ДЗ

1. Домашнее задание

1. Знать законы алгебры логики.
Обратите внимание, что результат тождества можно получить, зная
правила истинности для логических операций.
Законы поглощения можно получить самостоятельно, зная законы
для И и ИЛИ: переместительный, сочетательный и распределительный.
Необходимо знать законы для И и ИЛИ:
• переместительный;
• сочетательный;
• распределительный;
• закон отрицания (закон де Моргана).
А также законы для импликации, эквиваленции, строгой дизъюнкции —
они приводят формулы к нормальной форме.

2.

3. Задание 6

Решите задачу методом упрощения логического выражения.
На вопрос о дежурстве классный руководитель, он же учитель информатики, ответил
ребятам тремя утверждениями:
1. «Если не будет дежурить Виктор, то будет дежурить Павел без Димы».
2. «Если будет дежурить Дима, то будет дежурить Павел, но без Вити».
3. «Если Павел выйдет на дежурство, то Дима тоже дежурный, но без Вити».
«С помощью алгебры логики определите, кто будет дежурить», — дал задание
ребятам их учитель информатики.

4. Справочный материал

5. ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ

• Законы алгебры логики (свойства логических операций) позволяют
упростить процесс анализа истинности логического выражения с
большим количеством переменных и операций.
Закон двойного
отрицания
ന =A
A
Закон исключённого
третьего
A ∨ A= 1
Закон противоречия
A & A= 0
Законы работы с
константами
A∨1=1
A∨0=A
A&1=A
A&0=0
Законы
идемпотентности
A&A=A
A∨A=A
A А
0 1
1 0
ന
A
0
1
A А A∨А
0 1
1
1 0
1
A А A&А
0 1
0
1 0
0

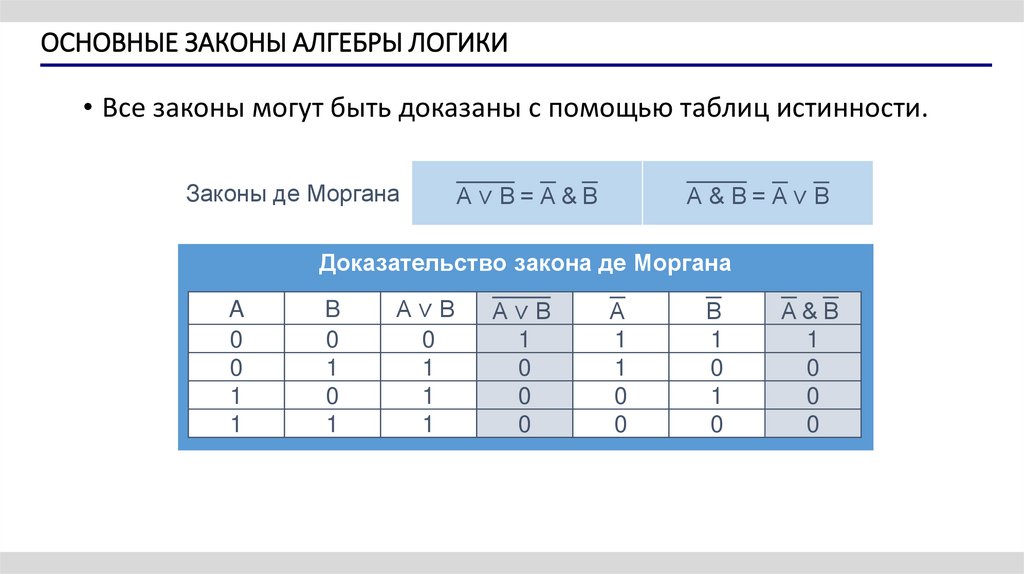
6. ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ

• Все законы могут быть доказаны с помощью таблиц истинности.
Законы де Моргана
A∨B=A&B
A&B=A∨B
Доказательство закона де Моргана
A
0
0
1
1
B
0
1
0
1
A∨B
0
1
1
1
A∨B
1
0
0
0
A
1
1
0
0
B
1
0
1
0
A&B
1
0
0
0

7.

ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
Переместительные
законы
A∨B=B∨A
Сочетательные
(ассоциативные) законы
(A & B) & C = A & (B & C)
(A ∨ B) ∨ C = A ∨ (B ∨ C)
Распределительный
(дистрибутивный) закон (I)
A & (B ∨ C) = (A & B) ∨ (A & C)
A&B=B&A
Упростить выражения: A ∨ A & B; A & (A ∨ B)
A ∨ A & B = A &1 ∨ A & B = A & (1 ∨ B) = A & 1 = A
(A B)
& C)
A & 1= A (I)A & (B ∨ C) = (A
Закон поглощения
A &∨ B)(A∨ &
=AA∨ 1= 1 A & 1= A
A & (A ∨ B) = A & A ∨ A & B = A ∨ A & B = A
A & (B
∨ C) = (A & B)(II)
∨ (A & C) A &AA&
=A
Закон
поглощения
(A ∨ B)A=∨AA & B = A

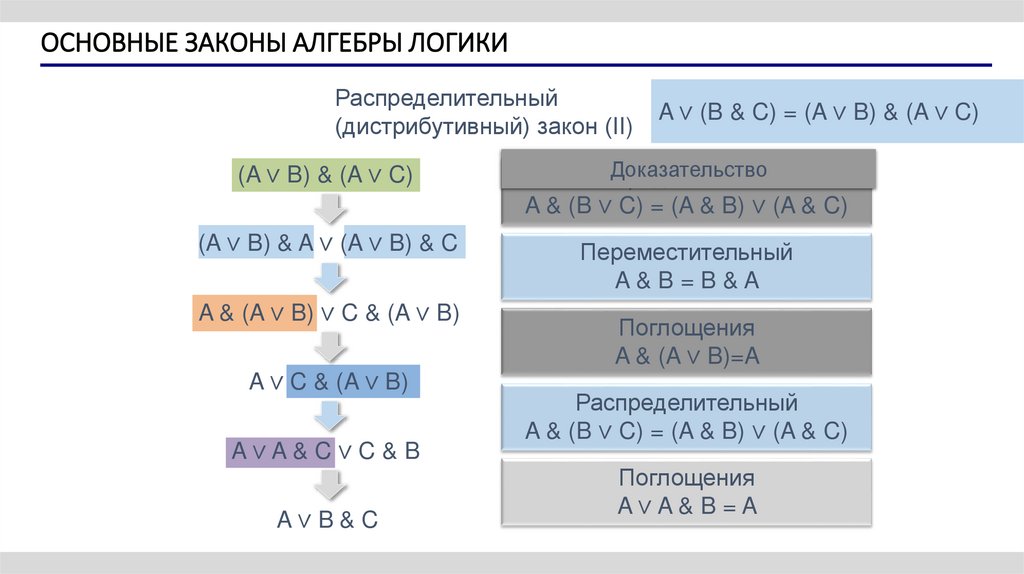
8. ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ

Распределительный
(дистрибутивный) закон (II)
A ∨ (B & C) = (A ∨ B) & (A ∨ C)
(A ∨ B) & (A ∨ C)
Доказательство
Распределительный
A & (B ∨ C) = (A & B) ∨ (A & C)
(A ∨ B) & A ∨ (A ∨ B) & C
Переместительный
A&B=B&A
A & (A ∨ B) ∨ C & (A ∨ B)
Поглощения
A & (A ∨ B)=A
A ∨ C & (A ∨ B)
A∨A&C∨C&B
A∨B&C
Распределительный
A & (B ∨ C) = (A & B) ∨ (A & C)
Поглощения
A∨A&B=A

9. ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ

Законы

10. Законы

ПРИМЕР 1
Упростим логическое выражение A & B & C ⋁ A & B & С.
A & B & C ⋁ A & B & С = A & B & (С ⋁ С ) = A & B & 1 = A & B

11. ПРИМЕР 1

ПРИМЕР 2
Упростим логическое выражение (A ⋁ B) & (A ⋁ B ⋁ C) & (A ⋁ B ⋁ С).
(A ⋁ B) & (A ⋁ B ⋁ C) & (A ⋁ B ⋁ С)= (A ⋁ B) & (1 ⋁ C ⋁ С) =(A ⋁ B) & 1 = A ⋁ B