Глава 8.ТеорВер

1. Глава 8. Статистическое изучение взаимосвязи социально-экономических явлений

ГЛАВА 8. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ
ВЗАИМОСВЯЗИ СОЦИАЛЬНОЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ

2. Причинность, регрессия, корреляция

Признаки
Факторные
Результативные
Признаки, обуславливающие изменения других,
связанных с ними признаков
Признаки, изменяющиеся под действием
факторных признаков

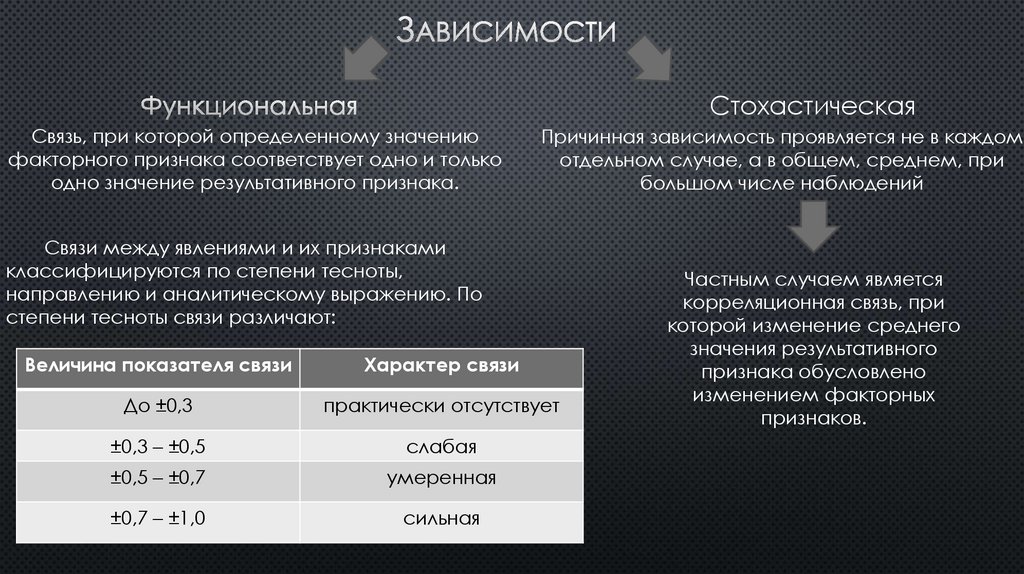
3. Функциональная

Стохастическая
Связь, при которой определенному значению
факторного признака соответствует одно и только
одно значение результативного признака.
Причинная зависимость проявляется не в каждом
отдельном случае, а в общем, среднем, при
большом числе наблюдений
Связи между явлениями и их признаками
классифицируются по степени тесноты,
направлению и аналитическому выражению. По
степени тесноты связи различают:
Величина показателя связи
Характер связи
До ±0,3
практически отсутствует
±0,3 – ±0,5
слабая
±0,5 – ±0,7
умеренная
±0,7 – ±1,0
сильная
Частным случаем является
корреляционная связь, при
которой изменение среднего
значения результативного
признака обусловлено
изменением факторных
признаков.

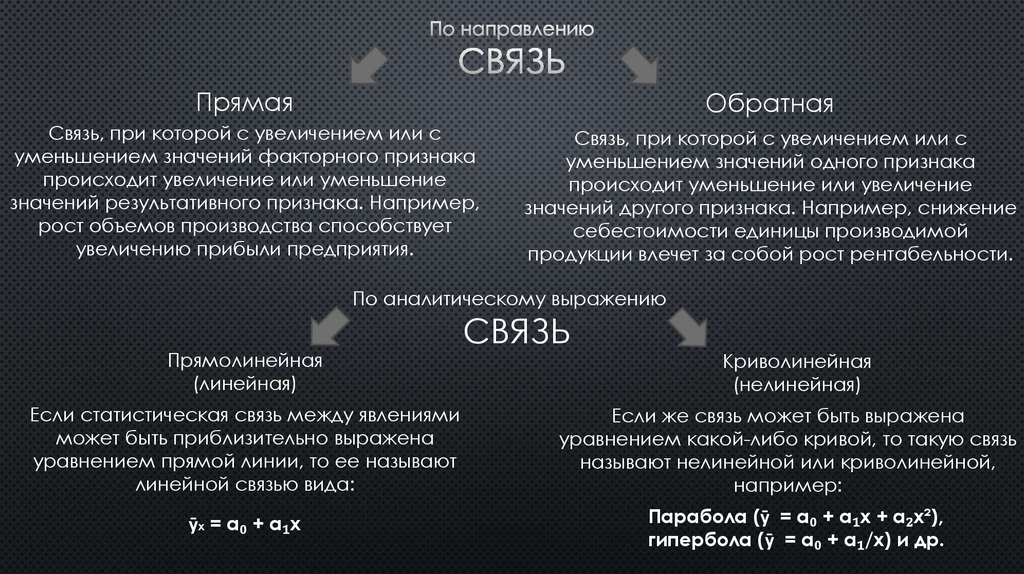
4. По направлению связь

Прямая
Обратная
Связь, при которой с увеличением или с
уменьшением значений факторного признака
происходит увеличение или уменьшение
значений результативного признака. Например,
рост объемов производства способствует
увеличению прибыли предприятия.
Связь, при которой с увеличением или с
уменьшением значений одного признака
происходит уменьшение или увеличение
значений другого признака. Например, снижение
себестоимости единицы производимой
продукции влечет за собой рост рентабельности.
По аналитическому выражению
Прямолинейная
(линейная)
СВЯЗЬ
Криволинейная
(нелинейная)
Если статистическая связь между явлениями
может быть приблизительно выражена
уравнением прямой линии, то ее называют
линейной связью вида:
Если же связь может быть выражена
уравнением какой-либо кривой, то такую связь
называют нелинейной или криволинейной,
например:
ȳx = a₀ + a₁x
Парабола (ȳ = a₀ + a₁x + a₂x²),
гипербола (ȳ = a₀ + a₁/x) и др.

5. Методы выявления связи

Приведение
параллельных данных
Графический
основан на
сопоставлении двух
или нескольких
рядов
статистических
величин. Такое
сопоставление
позволяет установить
наличие связи и
получить
представление о ее
характере.
взаимосвязь двух
признаков
изображается с
помощью поля
корреляции. На оси
абсцисс значения
факторного признака,
а на оси ординат –
результативного.
Каждое пересечение
линий обозначаются
точкой.
Аналитических
группировок
позволяет
выявить
влияние
одного
факторного
признака на
изменение
результативног
о при условии,
что все другие
факторы не
связаны с
изучаемым
признаком.
Корреляция
Регрессия
имеет своей
заключается в
задачей
определении
количественное аналитического
определение выражения связи,
тесноты и
в котором
направления
изменение
связи между
одной величины
двумя
(называемой
признаками
зависимой или
(при парной
результативным
связи) и между
признаком),
результативным
обусловлено
и множеством влиянием одной
факторных
или нескольких
признаков (при
независимых
многофакторн
величин
ой связи).
(факторных
признаков)

6. виды зависимостей

Парная корреляция
Частная корреляция
Множественная корреляция
Связь между двумя признаками
(результативным и факторным,
или двумя факторными).
Зависимость между
результативным и одним
факторным признаками при
фиксированном значении
других факторных признаков.
Зависимость результативного и
двух или более факторных
признаков, включенных в
исследование.
Теснота связи количественно выражается величиной коэффициентов корреляции, которые,
давая количественную характеристику тесноты связи между признаками, позволяют определять
«полезность» факторных признаков при построении уравнения множественной регрессии.
Знаки при коэффициентах корреляции характеризуют направление связи между признаками.

7. Парная регрессия на основе метода наименьших квадратов

ПАРНАЯ РЕГРЕССИЯ ПОЗВОЛЯЕТ ПОЛУЧИТЬ АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ СВЯЗИ МЕЖДУ ДВУМЯ ПРИЗНАКАМИ:
РЕЗУЛЬТАТИВНЫМ И ФАКТОРНЫМ.
S = ∑(yi-ȳx)²
min
Система нормальных уравнений для нахождения параметров линейной парной
регрессии методом наименьших квадратов имеет следующий вид:
na₀ + a₁∑xi = ∑yi
a₀∑xi + a₁∑xi² = ∑xiyi,
где n – объем исследуемой совокупности (число единиц наблюдения). В уравнениях регрессии параметр a0
показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков.
Коэффициент регрессии a1 показывает, на сколько в среднем изменяется значение результативного
признака при увеличении факторного признака на единицу собственного измерения.

8. Множественная (многофакторная) регрессия

ȳ1,2,…,k = f(x₁, x₂, ..., xₖ)
Построение моделей множественной регрессии включает несколько
этапов:
1. Выбор формы связи (уравнения регрессии);
2. Отбор факторных признаков;
3. Обеспечение достаточного объема совокупности.
Важным этапом построения уже выбранного уравнения множественной регрессии является
отбор и последующее включение факторных признаков. С одной стороны, чем больше
факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель
размерностью 100 и более факторных признаков сложно реализуема и требует больших затрат
машинного времени. Сокращение размерности модели за счет исключения второстепенных,
экономически и статистически несущественных факторов способствует простоте и качеству ее
реализации. В то же время построение модели регрессии малой размерности может привести к
тому, что такая модель будет недостаточно адекватна исследуемым явлениям и процессам.

9. шаговая регрессия (шаговый регрессионный анализ)

10.

ПРИ ПОСТРОЕНИИ МОДЕЛИ РЕГРЕССИИ ВОЗМОЖНА ПРОБЛЕМА МУЛЬТИКОЛЛИНЕАРНОСТИ, ПОД КОТОРОЙ
ПОНИМАЕТСЯ ТЕСНАЯ ЗАВИСИМОСТЬ МЕЖДУ ФАКТОРНЫМИ ПРИЗНАКАМИ, ВКЛЮЧЕННЫМИ В МОДЕЛЬ (RXIJ > 0,8)
Наличие мультиколлинеарности между признаками вызывает:
• искажение величины параметров модели, которые имеют тенденцию к завышению, чем осложняется
процесс определения наиболее существенных факторных признаков;
• изменение смысла экономической интерпретации коэффициентов регрессии.
В качестве причин возникновения мультиколлинеарности между признаками можно выделить следующие:
• изучаемые факторные признаки являются характеристикой одной и той же стороны изучаемого явления или
процесса. Например: показатели объема производимой продукции и среднегодовой стоимости основных
фондов одновременно включать в модель не рекомендуется, так как они оба характеризуют размер
предприятия;
• факторные признаки являются составляющими элементами друг друга. Например: показатели выработки
продукции на одного работающего и численность работающих одновременно в модель включать нельзя, так
как в основе расчета показателей лежит один и тот же показатель – численность работающих на предприятии.
• факторные признаки по экономическому смыслу дублируют друг друга.
Устранение мультиколлинеарности может реализовываться через исключение из корреляционной модели
одного или нескольких линейно-связанных факторных признаков или преобразование исходных факторных
признаков в новые, укрупненные факторы.

11.

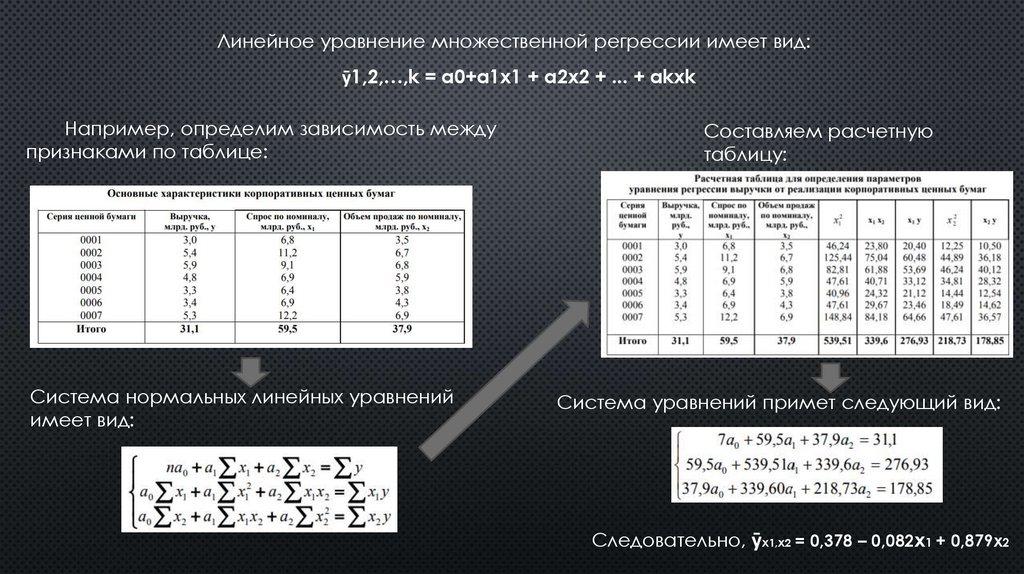
Линейное уравнение множественной регрессии имеет вид:
ȳ1,2,…,k = a0+a1x1 + a2x2 + ... + akxk
Например, определим зависимость между
признаками по таблице:
Система нормальных линейных уравнений
имеет вид:
Составляем расчетную
таблицу:
Система уравнений примет следующий вид:
Следовательно, ȳx1,x2 = 0,378 – 0,082x1 + 0,879x2

12. Собственно-корреляционные параметрические методы изучения связи

Линейный коэффициент корреляции
(К. Пирсона)
Характеризует тесноту и направление связи между
двумя коррелируемыми признаками в случае наличия
между ними линейной зависимости.
ഥ*