Алгоритмизация

1.

Задача о рюкзаке:
Рекурсивный и
динамический подходы
Смолин Захар, Зайцев Савелий. ВТ-11
Основы алгоритмизации

2.

Введение: Что такое задача о рюкзаке?
Представьте, что вы собираетесь в поход, и у вас есть рюкзак с
ограниченной вместимостью. Вам нужно выбрать из множества
предметов (каждый со своим весом и ценностью) те, которые
поместятся в рюкзак, принесут наибольшую пользу и не превысят
допустимый вес.
Именно в этом суть «Задачи о рюкзаке»: выбрать подмножество
предметов, чтобы максимизировать их общую ценность, не
превышая при этом заданное ограничение по весу.

3.

Формулировка задачи и пример
У нас есть набор из n предметов. Каждый предмет i характеризуется:
Весом: w[i]
Ценностью: v[i]
Максимальная вместимость рюкзака составляет W.
Задача: Найти такую комбинацию предметов, чтобы их общая ценность была максимальной, а общий вес не превышал W.
Предмет
Вес (кг)
Ценность
Палатка
4
60
Еда
5
100
Вода
3
70
Спальник
2
20
Если рюкзак вмещает 10 кг, какие предметы взять, чтобы получить наибольшую суммарную ценность?

4.

Рекурсивный подход: Идея
Принцип выбора
Рекурсивное решение
Для каждого предмета мы
Мы рекурсивно исследуем обе эти
сталкиваемся с двумя возможными
ситуации для каждого предмета,
решениями:
начиная с последнего. Функция
Взять предмет в рюкзак (если
он помещается).
Не брать предмет.
Поиск максимума
В итоге, решение находит
максимальную ценность,
перебирая все возможные
комбинации предметов. Это
похоже на дерево, где каждая
ветвь представляет собой выбор
"взять" или "не взять".
вычисляет максимальную ценность
для текущей вместимости рюкзака
и оставшихся предметов.

5.

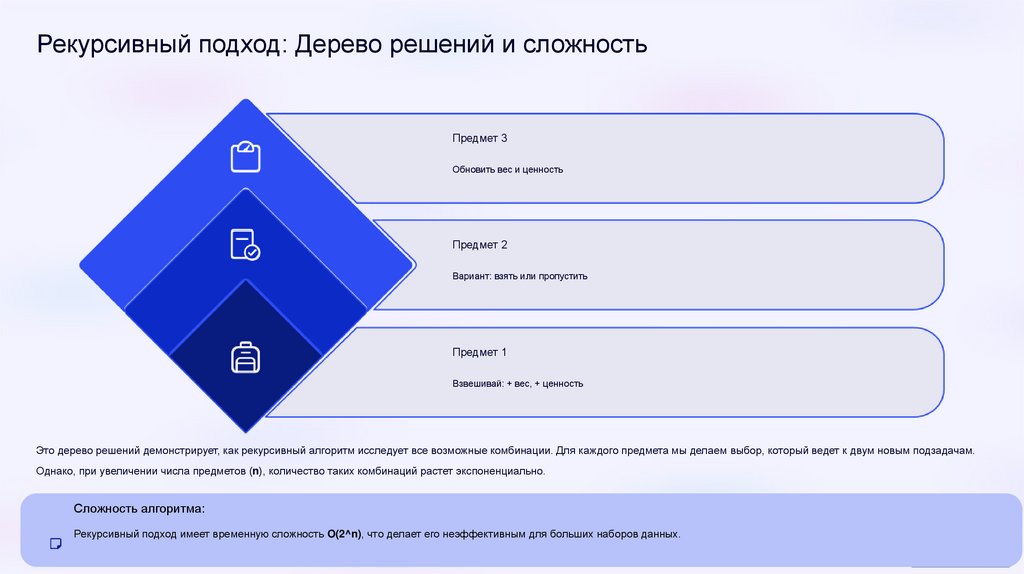
Рекурсивный подход: Дерево решений и сложность
Предмет 3
Обновить вес и ценность
Предмет 2
Вариант: взять или пропустить
Предмет 1
Взвешивай: + вес, + ценность
Это дерево решений демонстрирует, как рекурсивный алгоритм исследует все возможные комбинации. Для каждого предмета мы делаем выбор, который ведет к двум новым подзадачам.
Однако, при увеличении числа предметов (n), количество таких комбинаций растет экспоненциально.
Сложность алгоритма:
Рекурсивный подход имеет временную сложность O(2^n), что делает его неэффективным для больших наборов данных.

6.

Рекурсивный подход: Псевдокод
def knapsack_recursive(W, weights, values, n):
# Базовый случай: если нет предметов или вместимость рюкзака равна 0
if n == 0 or W == 0:
return 0
# Если вес текущего предмета больше текущей вместимости рюкзака
if weights[n-1] > W:
# Не берем предмет, переходим к следующему
return knapsack_recursive(W, weights, values, n-1)
else:
# Два варианта:
# 1. Взять текущий предмет: ценность предмета + решение для оставшегося веса и предметов
# 2. Не брать текущий предмет: решение для того же веса и оставшихся предметов
return max(
values[n-1] + knapsack_recursive(W - weights[n-1], weights, values, n-1),
knapsack_recursive(W, weights, values, n-1)
Этот псевдокод показывает логику перебора всех вариантов «взять» или «не взять» для каждого предмета, чтобы найти оптимальное решение.

7.

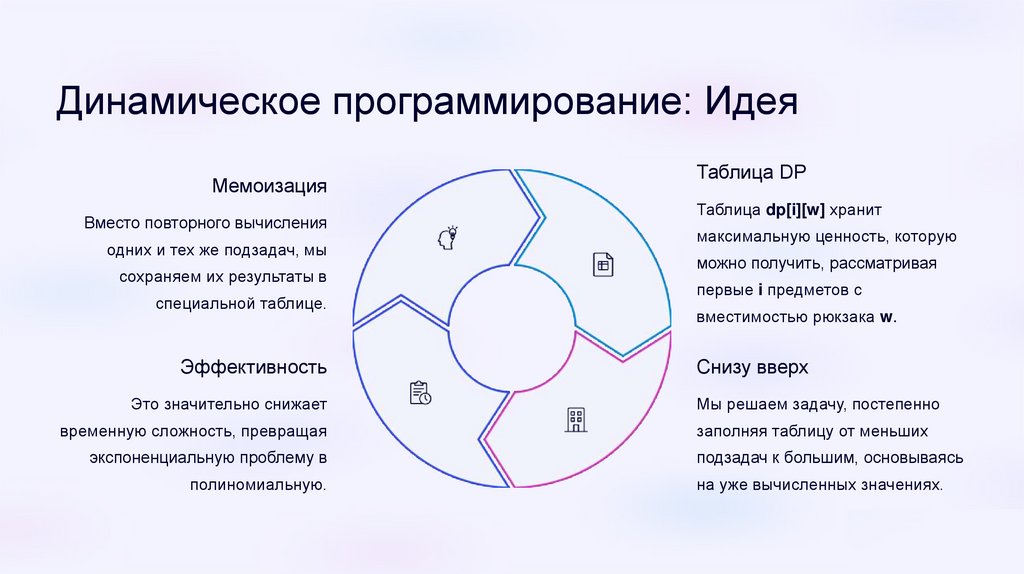
Динамическое программирование: Идея
Мемоизация
Вместо повторного вычисления
одних и тех же подзадач, мы
сохраняем их результаты в
специальной таблице.
Эффективность
Это значительно снижает
временную сложность, превращая
экспоненциальную проблему в
полиномиальную.
Таблица DP
Таблица dp[i][w] хранит
максимальную ценность, которую
можно получить, рассматривая
первые i предметов с
вместимостью рюкзака w.
Снизу вверх
Мы решаем задачу, постепенно
заполняя таблицу от меньших
подзадач к большим, основываясь
на уже вычисленных значениях.

8.

Динамическое решение: Формула и псевдокод
Основная идея: для каждого предмета и каждой возможной вместимости рюкзака w мы либо включаем предмет (если его вес не превышает w), либо не включаем его. Мы выбираем тот вариант, который
дает большую ценность.
def knapsack_dp(W, weights, values, n):
# Создаем таблицу dp, где dp[i][w] будет хранить максимальную ценность
# для первых i предметов и вместимости w
dp = [[0]*(W+1) for _ in range(n+1)]
# Заполняем таблицу
for i in range(1, n+1): # Проходим по каждому предмету
for w in range(1, W+1): # Проходим по каждой возможной вместимости
# Если текущий предмет (weights[i-1]) помещается в рюкзак
if weights[i-1] <= w:
# Выбираем максимум из двух вариантов:
# 1. Взять предмет: ценность предмета + ценность от оставшегося веса и предыдущих предметов
# 2. Не брать предмет: ценность от предыдущих предметов с той же вместимостью
dp[i][w] = max(
values[i-1] + dp[i-1][w - weights[i-1]],
dp[i-1][w]
)
else:
# Если предмет не помещается, его нельзя взять,
# поэтому берем ценность от предыдущих предметов с той же вместимостью
dp[i][w] = dp[i-1][w]
return dp[n][W]
Этот псевдокод строит таблицу dp постепенно, ячейка за ячейкой, где каждая ячейка представляет собой решение подзадачи. Конечный результат находится в dp[n][W].

9.

Сравнение подходов
Рекурсивный подход
Динамическое
программирование
Интуитивно понятный
Прямое следование логике перебора.
Более сложный
Требует понимания структуры подзадач.
Медленный
Экспоненциальная сложность O(2^n) из-за
повторных вычислений.
Быстрый
Полиномиальная сложность O(n*W) за счет
мемоизации.
Риск переполнения стека
Может произойти при больших n.
Использует память
Для хранения таблицы DP.

10.

Заключение
Классический пример
Задача о рюкзаке — это фундаментальная проблема оптимизации в информатике.
Понимание рекурсии
Рекурсивный подход помогает понять основную идею, но неэффективен для больших данных.
Мощь ДП
Динамическое программирование предоставляет эффективное решение, значительно сокращая время вычислений.
Применение в жизни
Эти подходы используются в логистике, планировании ресурсов, экономике, финансовом моделировании и ITпроектах.