8 класс_урок 9. Презентация информ

1.

Введение в таблицы истинности и
логические выражения
Краткий обзор логических переменных, выражений и значения операций И,
ИЛИ, НЕ.

2.

Основы логики и правила вычисления
Логическое выражение принимает значения
ИСТИНА или ЛОЖЬ.
Основные операции: НЕ, И, ИЛИ.
Порядок выполнения: сначала отрицание, затем
конъюнкция, после — дизъюнкция с учетом скобок.
2

3.

Что такое таблица истинности
Таблица истинности отображает
результат логического выражения для
всех вариантов значений входных
переменных. Это формализованный
способ вычисления логических
функций.
Каждая строка таблицы соответствует
одной комбинации истинностных
значений переменных, показывая итог
вычисления выражения для неё.
3
Таблицы лежат в основе
проектирования цифровых схем,
обеспечивая точность и однозначность
при работе с логикой.

4.

Зачем нужны таблицы
истинности?
Формальное определение истинности
Таблицы позволяют без лишних рассуждений точно
определить истинность сложных логических
выражений, опираясь на формальные правила логики.
Основы работы цифровых систем
Их применение критично для программирования и
проектирования аппаратного обеспечения, где
требуется надёжное вычисление логических функций.
4

5.

n
2
число строк зависит от количества логических
переменных и отображает все возможные
комбинации.
5
Количество строк вычисляется как степень
двойки по количеству переменных n —
важнейший параметр для построения
таблицы.

6.

Количество столбцов и заполнение таблицы
6
Число столбцов равно сумме переменных
и выражений, участвующих в вычислении
итогового результата.
Таблица начинается с заполнения
столбцов переменных всеми двоичными
комбинациями от 0 до 2n - 1.
Значения промежуточных выражений
заполняются поочерёдно в соответствии
с порядком вычисления операций.
Такая пошаговая организация облегчает
понимание и проверку результатов
логического выражения.

7.

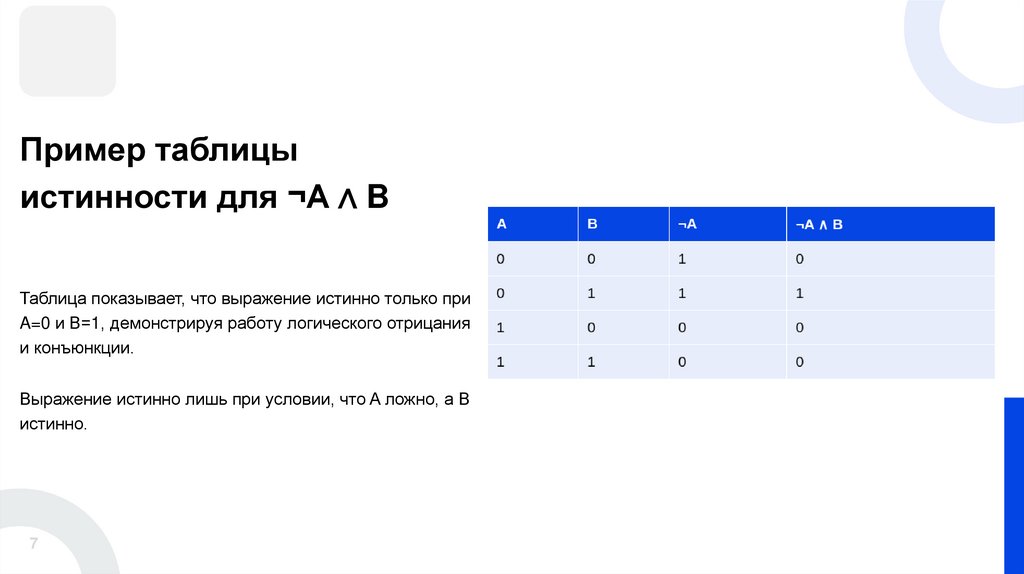
Пример таблицы
истинности для ¬A ∧ B
Таблица показывает, что выражение истинно только при
A=0 и B=1, демонстрируя работу логического отрицания
и конъюнкции.
Выражение истинно лишь при условии, что A ложно, а B
истинно.
7

8.

Анализ выражения (A ∨ B) ∧ ¬A
Выражение истинно, когда
переменная A принимает
значение ЛОЖЬ, а B — ИСТИНА,
что соответствует тонкой
логической комбинации.
8
Оно означает, что хотя бы одно
из двух условий A или B
выполняется, однако A при этом
не выполняется.
Такое выражение позволяет
выделить роль B в обеспечении
истинности при ложности A.

9.

Таблица истинности для выражения (A ∨ B) ∧ ¬A
В таблице изображены все логические значения и
финальный результат выражения, показывающий
истинность при специфичной комбинации.
Выражение истинно только когда A ложно, а B
истинно.
9

10.

4
число строк соответствует всем возможным
комбинациям двух переменных, необходимых
для анализа выражения.
10
Для двух переменных таблица содержит 4
строки, что позволяет полностью учесть все
варианты истинностных значений.

11.

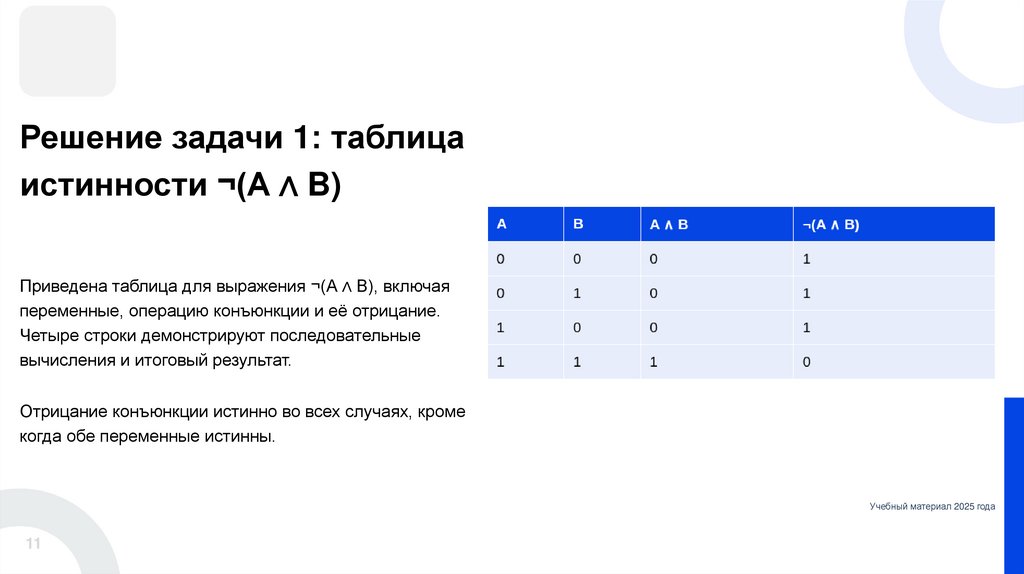
Решение задачи 1: таблица
истинности ¬(A ∧ B)
Приведена таблица для выражения ¬(A ∧ B), включая
переменные, операцию конъюнкции и её отрицание.
Четыре строки демонстрируют последовательные
вычисления и итоговый результат.
Отрицание конъюнкции истинно во всех случаях, кроме
когда обе переменные истинны.
Учебный материал 2025 года
11

12.

Задача 2: построение таблицы для ¬A ∨ ¬B
Необходимо построить таблицу истинности для выражения
¬A ∨ ¬B, рассматривая значение дизъюнкции отрицаний двух
переменных, чтобы понять её поведение.
Задача направлена на демонстрацию применения
закона де Моргана, устанавливающего эквивалентность
¬A ∨ ¬B и ¬(A ∧ B), что важно для понимания логических
преобразований.
Предполагается сравнение полученной таблицы с таблицей для
¬(A ∧ B), чтобы выявить их полную идентичность по результатам
и убедиться в логической эквивалентности.
Задание помогает закрепить навыки построения и анализа таблиц
истинности для разных логических выражений, развивая формальное
мышление и умение работать с преобразованиями логики.
12

13.

Решение задачи 2: таблица истинности для ¬A ∨
¬B
Таблица показывает значения для переменных, их
отрицаний и результата дизъюнкции ¬A ∨ ¬B.
Демонстрируется совпадение с результатами
¬(A ∧ B).
Эквивалентность выражений ¬A ∨ ¬B и ¬(A ∧ B)
подтверждена идентичными результатами таблиц
истинности.
13

14.

Задача 3: анализ выражения (A ∨ ¬B) ∨ B
Постройте таблицу
истинности для выражения
(A ∨ ¬B) ∨ B, чтобы
проверить его истинность
при всех вариантах входных
значений A и B.
14
Необходимо доказать, что
результат выражения всегда
равен истине, показав, что
внутри него присутствует
тавтология, гарантирующая
истинность независимо от
переменных.
Разберем упрощение:
(A ∨ ¬B) ∨ B = A ∨ (¬B ∨ B) =
A ∨ 1 = 1, что формально
подтверждает
тавтологичность выражения.

15.

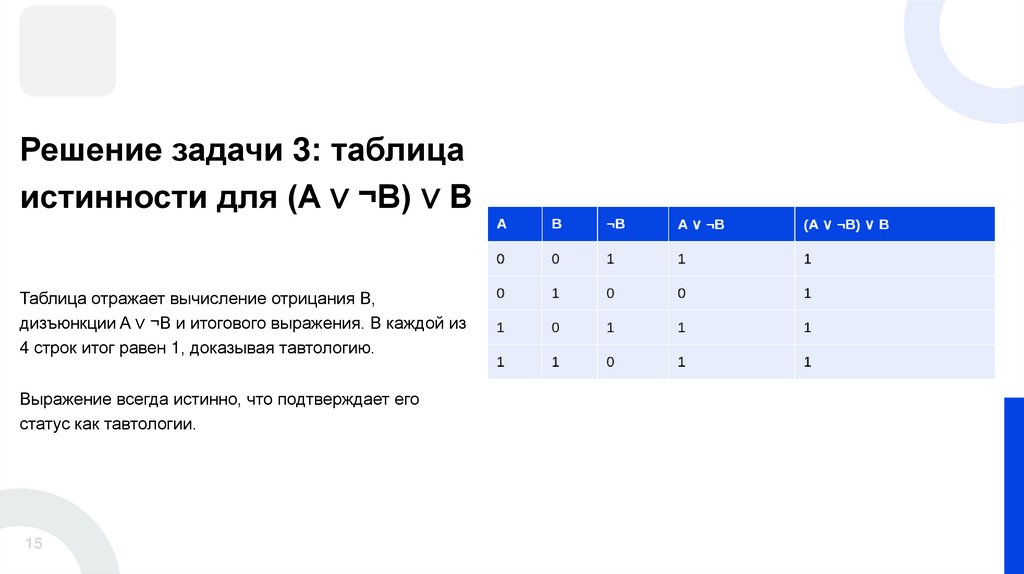
Решение задачи 3: таблица
истинности для (A ∨ ¬B) ∨ B
Таблица отражает вычисление отрицания B,
дизъюнкции A ∨ ¬B и итогового выражения. В каждой из
4 строк итог равен 1, доказывая тавтологию.
Выражение всегда истинно, что подтверждает его
статус как тавтологии.
15

16.

Задача 4: таблица истинности с тремя
переменными
16
Постройте таблицу истинности для
выражения A ∧ (B ∨ C), где участвуют три
переменные, что требует учёта всех
восьми комбинаций их значений.
Данная задача позволяет практиковать
формирование табличных данных с 8
строками, расширяя понимание
вложенных логических операций и
комплексных выражений.
При расчёте значений важно поэтапно
вычислять сначала дизъюнкцию B ∨ C, а
затем конъюнкцию с A, соблюдая порядок
операций.
Результат помогает закрепить навык
создания таблиц истинности для более
сложных выражений и анализировать
влияние каждой переменной.

17.

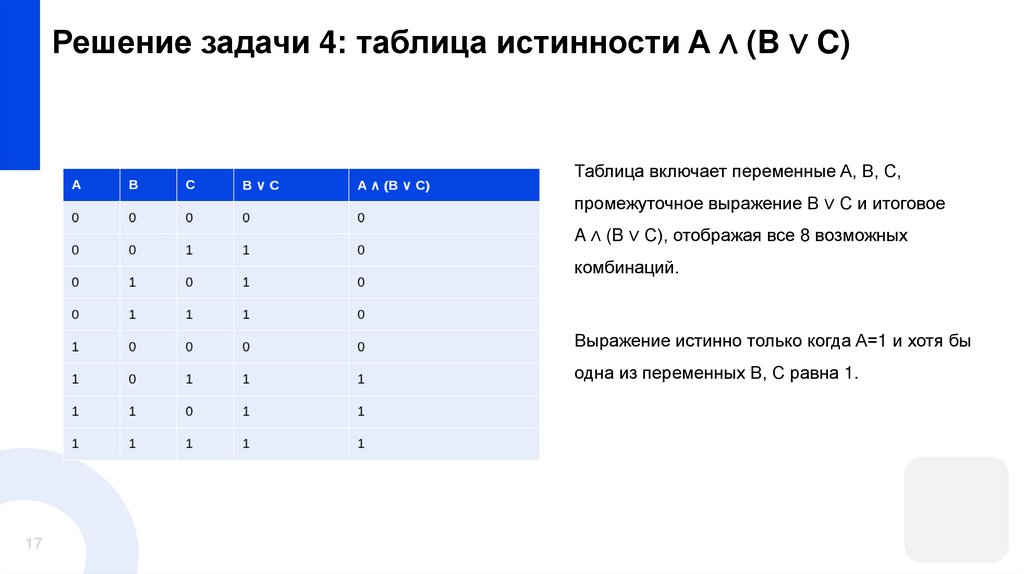
Решение задачи 4: таблица истинности A ∧ (B ∨ C)
Таблица включает переменные A, B, C,
промежуточное выражение B ∨ C и итоговое
A ∧ (B ∨ C), отображая все 8 возможных
комбинаций.
Выражение истинно только когда A=1 и хотя бы
одна из переменных B, C равна 1.
17

18.

Задача 5: восстановление логического выражения
по таблице
Дана таблица с переменными A, B и
результатом F, где F принимает
значения 1 и 0 для разных
комбинаций.
Требуется выявить логическое
выражение, удовлетворяющее
таблице, анализируя строки, в которых
F равно 1, и сопоставляя с значениями
переменных.
18
Этот приём тренирует навыки
обратного построения логических
выражений из таблицы, что полезно
для понимания логики и алгоритмов.

19.

Решение задачи 5:
восстановленное
выражение F = ¬B
Таблица демонстрирует значения A, B и результата F.
Анализируем строки с F=1, выводя, что F равняется
отрицанию переменной B.
Выражение F эквивалентно ¬B, так как результаты
совпадают с отрицанием B во всех строках.
Учебный материал 2025 года
19

20.

Заключение: важность таблиц
истинности и логического
мышления в обучении
Таблицы истинности облегчают понимание и анализ сложных логических выражений,
способствуют освоению булевой алгебры и развития критического мышления,
являясь фундаментом для цифровых технологий и образования школьников.