Поветкин ДИ 2401 (ДИ-21) - Алгоритмы Дейкстра и Уоршела

1.

Построение графов и
анализ кратчайших
путей
Выполнил: Поветкин Данил Константинович, студент группы ДИ-2401 (ДИ-21)
Преподаватель: Докучаев Сергей Аркадьевич

2.

Исходные данные и
постановка задачи
Задачи работы
Типы графов
Реализовать алгоритм
Граф 1: Ориентированный
Дейкстра для поиска
взвешенный граф (матрица
кратчайших путей
смежности)
Построить матрицу
Граф 2: Ориентированный
достижимости вершин по
невзвешенный граф (анализ
алгоритму Уоршелла
достижимости)
Визуализировать полученные
графы.

3.

Представление
данных
Вершины
Рёбра
Пронумерованы от 1 до N
Вес > 0; отсутствие = 0
Матрица смежности
Хранение графа в памяти

4.

Алгоритм Дейкстра: Структура
Инициализация
Установка начальных расстояний и приоритетной очереди
Выбор вершины
Извлечение вершины с минимальным расстоянием из
очереди
(heapq)
Релаксация рёбер
Обновление расстояний до соседних вершин
Результат
Массив кратчайших путей и восстановление пути

5.

Поддерживаемые
структуры данных
dist[]
prev[]
Кратчайшие расстояния от
Предыдущие вершины для
стартовой вершины до всех
восстановления оптимального
остальных
пути
visited[]
Отслеживание обработанных
вершин для избежания
повторений

6.

Вывод результатов
Кратчайшие
расстояния
Визуализация
графа
От вершины 1 до всех остальных
Полная последовательность вершин,
вершин графа с указанием
образующих ориентированный
минимальных весов пути
взвешенный граф

7.

Матрица достижимости: Алгоритм
Флойда–Уоршелла
1
Инициализация
Построение начальной матрицы
на основе рёбер графа
2 Итерация по
промежуточным
вершинам
Для каждой вершины k
проверяются пути через неё: если i
→ k и k → j, то i → j
3 Построение
матрицы
Результат: reachable[i][j] = 1, если
существует путь от i к j

8.

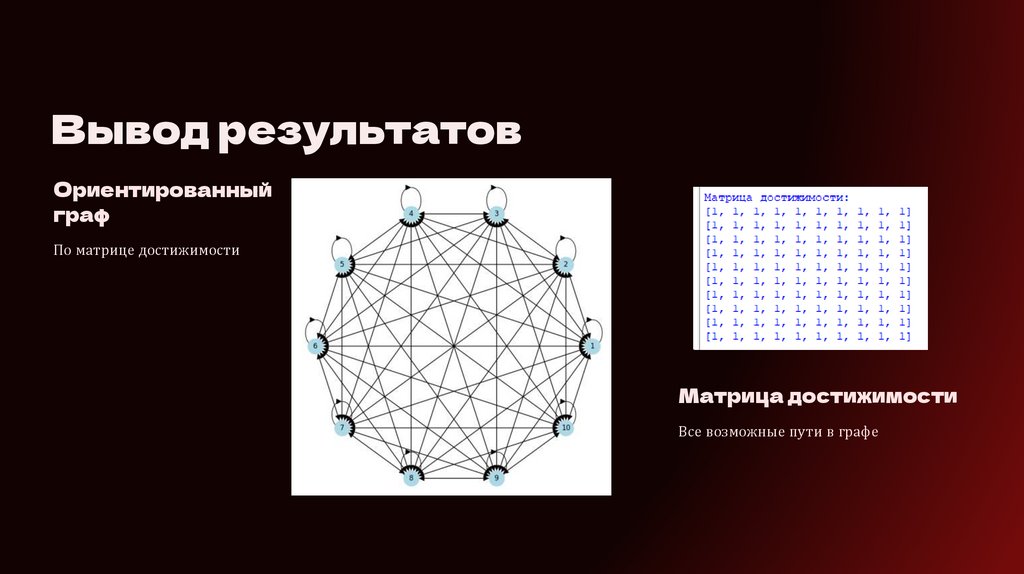
Вывод результатов
Ориентированный
граф
По матрице достижимости
Матрица достижимости
Все возможные пути в графе

9.

Ключевые выводы
Алгоритм Дейкстры
Флойд–Уоршелл
Визуализация
Эффективен для поиска кратчайших
Универсальный метод анализа
Python обеспечивает мощные
путей во взвешенных графах с
достижимости для невзвешенных и
инструменты для анализа и
неотрицательными весами
взвешенных графов
графического представления
сложных структур данных

10.

Практическое применение
Реальные приложения
Дальнейшее развитие
Навигация и маршрутизация
Параллельная обработка больших графов
Сетевые протоколы
Адаптивные алгоритмы для динамических графов
Анализ социальных сетей
Интеграция машинного обучения
Оптимизация логистики