Похожие презентации:
Лекция_№_01_туннельный_эффект,_кристаллы,_акустика
1.
ФИЗИЧЕСКИЕ ОСНОВЫСОВРЕМЕННЫХ
ТЕХНОЛОГИЙ
25.04.01 –Техническая эксплуатация летательных
аппаратов и двигателей Управление технологическими
процессами авиатопливообеспечения воздушных судов
МАГИСТРАТУРА, заочное отделение
Лектор: профессор каф.Физики, д.т.н.,
Капуткин Дмитрий Ефимович
E-mail: d.kaputkin@mail.ru
Телефон, WhatsApp: +7-985-9837710
2. Лекция №1
3. Основная литература
1. Савельев И.В. Курс общей физики.- М.: Наука, том 1, 2, 3.2. Трофимова Т.И. Курс физики. - М.: Высшая школа. 20052012.
3. Бутюгин М.А., Куколева А.А., Захарченко К.В. Физические
основы современных технологий. Пособие по изучению
дисциплины и контрольные задания. - М. МГТУ ГА, 2020.
4. Физическое материаловедение: Учебник для вузов:1-5т.Под
общей ред. Б. А. Калина. – М.: МИФИ, 2007.
5. Бутюгин М.А., Куколева А.А. Изучение процесса
намагничивания ферромагнетиков. Пособие по
выполнению лабораторной работы. – МГТУ ГА, 2018
6. Камзолов С.К., Новиков С.М. Физические основы работы p –
n-переходов. Пособие по выполнению лабораторной
работы. – МГТУ ГА, 2015
в начало
4.
Основные единицы измеренияфизических величин в системе СИ
(ГОСТ 8.417-81) :
Основные единицы:
Дольные
приставки:
Кратные
приставки:
Длина – метр (м)
Деци (д) – 10-1
Дека (да) – 101
Санти (с) - 10-2
Гекто (г) – 102
Милли (м) - 10-3
Кило (к) - 103
Микро (мк) - 10-6
Мега (М) - 106
Нано (н) - 10-9
Гига (Г) – 109
Пико (п) - 10-12
Тера (Т) - 1012
Масса – килограмм (кг)
Термодинамическая
температура – Кельвин (К)
Время – секунда (с)
Сила электрического тока – Фемто (ф) - 10-15
ампер (А)
-18
Пета (П) – 1015
Атто (а) – 10
Экса (Э) – 1018
Сила света – канделла (кд)
Зепто (з) – 10-21
Зетта (З) – 1021
Йопто (й) – 10-24
в начало 24
Йотта (Й)–
10
5.
хДвойственная природа света
Основной постулат корпускулярной теории
электромагнитного излучения, звучит так:
Электромагнитное излучение (и в частности,
свет) – это поток частиц, называемых фотонами.
Фотоны распространяются в вакууме со
скоростью с = 3∙108 м/с.
Масса и энергия покоя фотона равны нулю.
Энергия фотона E связана с частотой
электромагнитного излучения ν и длиной волны λ
формулой:
hc
E hν
λ
6.
хВиды фотоэффекта
Различают фотоэффект внешний, внутренний, вентильный.
Внешний фотоэффект может быть одно- и многофотонный.
Внешним фотоэффектом называется испускание электронов
веществом под действием электромагнитного излучения.
Внутренний фотоэффект – это вызванные электромагнитным
излучением переходы электронов внутри полупроводника или
диэлектрика из связанных состояний в свободные без вылета
наружу.
Вентильный фотоэффект, – возникновение эдс (фото-эдс) при
освещении контакта двух разных полупроводников или
полупроводника
и
металла
(при
отсутствии
внешнего
электрического поля).
Многофотонный фотоэффект возможен, если интенсивность
света очень большая (при использовании лазерных пучков). При
этом электрон, испускаемый металлом, может одновременно
получить энергию не от одного, а от нескольких фотонов.
7.
Законы фотоэффекта:1.
Закон Столетова: при фиксированной частоте
падающего света число фотоэлектронов, вырываемых
из катода в единицу времени, пропорционально
интенсивности света.
2.
Максимальная скорость фотоэлектронов не
зависит от интенсивности падающего света, а
определяется только его частотой ν.
3.
Для каждого вещества существует красная
граница фотоэффекта, т.е. минимальная частота ν0
света (зависящая от химической природы вещества и
состояния его поверхности), ниже которой
A
0
фотоэффект невозможен:
h
8.
Объяснениенаблюдаемых
экспериментально закономерностей было дано
Эйнштейном:
Свет не только испускается (Планк), но
и распространяется, и поглощается
веществом отдельными порциями
(квантами), энергия которых :
ε = hν.
Уравнение Эйнштейна для фотоэффекта:
mv
h
2
2
max
А – работа выхода электронов.
A.
9.
хМасса, энергия и импульс фотона
Фотон обладает энергией Е = hν = h(c/λ).
Для видимого света λ = 500 Å и Е = 2,2 эВ,
для рентгеновских лучей λ = 10–4 Å и Е = 0,5 эВ.
hν
mф 2
ф
c
Фотон движется со скоростью света c = 3·108 м/с.
Подставим это значение скорости в выражение:
m0
m0
m0
Фотон – частица, не обладающая
m
.массой
покоя потому, что она
2
0
1 1
υ
может существовать только
1 2
двигаясь со скоростью света c.
c
Е = mc2 m
= Е/c2 = hc/λc2 = h/cλ;
10.
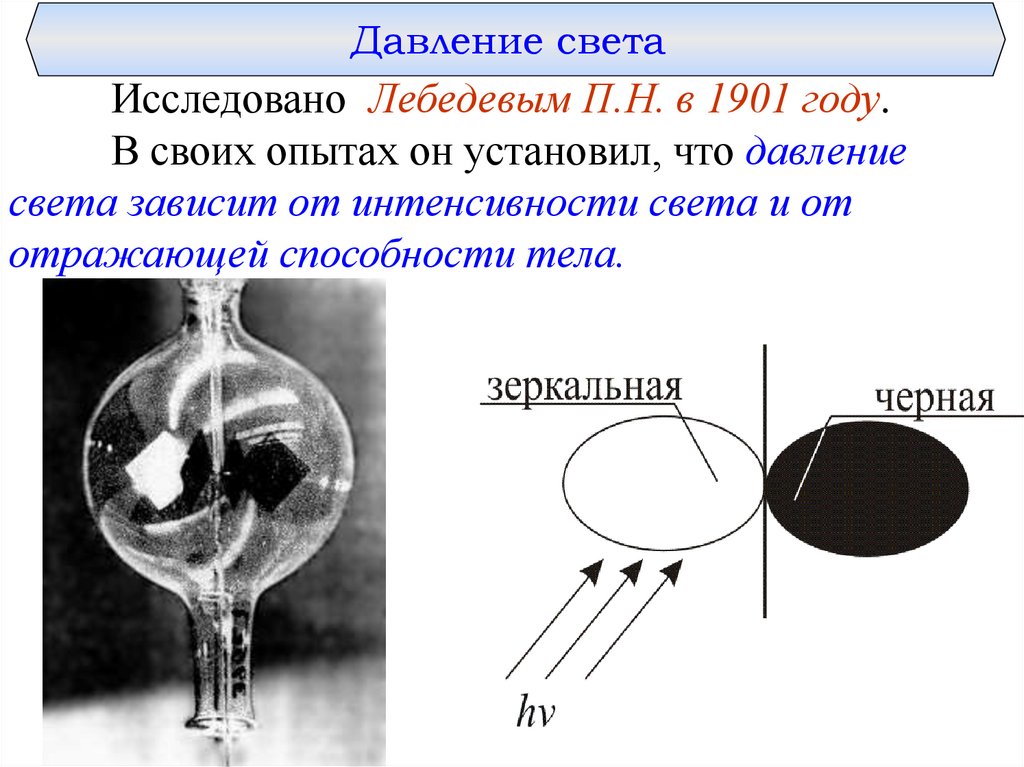
Давление светаИсследовано Лебедевым П.Н. в 1901 году.
В своих опытах он установил, что давление
света зависит от интенсивности света и от
отражающей способности тела.
11.
В единицу времени все N квантовсообщают телу импульс р: p (1 K ) N h
c
Давление P F / S
J – интенсивность излучения
hνN
(1 K )
P
(1 K ) J
,
cS
c
.
(1 K ) Световое
P J
давление
c
если тело зеркально отражает, то K = 1 и
если полностью поглощает
(абсолютно черное тело) K = 0
J
P
c
2J
P
,
c
т.о. световое давление на абсолютно черное тело в два
раза меньше, чем на зеркальное.
12.
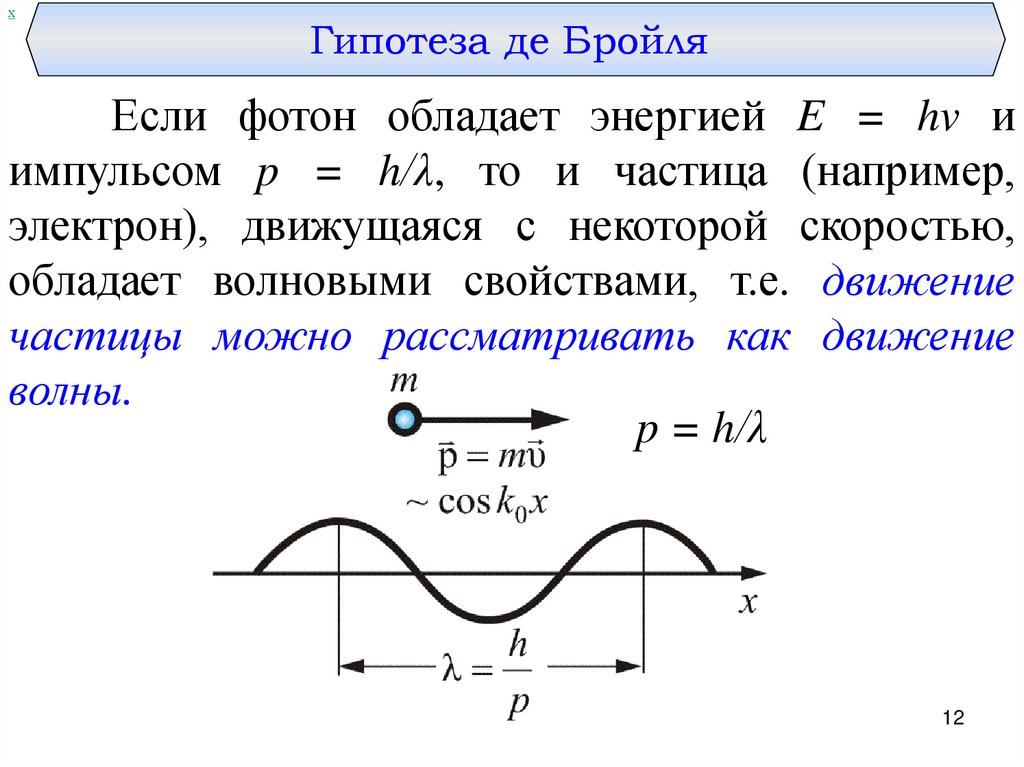
хГипотеза де Бройля
Если фотон обладает энергией E = hv и
импульсом p = h/λ, то и частица (например,
электрон), движущаяся с некоторой скоростью,
обладает волновыми свойствами, т.е. движение
частицы можно рассматривать как движение
волны.
p = h/λ
12
13.
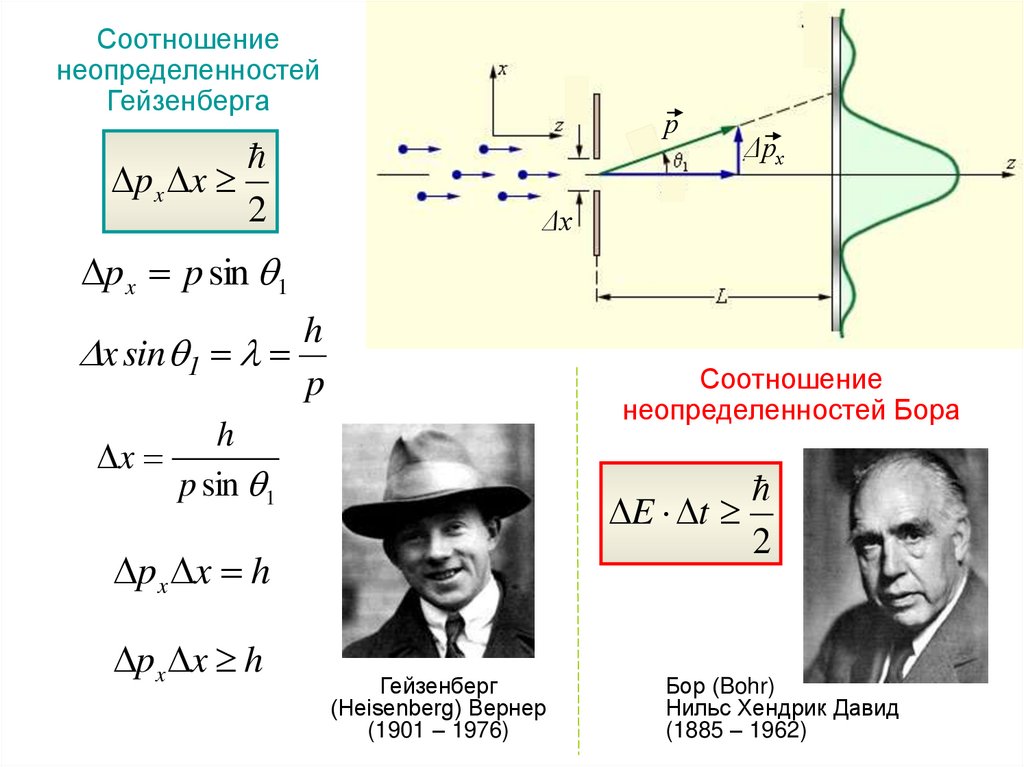
Соотношениенеопределенностей
Гейзенберга
p x x
2
р
Δрх
Δх
px p sin 1
h
x sin 1
p
Соотношение
неопределенностей Бора
h
x
p sin 1
E t
2
px x h
px x h
Гейзенберг
(Heisenberg) Вернер
(1901 – 1976)
Бор (Bohr)
Нильс Хендрик Давид
(1885 – 1962)
14. Следствия из соотношения неопределенностей
1.Невозможно состояние, в котором частицанаходилась бы в состоянии покоя.
2.При рассмотрении квантовых объектов
нельзя говорить о классической траектории.
3.Часто теряет смысл разделения полной
энергии на потенциальную и кинетическую.
4.В отличие от классической физики , в
квантовой существует естественный предел
точности измерений.
14
15. Описание движения квантовых частиц
хОПИСАНИЕ ДВИЖЕНИЯ
КВАНТОВЫХ ЧАСТИЦ
Свободная квантовая частица – частица,
движущаяся в отсутствие внешних полей.
Потенциальную энергию этой частицы
можно принять равной нулю: (U=0).
Тогда полная энергия частицы совпадает с
ее кинетической энергией.
В таком случае уравнение Шредингера для
этой частицы примет вид:
Ψ 2m
2 EΨ 0
2
x
2
(1)
15
16.
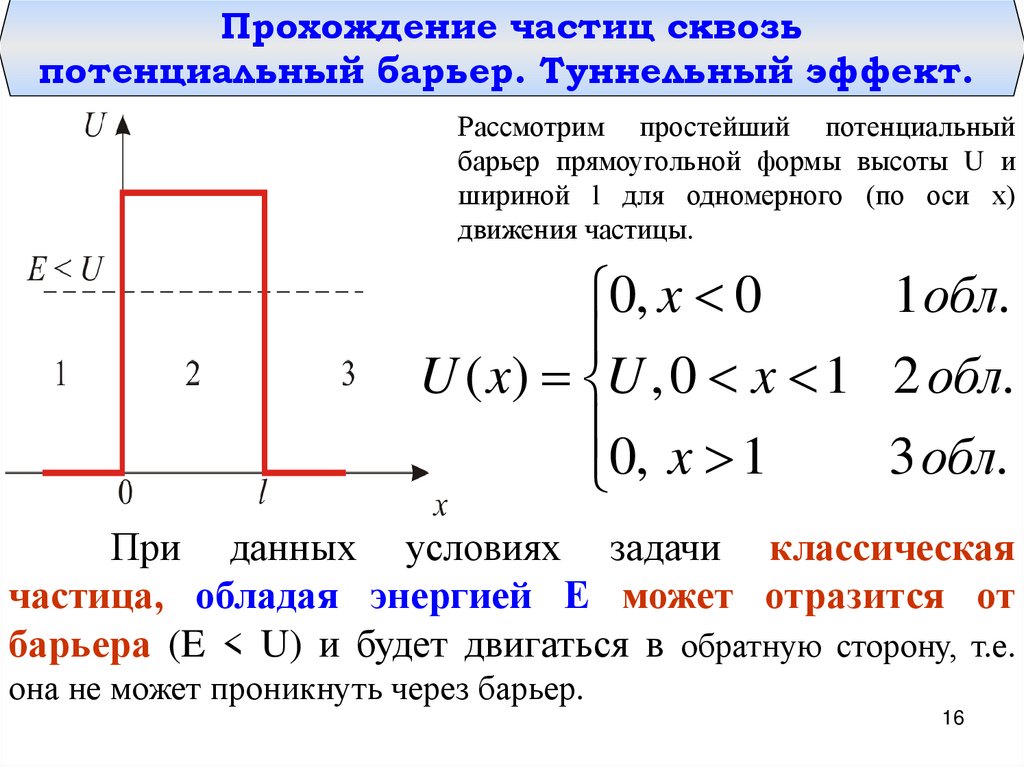
хПрохождение частиц сквозь
потенциальный барьер. Туннельный эффект.
Рассмотрим простейший потенциальный
барьер прямоугольной формы высоты U и
шириной l для одномерного (по оси х)
движения частицы.
Рисунок 5
1обл.
0, x 0
U ( x) U , 0 x 1 2 обл.
0, x 1
3 обл.
При данных условиях задачи классическая
частица, обладая энергией Е может отразится от
барьера (E < U) и будет двигаться в обратную сторону, т.е.
она не может проникнуть через барьер.
16
17.
1обл.0, x 0
U ( x) U , 0 x 1 2 обл.
0, x 1
3 обл.
Уравнение Шредингера для состояний в
области 1 имеет вид: 2Ψ 2m
EΨ 0 или
x
Ψ
2
k Ψ 0,
2
x
2
2
где
2
2mE
k 2 .
2
17
18.
1обл.0, x 0
U ( x) U , 0 x 1 2 обл.
0, x 1
3 обл.
Уравнение Шредингера для состояний в
области 2 имеет вид:
2 2m
x
или
2 2
q 0,
2
x
где
2
2
E U 0
q
2
2 m( E U )
2
.
18
19.
1обл.0, x 0
U ( x) U , 0 x 1 2 обл.
0, x 1
3 обл.
Уравнение Шредингера для состояний в
области 3 имеет вид:
Ψ
2
k
Ψ
0
,
2
x
2
где
2mE
k 2 .
2
19
20.
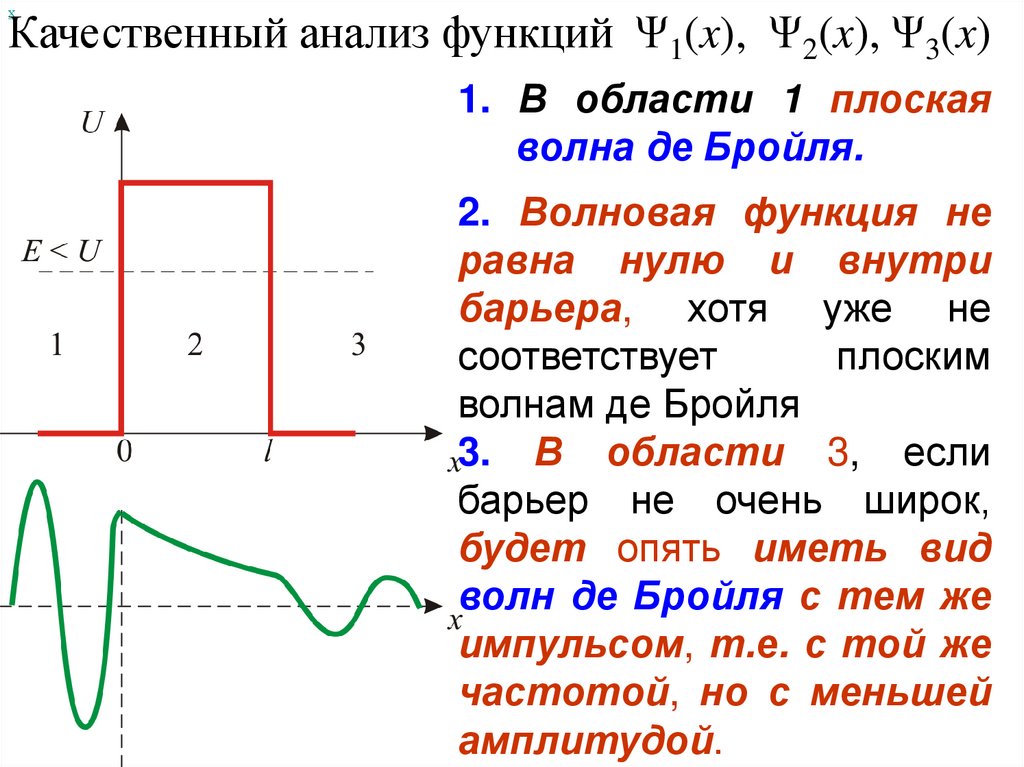
хКачественный анализ функций Ψ1(x), Ψ2(x), Ψ3(x)
1. В области 1 плоская
волна де Бройля.
2. Волновая функция не
равна нулю и внутри
барьера, хотя уже не
соответствует
плоским
волнам де Бройля
3. В области 3, если
барьер не очень широк,
будет опять иметь вид
волн де Бройля с тем же
импульсом, т.е. с той же
частотой, но с меньшей
амплитудой.
21.
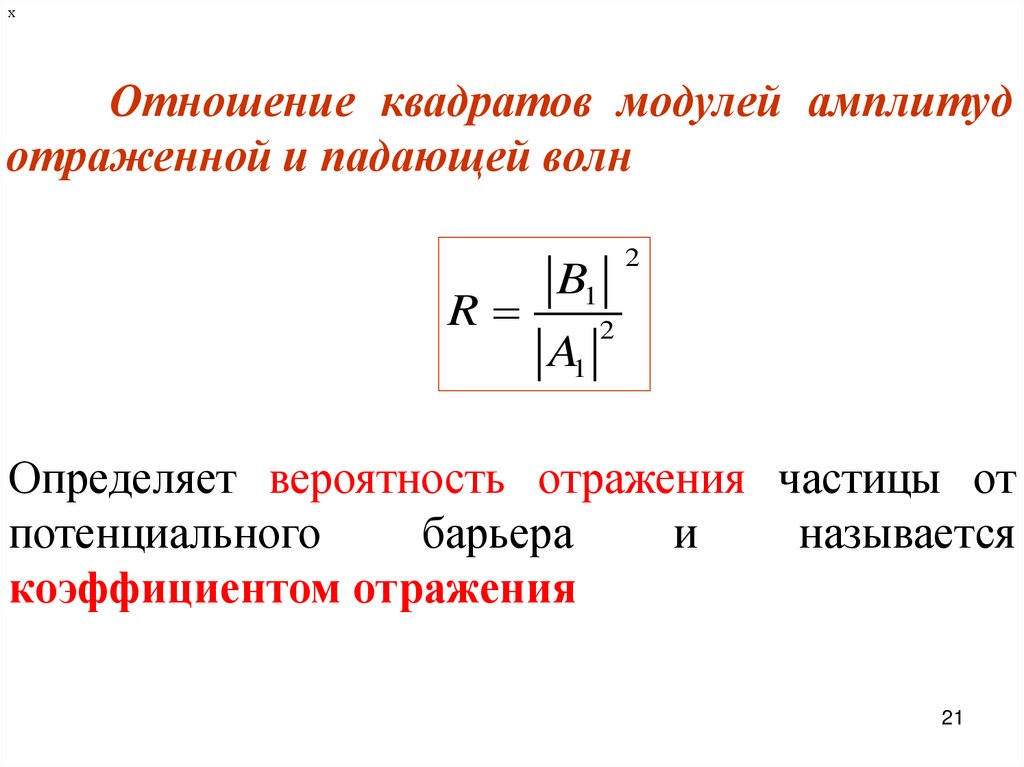
хОтношение квадратов модулей амплитуд
отраженной и падающей волн
R
2
B1
A1
2
Определяет вероятность отражения частицы от
потенциального
барьера
и
называется
коэффициентом отражения
21
22.
хОтношение квадратов модулей амплитуд
прошедшей и падающей волн
D
A3
A1
2
2
Определяет вероятность прохождения частицы
через потенциальный барьер и называется
коэффициентом прохождения (прозрачности).
22
23.
E;UE
ψ
U0
U=0
ψ2
U=0
0
l
x
l
x
l
x
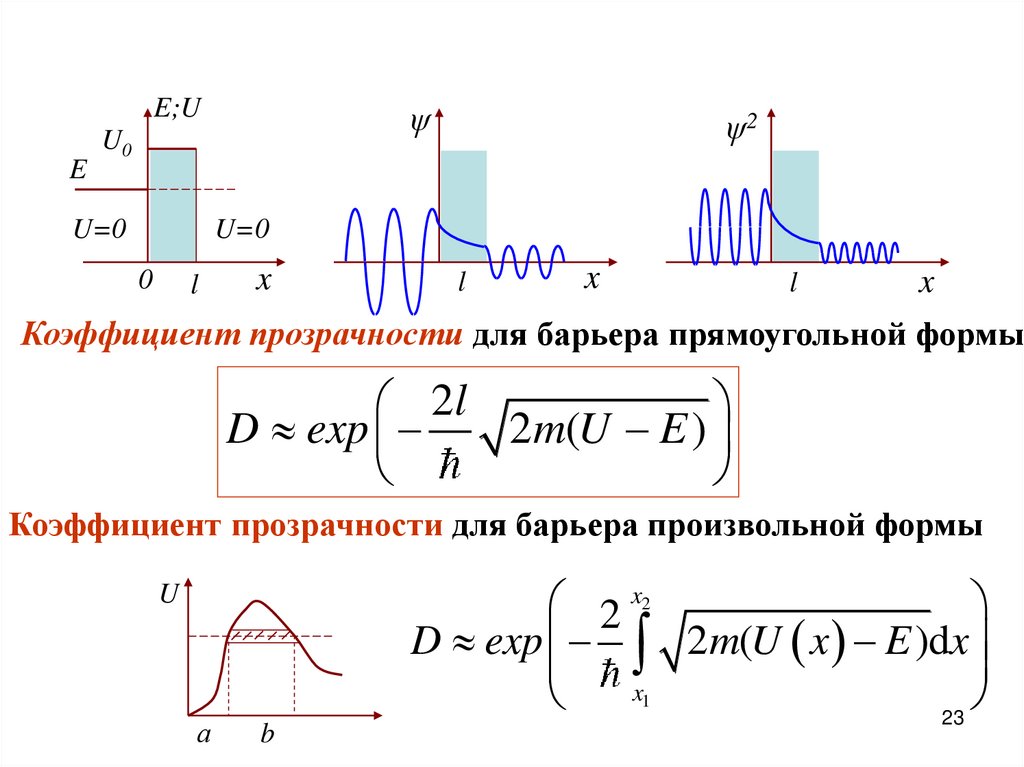
Коэффициент прозрачности для барьера прямоугольной формы
2l
D exp
2 m(U E )
Коэффициент прозрачности для барьера произвольной формы
U
E
а а b
x
2 x2
D exp 2m(U x E )dx
x
1
23
24.
Таким образом, квантоваямеханика приводит к принципиально
новому квантовому явлению туннельному эффекту,
в результате которого микрообъект
может пройти через барьер.
24
25. Эмиссия электронов из проводников
• Электрон свободен только в границах металла. Кактолько он пытается перейти границу «металл –
вакуум», возникает кулоновская сила притяжения
между электроном и образовавшимся на
поверхности избыточным положительным зарядом
26.
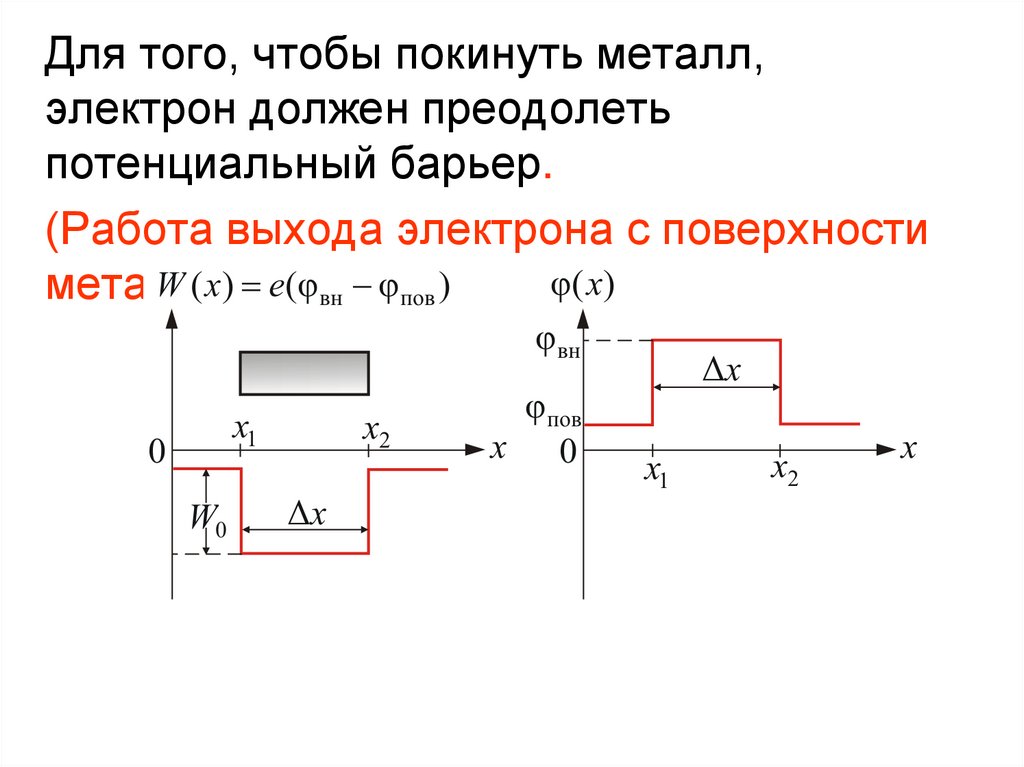
Для того, чтобы покинуть металл,электрон должен преодолеть
потенциальный барьер.
(Работа выхода электрона с поверхности
металла).
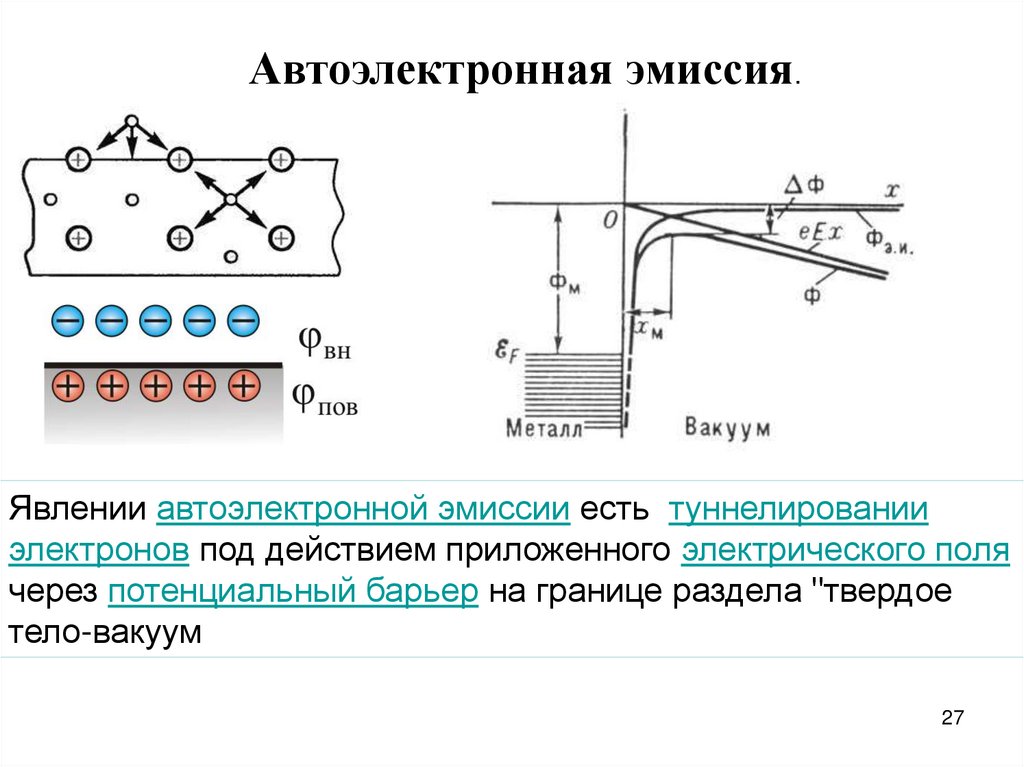
27.
Автоэлектронная эмиссия.Явлении автоэлектронной эмиссии есть туннелировании
электронов под действием приложенного электрического поля
через потенциальный барьер на границе раздела "твердое
тело-вакуум
27
28.
Какой же должна быть напряженность поля, чтобы ток холоднойэмиссии во внешней цепи достиг максимального значения?
Очевидно, это может произойти при такой напряженности поля,
когда работа выхода обратится в нуль. Оценка напряженности поля
для вольфрама показывает, что эта величина поля E=U/d=200 000
000 В/см, т. е. если расстояние между анодом и катодом сделать
равным 1 см, то батарея должна иметь напряжение 200 000 000 В.
Если же расстояние сделать равным 1 мкм (0,0001 см), то
напряжение должно быть 20 000 В. Отсюда следует, что даже в
последнем случае практическое осуществление подобного прибора
весьма затруднительно.
Однако экспериментальная проверка доказала, что для
вольфрамового катода достаточно большие токи удается получить
уже при напряженности поля порядка 106 В/см, т. е. при расстоянии
в 1 мкм достаточно иметь батарею напряжением 100 В.
29.
Столь сильные расхождения между первоначальнопредложенной теорией и опытом удалось объяснить с
помощью туннельного эффекта. Дело в том, что силы,
препятствующие выходу электрона из металла,
образуют у его поверхности так
называемый потенциальный барьер для преодоления
которого согласно классической теории электрон
должен сначала «подняться» на него, затратив работу,
равную работе выхода, а затем уже свободно
перемещаться от катода к аноду.
Согласно же квантовой механике электрону нет
необходимости «подниматься» на барьер; при
определенных условиях он может, не затрачивая
энергии, пройти «сквозь» него, как через туннель.
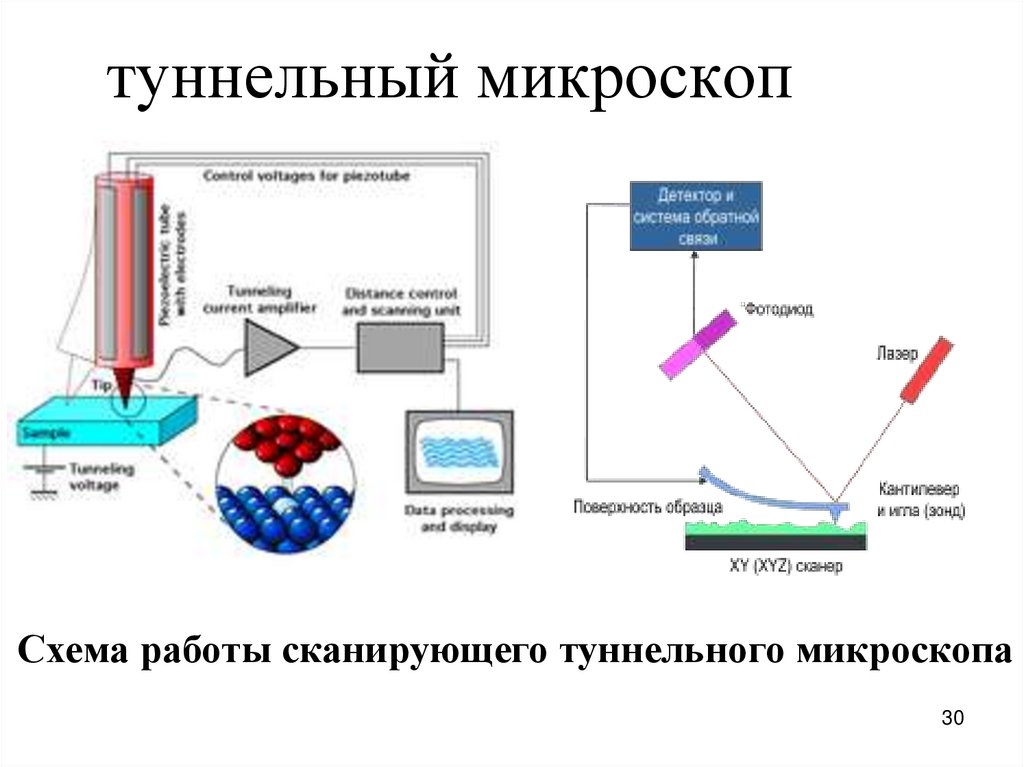
30. туннельный микроскоп
Схема работы сканирующего туннельного микроскопа30
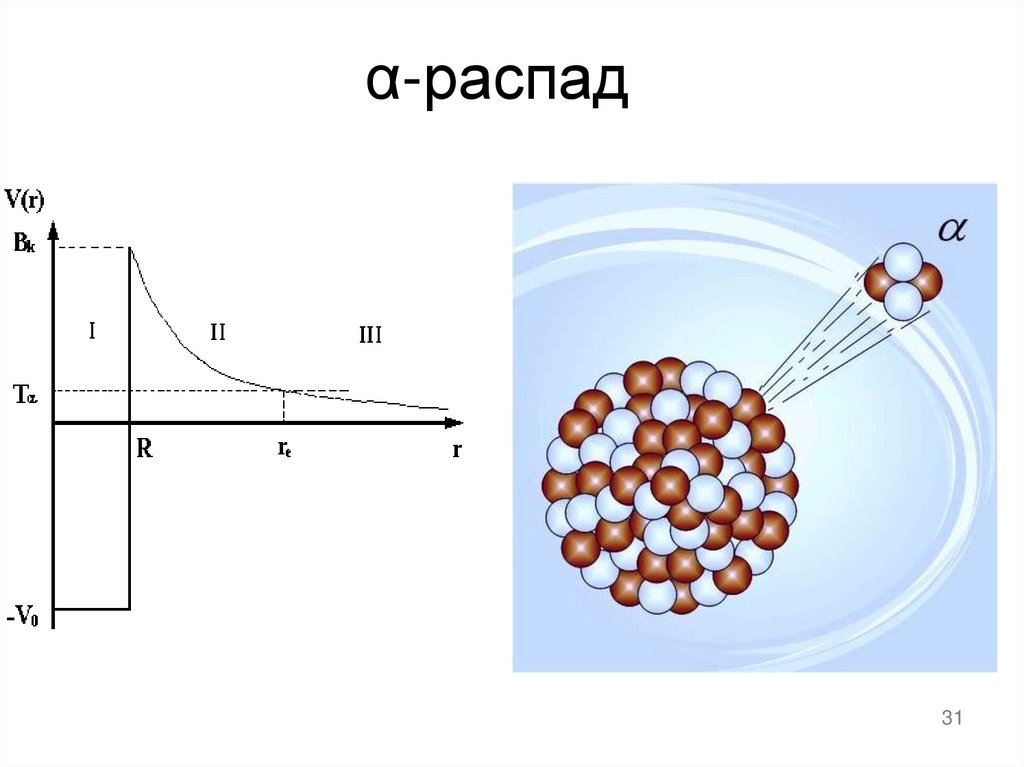
31. α-распад
3132. α-распад
Простейшая модель была предложена в 1928 году Г. Гамовым инезависимо от него Г. Герни . В этой модели предполагалось, что αчастица постоянно существует в ядре. Пока α-частица находится в
ядре на нее действуют ядерные силы притяжения и кулоновские.
Для того, чтобы выйти за пределы ядра α-частица должна пройти
через кулоновский потенциальный барьер.
Таким образом, вылет α-частиц из радиоактивных ядер
обусловлен туннельным эффектом. Это квантовомеханическое
явление называют “туннельным эффектом” или “туннелированием”.
Чем выше барьер, тем меньше вероятность туннелирования, а
период полураспада больше. Огромный диапазон периодов
полураспада α-излучателей объясняется различным сочетанием
кинетических энергий α-частиц и высот потенциальных барьеров.
Если бы барьера не существовало, то альфа-частица за время ≈1021 – 10-23 с покинула бы ядро.
33. Кристаллы
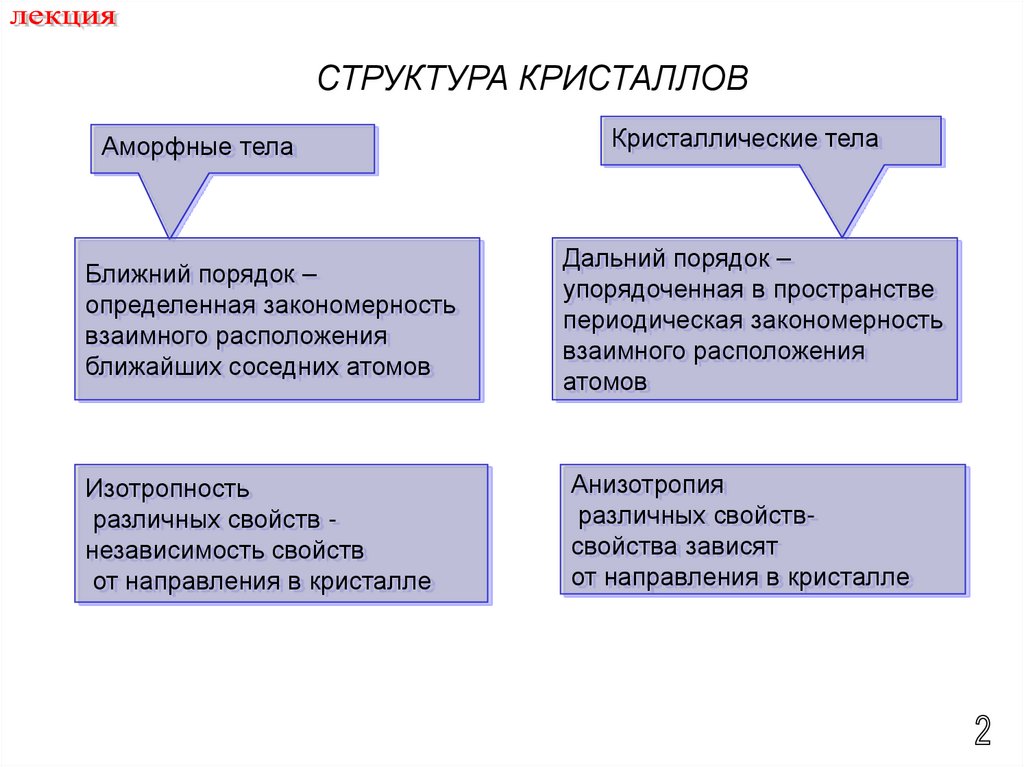
3334.
СТРУКТУРА КРИСТАЛЛОВАморфные тела
Кристаллические тела
Ближний порядок –
определенная закономерность
взаимного расположения
ближайших соседних атомов
Дальний порядок –
упорядоченная в пространстве
периодическая закономерность
взаимного расположения
атомов
Изотропность
различных свойств независимость свойств
от направления в кристалле
Анизотропия
различных свойствсвойства зависят
от направления в кристалле
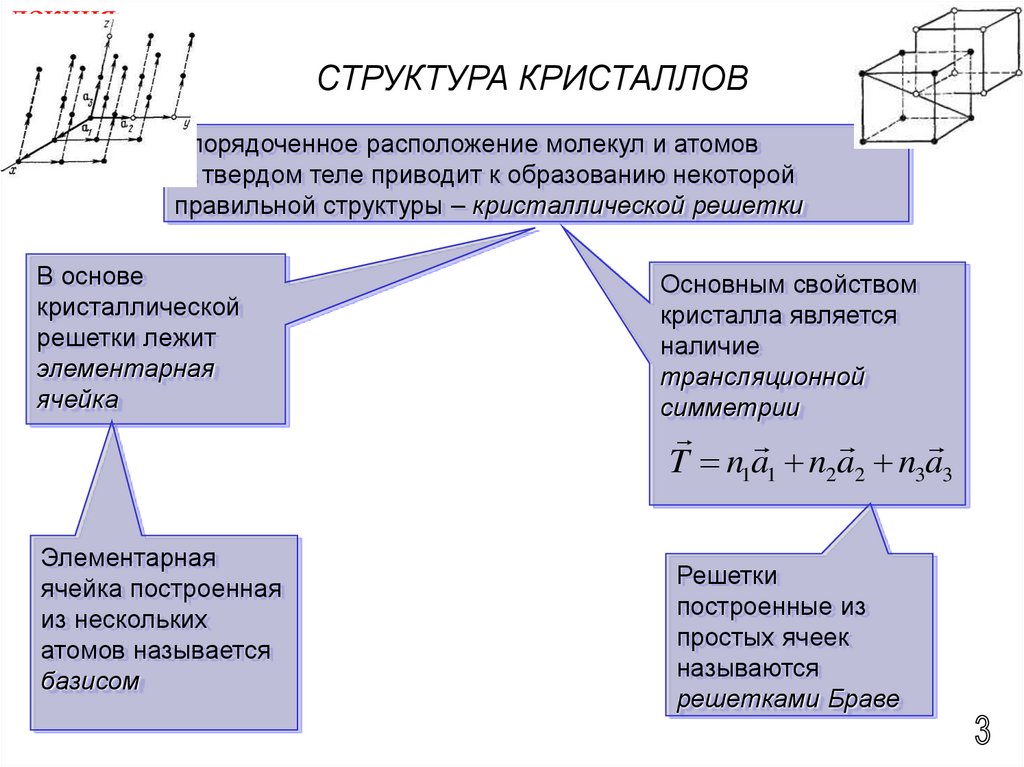
35.
СТРУКТУРА КРИСТАЛЛОВУпорядоченное расположение молекул и атомов
в твердом теле приводит к образованию некоторой
правильной структуры – кристаллической решетки
В основе
кристаллической
решетки лежит
элементарная
ячейка
Основным свойством
кристалла является
наличие
трансляционной
симметрии
T n1a1 n2a2 n3a3
Элементарная
ячейка построенная
из нескольких
атомов называется
базисом
Решетки
построенные из
простых ячеек
называются
решетками Браве
36.
3637.
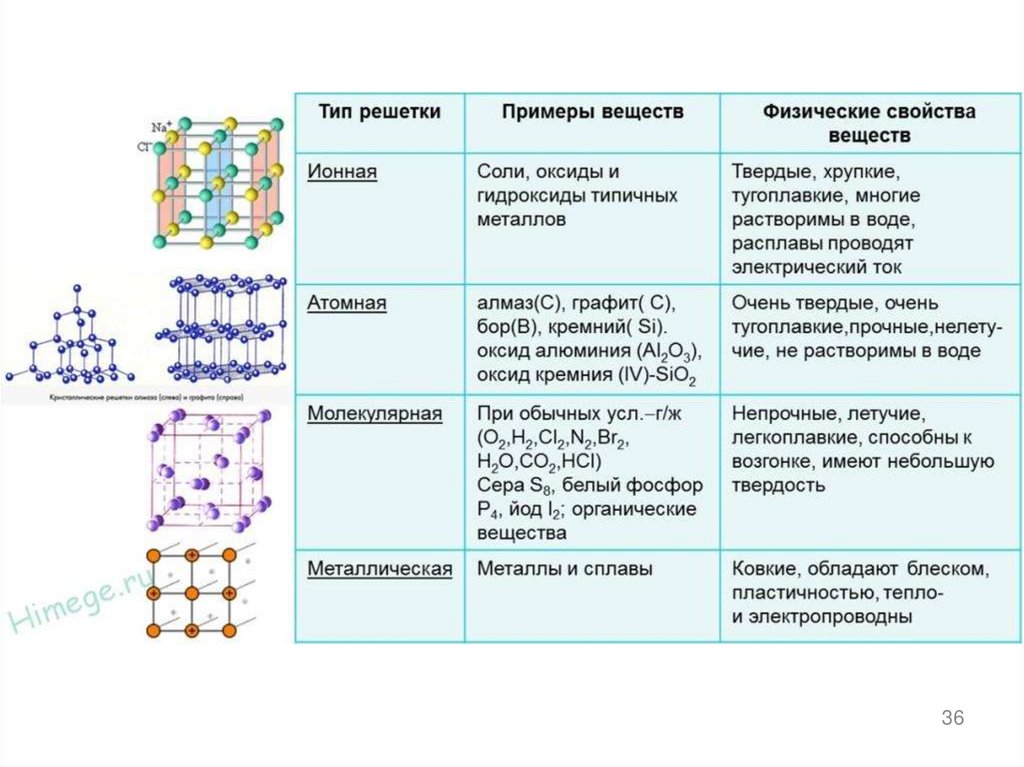
КЛАССИФИКАЦИЯ КРИСТАЛЛОВ ПО ТИПАМ СВЯЗИТип
Кристалла
1. Ионные
Пример
Энергия
связи,
ккал/моль
NaCl
LiF
180
240
2.4
2. Ковалентные
3. Металлические
Алмаз
SiC
Na
Fe
170
283
26
94
4. Молекулярные
Ar
CCl4
1,8
2,4
5. С водородными
связями
HF
Лед
7
12
Свойства
Диэлектрики (низкая проводимость
при низких температурах; при высоких
- ионная проводимость); сильное ИК
поглощение; твердые, хрупкие.
Диэлектрики,
высокая
твердость,
высокая температура плавления
Высокая электропроводность, высокий
коэффициент отражения
Диэлектрики, низкая точка плавления,
высокая сжимаемость.
Тенденция к полимеризации
+5 ккал/моль
37
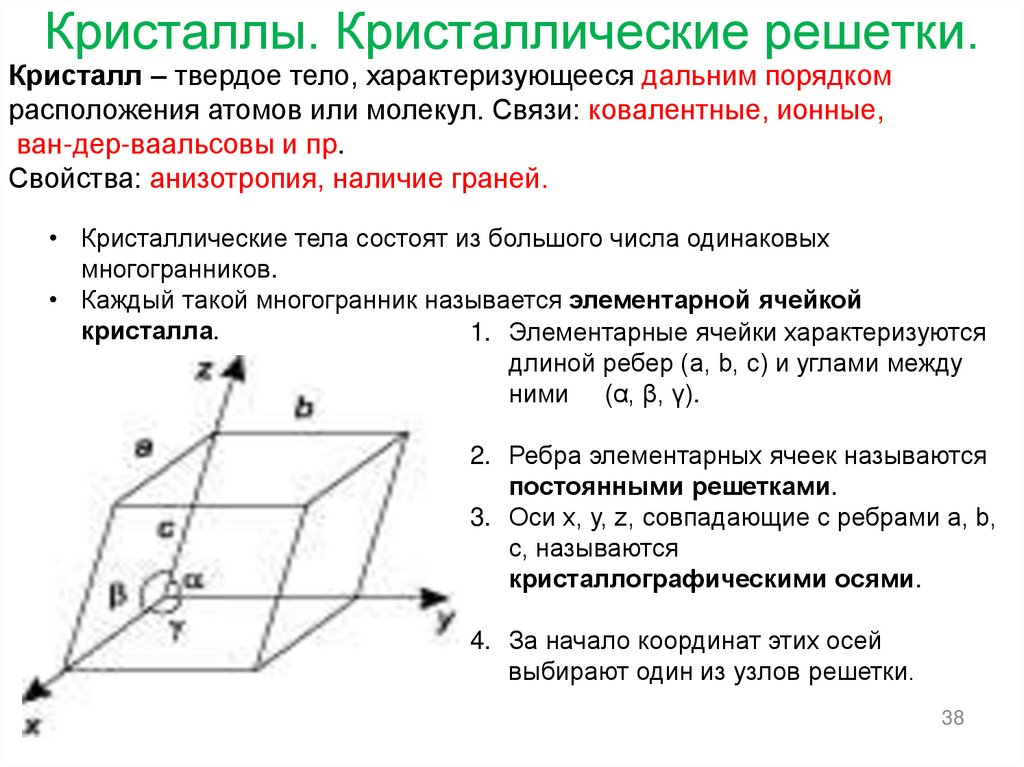
38. Кристаллы. Кристаллические решетки.
Кристалл – твердое тело, характеризующееся дальним порядкомрасположения атомов или молекул. Связи: ковалентные, ионные,
ван-дер-ваальсовы и пр.
Свойства: анизотропия, наличие граней.
• Кристаллические тела состоят из большого числа одинаковых
многогранников.
• Каждый такой многогранник называется элементарной ячейкой
кристалла.
1. Элементарные ячейки характеризуются
длиной ребер (а, b, c) и углами между
ними (α, β, γ).
2. Ребра элементарных ячеек называются
постоянными решетками.
3. Оси x, y, z, совпадающие с ребрами a, b,
c, называются
кристаллографическими осями.
4. За начало координат этих осей
выбирают один из узлов решетки.
38
39.
Координационное число. Сингония.Координационное число – характеристика, которая
определяет число ближайших равноудаленных одинаковых
частиц (ионов или атомов) в кристаллической решётке.
Прямые линии, соединяющие центры ближайших атомов или
ионов в кристалле, образуют координационный
многогранник, в центре которого находится данный атом.
Число ближайших соседей отражает плотность упаковки
вещества.
Для простой кубической решетки координационное число равно шести, для ОЦК
— 8, ГЦК и ГП (гексагональной плотноупакованной) — 12.
Сингония кристаллографическая, - подразделение
кристаллов по признаку симметрии их элементарной
ячейки. Сингония характеризуется соотношениями между
ребрами а, b, с и углами α, β, γ ячейки.
39
40. Типы кристаллических решеток
В зависимости от пространственной симметрии, все кристаллическиерешётки подразделяются на
7 кристаллических систем.
По форме элементарной ячейки они могут быть разбиты на
7сингоний.
Все возможные сочетания имеющихся в кристаллической решётке
поворотных осей симметрии и зеркальных плоскостей симметрии
приводят к делению кристаллов на 32 класса симметрии.
С учётом винтовых осей симметрии и скользящих плоскостей
симметрии на 230 пространственных групп.
40
41.
Решетки БравеПомимо основных трансляций, на которых строится кристаллическая решётка
могут присутствовать дополнительные трансляции, называемые
решётками Браве.
Ячейка, обладающая симметрией структуры, и имеющая минимальный объем из
всех ячеек такого же качества, называется характеристической ячейкой, или
ячейкой Браве.
Типы трёхмерных решёток Браве:
1. гранецентрированная (F),
2. объёмноцентрированная (I),
3. базоцентрированная (A, B или C),
4. примитивная (P)
5. ромбоэдрическая (R).
Примитивная система трансляций состоит из множества векторов (a, b, c).
Объёмноцентрированная состоит из 4 векторов (a, b, c, ½(a+b+c))
Гранецентрированная состоит из 6 векторов (a, b, c, ½(a+b), ½(b+c), ½(a+c)).
41
42. Классификация решёток по симметрии. Сингония.
4243. Классификация решёток по симметрии. Сингония.
1. триклинная сингония — наименьшая симметрия, нет одинаковыхуглов,
нет ребер одинаковой длины
; и у которой
атомы расположены только в вершинах элементарной ячейки.
43
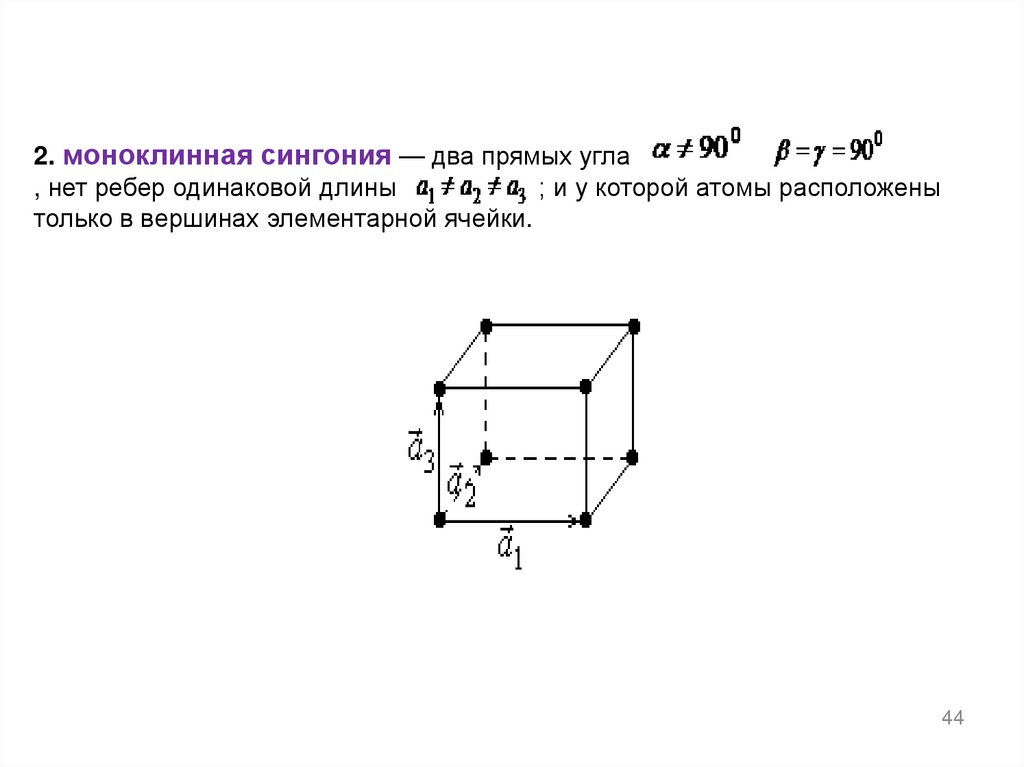
44.
2. моноклинная сингония — два прямых угла, нет ребер одинаковой длины
; и у которой атомы расположены
только в вершинах элементарной ячейки.
44
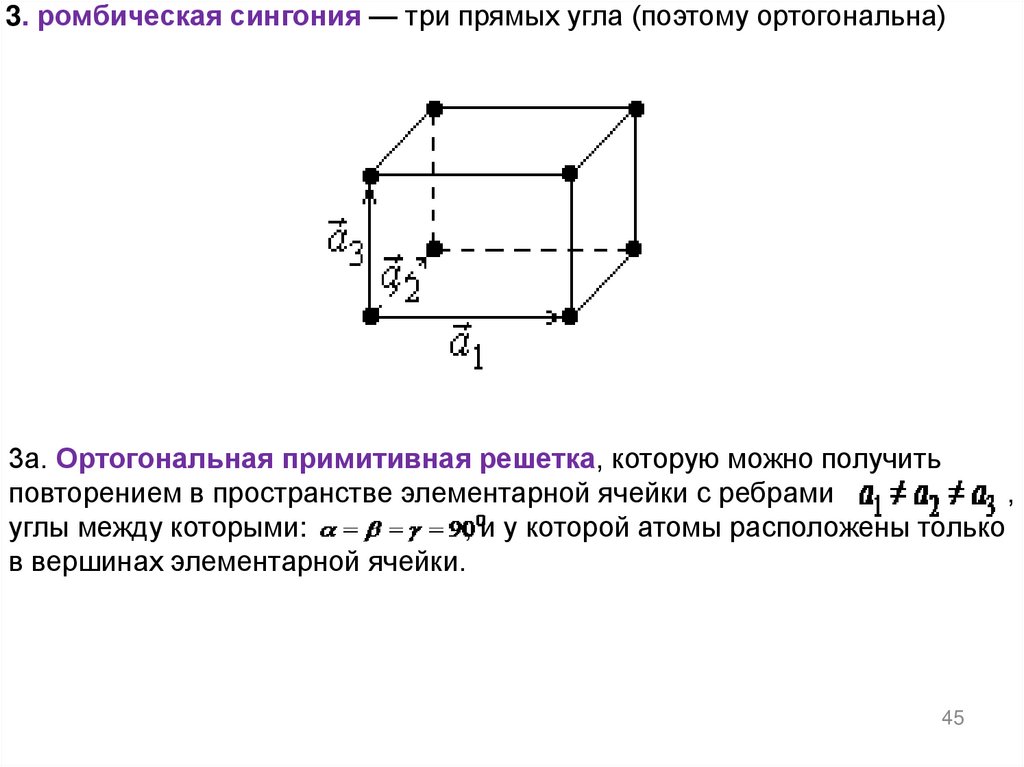
45.
3. ромбическая сингония — три прямых угла (поэтому ортогональна)3а. Ортогональная примитивная решетка, которую можно получить
повторением в пространстве элементарной ячейки с ребрами
,
углы между которыми:
, и у которой атомы расположены только
в вершинах элементарной ячейки.
45
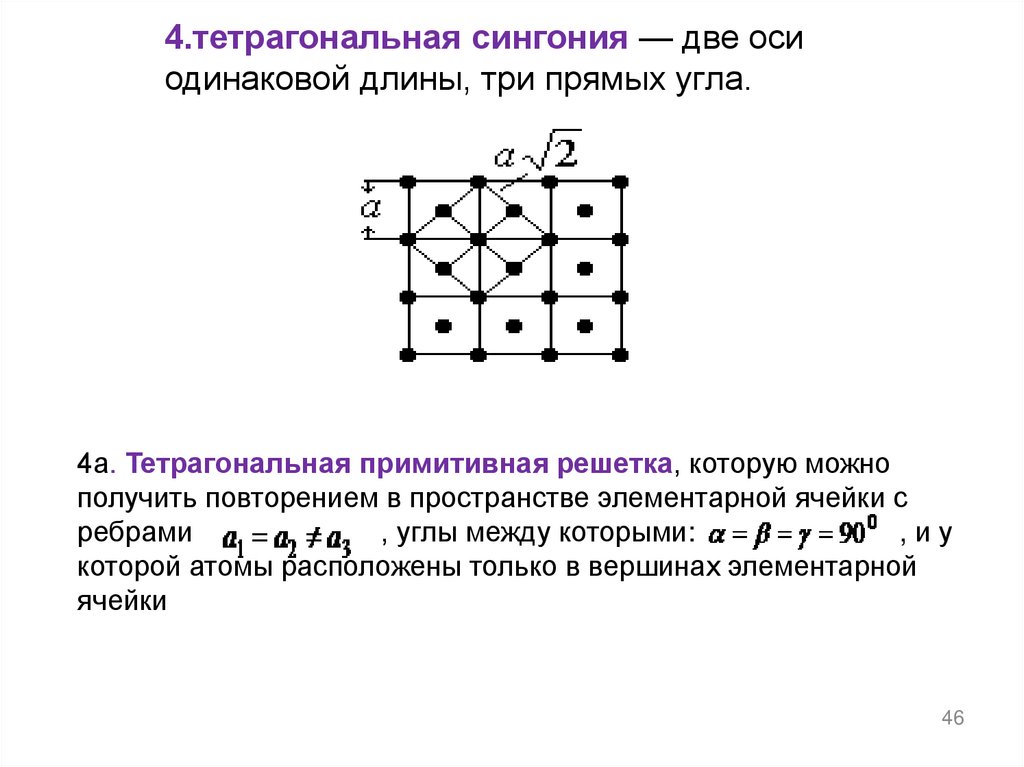
46.
4.тетрагональная сингония — две осиодинаковой длины, три прямых угла.
4а. Тетрагональная примитивная решетка, которую можно
получить повторением в пространстве элементарной ячейки с
ребрами
, углы между которыми:
,иу
которой атомы расположены только в вершинах элементарной
ячейки
46
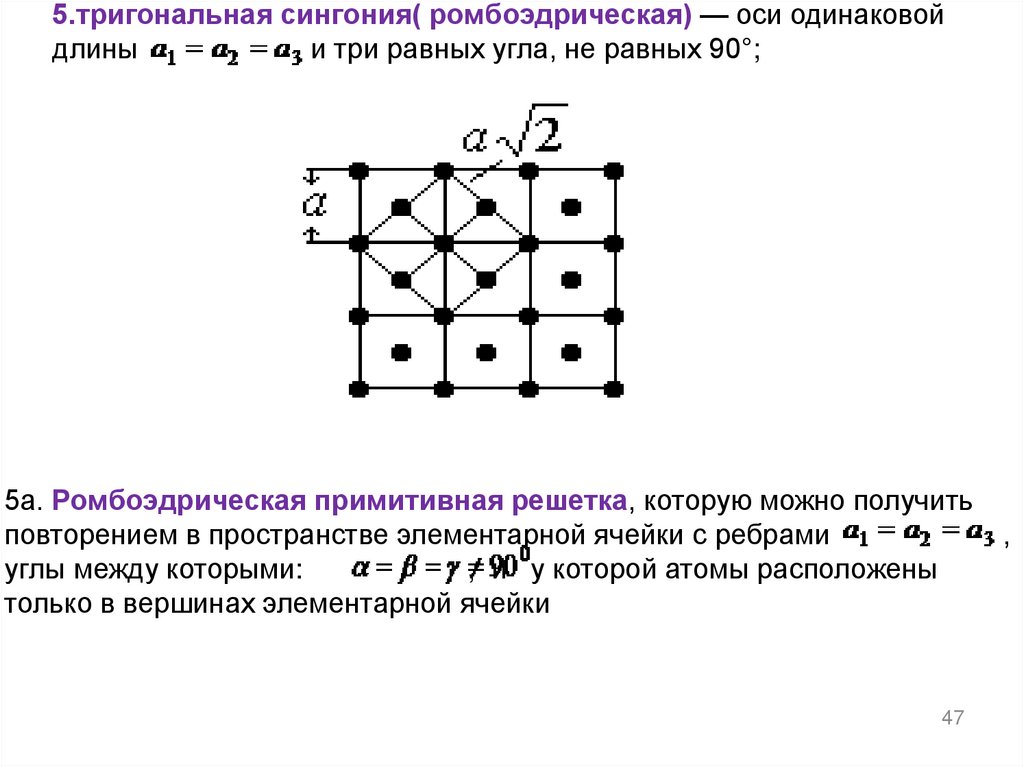
47.
5.тригональная сингония( ромбоэдрическая) — оси одинаковойдлины
и три равных угла, не равных 90°;
5а. Ромбоэдрическая примитивная решетка, которую можно получить
повторением в пространстве элементарной ячейки с ребрами
углы между которыми:
, и у которой атомы расположены
только в вершинах элементарной ячейки
47
,
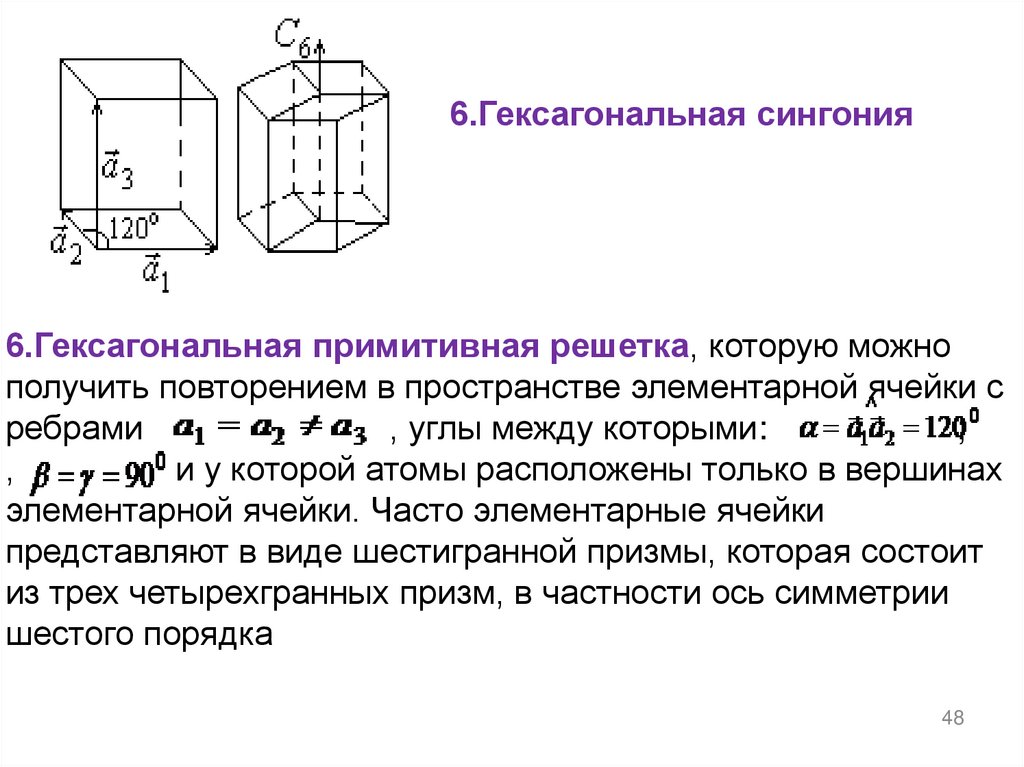
48.
6.Гексагональная сингония6.Гексагональная примитивная решетка, которую можно
получить повторением в пространстве элементарной ячейки с
ребрами
, углы между которыми:
;
,
и у которой атомы расположены только в вершинах
элементарной ячейки. Часто элементарные ячейки
представляют в виде шестигранной призмы, которая состоит
из трех четырехгранных призм, в частности ось симметрии
шестого порядка
48
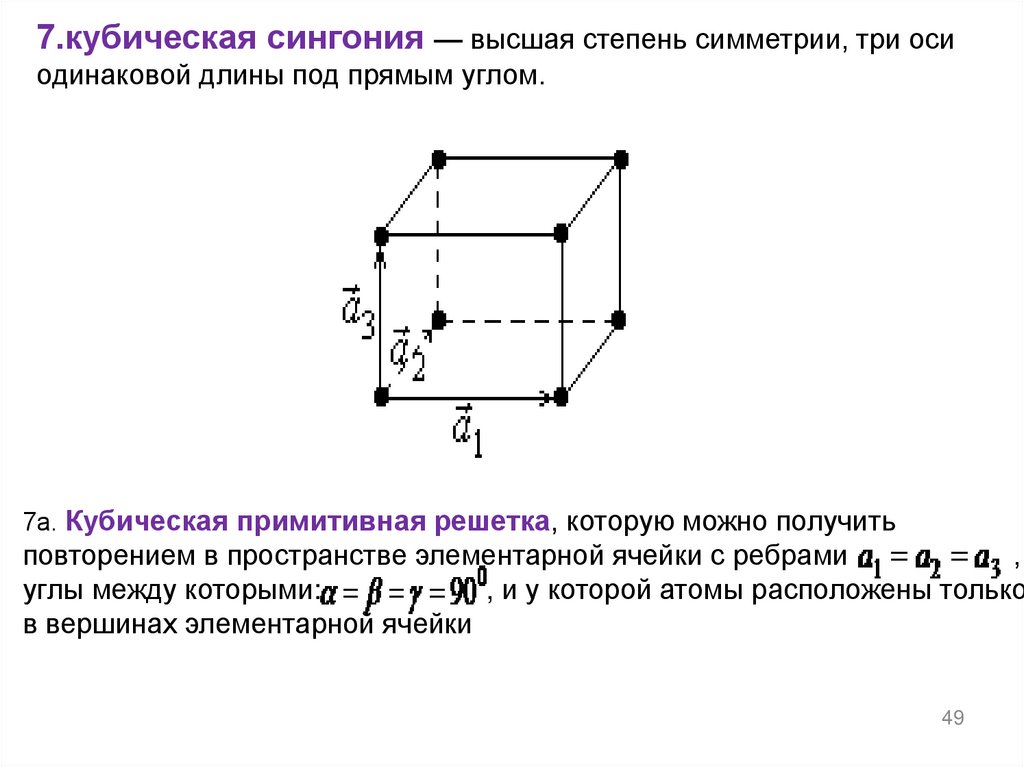
49.
7.кубическая сингония — высшая степень симметрии, три осиодинаковой длины под прямым углом.
7а. Кубическая примитивная решетка, которую можно получить
повторением в пространстве элементарной ячейки с ребрами
,
углы между которыми:
, и у которой атомы расположены только
в вершинах элементарной ячейки
49
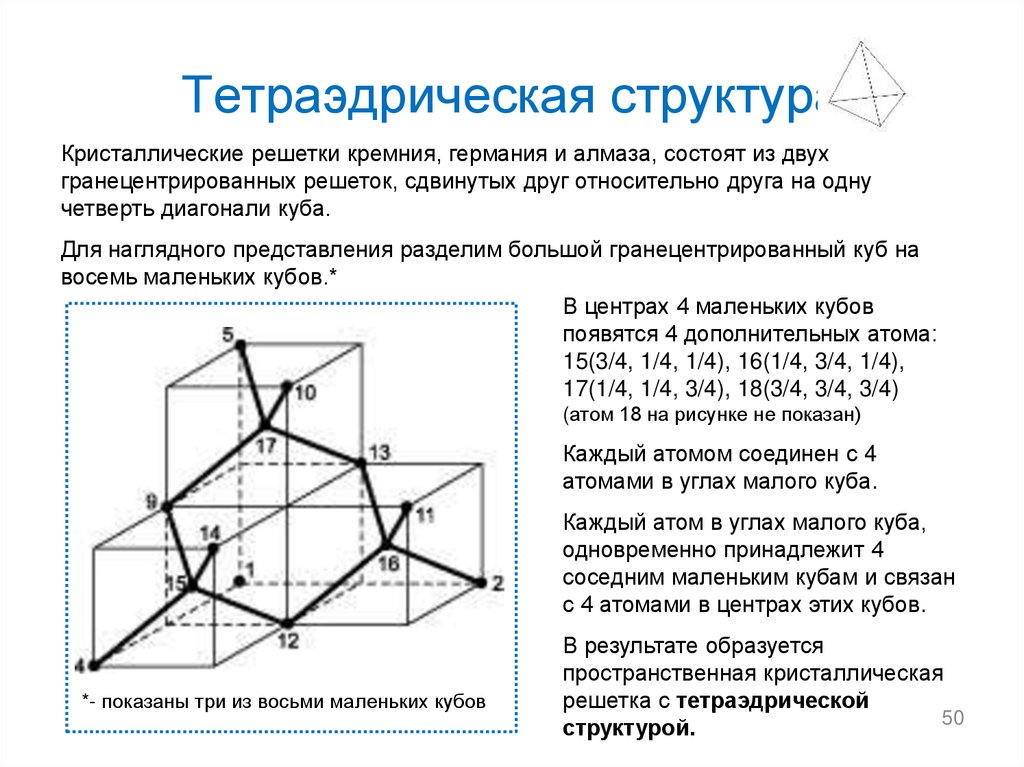
50. Тетраэдрическая структура
Кристаллические решетки кремния, германия и алмаза, состоят из двухгранецентрированных решеток, сдвинутых друг относительно друга на одну
четверть диагонали куба.
Для наглядного представления разделим большой гранецентрированный куб на
восемь маленьких кубов.*
В центрах 4 маленьких кубов
появятся 4 дополнительных атома:
15(3/4, 1/4, 1/4), 16(1/4, 3/4, 1/4),
17(1/4, 1/4, 3/4), 18(3/4, 3/4, 3/4)
(атом 18 на рисунке не показан)
Каждый атомом соединен с 4
атомами в углах малого куба.
Каждый атом в углах малого куба,
одновременно принадлежит 4
соседним маленьким кубам и связан
с 4 атомами в центрах этих кубов.
*- показаны три из восьми маленьких кубов
В результате образуется
пространственная кристаллическая
решетка с тетраэдрической
50
структурой.
51. Симметрия кристаллов. Трансляционная симметрия.
Для описания кристаллической решетки используютспецифические операции
1. трансляционная (переносная) симметрия.
2. поворотная (вращательная) симметрия.
Трансляционная симметрия – повторяемость объекта в
пространстве через определенное расстояние вдоль
прямой, называемой осью трансляции.
.
51
52. Симметрия кристаллов. Поворотная симметрия.
Поворотная симметрия – свойство кристалла совмещаться с самимсобой при вращении на некоторый определенный угол вокруг оси
симметрии
При наличии трансляционной симметрии возможны только оси
симметрии, отвечающие поворотам на 180, 120, 90 и 60 град.
Эти оси обозначают символами (порядок симметрии) 2, 3, 4 и 6 .
1. Нет оси симметрии 5 порядка соответствующей углу поворота 72
градуса.
.
2. Запрещены оси симметрии выше 6 порядка, так как они
несовместимы с представлением о трансляционной симметрии.
52
53. Симметрия кристаллов. Зеркально – поворотная ось симметрии
Зеркально – поворотная ось симметрии n –малого порядка (Sn) – это такая операция, при
которой кристалл совмещается сам с собой, если
произвести его поворот вокруг обычной оси n –
малого порядка с последующем отражением
кристалла в плоскости σh перпендикулярной оси n –
го порядка.
53
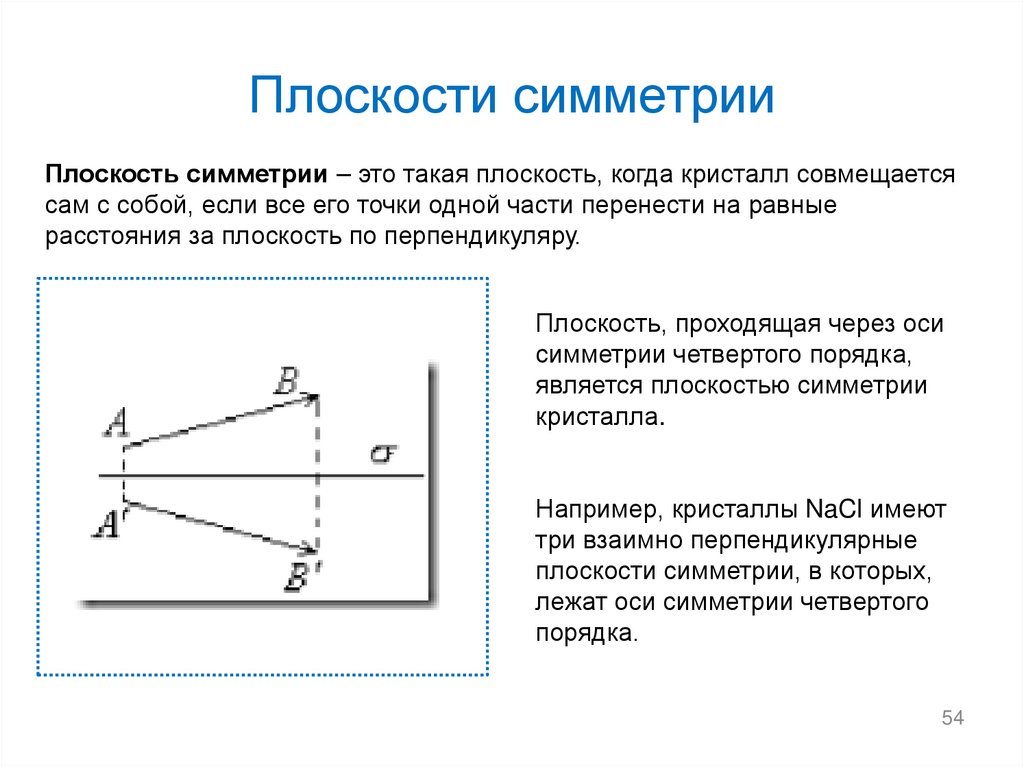
54. Плоскости симметрии
Плоскость симметрии – это такая плоскость, когда кристалл совмещаетсясам с собой, если все его точки одной части перенести на равные
расстояния за плоскость по перпендикуляру.
Плоскость, проходящая через оси
симметрии четвертого порядка,
является плоскостью симметрии
кристалла.
Например, кристаллы NaCl имеют
три взаимно перпендикулярные
плоскости симметрии, в которых,
лежат оси симметрии четвертого
порядка.
54
55.
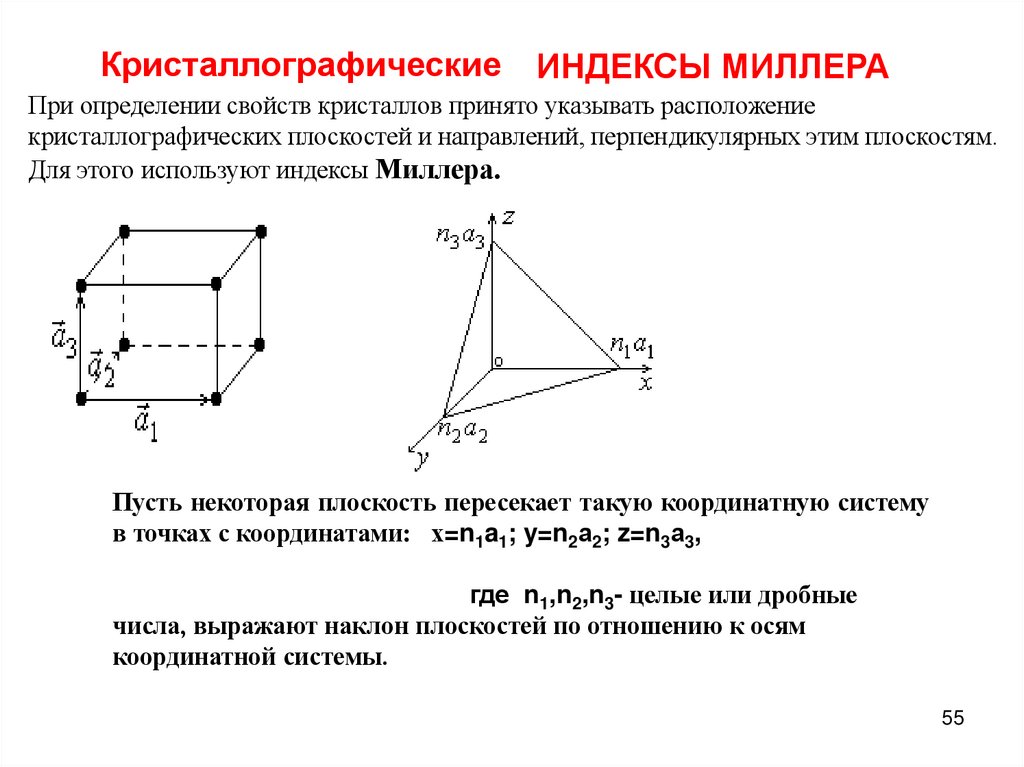
КристаллографическиеИНДЕКСЫ МИЛЛЕРА
При определении свойств кристаллов принято указывать расположение
кристаллографических плоскостей и направлений, перпендикулярных этим плоскостям.
Для этого используют индексы Миллера.
Пусть некоторая плоскость пересекает такую координатную систему
в точках с координатами: х=n1a1; y=n2а2; z=n3а3,
где n1,n2,n3- целые или дробные
числа, выражают наклон плоскостей по отношению к осям
координатной системы.
55
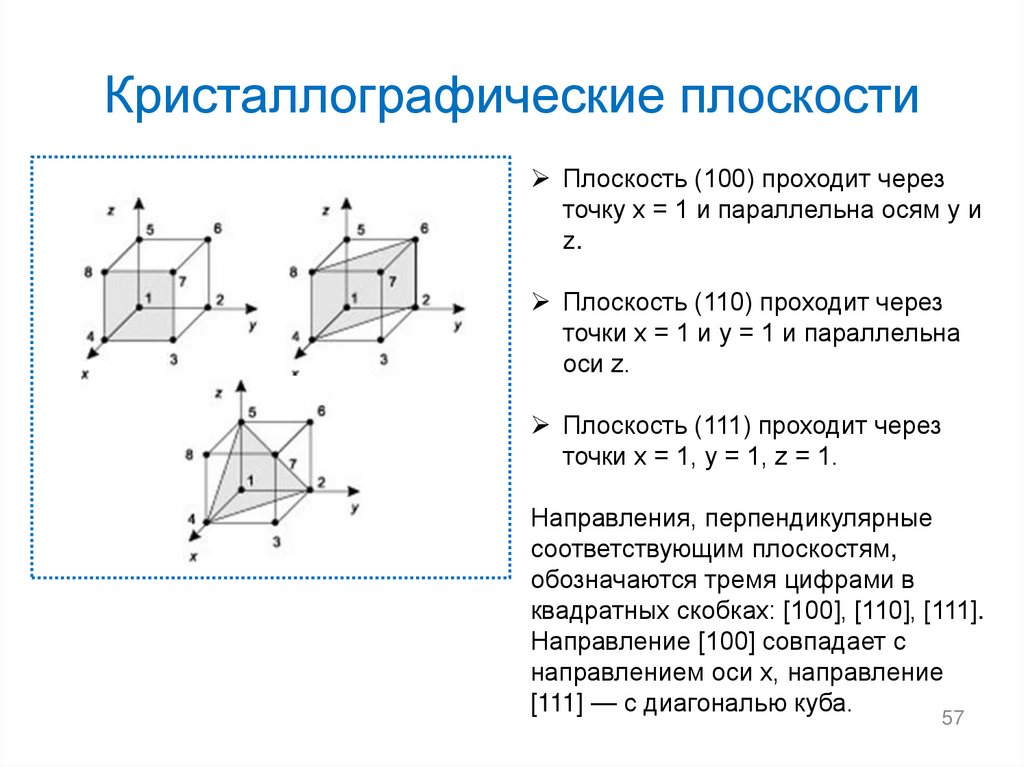
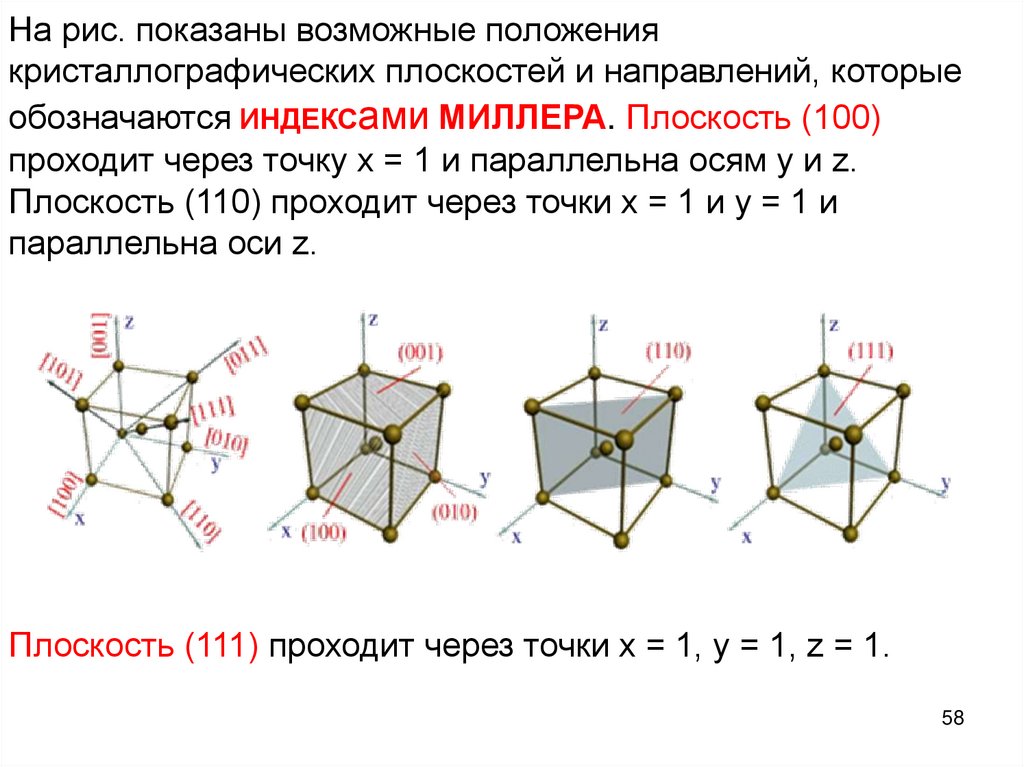
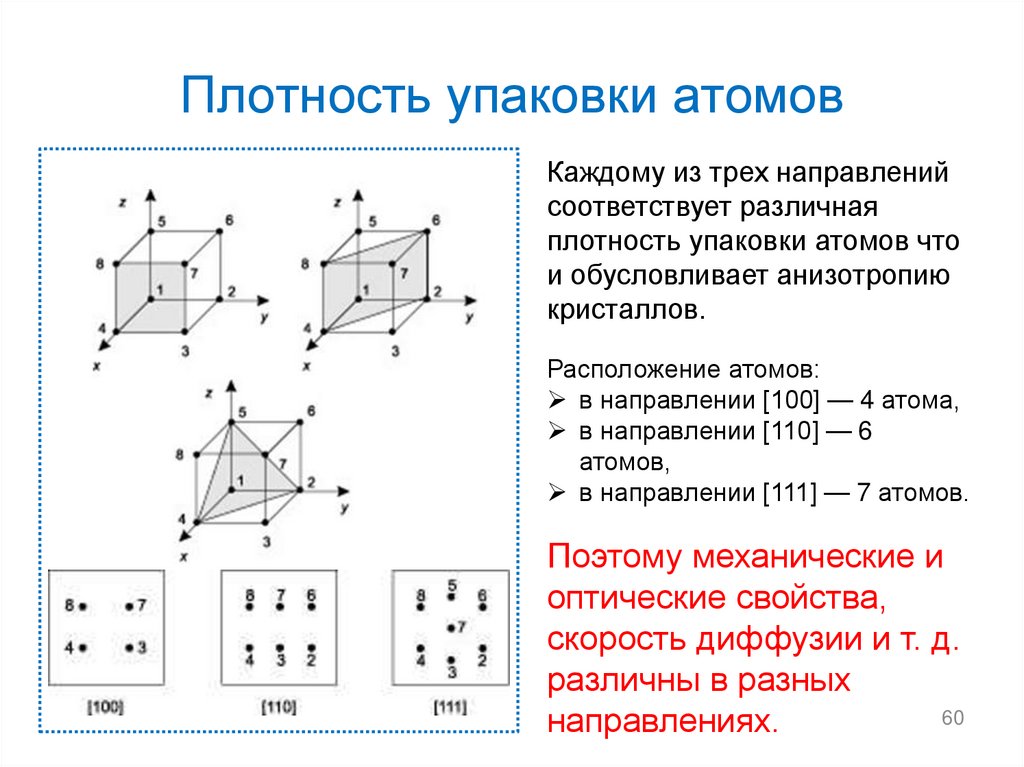
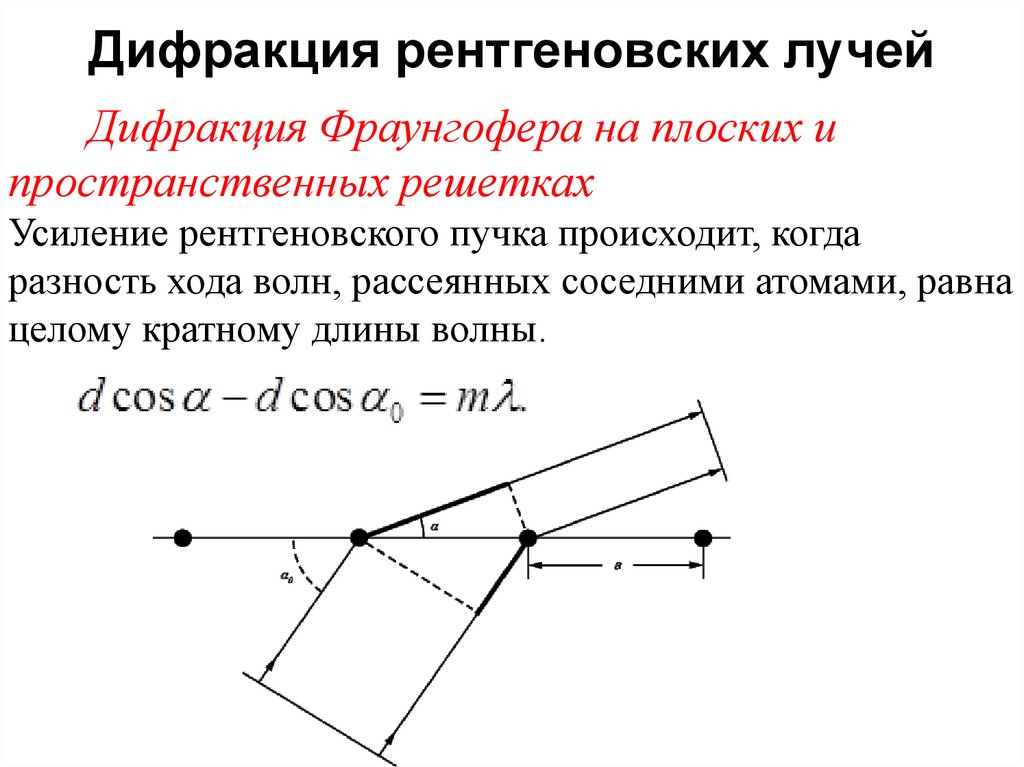
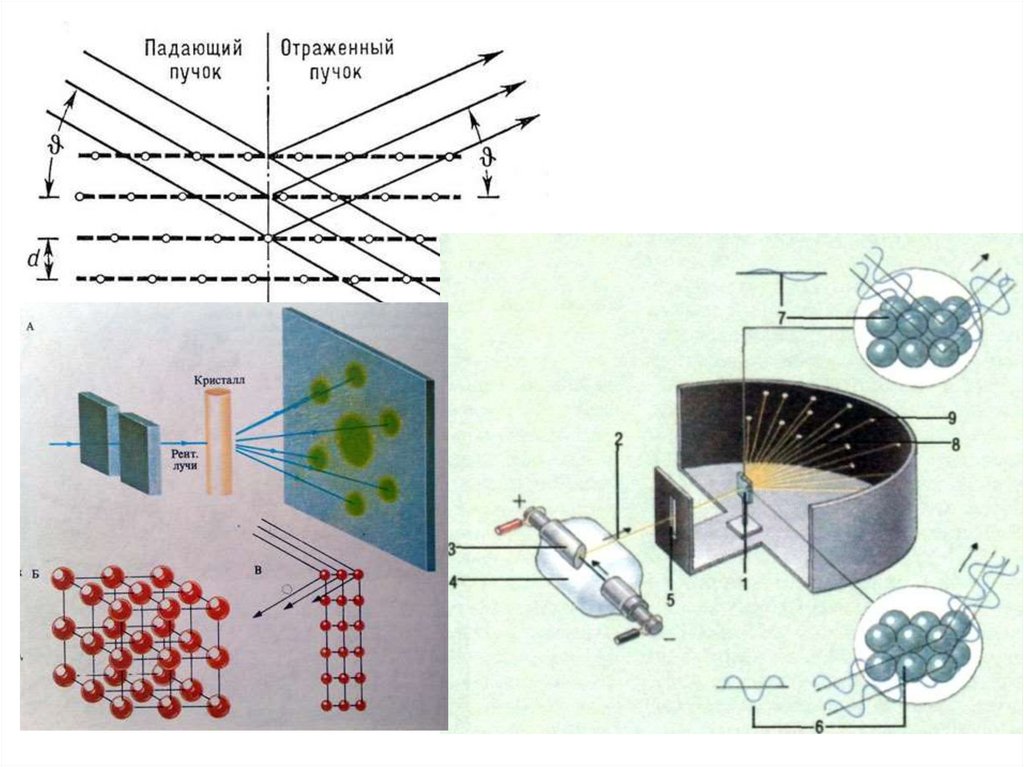
56.
КристаллографическиеИНДЕКСЫ МИЛЛЕРА
Теперь составим отношение обратных чисел







































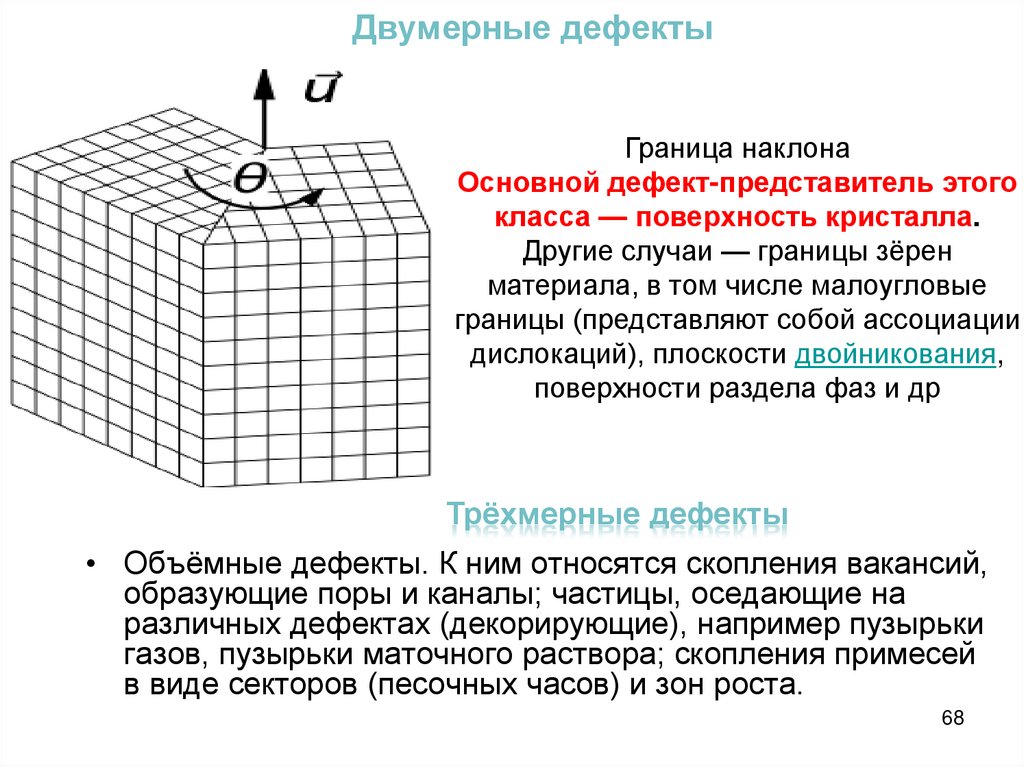



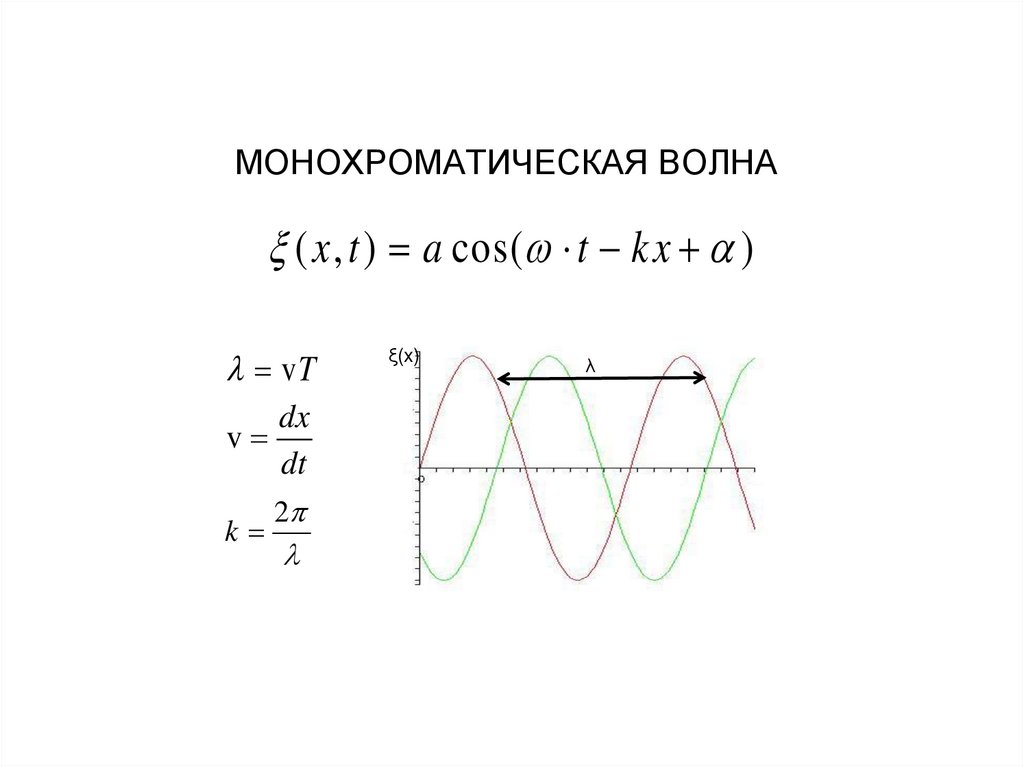


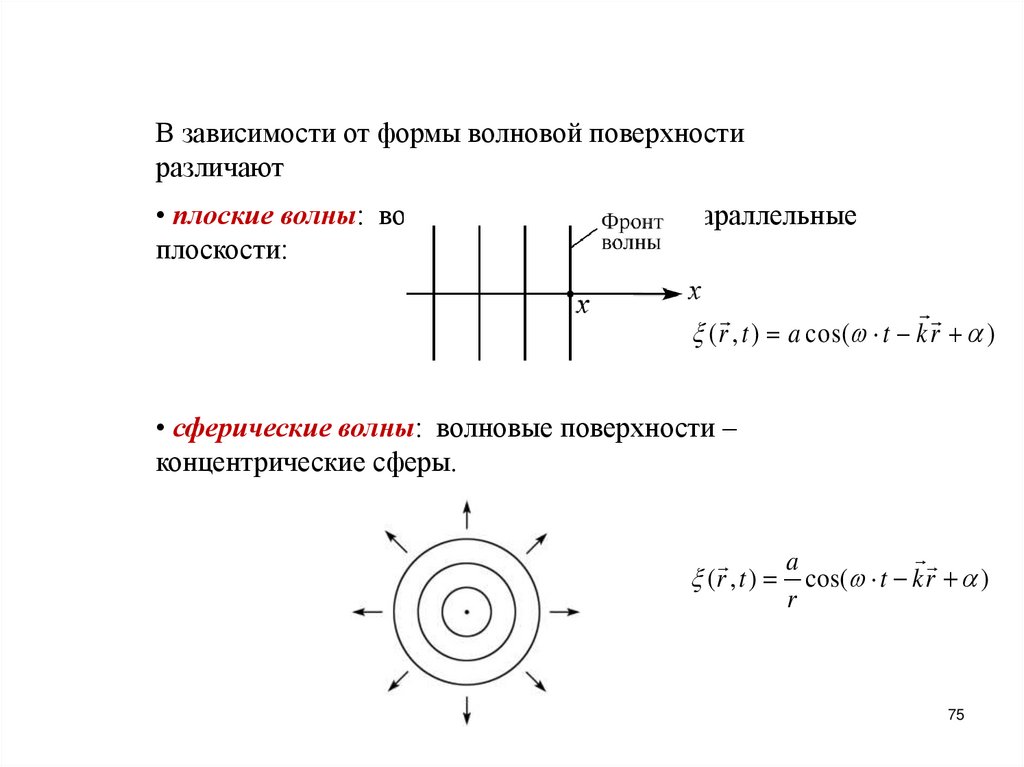




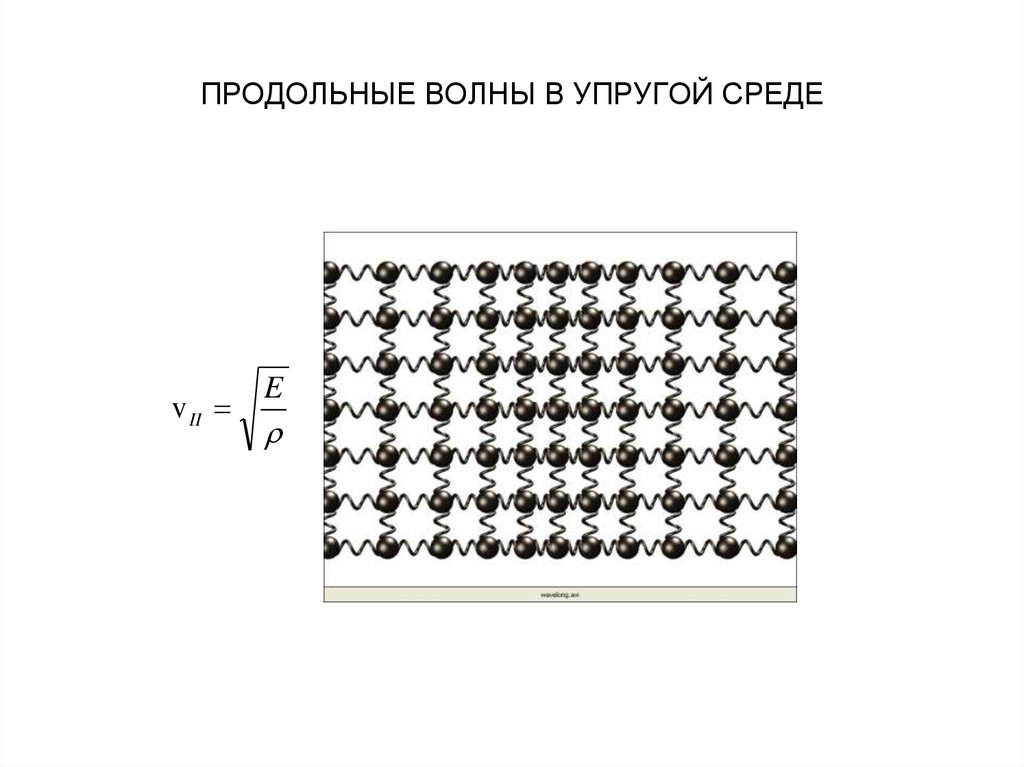




























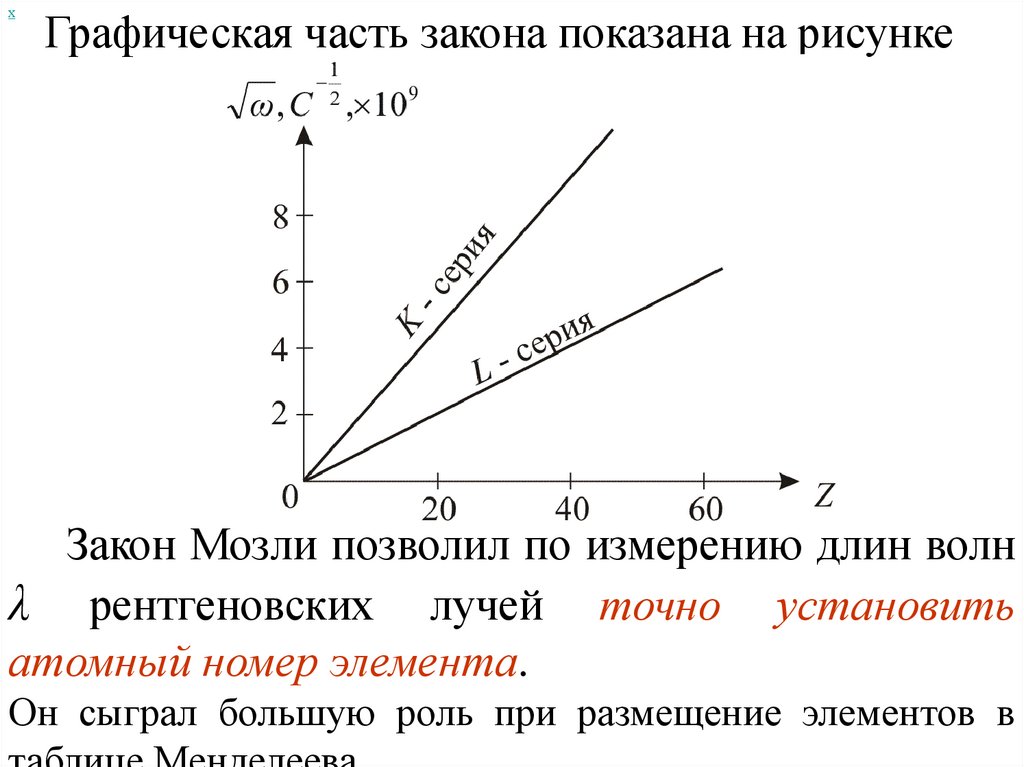

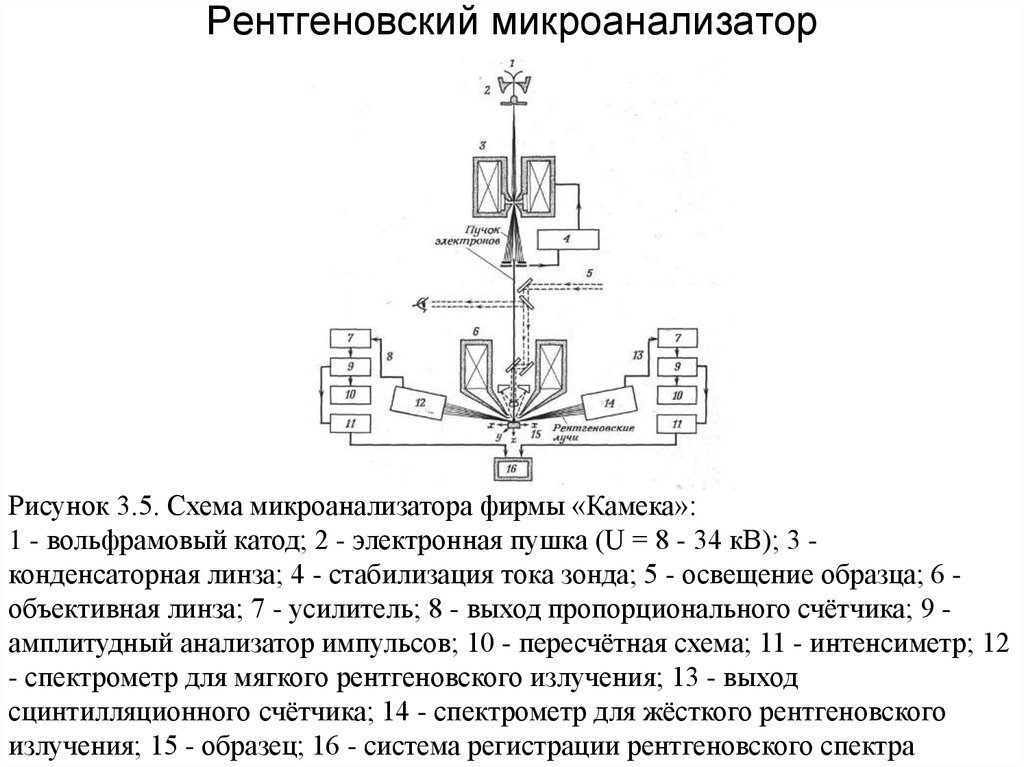
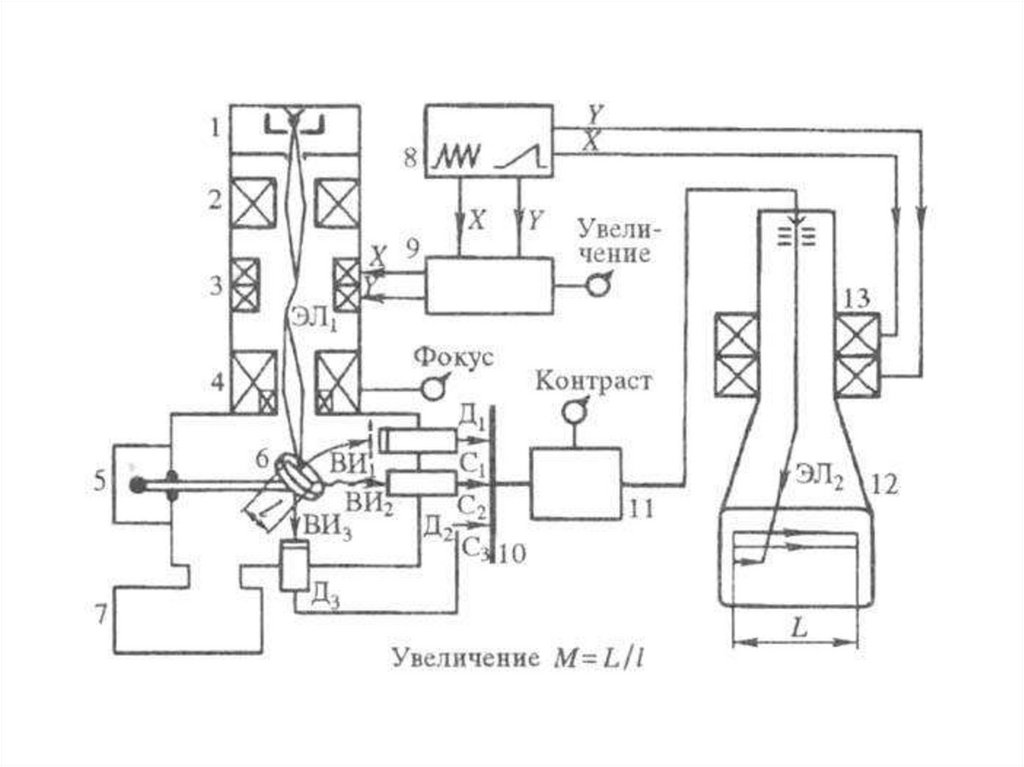
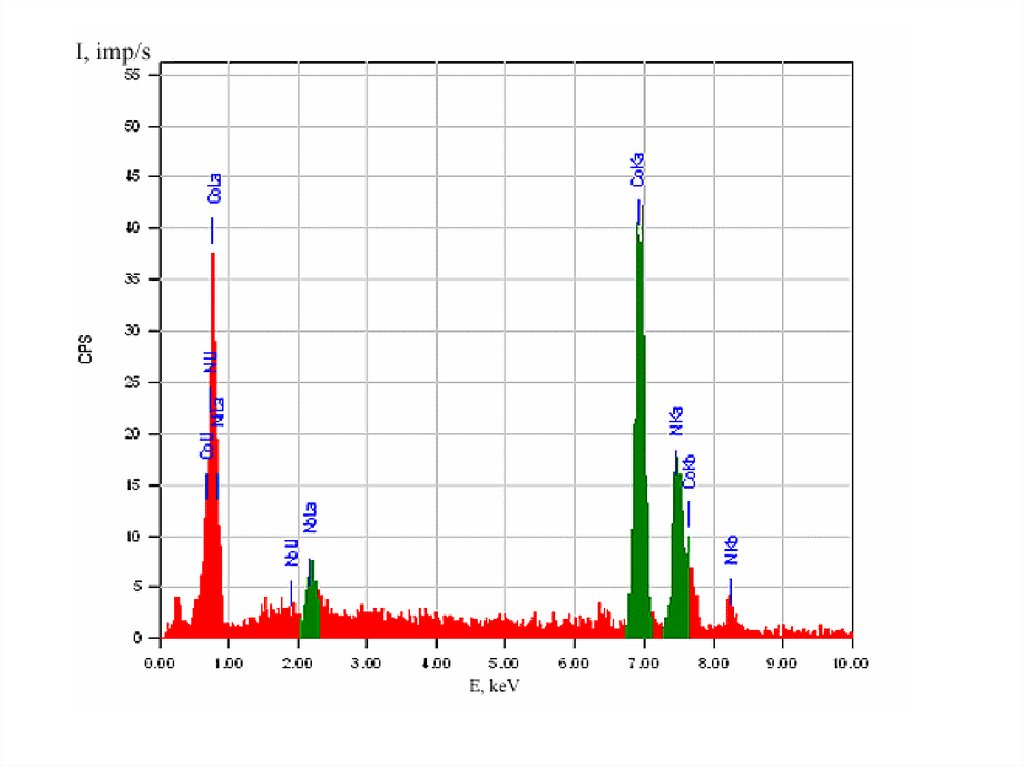






 Химия
Химия








