учебное пособие по 1 домашней работе

1.

Министерство науки и высшего образования Российской Федерации
Калужский филиал федерального государственного автономного
образовательного учреждения высшего образования
«Московский государственный технический университет имени Н.Э.
Баумана
(национальный исследовательский университет)»
(КФ МГТУ им. Н.Э. Баумана)
Е.А. Шестернина, О.В. Сулина, В.В. Сахаров
Домашняя работа «Плоская и пространственная фигура»
по дисциплине
«Начертательная геометрия»
учебное пособие
Калуга, 2025

2.

УДК 514.18
Рецензенты:
профессор кафедры «Колесные машины и прикладная механика»
КФ МГТУ им. Н.Э. Баумана, профессор, д.т.н., В.В. Булычев
главный конструктор ПАО «Калужский двигатель» 9г. Калуга) В.В. Рунько
Утверждено Методической комиссией КФ МГТУ им. Н.Э. Баумана
(протокол №__ от 03.06.2025 г. рег. номер 055/МК2025-03)
Сулина О.В., Шестернина Е.А., Сахаров В.В.
Домашняя работа «Плоская и пространственная фигура» по дисциплине
«Начертательная геометрия»: учебное пособие /О.В. Сулина, Е.А. Шестернина,
В.В. Сахаров.— Калуга: КФ МГТУ им. Н.Э. Баумана, 2025 .— 28с.
В учебном пособии приведены теоретические сведения и исходные
данные для выполнения домашней работы «Плоская и пространственная
фигура» по дисциплине «Начертательная геометрия», даны рекомендации по
выполнению, форма отчетности о выполненной работе, требования к
оформлению, рекомендуемые источники информации.
Учебное пособие предназначено для студентов всех направлений
подготовки и специальностей КФ МГТУ им. Н.Э. Баумана.
© КФ МГТУ им. Н.Э. Баумана, 2025
© Сулина О.В., Шестернина Е.А., Сахаров В.В., 2025
2

3.

ОГЛАВЛЕНИЕ
Введение .........................................................................................................................................
Теоретические сведения и характеристика исходных данных ..................................................
1. Определение длины отрезка прямой общего положения и углов наклона его
к плоскостям проекций .............................................................................................................
2. Теорема о частном случае проецирования прямого угла ..................................................
3. Взаимное положение прямых и плоскостей .......................................................................
4. Пересечение прямой с плоскостью ......................................................................................
5. Характеристика исходных данных ......................................................................................
Рекомендации по выполнению работы ....................................................................................
Форма отчетности о выполненной работе, требования к оформлению ...................................
Индивидуальные задания ..........................................................................................................
Контрольные вопросы и задания ..............................................................................................
Рекомендуемые источники информации .................................................................................
3

4.

ВВЕДЕНИЕ
Цель работы: изучить способы решения на чертеже различных задач,
позволяющих определять метрические характеристики геометрических фигур и
позиционные отношения между фигурами.
Задачи:
1. закрепить теоретический материал;
2. выполнить построение плоской или пространственной фигуры по
исходным данным методом прямоугольного проецирования с помощью
чертежных приборов и инструментов;
3. составить алгоритм решения задачи с применением математических
символов и выражений.
4. выполнить защиту домашней работы.
4

5.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И ХАРАКТЕРИСТИКА
ИСХОДНЫХ ДАННЫХ
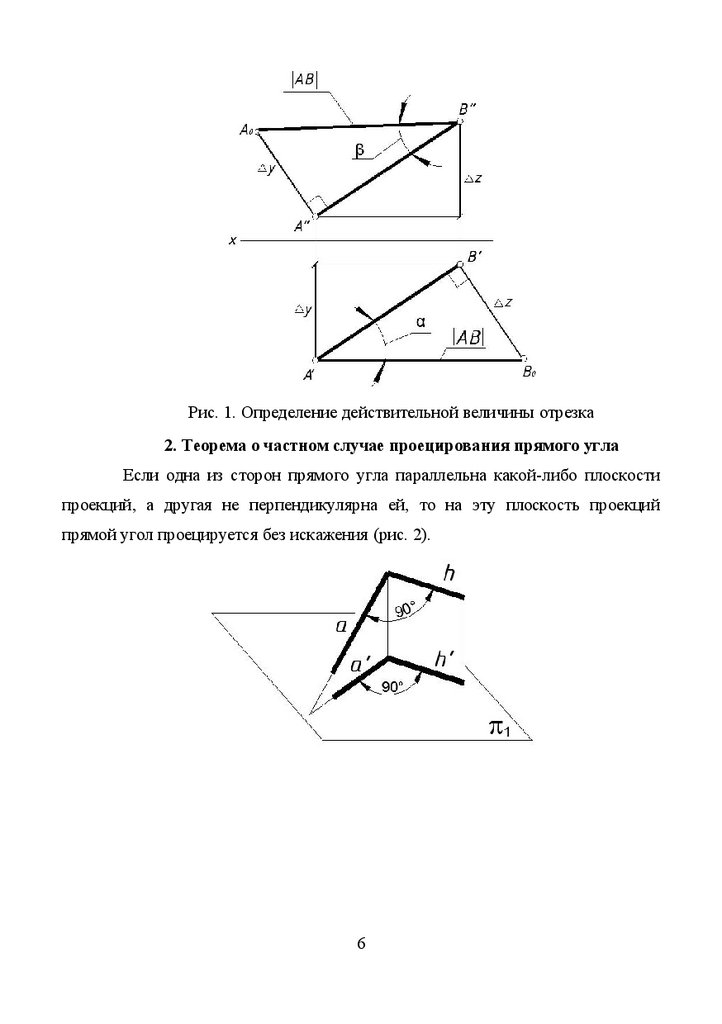
1. Определение длины отрезка прямой общего положения и углов
наклона его к плоскостям проекций
Для определения длины отрезка прямой общего положения и углов
наклона его к плоскостям проекций необходимо построить прямоугольный
треугольник, одним катетом которого является отрезок, равный по величине
горизонтальной (фронтальной) проекции отрезка, а вторым катетом — отрезок,
равный по величине алгебраической разности координат Z ( Y ) крайних точек
отрезка прямой. Гипотенуза построенного прямоугольного треугольника равна
по величине отрезку прямой (рис. 1).
Если при построении за один из катетов прямоугольного треугольника
взят отрезок, равный по величине горизонтальной проекции отрезка, то угол
между этим отрезком и гипотенузой прямоугольного треугольника определяет
величину угла
a
— угла наклона прямой к горизонтальной плоскости
проекций.
Если при построении за один из катетов прямоугольного треугольника
взят отрезок, равный по величине фронтальной проекции отрезка, то угол между
этим отрезком и гипотенузой прямоугольного треугольника определяет
величину угла b — угла наклона прямой к фронтальной плоскости проекций
(рис. 1).
5

6.

Рис. 1. Определение действительной величины отрезка
2. Теорема о частном случае проецирования прямого угла
Если одна из сторон прямого угла параллельна какой-либо плоскости
проекций, а другая не перпендикулярна ей, то на эту плоскость проекций
прямой угол проецируется без искажения (рис. 2).
6

7.

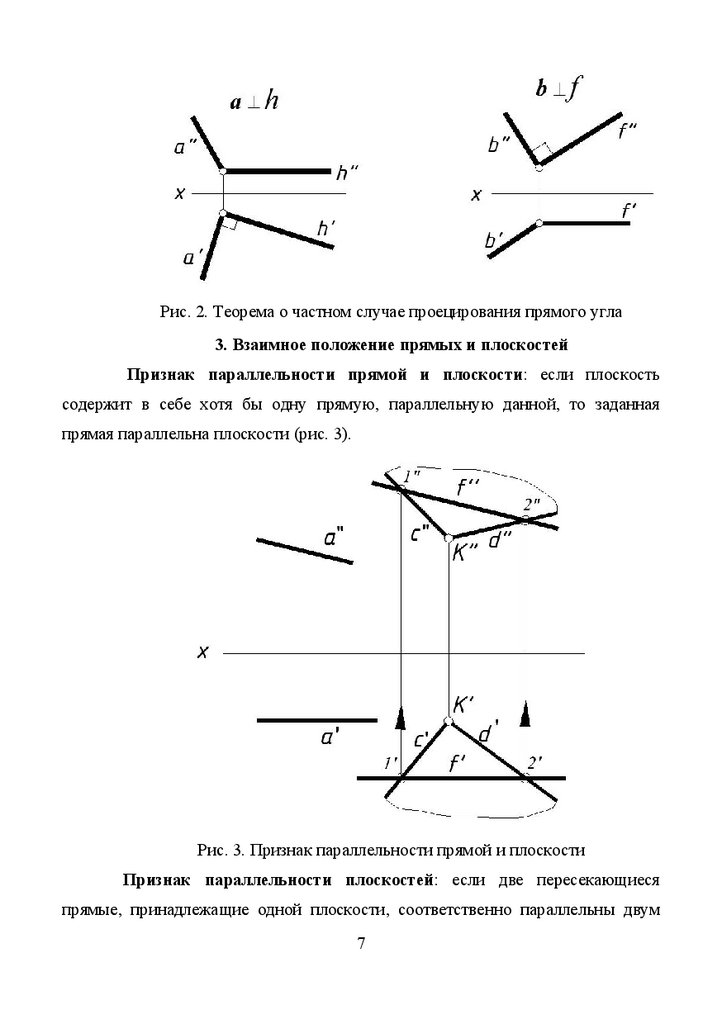
Рис. 2. Теорема о частном случае проецирования прямого угла
3. Взаимное положение прямых и плоскостей
Признак параллельности прямой и плоскости: если плоскость
содержит в себе хотя бы одну прямую, параллельную данной, то заданная
прямая параллельна плоскости (рис. 3).
Рис. 3. Признак параллельности прямой и плоскости
Признак параллельности плоскостей: если две пересекающиеся
прямые, принадлежащие одной плоскости, соответственно параллельны двум
7

8.

пересекающимся прямым, принадлежащим другой плоскости, то такие
плоскости параллельны. Если плоскости параллельны, то параллельны
одноименные проекции фронталей и горизонталей (рис. 4).
Рис. 4.
Признак
перпендикулярности
прямой
и
плоскости:
прямая
перпендикулярна плоскости, если она перпендикулярна двум пересекающимся
прямым, принадлежащим данной плоскости.
Если
горизонтальная
прямая
перпендикулярна
проекция
плоскости,
перпендикулярна
то
на
горизонтальной
чертеже
ее
проекции
произвольной горизонтали плоскости и горизонтальному следу плоскости, а
фронтальная проекция перпендикулярна фронтальной проекции произвольной
фронтали плоскости и фронтальному следу плоскости. Это правило вытекает из
теоремы о частном случае проецирования прямого угла. (рис. 5).
8

9.

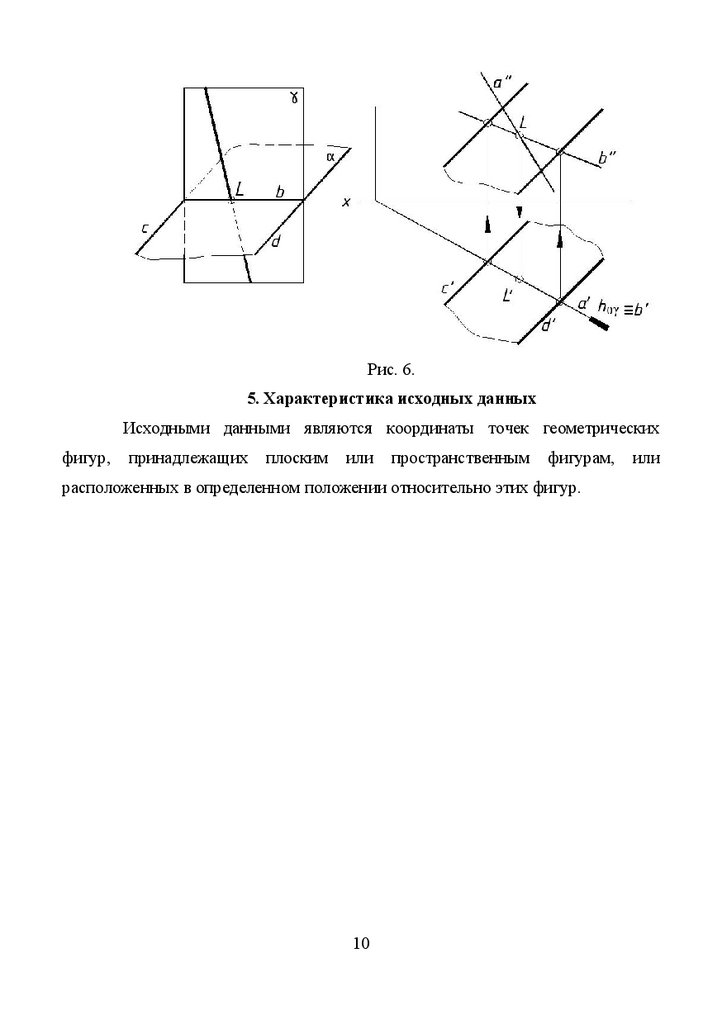
Рис. 5.
4. Пересечение прямой с плоскостью
Определение
точки
пересечение
прямой
общего
положения
с
плоскостью общего положения решается с помощью универсального алгоритма
(рис. 6):
1. заключают
прямую
(прямая
a
)
во
вспомогательную
проецирующую плоскость. На рисунке 6 - это горизонтально проецирующая
плоскость g ;
2. находят пересечение этой вспомогательной плоскости с заданной
(прямая b );
3.
на пересечении полученной прямой с заданной находят искомую
точку L .
9

10.

Рис. 6.
5. Характеристика исходных данных
Исходными данными являются координаты точек геометрических
фигур,
принадлежащих
плоским
или
пространственным
фигурам,
расположенных в определенном положении относительно этих фигур.
10
или

11.

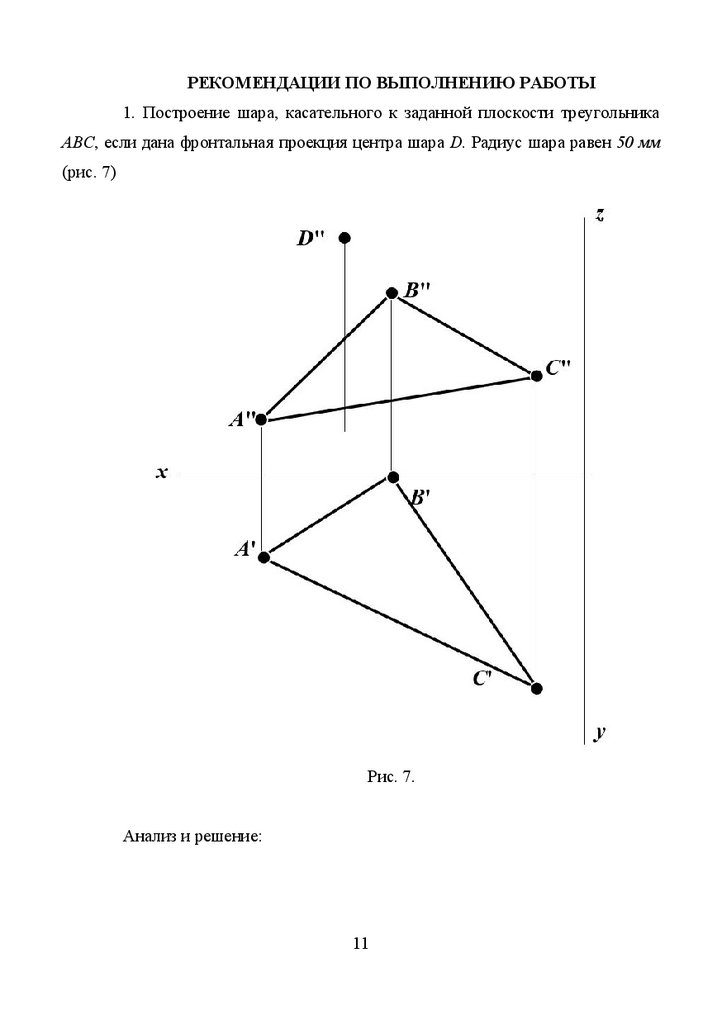
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ РАБОТЫ
1. Построение шара, касательного к заданной плоскости треугольника
AВС, если дана фронтальная проекция центра шара D. Радиус шара равен 50 мм
(рис. 7)
Рис. 7.
Анализ и решение:
11

12.

Задача практически сводится к построению плоскости, параллельной
плоскости АВС, удалённой от неё на расстояние 50 мм. В построенной
плоскости будет находиться центр шара.
1. Построение плоскости, параллельной плоскости АВС на требуемом
расстоянии от неё (рис. 8):
а) Построить в плоскости треугольника ABC горизонталь и фронталь (h
и f).
б) Из любой вершины треугольника АВС, например, А построить
прямую п, перпендикулярную плоскости АВС : n' h' n" h".
в) На проекциях прямой п найти точку А1, удалённую от точки А на 50
мм. Для этого: на прямой n'(n") взять произвольную точку K'(K") и найти
действительную величину отрезка AK. На полученном луче действительных
величин отложить от точки A' 50мм, получить точку А1. Найти проекции точки
А1 ', опустив из точки А1 перпендикуляр на проекцию прямой n'.
г) Через проекции точки А1 с помощью двух пересекающихся прямых
a'(a") и b'(b") задать плоскость, параллельную плоскости треугольника АВС.
2. Центр шара D будет принадлежать построенной плоскости, т.к. R
50мм и шар касателен к плоскости треугольника АВС
Если точка принадлежит прямой, то проекция точки принадлежит
проекции этой прямой. Если прямая принадлежит плоскости, то проекция
прямой принадлежит проекции плоскости.
а) Через D" провести фронтальную проекцию произвольной прямой
M"N", принадлежащую плоскости пересекающихся прямых а и b. С помощью
точек M и N построить горизонтальную проекцию прямой, на которой найти
проекцию искомой точки D'.
б) Имея две проекции центра шара, с помощью циркуля построить
проекции шара R 50мм. (на примере шар не показан).
12

13.

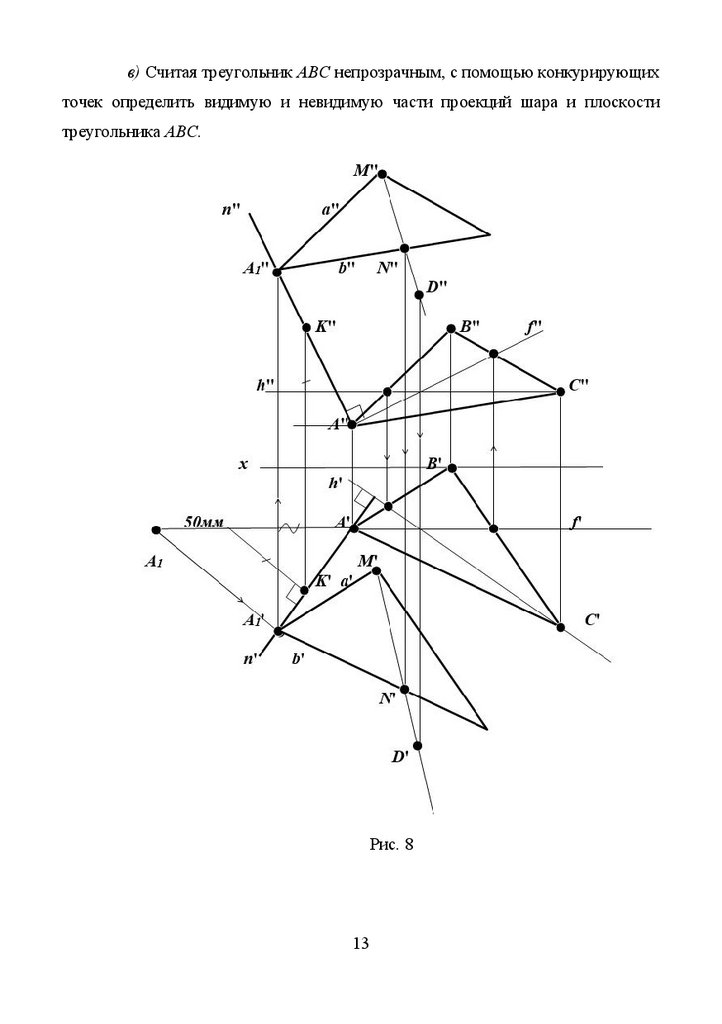
в) Считая треугольник АВС непрозрачным, с помощью конкурирующих
точек определить видимую и невидимую части проекций шара и плоскости
треугольника ABC.
Рис. 8
13

14.

2. Построение проекций прямой призмы, высота которой равна 70 мм,
исходя из условия, что её основание—равнобедренный треугольник АВС с
вершиной А, лежащей на прямой ЕF (рис. 9).
Рис. 9.
Анализ и решение:
1. Построение основания призмы - треугольника АВС (рис. 10).
Недостающая вершина А равноудалена от концов отрезка BC, т.к.
треугольник АВС—равнобедренный, таким образом, точка А находится в
плоскости, перпендикулярной отрезку BС и проходящей через середину отрезка
BC. С другой стороны, точка А по условию, принадлежит прямой EF. Точка,
удовлетворяющая этим двум условиям, находится на пересечении прямой EF с
этой плоскостью.
а) Построить плоскость a, перпендикулярную BC и проходящую через
середину BC. На эпюре Монжа эта плоскость задаётся проекциями двух
14

15.

пересекающихся прямых: фронталь f'(f") и горизонталь h'(h"), которые проходят
через середины проекций отрезка ВС. Причём, h' B'C' , f" B"C".
б) Найти точку пересечения построенной плоскости a с прямой EF. Для
этого: заключить EF в проецирующую плоскость (на примере горизонтальнопроецирующая плоскость ) ; найти линию пересечения 12 проецирующей
плоскости с данной плоскостью a; пересечение фронтальных проекций прямых
1"2" и E"F" является фронтальной проекцией искомой проекции точки А"; на
горизонтальной проекции А' принадлежит прямой E'F'.
в) Соединить отрезками найденную вершину А (A'A") c точками B(B'B")
и C(C'C"), получить проекции основания прямой призмы.
2. Построение основания призмы A1B1C1.
Призма
прямая,
следовательно,
боковые
рёбра
перпендикуляры
основанию призмы, а сами основания призмы лежат в параллельных плоскостях.
а) Из любой вершины основания АВС, например, B построить прямую п,
перпендикулярную к плоскости основания, для этого в проекциях плоскости
треугольника АВС провести фронталь f1(f1' f1") и горизонталь h1 (h1'h1"): n' h1'
n" f1" .
б) Длина ребра составляет 70 мм, следовательно, необходимо на
проекциях прямой п найти точку B1, удалённую от точки B на 70 мм. Для этого:
на прямой n'(n") взять произвольную точку K'(K") и найти действительную
величину отрезка BK. На полученном луче действительных величин (B"K0)
отложить от точки B" 70 мм, получить точку B1. Найти проекции точки B1",
опустив из точки B1 перпендикуляр на проекцию прямой n".
в) Все рёбра призмы имеют равную длину и параллельны, поэтому и их
проекции будут иметь равную длину и будут параллельны между собой.
A'A1'//C'C1'//B'B1',
/A'A1'/= /C'C1'/= /B'B1'/
A"A1//C"C1"//B"B1", /A"A1"/= /C"C1"/= /B"B1"/
г) Соединить проекции точек А1В1С1/
15

16.

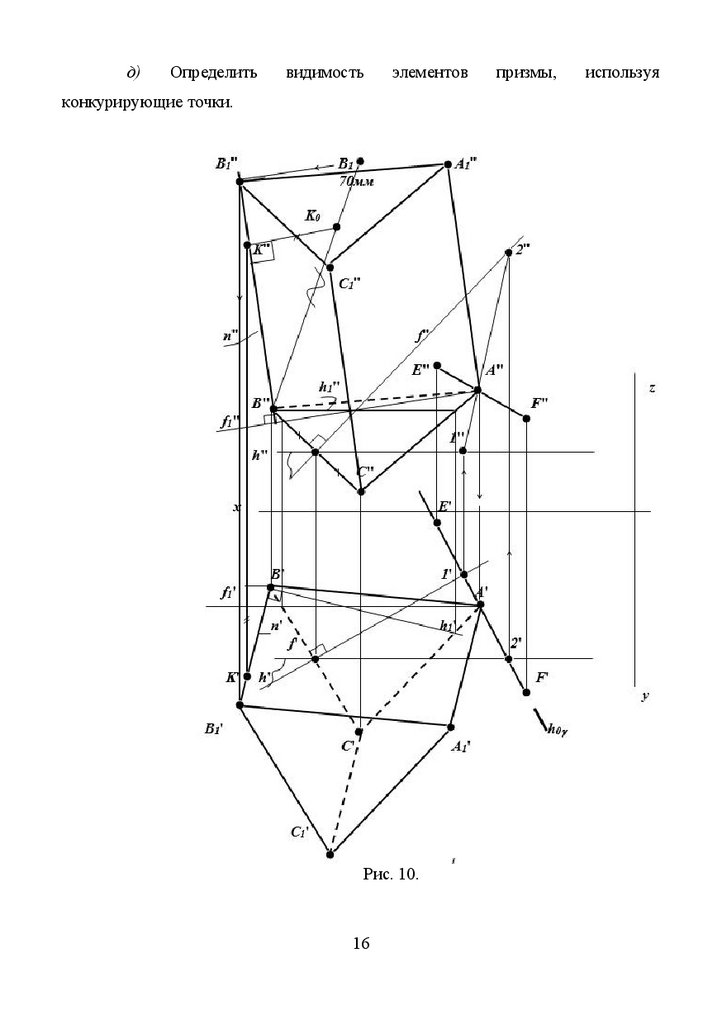
д)
Определить
видимость
элементов
конкурирующие точки.
Рис. 10.
16
призмы,
используя

17.

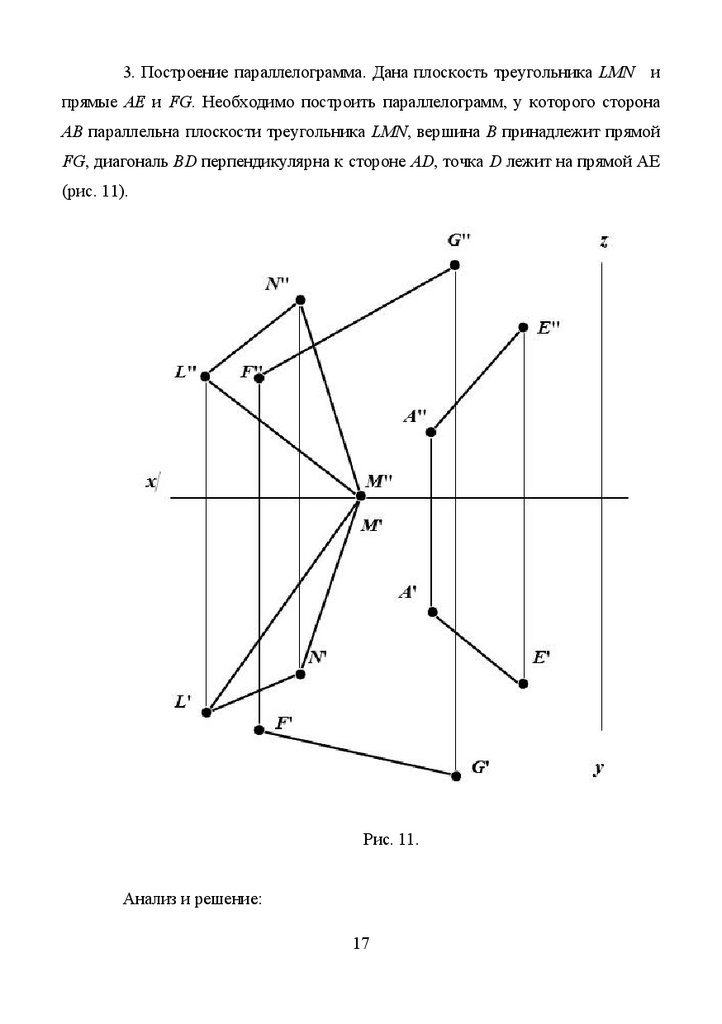
3. Построение параллелограмма. Дана плоскость треугольника LMN
и
прямые АЕ и FG. Необходимо построить параллелограмм, у которого сторона
AB параллельна плоскости треугольника LMN, вершина В принадлежит прямой
FG, диагональ BD перпендикулярна к стороне AD, точка D лежит на прямой АЕ
(рис. 11).
Рис. 11.
Анализ и решение:
17

18.

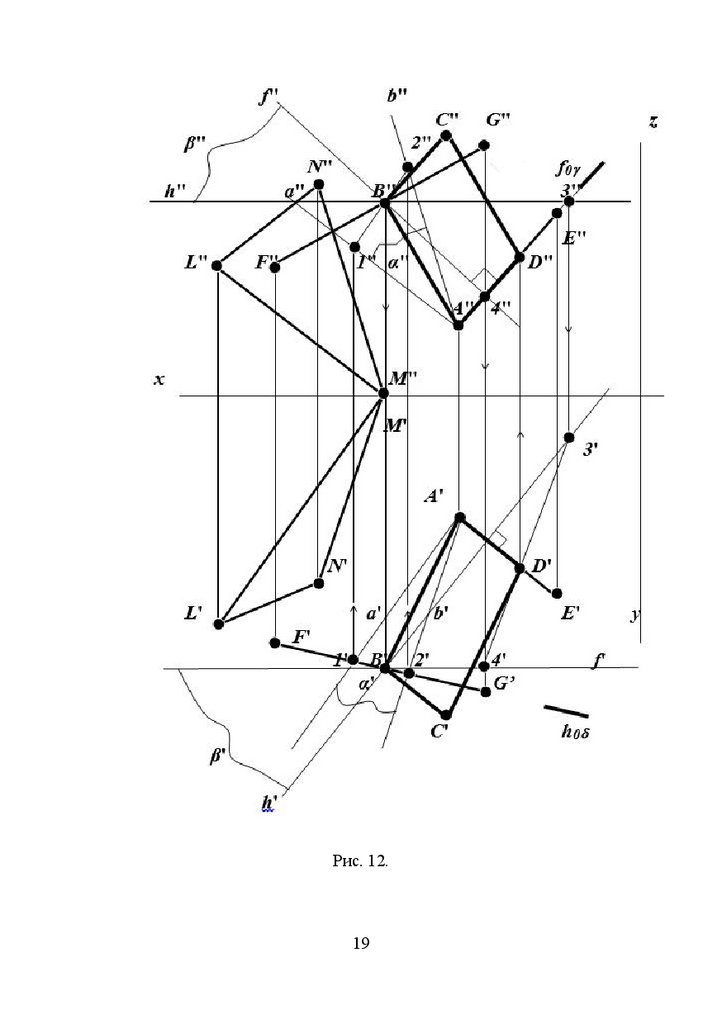
1. Находим проекции вершины В (рис. 12). Для этого:
Сторона
AB
параллелограмма
параллельна
плоскости
LMN,
следовательно, вершина В будет лежать в плоскости a , параллельной LMN ,
проведённой через вершину А . В принадлежит прямой FG. Искомая точка В,
таким образом, находится на пересечении FG с плоскостью a.
а) Через проекции точки А(А'A") провести проекции прямых а(а'a") и
b(b'b"), соответственно параллельно проекциям отрезков ML и MN, плоскость a
будет задана прямыми a и b.
б) Найти точку пересечения прямой FG с плоскостью a . Для этого:
заключить FG в проецирующую плоскость (на примере горизонтальнопроецирующая плоскость ). Найти линию пересечения 12 проецирующей
плоскости с плоскостью a, найти проекции искомой точки В(B'B"):
B''=1''2'' F''G'' B'.
2. Найти проекции вершины D.
По условию точка D AE и BD AD или BD AE.
а) Через точку В задать плоскость b
AE (с помощью двух
пересекающихся прямых h и f : h' A'E' и f" A"E".
б) Найти точку пересечения AE с плоскостью b . Для этого, заключить
AE в проецирующую плоскость (на примере фронтально-проецирующая
плоскость ) . Найти линию 34 пересечения
проецирующей плоскости с
плоскостью b ; пересечение горизонтальной проекций прямых
3'4' и A'E'
является горизонтальной проекцией D'искомой точки D; найти D".
3. Противоположные стороны параллелограмма параллельны и равны,
следовательно, и проекции также будут равны и параллельны между собой.
Таким образом, имея проекции трёх вершины параллелограмма, необходимо
достроить его.
18

19.

Рис. 12.
19

20.

ФОРМА ОТЧЕТНОСТИ О ВЫПОЛНЕННОЙ РАБОТЕ,
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ
Министерство науки и высшего образования Российской
Федерации
Калужский филиал
федерального государственного автономного
образовательного учреждения высшего образования
«Московский государственный технический университет
имени Н.Э. Баумана (национальный исследовательский
университет)»
(КФ МГТУ им. Н.Э. Баумана)
ФАКУЛЬТЕТ _МК «Машиностроительный»____________________
КАФЕДРА __МК4 «Инженерная графика»__________
ДОМАШНЯЯ РАБОТА
«Плоская и пространственная фигура»
ДИСЦИПЛИНА: «Начертательная геометрия»
Выполнил: студент гр. _________
_________________
(_____________________)
(Подпись)
(Ф.И.О.)
Проверил:
_________________
(_____________________)
(Подпись)
(Ф.И.О.)
Дата сдачи (защиты):
Результаты сдачи (защиты):
- Балльная оценка:
- Оценка:
Калуга , 2025
20

21.

Цель: формирование практических навыков представления в графическом виде
плоских и пространственных геометрических фигур и поверхностей деталей
машин и механизмов
Задачи: выполнить анализ исходных данных, разработать алгоритм решения
задач, построить проекции плоской и пространственной фигуры.
Выводы:
Литература:
Построение плоской или пространственной фигуры осуществляется на формате
А3 ватман. Оформление выполняется в соответствии с ЕСКД. Построения
осуществлять простым карандашом. Проекции фигуры допускается обвести
цветным
карандашом.
Толщина
и
тип
линий
построения
должны
соответствовать ЕСКД. Обозначения в работе выполняются шрифтом № 7 типа
Б с наклоном.
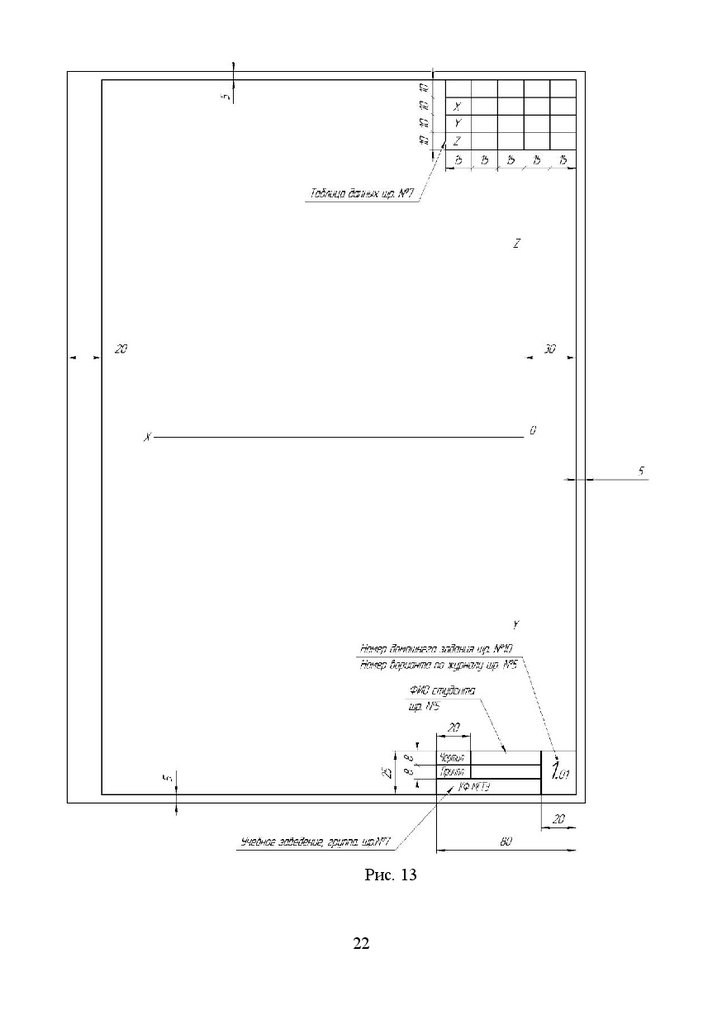
На чертеж наносят рамку чертежа и строят упрощенную
основную надпись (рис. 13).
21

22.

Рис. 13
22

23.

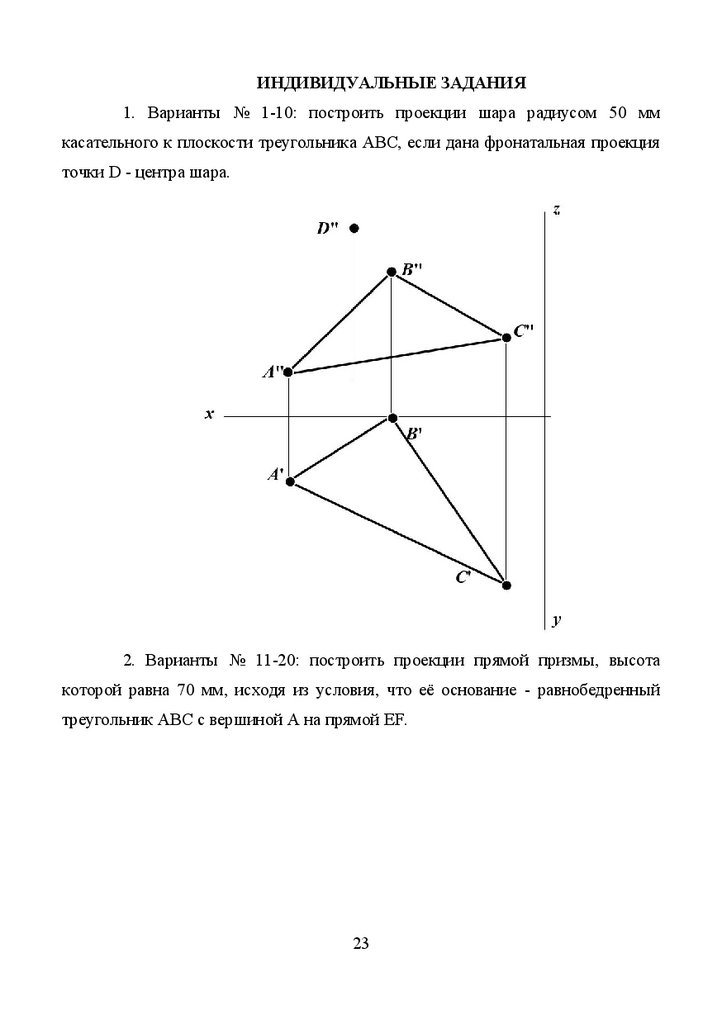
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
1. Варианты № 1-10: построить проекции шара радиусом 50 мм
касательного к плоскости треугольника ABC, если дана фронатальная проекция
точки D - центра шара.
2. Варианты № 11-20: построить проекции прямой призмы, высота
которой равна 70 мм, исходя из условия, что её основание - равнобедренный
треугольник ABC с вершиной A на прямой EF.
23

24.

3. Варианты № 21-30: даны: плоскость треугольника LMN и прямые AE
и FG. Построить параллелограмм, у которого сторона AD лежит на прямой AE,
сторона AB параллельна плоскости треугольника, вершина B принадлежит
прямой FG, диагональ BD перпендикулярна к стороне AD.
24

25.

25

26.

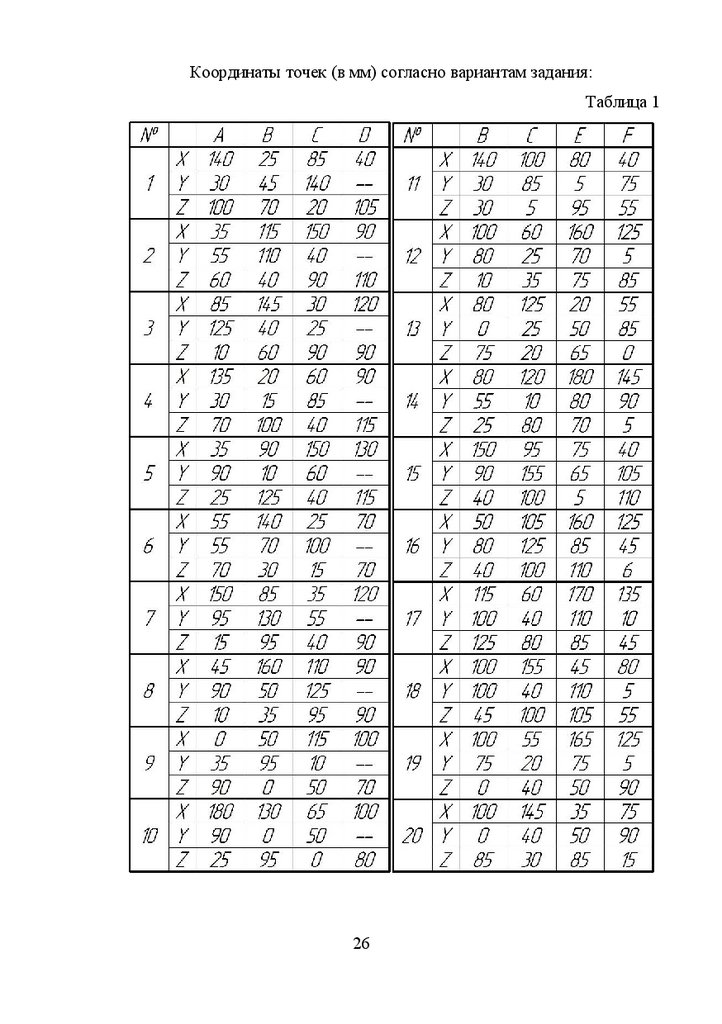
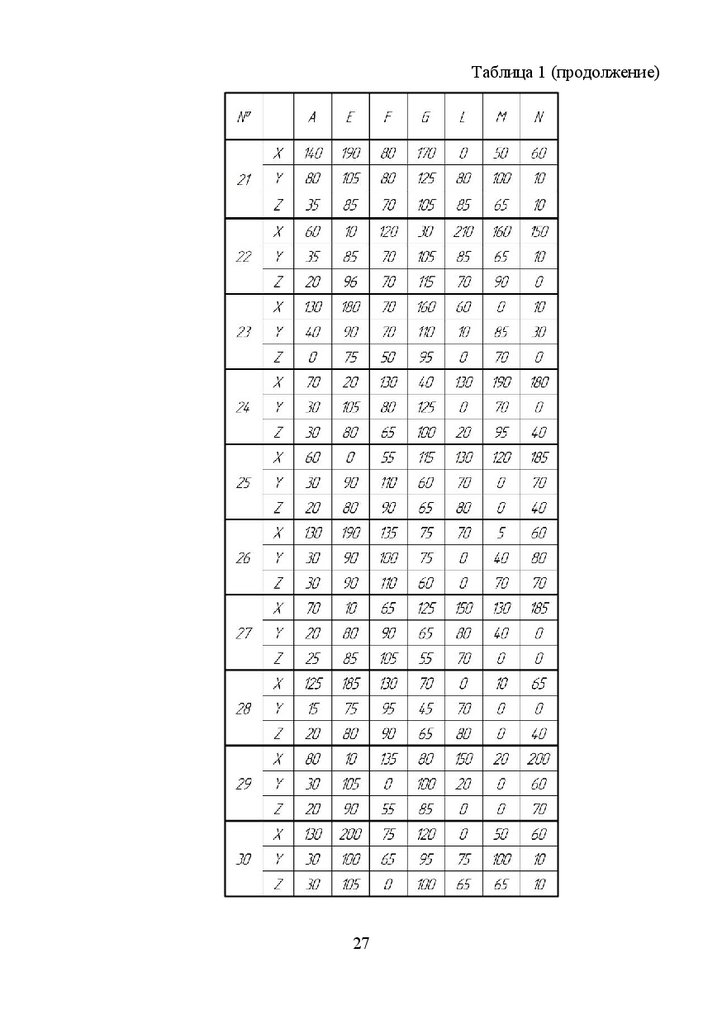
Координаты точек (в мм) согласно вариантам задания:
Таблица 1
26

27.

Таблица 1 (продолжение)
27

28.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1.
Опишите алгоритм нахождения действительной величины отрезка
прямой общего положения. Когда отрезок проецируется в натуральную
величину?
2.
Опишите алгоритм определения положения отрезка в пространстве.
3.
Дайте определение терминам «Прямая частного положения», «Прямая
общего положения», приведите примеры из домашней работы прямых
общего и частного положения.
4.
Опишите алгоритм определения следов прямой общего положения на
эпюре.
5.
У
какой
прямой
нет
фронтального
следа?
Горизонтального?
Профильного?
6.
Приведите варианты взаимного положения прямых в пространстве.
Укажите взаимное положение прямых в домашней работе.
7.
Какие инвариантные свойства ортогонального проецирования вы
использовали при решении задачи в домашней работе?
8.
Сформулируйте теорему о частном случае проецирования плоского
прямого угла.
9.
Перечислите способы задания плоскости на эпюре. Приведите примеры
из домашней работы.
10. Дайте определение термину «Плоскость частного положения».
28

29.

РЕКОМЕНДУЕМЫЕ ИСТОЧНИКИ ИНФОРМАЦИИ
1.
Сулина О. В., Сломинская Е. Н. Начертательная геометрия: курс
лекций : учебное пособие / Сулина О. В., Сломинская Е. Н. - Калуга :
Издательство Манускрипт, 2025. - 72 с. - ISBN 978-5-94627-257-5.
2.
Жирных Б. Г., Новоселова Л. В. Начертательная геометрия. Рабочая
тетрадь для использования на лекционных занятиях / Жирных Б. Г., Новоселова
Л. В. - М. : Изд-во МГТУ им. Н. Э. Баумана, 2024. - [44] с. - ISBN 978-5-70386338-1.
3.
Жирных Б. Г., Новоселова Л. В. Начертательная геометрия. Рабочая
тетрадь для семинарских занятий / Жирных Б. Г., Новоселова Л. В. - М. : Изд-во
МГТУ им. Н. Э. Баумана, 2024. - [36] с. - ISBN 978-5-7038-6337-4.
4.
Новожилов Ю. Н. Начертательная геометрия : учебное пособие /
Новожилов Ю. Н. ; МГТУ им. Н. Э. Баумана (Национальный исследовательский
университет). - М. : Изд-во МГТУ им. Н. Э. Баумана, 2024. - 93 с. : ил. Библиогр.: с. 91. - ISBN 978-5-7038-6219-3.
29