АиСД_Лекция 2

1.

Алгоритмы и структуры данных
Преподаватель:
Ряскова Елена Борисовна
Кафедра АПУ СПбГЭТУ «ЛЭТИ»
1

2.

Тема 2. Классификация структур данных в
С++. Линейные структуры данных.
Нелинейные структуры данных.
2

3.

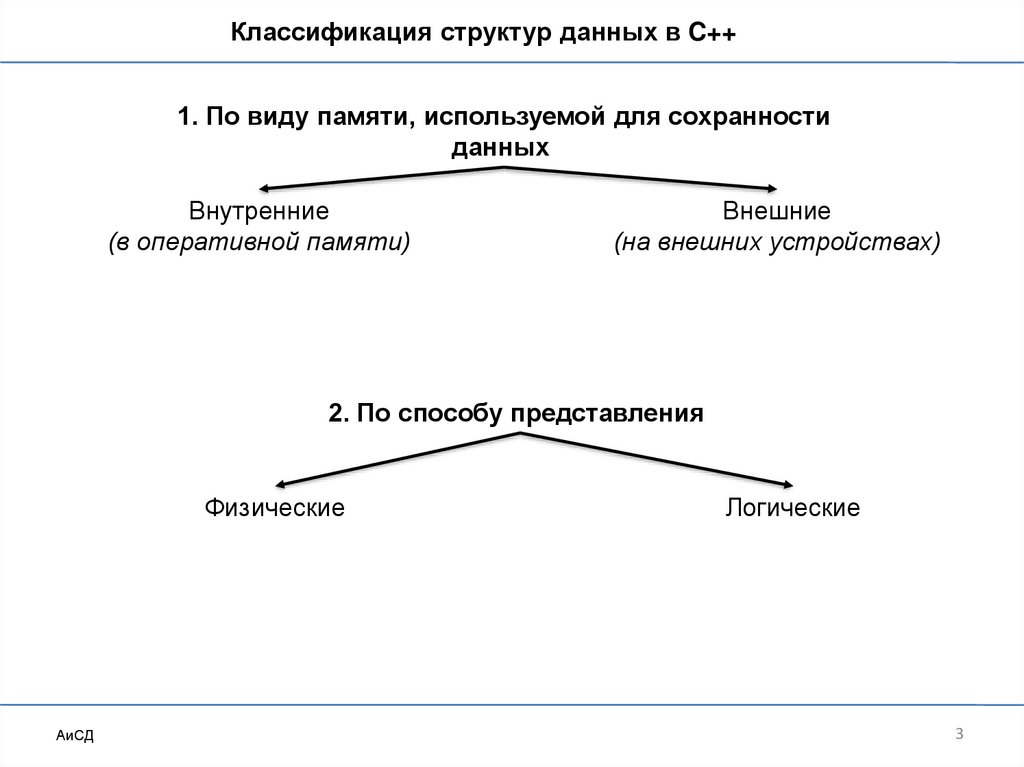
Классификация структур данных в C++
1. По виду памяти, используемой для сохранности
данных
Внутренние
(в оперативной памяти)
Внешние
(на внешних устройствах)
2. По способу представления
Физические
АиСД
Логические
3

4.

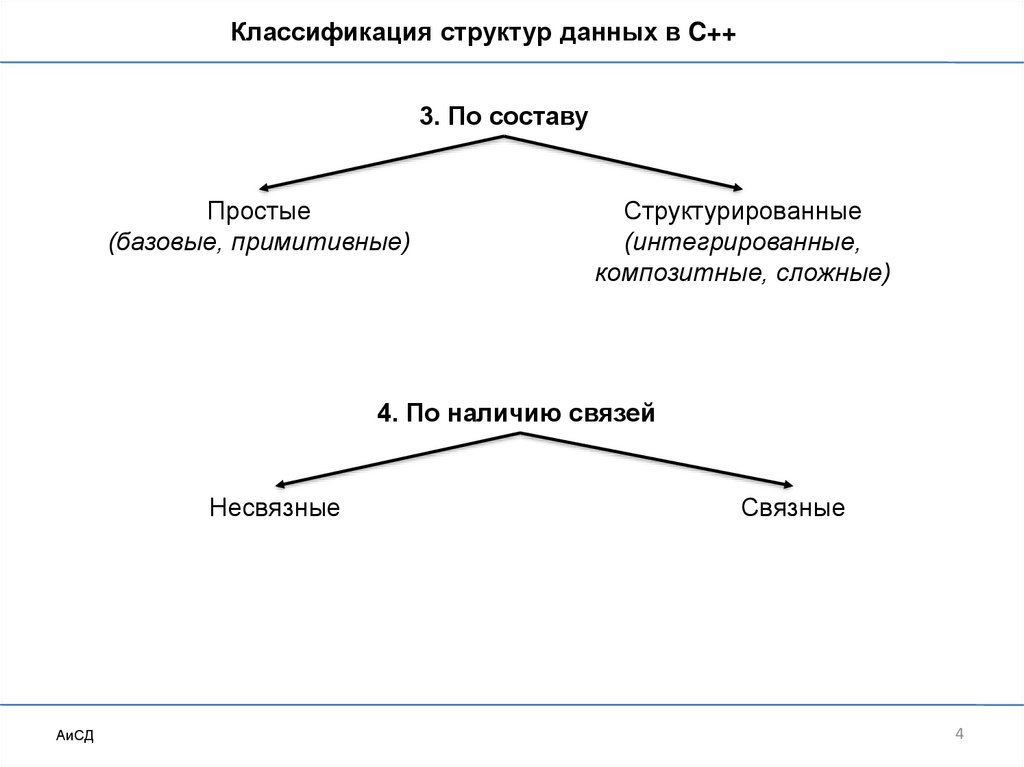
Классификация структур данных в C++
3. По составу
Простые
(базовые, примитивные)
Структурированные
(интегрированные,
композитные, сложные)
4. По наличию связей
Несвязные
АиСД
Связные
4

5.

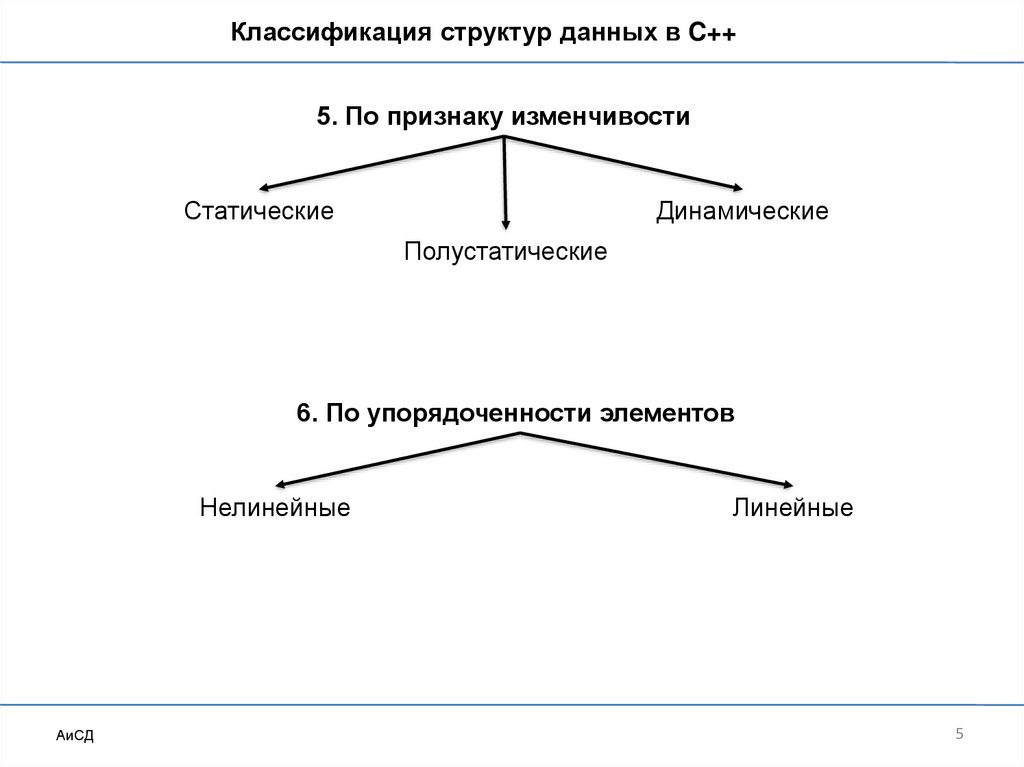
Классификация структур данных в C++
5. По признаку изменчивости
Статические
Динамические
Полустатические
6. По упорядоченности элементов
Нелинейные
АиСД
Линейные
5

6.

Линейные структуры данных
6

7.

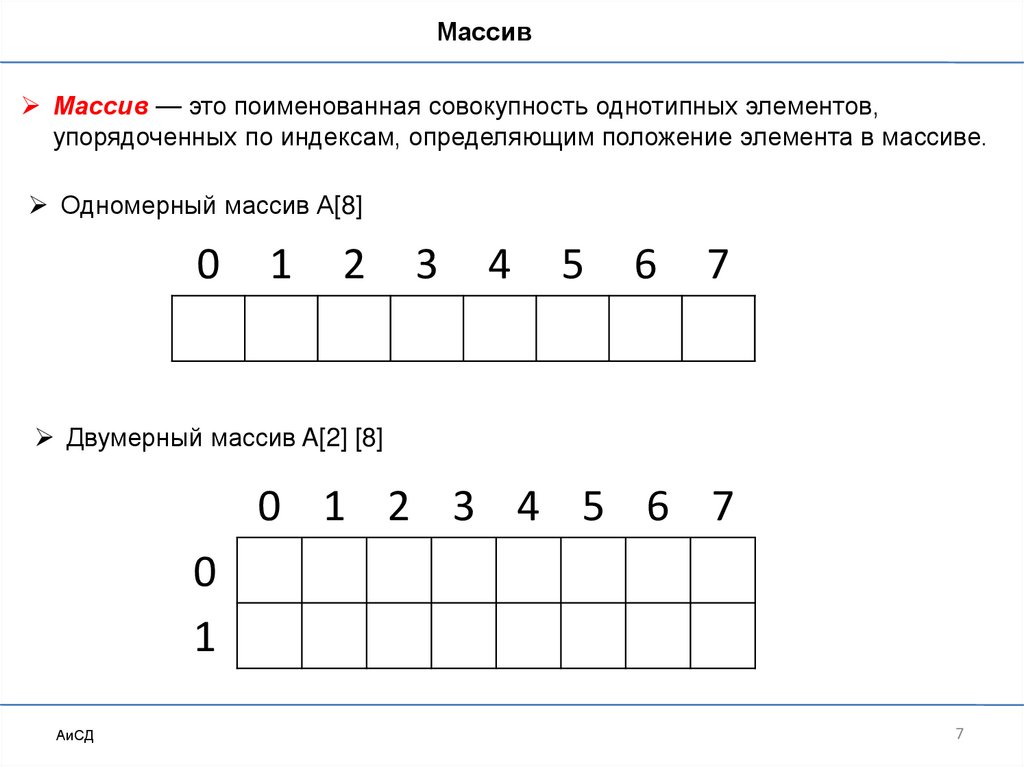
Массив
Массив — это поименованная совокупность однотипных элементов,
упорядоченных по индексам, определяющим положение элемента в массиве.
Одномерный массив А[8]
0
1
2
3
4
5
6
7
Двумерный массив A[2] [8]
0 1 2 3 4 5 6 7
0
1
АиСД
7

8.

Массив. Описание в C++
Объявление одномерного массива: T a[N],
где Т – тип элементов массива, а - название массива, а N – размерность
(количество элементов в массиве).
Пример 1:
int x[10]; //Описание массива из 10 целых чисел.
float a[20]; //Описание массива из 20 вещественных чисел.
Пример 2:
const int n=15; //Определена целая положительная константа.
double B[n]; //Описан массив из 15 вещественных чисел.
Пример 3:
int x[ ]={1, 2, 3, 4}; //размерность массива - 4
N=8
АиСД
0
1
2
3
4
5
6
7
8

9.

Массив. Операции в C++
Обращения к элементу массива:
имя_массива [индекс];
const int n=15;
double C[n], S;
S=C[0]+C[n-1]; //Сумма первого и последнего элементов массива С.
Инициализация массива:
тип имя_пременной [размерность] = {элемент 0, элемент_1, …};
float a[6] = { 1.2, 3.4, 5.6, 6.1 }; //Формируется массив из шести
вещественных чисел, значения элементам присваиваются по
порядку. Элементы, значения которых не указаны (в данном случае
a[4], a[5]), обнуляются.
С элементами объявленного массива можно выполнять все действия,
допустимые для обычных переменных этого типа
Массив является статической структурой данных, то есть не поддерживает
операции добавления и удаления элементов.
АиСД
9

10.

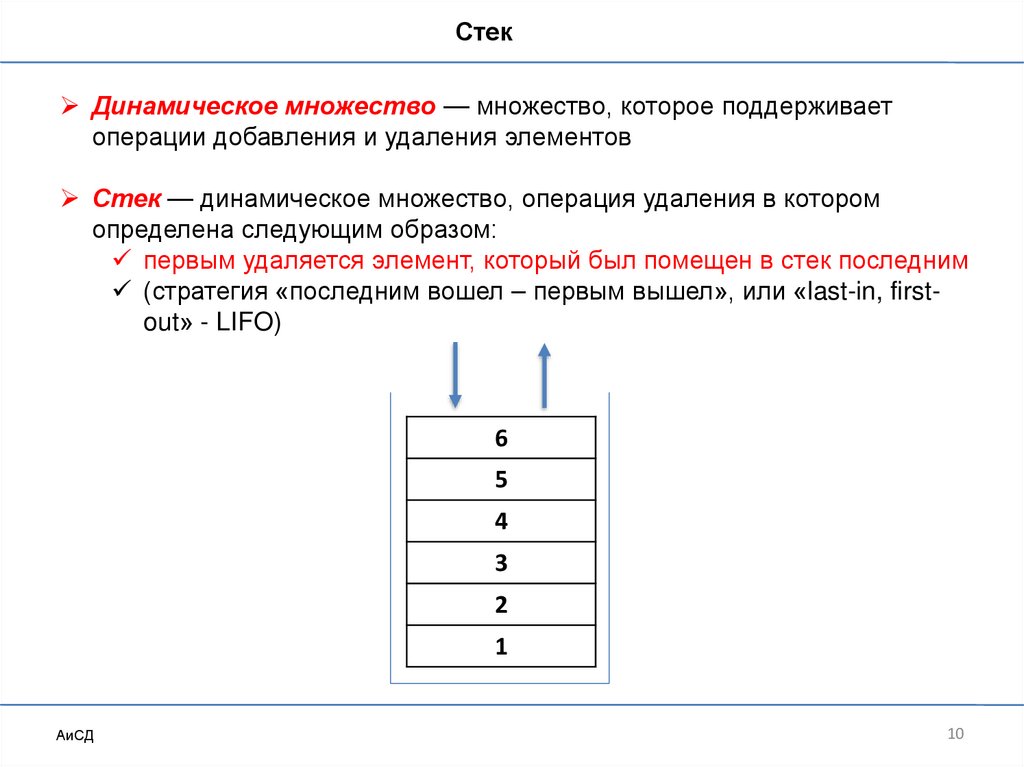
Стек
Динамическое множество — множество, которое поддерживает
операции добавления и удаления элементов
Стек — динамическое множество, операция удаления в котором
определена следующим образом:
первым удаляется элемент, который был помещен в стек последним
(стратегия «последним вошел – первым вышел», или «last-in, firstout» - LIFO)
6
5
4
3
2
1
АиСД
10

11.

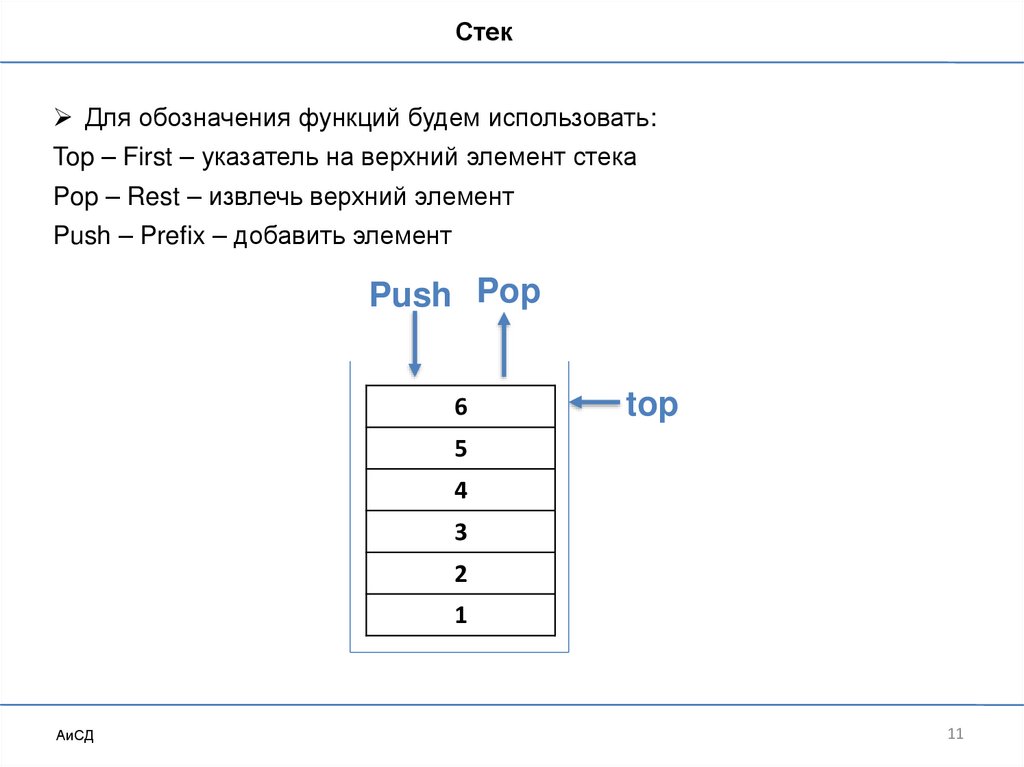
Стек
Для обозначения функций будем использовать:
Top – First – указатель на верхний элемент стека
Pop – Rest – извлечь верхний элемент
Push – Prefix – добавить элемент
Push Pop
6
top
5
4
3
2
1
АиСД
11

12.

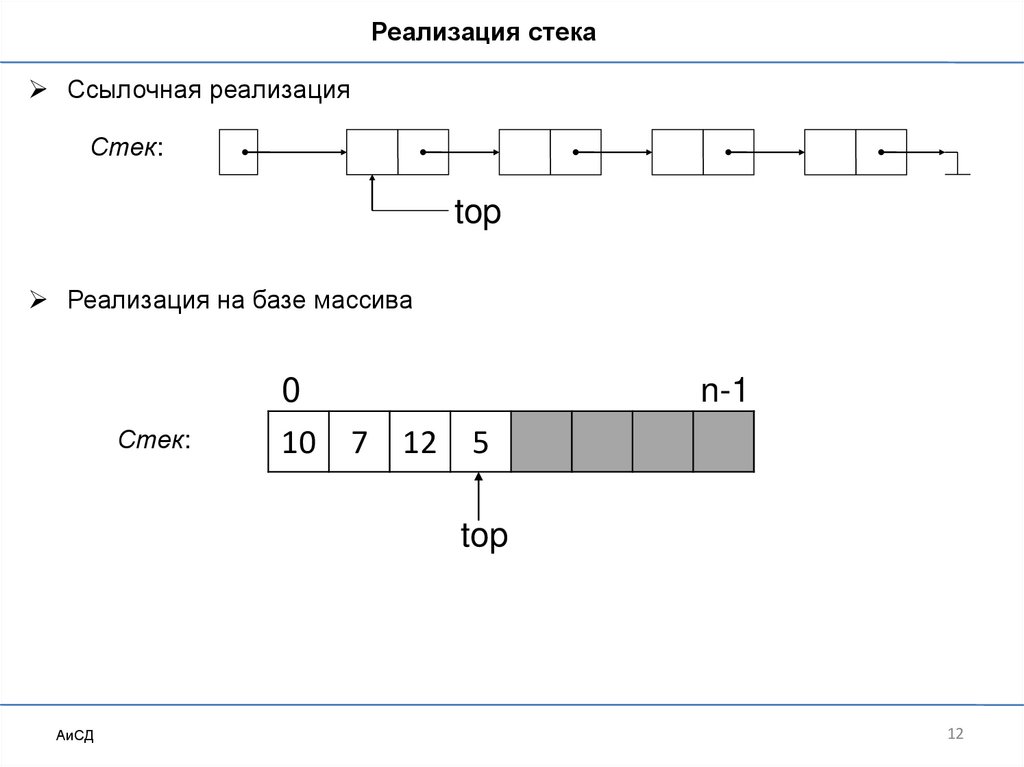
Реализация стека
Ссылочная реализация
Стек:
top
Реализация на базе массива
0
Стек:
10
n-1
7
12
5
top
АиСД
12

13.

Оценка времени работы алгоритма
При создании пустого стека переменную top инициализируем значением, которое
не может принимать индекс массива - «-1»
Is_Empty(S) – проверка стека S на пустоту.
Is_Empty(S)
1: if top[S] = -1 then
2: return TRUE
3: else
4: return FALSE
Время работы операции Is_Empty(S) – O(1)
АиСД
13

14.

Оценка времени работы алгоритма
Push(S,x) – добавить элемент
x в стек S
Push(S,x)
1: if top[S] = n-1 then
2: error “overflow”
3: else
4: top[S] ← top[S] + 1
5: S[top[S]] ← x
Пример: S = [10, 7, 12, 5], top = 3
10
7
12
5
top
Push(S, 17), top = 4
10
7
12
5
17
top
Время работы операции Push(S,x) – O(1)
АиСД
14

15.

Оценка времени работы алгоритма
Pop(S) – извлечь элемент из
стека S
Pop(S)
Пример: S = [10, 7, 12, 5, 17], top = 4
10
7
12
5
17
top
1: if Is_Empty(S) then
2: error “underflow”
3: else
4: top[S] ← top[S] − 1
5: return S[top[S] + 1]
Pop(S) = 17, top = 3
10
7
12
5
17
top
Время работы операции Pop(S) – O(1)
АиСД
15

16.

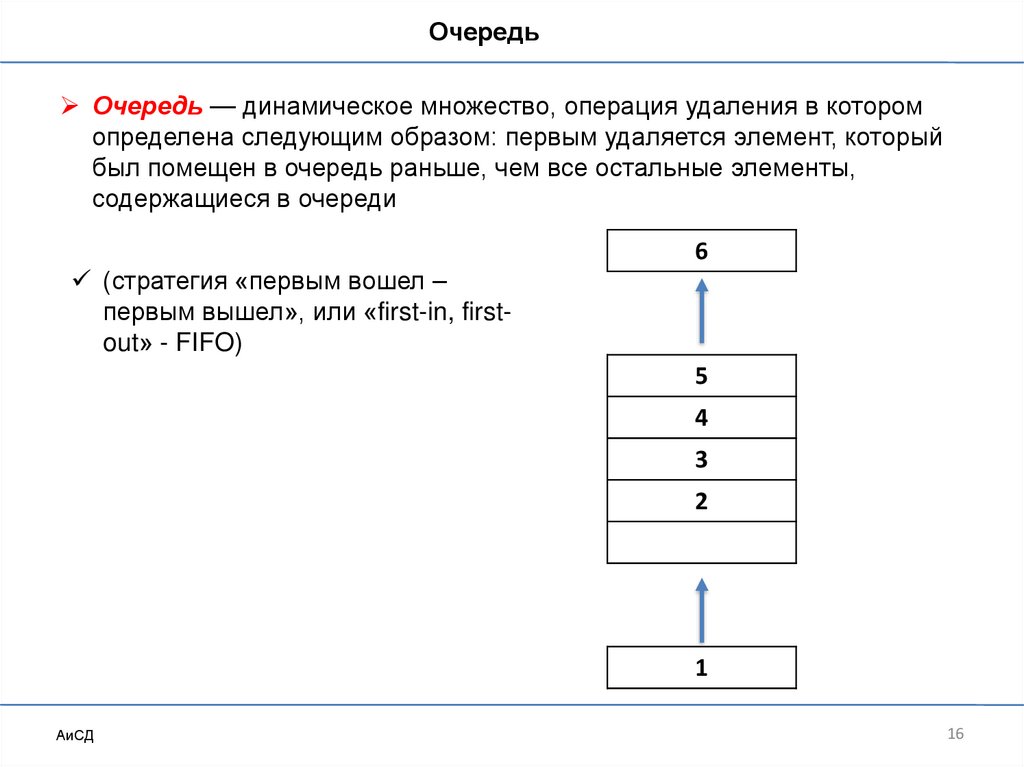
Очередь
Очередь — динамическое множество, операция удаления в котором
определена следующим образом: первым удаляется элемент, который
был помещен в очередь раньше, чем все остальные элементы,
содержащиеся в очереди
6
(стратегия «первым вошел –
первым вышел», или «first-in, firstout» - FIFO)
5
4
3
2
1
АиСД
16

17.

Очередь
Для обозначения функций будем использовать:
Head – указатель на голову очереди
6
Tail – указатель на конец очереди
Dequeue – извлечь первый элемент (обслужить)
Enqueue – добавить элемент в конец очереди
head
Dequeue
5
4
3
2
tail
Enqueue
1
АиСД
17

18.

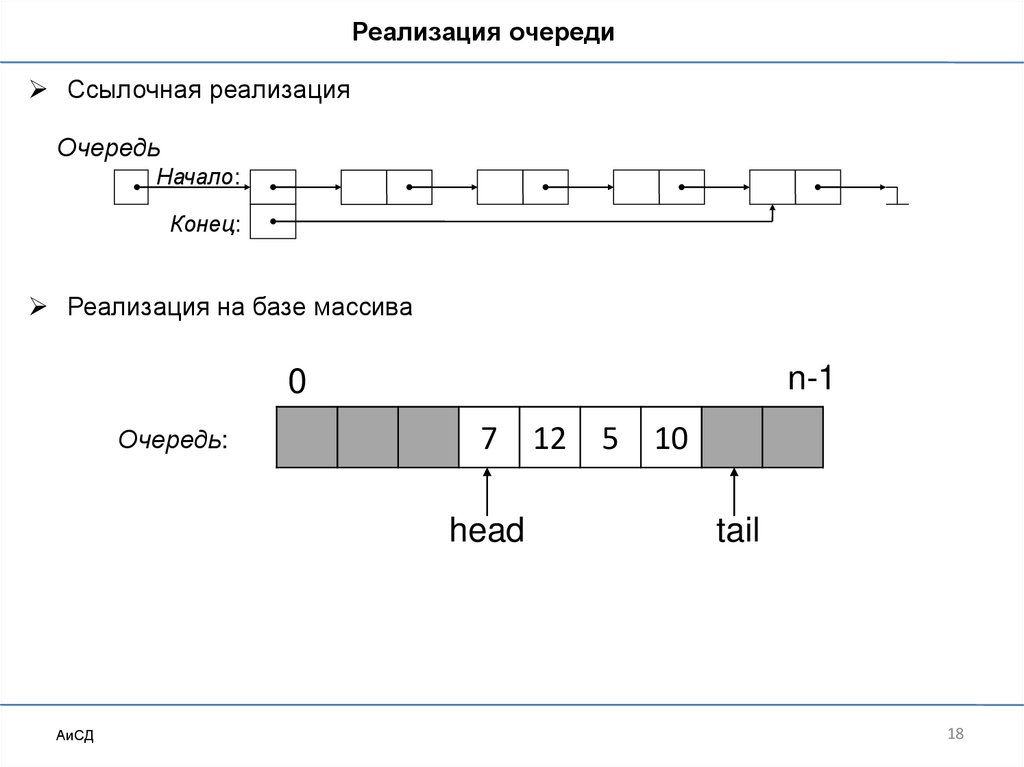
Реализация очереди
Ссылочная реализация
Очередь
Начало:
Конец:
Реализация на базе массива
n-1
0
Очередь:
7
head
АиСД
12
5
10
tail
18

19.

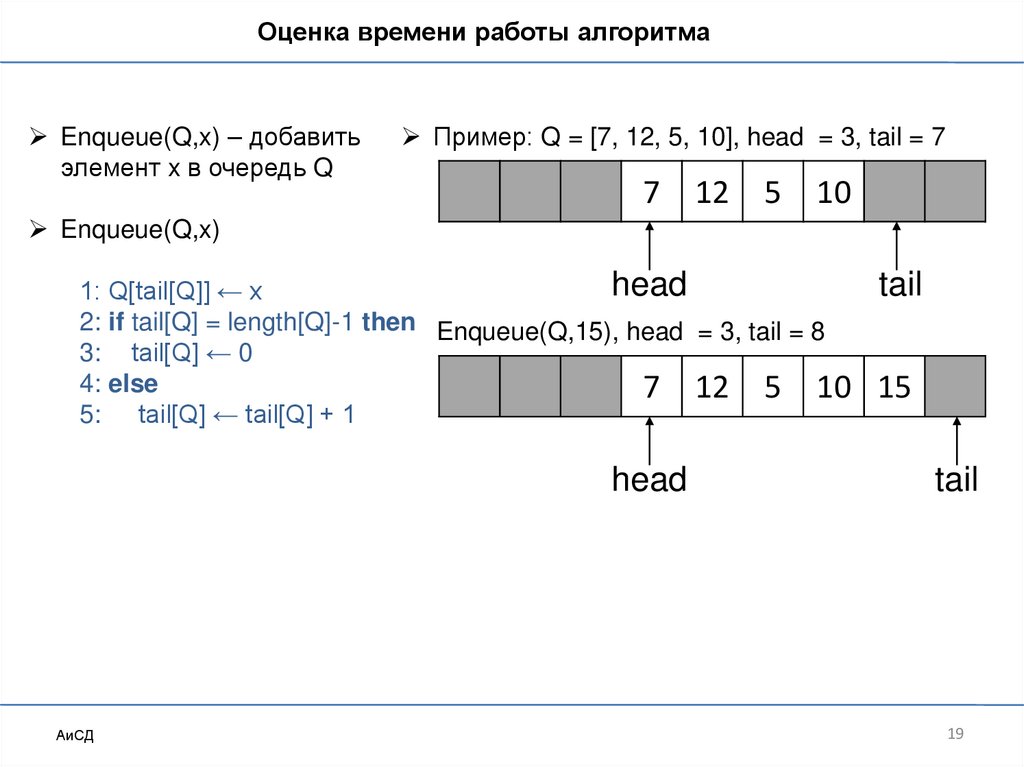
Оценка времени работы алгоритма
Enqueue(Q,x) – добавить
элемент x в очередь Q
Пример: Q = [7, 12, 5, 10], head = 3, tail = 7
7
12
5
10
Enqueue(Q,x)
head
1: Q[tail[Q]] ← x
2: if tail[Q] = length[Q]-1 then Enqueue(Q,15), head = 3, tail = 8
3: tail[Q] ← 0
4: else
7 12 5 10
5: tail[Q] ← tail[Q] + 1
head
АиСД
tail
15
tail
19

20.

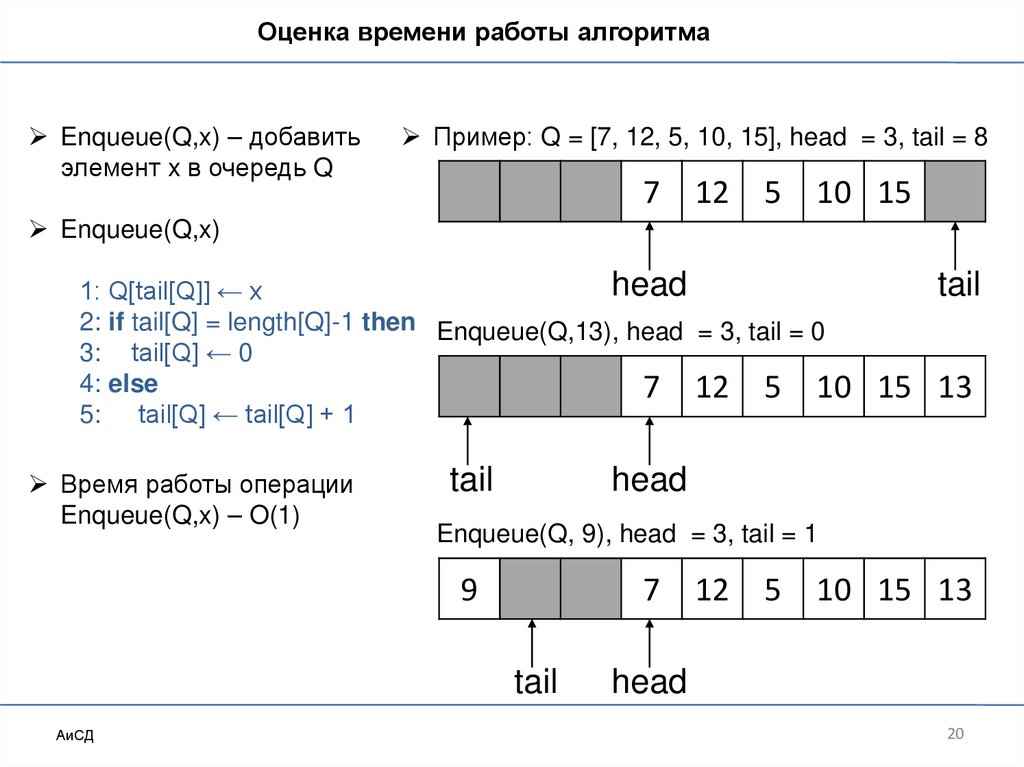
Оценка времени работы алгоритма
Enqueue(Q,x) – добавить
элемент x в очередь Q
Пример: Q = [7, 12, 5, 10, 15], head = 3, tail = 8
7
12
5
10 15
Enqueue(Q,x)
head
1: Q[tail[Q]] ← x
2: if tail[Q] = length[Q]-1 then Enqueue(Q,13), head = 3, tail = 0
3: tail[Q] ← 0
4: else
7 12 5 10
5: tail[Q] ← tail[Q] + 1
Время работы операции
Enqueue(Q,x) – O(1)
tail
15 13
head
Enqueue(Q, 9), head = 3, tail = 1
9
7
tail
АиСД
tail
12
5
10 15 13
head
20

21.

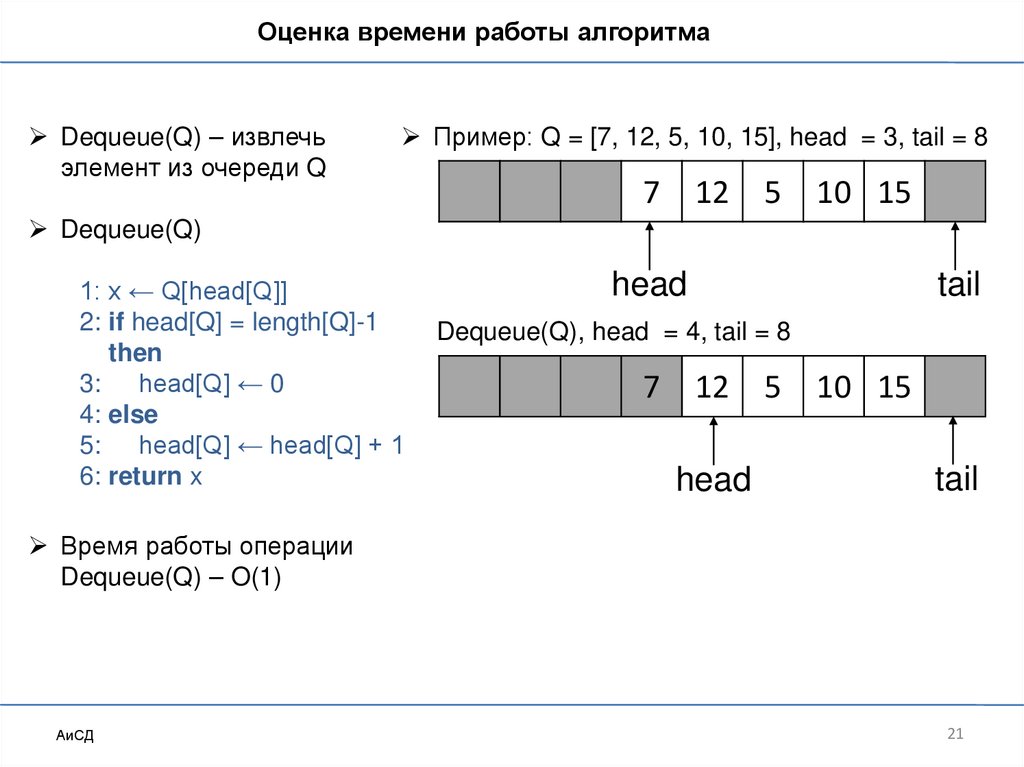
Оценка времени работы алгоритма
Dequeue(Q) – извлечь
элемент из очереди Q
Пример: Q = [7, 12, 5, 10, 15], head = 3, tail = 8
7
12
5
10 15
Dequeue(Q)
1: x ← Q[head[Q]]
2: if head[Q] = length[Q]-1
then
3: head[Q] ← 0
4: else
5: head[Q] ← head[Q] + 1
6: return x
head
tail
Dequeue(Q), head = 4, tail = 8
7
12
head
5
10 15
tail
Время работы операции
Dequeue(Q) – O(1)
АиСД
21

22.

Дек
Дек – это структура данных, представляющая собой последовательность
элементов, в которой можно добавлять и удалять в произвольном
порядке элементы с двух сторон. Первый и последний элементы дека
соответствуют входу и выходу дека
6
Выделяют ограниченные деки:
дек с ограниченным входом – из конца дека можно
только извлекать элементы;
дек с ограниченным выходом – в конец дека
5
можно только добавлять элементы.
4
Данная структура является наиболее универсальной из
3
рассмотренных линейных структур: поддерживает как
2
FIFO, так и LIFO, поэтому на ней можно реализовать
как стек, так и очередь.
1
АиСД
22

23.

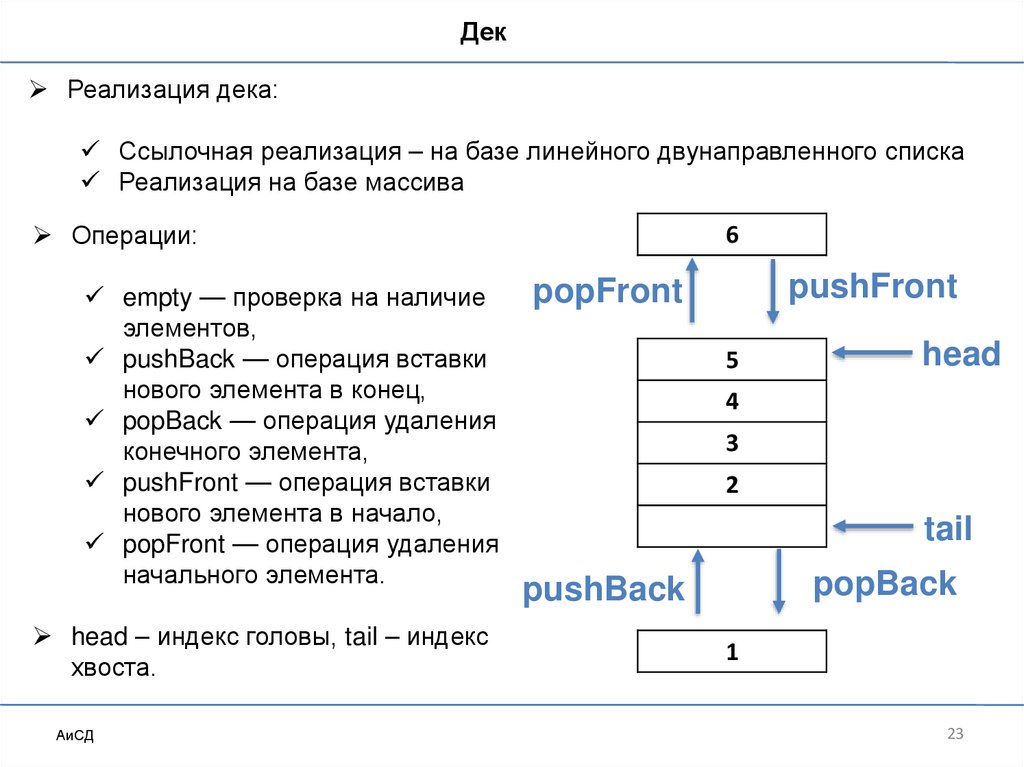
Дек
Реализация дека:
Ссылочная реализация – на базе линейного двунаправленного списка
Реализация на базе массива
Операции:
empty — проверка на наличие
элементов,
pushBack — операция вставки
нового элемента в конец,
popBack — операция удаления
конечного элемента,
pushFront — операция вставки
нового элемента в начало,
popFront — операция удаления
начального элемента.
head – индекс головы, tail – индекс
хвоста.
АиСД
6
pushFront
popFront
5
head
4
3
2
tail
popBack
pushBack
1
23

24.

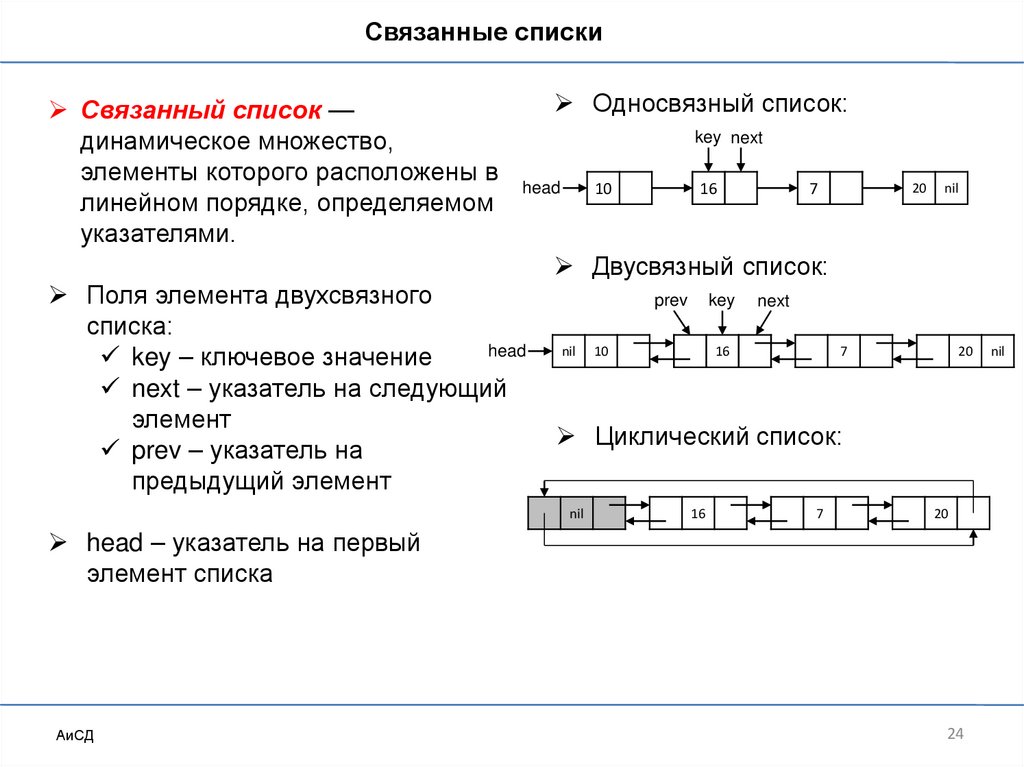
Связанные списки
Связанный список —
динамическое множество,
элементы которого расположены в
линейном порядке, определяемом
указателями.
Односвязный список:
key next
head
10
16
7
20
nil
Двусвязный список:
Поля элемента двухсвязного
списка:
head
key – ключевое значение
next – указатель на следующий
элемент
prev – указатель на
предыдущий элемент
prev
nil
key
10
next
16
7
20
Циклический список:
nil
16
7
20
head – указатель на первый
элемент списка
АиСД
24
nil

25.

Реализация односвязного списка
Представление и реализация линейных списков:
Непрерывная реализация
Ссылочное представление в связанной (динамической) памяти
Ссылочное представление на базе вектора
АиСД
25

26.

Непрерывная реализация на базе вектора
ч
е
р
е
д
а
б
у
к
в
ч
е
р
е
д
а
б
у
к
в
1
2
3
4
5
6
7
8
9
10
ч
е
р
е
д
а
б
у
к
в
ч
р
е
д
а
б
у
к
в
в
1
2
3
4
5
6
7
8
9
10
11
12
11
12
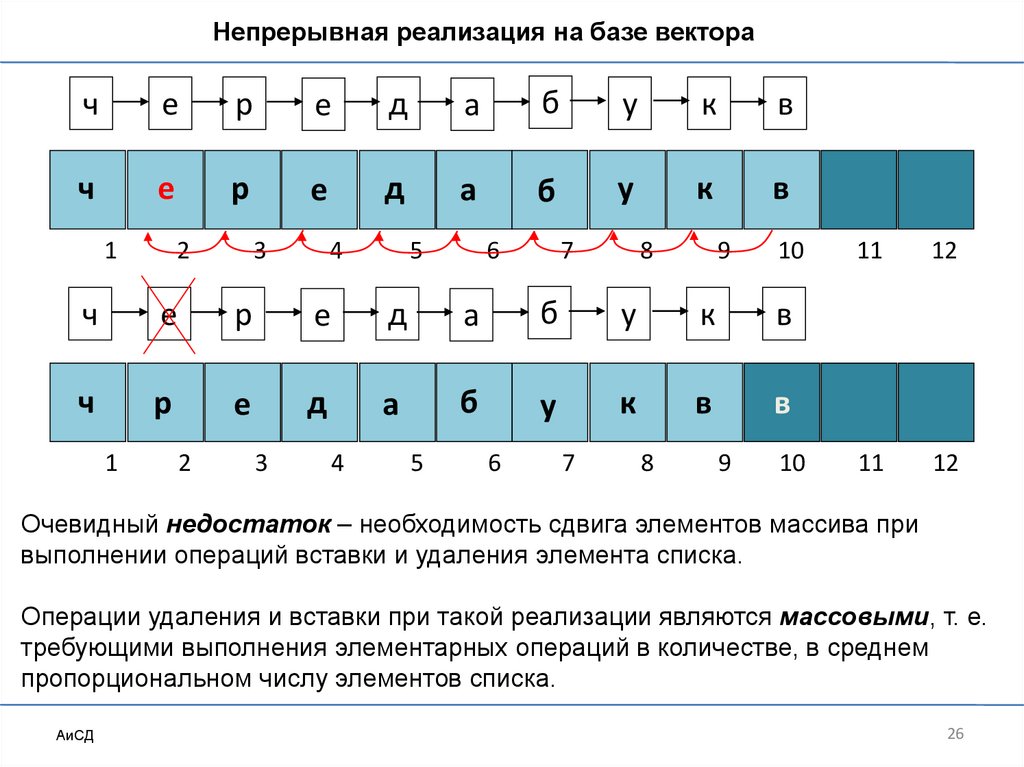
Очевидный недостаток – необходимость сдвига элементов массива при
выполнении операций вставки и удаления элемента списка.
Операции удаления и вставки при такой реализации являются массовыми, т. е.
требующими выполнения элементарных операций в количестве, в среднем
пропорциональном числу элементов списка.
АиСД
26

27.

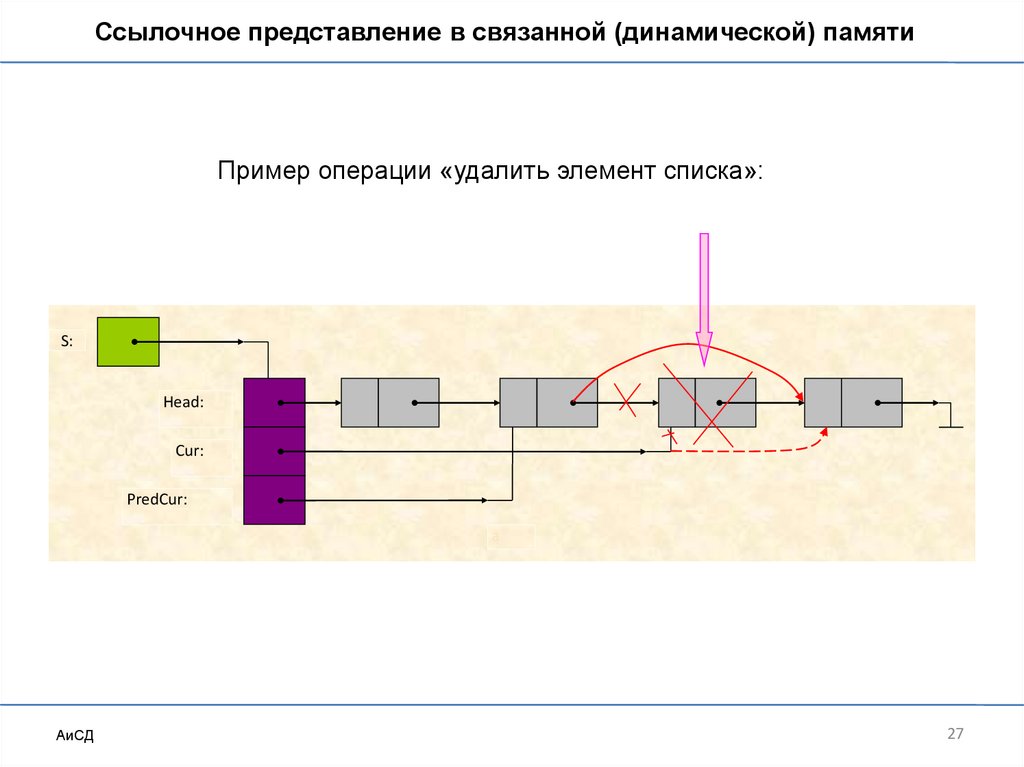
Ссылочное представление в связанной (динамической) памяти
Пример операции «удалить элемент списка»:
S:
Head:
Cur:
PredCur:
а
АиСД
27

28.

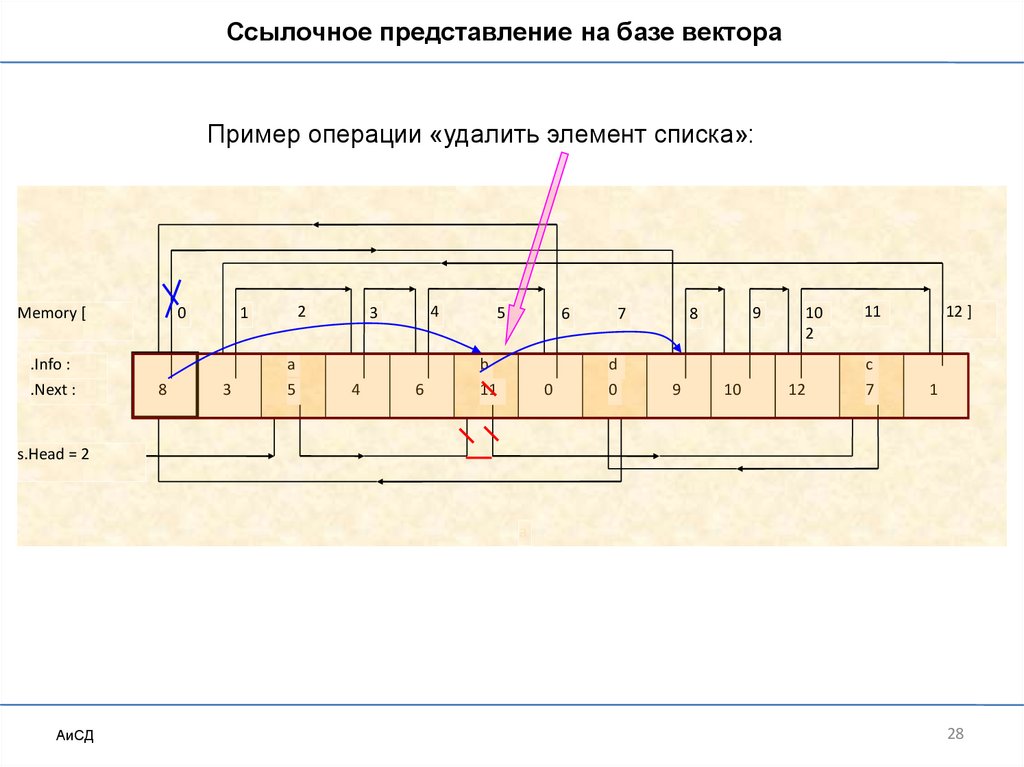
Ссылочное представление на базе вектора
Пример операции «удалить элемент списка»:
Memory [
S:
0
.Info :
.Next :
2
1
4
3
a
8Head:
3
5
5
6
b
4
6
7
9
8
10
2
d
11
0
0
11
12 ]
c
9
10
12
7
1
Cur:
s.Head = 2
PredCur:
а
АиСД
a
28

29.

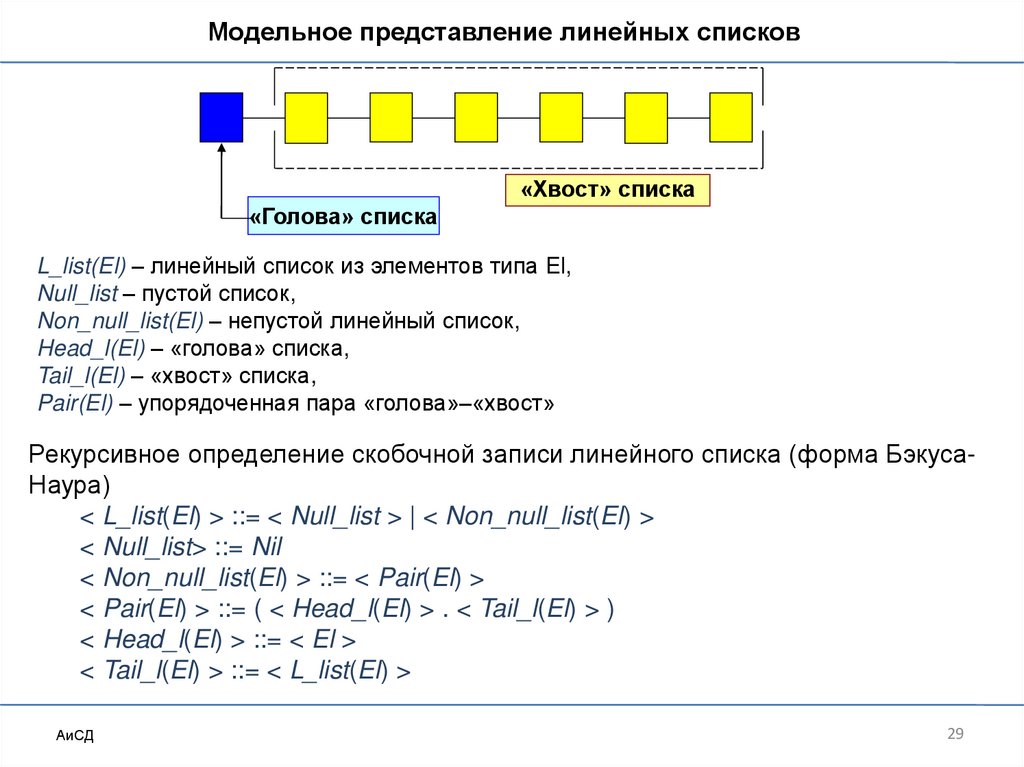
Модельное представление линейных списков
«Хвост» списка
«Голова» списка
L_list(El) – линейный список из элементов типа El,
Null_list – пустой список,
Non_null_list(El) – непустой линейный список,
Head_l(El) – «голова» списка,
Tail_l(El) – «хвост» списка,
Pair(El) – упорядоченная пара «голова»–«хвост»
Рекурсивное определение скобочной записи линейного списка (форма БэкусаНаура)
< L_list(El) > ::= < Null_list > | < Non_null_list(El) >
< Null_list> ::= Nil
< Non_null_list(El) > ::= < Pair(El) >
< Pair(El) > ::= ( < Head_l(El) > . < Tail_l(El) > )
< Head_l(El) > ::= < El >
< Tail_l(El) > ::= < L_list(El) >
АиСД
29

30.

Рекурсивное определение скобочной записи линейных списков
Скобочная запись: (a . (b . (c . (d . Nil))))
В сокращенной записи: (a b c d)
Пустой список: Nil или ( )
Список из одного элемента: (a . Nil) или (a)
АиСД
30

31.

Функции обработки линейных списков
Sum – вычисление суммы элементов списка
Sum(x)
1: if Null(x) = true then
2: return 0
3: else
4: return Head[x] + Sum(Tail[x])
Concat – соединение двух списков в один
Concat(x,y)
1: if Null(x) = true then
2: return y
3: else
4: return Cons(Head[x], Concat(Tail[x], y)
Concat(x,y) = (a b c d) для x = (a b) и y = (c d)
АиСД
31

32.

Функции обработки линейных списков
Append – добавление элемента в конец списка
Append(x,у)
Concat(x, Cons(y, Nil))
Append(x,y) = (a b c) для x = (a b) и y = (c)
Reverse – обращение списка
Reverse(x)
1: if Null(x) = true then
2: return Nil
3: else
4: return Concat(Reverse (Tail(x)), Cons(Head(x), Nil))
Reverse(x) = (d b c a) для x = (a b c d)
АиСД
32

33.

Поиск в связанном списке
List_Search(L, k) – поиск элемента с ключом k в списке L
List_Search(L, k)
1: x ← Head[L]
2: while (x ≠ nil и x.key ≠ k) do
3: x ← x.next
4: return x
Пример:
head
10
16
7
20
nil
List_Search(L, 16) вернет указатель на второй элемент
List_Search(L, 1) вернет значение nil
Время работы операции List_Search(L, k) – O(n), где n – число элементов в
списке L.
АиСД
33

34.

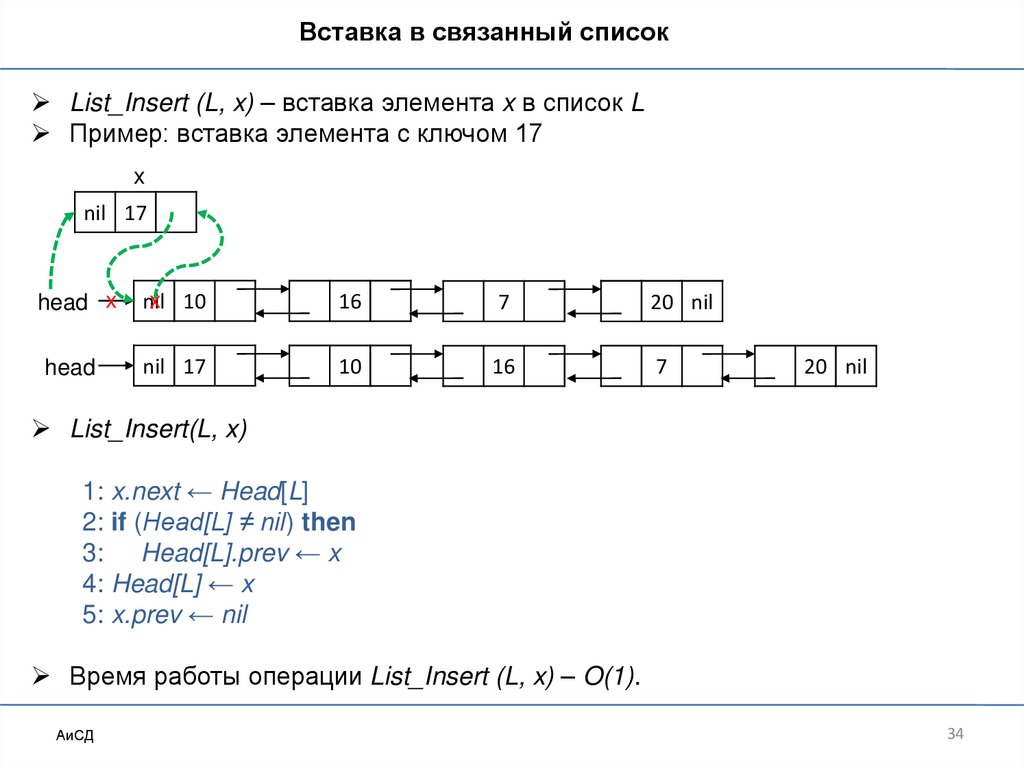
Вставка в связанный список
List_Insert (L, x) – вставка элемента x в список L
Пример: вставка элемента с ключом 17
x
nil 17
head x
x 10
nil
16
7
20 nil
head
nil 17
10
16
7
20 nil
List_Insert(L, x)
1: x.next ← Head[L]
2: if (Head[L] ≠ nil) then
3: Head[L].prev ← x
4: Head[L] ← x
5: x.prev ← nil
Время работы операции List_Insert (L, x) – O(1).
АиСД
34

35.

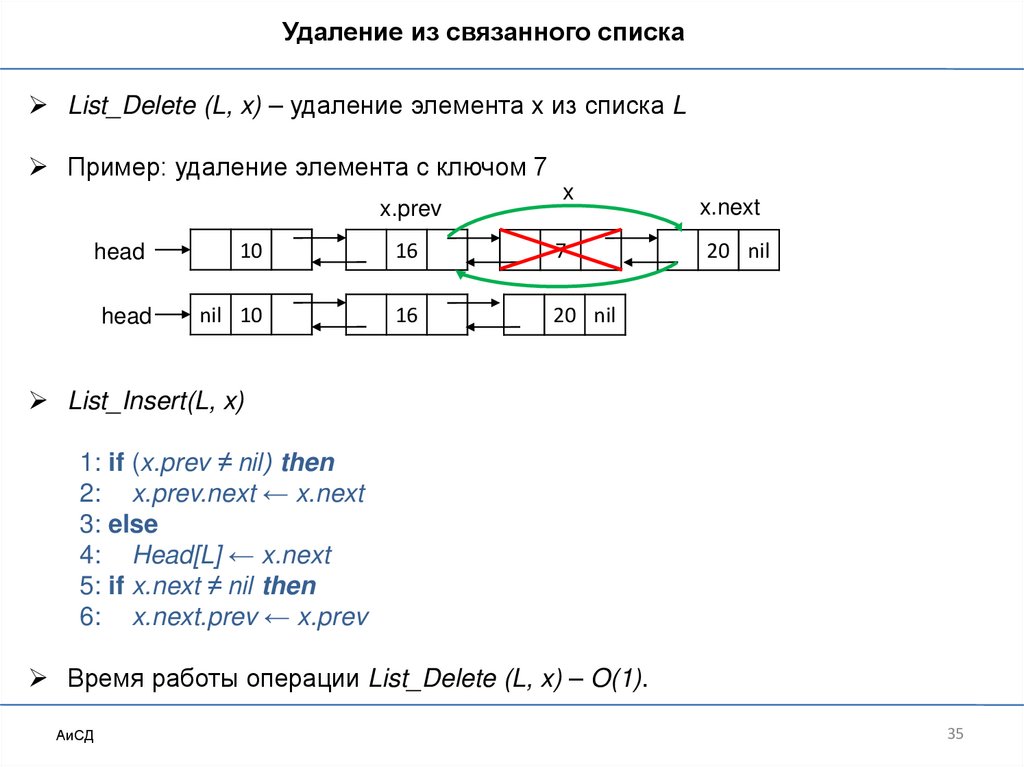
Удаление из связанного списка
List_Delete (L, x) – удаление элемента x из списка L
Пример: удаление элемента с ключом 7
x.prev
x
head
10
16
7
head
nil 10
16
20 nil
x.next
20 nil
List_Insert(L, x)
1: if (x.prev ≠ nil) then
2: x.prev.next ← x.next
3: else
4: Head[L] ← x.next
5: if x.next ≠ nil then
6: x.next.prev ← x.prev
Время работы операции List_Delete (L, x) – O(1).
АиСД
35

36.

Тема 3. Нелинейные структуры данных
36

37.

Нелинейные структуры данных
Мультисписки
Слоеные списки
Графы
Деревья
АиСД
37

38.

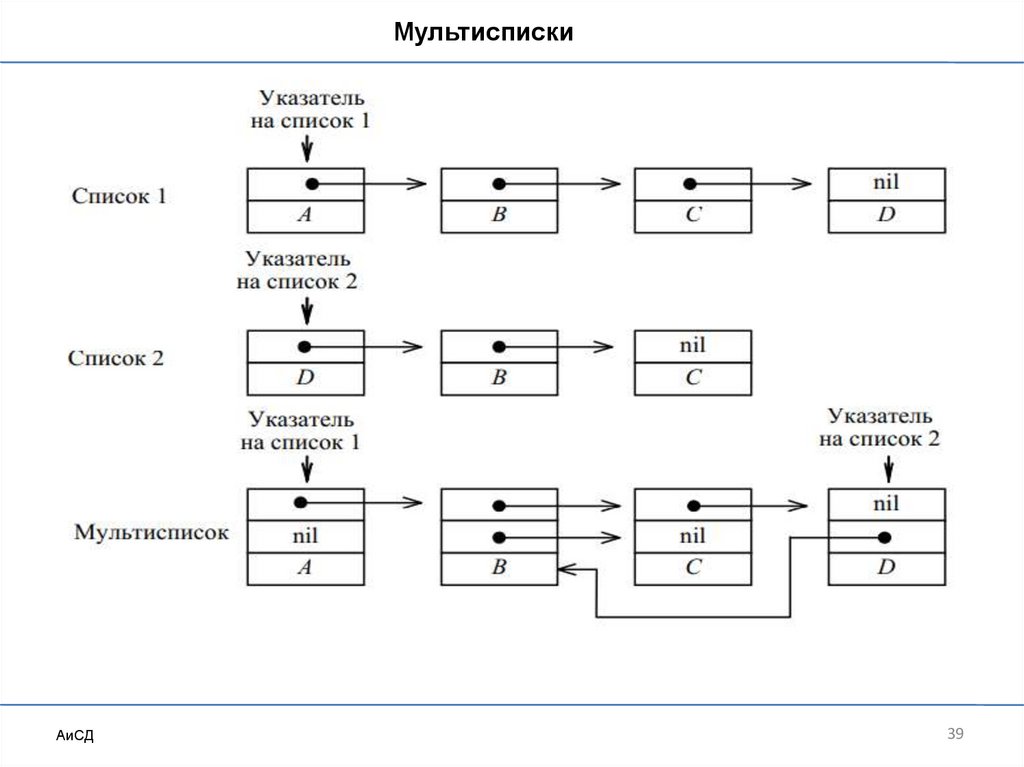
Мультисписки
Мультисписок – это структура данных, состоящая из элементов,
содержащих такое число указателей, которое позволяет организовать их
одновременно в виде нескольких различных списков.
В элементах мультисписка важно различать поля указателей для разных
списков, чтобы можно было проследить элементы одного списка, не вступая
в противоречие с указателями другого списка.
АиСД
38

39.

Мультисписки
АиСД
39

40.

Слоеные списки
Слоеные, или разделенные, списки – это связанные списки, которые
позволяют перескакивать через некоторое количество элементов.
Позволяет преодолеть ограничения последовательного поиска, являющегося
основной причиной низкой эффективности поиска в линейных списках.
Вставка и удаление остаются сравнительно эффективными.
В отличие от элементов обычных линейных списков, элементы этих списков
имеют дополнительный указатель. Все элементы списка группируются по
определенному признаку, и первый элемент каждой группы содержит
указатель на первый элемент следующей группы.
Можно добавлять нужное число дополнительных указателей, группируя
группы элементов и т. д. на нужном количестве уровней.
АиСД
40

41.

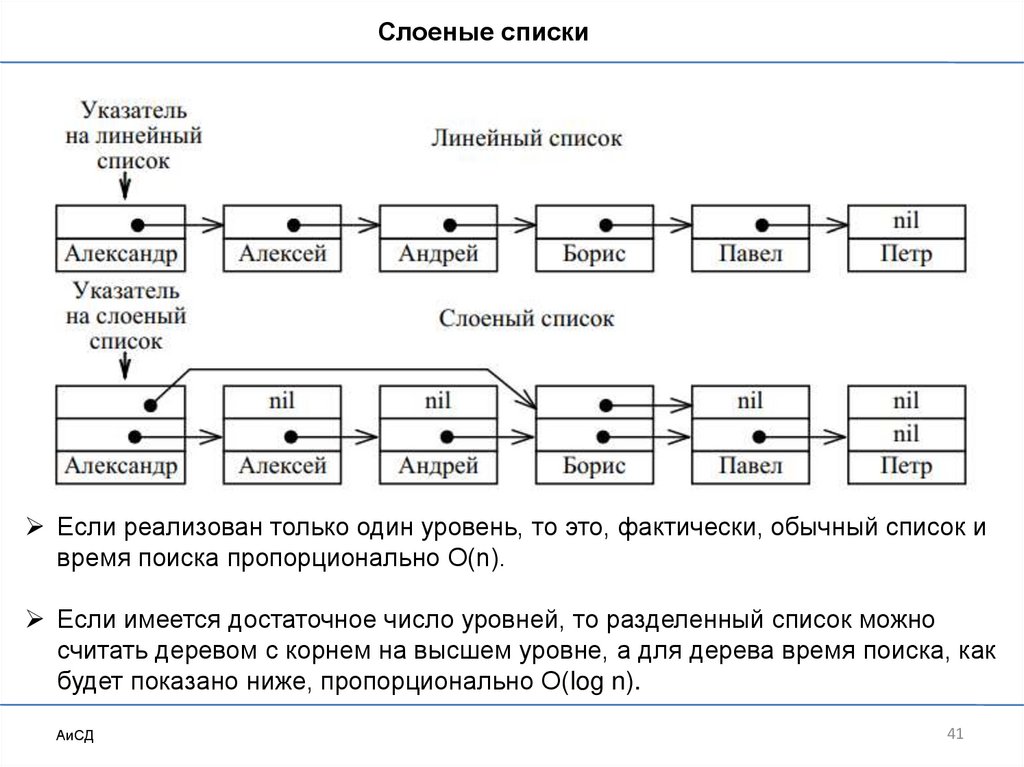
Слоеные списки
Если реализован только один уровень, то это, фактически, обычный список и
время поиска пропорционально O(n).
Если имеется достаточное число уровней, то разделенный список можно
считать деревом с корнем на высшем уровне, а для дерева время поиска, как
будет показано ниже, пропорционально O(log n).
АиСД
41

42.

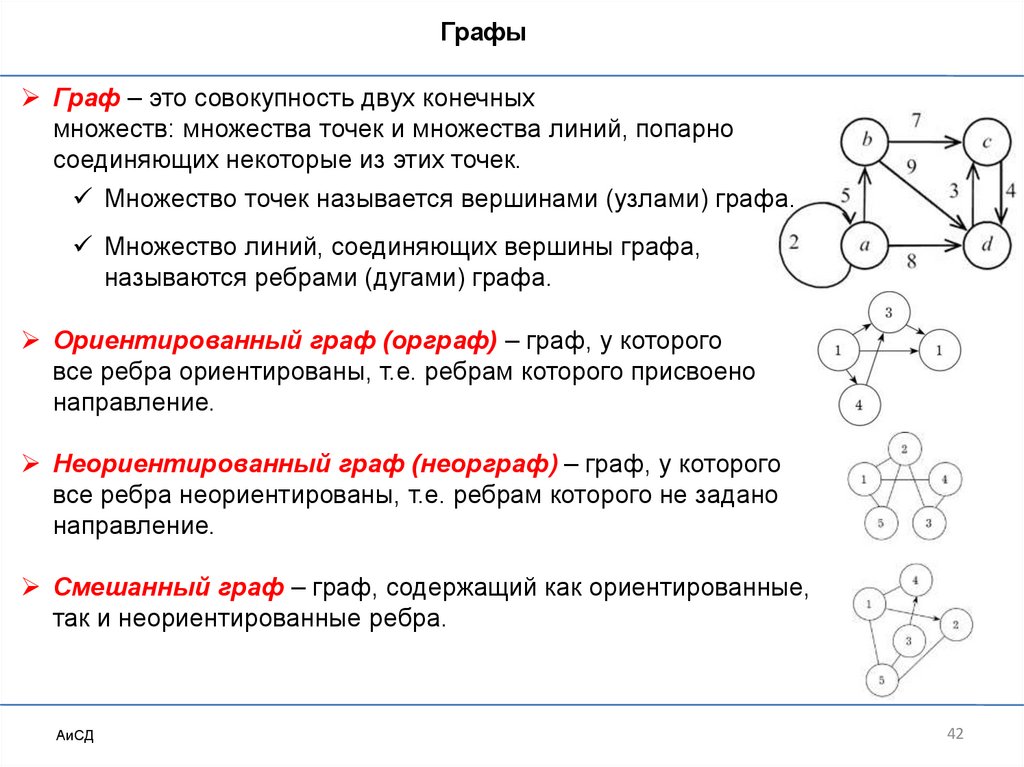
Графы
Граф – это совокупность двух конечных
множеств: множества точек и множества линий, попарно
соединяющих некоторые из этих точек.
Множество точек называется вершинами (узлами) графа.
Множество линий, соединяющих вершины графа,
называются ребрами (дугами) графа.
Ориентированный граф (орграф) – граф, у которого
все ребра ориентированы, т.е. ребрам которого присвоено
направление.
Неориентированный граф (неорграф) – граф, у которого
все ребра неориентированы, т.е. ребрам которого не задано
направление.
Смешанный граф – граф, содержащий как ориентированные,
так и неориентированные ребра.
АиСД
42

43.

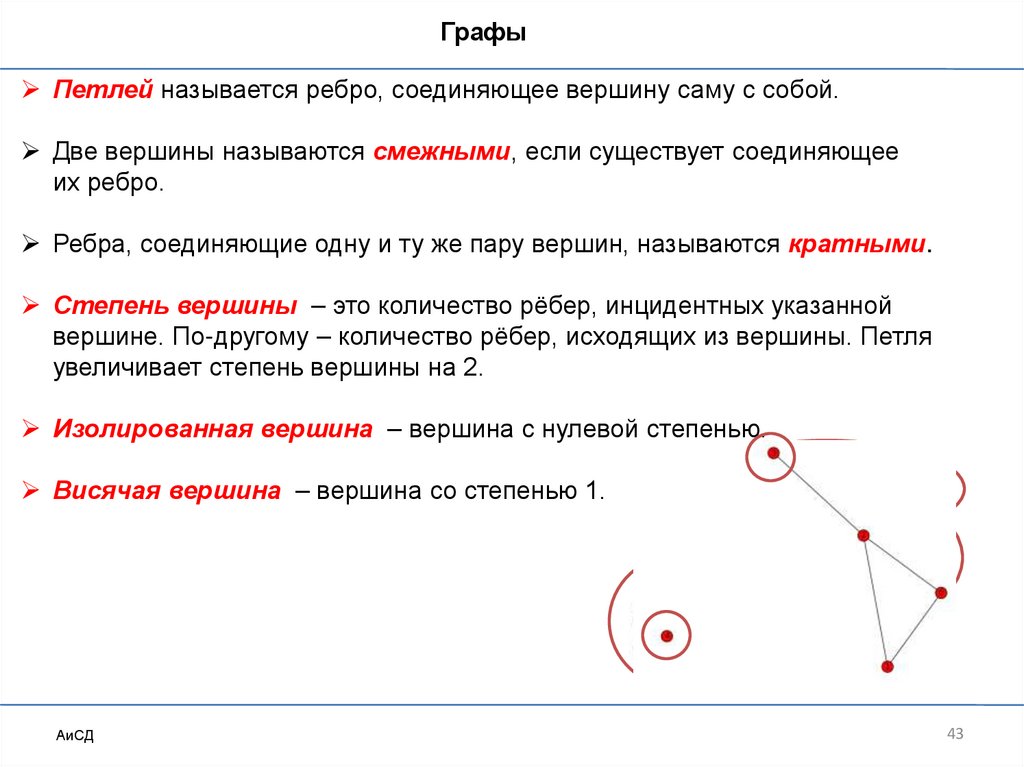
Графы
Петлей называется ребро, соединяющее вершину саму с собой.
Две вершины называются смежными, если существует соединяющее
их ребро.
Ребра, соединяющие одну и ту же пару вершин, называются кратными.
Степень вершины – это количество рёбер, инцидентных указанной
вершине. По-другому – количество рёбер, исходящих из вершины. Петля
увеличивает степень вершины на 2.
Изолированная вершина – вершина с нулевой степенью.
Висячая вершина – вершина со степенью 1.
АиСД
43

44.

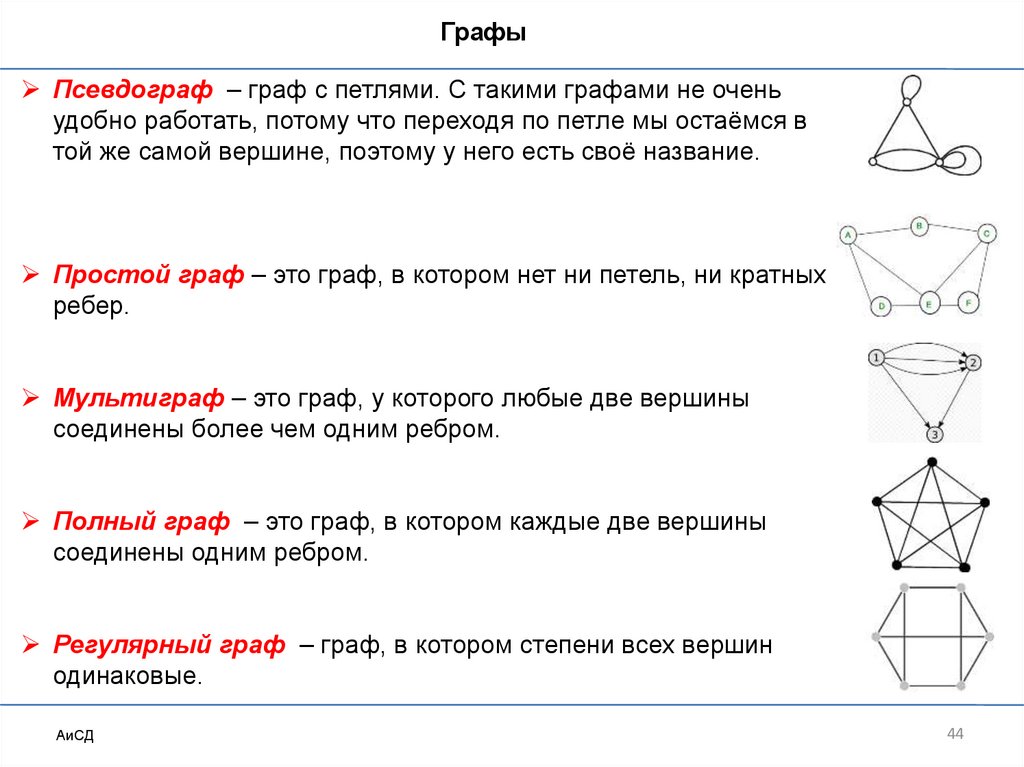
Графы
Псевдограф – граф с петлями. С такими графами не очень
удобно работать, потому что переходя по петле мы остаёмся в
той же самой вершине, поэтому у него есть своё название.
Простой граф – это граф, в котором нет ни петель, ни кратных
ребер.
Мультиграф – это граф, у которого любые две вершины
соединены более чем одним ребром.
Полный граф – это граф, в котором каждые две вершины
соединены одним ребром.
Регулярный граф – граф, в котором степени всех вершин
одинаковые.
АиСД
44

45.

Графы
Маршрут в графе – это конечная чередующаяся последовательность
смежных вершин и ребер, соединяющих эти вершины.
Маршрут называется открытым, если его начальная и конечная вершины
различны, в противном случае он называется замкнутым.
Цепь – маршрут, у которого все ребра различны.
Путь – открытая цепь, у которой все вершины различны.
Цикл (контур) – замкнутая цепь, у которой различны все вершины, за
исключением концевых.
Граф называется связным, если для любой пары вершин существует
соединяющий их путь.
АиСД
45

46.

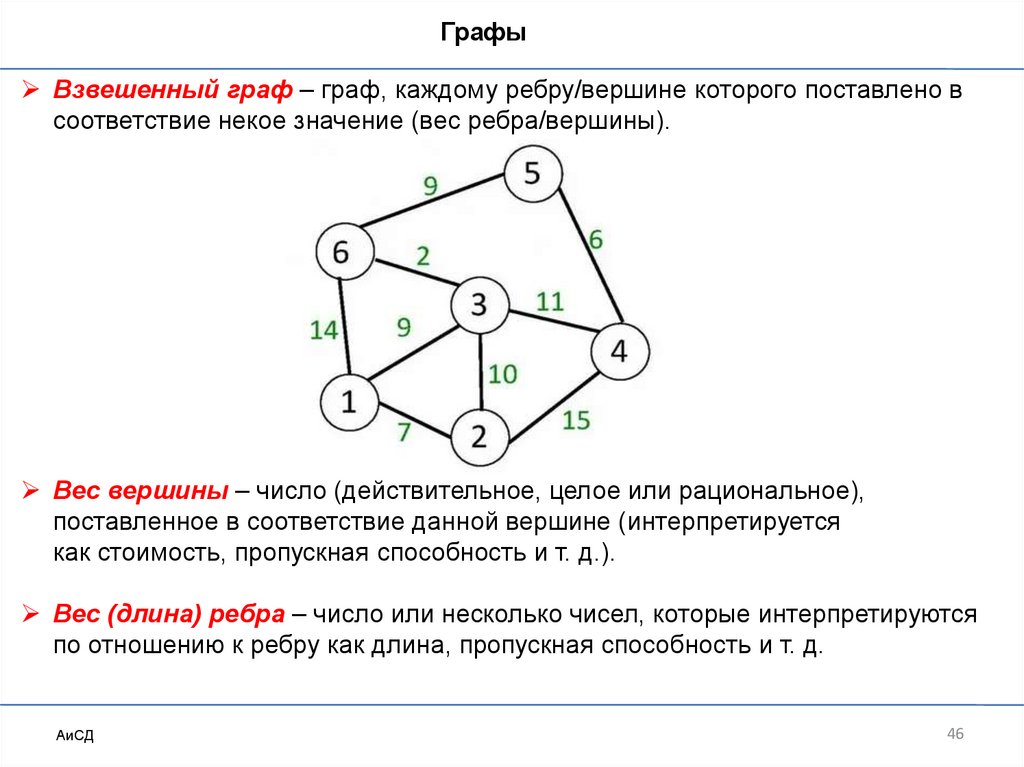
Графы
Взвешенный граф – граф, каждому ребру/вершине которого поставлено в
соответствие некое значение (вес ребра/вершины).
Вес вершины – число (действительное, целое или рациональное),
поставленное в соответствие данной вершине (интерпретируется
как стоимость, пропускная способность и т. д.).
Вес (длина) ребра – число или несколько чисел, которые интерпретируются
по отношению к ребру как длина, пропускная способность и т. д.
АиСД
46

47.

Представления графов
Матрица смежности
Матрица инцидентности
Списки смежных вершин
Список ребер
Списки вершин и ребер
АиСД
47

48.

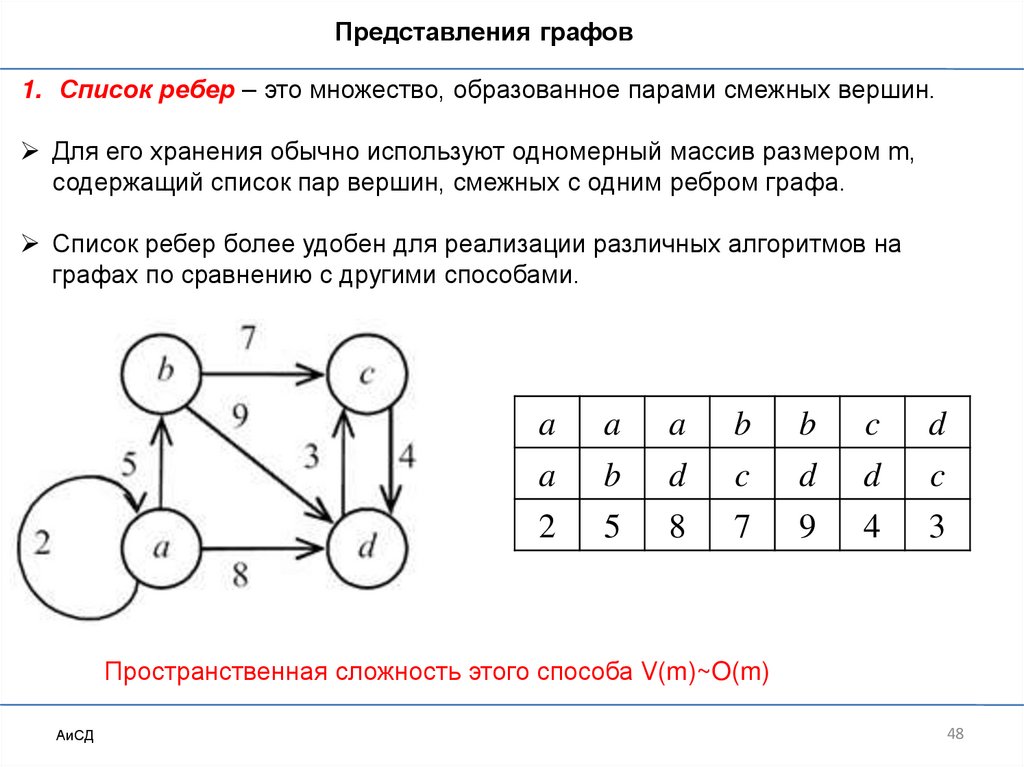
Представления графов
1. Список ребер – это множество, образованное парами смежных вершин.
Для его хранения обычно используют одномерный массив размером m,
содержащий список пар вершин, смежных с одним ребром графа.
Список ребер более удобен для реализации различных алгоритмов на
графах по сравнению с другими способами.
a
a
a
b
b
c
d
a
2
b
5
d
8
c
7
d
9
d
4
c
3
Пространственная сложность этого способа V(m)~O(m)
АиСД
48

49.

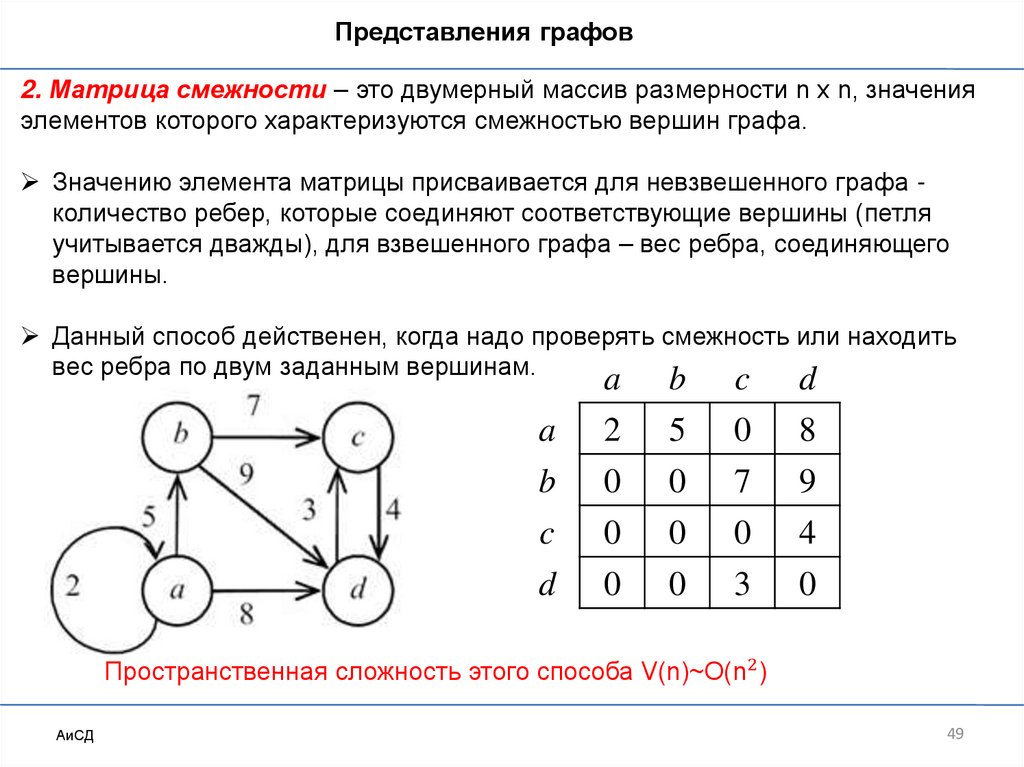
Представления графов
2. Матрица смежности – это двумерный массив размерности n x n, значения
элементов которого характеризуются смежностью вершин графа.
Значению элемента матрицы присваивается для невзвешенного графа количество ребер, которые соединяют соответствующие вершины (петля
учитывается дважды), для взвешенного графа – вес ребра, соединяющего
вершины.
Данный способ действенен, когда надо проверять смежность или находить
вес ребра по двум заданным вершинам.
a
b
a
2
0
b
5
0
c
0
7
d
8
9
c
0
0
0
4
d
0
0
3
0
Пространственная сложность этого способа V(n)~O(n2 )
АиСД
49

50.

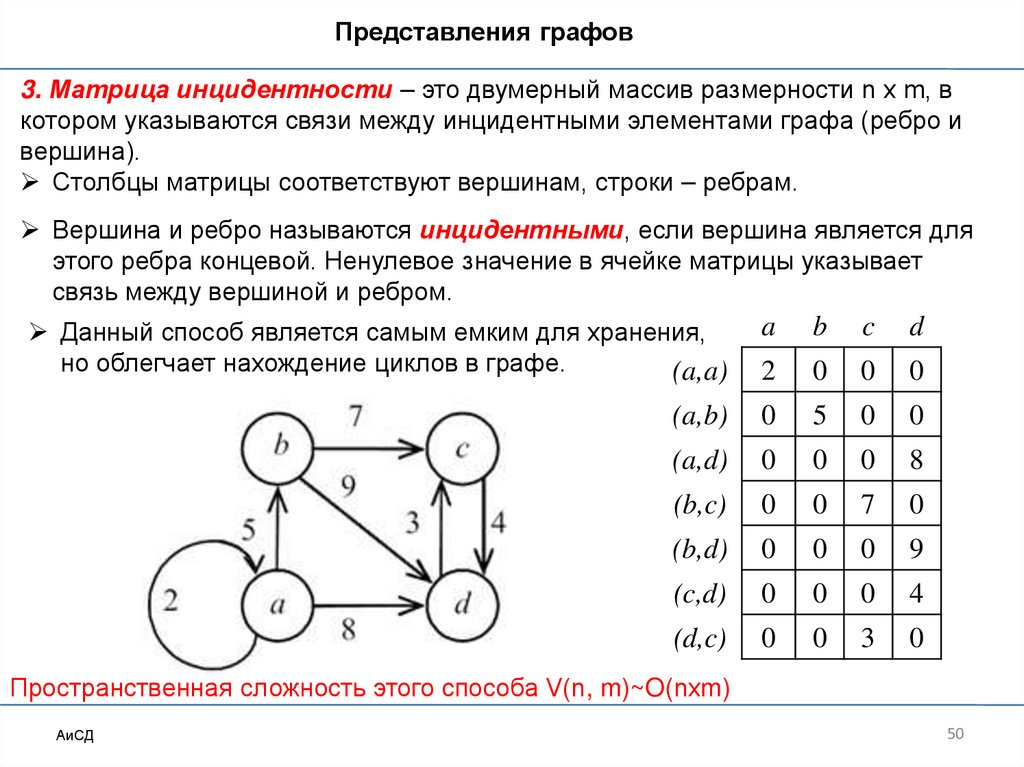
Представления графов
3. Матрица инцидентности – это двумерный массив размерности n x m, в
котором указываются связи между инцидентными элементами графа (ребро и
вершина).
Столбцы матрицы соответствуют вершинам, строки – ребрам.
Вершина и ребро называются инцидентными, если вершина является для
этого ребра концевой. Ненулевое значение в ячейке матрицы указывает
связь между вершиной и ребром.
Данный способ является самым емким для хранения,
но облегчает нахождение циклов в графе.
(a,a)
a
b
c
d
2
0
0
0
(a,b)
0
5
0
0
(a,d)
0
0
0
8
(b,c)
0
0
7
0
(b,d)
0
0
0
9
(c,d)
0
0
0
4
(d,c)
0
0
3
0
Пространственная сложность этого способа V(n, m)~O(nхm)
АиСД
50

51.

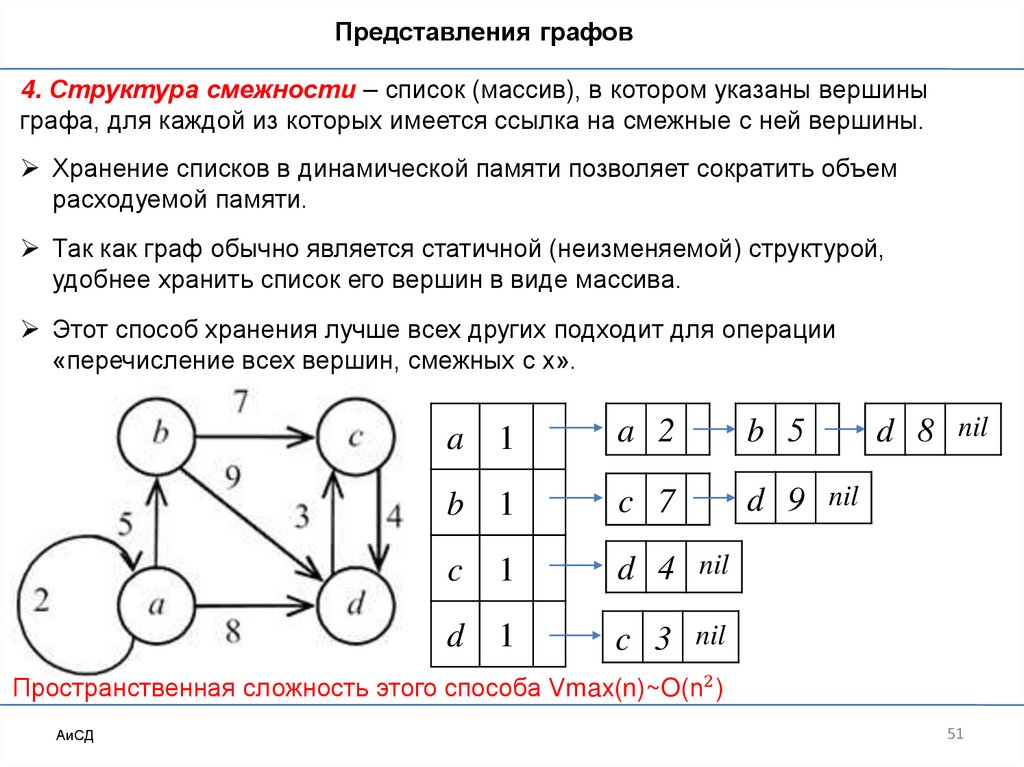
Представления графов
4. Структура смежности – список (массив), в котором указаны вершины
графа, для каждой из которых имеется ссылка на смежные с ней вершины.
Хранение списков в динамической памяти позволяет сократить объем
расходуемой памяти.
Так как граф обычно является статичной (неизменяемой) структурой,
удобнее хранить список его вершин в виде массива.
Этот способ хранения лучше всех других подходит для операции
«перечисление всех вершин, смежных с x».
a 1
a 2
b 5
b 1
c 7
d 9 nil
c
1
d 4 nil
d 1
c 3 nil
d 8 nil
Пространственная сложность этого способа Vmax(n)~O(n2 )
АиСД
51