17fa4df4452a40a1b3f6ee8be73aaec3

1.

Свойства операций над
множествами: переместительное,
сочетательное, распределительное,
включения.
Ст а т и с т и ка – это н ау ка ,
изу чающая процессы,
происходящие в обществе,
оценивающ ая и х
количественные и
качественные параметры.
Вероя́ т ность — степень
возможности наступления
некоторого события.
22.11.2025

2.

Повторение
Вопросы:
Что такое множество?
Какие способы задания множеств вам известны?
Что такое подмножество?
Какое множество называется пустым?
Какие множества являются равными?
Какая операция над множествами называется
дополнение?
Какая операция над множествами называется
объединение?
Какая операция над множествами называется
пересечение?
Какая операция над множествами называется
разностью?
Что понимают под мощностью множества?

3. Повторение

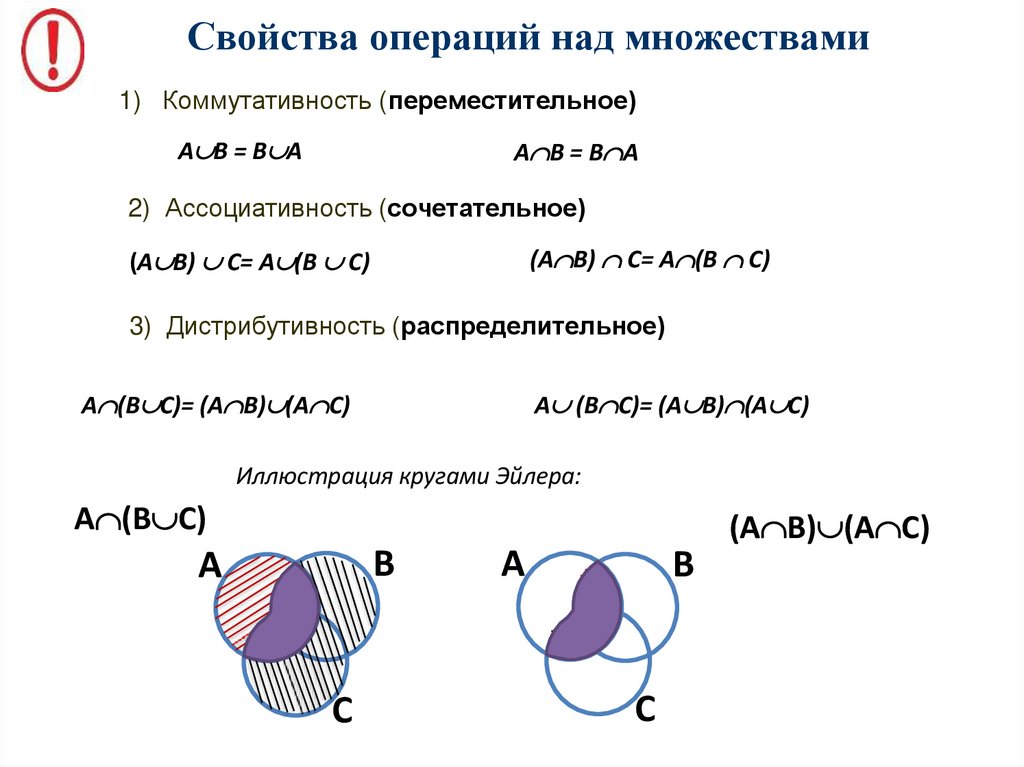
Свойства операций над множествами
1) Коммутативность (переместительное)
A B = B A
A B = B A
2) Ассоциативность (сочетательное)
(A B) С= A (B С)
(A B) С= A (B С)
3) Дистрибутивность (распределительное)
A (B С)= (A B) (A С)
A (B С)= (A B) (A С)
Иллюстрация кругами Эйлера:
A (B С)
B
А
C
(A B) (A С)
А
B
C

4.

3. Дистрибутивность
A (B С)= (A B) (A С)
Доказательство:
1) x A (B С)
x A и одновременно x (B С)
(по опр. пересечения)
x A и одновременно или x B,
или x С (по опр. объединения)
x A и одновременно x B, либо
x A и одновременно x С
x (A B) (A С)
A (B С) (A B) (A С)
1)
2)
2) x (A B) (A С)
x A и одновременно x B, либо
x A и одновременно x С
x A и одновременно или x B,
или x С
x A и одновременно x (B С)
x A (B С)
(A B) (A С) A (B С)
A (B С)= (A B) (A С)

5.

Свойства операций над множествами
4)
Закон поглощения.
8)
Свойство единицы.
5)
Идемпотентность.
9)
Закон де Моргана
6)
Инволютивность.
7)
Свойство нуля.
А
Ø=А
А
Ø= Ø

6.

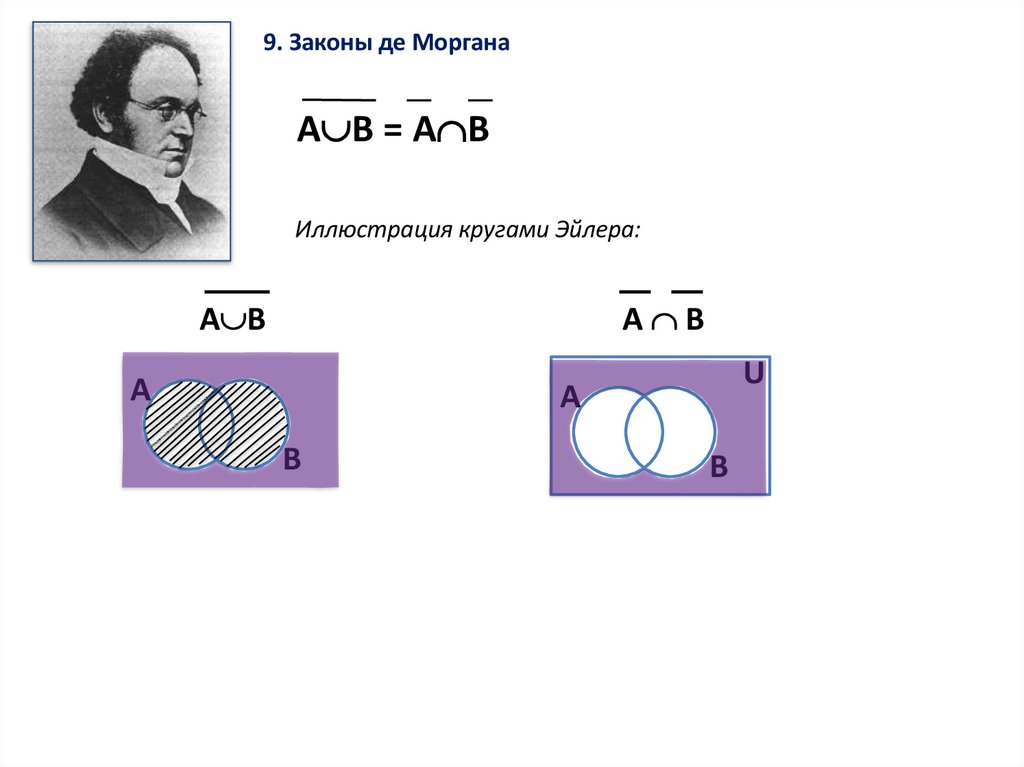
9. Законы де Моргана
A В = A B
Иллюстрация кругами Эйлера:
A B
A В
A
U
A
B
B

7.

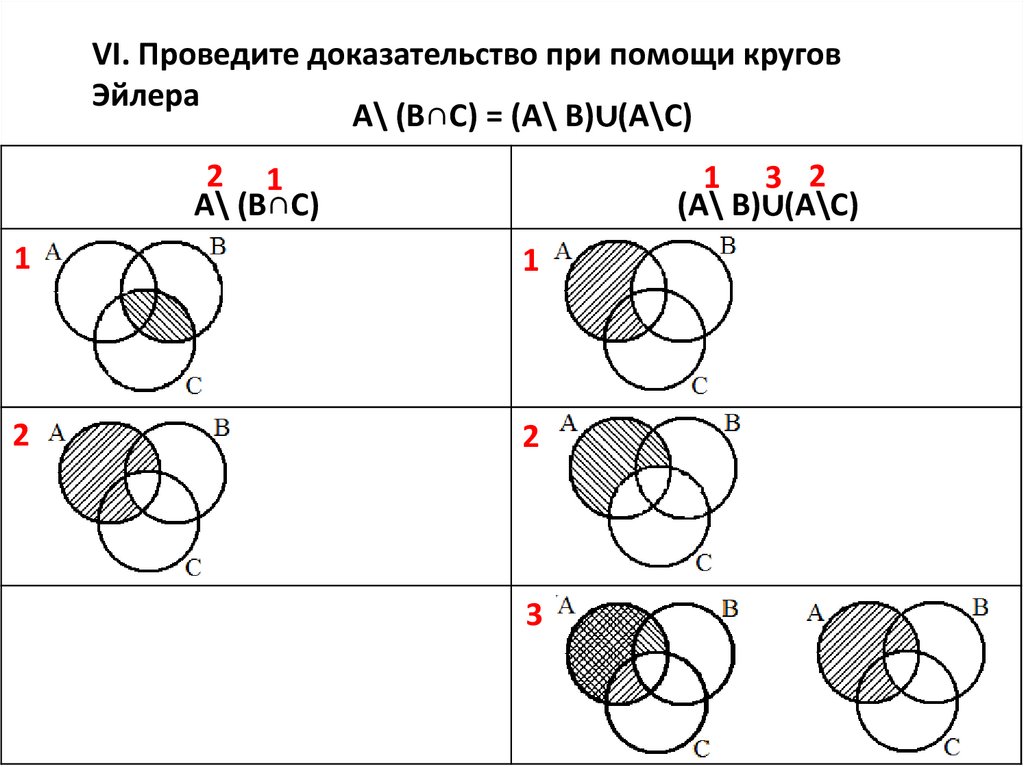
VI. Проведите доказательство при помощи кругов
Эйлера
А\ (В∩С) = (А\ В)∪(А\С)
2 1
А\ (В∩С)
1 3 2
(А\ В)∪(А\С)
1
1
2
2
3

8.

Упражнения
№ 19
№ 20

9. Упражнения

Приложение к уроку
Домашнее задание
Выполнить 207