Урок№16-18(Параллельность плоскостей) —в эльжур№1

1.

§ Параллельность плоскостей.
Параллельные плоскости.

2.

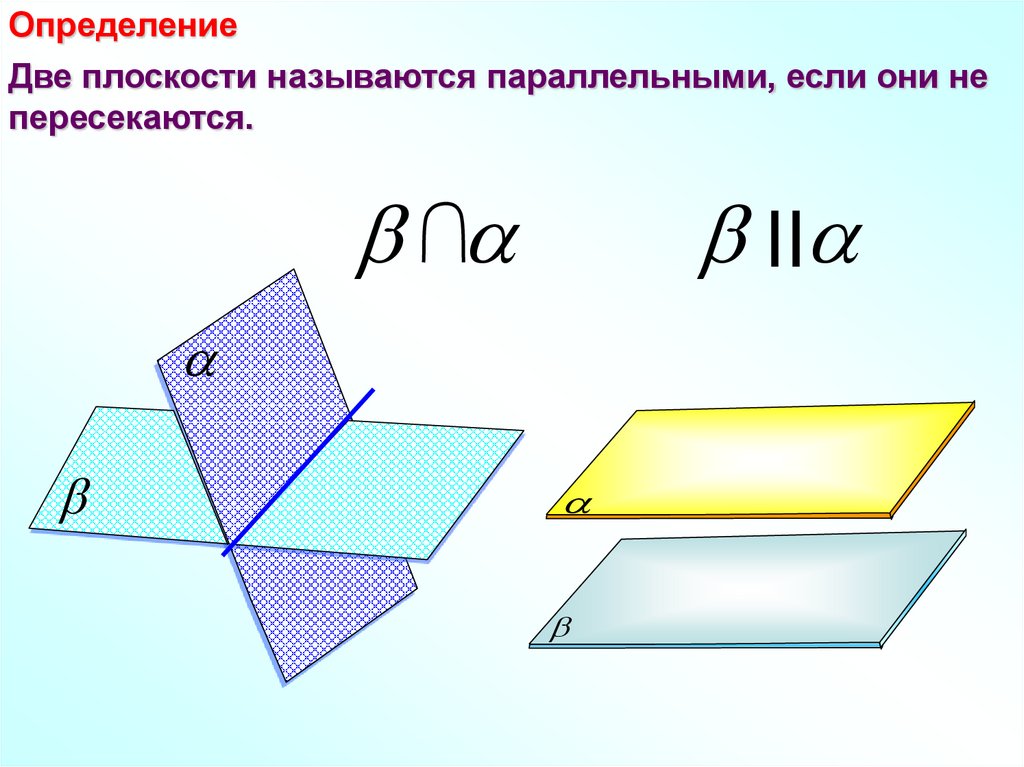
Определение
Две плоскости называются параллельными, если они не
пересекаются.
II

3.

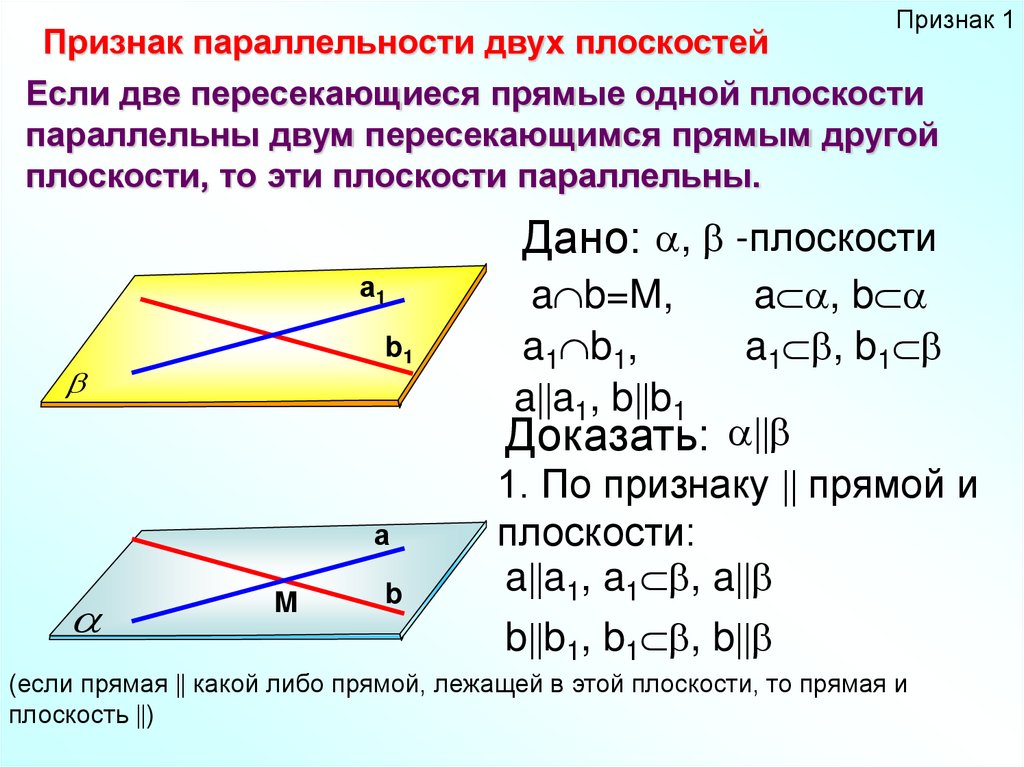
Признак 1
Признак параллельности двух плоскостей
Если две пересекающиеся прямые одной плоскости
параллельны двум пересекающимся прямым другой
плоскости, то эти плоскости параллельны.
Дано: , -плоскости
а1
b1
a b=M,
a1 b1,
a a1, b b1
a , b
a1 , b1
Доказать:
а
M
b
1. По признаку прямой и
плоскости:
a a1, a1 , a
b b1, b1 , b
(если прямая какой либо прямой, лежащей в этой плоскости, то прямая и
плоскость )

4.

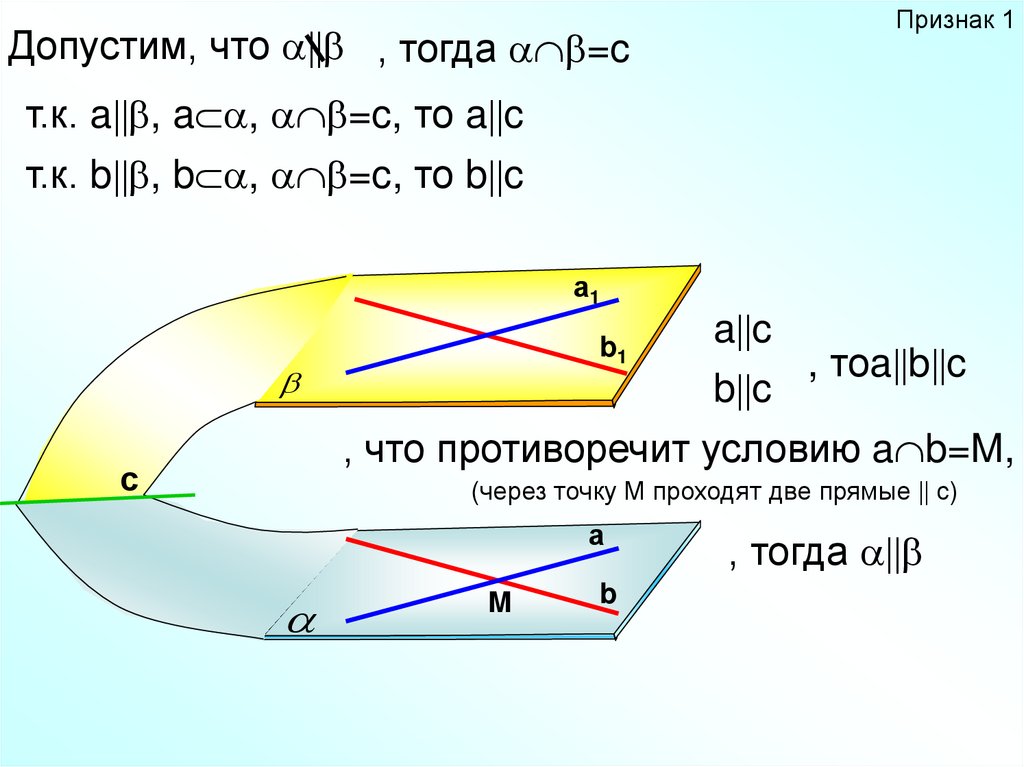
Признак 1
Допустим, что , тогда =c
т.к. a , a , =c, то a c
т.к. b , b , =c, то b c
а1
b1
a c
b c
, тоa b c
, что противоречит условию a b=M,
с
(через точку М проходят две прямые с)
а
M
b
, тогда

5.

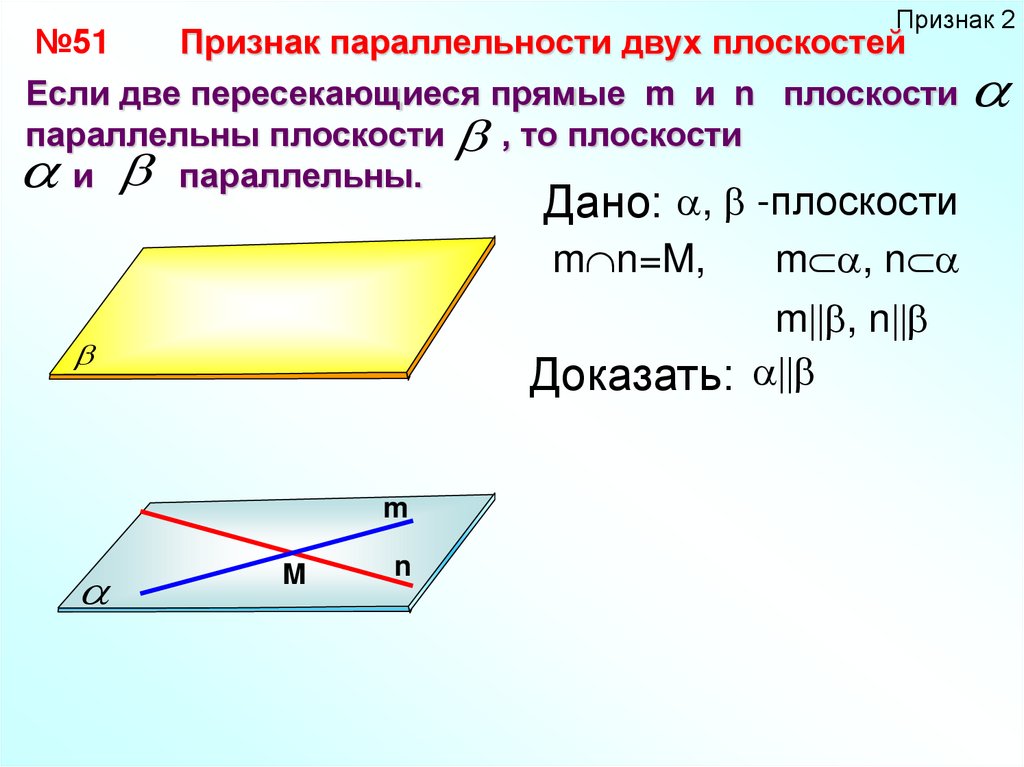
Признак 2
№51
Признак параллельности двух плоскостей
Если две пересекающиеся прямые m и n плоскости
параллельны плоскости , то плоскости
и параллельны.
Дано: , -плоскости
m n=M,
m , n
Доказать:
m
m , n
M
n

6.

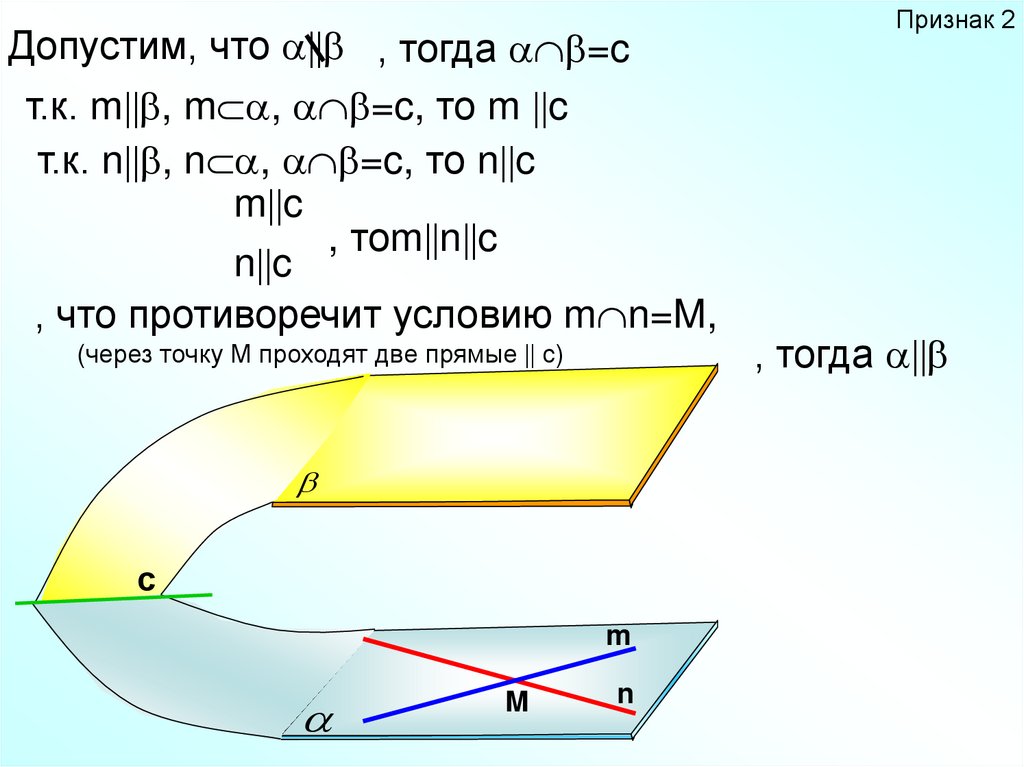
Допустим, что , тогда =c
т.к. m , m , =c, то m c
т.к. n , n , =c, то n c
m c
, тоm n c
n c
, что противоречит условию m n=M,
(через точку М проходят две прямые с)
с
m
M
n
Признак 2
, тогда

7.

Параллельные плоскости.

8.

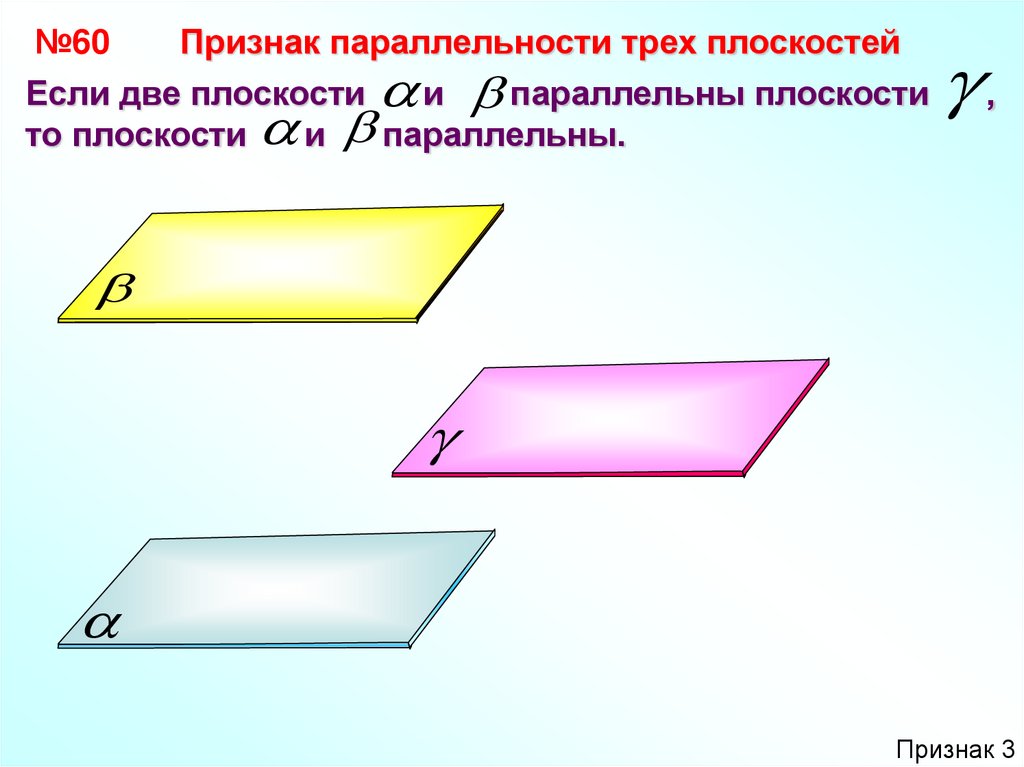
№60
Признак параллельности трех плоскостей
Если две плоскости
и параллельны плоскости
то плоскости
и параллельны.
,
Признак 3

9.

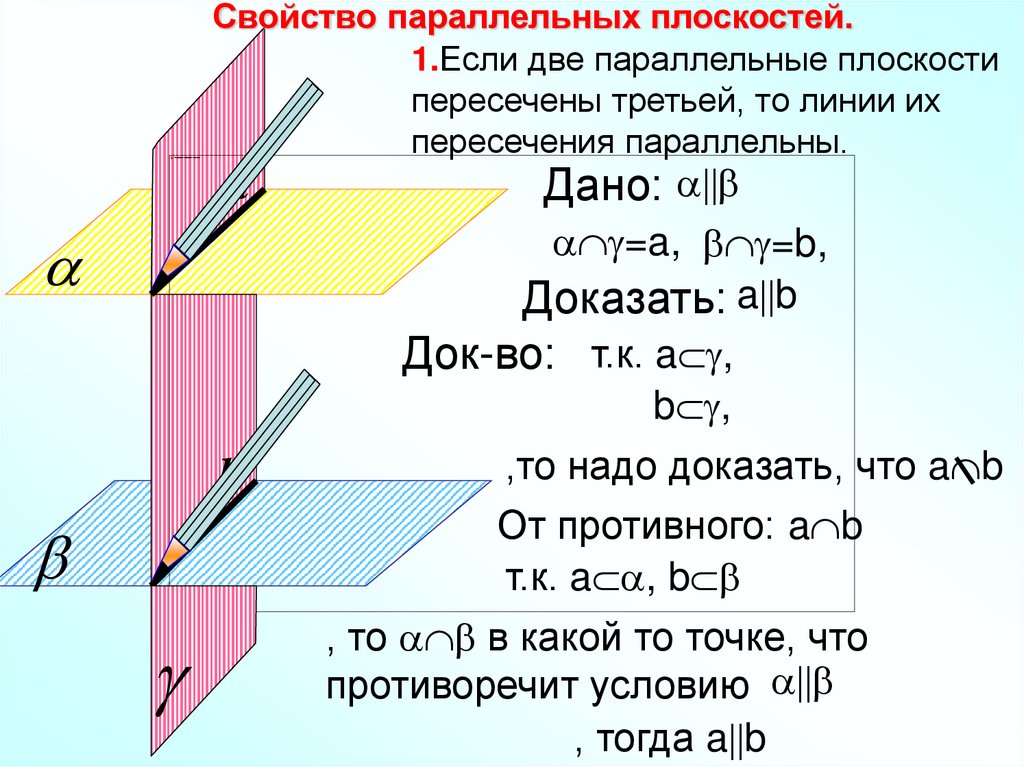
Свойство параллельных плоскостей.
1.Если две параллельные плоскости
пересечены третьей, то линии их
пересечения параллельны.
а
Дано:
=a, =b,
Доказать: a b
Док-во: т.к. a ,
b ,
b
,то надо доказать, что a b
От противного: a b
т.к. a , b
, то в какой то точке, что
противоречит условию
, тогда a b

10.

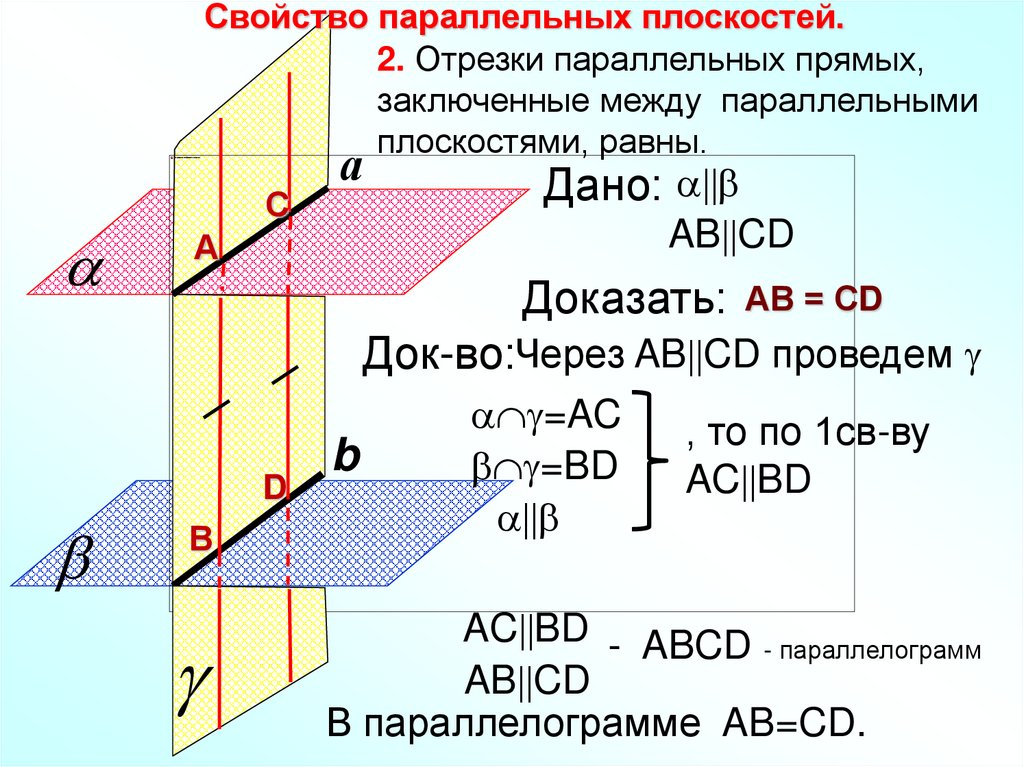
Свойство параллельных плоскостей.
2. Отрезки параллельных прямых,
заключенные между параллельными
плоскостями, равны.
С
а
Дано:
AB CD
А
Доказать: АВ = СD
Док-во:Через AB CD проведем
D
В
b
=AC
=BD
, то по 1св-ву
AC BD
AC BD - ABCD - параллелограмм
AB CD
В параллелограмме AB=CD.