83-84 векторы

1. Координаты и векторы

2. Действия с векторами

Сложение
Вычитание
Умножение вектора на число
Скалярное произведение

3. Сложение векторов

Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
Свойства сложения

4. Правило треугольника

Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А вектор
AB, равный а
2. от точки В отложить вектор BC , равный b
3. вектор AC называется суммой векторов a и b
B
a
a
b
А
b
a b
C

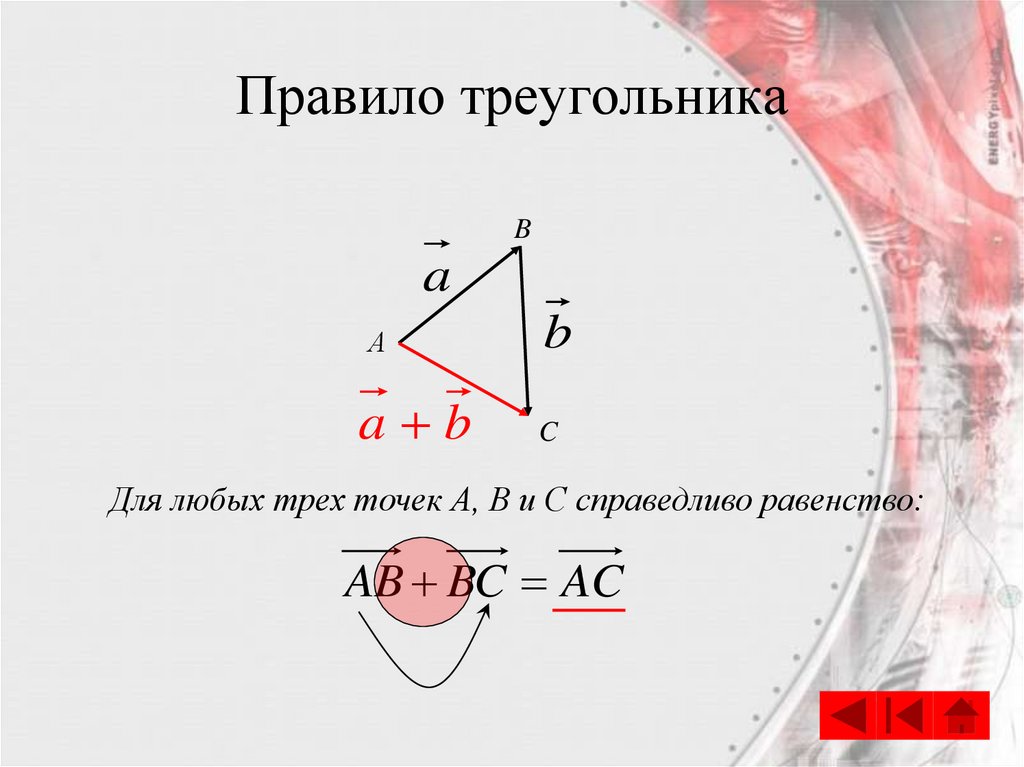
5. Правило треугольника

B
a
А
b
a b
C
Для любых трех точек А, В и С справедливо равенство:
AB BC AC

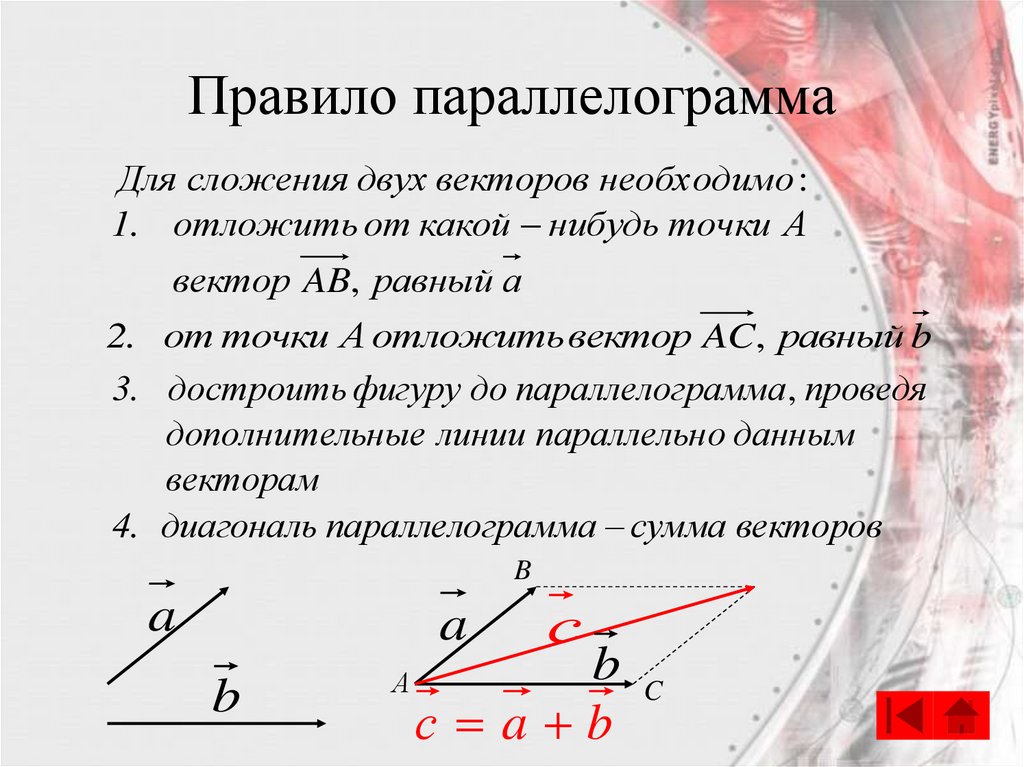
6. Правило параллелограмма

Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от точки А отложить вектор AC, равный b
3. достроить фигуру до параллелограмма , проведя
дополнительные линии параллельно данным
векторам
4. диагональ параллелограмма сумма векторов
B
a
a
b
А
с
b C
с a b

7. Свойства сложения

Для любых векторов a , b и c справедливы
равенства :
a b b a
переместительный закон
a b с а b с сочетательный закон

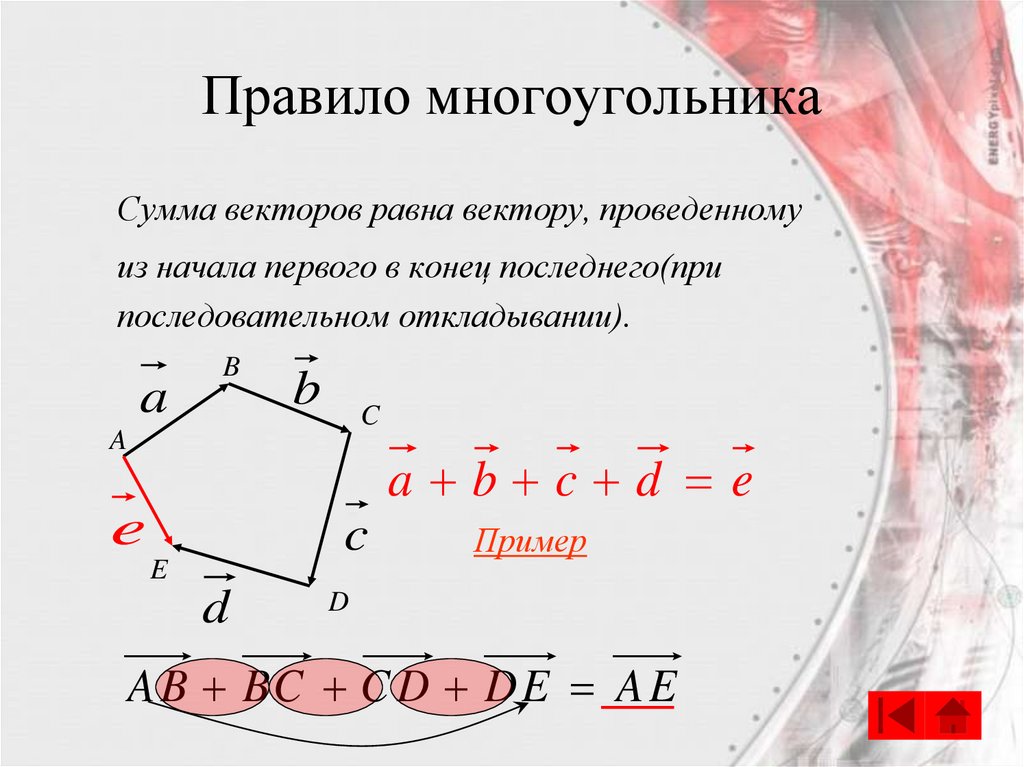
8. Правило многоугольника

Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
a b c d e
e
c
E
d
Пример
D
A B BC C D DE A E

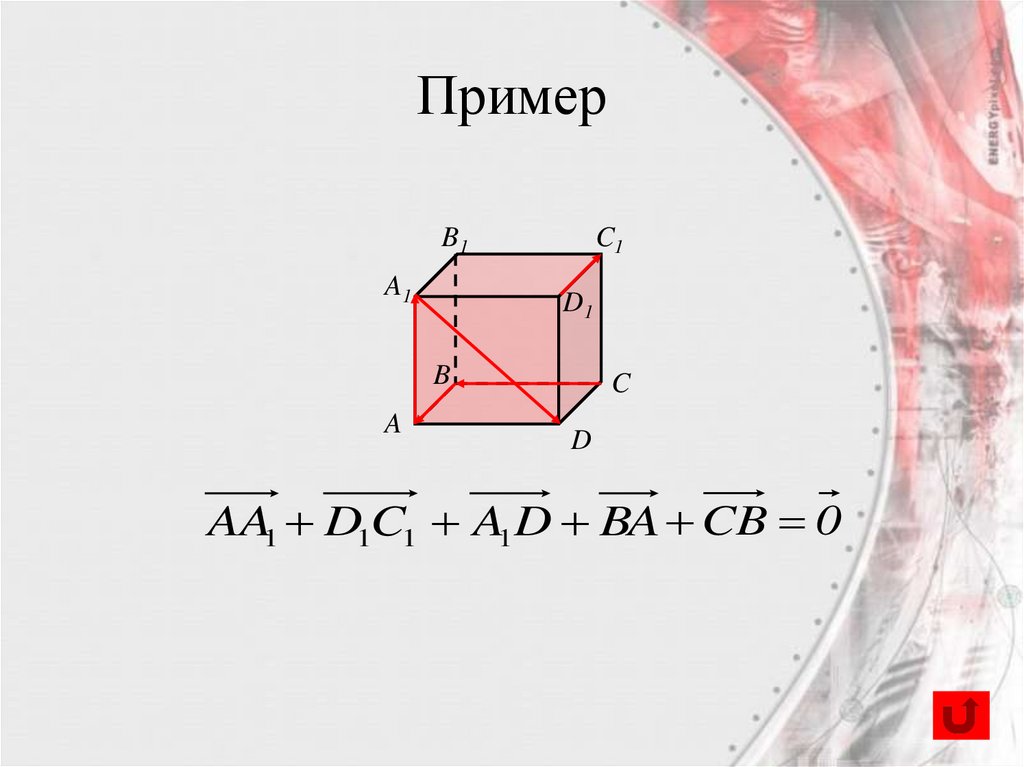
9. Пример

B1
A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0

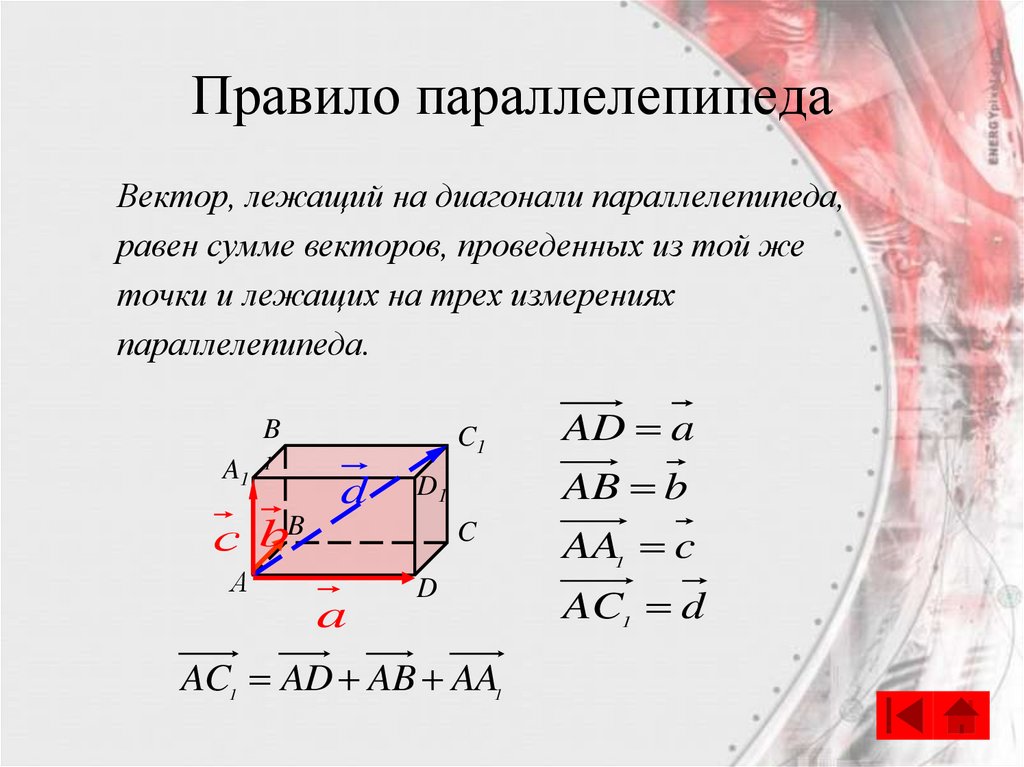
10. Правило параллелепипеда

Вектор, лежащий на диагонали параллелепипеда,
равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B
A1 1
C1
d
AB b
D1
с bB
C
А
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d

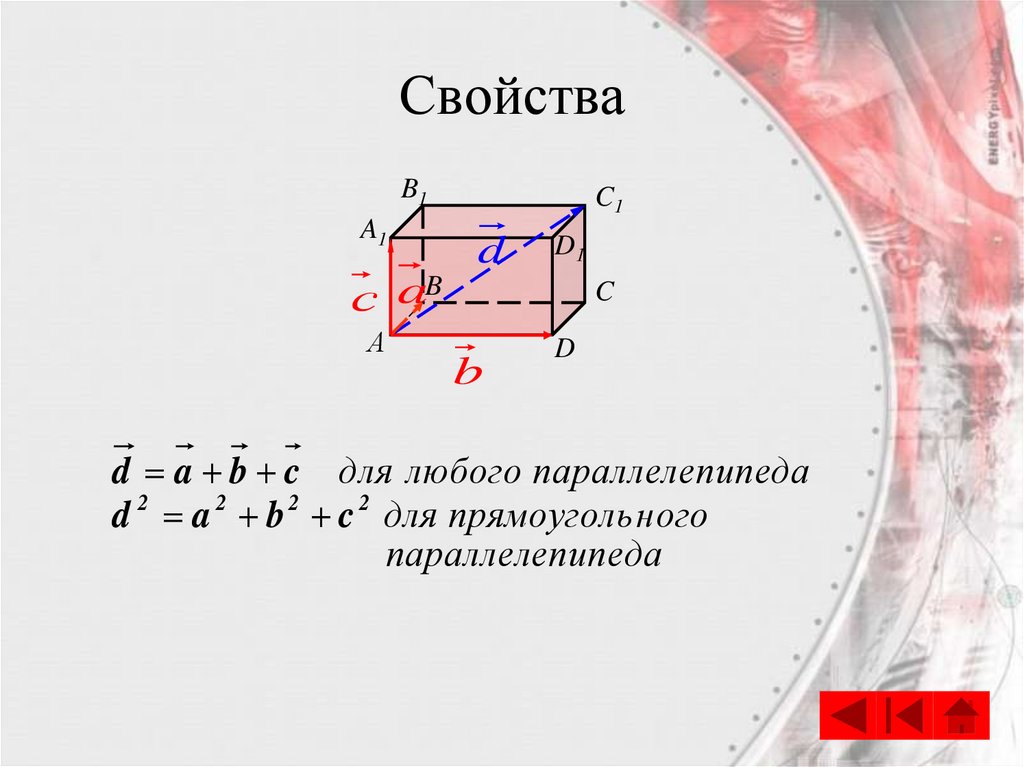
11. Свойства

B1
A1
C1
d
D1
с aB
А
C
b
D
d a b c для любого параллелеп ипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелеп ипеда

12. Вычитание векторов

• Вычитание
• Сложение с противоположным

13. Вычитание

Разностью векторов a и b называется такой
вектор, сумма которого с вектором b равна
вектору a .

14. Вычитание

Для вычитания одного вектора из другого необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
Правило трех точек
a
a b
A
b
C

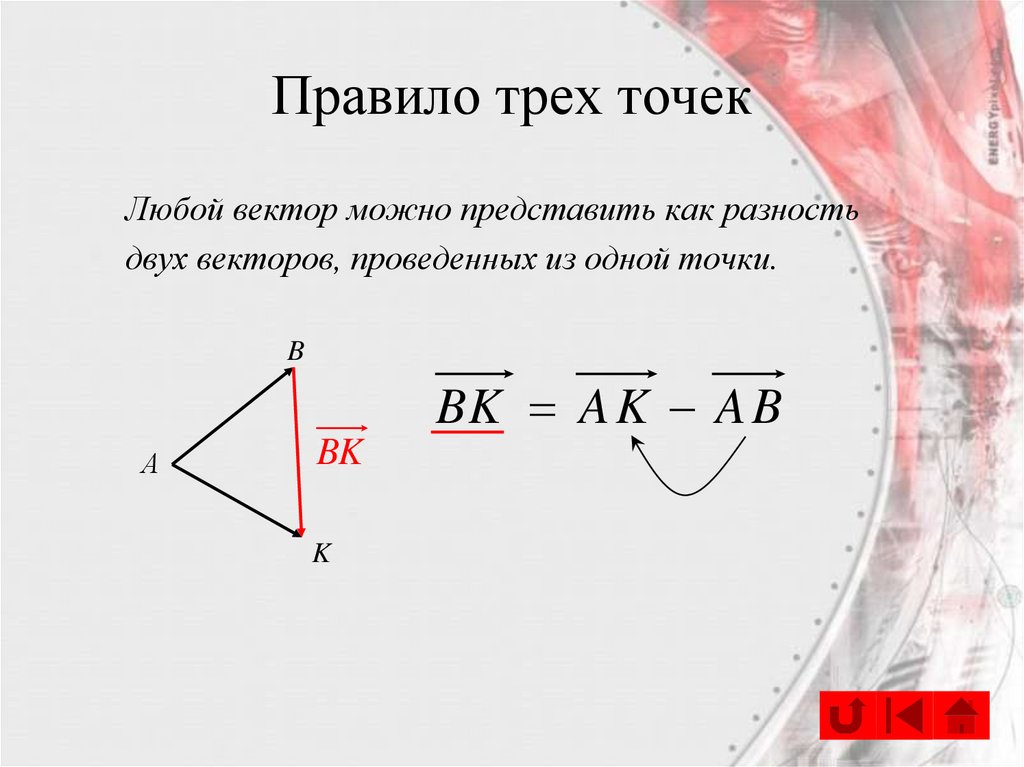
15. Правило трех точек

Любой вектор можно представить как разность
двух векторов, проведенных из одной точки.
B
BK A K A B
А
BK
K

16. Сложение с противоположным

Разность векторов a и b можно представить
как сумму вектора a и вектора,
противоположного вектору b.
a b a b
a
B
b
a b
b
O
А
a

17. Умножение вектора на число

Произведением ненулевог о вектора a на число k
называется такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3

18. Свойства

• Произведением нулевого вектора на любое число
считается нулевой вектор.
0 n 0
• Произведение любого вектора на число нуль есть
нулевой вектор.
n 0 0

19. Свойства

Для любыхвект оровa и b и любых
чисел k, l справедливы равенст ва:
(kl)a k(la )
сочет ат ельный закон
k( a b ) k a k b
1 ый распределит ельный
закон
(k l)a k a l a
2 ой распределит ельный
закон

20. Скалярное произведение

Скалярным произведением двух векторов
называется произведение их длин на косинус угла
между ними.
ab a b cos( a ; b )
Справедливые утверждения
Вычисление скалярного произведения в координатах
Свойства скалярного произведения

21. Справедливые утверждения

• скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти
векторы перпендикулярны
a b 0 a 0 b 0 a b
• скалярный квадрат вектора (т.е. скалярное
произведение вектора на себя) равен квадрату
его длины
2
a
а
2
а
2

22. Вычисление скалярного произведения в координатах

Скалярное произведение векторов a x1 ; y1 ; z1
и b x 2 ; y2 ; z 2 выражается формулой
a b x 1 x 2 y1 y 2 z 1 z 2

23. Свойства скалярного произведения

Для любых векторов a , b и с и любого
числа k справедливы равенства :
10.
2
a 0 причем a 0 при a 0
20. a b ba (переместительный закон)
(распределительный
0
a
b
c
a
c
b
c
3.
закон)
40. k a b k a b (сочетательный закон)

24. Разложение вектора

• По двум неколлинеарным векторам
• По трем некомпланарным векторам

25. Разложение вектора по двум неколлинеарным векторам

Теорема.
Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем
коэффициенты разложения определяются
единственным образом.

26. Разложение вектора по трем некомпланарным векторам

Если вектор p представлен в виде
p xa yb zc
где x, y, z – некоторые числа, то говорят, что вектор
p разложен по векторам a , b и c .
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.