Похожие презентации:
лекция 6_СВ_ДСВ
1. Теория вероятностей и математическая статистика
6. СЛУЧАЙНЫЕВЕЛИЧИНЫ
2. ФЕДЕРАЛЬНАЯ РАБОЧАЯ ПРОГРАММА
БАЗОВЫЙУРОВЕНЬ
9 КЛАСС
3. ФЕДЕРАЛЬНАЯ РАБОЧАЯ ПРОГРАММА
БАЗОВЫЙУРОВЕНЬ
10-11 КЛАСС
4. ФЕДЕРАЛЬНАЯ РАБОЧАЯ ПРОГРАММА
УГЛУБЛЁННЫЙУРОВЕНЬ
9 КЛАСС
5. ФЕДЕРАЛЬНАЯ РАБОЧАЯ ПРОГРАММА
10 КЛАССУГЛУБЛЁННЫЙ
УРОВЕНЬ
6. ФЕДЕРАЛЬНАЯ РАБОЧАЯ ПРОГРАММА
11 КЛАССУГЛУБЛЁННЫЙ
УРОВЕНЬ
7. СЛУЧАЙНАЯ ВЕЛИЧИНА (СВ)
• Случайной величиной называют величину,которая в результате испытания принимает одно
и только одно возможное значение, наперед
неизвестное и зависящее от случайных причин,
которые заранее не могут быть учтены.
• Случайной величиной Х называется числовая
функция Х=Х(ω), определенная на пространстве
элементарных исходов , которая каждому
элементарному исходу ставит в соответствие
некоторое число х таким образом, что множество
элементарных исходов ω∈ , для которых
выполняется неравенство Х<x, является
событием.
8. Примеры случайных величин
• число очков, выпавших на верхней граникубика;
• число студентов, пришедших на лекцию;
• сумма выплаты по очередному страховому
случаю;
• время за которое спортсмен пробежал
дистанцию;
• индикатор события. Пусть А – некоторое
событие. Случайная величина, которая
принимает значение, равное единице, если
событие А происходит и нулю в противном
случае, называется индикатором IA события А.
9. Связь случайной величины и случайного события
• Принятие случайной величиной Х некоторогочислового значения хi из набора возможных
(т.е. выполнение равенства Х=хi) есть
случайное событие, характеризующееся
вероятностью Р(Х=хi)=рi
10. Закон распределения
• Закономраспределения
случайной
величины называется всякое соотношение,
устанавливающее
связь
между
всеми
возможными значениями случайной величины
и соответствующими им вероятностями.
• Говорят,
что
случайная
величина
распределена по данному закону или
подчинена данному закону распределения.
Дискретные случайные
величины (ДСВ)
Непрерывные случайные
величины (НСВ)
11. Дискретные случайные величины
• Случайная величина, которая может приниматьлишь конечное или счётное число значений,
называется дискретной.
• Значения случайной величины записываются в виде
конечной или бесконечной последовательности
x1, x2, , xn,
• Примеры дискретных случайных величин:
• Число очков, выпавших на верхней грани игральной
кости. Множество возможных значений содержит 6
элементов.
• Количество звонков, принятых на телефонной
станции в течение суток. Возможные значения
образуют счетное множество: 0; 1; 2; .
12. Закон распределения дискретной случайной величины
• Закон распределения содержит всюинформацию о случайной величине, и задать
случайную величину можно, просто
представив её закон распределения.
• Законом распределения дискретной случайной
величины Х называется совокупность пар
чисел (хi; рi), т.е. её возможных значений и
соответствующих им вероятностей, причем
p 1
i
i
13. Способы задания ДСВ
• Табличный(в виде ряда
распределения)
х1
X
р1
P
х2
p2
х3
p3
хn
pn
n
p 1.
i 1
i
Вероятности, соответствующие
значениям с.в.Х
• Графический
(в
виде
многоугольника
распределения)
• Аналитический
(в виде формулы)
0,4
Р
0,3
0,2
0,1
0
х1
х2
х3
х4
х5
Х
ломаная линия с
вершинами в точках
(xi, pi)
P( X x k ) ( x k )
14. Функция распределения
• Функцией распределения случайной величиныХ называется функция F(x), значение которой для
любого действительного числа х равно
вероятности события «X<x», то есть вероятность
того, что случайная величина Х принимает
значения меньшие х: F(x)=P(X<x).
Свойства функции распределения
• 1. 0⩽F(x)⩽1 для любого x∈R.
• 2. Функция F(x) является неубывающей.
F ( x) 0,
lim F ( x) 1.
• 3. xlim
x
• 4. P(a⩽X<b)=F(b) – F(a)
• 5. Функция F(x) непрерывна слева в любой точке.
15. Функция распределения ДСВ
F(x)=P(X<x)Функция распределения ДСВ является кусочно-постоянной
X
P
х1
р1
х2
p2
х3
p3
хn
pn
n
p 1.
i 1
0
р1
р1 + р2
F ( x)
р1 + р2 + …+рn–1
1
если х х1 ;
если х1 х х2 ;
если х2 х х3 ;
если хn 1 х хn ;
если х хn .
i
16. Функция распределения ДСВ
F(x)=P(X<x)Функция распределения ДСВ является кусочно-постоянной
X
P
х1
р1
х2
p2
х3
p3
хn
n
pn
p 1.
i 1
i
0,
если х х1 ;
p1 ,
если х1 х х2 ;
p1 p2 ,
если х2 х х3 ;
F ( x) P( X xi )
xi x
p1 p2 pn 1 , если хn 1 х хn ;
1
если х хn .
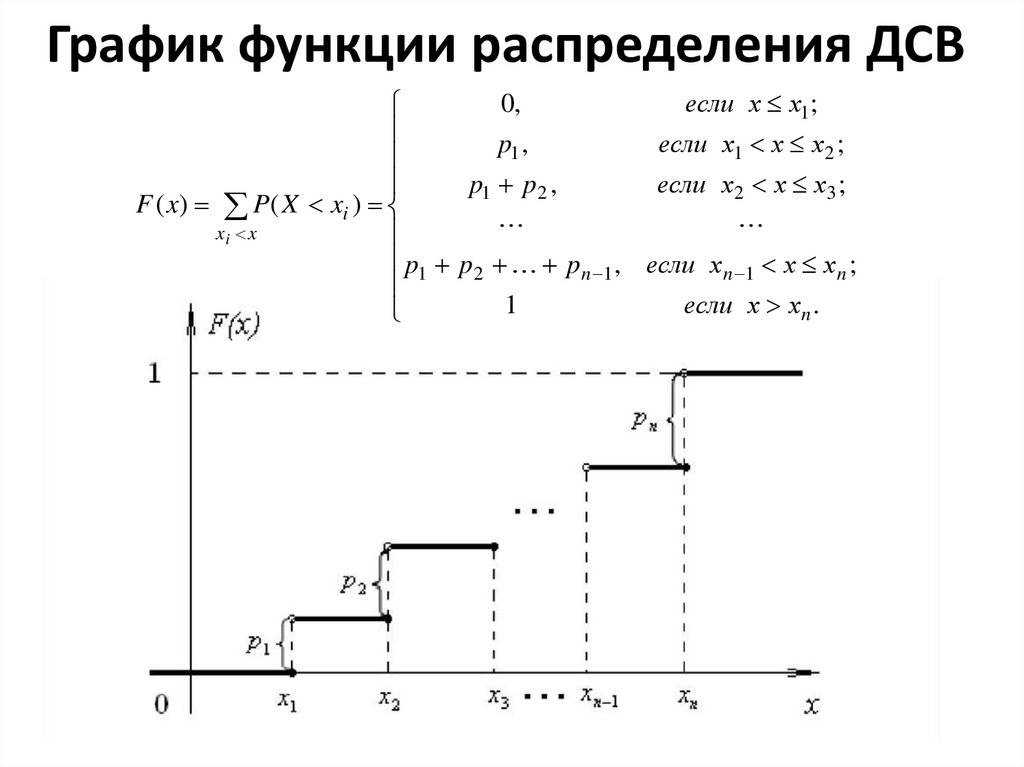
17. График функции распределения ДСВ
0,если х х1 ;
p1 ,
если х1 х х2 ;
p1 p2 ,
если х2 х х3 ;
F ( x) P( X xi )
xi x
p1 p2 pn 1 , если хn 1 х хn ;
1
если х хn .
18. Задача.
• Охотник имеет четыре патрона. Он стреляет по дичи дотех пор, пока не попадет или пока не закончатся все
патроны. Вероятность попадания при первом выстреле
равна 0,7 и при каждом следующем уменьшается на 0,1.
• Составить ряд распределения числа израсходованных
патронов. Записать функцию распределения.
Х
1
2
3
4
р1 Р( А1 ) 0,7 q1 P( A1 ) 1 р1 1 0,7 0,3;
p2 0,6 q2 0,4,
p3 0,5 q3 0,5,
p4 0,4 q4 0,6
19. Задача.
• Охотник имеет четыре патрона. Он стреляет по дичи до техпор, пока не попадет или пока не закончатся все патроны.
Вероятность попадания при первом выстреле равна 0,7 и при
каждом следующем уменьшается на 0,1.
• Составить ряд распределения числа израсходованных
патронов. Записать функцию распределения.
р1 0,7 q1 0,3; p2 0,6 q2 0,4,
p3 0,5 q3 0,5; p4 0,4 q4 0,6.
Х
1
2
3
4
0,7
0,18
0,06
0,06
1
P( X 1) P( A1 ) р1 0,7;
P( X 2) P( A1 A2 ) q1 p2 0,3 0,6 0,18;
P( X 3) P( A1 A2 А3 ) q1 q2 p3 0,3 0,4 0,5 0,06;
P( X 4) P( A1 A2 А3 ) q1 q2 q3 0,3 0,4 0,5 0,06.
20. Задача.
• Охотник имеет четыре патрона. Он стреляет по дичи до техпор, пока не попадет или пока не закончатся все патроны.
Вероятность попадания при первом выстреле равна 0,7 и при
каждом следующем уменьшается на 0,1.
• Составить ряд распределения числа израсходованных
патронов. Записать функцию распределения.
Х
1
0,7
2
0,18
3
0,06
4
0,06
1
0
x 1;
x 1;
0,
0,7, 1 x 2;
0
,
7
1
x
2
;
F (x) 0,7 0,18
2 x 3; 0,88 2 x 3;
0,7 0,18 0,06 3 x 4;
0,94, 3 x 4;
x 4.
1
1,
x 4.
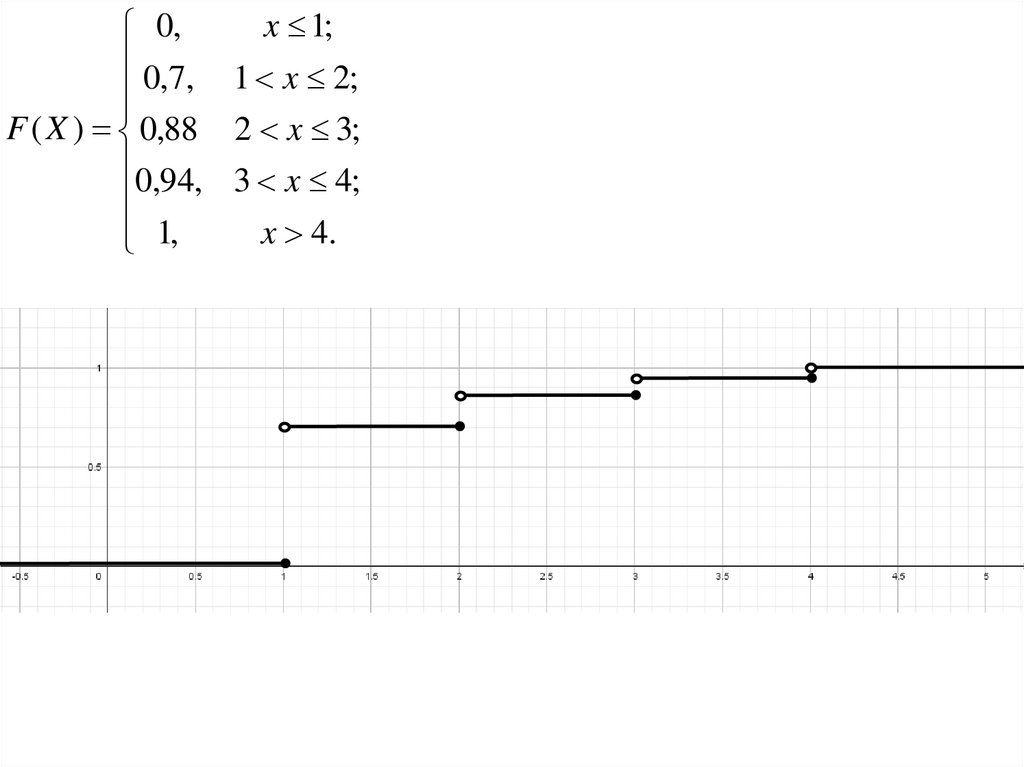
21.
x 1;0,
0,7, 1 x 2;
F ( X ) 0,88 2 x 3;
0,94, 3 x 4;
1,
x 4.
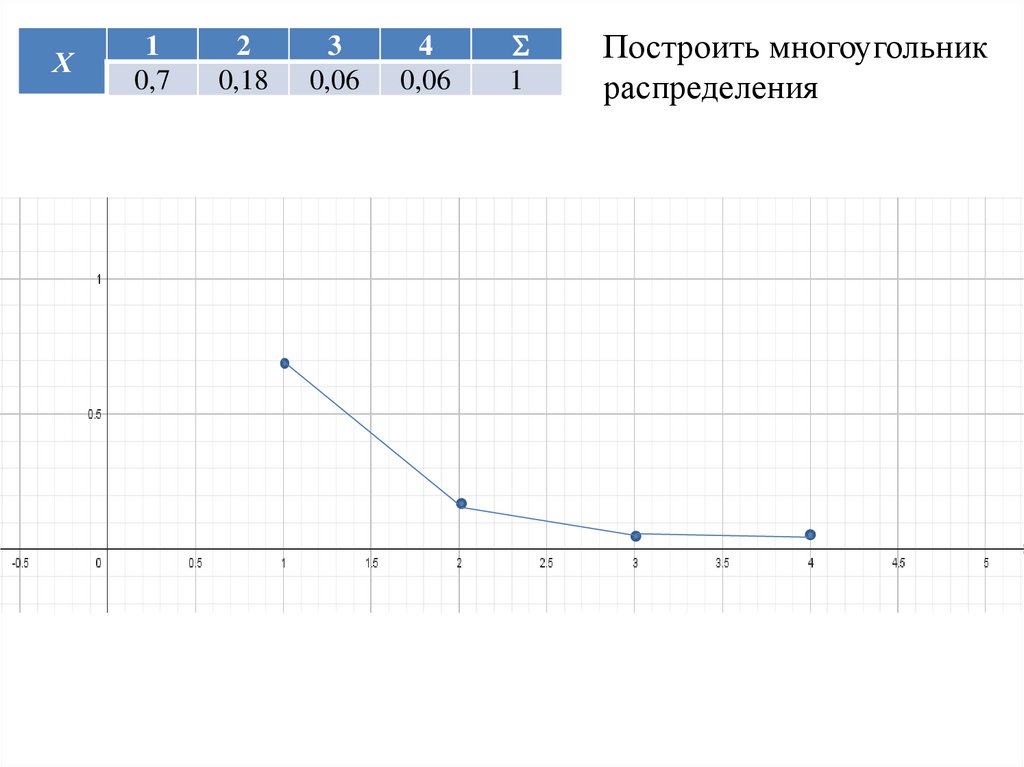
22.
Х1
0,7
2
0,18
3
0,06
4
0,06
1
Построить многоугольник
распределения
23. Действия над независимыми случайными величинами
• Дискретные случайные величины X и Yназываются независимыми, если для любых
i=1, 2, ..., n и j=1, 2, …, m события (Х=хi) и
(Y=yj) являются независимыми, то есть
вероятность совместного наступления этих
событий равна произведению их вероятностей:
P( X xi , Y y j ) P( X xi ) P(Y y j ), i, j
X = {x1,x2, ,xn}; Y = {у1, у2, ,уm}
X
P
х1
р1
х2
p2
хn
pn
Y
P
y1
р/1
y2
p/2
ym
p/m
24.
• Пусть Х – дискретная случайная величина. Новаяслучайная величина Y может быть построена по Х
с помощью заданной числовой функции Y= (Х).
n
xi
X
pi i 1
( xi )
Y
pi i 1
n
xi 2
Y X 2 p
i i 1
n
n
4x 5
Z 4 X 5
p
i
i 1
3
3
i
Замечание. Если среди полученных значений
встретятся равные, то соответствующие столбцы надо
объединить в один, сложив вероятности.
25. Пример.
12
2 1 0
.
X
0,2 0,1 0,3 0,1 0,3
( 2) 2 1 ( 1) 2 1
Y
0,1
0,2
02 1
0,3
0 1 0
3
3
0,2 0,1 0,3 0,1 0,3
3
1 0
.
Y
0,3 0,2 0,5
Y X 2 1 ?
1 1
2
0,1
2 2 1
0,3
26.
nxi
X
pi i 1
yi
; Y
p j
m
j 1
• - известны законы распределения независимых
дискретных случайных величин X и Y.
• Тогда случайная величина Z= (X, Y) также будет
дискретной, возможными значениями которой
будут числа: z11= (x1, y1), z12= (x1, y2), ,
z21= (x2, y1), z22= (x2, y2), , с вероятностями
pij P(Z zij ) P( X xi , Y y j ) pi p j .
27. Пример.
12
0
.
Х
0,5 0,2 0,3
Пример.
1
1 0
.
Y
0,1 0,6 0,3
Составить закон распределения случайной величины U=X Y
U X Y
0 ( 1) 1,
1 ( 1) 2,
2 ( 1) 3,
0 0 0,
1 0 1,
2 0 2,
0 1 1,
1 1 0,
2 1 1
pij P(Z zij ) P( X xi , Y y j ) pi p j .
0
1
2
1
0
3
2
1
1
U
0,05 0,3 0,15 0,02 0,12 0,06 0,03 0,18 0,09
0
1
2
3
1
U
0,15 0,36 0,26 0,2 0,03
n
p 1.
i 1
i
28. Основные числовые характеристики CВ
Математическоеожидание СВ
М(Х)
• - число,
характеризующее
среднее значение СВ Х
Дисперсия СВ
D(X)
• - число, характеризующее
разброс или рассеяние
значений СВ Х около ее
математического ожидания
дополнительная характеристика
рассеяния значений СВ Х вокруг
ее математического ожидания,
совпадающая по размерности со
СВ
D( X ) M ( X M ( X )) 2
Среднее квадратическое
отклонение (СКО) или
стандартное отклонение
σХ
29. Математическое ожидание ДCВ
• число, равное сумме произведений всехвозможных значений случайной величины на
n
соответствующие им вероятности
x
X i
pi i 1
n
M ( X ) x1 p1 x2 p2 ... xn pn xi pi
i 1
M ( X ) xi pi .
i 1
2
3
4
1
Х
0,7 0,18 0,06 0,06
n
среднее число израсходованных патронов
M ( X ) xi pi 1 0,7 2 0,18 3 0,06 4 0,06 1,48.
i 1
30. Свойства математического ожидания
M (X ) x p .n
M (С ) С
i 1
i
i
С=const
M (СХ ) С M ( X );
M ( X Y ) M ( X ) M (Y ) M ( X С ) M ( X ) С
M ( X Y ) M ( X ) M (Y ) для независимых случайных величин
M ( X M ( X )) 0
31. Дисперсия ДСВ
• Дисперсией случайной величины Х называетсяматематическое ожидание квадрата отклонения
случайной величины от ее математического
ожидания: D( X ) M ( X M ( X )) 2
n
D( X ) xi M ( X ) pi
i 1
2
32. Дисперсия
D( X ) M ( X M ( X ))2
D( X ) M ( X M ( X )) M ( X 2 2 X M ( X ) ( M ( X )) 2 )
2
M ( X 2 ) 2 M ( X ) M ( X ) ( M ( X )) 2 M ( X 2 ) M 2 ( X )
D( Х ) M ( X 2 ) M 2 ( X )
n
D( Х ) M ( X ) M ( X ) xi2 pi ( MX ) 2
2
2
i 1
33.
• Средним квадратическим отклонением(СКО) или стандартным отклонением
случайной величины называется
арифметический квадратный корень из ее
дисперсии:
X D( X )
34.
23
4
1
Х
0,7 0,18 0,06 0,06
среднее число израсходованных патронов
M ( X ) 1,48
D( X ) M ( X M ( X )) 2
n
D( Х ) xi MX pi (1 1,48) 2 0,7 (2 1,48) 2 0,18 (3 1,48) 2 0,06
2
i 1
(4 1,48) 2 0,06 0,16128 0,048672 0,138624 0,381024 0,7296.
M ( X 2 ) 12 0,7 2 2 0,18 32 0,06 4 2 0,06 2,92;
DX M ( X 2 ) M 2 ( X ) 2,92 (1,48) 2 2,92 2,1904 0,7296.
X 0,7296 0,854.
35. Свойства дисперсии
D( X ) 0.D(C ) 0.
Верно и обратное: если дисперсия случайной величины
равна нулю, то это постоянная случайная величина
D(СХ ) С 2 D( X ).
D( X Y ) D( X ) D(Y ) для независимых случайных величин
D( XY ) DX DY M ( X ) DY M (Y ) DX .
2
2
для независимых случайных величин
36. Пример
• Найти математическое ожидание и дисперсиюслучайной величины Z=3X-5Y-6, если известно,
что случайные величины Х и Y независимы,
M(X)=20, M(Y)=15, D(X)=4, D(Y)=2
M ( Z ) M (3 X 5Y 6) 3 M ( X ) 5 M (Y ) 6 3 20 5 15 6 21.
D( Z ) D(3 X 5Y 6) 32 DX 52 DY 0 9 4 25 2 86.
37. Основные дискретные распределения
• Распределение Бернулли (биномиальноераспределение) определяется как закон
распределения случайной величины, равной
числу успехов в испытаниях Бернулли. Эта
случайная величина имеет два параметра: n∈N и
0<p<1, может принять любое из значений:
0,1,2,…,n вероятности которых вычисляются по
формуле Бернулли P( X m) Cnm p m q n m .
X ~ Bin(n; p)
M ( X ) np; D( X ) npq.
38. Основные дискретные распределения
• Случайная величина, распределенная по законуПуассона, может принять любое из значений 0, 1,
2, …, k, … с вероятностями, вычисляемыми по
формулам Пуассона:
m
Р( X m)
X ~ П ( )
M ( X ) ;
m!
e .
D( X ) .
Потоком событий называют последовательность событий,
которые наступают в случайные моменты времени.
Интенсивностью потока λ называют среднее число событий,
которые появляются в единицу времени.
Если постоянная интенсивность потока известна, то вероятность
появления m событий за время t определяется формулой: m
( t )
Pt (m)
e t .
m!
39. Основные дискретные распределения
Геометрическое распределение имеет случайнаявеличина Х, равная числу испытаний Бернулли до
первого «успеха» включительно. Эта случайная
величина полностью определяется одним параметром
0<p<1 вероятностью успеха в одном испытании, она
принимает значения 1, 2, 3, …, m, ... с вероятностями,
которые определяются формулой
Р( X m) q m 1 p,



























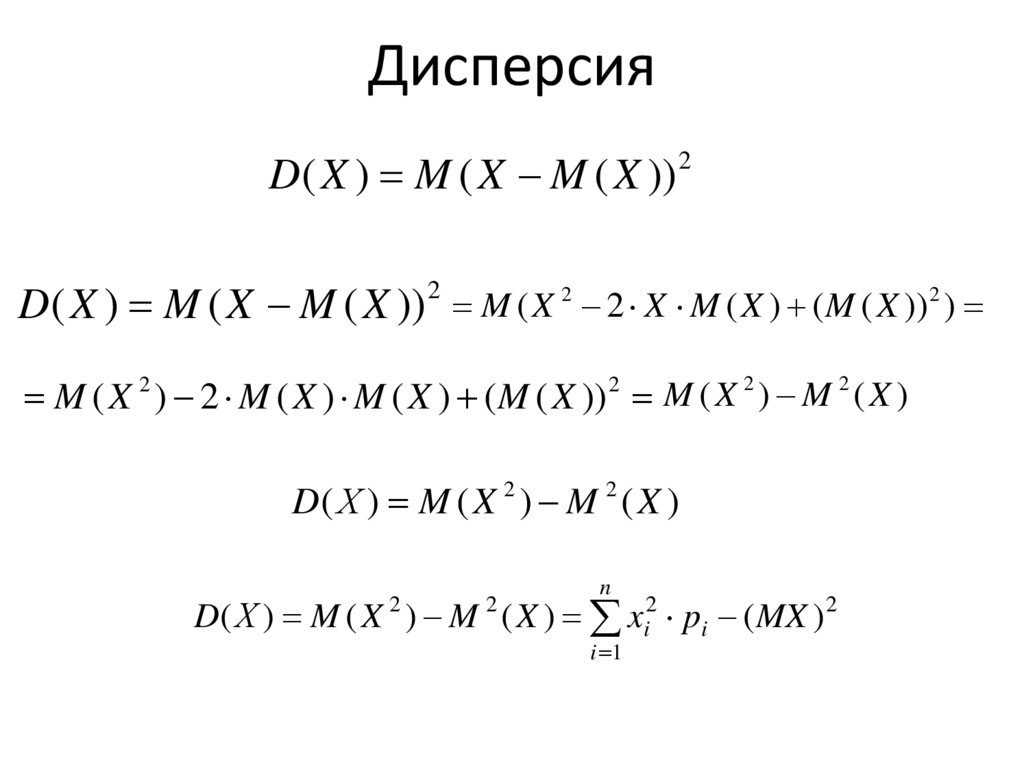








 Математика
Математика








