Похожие презентации:
Использование фотохромных превращений центров окраски в кристаллах фторида кальция для создания голографической среды
1. Выпускная квалификационная работа ИСПОЛЬЗОВАНИЕ ФОТОХРОМНЫХ ПРЕВРАЩЕНИЙ ЦЕНТРОВ ОКРАСКИ В КРИСТАЛЛАХ ФТОРИДА КАЛЬЦИЯ ДЛЯ СОЗДАНИЯ ГОЛО
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕВЫСШЕГО ОБРАЗОВАНИЯ
“САНКТ-ПЕТЕРБУРГСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ,
МЕХАНИКИ И ОПТИКИ”
Факультет фотоники и оптоинформатики
кафедра оптоинформационных технологий и материалов
Выпускная квалификационная работа
ИСПОЛЬЗОВАНИЕ ФОТОХРОМНЫХ ПРЕВРАЩЕНИЙ ЦЕНТРОВ ОКРАСКИ В
КРИСТАЛЛАХ ФТОРИДА КАЛЬЦИЯ ДЛЯ СОЗДАНИЯ ГОЛОГРАФИЧЕСКОЙ
СРЕДЫ В ВИДИМОЙ И ИНФРАКРАСНОЙ ОБЛАСТЯХ СПЕКТРА
Студентка группы 4351: Аксенова К.А.
Научный руководитель:Щеулин А.С., д.ф.-м.н.
Санкт-Петербург, 2015
2.
Актуальность работыПостэкспозиционная
фототермическая
обработка
кристалла фторида кальция предоставляет возможность
получать эффективные голограммы для ИК диапазона
спектра.
Метод, основанный на теории Крамерса- Кронига,
позволяет прогнозировать свойства таких голограмм
по спектру поглощения фотохромного кристалла.
Такие голограммы могут быть использованы в качестве
пропускающих
и
отражательных
голографических
интерференционных
фильтров
с
необходимым
пропусканием или отражением на той или иной длине
волны.
2
3.
Цель и задачи работыЦель : получение данных о голографических свойствах кристалла
флюорита в инфракрасной области спектра
Задачи :
1. Исследование спектральных характеристик кристаллов флюорита,
содержащих фотохромные центры окраски, описание методики их
измерения
2. Рассмотрение процессов записи голограммы в кристаллах фторида
кальция
3. Разработка методики расчета голографических характеристик
объемных пропускающих и отражательных голограмм в кристалле фторида
кальция с помощью теории Крамерса-Кронига
4. Расчет голографических характеристик кристалла фторида кальция с
фотохромными центрами окраски в ближнем и среднем ИК-диапазоне
спектра по измеренным спектрам поглощения кристалла
5. Анализ полученных данных и формулировка выводов о возможности
использования среды в ближней и средней ИК-области спектра.
3
4.
Спектральные характеристики кристаллафлюорита
1.0
Толщина образца 10 мм
Пропускание T,%
0.8
0.6
0.4
0.2
0.0
0.1
Спектр пропускания чистого
флюорита
1
Длина волны, мкм
10
Пропускание аддитивноокрашенного кристалла
4
5.
Формирование центров окраски в кристаллахфторида кальция
Структура
флюорита
2+
Ca
F
Li
Fv
Постоянная решетки
0.54626 нм
Плотность
3.180 г/см3
Показатель преломления
1.433
Область прозрачности
130–10000 нм
Температурная
-8.65·10-6 1/K
дисперсия
показателя
преломления
Коэффициент линейного 18.9·10-6 1/K
расширения
Выращенный (справа) и равномерно
окрашенный по объему (слева) образцы CaF2
толщиной 6 мм и диаметром 15 мм
5
6.
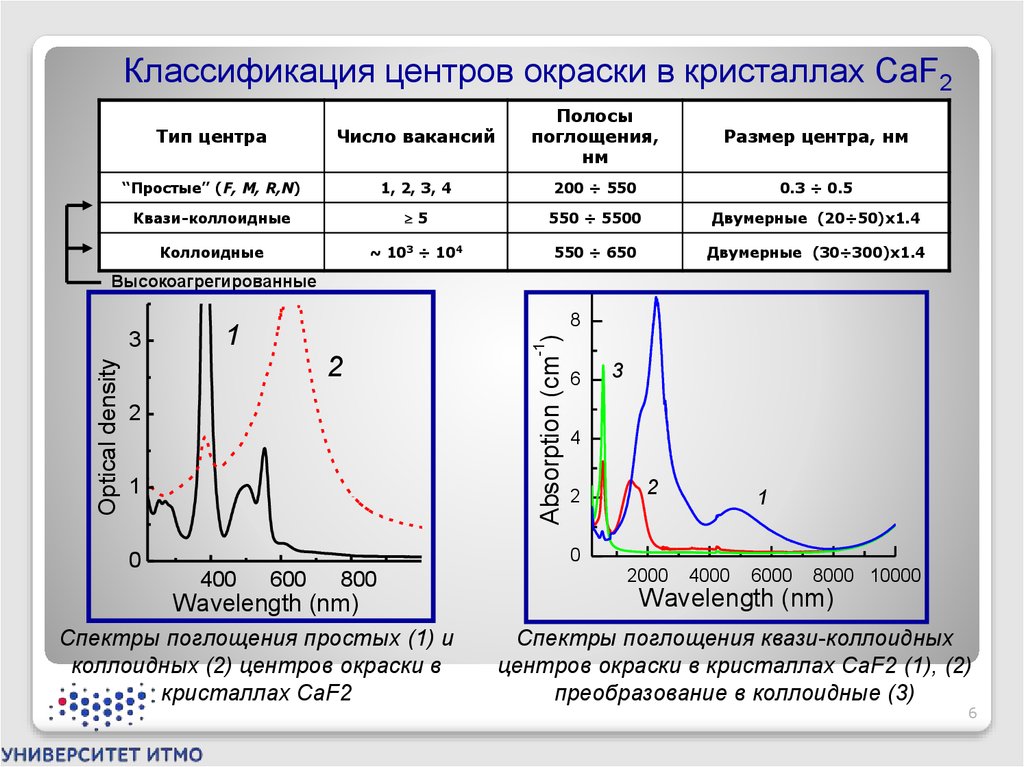
Классификация центров окраски в кристаллах CaF2Тип центра
Число вакансий
Полосы
поглощения,
нм
“Простые” (F, M, R,N)
1, 2, 3, 4
200 ÷ 550
0.3 ÷ 0.5
Квази-коллоидные
5
550 ÷ 5500
Двумерные (20÷50)х1.4
Коллоидные
~ 103 ÷ 104
550 ÷ 650
Двумерные (30÷300)х1.4
Размер центра, нм
Высокоагрегированные
-1
2
2
1
0
Absorption (cm )
Optical density
3
8
1
6
3
4
2
2
1
0
400
600
800
Wavelength (nm)
Спектры поглощения простых (1) и
коллоидных (2) центров окраски в
кристаллах CaF2
2000
4000
6000
8000 10000
Wavelength (nm)
Спектры поглощения квази-коллоидных
центров окраски в кристаллах CaF2 (1), (2)
преобразование в коллоидные (3)
6
7.
Оптическая плотность6
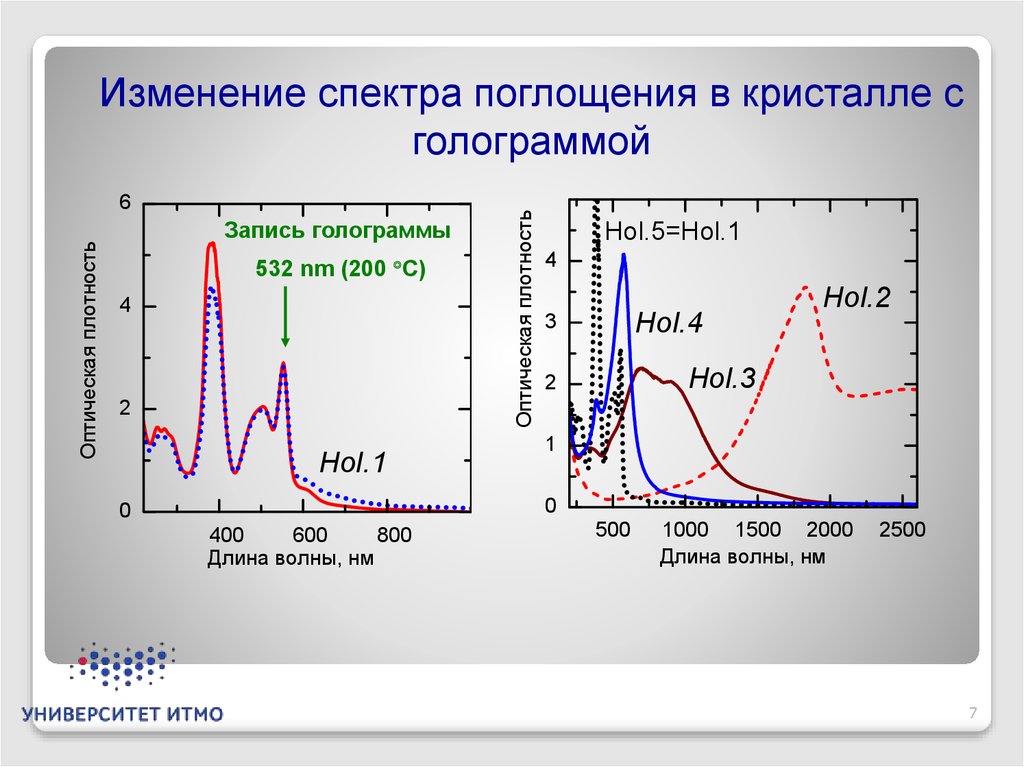
Запись голограммы
532 nm (200 C)
4
2
Hol.1
Оптическая плотность
Изменение спектра поглощения в кристалле с
голограммой
Hol.5=Hol.1
4
Hol.4
3
Hol.2
Hol.3
2
1
0
0
400
600
800
Длина волны, нм
500
1000 1500 2000
Длина волны, нм
2500
7
8.
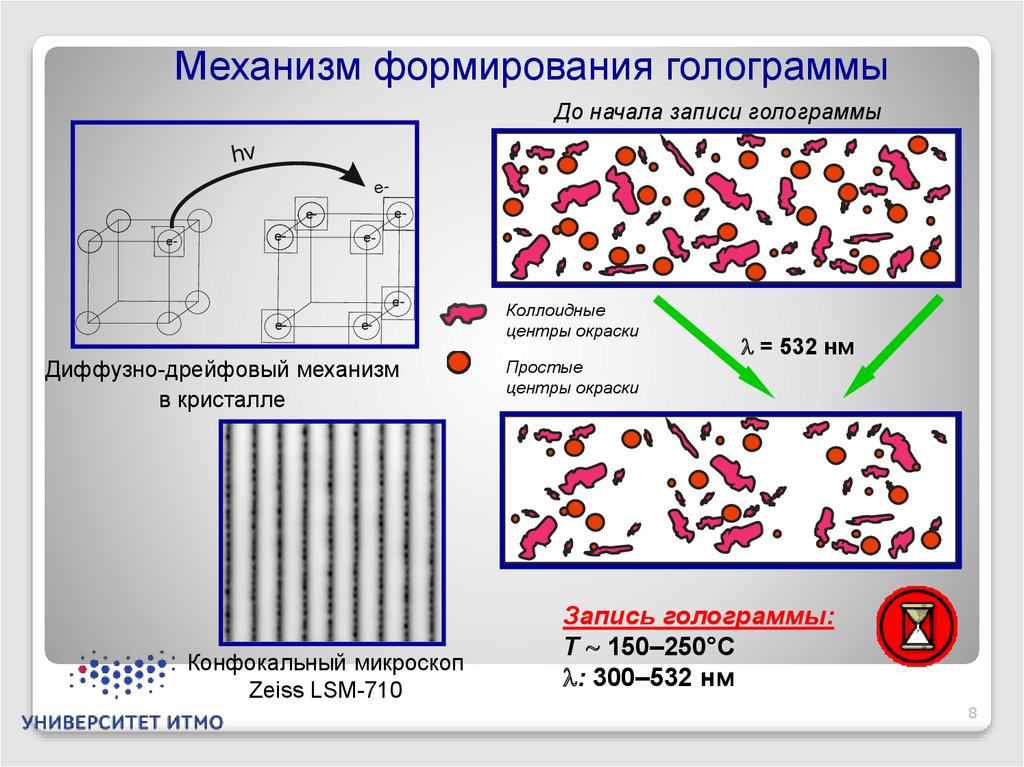
Механизм формирования голограммыДо начала записи голограммы
hv
ee-
ee-
e-
e-
ee-
e-
Диффузно-дрейфовый механизм
в кристалле
Конфокальный микроскоп
Zeiss LSM-710
Коллоидные
центры окраски
Простые
центры окраски
= 532 нм
Запись голограммы:
T 150–250°C
: 300–532 нм
8
9.
Степень пространственногоперераспределения центров окраски
10
8
15
6
10
4
5
0
-40
ДЭ, %
Пропускание, %
20
2
0
-20
0
20
Угол, угл. мин.
40
Контура угловой селективности ДЭ в нулевом
(пропускание) и первом порядках дифракции
9
10.
Расчет по методу Крамерса- Кронигаc0 ( )d Формула Крамерса-Кронига
n( 1 ) 2 2 2 .
2 0 1
гдес0 – скорость света, ν – волновое число, δα(ν) – амплитуда модуляции
показателя поглощения в образце сголограммой на длине волны =1/ν, δn(ν1) –
амплитуда модуляции показателя преломления в образце с голограммой.
2 x
( x) cos
h
Пространственная
зависимость
показателя
поглощения
(α)от
координаты χ в кристалле с
голограммой
Область интегрирования в формуле выбирается равной области
прозрачности кристалла 200нм - 9,6 мкм
Амплитуда
модуляции
концентрации
центров
окраски
предполагается равной 100%. Эта величина равна среднему спектру
поглощению кристалла.
( ) ( )
10
11.
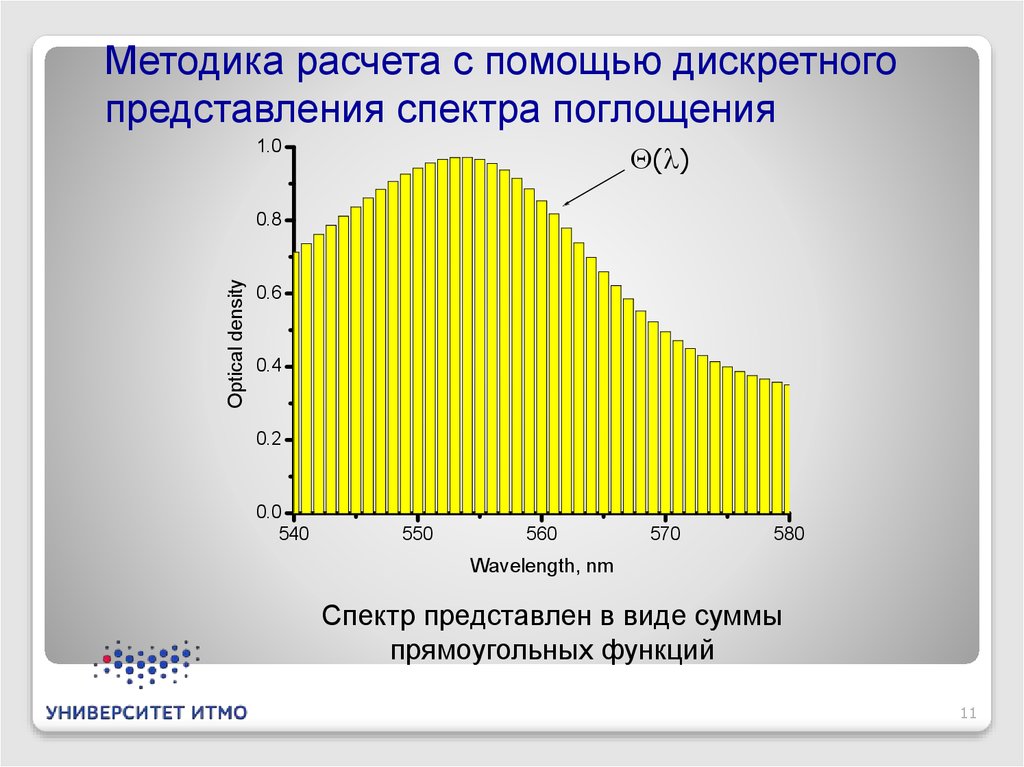
Методика расчета с помощью дискретногопредставления спектра поглощения
1.0
( )
Optical density
0.8
0.6
0.4
0.2
0.0
540
550
560
570
580
Wavelength, nm
Спектр представлен в виде суммы
прямоугольных функций
11
12.
Результаты расчета-4
2.5x10
-4
2.0x10
-4
n
1.5x10
-4
1.0x10
-5
5.0x10
0
1
2
3
-5
-5.0x10
-4
-1.0x10
2000
4000
6000
Длина волны, нм
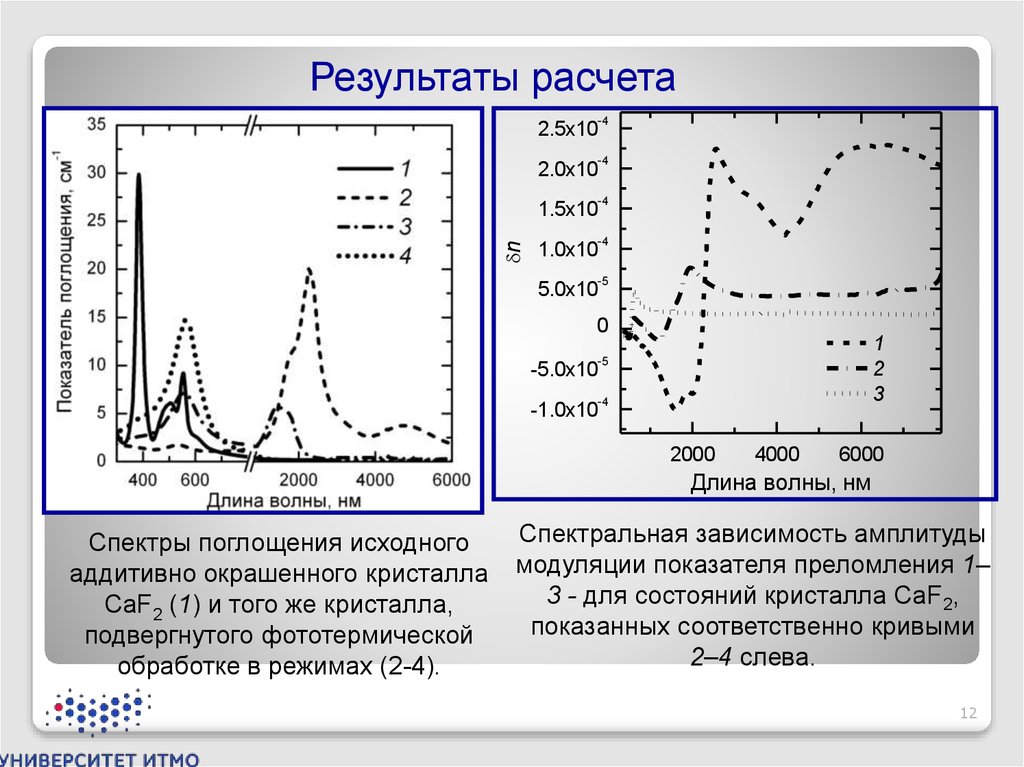
Спектры поглощения исходного
аддитивно окрашенного кристалла
CaF2 (1) и того же кристалла,
подвергнутого фототермической
обработке в режимах (2-4).
Спектральная зависимость амплитуды
модуляции показателя преломления 1–
3 - для состояний кристалла CaF2,
показанных соответственно кривыми
2–4 слева.
12
13.
Расчет дифракционной эффективностиФормулы для расчета дифракционной эффективности по величине
амплитуд модуляции показателя преломления и показателя поглощения
0
0
z
T
cos
z
T
sin
2
2
2
0
0
2
2 T 1 2
m ( ) 2 exp
cosh
cos
cos
cos
cos z 0
где 0( ), m( ) (m ≥ 1)-нулевой и следующие порядки
где – средний коэффициент поглощения образца с голограммой на
длине волны считывания, n = 1.43 – средний показатель преломления для той
же длины волны, T – эффективная толщина голограммы, κ1 = π n/λ, κ2 = /2,
4 n sin m
[ 2 4( 12 22 )]
0 acos
z0
(sin sin m )
1/ 2
z0 ( 4( )) (8 1 2 )
2
2
1
2
2
2
2
Carretero L., Madrigal R.F., Fimia A., Blaya S., Beléndez A. Study of angular responses
of mixed amplitude–phase holographic gratings: shifted Borrmann effect // Opt. Lett.
2001. V. 26. № 11. P. 786-788.
13
14.
Спектральные зависимости дифракционнойэффективности пропускающих голограмм
30
25
ДЭ, %
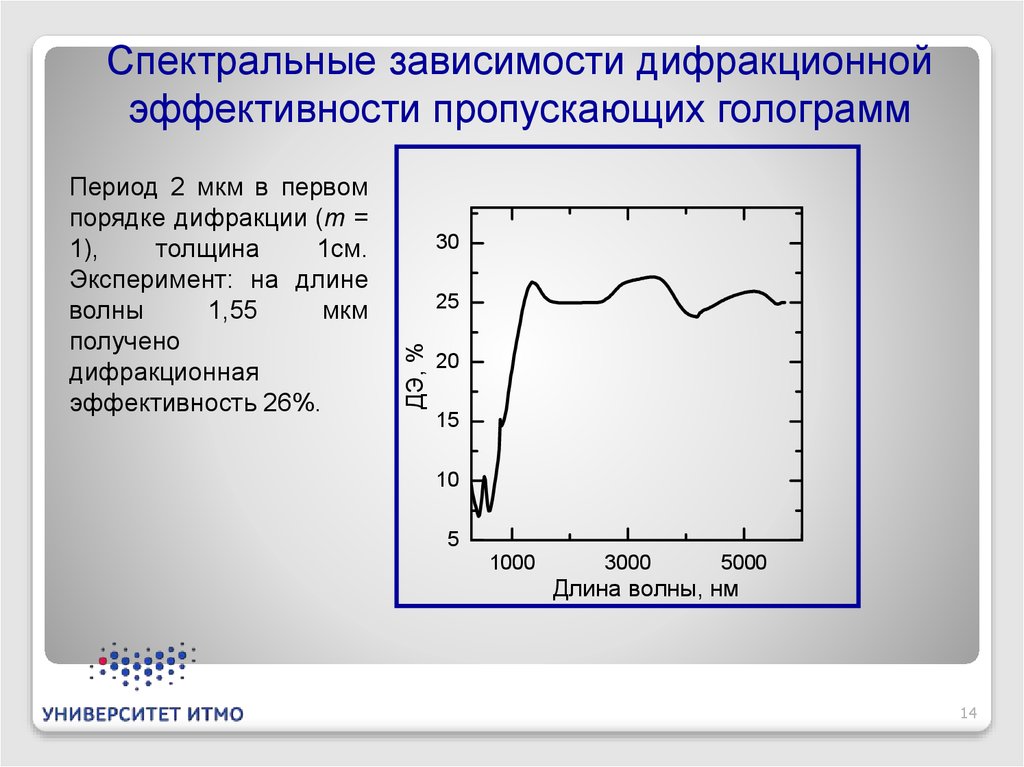
Период 2 мкм в первом
порядке дифракции (m =
1),
толщина
1см.
Эксперимент: на длине
волны
1,55
мкм
получено
дифракционная
эффективность 26%.
20
15
10
5
1000
3000
5000
Длина волны, нм
14
15.
ВыводыРазработана
модель
формирования
голограммы
позволяющая
рассчитывать
ее
дифракционные
характеристики по спектру поглощения.
2)установлена
высокая
степень
пространственной
модуляции концентрации центров окраски в кристалле с
голограммой.
3)Для получения образцов голограмм в кристаллах
толщиной менее 10 мм необходимо использовать более
интенсивно окрашенные кристаллы с большим показателем
поглощения.
15
16.
Благодарю за внимание!!!E-mail: Aksen.a.k@mail.ru
16










 Физика
Физика








