Функция у=х2 и её график

1. Функция y = x2 и её график

Функция y =
и её график
2
x
Урок алгебры в 7 классе.

2. «Величие человека в его способности мыслить»

Блез Паскаль

3. Фалес:

- Что есть больше всего на свете?
- Пространство.
- Что быстрее всего?
- Ум.
-
Что мудрее всего?
Время.
Что приятнее всего?
Достичь желаемого результата.

4.

(2;-2)
(- 2;2)
(1;2)
(-2; 2)
(-1;1)
(1;-1)
(2;2)
Ф
У
Н
К
Ц
И
Я

5.

Объясните термины
Функция
График функции
Область
определения
Аргумент
Линейная функция

6.

Укажите
область определения функции:
y = 16 – 5x
10
y
х
х – любое
число
х≠0
1
y
х 7
х≠7

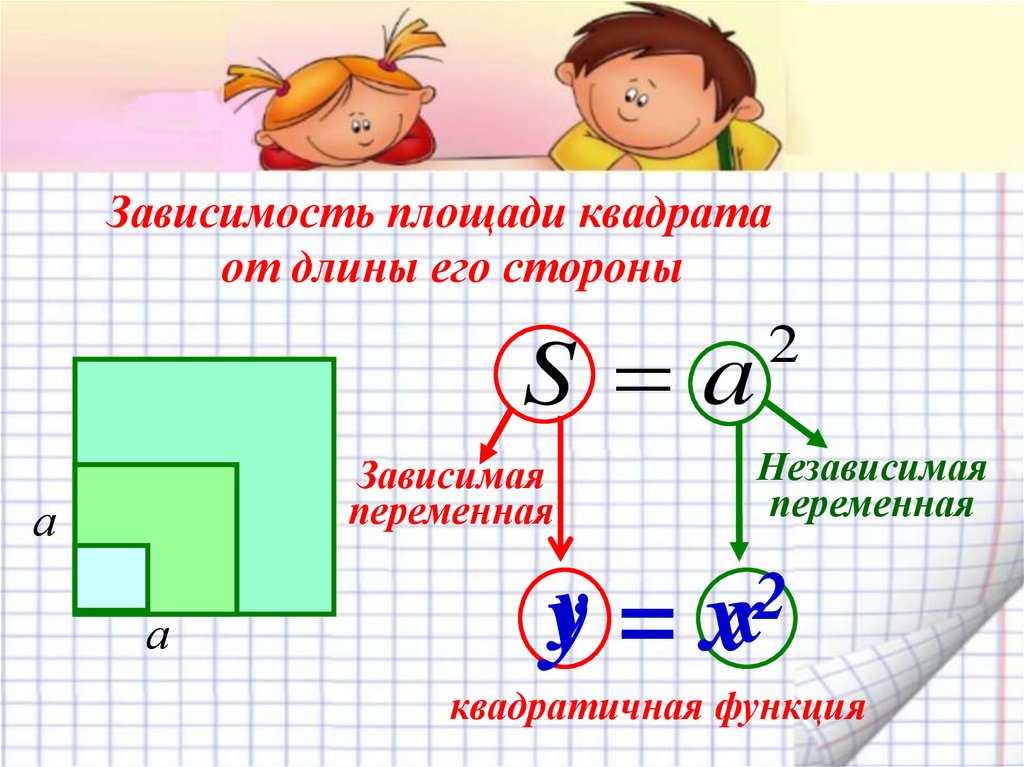
7. Зависимость площади квадрата от длины его стороны

S a
Зависимая
переменная
а
а
2
Независимая
переменная
2
y
y = xx
квадратичная функция

8. Функция y = x2 и её график

Функция y =
и её график
2
x

9. Цели урока:

• рассмотреть график и свойства
функции у = х2 ;
• научиться строить и «читать» график
данной функции.

10.

Оноре де Бальзак
Ключом ко всякой науке
является вопросительный
знак?

11.

Математическое
исследование
Функция y =
2
x

12.

Заполните таблицу значений функции y = x2:
х
y
- 3 - 2,5
9
6,25
4
2,25
1
0,25
0
х
y
0
0,5
1
1,5
2
2,5
3
0
0,25
1
2,25
4
6,25
9
- 2 - 1,5
- 1 - 0,5
0

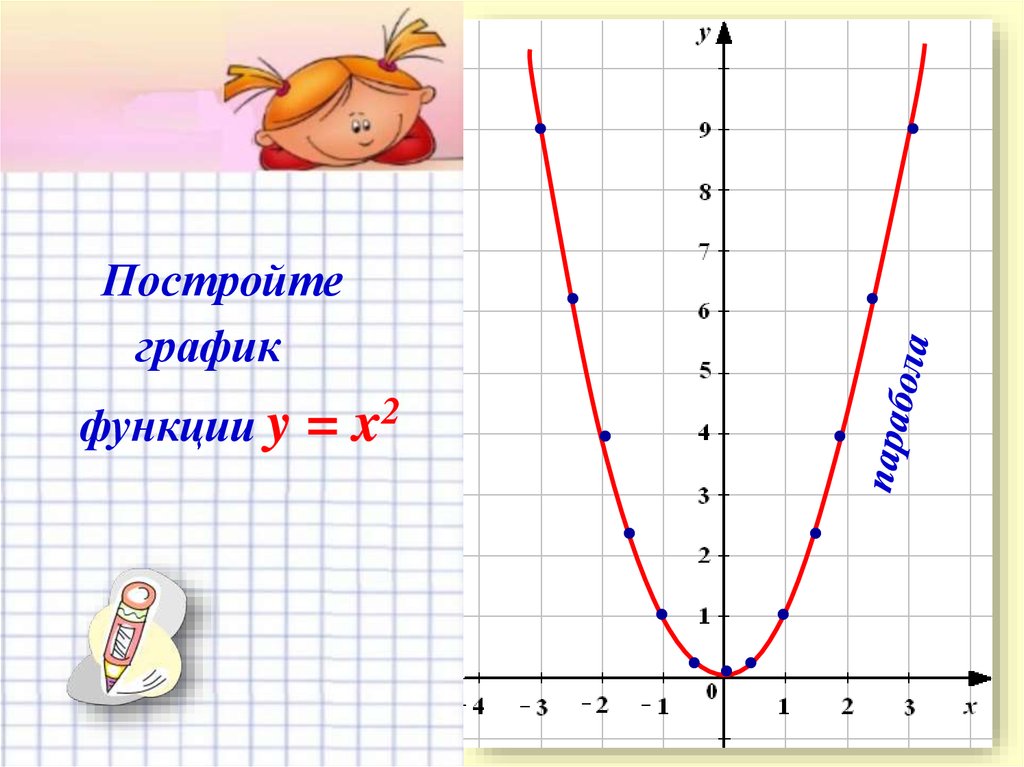
13.

Постройте
график
функции y
= x2

14.

Историческая справка
Древнегреческий математик
Аполлоний Пергский
( Перге, 262 до н.э. — 190 до н.э.)
разрезав конус, линию среза назвал
параболой, что в переводе с греческого
означает «приложение» или «притча»,
о чём математик и написал в
восьмитомнике «Конические сечения».
И долгое время параболой называли
лишь линию среза конуса, пока не
появилась квадратичная функция.

15.

Знаете ли вы?
Траектория камня,
брошенного под углом к
горизонту

16.

Невероятно,
но факт!
Перевал Парабола

17. Свойства функции y = x2

Свойства функции
y=
2
x

18.

• Область
определения
функции :
х – любое число.
• Область значений
функции:
все значения у ≥ 0.

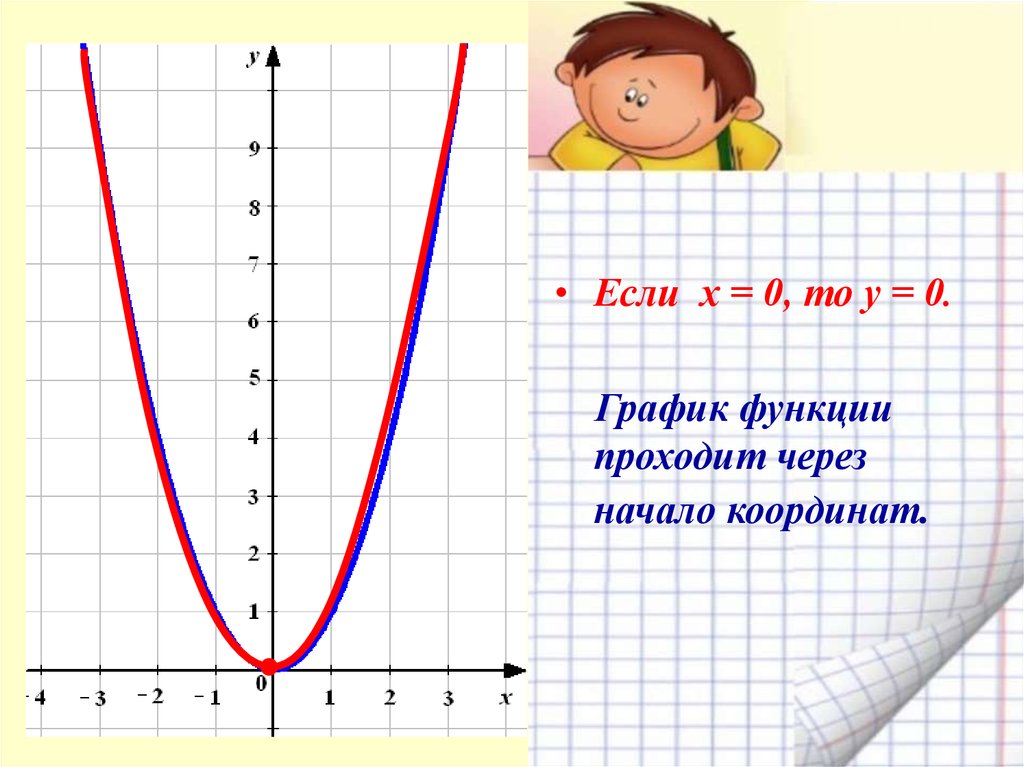
19.

• Если х = 0, то у = 0.
График функции
проходит через
начало координат.

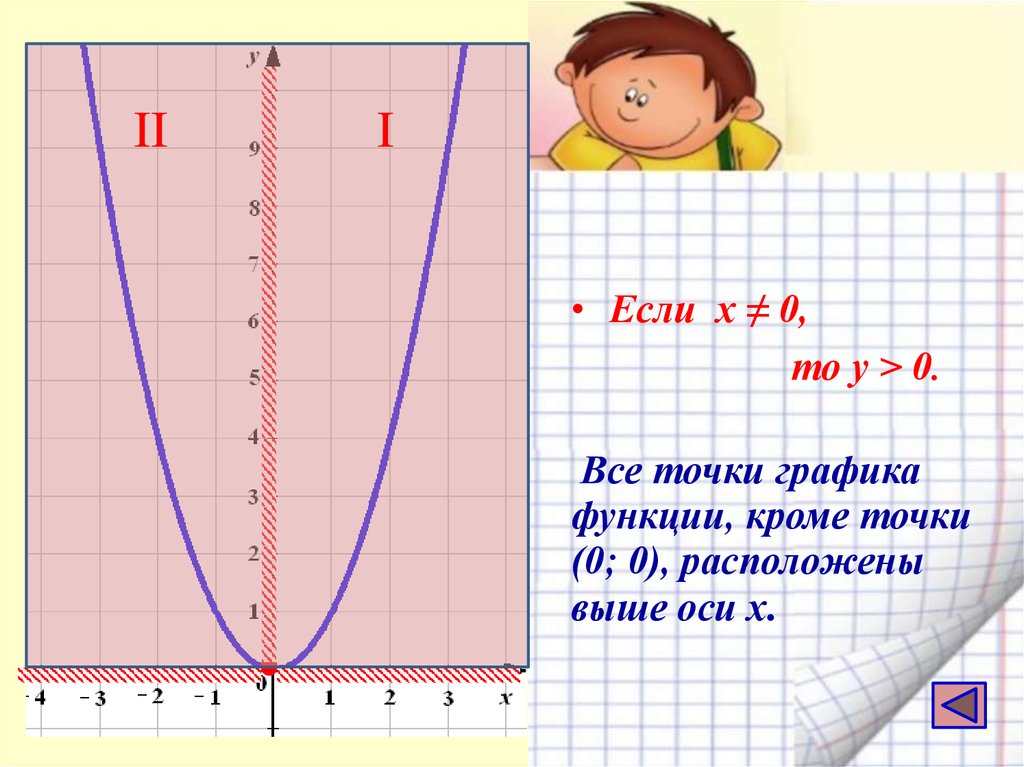
20.

II
I
• Если х ≠ 0,
то у > 0.
Все точки графика
функции, кроме точки
(0; 0), расположены
выше оси х.

21.

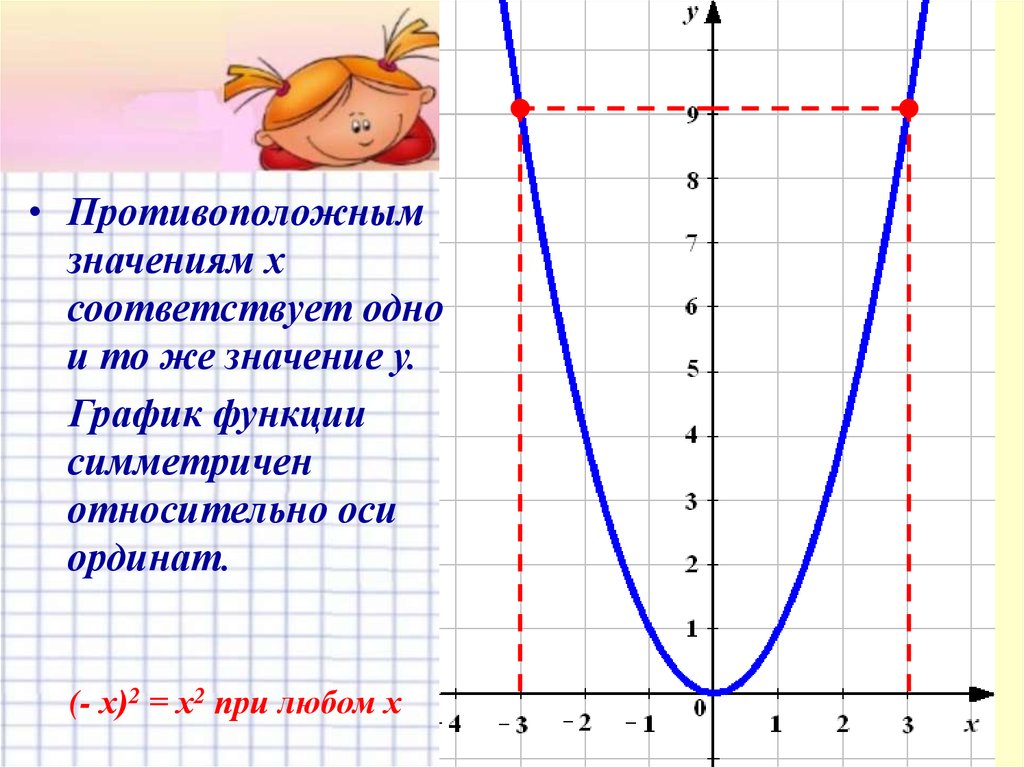
• Противоположным
значениям х
соответствует одно
и то же значение у.
График функции
симметричен
относительно оси
ординат.
(- х)2 = х2 при любом х

22.

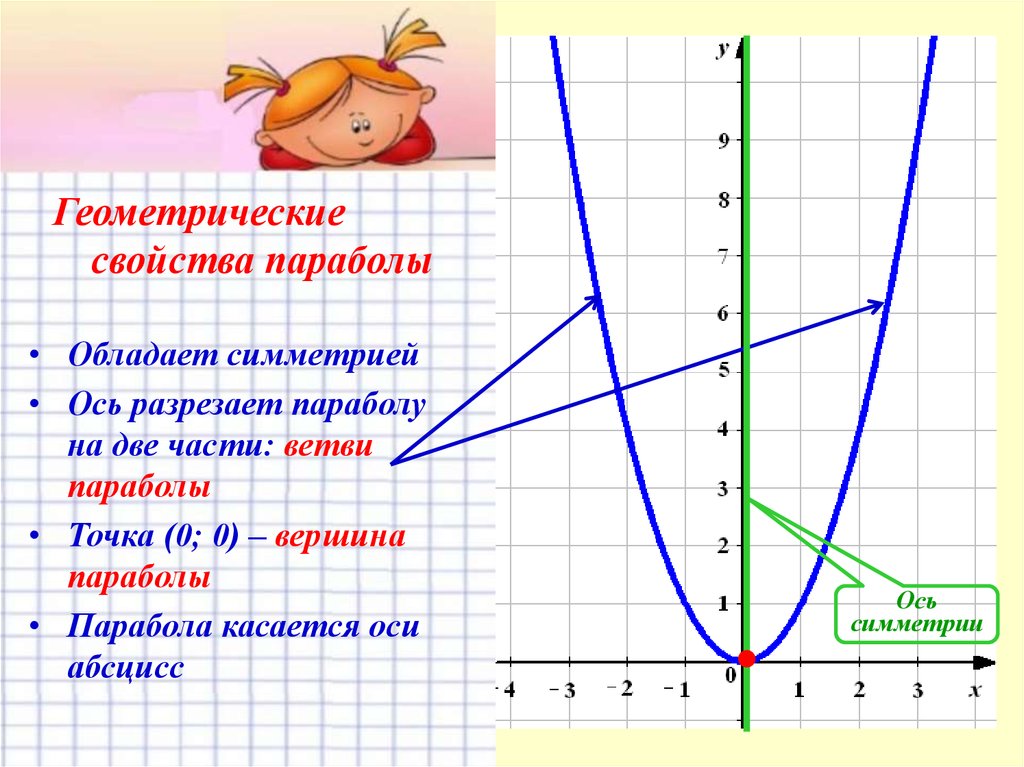
Геометрические
свойства параболы
• Обладает симметрией
• Ось разрезает параболу
на две части: ветви
параболы
• Точка (0; 0) – вершина
параболы
• Парабола касается оси
абсцисс
Ось
симметрии

23.

Найдите у, если:
«Знание – орудие,
а не цель»
х = 1,4 - 1,4
у ≈ 1,9
х = - 2,6
у ≈ 6,7
х = 3,1 - 3,1
у ≈ 9,6
Найдите х, если:
Л. Н. Толстой
у=6
у=4
х ≈ 2,5 х ≈ -2,5
х=2
х=-2

24.

Найдите
несколько значений
х, при которых
значения функции :
меньше 4
больше 4

25.

• Принадлежит ли графику функции у = х2 точка:
P(-18; 324)
R(-99; -9081)
принадлежит
не принадлежит
S(17; 279)
не принадлежит
• Не выполняя вычислений, определите, какие из
точек не принадлежат графику функции у = х2:
(-1; 1)
(-2; 4)
(0; 8)
(3; -9)
(1,8; 3,24)
(16; 0)
• При каких значениях а точка Р(а; 64) принадлежит
графику функции у = х2.
а = 8; а = - 8

26.

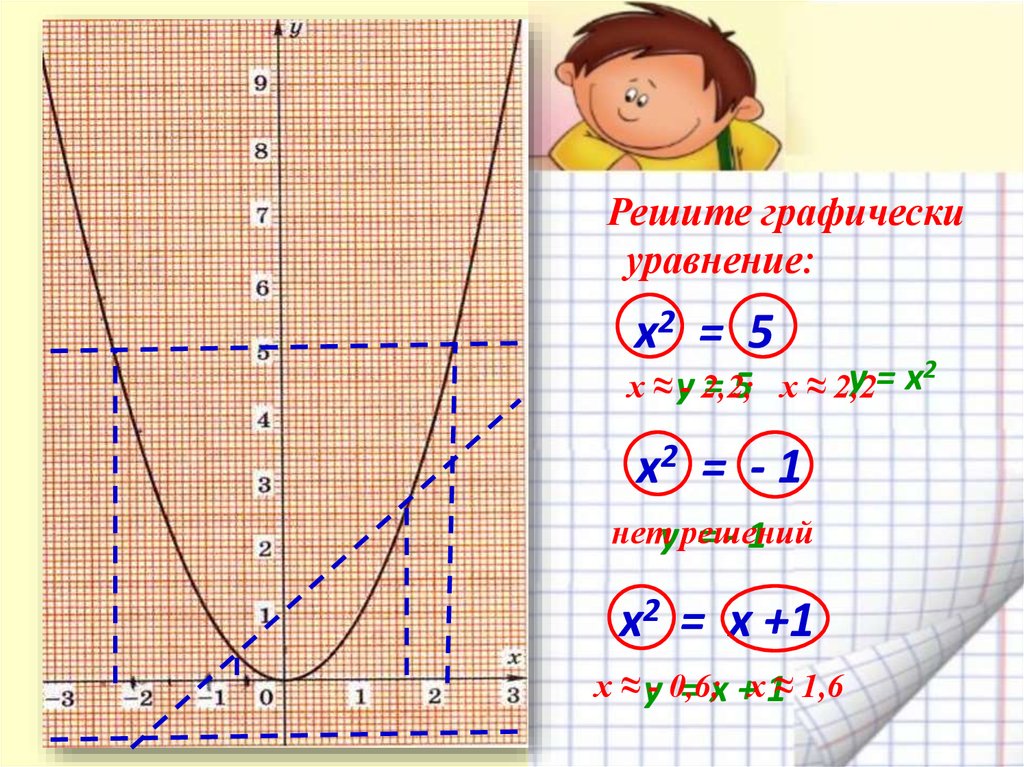
Решите графически
уравнение:
х2 = 5
y=х
х ≈ y- 2,2;
= 5 х ≈ 2,2
х2 = - 1
нетy решений
=-1
x2 = х +1
х ≈ y- 0,6;
= x +х1≈ 1,6
2

27. Цели урока:

• рассмотреть график и свойства
функции у = х2 ;
• научиться строить и «читать» график
данной функции.

28.

Я узнал …
Я почувствовал ….
Я увидел….
Я сначала испугался, а потом ….
Я заметил, что ….
Я сейчас слушаю и думаю …..
Мне интересно следить за ….