мат_предложения[1]

1.

Математические
понятия, предложения.

2.

Понятием называется форма мышления о целостной совокупности
свойств объектов реального мира.
Математическим понятиям присуще следующая особенность:
математические объекты, о которых составляются понятия в реальности
не существует.
Примеры математических понятий:
• Множество;
• Число;
• Величина - длина, время;
• Геометрические понятия - фигура, угол, прямоугольник, квадрат;
• Алгебраические понятия - выражение, уравнение, равенсвто;
• Операции - сложение, умножение, площадь геметрической фигуры.

3.

Математическое понятия - это совокупность всех
существенных свойств объекта.
Существенные свойства объекта - это свойства,
присущие данному объекту, без которых его
существование невозможно.
Несущественные свойства - это свойства, отсутсвие
которых не влияет на существование объекта.

4.

Назовите существенные и несущественные
свойства круга
Существенные свойства
Несущественные свойства
Радиус
Диаметр
Хорда
Сектор
Состоит из всех точек
плоскости, находящихся на
расстоянии, не
превышающем радиус, от
заданного центра
Цвет
Размер
Положение
Ориентация

5.

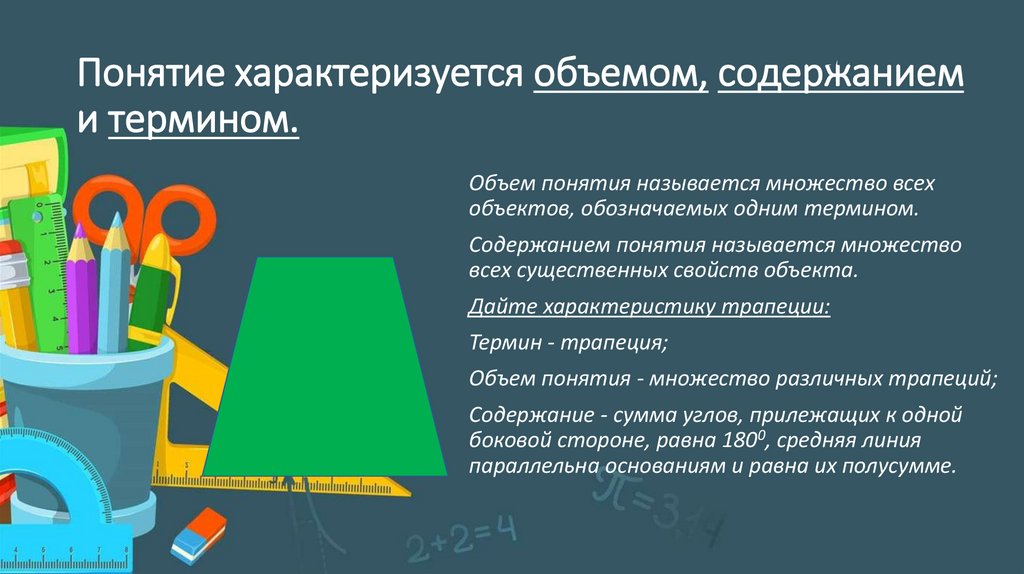
Понятие характеризуется объемом, содержанием
и термином.
Объем понятия называется множество всех
объектов, обозначаемых одним термином.
Содержанием понятия называется множество
всех существенных свойств объекта.
Дайте характеристику трапеции:
Термин - трапеция;
Объем понятия - множество различных трапеций;
Содержание - сумма углов, прилежащих к одной
боковой стороне, равна 1800, средняя линия
параллельна основаниям и равна их полусумме.

6.

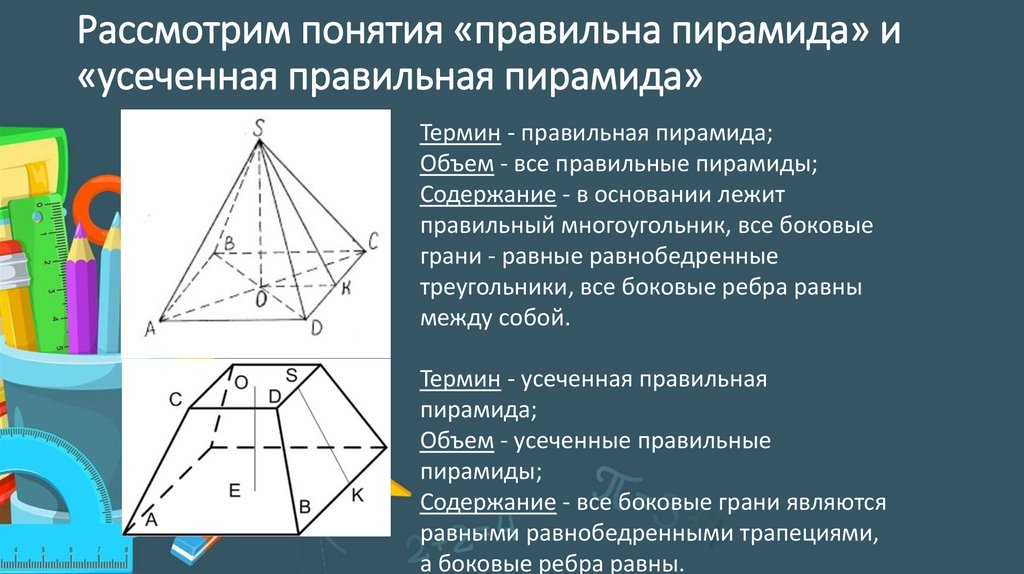
Рассмотрим понятия «правильна пирамида» и
«усеченная правильная пирамида»
Термин - правильная пирамида;
Объем - все правильные пирамиды;
Содержание - в основании лежит
правильный многоугольник, все боковые
грани - равные равнобедренные
треугольники, все боковые ребра равны
между собой.
Термин - усеченная правильная
пирамида;
Объем - усеченные правильные
пирамиды;
Содержание - все боковые грани являются
равными равнобедренными трапециями,
а боковые ребра равны.

7.

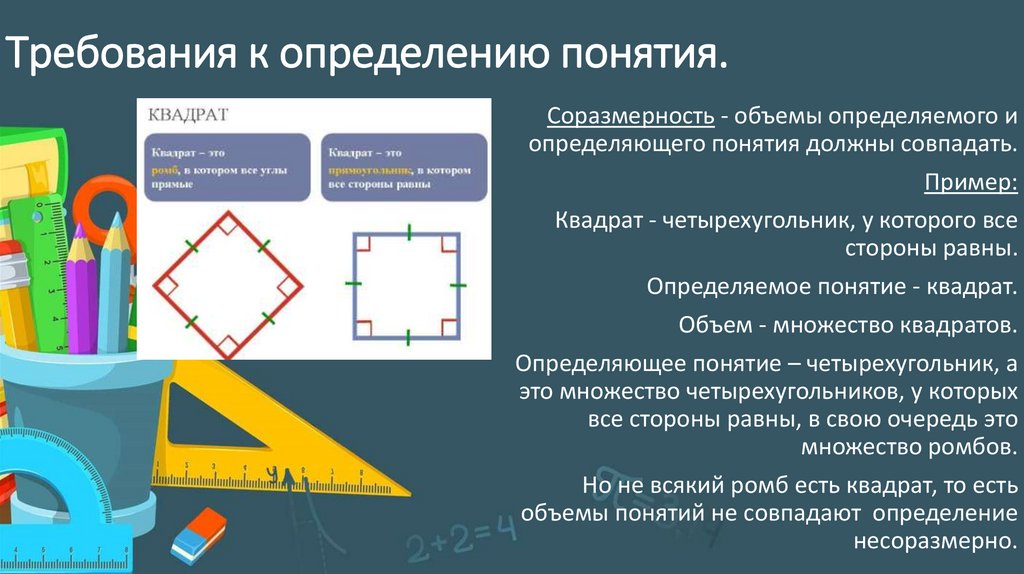
Требования к определению понятия.
Соразмерность - объемы определяемого и
определяющего понятия должны совпадать.
Пример:
Квадрат - четырехугольник, у которого все
стороны равны.
Определяемое понятие - квадрат.
Объем - множество квадратов.
Определяющее понятие – четырехугольник, а
это множество четырехугольников, у которых
все стороны равны, в свою очередь это
множество ромбов.
Но не всякий ромб есть квадрат, то есть
объемы понятий не совпадают определение
несоразмерно.

8.

Требования к определению понятия.
Запрещается определять понятие через само себя.
Например:
Деление чисел - это действие при помощи которого
находят частное чисел.
Равные треугольники - это труегольники которые
равны.

9.

Требования к определению понятия.
Определение не должно быть избытычным или
недостаточным.
Пример: окружностью называется
геометрической фигурой, точки которой
находятся на одинаковом расстоянии от одной
центральной точки.
Это описание подходит не только для
окружности, но и для сферы.
В определении не указан ключевой признак
окружности:
• Плоскость.
Окружность - это множество точек на
плоскости, равноудаленных от центра.
Сфера - это множество точек в пространстве,
равноудаленных от центра.

10.

Понятие о математических предложениях.
В языке связи между объектами и их
свойствами выражаются с помощью
предложений, которые образуются из
понятий.
Каждое математическое предложение
характеризуется содержанием и
логической структурой.
В математике по структуре различают
элементарные и составные
предложения.
Составные образуются из элементарных с
помощью союзов «и», «или», частицы
«не» и некоторых других. Эти слова в
математике называются логическими
связками.
Элементарное предложение:
«Число 30 делится на 3»;
«6+9=15»;
«Число 8 является
натуральным».
Составное предложение:
«Если треугольник
равнобедренный, то углы при
основании равны»;
«Число 32 четное и делится на
4»;
«Если у параллелограмма все
стороны равны и углы прямые,
тогда это квадрат».

11.

Среди суждений, устанавливающих различные
отношения между математическими понятиями,
выделяют высказывания и высказывательные
формы.
Высказыванием называется предложение,
относительно которого имеет смысл вопрос,
истинно оно или ложно.
«число 10 четное» - истинное высказывание;
«1+1=3» - ложное высказывание.
Если высказывание элементарное, то его значение
истинности определяют по содержанию, опираясь
на известные знания.

12.

Если высказывание составное, то считают, что что:
1) Высказывание вида «А и В» истинное, если истинны
оба высказывания А и В.
Если же хотя бы одно из них ложно, то высказывание «А и
В» ложно.
Например:
- высказывание «9>1 и 15<20» истинно, т.к. истинно каждое
высказывание
- высказывание «число -100 положительное и делится на 5»
ложно, т.к. А - ложно, но В - истинно.
2) Высказывание вида «А или В» истинно, если истинно
хотя бы одно из высказываний. Ложно тогда, когда
ложны оба высказывания.
Например:
- высказывание «число -100 отрицательное или делится на
5» истинно, т.к. оба высказывания истинны;
- высказывание «≦8» истинно, т.к. одно из высказываний
истинно (5<8), но другое ложное (5=8);
- высказывание «6≧10» ложно, т.к. оба высказывания
ложные.

13.

Высказывательная форма - это предложение с
одной или несколькими перменными, которое
обращается в высказывание при подстановке
в него конкретных значений переменных.
В математике часто встречаются
предложения, содержащие одну или
несколько переменных. Например,
x+7=10, x-y=12.
Эти предложения не являются
высказываниями, т.к. относительно
таких предложений нельзя сказать,
истинны они или ложны. Предложения
такого вида называют
высказывательными формами.

14.

Понятие «высказывательная форма» можно рассматривать как
обобщение известных понятий: уравнения с одной
переменной, неравенства с переменными и т.д.
Если высказывательная форма - уравнения или неравенство,
то, чтобы дать ответ на этот вопрос, надо уравнения или
неравенство решить.
Например, при каком значении переменной х
высказывательная форма «2х-8=10»; «x2-12x+32≦0»;