2.12 Операции над событиями измен

1.

Операции над событиями

2.

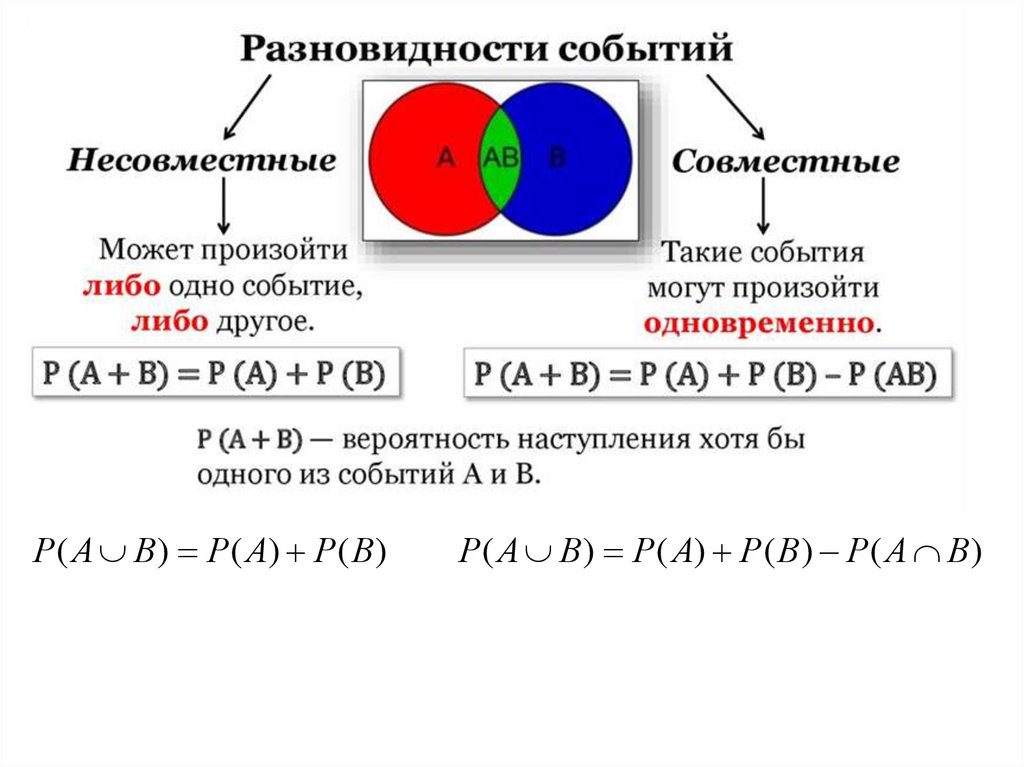
Два события называются несовместными событиями,
в которых появление одного из событий исключает
появление другого (при условии одного и того же
испытания)
Событию А противоположное событие А
Вероятность противоположных событий равна 1
Р( А) Р( А ) 1

3.

Два события называются совместными событиями,
если появление одного из них не исключает
появление другого в одном и том же испытании

4.

Определите события:
1)В торговом центре два одинаковых автомата продают кофе.
Событие «к концу дня кофе останется в обоих автоматах»
Совместные события
2)Брошена монета. Появление «герба» исключает появление
«решки». События «появился герб» и «появилась решка»
Не совместные события
3)Однократно бросают игральный кубик:
А: выпадает число 2
В: выпадает число 5
Не совместные события
4)Однократно бросают одновременно два игральных кубика:
А: выпадает число 2
В: выпадает число 5
Совместные события

5.

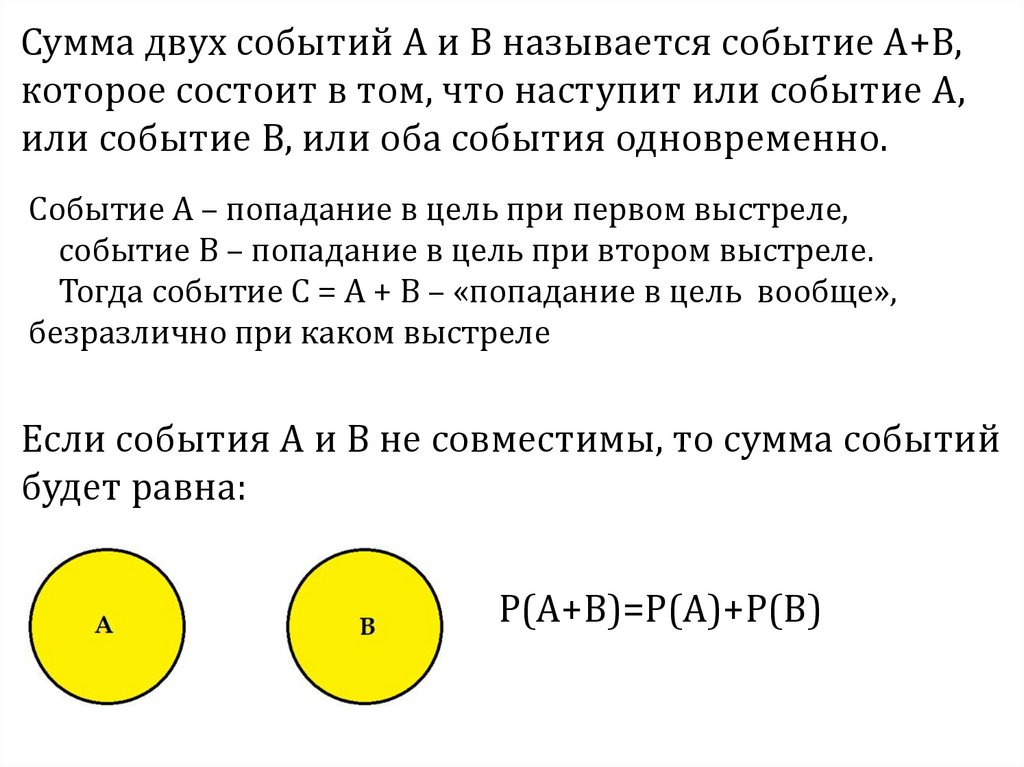
Сумма двух событий А и В называется событие А+В,
которое состоит в том, что наступит или событие А,
или событие В, или оба события одновременно.
Событие А – попадание в цель при первом выстреле,
событие В – попадание в цель при втором выстреле.
Тогда событие С = А + В – «попадание в цель вообще»,
безразлично при каком выстреле
Если события А и В не совместимы, то сумма событий
будет равна:
Р(А+В)=Р(А)+Р(В)

6.

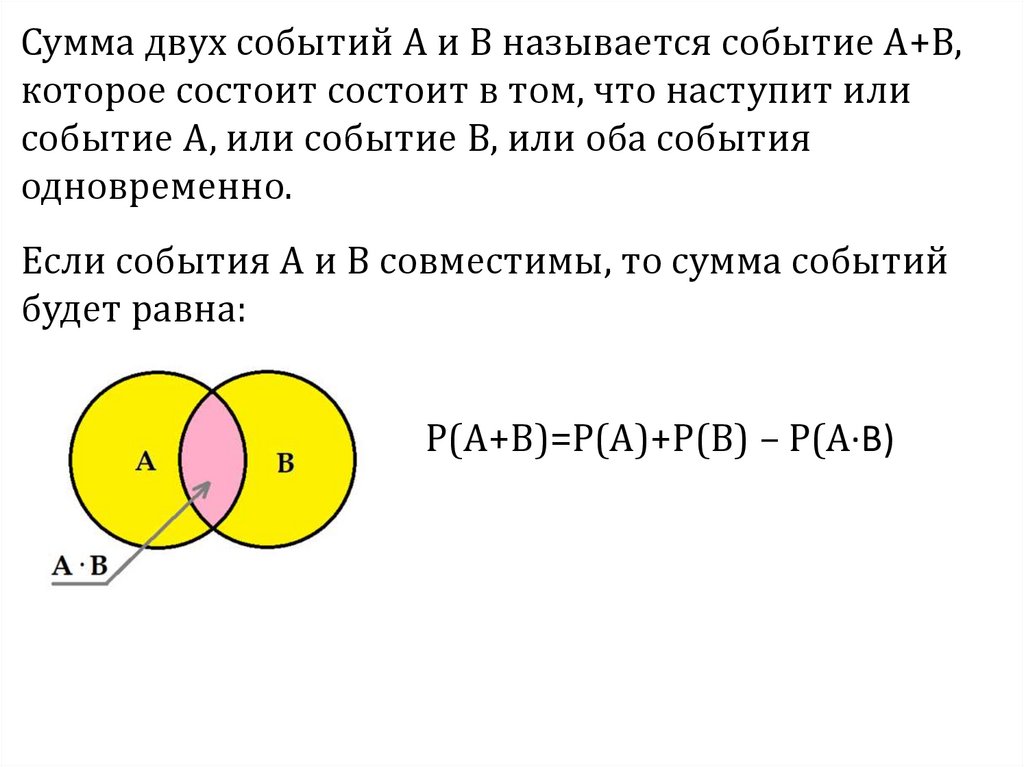
Сумма двух событий А и В называется событие А+В,
которое состоит состоит в том, что наступит или
событие А, или событие В, или оба события
одновременно.
Если события А и В совместимы, то сумма событий
будет равна:
Р(А+В)=Р(А)+Р(В) – Р(А∙В)

7.

Вероятность появления хотя бы одного из двух
совместных событий равна сумме
вероятностей этих событий без вероятности их
совместного появления:
P(A + B) = P(A) + P(B) − P(A·B)
Заметим, что если при определении нового события,
мы употребляем союз «ИЛИ», то имеет место сумма
некоторых событий.

8.

Р( А В) Р( А) Р( В)
Р( А В) Р( А) Р( В) Р( А В)

9.

№ 1. В торговом центре два автомата продают шоколадки. Вероятность
того, что к концу дня в автомате заканчиваются шоколадки , равна 0,3.
Вероятность того, что шоколадки заканчиваются в обеих автоматах,
равна 0,12. Найдите вероятность того, что к концу дня шоколадки
останутся в обоих автоматах.
Событие А: шоколадки заканчиваются хотя бы в одном автомате и
вероятность равна – 0,3.
Событие В: шоколадки заканчиваются в обоих автоматах и вероятность
равна – 0,12.
Совместные события
Вероятность, что хотя бы где-то шоколадки заканчиваются равна
Р(А+В) = Р(А)+Р(В) – Р(АВ) = 0,3+0,3 – 0,12= 0,48
А вероятность, что шоколадки не закончатся к концу дня в автоматах
равна
Р А В 1 0,48 0,52
Ответ: 0,52

10.

№ 2. В торговом центре два одинаковых автомата продают кофе.
Вероятность того, что к концу дня в автомате закончится кофе, равна 0,35.
Вероятность того, что кофе закончится в обоих автоматах, равна 0,2.
Найдите вероятность того, что к концу дня кофе останется в обоих
автоматах.
Событие А и В совместные, то
Вероятность, что хотя бы где-то кофе заканчиваются равна
Р(А+В) = Р(А)+Р(В) – Р(АВ) = 0,35+0,35 – 0,2= 0,5
А вероятность, что кофе не закончатся к концу дня в автоматах равна
Р А В 1 0,5 0,5
Ответ: 0,5

11.

№ 3. Вероятность того, что новый сканер прослужит больше года равна
0,96. Вероятность того, что он прослужит больше двух лет равна 0,87.
Найдите вероятность того, что сканер прослужит меньше двух лет, но
больше года.
Событие А: сканер прослужит больше года и вероятность равна – 0,96.
Событие В: сканер прослужит больше двух лет и вероятность равна – 0,87.
Больше 1 года
0,96
?
1 год
2 года
Больше 2 лет
0,87
Вероятность того, что сканер прослужит меньше двух лет, но больше года равна
Р(В – А ) = Р(В)– Р(А) = 0,96 – 0,87= 0,09

12.

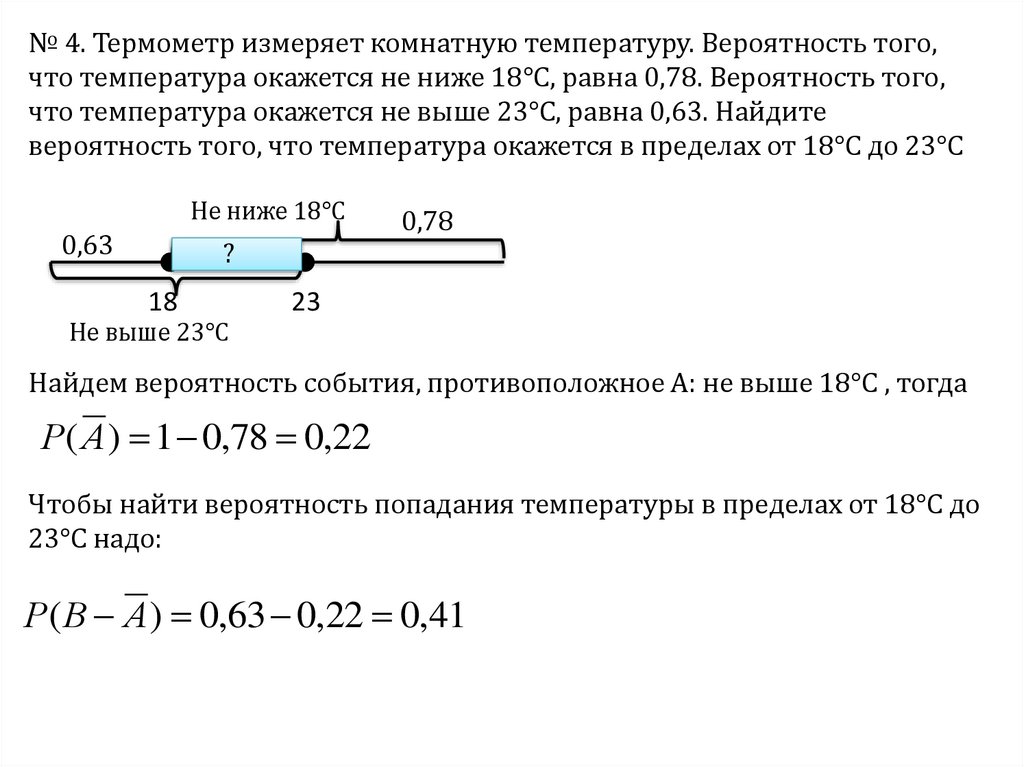
№ 4. Термометр измеряет комнатную температуру. Вероятность того,
что температура окажется не ниже 18°С, равна 0,78. Вероятность того,
что температура окажется не выше 23°С, равна 0,63. Найдите
вероятность того, что температура окажется в пределах от 18°С до 23°С
Не ниже 18°С
0,63
?
18
Не выше 23°С
0,78
23
Найдем вероятность события, противоположное А: не выше 18°С , тогда
Р( А ) 1 0,78 0,22
Чтобы найти вероятность попадания температуры в пределах от 18°С до
23°С надо:
Р( В А ) 0,63 0,22 0,41

13.

№ 150 (учебника) В отделении банка стоят два автомата. Первый может
выдавать и приминать купюры, второй – только выдавать. Вероятность,
что к концу дня купюры закончатся в первом автомате, равна 0,1, а что
закончатся во втором – 0,3. Вероятность, что они закончатся в двух
автоматах , равна 0,06. Найдите вероятность того, что к концу дня
купюры:
А) останутся в обоих автоматах;
Р( А) 0,1
Р( В) 0,3
Р( А В) 0,06
Вероятность, что купюру останутся в обоих автоматах, означает, что
купюры не закончатся ни в 1, ни во 2 автоматах
С начало найдем, что вероятность события, когда купюры закончатся
хотя бы в одном автомате:
Р( А В) Р( А) Р( В) Р( А В) 0,1 0,3 0,06 0,34
Найдем вероятность противоположного события:
Р( А В) 1 Р( А В) 1 0,34 0,66

14.

№ 150 (учебника) В отделении банка стоят два автомата. Первый может
выдавать и приминать купюры, второй – только выдавать. Вероятность,
что к концу дня купюры закончатся в первом автомате, равна 0,1, а что
закончатся во втором – 0,3. Вероятность, что они закончатся в двух
автоматах , равна 0,06. Найдите вероятность того, что к концу дня
купюры:
Б) останутся хотя бы в одном автомате;
Это вероятность, что купюру не закончатся хотя бы в одном автомате.
Это противоположное событие к тому, что они закончатся в обоих
автоматах т.е.
Р( А В) 1 Р( А В) 1 0,06 0,94

15.

№ 150 (учебника) В отделении банка стоят два автомата. Первый может
выдавать и приминать купюры, второй – только выдавать. Вероятность,
что к концу дня купюры закончатся в первом автомате, равна 0,1, а что
закончатся во втором – 0,3. Вероятность, что они закончатся в двух
автоматах , равна 0,06. Найдите вероятность того, что к концу дня
купюры:
В) закончатся хотя бы в одном автомате;
Р( А В) Р( А) Р( В) Р( А В) 0,1 0,3 0,06 0,34

16.

№ 150 (учебника) В отделении банка стоят два автомата. Первый может
выдавать и приминать купюры, второй – только выдавать. Вероятность,
что к концу дня купюры закончатся в первом автомате, равна 0,1, а что
закончатся во втором – 0,3. Вероятность, что они закончатся в двух
автоматах , равна 0,06. Найдите вероятность того, что к концу дня
купюры:
Г) закончатся только во втором, а в первом останутся;
Р( А В) Р( В) Р( А В) 0,3 0,06 0,24

17.

№ 150 (учебника) В отделении банка стоят два автомата. Первый может
выдавать и приминать купюры, второй – только выдавать. Вероятность,
что к концу дня купюры закончатся в первом автомате, равна 0,1, а что
закончатся во втором – 0,3. Вероятность, что они закончатся в двух
автоматах , равна 0,06. Найдите вероятность того, что к концу дня
купюры:
Д) закончатся только в первом автомате, а во втором останутся;
Р( А В ) Р( А) Р( А В) 0,1 0,06 0,04

18.

№ 152 (учебника) Друзья Петров и Васечкин часто прогуливают лекции.
Вероятность их совместного появления на лекции равна 0,1, а
вероятность, что оба не придут на лекцию равна 0,8. Петров прогулял
87% лекций. Сколько процентов лекций прогулял Васечкин?
Событие А: не приход Петрова на лекции и вероятность равна –
87%=0,87.
Событие В: не приход Васечкина и вероятность – х
Совместные события
Р( А В) Р( А) Р( В) Р( А В)
Не приход их совместно равно: 1 – 0,1=0,9, тогда
0,9 0,87 х 0,8
0,9 0,87 0,8 х
0,83 х
Значит 0,83=83% – прогулял Васечкин

19.

№ 153 (учебника) Вероятность того, что на тестировании по истории
ученик верно ответит больше, чем на 8 вопросов, равна 0,65. Вероятность
того, что он верно ответит больше, чем 7 вопросов, равна 0,74. Найдите
вероятность того, что ученик ответит ровно на 8 вопросов.
?
Больше 8 задач – 0,65
7задач
8 задач
Больше 7 задач – 0,74
0,74 – 0,65 = 0,09

20.

Домашнее задание
№ 154
№ 155