10. Greefy algorithms

1. Жадные алгоритмы

2.

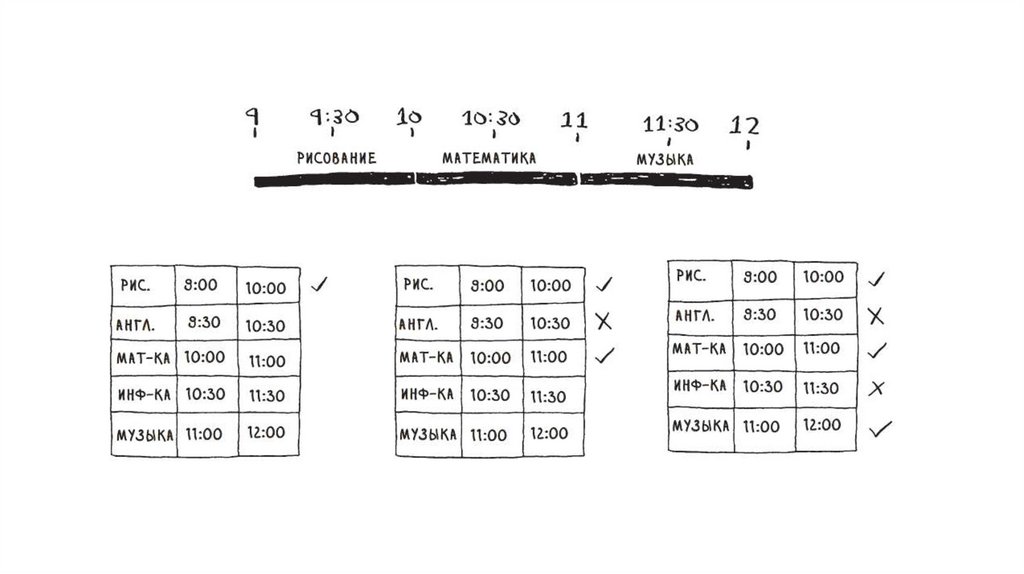
Нужно провести как можно больше уроков, чтоб они
не накладывались друг на друга. Как это сделать?
Алгоритм:
• Выбрать урок, завершающийся раньше всех.
Это первый урок, который будет проведён.
• Затем выбирается урок, начинающийся после
завершения первого урока. И снова следует
выбрать урок, завершающийся раньше всех. Он
становится вторым уроком в расписании.

3.

4.

Задача о рюкзаке
Воришка забрался в магазин с рюкзаком, вмещающим до
35 фунтов. Хочется утащить как можно больше ценного.
Мысль проста:
1. Выбираем самый дорогой предмет, который поместится в рюкзаке.
2. Выбираем следующий по стоимости предмет, помещающийся в рюкзаке.
В этот раз не сработало!

5.

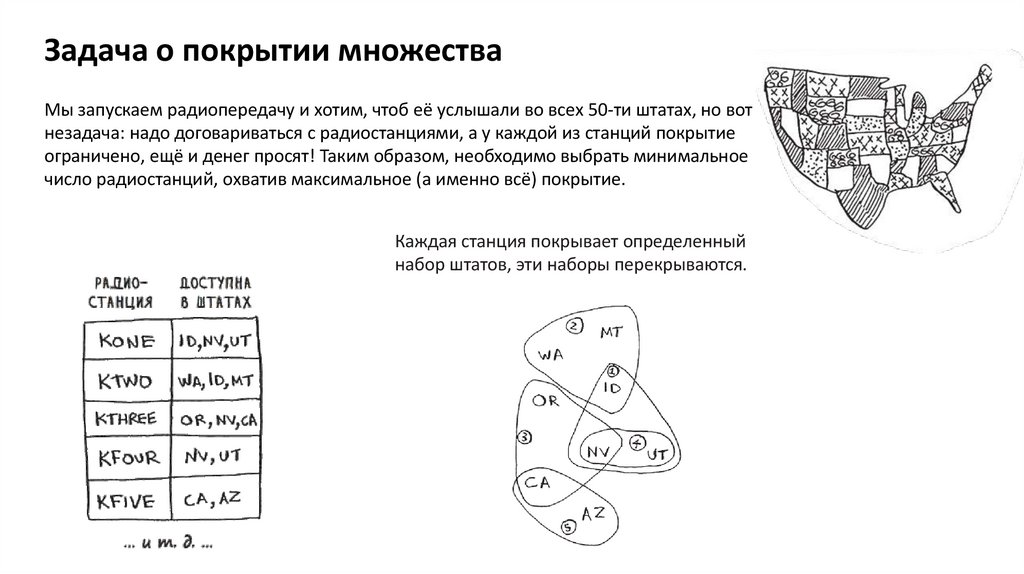
Задача о покрытии множества
Мы запускаем радиопередачу и хотим, чтоб её услышали во всех 50-ти штатах, но вот
незадача: надо договариваться с радиостанциями, а у каждой из станций покрытие
ограничено, ещё и денег просят! Таким образом, необходимо выбрать минимальное
число радиостанций, охватив максимальное (а именно всё) покрытие.
Каждая станция покрывает определенный
набор штатов, эти наборы перекрываются.

6.

Как найти минимальный набор станций, покрывающий все 50 штатов? Вроде бы
простая задача, верно? Оказывается, она чрезвычайно сложна. Вот как это делается:
1. Составить список всех возможных подмножеств станций — степенное
множество. В нем содержатся 2^n возможных подмножеств.
2. Из этого списка выбирается множество с наименьшим набором станций,
покрывающих все 50 штатов.
Не существует алгоритма, который будет вычислять
подмножества с приемлемой скоростью! Что же делать?

7.

8.

9.

Жадный алгоритм не всегда даст точный ответ, но он очень
быстр. Задача о покрытии множеств относится к NPтрудным задачам. Если вы хотите узнать немного больше
об NP-трудных задачах, обратитесь к приложению Б.
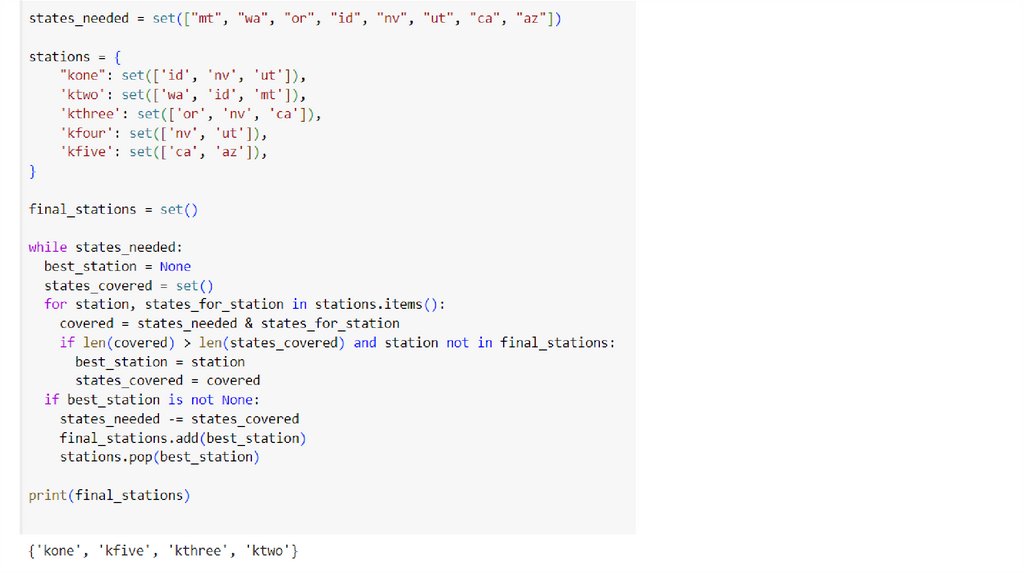
----------------- станция, обслуж-я больше всего штатов не входящих в текущие покрытие
----------------- штаты, обслуживаемые этой станцией и не входящие в текущее покрытие