Curs_01_Teams_PAT (1)

1. Proiectare Asistată în Transporturi - note de curs -

Șef de Disciplină
Conf. Dr. Ing. Relly-Victoria Petrescu

2.

Prima parte
– Geometria Descriptivă, baza proiectării grafice –

3.

DEFINIȚIE
Geometria Descriptivă este o ramură matematică a
Geometriei Proiective, iar problema fundamentală a acesteia o
constituie transformarea spaţiului tridimensional în spaţiul
bidimensional şi reciproc.
Altfel spus, ea se ocupă atât cu
reprezentarea în plan a figurilor geometrice din spaţiul tridimensional
cât şi cu deducerea figurilor din spaţiul tridimensional pornind de la
reprezentările plane ale acestora.
În tehnică, ea constituie fundamentul teoretic al ştiinţei reprezentării
corpurilor pe un plan şi al deducerii formei spaţiale ale acestora
pornind de la reprezentările lor plane.
Originea şi scopul Geometriei Descriptive
Nevoia de a reprezenta, obiectele din spaţiu prin desene este pentru
om o necesitate comparabilă cu aceea de a exprima graiul prin scris. După
cum a inventat scrisul pentru a fixa ceea ce vorbeşte, omul a imaginat
desenul pentru a exprima ceea ce vede. Acest îndemn natural a dat naştere
diverselor sisteme convenţionale de reprezentare imaginate de-a lungul
secolelor, conform cărora, orice obiect din spaţiu este reprezentat printr-o
imagine plană construită după anumite reguli, numită desen. Problema
este de a desena, pe o foaie de hârtie, deci pe o suprafaţă plană cu numai
două dimensiuni, un obiect din spaţiu având trei dimensiuni. Metoda de
rezolvare a acestei probleme este cea geometrică; ea constă în utilizarea
regulilor geometriei care stabilesc legătura dintre obiectul din spaţiu şi
imaginea lui pe hârtie. Aceste reguli trebuie cunoscute atât de cel care
alcătuieşte desenul cât şi de cel care îl citeşte. Astfel, pentru a putea
proiecta o clădire şi a construi apoi clădirea după proiect, regulile de
reprezentare trebuie cunoscute atât de proiectant cât şi de executant.
Deprinderea de a reprezenta corpurile din spaţiu prin imagini plane şi
respectiv de a imagina corpurile în spaţiu prin simpla citire a desenelor,
duce la rezolvarea aşa-numitei „vederi în spaţiu", însuşire de primă
importanţă pentru ingineri.
Dea lungul istoriei, proiectarea grafică a trecut prin mai multe etape
principale. Cea mai importantă dintre acestea, a fost etapa proiecției
centrale concentrată în Geometria Proiectivă, care a sta la baza dezvoltării
de mai târziu a Geometriei Descriptive prin proiecția paralelă ortogonală.

4.

Geometria Proiectivă
Scurt istoric
Problema reprezentării corpurilor pe un plan a fost una din preocupările omului încă din cele
mai vechi timpuri. Ea a apărut, sub diferite forme, în două domenii: în artă, îndeosebi în pictură şi
în tehnică, mai ales în proiectarea clădirilor. Grecii şi romanii alcătuiesc decoruri scenice care dau
spectatorului iluzia realităţii, ce se vor numi apoi perspective. Necesitatea de a tăia cu exactitate
blocurile de piatră pentru monumente după anumite forme geometrice, a dus în Evul Mediu la
planurile de tăiere a pietrelor, adică „epurele de stereotomie". În timpul Renaşterii, perspectiva
cunoaşte o largă dezvoltare atât în domeniul picturii cât şi în cel al arhitecturii și ingineriei.
Inginerul și matematicianul Gerard Desargues (n. 21 februarie 1591 – m. 9 octombrie 1661) este
cel care a pus bazele Geometriei Proiective, ramură a matematicii care utiliza în rezolvarea
problemelor proiecția centrală și care mai târziu, a stat la baza dezvoltării Geometriei Descriptive.
Inginerul și matematicianul Gerard Desargues (n.21 februarie 1591 –
m.octombrie 1661), cel care a pus bazele Geometriei Proiective, ramură a
matematicii care a stat la baza dezvoltării Geometriei Descriptive.(Pictură în ulei
reprezentându-l în curtea Palatului Louvre din Paris)

5.

Cardinalul Richelieu consultându-l pe Gerard Desargues cu privire la
construcția tranșeelor și a forturilor, la asediul din La Rochelle, în timpul
domniei regelui Ludovic al XIII-lea.

6.

Cele mai importante teoreme enunțate de Desargues au contribuit la dezvoltarea teoriei
rețelelor prin studierea renumitelor configurații care-i poartă numele.
Configurații Desargues
În geometria euclidiană, teorema lui Desargues este o problemă de geometrie sintetică.
Geometria sintetică este cea mai veche ramură a geometriei, care se sprijină în mod esențial pe
desene geometrice și apelează preponderent în rezolvarea problemelor la construcții auxiliare
care pot fi reduse la operații efectuate cu rigla și compasul, și la considerații vizuale sintetice.
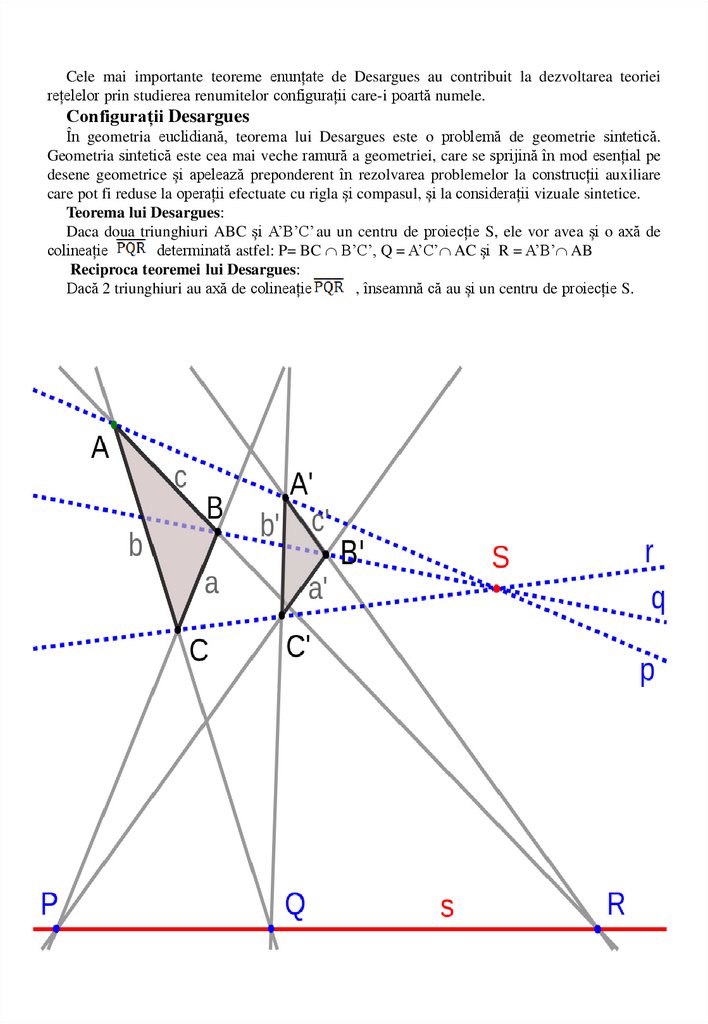
Teorema lui Desargues:
Daca doua triunghiuri ABC și A’B’C’ au un centru de proiecție S, ele vor avea și o axă de
colineație
determinată astfel: P= BC B’C’, Q = A’C’ AC și R = A’B’ AB
Reciproca teoremei lui Desargues:
Dacă 2 triunghiuri au axă de colineație
, înseamnă că au și un centru de proiecție S.

7.

În cazul în care segmentele AB și A'B' sunt egale, ABA'B' este un
paralelogram. De aici rezultă AA' || BB'. Tot din AB = A'B' rezultă egalitatea
triunghiurilor ΔABC = ΔA'B'C' deci și a segmentelor BC și B'C'. Ca și mai
înainte, vom avea BB’ || CC'. În concluzie, AA' || BB' || CC' .
În cazul în care segmentele AB și A'B' au lungimi diferite, dreptele AA' și
BB' se vor întâlni într-un punct S. (În caz contrar, ar rezulta că ABB’A’ ar fi un
paralelogram ceea ce contravine ipotezei)
SA/SA' = AB/A'B'
Tot în acest caz, triunghiurile ΔABC și ΔA'B'C' sunt asemenea, fără a fi
egale:
AB/A'B' = BC/B'C' ≠ 1
Fie acum S' punctul de intersecție al dreptelor BB' și CC'.
Avem S'B/S'B’ = BC/B'C' = AB/A'B' = SB/SB'.
Va rezulta: SB/SB' - 1 = S'B/S'B' - 1, apoi BB'/SB' = BB'/S'B' și deci SB' =
S'B'.
Dacă luăm în compas lungimea B'S, ridicăm compasul, punem la loc un vârf
în B' și trasăm punctul S', acesta va coincide cu punctul de plecare S, așadar
S = S' iar dreptele date sunt concurente.
Pe site-ul https://www.geogebra.org/m/efHaaabw se poate vedea
Configurația lui Desargues cel mai bine, deoarece configuratorul ne oferă
posibilitatea de a așeza punctele într-un număr infinit de modalități.

8.

Din punct de vedere matematic, Geometria Descriptivă - se ocupă cu
studiul proiecțiilor paralele ortogonale, având ca scop reprezentarea
plană a elementelor din spațiu, a poziției relative dintre acestea, a
secționării, intersectării și desfășurării suprafețelor sau corpurilor.
Forma actuală a acestei ramuri a geometriei o datorăm lui Gaspard
Monge (n. 10 mai1746 - m. 28 iulie 1818) inginer şi matematician
francez care a profesat la şcoala Politehnică din Paris.
La 25 de ani este numit profesor de Matematicã și de Geometrie
Descriptivã la Școala Militarã din Mezieres.
In 1780, renumele lui Monge ajunsese pânã la Paris. Atunci, Turgot,
ministrul lui Ludovic al XVI-lea, i-a încredintat postul de profesor de
Hydraulicã la Louvre. În același an a intrat în Academia de Științe
Francezã, deși avea numai 34 ani și Senator din partea partidului
Conservator.

9.

10.

11.

12.

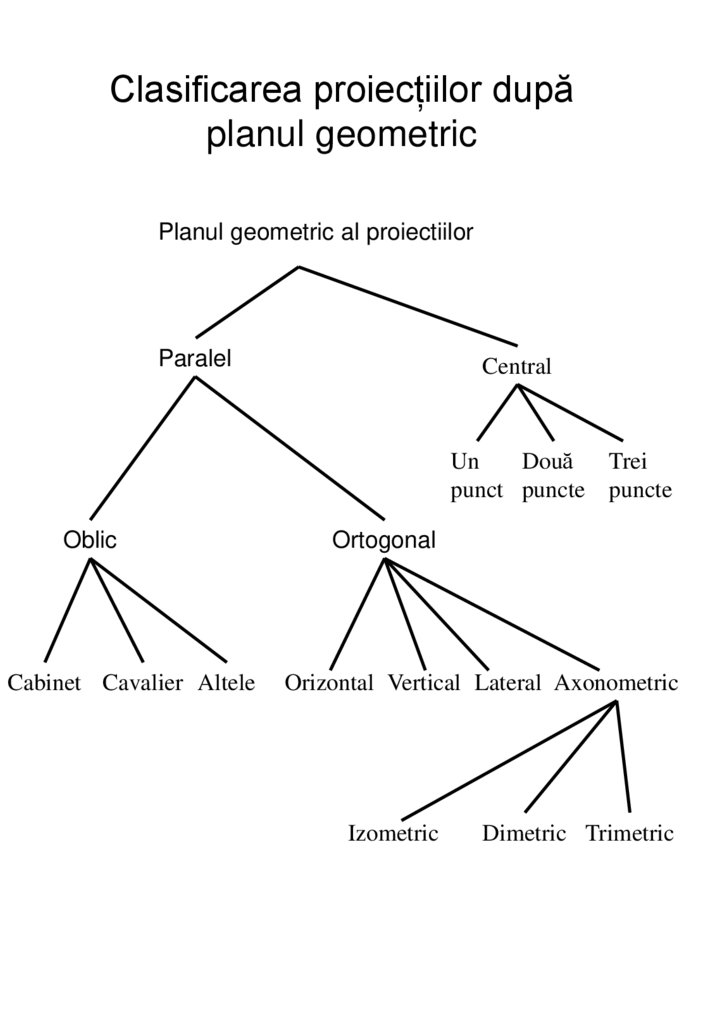
Clasificarea proiecțiilor după
planul geometric
Planul geometric al proiectiilor
Paralel
Central
Un
Două
Trei
punct puncte puncte
Oblic
Cabinet Cavalier Altele
Ortogonal
Orizontal Vertical Lateral Axonometric
Izometric
Dimetric Trimetric

13.

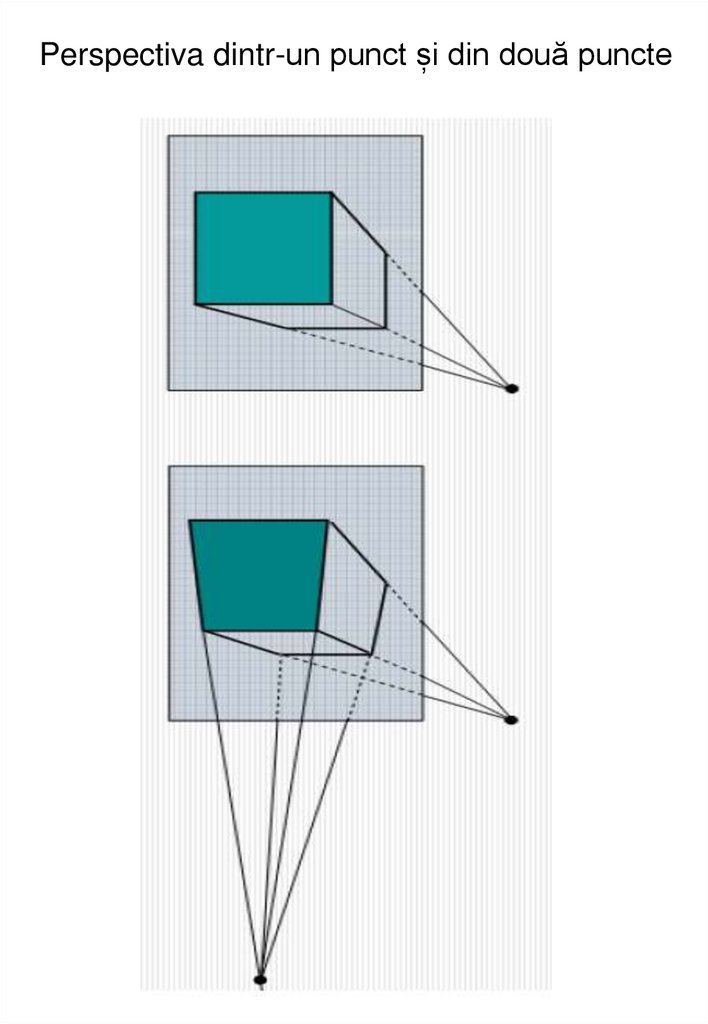
Perspectiva dintr-un punct și din două puncte

14.

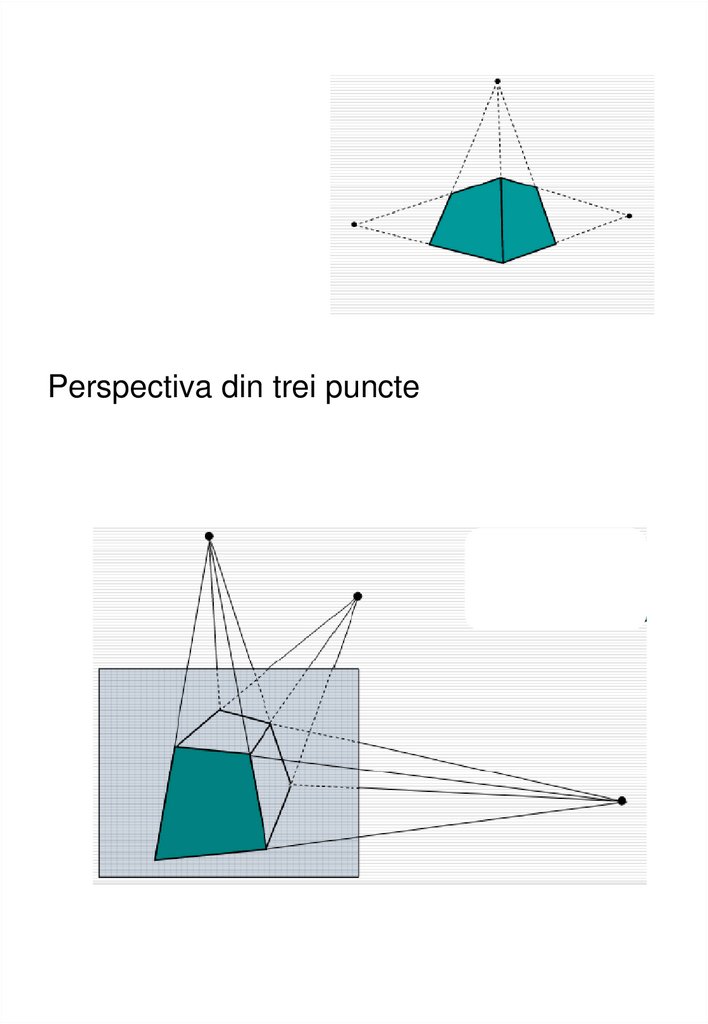
Perspectiva din trei puncte

15.

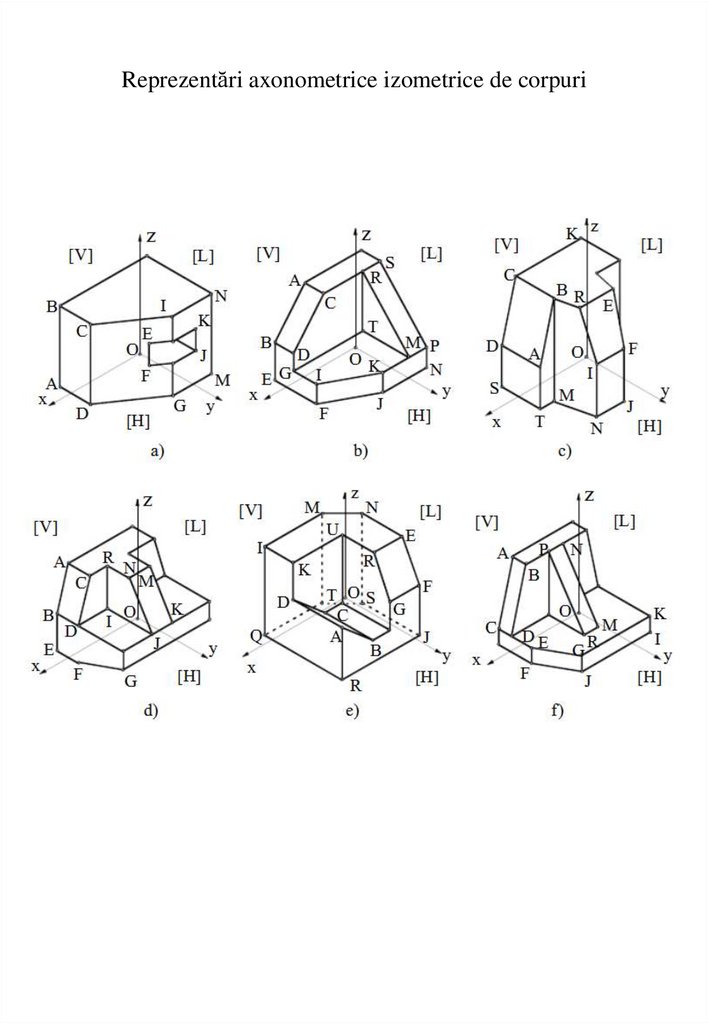
Reprezentări axonometrice izometrice de corpuri

16.

17.

18.

19.

20.

21.

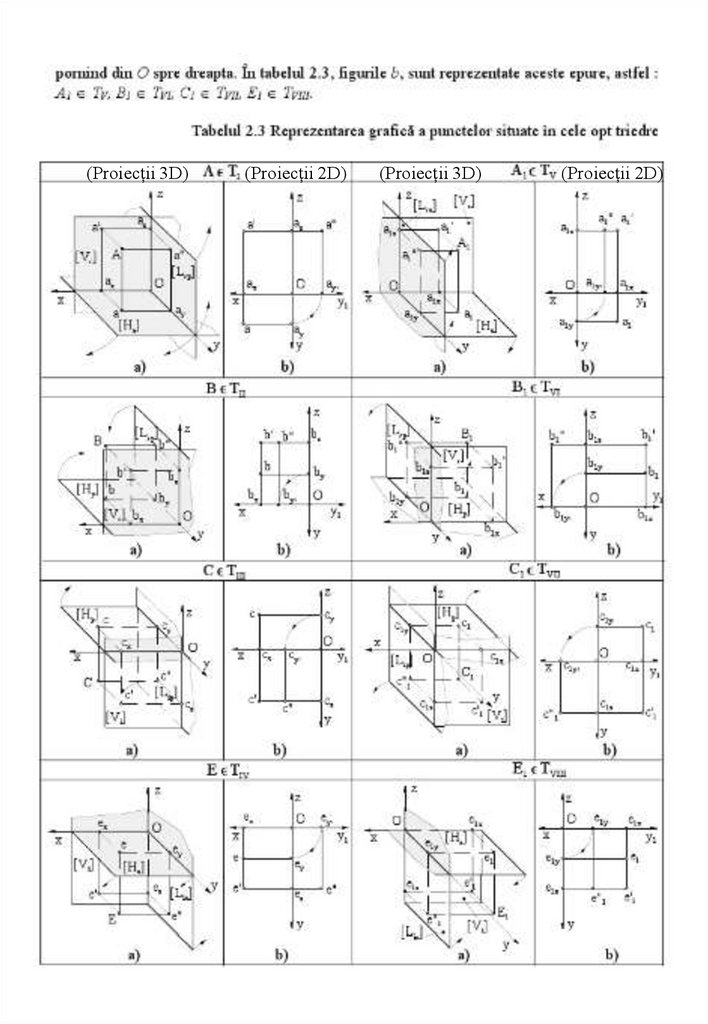
(Proiecții 3D)
(Proiecții 2D)
(Proiecții 3D)
(Proiecții 2D)