Проект

1.

ПРЕЗЕНТАЦИЯ ОТЧЕТА ПО
ДИСЦИПЛИНЕ
«ПРОЕКТНАЯ ДЕЯТЕЛЬНОСТЬ»
НА ТЕМУ:
ПРОЕКТИРОВАНИЕ СИСТЕМ
ИСКУССТВЕННОГО ИНТЕЛЛЕКТА.
КЛАСТЕРНЫЙ АНАЛИЗ
ТЕХНИЧЕСКИХ ОБЪЕКТОВ
Выполнили: студенты группы УИБ-212
Никитин Вадим Александрович
Батаев Алексей Максимович
Никитин Максим Александрович
Руководитель проекта:
Никитин Максим Александрович

2.

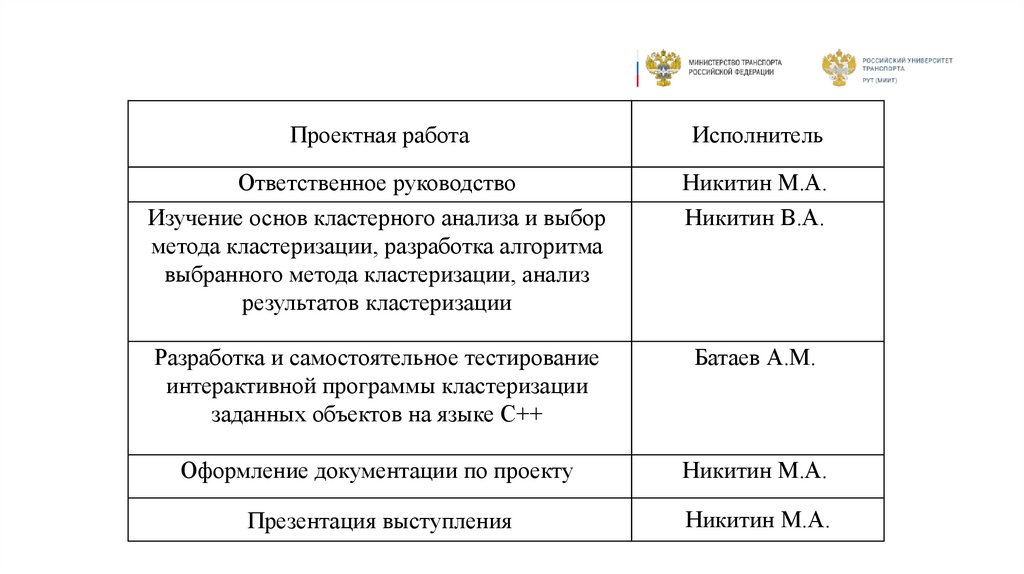
Проектная работа
Исполнитель
Ответственное руководство
Изучение основ кластерного анализа и выбор
метода кластеризации, разработка алгоритма
выбранного метода кластеризации, анализ
результатов кластеризации
Никитин М.А.
Никитин В.А.
Разработка и самостоятельное тестирование
интерактивной программы кластеризации
заданных объектов на языке C++
Батаев А.М.
Оформление документации по проекту
Никитин М.А.
Презентация выступления
Никитин М.А.

3. Цели и задачи проекта

Цель:
Определение пары наиболее информативных признаков с помощью алгоритма k-средних
и последующая оценка эффективности кластеризации в двумерном пространстве этих
признаков.
Задачи:
1. Провести теоретическое исследование: изучить существующие подходы к
кластерному анализу и, сравнив их, обосновать выбор именно алгоритма k-средних
для целей данной работы.
2. Разработать и реализовать алгоритм k-средних на языке C++ для кластеризации
данных в двумерных признаковых пространствах.
3. Провести вычислительный эксперимент: выполнить кластеризацию для шести
различных пар признаков, визуализировать результаты и провести их сравнительный
анализ.
4. Определить пару наиболее информативных признаков на основе анализа результатов
эксперимента и оценить эффективность кластеризации в этом двумерном
пространстве.

4.

Задание:
Для каждого варианта заданы:
1. Обучающая выборка - таблица экспериментальных данных (ТЭД) размерностью
60/45 x 4, с количественными (4 признака) описаниями 60/45 объектов.
2. Объекты, представленные в обучающей выборке, относятся к 4/3 классам
(кластерам);
3. Метрикой расстояния между объектами является метрика Евклида;
4. Кластерный анализ выполняется методом k-средних.
Необходимо проанализировать заданную обучающую выборку методом кластерного
анализа (обучение «без учителя») с целью найти 2 наиболее информативных признака.

5.

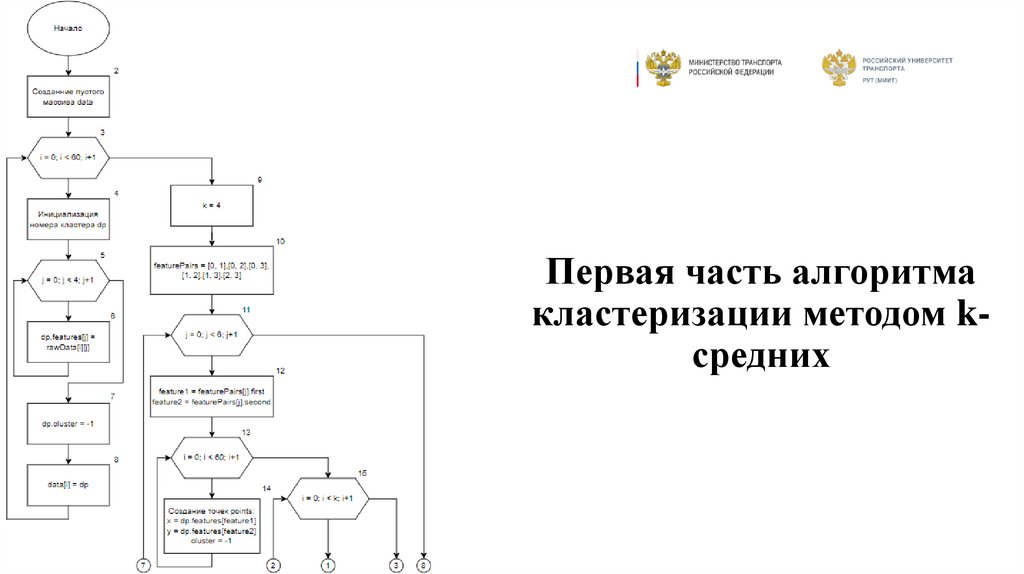
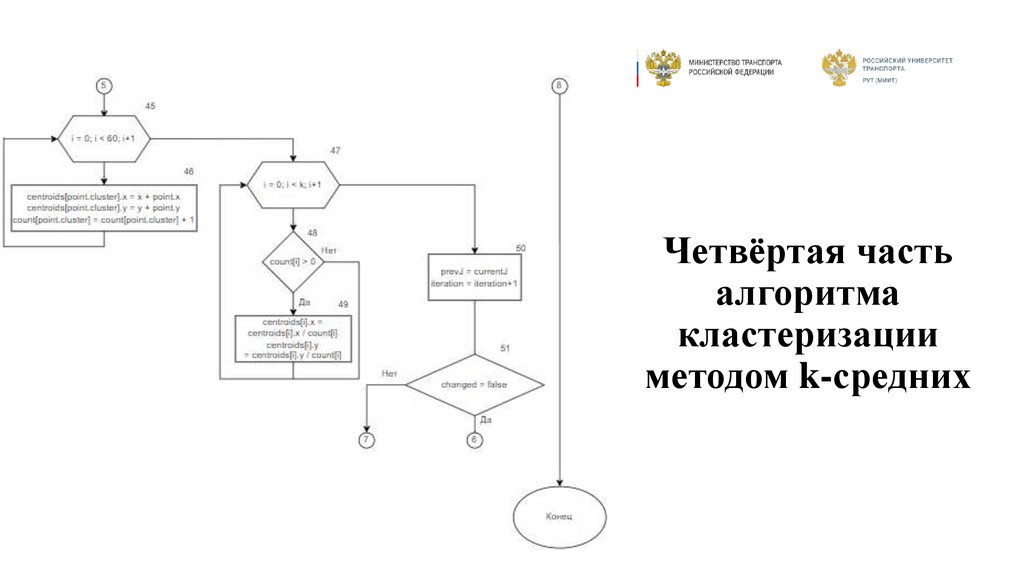
Метод k-средних
1. Задать число кластеров k.
2. Случайно сгенерировать координаты
центроидов.
3. Для каждой точки найти ближайший центроид.
4. Пересчитать центроиды как среднее
арифметическое точек своего кластера.
5. Повторять шаги 3-4, пока центроиды не
будут меняться незначительно.

6.

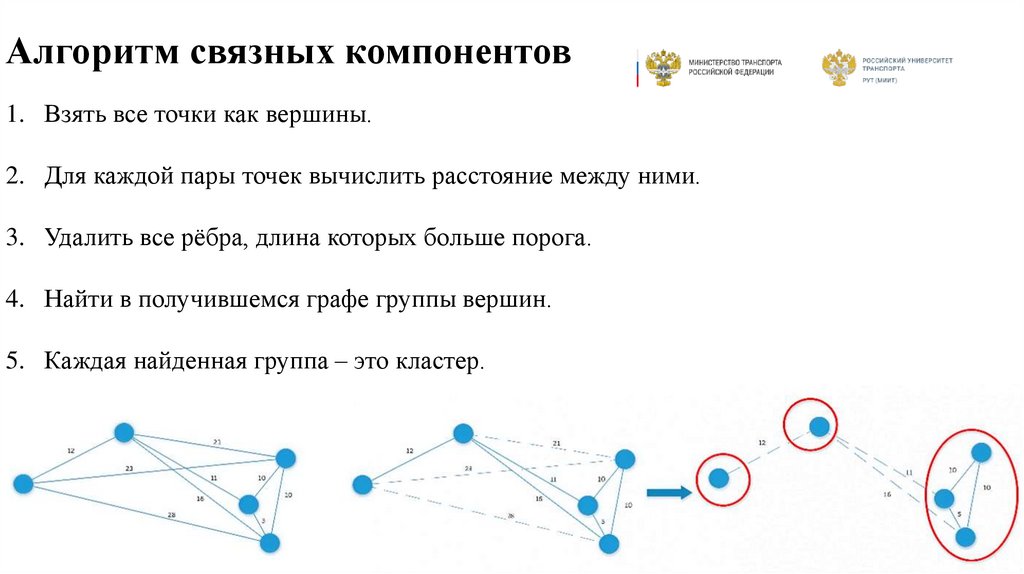
Алгоритм связных компонентов
1. Взять все точки как вершины.
2. Для каждой пары точек вычислить расстояние между ними.
3. Удалить все рёбра, длина которых больше порога.
4. Найти в получившемся графе группы вершин.
5. Каждая найденная группа – это кластер.

7.

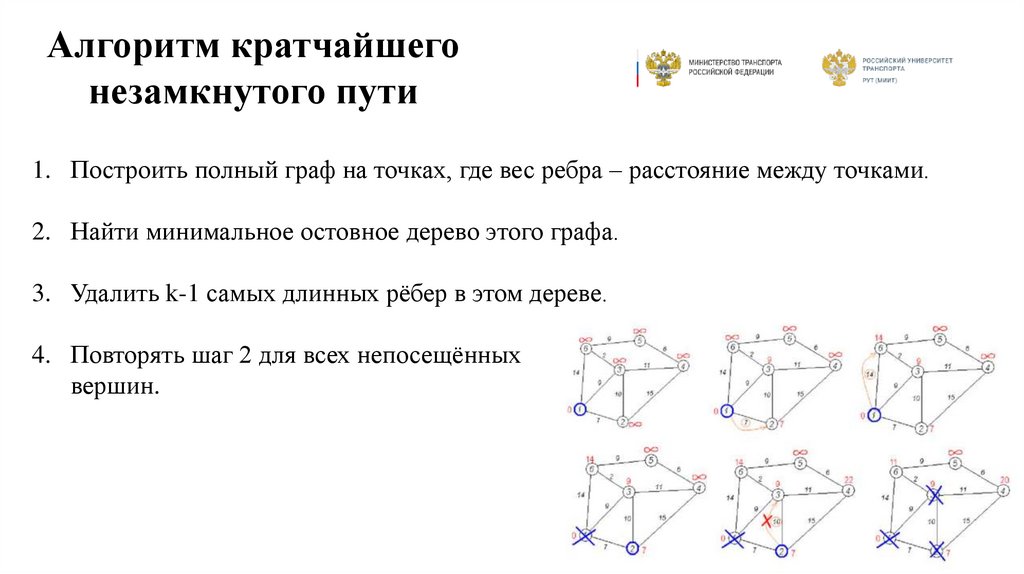
Алгоритм кратчайшего
незамкнутого пути
1. Построить полный граф на точках, где вес ребра – расстояние между точками.
2. Найти минимальное остовное дерево этого графа.
3. Удалить k-1 самых длинных рёбер в этом дереве.
4. Повторять шаг 2 для всех непосещённых
вершин.

8.

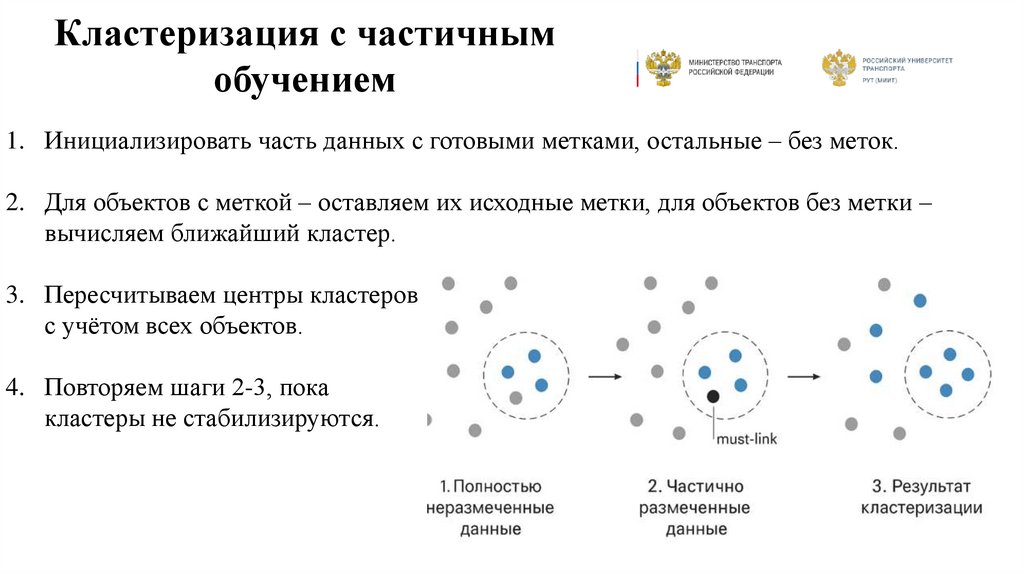
Кластеризация с частичным
обучением
1. Инициализировать часть данных с готовыми метками, остальные – без меток.
2. Для объектов с меткой – оставляем их исходные метки, для объектов без метки –
вычисляем ближайший кластер.
3. Пересчитываем центры кластеров
с учётом всех объектов.
4. Повторяем шаги 2-3, пока
кластеры не стабилизируются.

9.

Иерархическая кластеризация
1. Вычисляем попарные расстояния между всеми кластерами как расстояния между
объектами.
2. Находим пары кластеров U и V с минимальными расстояниями R(U, V), и объединяем
их в новые кластеры W = U∪V.
3. Для каждого оставшегося кластера S вычисляем расстояние до W по формуле ЛансаУильямса.
4. Повторяем шаги 2-3, пока не останется один кластер.

10.

Иерархическая кластеризация
Формула Ланса-Уильямса:
R(W,S)=αU​R(U,S)+αV​R(V,S)+βR(U,V)+γ∣R(U,S)−R(V,S)∣
U,V – пара кластеров.
W – Новый кластер.
S – оставшийся кластер.
R(U, V) – расстояние между кластерами.

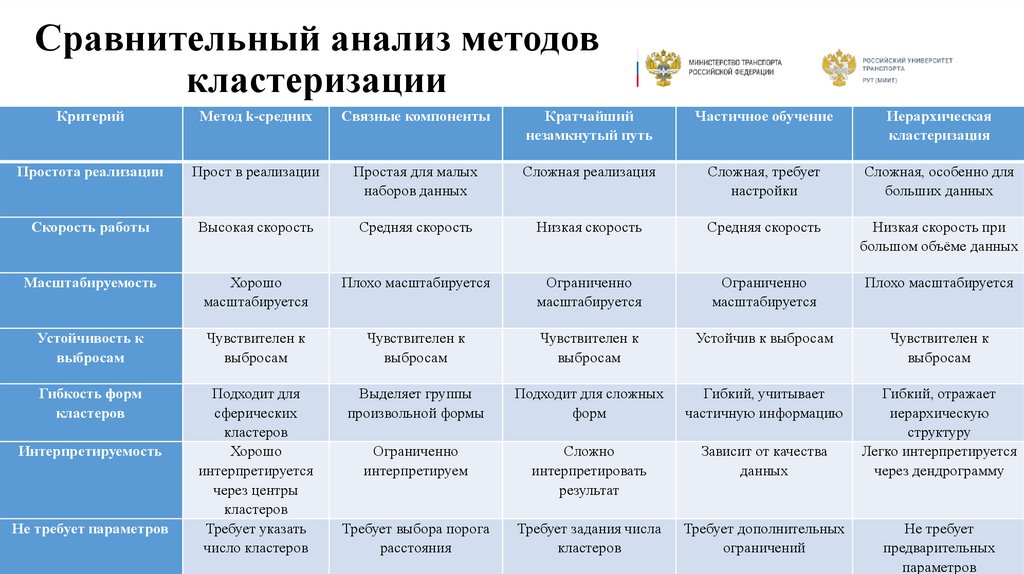
11. Сравнительный анализ методов кластеризации

Критерий
Метод k-средних
Связные компоненты
Кратчайший
незамкнутый путь
Частичное обучение
Иерархическая
кластеризация
Простота реализации
Прост в реализации
Простая для малых
наборов данных
Сложная реализация
Сложная, требует
настройки
Сложная, особенно для
больших данных
Скорость работы
Высокая скорость
Средняя скорость
Низкая скорость
Средняя скорость
Низкая скорость при
большом объёме данных
Масштабируемость
Хорошо
масштабируется
Плохо масштабируется
Ограниченно
масштабируется
Ограниченно
масштабируется
Плохо масштабируется
Устойчивость к
выбросам
Чувствителен к
выбросам
Чувствителен к
выбросам
Чувствителен к
выбросам
Устойчив к выбросам
Чувствителен к
выбросам
Гибкость форм
кластеров
Подходит для
сферических
кластеров
Хорошо
интерпретируется
через центры
кластеров
Требует указать
число кластеров
Выделяет группы
произвольной формы
Подходит для сложных
форм
Гибкий, учитывает
частичную информацию
Ограниченно
интерпретируем
Сложно
интерпретировать
результат
Зависит от качества
данных
Гибкий, отражает
иерархическую
структуру
Легко интерпретируется
через дендрограмму
Требует выбора порога
расстояния
Требует задания числа
кластеров
Требует дополнительных
ограничений
Интерпретируемость
Не требует параметров
Не требует
предварительных
параметров

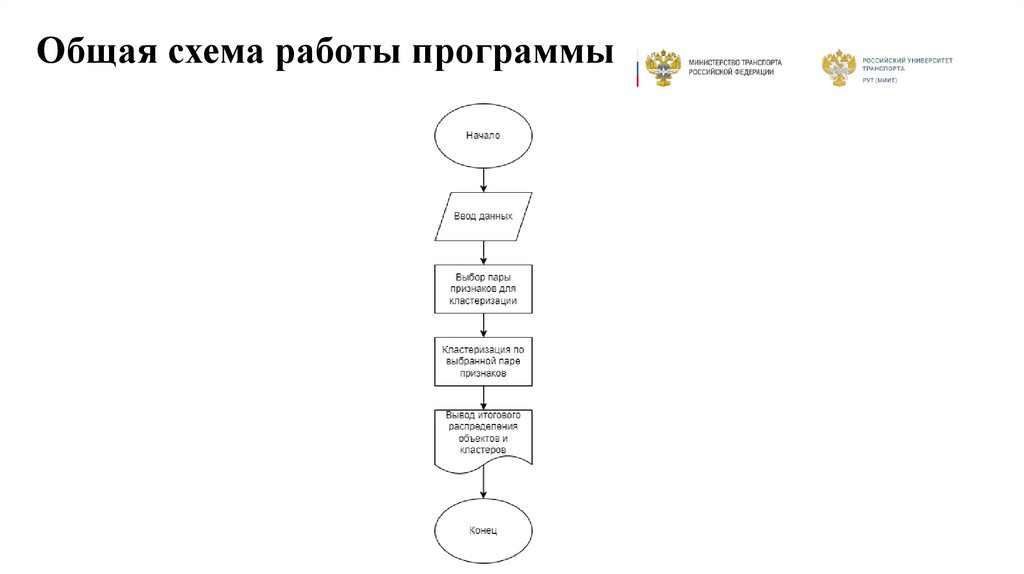
12. Общая схема работы программы

13. Первая часть алгоритма кластеризации методом k-средних

Первая часть алгоритма
кластеризации методом kсредних

14. Вторая часть алгоритма кластеризации методом k-средних

15. Третья часть алгоритма кластеризации методом k-средних

Третья часть алгоритма
кластеризации методом kсредних

16. Четвёртая часть алгоритма кластеризации методом k-средних

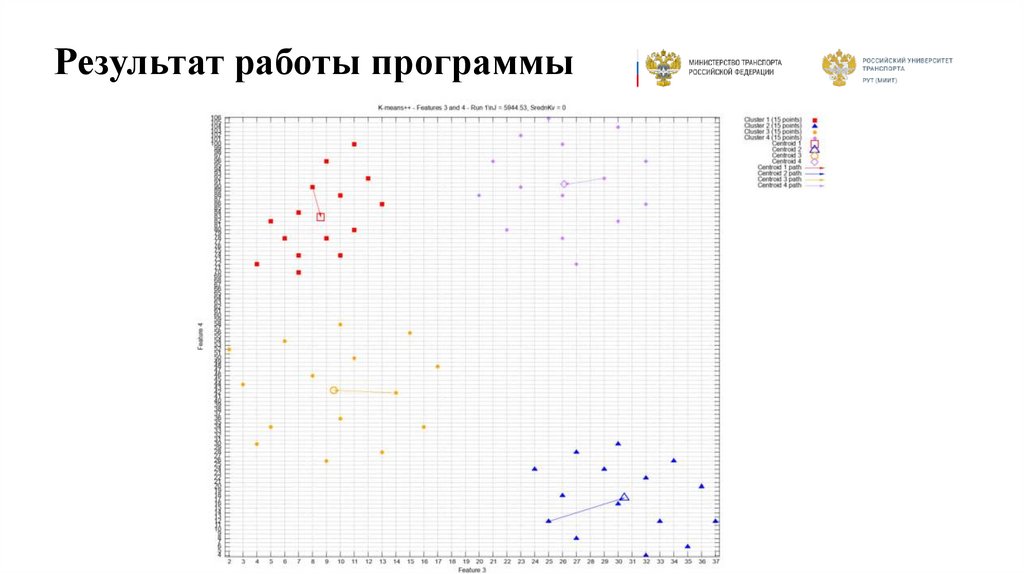
17. Результат работы программы

18. Результат работы программы

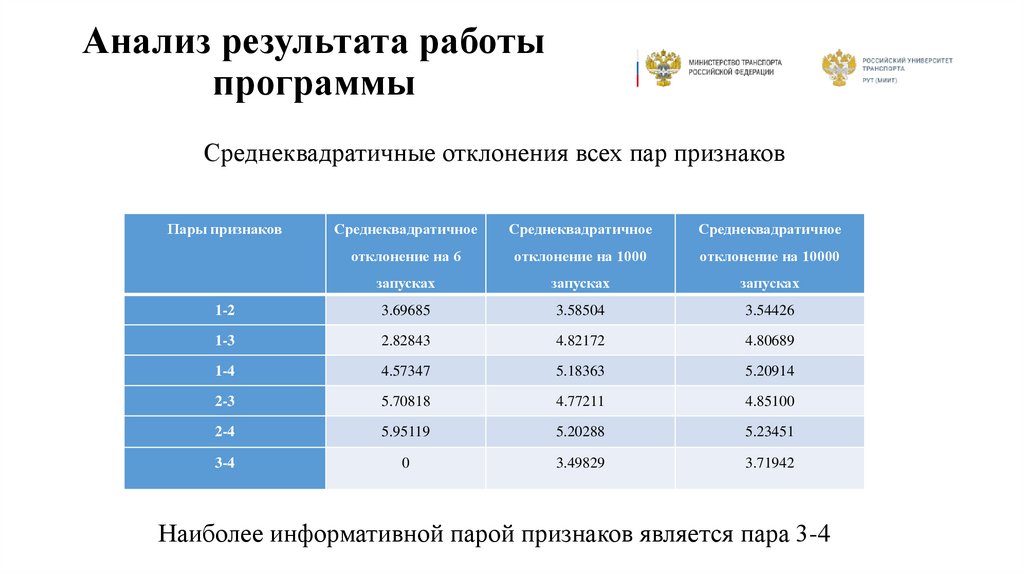
19. Анализ результата работы программы

Среднеквадратичные отклонения всех пар признаков
Пары признаков
Среднеквадратичное
Среднеквадратичное
Среднеквадратичное
отклонение на 6
отклонение на 1000
отклонение на 10000
запусках
запусках
запусках
1-2
3.69685
3.58504
3.54426
1-3
2.82843
4.82172
4.80689
1-4
4.57347
5.18363
5.20914
2-3
5.70818
4.77211
4.85100
2-4
5.95119
5.20288
5.23451
3-4
0
3.49829
3.71942
Наиболее информативной парой признаков является пара 3-4

20. Заключение

1. Был осуществлён комплексный анализ методов кластеризации, в рамках которого
изучены теоретические принципы и практические особенности применения алгоритмов
машинного обучения без учителя.
2. Основное внимание было уделено исследованию метода k-средних и его модификациям,
а также проведён сравнительный анализ с другими методами кластеризации, такими как
алгоритм связных компонентов, алгоритм кратчайшего незамкнутого пути,
кластеризация с частичным обучением и иерархическая кластеризация.
3. Программная реализация проекта выполнена на языке C++, что позволило эффективно
решить задачу кластеризации 60 объектов по 4 признакам с выделением 4 кластеров.
4. Проведено тестирование программы и сравнительный анализ шести вариантов
сочетаний признаков.
5. Определены два наиболее информативных признака.

21. СПАСИБО ЗА ВНИМАНИЕ! Мы готовы ответить на ваши вопросы