Копия - прямая в пространстве

1.

Прямая в
пространстве
1

2.

1 Общее уравнение прямой
Прямая определяется как линия пересечения двух плоскостей, т.е. совместным
заданием уравнений двух плоскостей:
A1 x B1 y C1 z D1 0,
-общее уравнение прямой.
.
0
D
z
C
y
B
x
A
2
2
2
2
В качестве нормали можно взять вектор N1 N 2 s .
(24)
2

3.

2. Векторное уравнение прямой.
Положение прямой в пространстве определено, если задать какую-нибудь
точку M 0 x0 ; y0 ; z 0 и направляющий вектор s m; n; p , параллельный этой
прямой.
Вывод: ▼ Возьмем на прямой произвольную точку M x; y; z . Введем в
рассмотрение радиус-векторы точек M 0 и M : r 0 OM 0 , r OM .
По правилу суммы векторов получаем: r r0 M 0 M .
Так как M 0 M || s , то M 0 M t s , где t R -параметр.
Таким образом, векторное уравнение прямой:
r r0 t s
3

4.

3. Параметрическое уравнение прямой
Так как r x; y; z , r 0 x0 ; y0 ; z 0 , t s tm; tn; tp ,
то согласно (24) xi y j z k x0 tm i y0 tn j z0 tp k , т.е.
x x0 mt
y y0 nt -параметрическое уравнение прямой.
z z0 pt
(26)
4

5.

4. Канонические уравнения прямой
Так как M 0 M x x0 ; y y0 ; z z0 коллинеарен направляющему вектору
s m; n; p , следовательно, координаты M 0 M пропорциональны координатам
s:
x x0 y y0 z z0
- канонические уравнения прямой.
m
n
p
(27)
Замечание. Обращение в нуль одного из знаменателей соответствует
обращению в нуль соответствующего числителя.
5

6.

5. Уравнение прямой, проходящей
через две точки.
Пусть точки M 1 и M 2 лежат на прямой. В качестве направляющего вектора s
взять M 1M 2 , следовательно x2 x1 ; y 2 y1 ; z 2 z1 m; n; p .
Согласно уравнению (27), взяв в качестве M 0 точку M 1 :
x x1
y y1
z z1
x2 x1 y2 y1 z 2 z1
(28)
уравнение прямой, проходящей через две точки.
6

7.

Пример:
Написать канонические уравнения прямой, заданной общим уравнением
x y z 1 0,
2 x y 3z 5 0.
Решение:
x y 1 0,
1. Пусть z 0 . Система примет вид
2 x y 5 0.
Решаем систему, получаем точку M 1 ( 2;1;0) L .
x z 1 0,
2. Пусть y 0 . Система примет вид
2 x 3z 5 0.
Решаем систему, получаем точку M 2 (2;0;3) L .
3. Теперь составим уравнение прямой, проходящей через две точки (28):
x 2 y 1 z
.
4
1 3
7

8.

Пример
Даны координаты точек: B 5; 4; 0 , D 1; 1;1 .
1. Составить уравнение прямой BD .
2. Построить прямую.
x x1
y y1
z z1
.
x2 x1 y2 y1 z 2 z1
Подставим координаты точек в данное уравнение:
x 5 y 4 z 0
.
1 5 1 4 1 0
Упростим его:
x 5 y 4 z
.
4
3
1
8

9.

Пример
x 1 y z 1
.
2
3
1
Составить параметрическое уравнение прямой.
Дано каноническое уравнение прямой
Рассмотрим исходное уравнение
x 1 y z 1
. Введём в рассмотрение
2
3
1
параметр t :
x 1 y z 1
t.
2
3 1
Составим систему уравнений:
x 1
2 t,
y
t,
3
z 1
1 t.
Выразим из системы x , y , и z :
x 1 2t ,
y 3t ,
z 1 t ;
9

10.

Пример
Составить
уравнение
прямой,
проходящей
через
точку
A 2;1; 3
перпендикулярно плоскости x 5 y 2 z 1 0 .
Решение.
1. Выполним схематичный чертёж к задаче. Пусть l – искомая прямая, –
плоскость, перпендикулярная прямой l .
x x0 y y0 z z0
,
m
n
p
где x0 , y0 , и z 0 – координаты точки, лежащей на прямой, m , n и p – координаты
направляющего вектора прямой.
Подставим координаты точки A 2;1; 3 и направляющего вектора s l 1; 5; 2
в уравнение:
Упростим его:
x 2 y 1 z 3
.
1
5
2
x 2 y 1 z 3
– искомое уравнение прямой l .
1
5
2
10

11.

Взаимное расположение прямых в
пространстве
1. Угол между двумя прямыми.
Если прямые заданы уравнениями
x a1 y b1 z c1
x a2 y b2 z c2
( L1 ) и
( L2 ) ,
m1
n1
p1
m2
n2
p2
то угол между ними вычисляется как угол между направляющими векторами
s1 m1; n1; p1 и s 2 m2 ; n2 ; p2 по формуле:
cos
m1m2 n1n2 p1 p2
m12 n12 p12
m22 n22 p22
-
(29)
угол между прямыми ( L1 ) и ( L2 ) .
11

12.

2. Условие параллельности прямых в пространстве.
Пусть даны две прямые
x x1 y y1 z z1
,
m1
n1
p1
x x2 y y 2 z z 2
.
m2
n2
p2
Данные прямые параллельны в том и только в том случае, когда их
направляющие векторы
s1 m1 ; n1 ; p1 и
s 2 m2 ; n2 ; p2 коллинеарны,
следовательно получаем условие параллельных двух прямых:
m2 n2 p2
.
m1 n1 p1
12

13.

3. Условие перпендикулярности прямых в пространстве.
Данные прямые перпендикулярны в том и только в том случае, когда их
направляющие векторы перпендикулярны (в пространстве эти прямые могут
быть
и
не
пересекающимися)
следовательно
получаем
условие
перпендикулярности двух прямых:
m1m2 n1n2 p1 p2 0 .
(31)
13

14.

4. Условие, при котором две прямые лежат в одной плоскости.
Пусть даны две прямые
x x1 y y1 z z1
,
m1
n1
p1
x x2 y y 2 z z 2
,
m2
n2
p2
где r 1 OM 1 , r 2 OM 2 , M1M 2 r 2 r1 .
14

15.

Прямые
лежат
в
одной
плоскости,
если
M 1M 2 ,
s1 m1 ; n1 ; p1
и
s 2 m2 ; n2 ; p2 компланарны, т.е. их смешанное произведение равно нулю.
M 1 M 2 s1 s 2 0 :
x2 x1
y 2 y1 z 2 z1
m1
n1
p1
m2
n2
p2
0.
(33)
При выполнении этого условия прямые ( L1 ) и ( L2 ) лежат в одной плоскости,
т.е. либо пересекаются, либо параллельны.
15

16.

Пример:
Найти угол между прямыми
2 x y z 1 0,
x y 2 z 2
( L1 ) ,
( L2 )
2
1
3
2 x y 3z 5 0.
Решение:
Найдем направляющие векторы прямых:
s1 2; 1; 3 , s 2 N 1 N 2 2; 8; 4 , s1 s 2 0 , 90 .
16

17.

Пример
Проверить, являются ли прямые
x 2
y
z 4
x 3 y 3 z 5
и
1
2
5
3
4
1
перпендикулярными.
Решение.
1. Из уравнений прямых выпишем координаты направляющих векторов:
s1 1; 2; 5 , s2 3; 4;1 .
2. Воспользуемся условием перпендикулярности прямых:
l1 l2 s1 s2 .
Найдём скалярное произведение векторов s1 и s 2 :
s1 s2 1 3 2 4 5 1 3 8 5 0 ,
следовательно, s1 s2 , а это означает, что прямые перпендикулярны
17

18.

Прямая и плоскость в пространстве
1. Угол между прямой и плоскостью.
Рассмотрим плоскость Q : Ax By Cz D 0 ,
прямую l :
x x0 y y 0 z z 0
.
m
n
p
Углом между плоскостью и прямой называется любой из двух смежных углов,
образованных прямой и ее проекцией на плоскость.
Обозначим - угол между плоскостью Q и прямой L ,
- угол между нормалью к плоскости N A; B; C и направляющим вектором
прямой s m; n; p .
cos
n s
n s
Пусть
cos
.
n s
cos , т.е.
, sin sin
2
2
n s
Am Bn Cp
A2 B 2 C 2 m 2 n 2 p 2
-
косинус угла между прямой и плоскостью.
(34)
18

19.

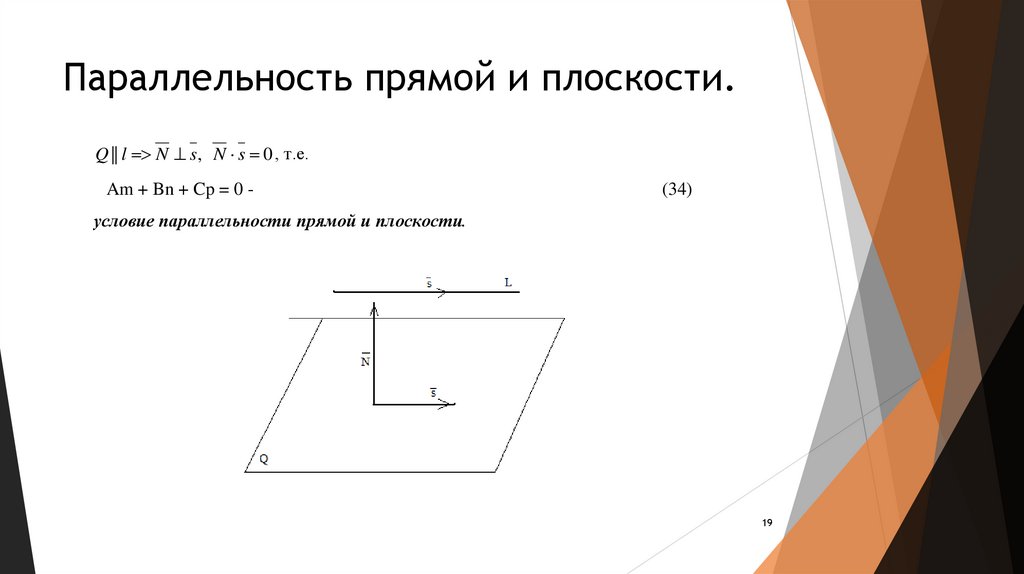
Параллельность прямой и плоскости.
Q || l N s, N s 0 , т.е.
Am + Bn + Cp = 0 -
(34)
условие параллельности прямой и плоскости.
19

20.

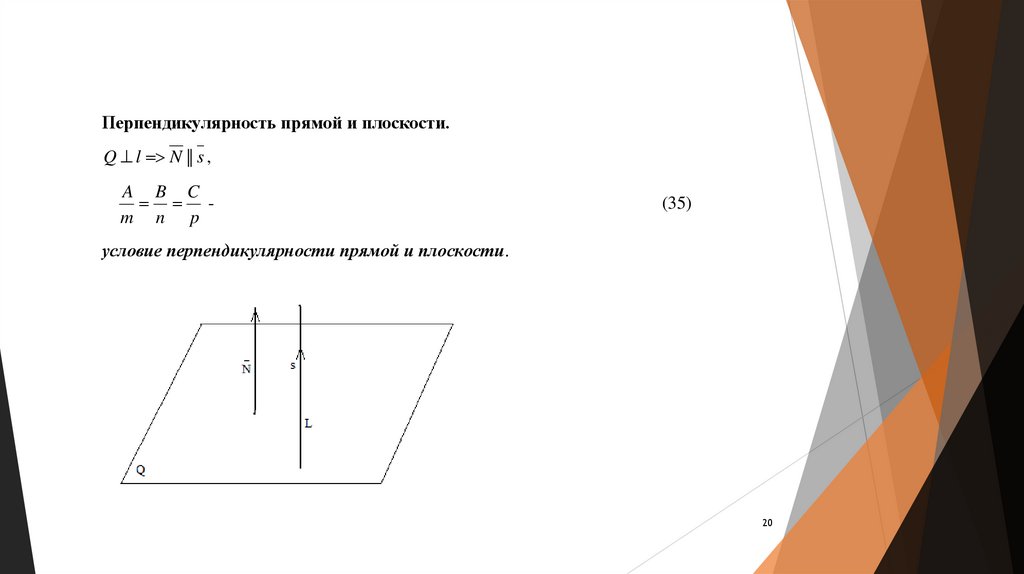
Перпендикулярность прямой и плоскости.
Q l N || s ,
A B C
m n p
(35)
условие перпендикулярности прямой и плоскости.
20

21.

Пересечение прямой и плоскости.
Ax By Cz D 0,
x x0 y y 0 z z 0
m n p .
Q
L
Чтобы найти пересечение прямой и плоскости, необходимо привести
уравнение прямой к параметрическому виду:
x x 0 mt,
L^ y y 0 nt ,
z z pt,
0
t R .
Далее подставляем найденные значения x, y, z в уравнение плоскости
A(x 0 mt ) B( y0 nt ) C ( z0 pt ) D 0 .
Находим параметр t.
Для полученного значения t находим координаты точки пересечения.
21

22.

Пример
Найти угол между прямой и плоскостью
4 x 2 y 2 z 3 0,
x 1 y 6 z 7
1 1 2 .
Решение:
s (1,1, 2) ,
n (4, 2, 2) .
По формуле (34) sin
1 4 1 ( 2) ( 2)( 2) 4 2 4 1
.
1 1 4 16 4 4
6 24 2
Найдем точку пересечения прямой и плоскости.
Запишем уравнение прямой в параметрическом виде:
x 1 t,
y 6 t,
z 7 2t.
22

23.

Подставим в уравнение плоскости полученную точку
4(1 + t) – 2(6 + t) – 2(-7 – 2t) + 3 = 0,
3
t , тогда
2
x0 1
1
3
,
2
2
y0 6
3
4,5 ,
2
z0 = -7 + 3 = -4,
1
M 0 ( ;4,5; 4) - точка пересечения прямой и плоскости.
2
23

24.

24