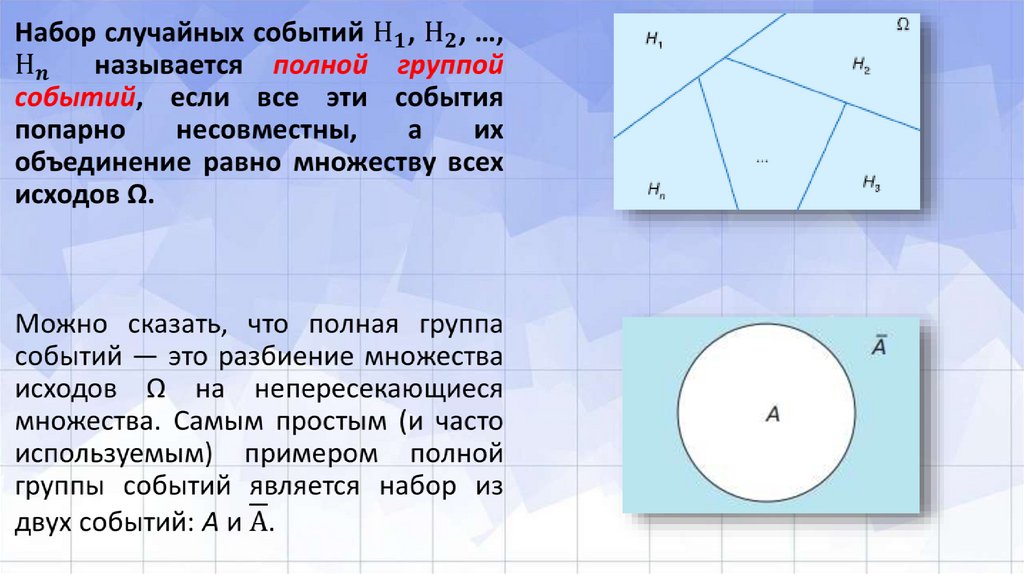
Похожие презентации:
Презентация к уроку вероятности и статистики по теме _Формула полной вероятности_ (10
1. Формула полной вероятности.
2. Пример 1
3.
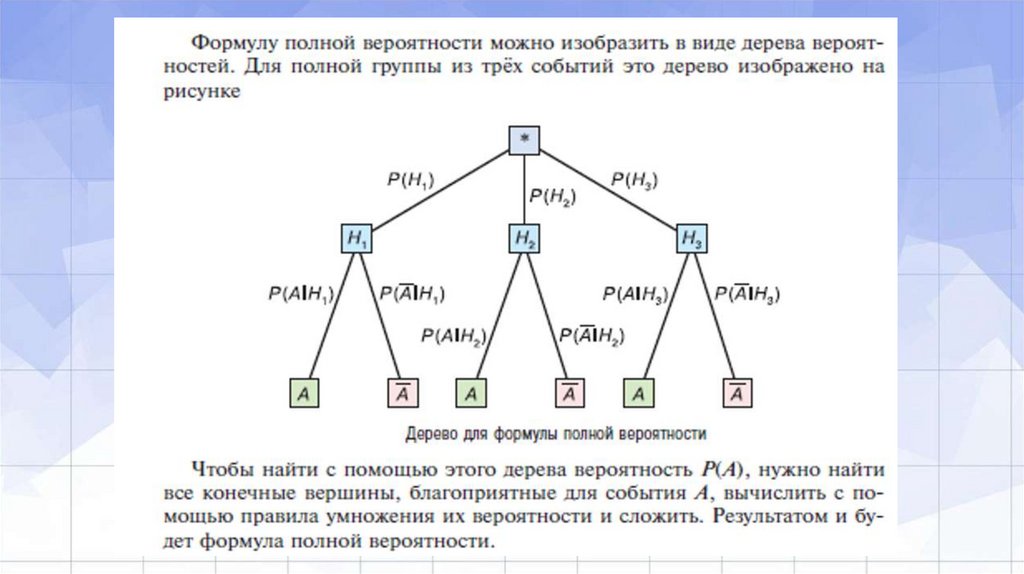
4. Формула полной вероятности
5.
6. Пример 2
7. Пример 3
8.
9. Задание 1
В ящике лежит 6 красных и 12 синих шаров. Из негоодин за другим вынимают 3 шара.
С какой вероятностью:
а) первый шар будет красным;
б) второй шар будет красным;
в) третий шар будет красным?
10. Задача 2
В Волшебной стране бывает два типа погоды: хорошая и отличная,причём погода, установившись утром, держится неизменной весь день.
Известно, что с вероятностью 0,9 погода завтра будет такой же, как и
сегодня. 5 апреля погода в Волшебной стране хорошая. Найдите
вероятность того, что 8 апреля в Волшебной стране будет отличная
погода.
Решение
Известно, что с вероятностью 0,9 погода завтра будет такой же, как и
сегодня. Тогда, если погода меняется, то её вероятность равна 0,1.
Для погоды на 6, 7 и 8 апреля есть 4 варианта: ХХО, ХОО, ОХО, ООО
(здесь Х — хорошая, О — отличная погода). Найдем вероятности
наступления такой погоды:
P(XXO) = 0,9·0,9·0,1 = 0,081;
P(XOO) = 0,9·0,1·0,9 = 0,081;
P(OXO) = 0,1·0,1·0,1 = 0,001;
P(OOO) = 0,1·0,9·0,9 = 0,081.
Указанные события несовместные, вероятность их суммы равна сумме
вероятностей этих событий:
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,081 + 0,081 + 0,001 + 0,081 = 0,24
4.
Ответ: 0,244.
11. Задача 3
В отдел технического контроляпоступает партия, содержащая 20
изделий, среди которых имеется 5
бракованных.
Контролёр
для
проверки отбирает 2 изделия, при
этом в бракованном изделии он
обнаруживает брак с вероятностью
0,9. Партия бракуется, если среди
отобранных для проверки изделий
обнаружено
хотя
бы
одно
бракованное. Найдите вероятность
того, что данная партия изделий
будут забракована.
12. Задача 3 (решение)
13. Задача 3 (решение)
14. Домашнее задание:
Выучить правила и формулы § 10 п.2Выполнить в тетради.
1.В долине Стабильности бывают только дождливые и
солнечные дни, причём с вероятностью 0,9 на
следующий день сохраняется та же погода, которая
была в предыдущий. 1 мая был дождь. С какой
вероятностью 5 мая будет солнце?
2. Из десяти студентов, пришедших на экзамен, Иванов
и Петров знают 20 билетов из 30, Сидоров — только 15,
а остальные выучили все 30 билетов. Знание билета
гарантирует сдачу экзамена профессору Злобину с
вероятностью 0,85, а незнание — только 0,1. С какой
вероятностью случайно вызванный студент сдаст
экзамен?