Тема №7. Растровая графика

1. Компьютерная графика

Москин Николай Дмитриевич
Институт математики и информационных
технологий
Петрозаводский государственный университет

2. § 7 Растровая графика

В отличие от векторных изображений здесь не
требуется математическое моделирование форм;
достаточно просто записать значение каждого
пикселя. Характеристиками изображения являются:
Размер в пикселях (например,
1024×768px);
Глубина цвета (количество
используемых цветов);
Цветовая модель (например,
RGB, CMYK, HSV и др.);
Разрешение изображения.

3. Разрешение устройств

Разрешение устройств (принтеров, сканеров и т.п.)
задается как количество точек на единицу длины:
dpi (dots per inch) – количество точек на дюйм.
Например, 5760x1440 dpi для принтера означает, что
его разрешающая способность 5760 точек по
горизонтали и 1440 точек по вертикали на квадрате
размером 1х1 дюйм.
ppi (pixels per inch) – количество пикселей на дюйм.
lpi (lines per inch) – количество линий на дюйм. Эта
характеристика разрешения печати полутоновых
изображений, используется в полиграфии.

4. Разрешение изображений

Физический размер изображения, отправленного на
устройство вывода = размер в пикселях / разрешение
устройства
Например, квадрат с шириной 128 пикселей при
отображении с разрешением 72 dpi имеет физическую
ширину 45 мм (1 дюйм = 2,54 см).
Если разрешение изображения < разрешения устройства,
необходимо масштабирование (интерполяция пикселей),
что приведет к ухудшению качества. Если разрешение
изображения > разрешения устройства вывода, то
изображение нужно масштабировать с уменьшением
размера. Данный процесс называется дискретизацией с
понижением частоты.

5. Выбор

Простейшими инструментами выбора являются
прямоугольная и эллиптическая бегущие рамки. Выбор
с помощью волшебной палочки осуществляется на
основе их цвета. При выборе можно указать допуск, т.е.
насколько цвет может отличаться от указанного.
Магнитное лассо не просто придерживается контура,
обрисованного пользователем, а подстраивается так,
что контур привязывается к краям, находящимся на
заданном расстоянии от курсора. Краем считаются
любые достаточно крупные изменения контраста.

6. Выбор с помощью «волшебной палочки»

7. Выбор с помощью «магнитного лассо»

8. Маска

Если нужно одно и то же
выделение использовать на
разных этапах редактирования,
то выбор представляется в виде
однобитовой маски, которую
можно хранить вместе с
изображением.
Используя несколько битов,
можно задавать различные
степени прозрачности. Такая
полутоновая маска называется
альфа-каналом.

9. Альфа-канал

При наложении двух пикселей друг на друга расчет
яркости результирующего пикселя выполняется по
формуле:
Result = Background * (1 − Alpha) + Foreground * Alpha,
где
Background − яркость фонового пикселя,
Foreground − яркость накладываемого пикселя,
Alpha (от 0 до 1) − прозрачность накладываемого
пикселя.

10. Смешивание с маской альфа-канала

11. Точечная обработка пикселей

Если расчет нового значения каждого пикселя выполняется на основе только его старого значения:
p’=f(p) – отображающая функция,
то подобная функция выполняет точечную обработку
пикселей. Например, для построения негатива по
полутоновому изображению
f(p) = W – p,
где W – значение пикселя, представляющее белый
цвет. Также можно определить f(p) для изменения
яркости и контраста.

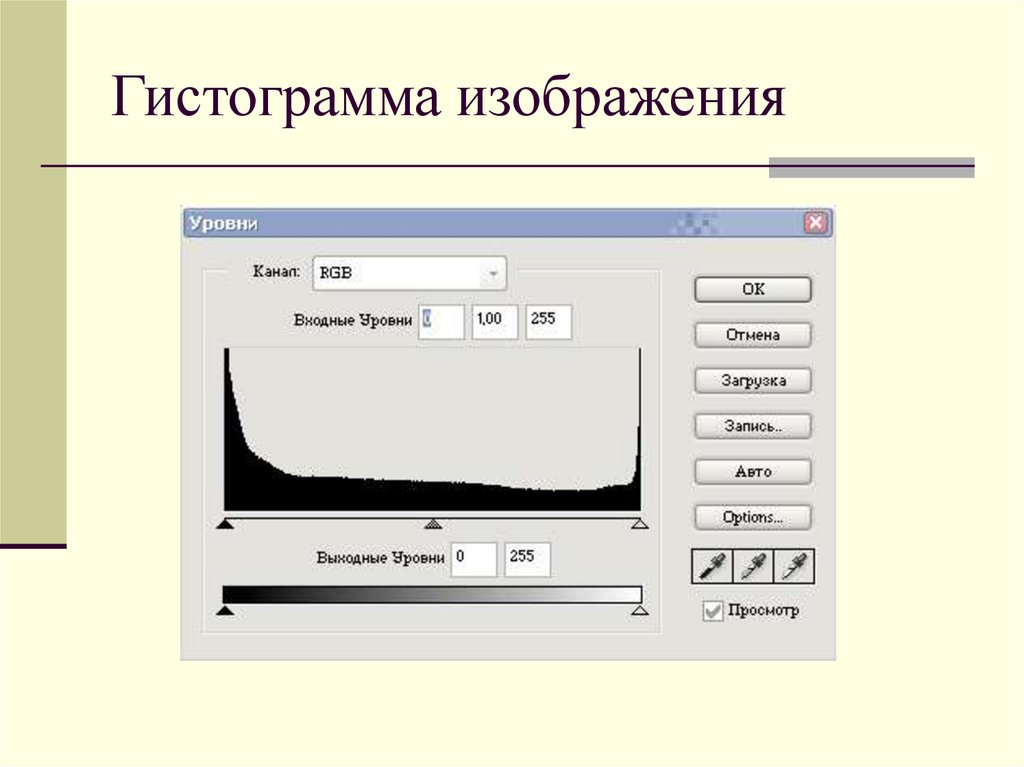
12. Гистограмма изображения

На гистограмме горизонтальная ось представляет
возможные значения (от 0 до 255 на 8-битовом
полутоновом изображении), а прямоугольники –
количество пикселей, имеющих указанное значение.
Верхний набор ползунков контролирует диапазон
входных значений. Левый ползунок задает значение,
которому будет поставлен в соответствие черный цвет,
правый – значение для белого цвета. Аналоги-чно
нижние ползунки отвечают за выходные значения
пикселей.

13. Гистограмма изображения

14. Гистограмма изображения

Гистограммы отображаются на дисплеях
современных цифровых фотоаппаратов, что
позволяет просматривать экспозицию фотографий
не только после съёмки, но и выбрать нужный
ракурс и параметры в процессе подготовки до
съёмки кадра.

15. Пример недоэкспонированного снимка

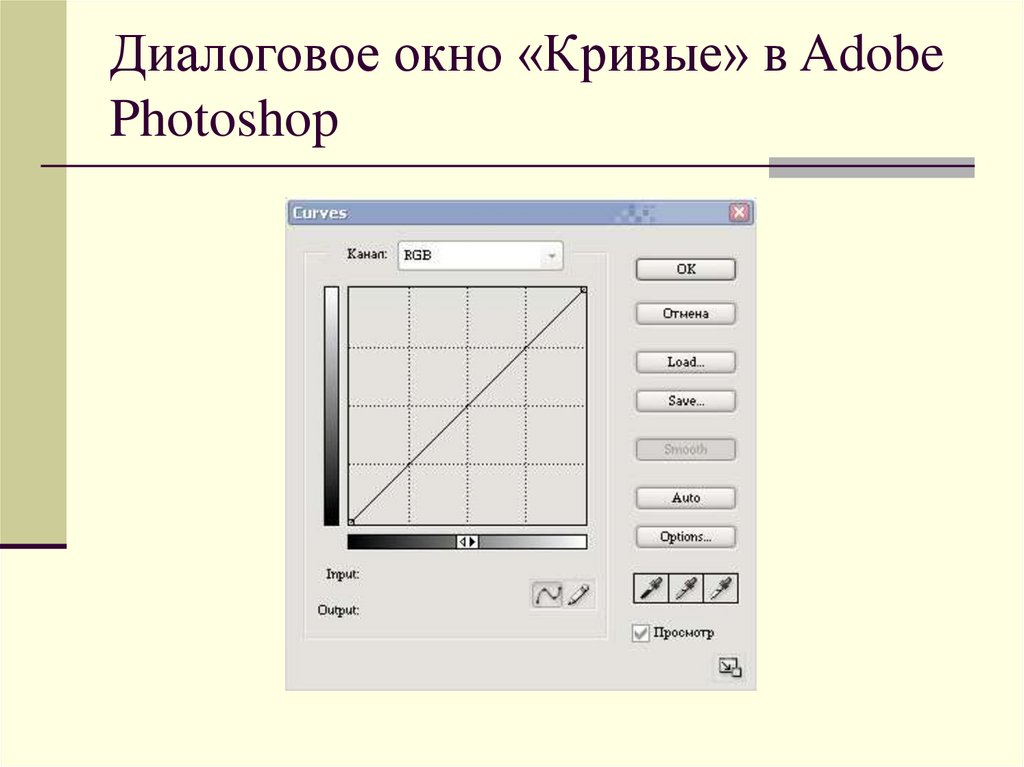
16. Диалоговое окно «Кривые» в Adobe Photoshop

В диалоговом окне «Кривые» можно
изменить форму функции f, перетаскивая
контрольные точки, или вообще
перерисовать полностью, используя
инструмент «карандаш».
До коррекции кривая представляет собой
тождественную функцию, где вход и выход
одинаковы.

17. Диалоговое окно «Кривые» в Adobe Photoshop

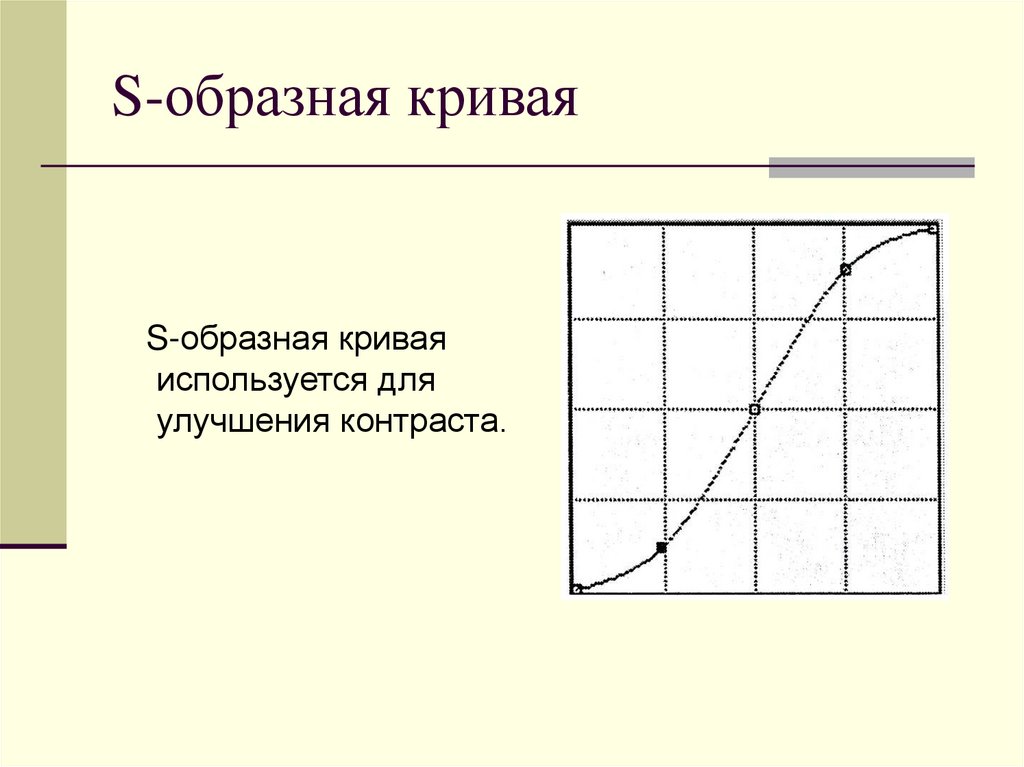
18. S-образная кривая

S-образная кривая
используется для
улучшения контраста.

19. Пакетная (групповая) обработка пикселей

При групповой (пакетной) обработке новое
значение пикселя рассчитывается как функция не
только прежнего значения, но и значений соседних
пикселей.
В общем случае, если пиксель имеет координаты
(x, y), ближайшие к нему пиксели располагаются в
точках (x-1, y+1), (x, y+1), … , (x, y-1), (x+1, y-1).

20. Свертка

Многие фильтры построены на основе операции
свертки (convolution). В одномерном случае,
если исходное изображение – это набор
значений a0, a1, …, an-1, то результат свертки
изображения с ядром k задается формулой
Величина N определяет размер ядра – массива
k-N, …, kN.

21. Свертка

Например, при наличии одномерного массива
входных данных a0, a1,…, an-1 в результате
применения свертки с ядром 3 получим
следующий набор значений:
При свертке для крайних элементов исходного
массива происходит выход за его пределы. Есть
несколько вариантов, как можно правильно
обрабатывать изображение в таких случаях.

22. Свертка

Один из вариантов заключается в том, что вместо
обращения к элементу за пределами массива мы
берем крайний элемент с соответствующей
границы массива, т. е. в результате применения
фильтра с ядром размера 3 к первому элементу
массива a0, a1, …, an-1 получим значение

23. Двухмерный случай

Для двухмерного случая используется формула:
В этом случае ядро свертки задается квадратной
матрицей k. Одним из простейших в применении
является фильтр, предназначенный для
выделения на исходном изображении резких
скачков яркости. Он использует свертку с ядром
размеров 3*3 к яркости изображения.

24. Результат применения фильтра

25. Фильтр тиснения (emboss)

Еще одним
интересным фильтром
является фильтр
тиснения (emboss).

26. Размывание (blurring)

Распространенным
эффектом является
«размытие»
(сглаживание
изображения).
Простейший вариант
сглаживания –
применение свертки
со следующим ядром.
В данном фильтре все соседние значения имеют
один и тот же вес (что и сам пиксел).

27. Фильтр Гаусса

Часто желательно, чтобы вес был тем больше,
чем ближе соответствующий элемент к центру
(это преобразование более естественно).
Один из самых
распространенных
подобных фильтров –
фильтр Гаусса. В
простейшем случае он
задается с помощью
следующего ядра.

28. Размывание

Для получения более качественного сглаживания
часто используют ядра с большим размером.
Коэффициенты подобного ядра определяются по
следующей формуле:
где C – нормированный коэффициент,
необходимый для того, чтобы сумма всех
элементов ядра равнялась единице.

29. Пример размывания

30. Резкость (sharpening)

Один из довольно простых фильтров,
применяемых не к яркости изображения, а по
отдельности к каждому из цветовых каналов –
фильтр повышения контрастности. Он
использует следующее ядро:
Здесь резкие края
больше подходят для
анализа изображения,
чем для его реалистичного восприятия.

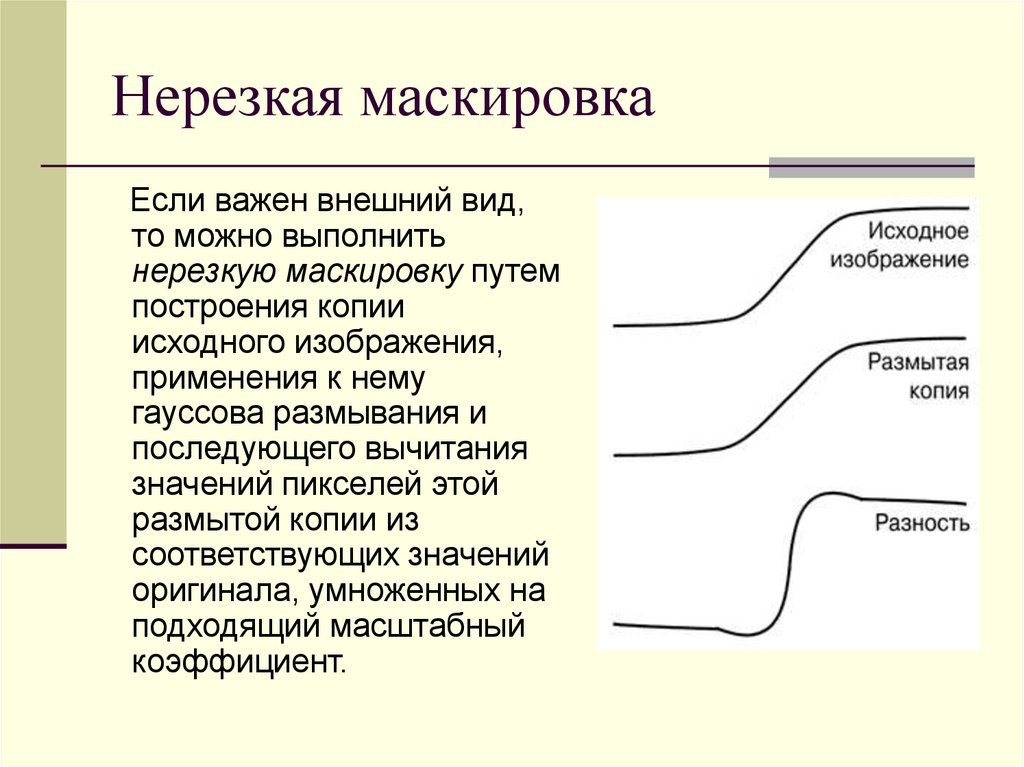
31. Нерезкая маскировка

Если важен внешний вид,
то можно выполнить
нерезкую маскировку путем
построения копии
исходного изображения,
применения к нему
гауссова размывания и
последующего вычитания
значений пикселей этой
размытой копии из
соответствующих значений
оригинала, умноженных на
подходящий масштабный
коэффициент.

32. Коррекция цвета

Красивым эффектом обработки изображений
является коррекция цвета. Для этого каждый
пиксел изображения переводят из цветового
пространства RGB в цветовое пространство HSV
и в этом пространстве изменяют насыщенность
цвета, после чего получившийся цвет переводят
обратно в RGB.
Иногда сложные эффекты можно представить как
результат последовательного применения ряда
простых фильтров.

33. Виды интерполяции

При применении к растровым
изображениям геометрических
преобразований (например,
масштабирование, поворот)
требуется интерполяция.
Пусть после преобразования
пиксель в точке (x’,y’) должен иметь
то же значение, что и точка (x,y)
оригинала, но x и y не являются
целыми числами. Пусть также в
точке (x,y) центрирован некий
целевой пиксель.

34. Интерполяция по ближайшему соседнему пикселю

Здесь учитывается
значение пикселя, центр
которого ближе всего
расположен к (x,y).
В результате преобразования изображение будет
демонстрировать все
признаки недостаточной
дискретизации: заметные
блоки пикселей и
зубчатые границы.

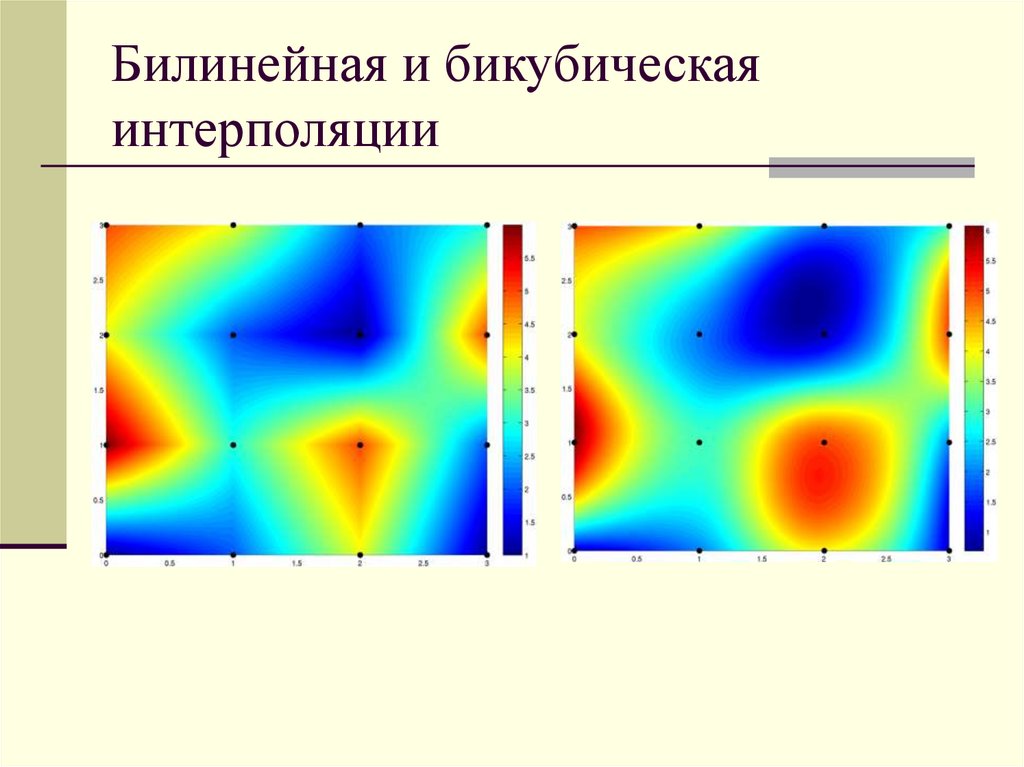
35. Билинейная интерполяция

Применяются значения четырех соседних пикселей
с весовыми коэффициентами, пропорциональными
площади их пересечения с целевым пикселем.
Пусть a и b – доли сторон целевого пикселя,
которые отсекаются вертикальной и горизонтальной
линиями соответственно. Тогда значение пикселя,
которому соответствует целевой пиксель с центром
в точке (x, y) равно
(1-a)(1-b)p1+a(1-b)p2+(1-a)bp3+abp4

36. Бикубическая интерполяция

В этом случае интерполяция основана на
кубических сплайнах, т.е. предполагается, что
промежуточные значения лежат не на прямой
линии, а на кривой Безье, соединяющей
записанные пиксели.
Кривые Безье используются по той же причине,
что и при рисовании кривых: они гладко
соединяются. В результате изображение с
пересчитанным разрешением также является
гладким.

37. Билинейная и бикубическая интерполяции