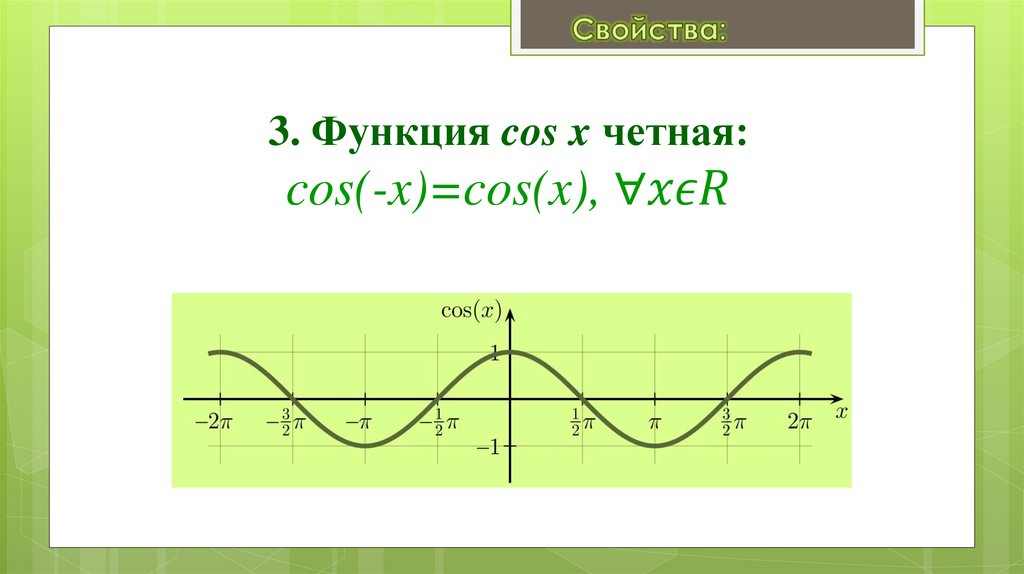
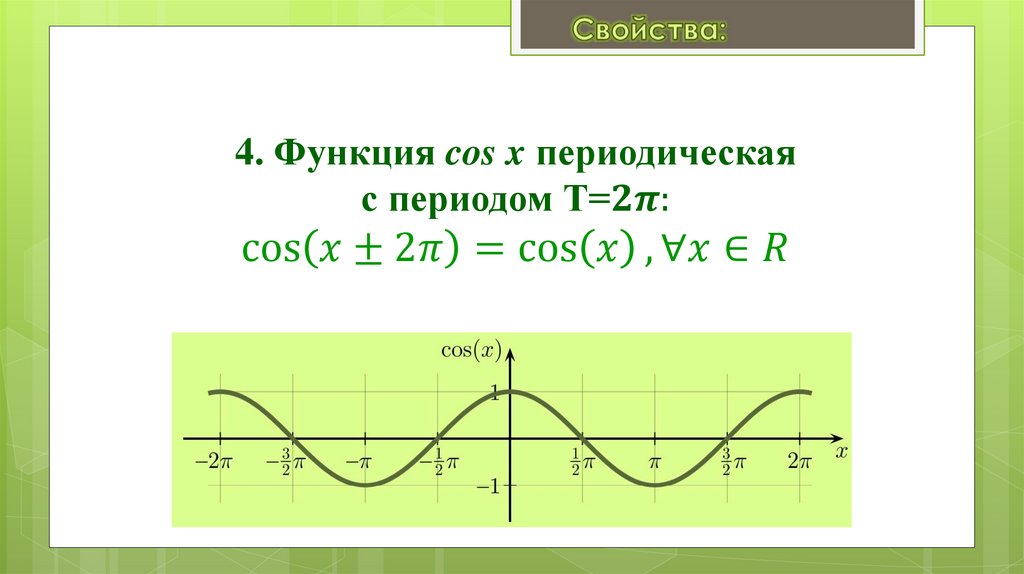
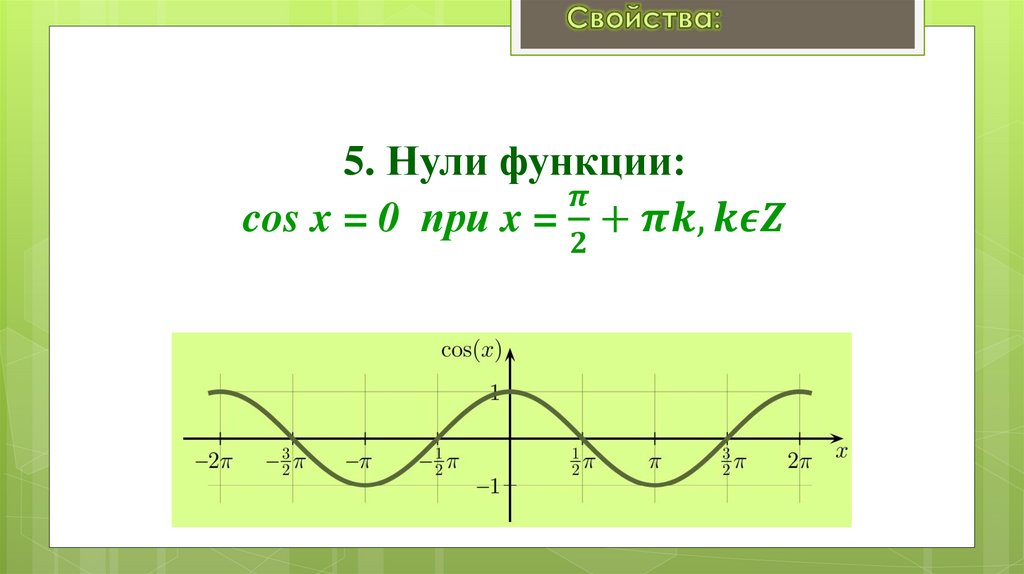
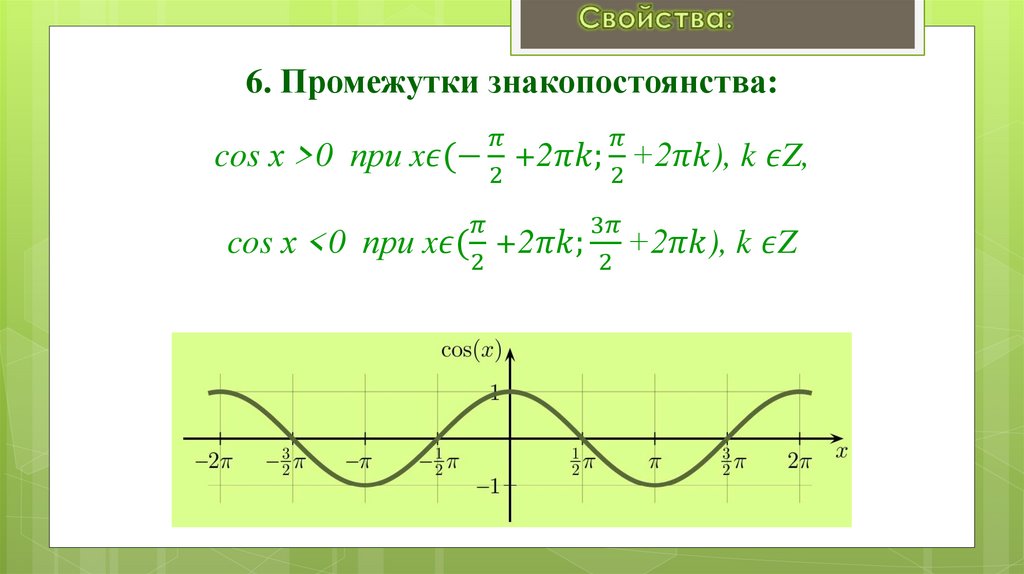
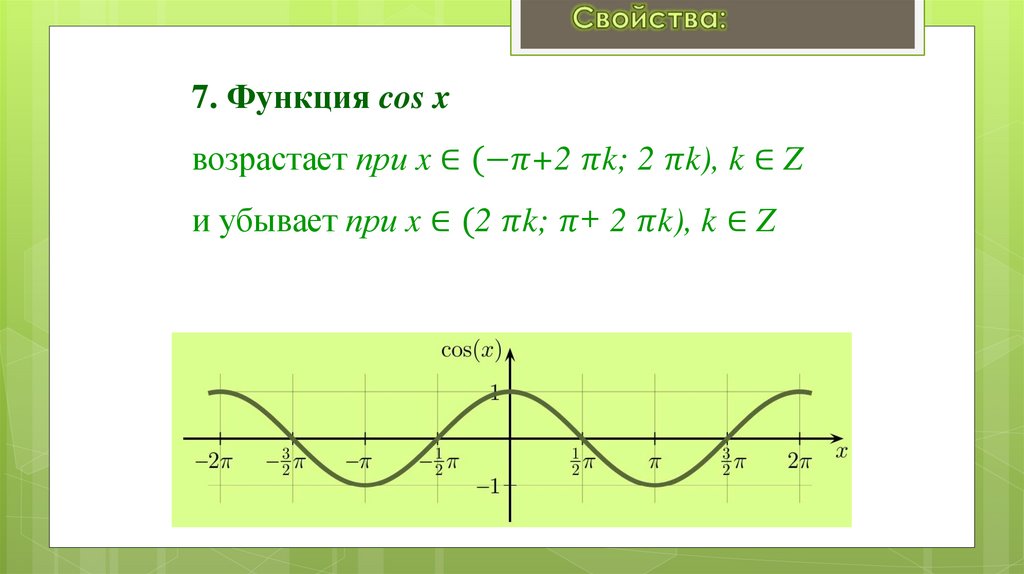
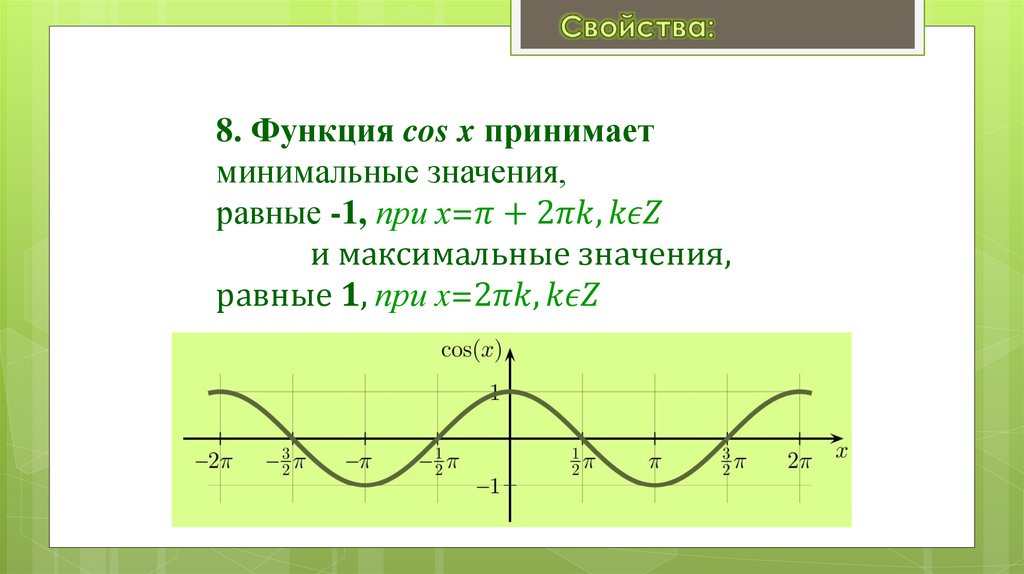
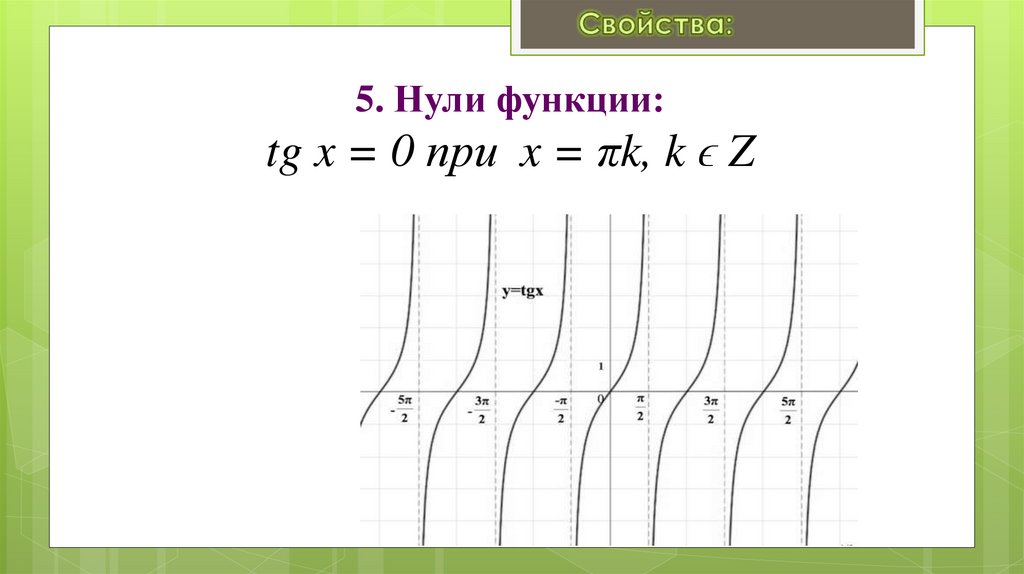
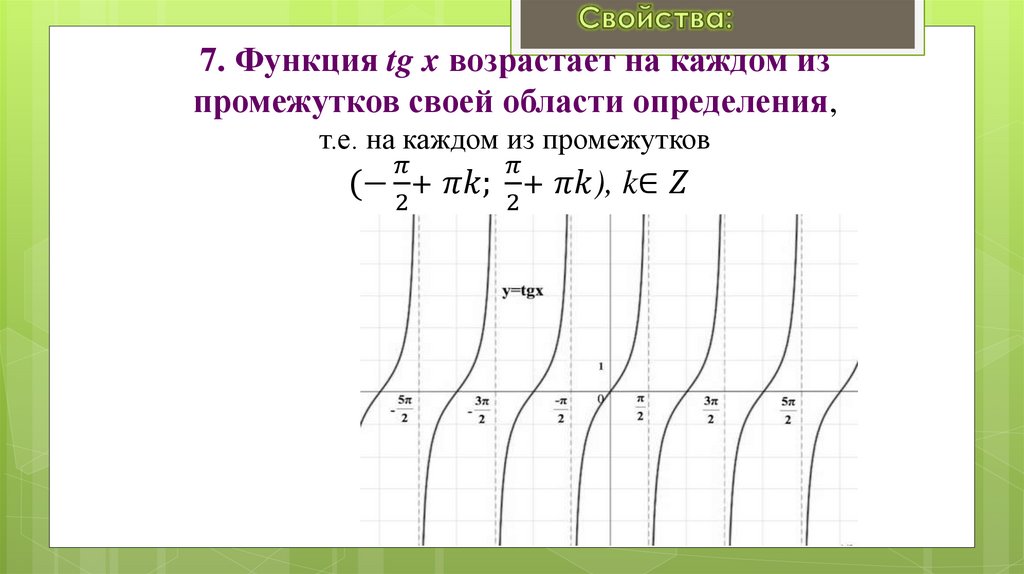
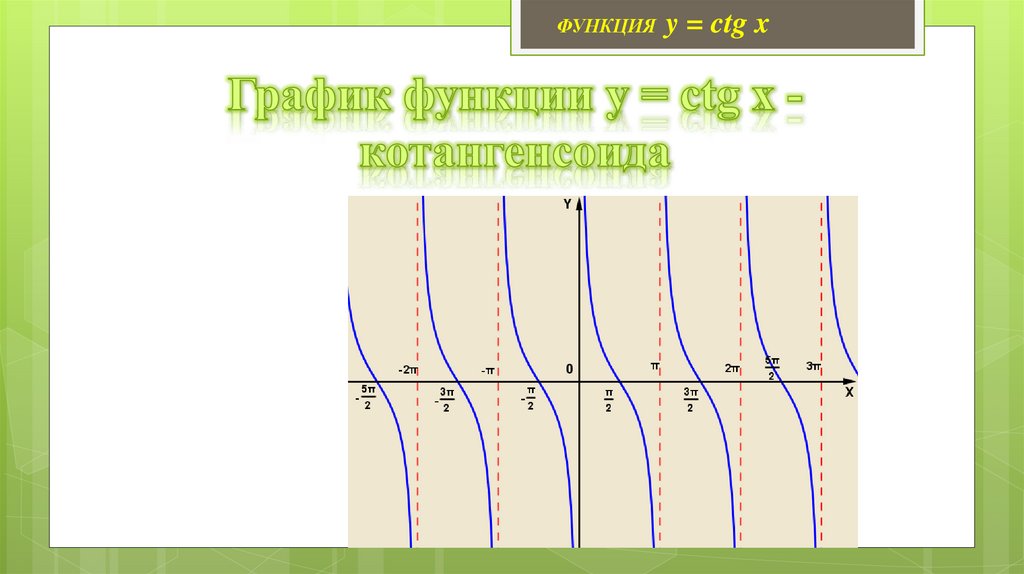
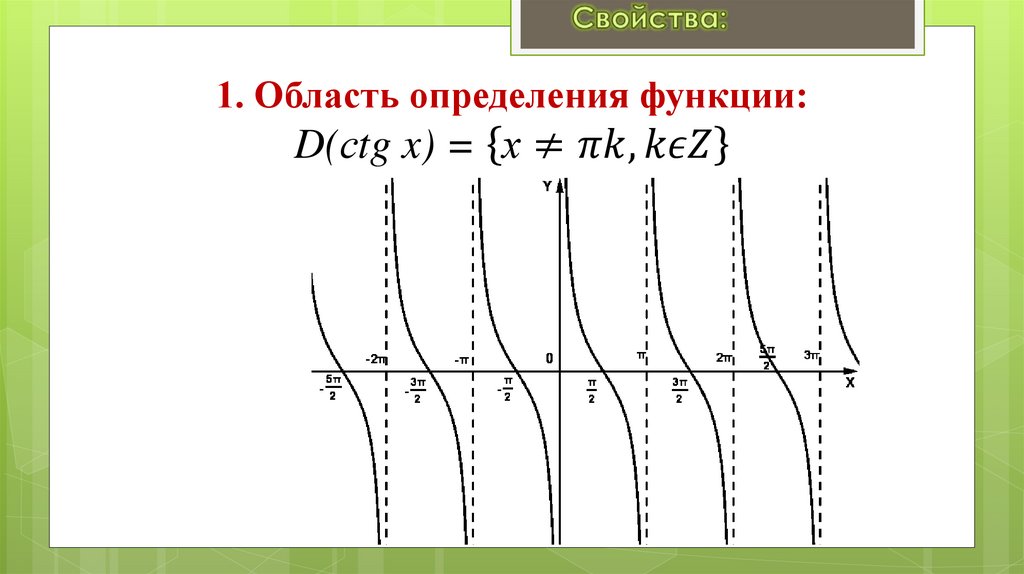
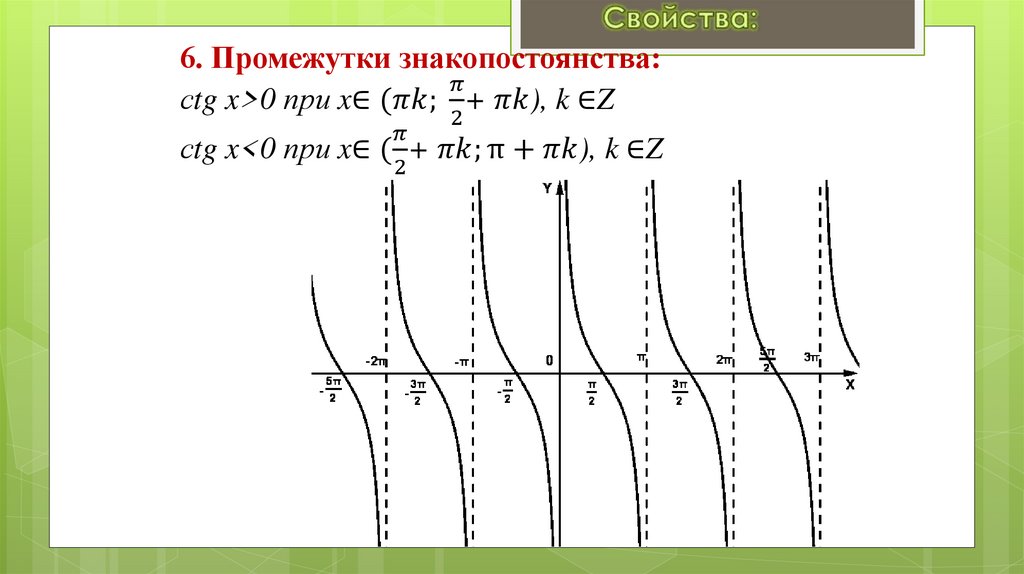
Занятие 17. Свойства и графики функций y = cos x
1. Свойства и графики функций y = cos x, y = sin x, y = tg x, y = сtg x.
2. Выполнить задания
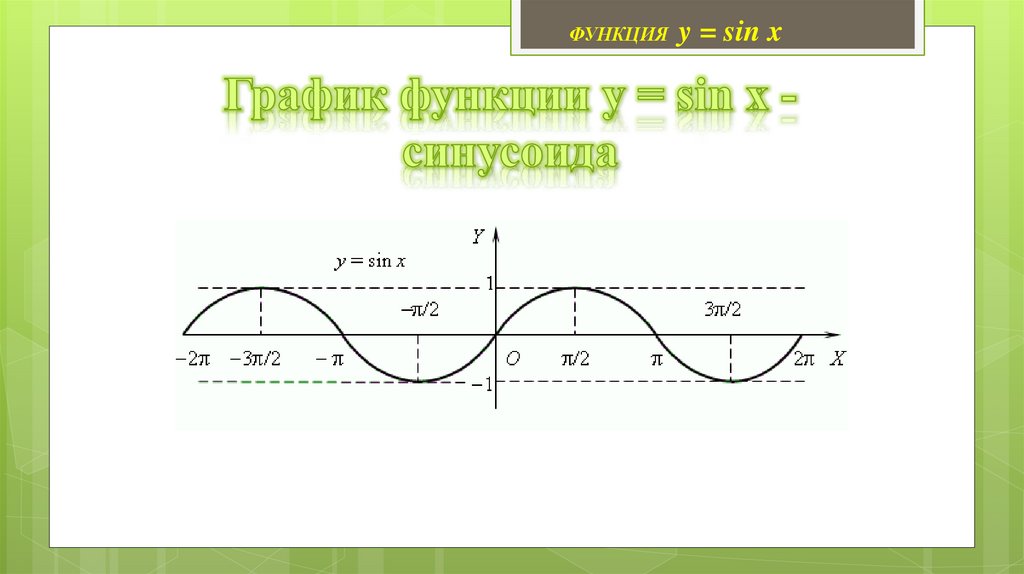
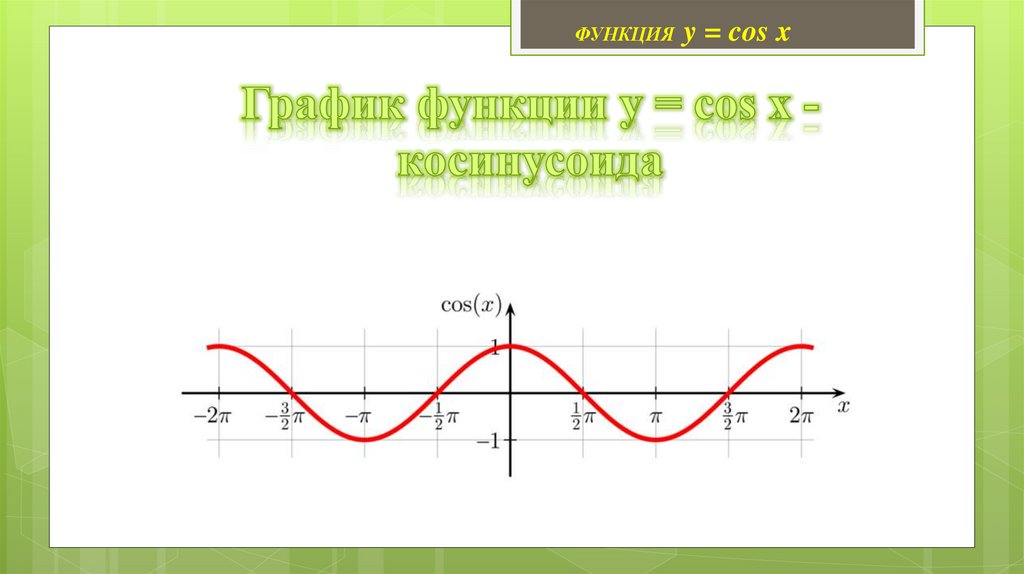
https://edu.skysmart.ru/student/mugagelafu3. График функции y = sin x - синусоида
ФУНКЦИЯ y = sin x4. 1. Область определения функции: D(sin x)=(-∞;+∞)
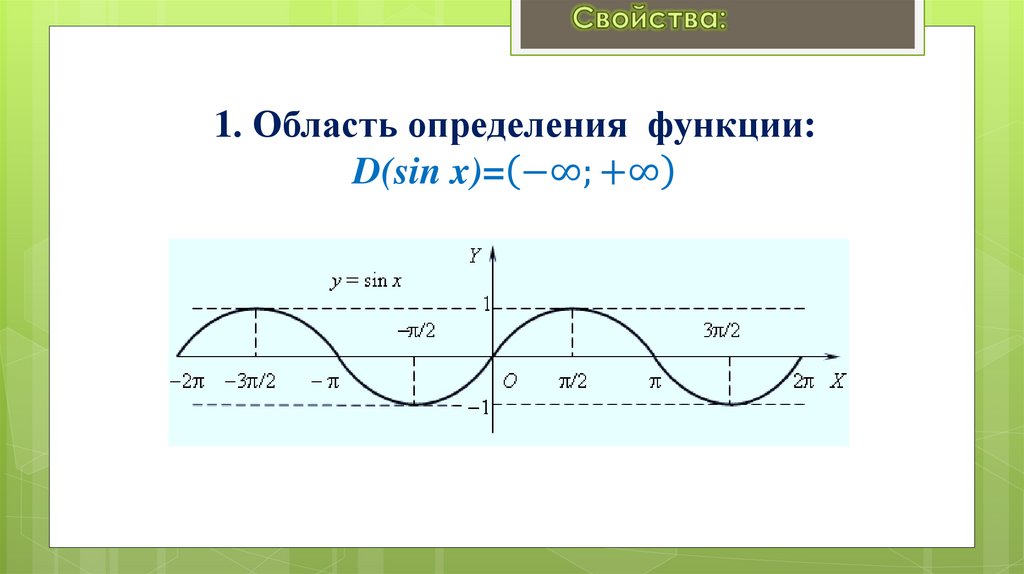
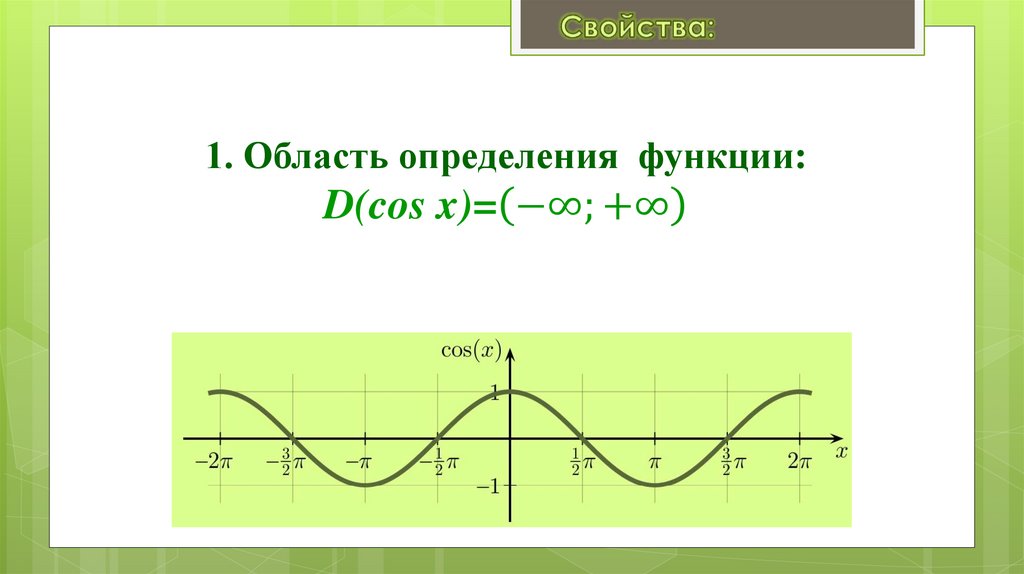
1. Область определения функции:D(sin x)= −∞; +∞
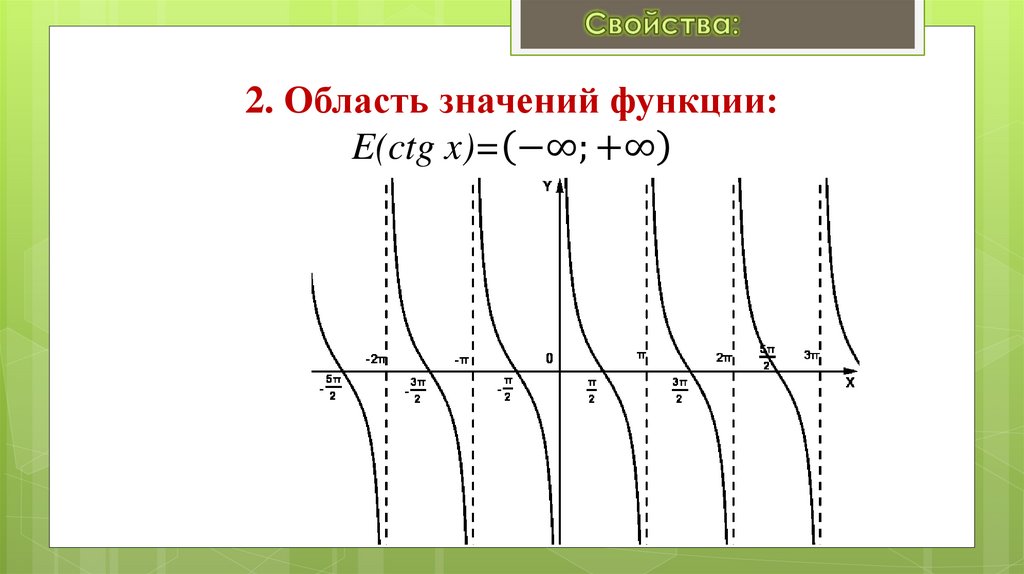
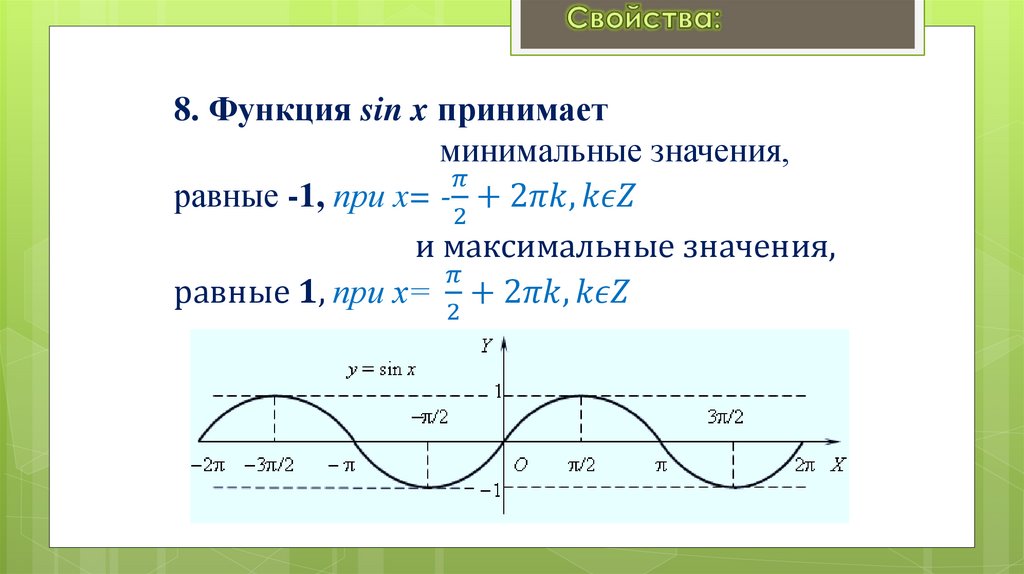
5. 2. Область значений функции: E(sin x)= [-1;1]
2. Область значений функции:E(sin x)= −


![2. Область значений функции: E(sin x)= [-1;1] 2. Область значений функции: E(sin x)= [-1;1]](https://cf5.ppt-online.org/files5/slide/j/JdLi5V1p2sIMhHc9TgOkBqGuDoSRXCjlr8vf6x/slide-4.jpg)
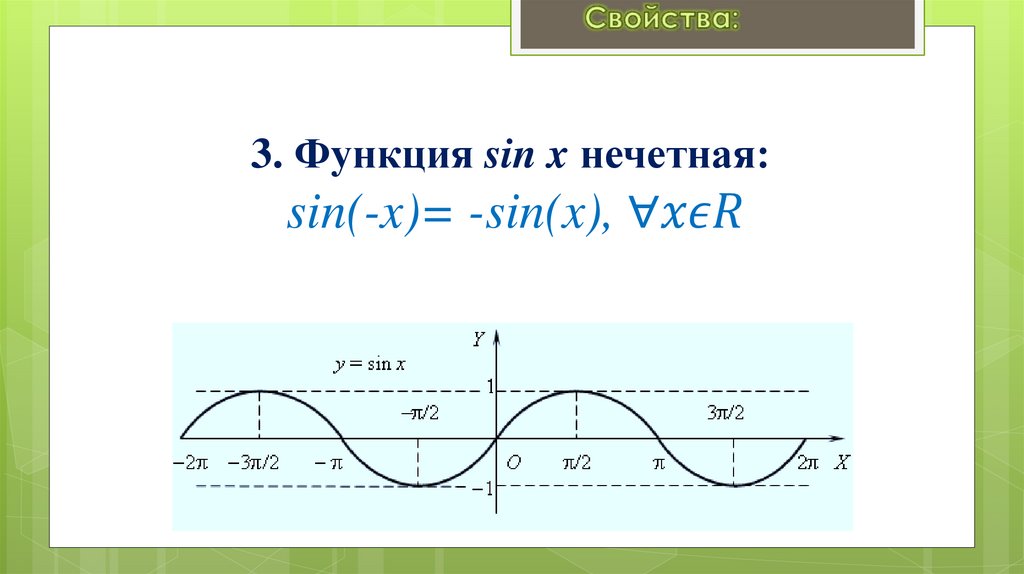
![2. Область значений функции: E(cos x)= [-1;1] 2. Область значений функции: E(cos x)= [-1;1]](https://cf5.ppt-online.org/files5/slide/j/JdLi5V1p2sIMhHc9TgOkBqGuDoSRXCjlr8vf6x/slide-13.jpg)