Лекция 8 Математическая логика

1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ ЛОГИКУ

Лекция 8
ВВЕДЕНИЕ В
МАТЕМАТИЧЕСКУЮ
ЛОГИКУ

2. ВОПРОСЫ:

1. Что такое логика? Формальная логика.
Математическая логика.
2. Применение математической логики.
3. Алгебра высказываний. Простые и сложные
высказывания.
4. Основные операции алгебры высказываний.
5. Таблицы истинности

3. ВОПРОС №1

Что такое логика?
Формальная
логика.
Математическая
логика.

4. Определения логики

5. КРАТКАЯ ИСТОРИЯ

Античность: рождение мысли. Древние греки (Аристотель) придумали логику как «инструкцию
к правильному мышлению». Это были первые правила игры, как правильно рассуждать.
XVII век: Лейбниц загорелся идеей создать «универсальный язык» для всех наук, где споры
заменятся вычислениями. Сейчас бы сказали, что он хотел сделать общий фундамент для
научных открытий. Он был гением, но опередил время на 200 лет.
XIX век: прорыв. Булева алгебра (Джордж Буль) наконец-то перевела логику на язык формул (И,
ИЛИ, НЕ). Логика стала полноценной математикой. Но пошли разговоры о неполноте теории.
Пока математики грустили о несовершенстве науки, их идеи подхватили технари. Тьюринг и
другие на этих принципах построили... компьютер. Смартфон работает на законах
математической логики.
Вывод: логика начиналась как философия, пережила кризис смысла и в итоге
покорила мир, став основой цифровой эпохи. Она не просто про истину, а про саму
структуру мысли, которую можно формализовать и заставить работать на нас.

6. LOGOS (ГРЕЧ.)- СЛОВО, ПОНЯТИЕ, РАССУЖДЕНИЕ, РАЗУМ.

СЛОВО «ЛОГИКА» ОБОЗНАЧАЕТ СОВОКУПНОСТЬ
ПРАВИЛ, КОТОРЫМ ПОДЧИНЯЕТСЯ ПРОЦЕСС
МЫШЛЕНИЯ.
ОСНОВНЫМИ ФОРМАМИ АБСТРАКТНОГО
МЫШЛЕНИЯ ЯВЛЯЮТСЯ: ПОНЯТИЯ, СУЖДЕНИЯ,
УМОЗАКЛЮЧЕНИЯ.

7. АРИСТОТЕЛЬ (384-322 ГГ. ДО Н.Э.) - ОСНОВОПОЛОЖНИК ЛОГИКИ.

АРИСТОТЕЛЬ (384-322 ГГ. ДО Н.Э.) ОСНОВОПОЛОЖНИК ЛОГИКИ.
КНИГИ:
• «КАТЕГОРИИ»
• «ПЕРВАЯ АНАЛИТИКА»
• «ВТОРАЯ АНАЛИТИКА»
(ИССЛЕДОВАЛ РАЗЛИЧНЫЕ ФОРМЫ РАССУЖДЕНИЙ , ВВЕЛ
ПОНЯТИЕ СИЛЛОГИЗМА)

8.

ЛОГИКА (ФОРМАЛЬНАЯ) - НАУКА О ЗАКОНАХ И ФОРМАХ ПРАВИЛЬНОГО
МЫШЛЕНИЯ.
МАТЕМАТИЧЕСКАЯ ЛОГИКА ИЗУЧАЕТ ЛОГИЧЕСКИЕ СВЯЗИ И
ОТНОШЕНИЯ, ЛЕЖАЩИЕ В ОСНОВЕ ЛОГИЧЕСКОГО (ДЕДУКТИВНОГО)
ВЫВОДА.

9.

ПОНЯТИЕ - ФОРМА МЫШЛЕНИЯ, В КОТОРОЙ ОТРАЖАЮТСЯ
СУЩЕСТВЕННЫЕ ПРИЗНАКИ ОТДЕЛЬНОГО ПРЕДМЕТА ИЛИ КЛАССА
ОДНОРОДНЫХ ПРЕДМЕТОВ. (ТРАПЕЦИЯ, ДЕРЕВО)
СУЖДЕНИЕ - МЫСЛЬ, В КОТОРОЙ ЧТО-ЛИБО УТВЕРЖДАЕТСЯ ИЛИ
ОТРИЦАЕТСЯ О ПРЕДМЕТАХ. (ВЕСНА НАСТУПИЛА, И ГРАЧИ ПРИЛЕТЕЛИ)
УМОЗАКЛЮЧЕНИЕ - ПРИЕМ МЫШЛЕНИЯ, в котором из двух или нескольких
суждений, называемых посылками, вытекает новое суждение, называемое заключением,
или выводом

10.

СИЛЛОГИЗМ - РАССУЖДЕНИЕ, В КОТОРОМ ИЗ ЗАДАННЫХ ДВУХ
СУЖДЕНИЙ ВЫВОДИТСЯ ТРЕТЬЕ.
Примеры типичных силлогизмов:
Все озера в Тверской области – пресноводные. Озеро Селигер расположено в Тверской
области. Озеро Селигер – пресноводное.
Многие студенты нашего факультета занимаются фундаментальной наукой. Те, кто
занимаются фундаментальной наукой, поступают в аспирантуру.
???

11.

АРИСТОТЕЛЬ ВЫДЕЛИЛ ВСЕ ПРАВИЛЬНЫЕ ФОРМЫ СИЛЛОГИЗМОВ,
КОТОРЫЕ МОЖНО СОСТАВИТЬ ИЗ РАССУЖДЕНИЙ ВИДА:
«Все А суть В»
«Некоторые А суть В»
«Все А не суть В»
«Некоторые А не суть В»
Логика, основанная на теории силлогизмов называется
классической.

12. Рене Декарт (1596-1650, французский философ, математик)

РЕКОМЕНДОВАЛ В ЛОГИКЕ
ИСПОЛЬЗОВАТЬ
МАТЕМАТИЧЕСКИЕ
МЕТОДЫ.

13. Лейбниц Г.В. (1646-1716, нем. ученый и математик) -

Лейбниц Г.В. (1646-1716, нем. ученый и
математик) ПРЕДЛОЖИЛ ИСПОЛЬЗОВАТЬ В ЛОГИКЕ
МАТЕМАТИЧЕСКУЮ СИМВОЛИКУ И ВПЕРВЫЕ
ВЫСКАЗАЛ МЫСЛЬ О ВОЗМОЖНОСТИ
ПРИМЕНЕНИЯ В НЕЙ ДВОИЧНОЙ СИСТЕМЫ.

14. Джордж Буль (1815-1864, анл.) - основоположник мат. логики.

Джордж Буль (1815-1864, анл.) основоположник мат. логики.
СОЗДАЛ БУЛЕВУ АЛГЕБРУ - ОДИН ИЗ
РАЗДЕЛОВ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.
РАЗРАБОТАЛ СВОЙ АЛФАВИТ,
ОРФОГРАФИЮ И ГРАММАТИКУ.

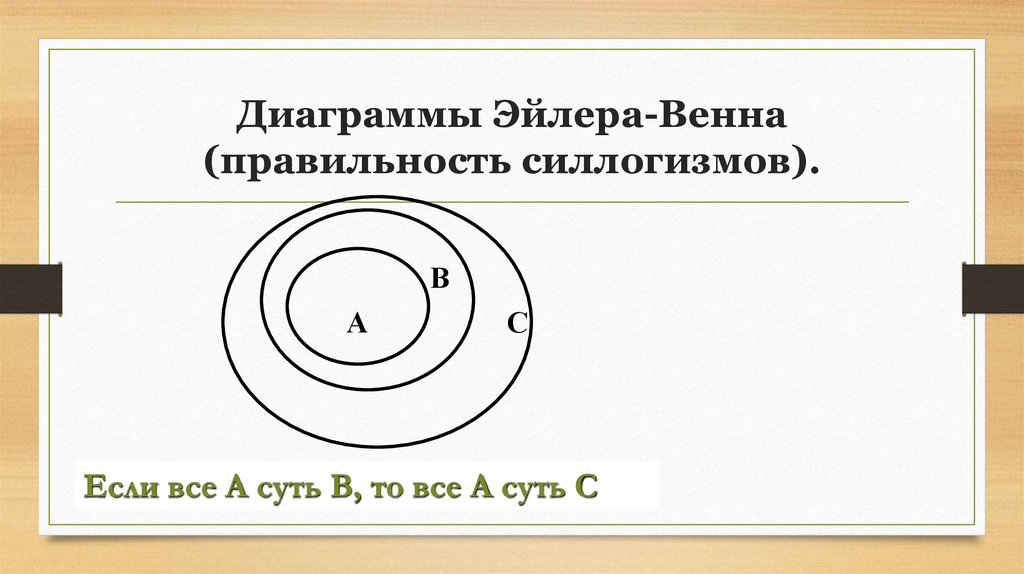
15. Диаграммы Эйлера-Венна (правильность силлогизмов).

В
А
С
Если все А суть В, то все А суть С

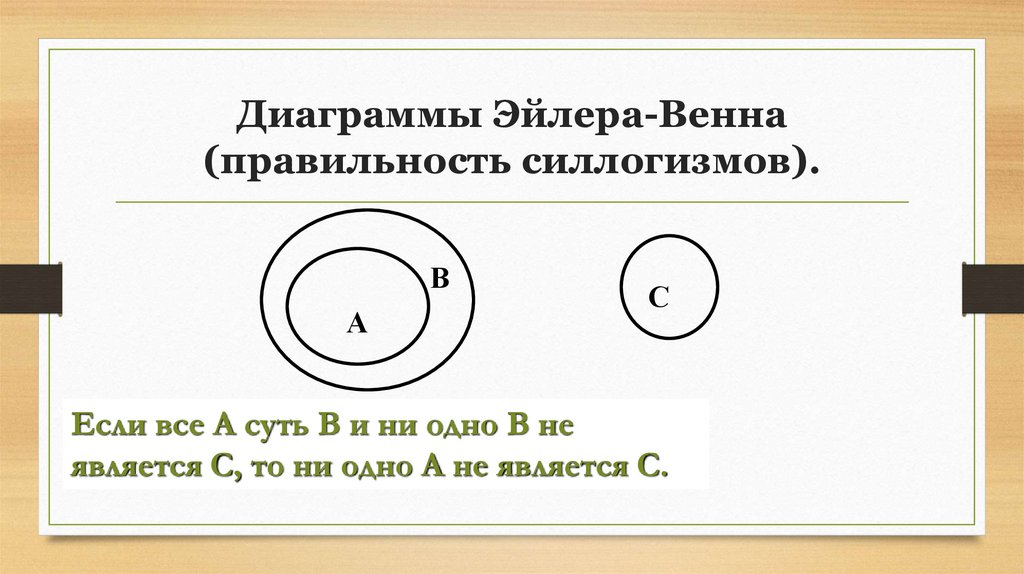
16. Диаграммы Эйлера-Венна (правильность силлогизмов).

В
А
С
Если все А суть В и ни одно В не
является С, то ни одно А не является С.

17. ВОПРОС №2

ПРИМЕНЕНИЕ
МАТЕМАТИЧЕСКОЙ
ЛОГИКИ.

18.

1) Логика оказала влияние на развитие математики, прежде всего теории множеств, функциональных
систем, алгоритмов, рекурсивных функций.
2) Идеи и аппарат логики используется в кибернетике, ВТ и электротехнике (построены компьютеры
на основе законов математической логики).
3) В гуманитарных науках (логика, криминалистика).
4) Математическая логика является средством для изучения деятельности мозга - для решения этой
самой важной проблемы биологии и науки вообще.

19. ВОПРОС №3

Алгебра
высказываний.
Простые и
сложные
высказывания.

20. АЛГЕБРА ЛОГИКИ ВЫСКАЗЫВАНИЙ – препозициональная логика

РАЗДЕЛ МАТЕМАТИЧЕСКОЙ ЛОГИКИ,
ИЗУЧАЮЩИЙ ВЫСКАЗЫВАНИЯ И
ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД
НИМИ.

21.

ВЫСКАЗЫВАНИЕ - ЭТО ПОВЕСТВОВАТЕЛЬНОЕ ПРЕДЛОЖЕНИЕ, О
КОТОРОМ МОЖНО СКАЗАТЬ, ЧТО ОНО ИСТИННО ИЛИ ЛОЖНО.
1) Земля - планета Солнечной системы.
2) 2+8<5
3) 5 •5=25

22.

ВЫСКАЗЫВАНИЕМ
НЕ ЯВЛЯЕТСЯ:
1) ВОСКЛИЦАТЕЛЬНЫЕ И ВОПРОСИТЕЛЬНЫЕ
ПРЕДЛОЖЕНИЯ.
2) ОПРЕДЕЛЕНИЯ.
3) ПРЕДЛОЖЕНИЯ ТИПА:
• «ОН СЕРОГЛАЗ»
• «X2-4X+3=0»

23. Принципы алгебры высказываний

1.
2.
3.
4.
Принцип тождества (если истинность какого-либо факта установлена, то она не
подвергается сомнению).
Принцип непротиворечивости (один и тот же факт не может быть одновременно и
истинным и ложным. Пример противоречия высказывание Сократа: «Я знаю лишь
то, что я ничего не знаю»).
Принцип исключенного третьего (нельзя одновременно отрицать и
высказывание и его отрицание. Любое высказывание либо истинно, либо ложно, –
третьего не дано)
Принцип достаточного основания (всякое высказывание должно быть
обосновано, выведено из каких-либо суждений)

24.

ВЫСКАЗЫВАНИЕ, КОТОРОЕ МОЖНО РАЗЛОЖИТЬ НА ЧАСТИ,
БУДЕМ НАЗЫВАТЬ СЛОЖНЫМ, А НЕРАЗЛОЖИМОЕ ДАЛЕЕ
ВЫСКАЗЫВАНИЕ - ПРОСТЫМ.
1) На улице светит солнце. (А)
2) На улице идет дождь. (В)
3) На улице светит солнце и идет дождь.
(А и В)
4) На улице светит солнце или идет дождь.
(А или В)
Если предложение истинно, то его значение истинности равно
1, если ложно - 0

25. ВОПРОС №4

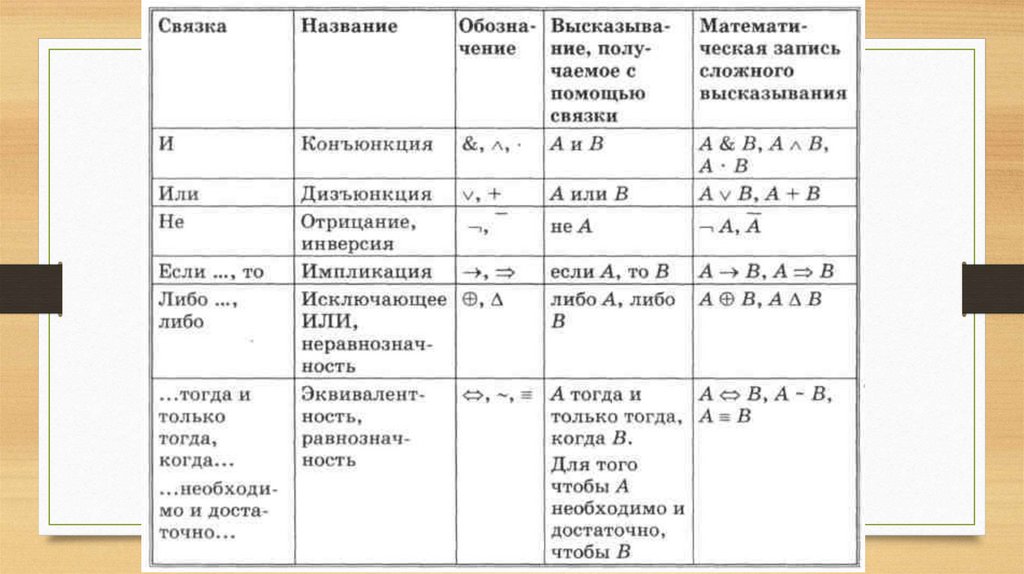
ОСНОВНЫЕ ОПЕРАЦИИ
(ЛОГИЧЕСКИЕ СВЯЗКИ)
АЛГЕБРЫ ЫСКАЗЫВАНИЙ.

26.

ИНВЕРСИЯ (ЛОГИЧЕСКОЕ ОТРИЦАНИЕ) -
ПРИСОЕДИНЕНИЕ ЧАСТИЦЫ «НЕ» К СКАЗУЕМОМУ ДАННОГО
ПРОСТОГО ВЫСКАЗЫВАНИЯ ИЛИ ПРИСОЕДИНЕНИЕ СЛОВ
«НЕВЕРНО ЧТО. . .» КО ВСЕМУ ВЫСКАЗЫВАНИЮ.
ИНВЕРСИЯ ЛОГИЧЕСКОЙ ПЕРЕМЕННОЙ
ИСТИННА, ЕСЛИ САМА ПЕРЕМЕННАЯ ЛОЖНА,
И, НАОБОРОТ, ИНВЕРСИЯ ЛОЖНА, ЕСЛИA
ПЕРЕМЕННАЯ ИСТИННА.

27. ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) -

ДИЗЪЮНКЦИЯ
(ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В в ОДНО С ПОМОЩЬЮ СОЮЗА «ИЛИ»,
УПОТРЕБЛЯЕМОГО В НЕИСКЛЮЧАЮЩЕМ ВИДЕ.
ДИЗЪЮНКЦИЯ ДВУХ
ЛОГИЧЕСКИХ ВЫСКАЗЫВАНИЙ
ЛОЖНА ТОГДА И ТОЛЬКО ТОГДА, КОГДА
ОБА ВЫСКАЗЫВАНИЯ
ЛОЖНЫ.

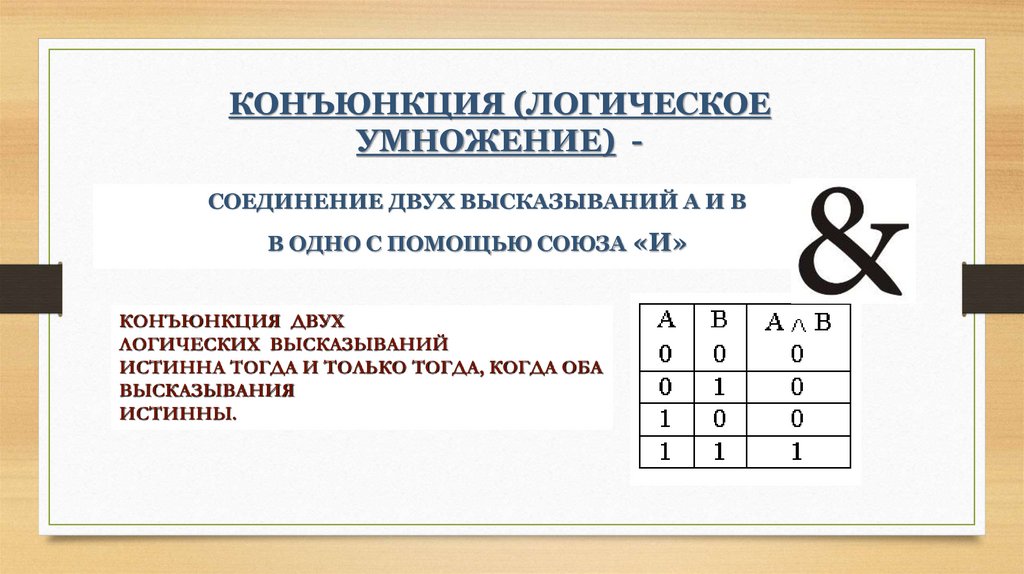
28. КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) -

КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ
УМНОЖЕНИЕ) СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В
В ОДНО С ПОМОЩЬЮ СОЮЗА «И»
КОНЪЮНКЦИЯ ДВУХ
ЛОГИЧЕСКИХ ВЫСКАЗЫВАНИЙ
ИСТИННА ТОГДА И ТОЛЬКО ТОГДА, КОГДА ОБА
ВЫСКАЗЫВАНИЯ
ИСТИННЫ.

29. ИМПЛИКАЦИЯ -

ИМПЛИКАЦИЯ ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ЕСЛИ . .
. , ТО . . .» («А влечет В», «из А следует В»)
ИМПЛИКАЦИЯ
ВЫСКАЗЫВАНИЙ
ЛОЖНА ЛИШЬ В СЛУЧАЕ,
КОГДА А ИСТИННО, а В
ЛОЖНО.

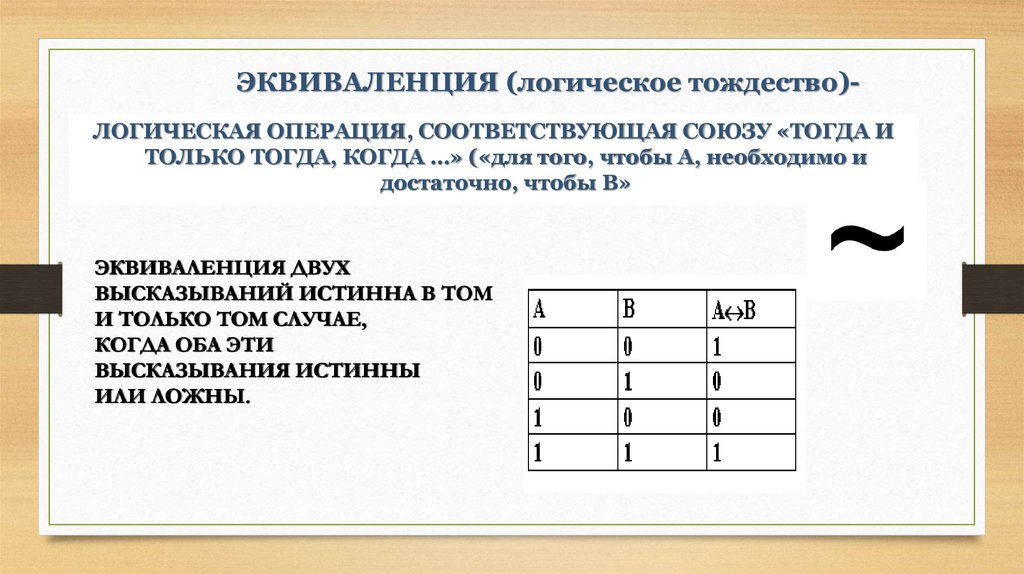
30. ЭКВИВАЛЕНЦИЯ (логическое тождество)-

ЭКВИВАЛЕНЦИЯ (логическое тождество)ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ТОГДА И
ТОЛЬКО ТОГДА, КОГДА …» («для того, чтобы А, необходимо и
достаточно, чтобы В»
ЭКВИВАЛЕНЦИЯ ДВУХ
ВЫСКАЗЫВАНИЙ ИСТИННА В ТОМ
И ТОЛЬКО ТОМ СЛУЧАЕ,
КОГДА ОБА ЭТИ
ВЫСКАЗЫВАНИЯ ИСТИННЫ
ИЛИ ЛОЖНЫ.

31. ИСКЛЮЧАЮЩЕЕ «ИЛИ» (неравнозначность)-

ИСКЛЮЧАЮЩЕЕ «ИЛИ» (неравнозначность)ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, КОТОРАЯ ЧИТАЕТСЯ «ЛИБО А,
ЛИБО В». А и В - ВЗАИМОИСКЛЮЧАЮЩИЕ ПОНЯТИЯ
НЕРАВНОЗНАЧНОСТЬ ДВУХ ВЫСКАЗЫВАНИЙ
ЛОЖНА В ТЕХ СЛУЧАЯХ КОГДА ОБА ЭТИ
ВЫСКАЗЫВАНИЯ ЛИБО ИСТИННЫ, ЛИБО
ЛОЖНЫ.

32.

33.

Другие логические операции
Стрелка Пирса –
антидизъюнкция
Обозначение A B
Лексический аналог – «ни…, ни…»
Функция истинности
Стрелка Пирса истинна в том и только в
том случает, когда оба высказывания A и B
ложны

34.

Другие логические операции
Штрих Шеффера –
антиконъюнкция
Обозначение A B
Лексический аналог –
««неверно, что
одновременно... и...»»
Функция истинности
Штрих Шеффера ложный в том и только в том случае,
когда оба высказывания A и B истинны

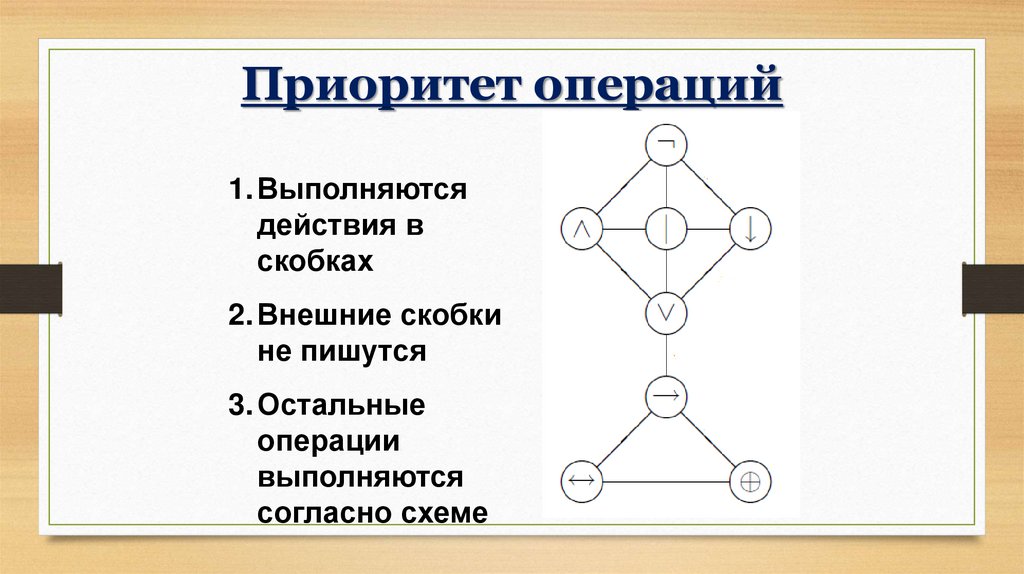
35.

Приоритет операций
1. Выполняются
действия в
скобках
2. Внешние скобки
не пишутся
3. Остальные
операции
выполняются
согласно схеме

36.

ФОРМУЛЫ АЛГЕБРЫ
ЛОГИКИ
Всякое сложное высказывание, которое может быть получено из
элементарных высказываний посредством применения логических
операций, называется формулой алгебры логики.
Логическое значение формулы алгебры логики полностью определяется
логическими значениями входящих в нее элементарных высказываний.
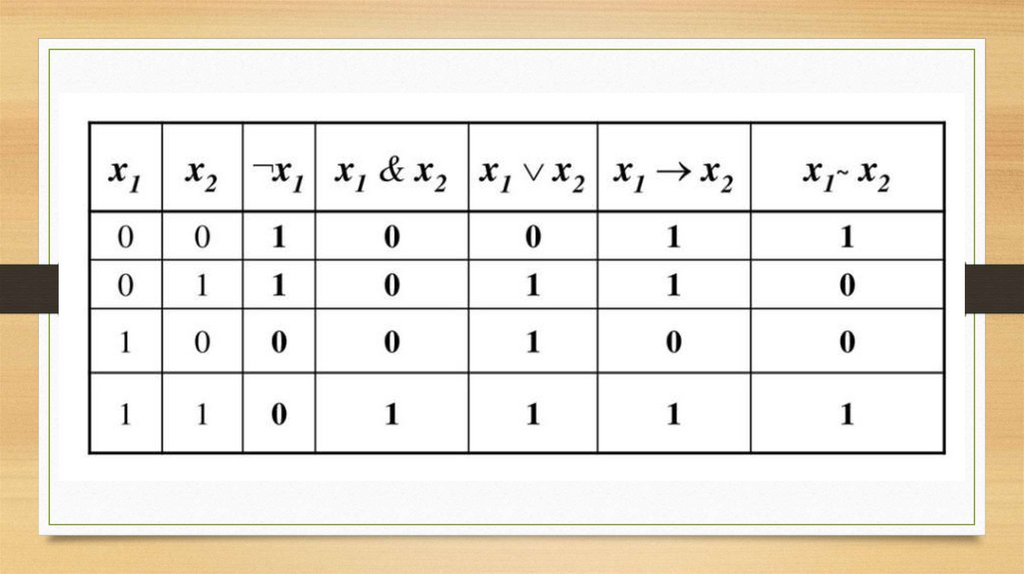
Все возможные логические значения формулы, в зависимости от значений
входящих в нее элементарных высказываний, могут быть описаны полностью с
помощью таблицы истинности.

37.

38.

39.

Построение таблицы истинности
1.
2.
3.
4.
5.
6.
Подсчитать количество переменных в формуле n.
Определить количество строк в таблице –
Подсчитать количество операций в формуле и определить
количество столбцов (m + n).
Записать названия столбцов с учетом последовательности
выполнения операций.
Заполнить столбцы переменных наборами от 00...0 до 11...1 в
лексикографическом порядке
Заполнить таблицу по столбцам.

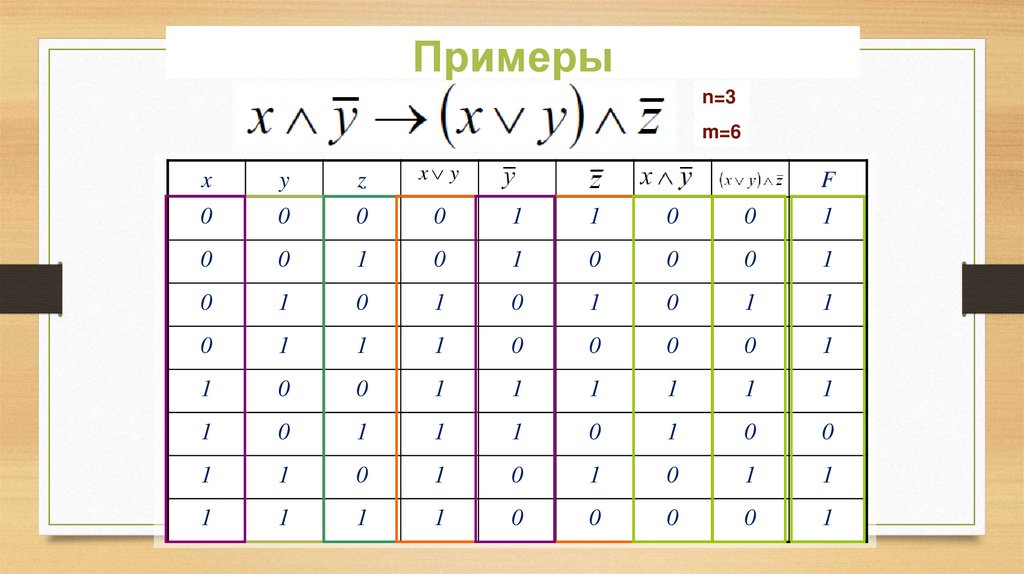
40.

Примеры
n=3
m=6
x
y
z
x y
0
0
0
0
1
1
0
0
1
0
0
1
0
1
0
0
0
1
0
1
0
1
0
1
0
1
1
0
1
1
1
0
0
0
0
1
1
0
0
1
1
1
1
1
1
1
0
1
1
1
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
1
1
0
0
0
0
1
F

41.

Виды формул Алгебры Логики
• Формула называется тавтологией, если она принимает только
истинные значения при любых значениях переменных. Другими
словами, тавтология – это тождественно истинная формула.
• Формула называется противоречием, если она принимает
только ложные значения при любых значениях переменных.
Другими словами, противоречивая – это тождественно ложная
формула.
• Формула называется выполнимой, если она принимает истинное
значение хотя бы на одном наборе переменных.
• Формула называется опровержимой, если она принимает
ложное значение хотя бы на одном наборе переменных.