Лекция 9. Логика предикатов

1.

ЛЕКЦИЯ 9

2. Повторяем изученный материал

1.
Какие из этих выражений представляют собой простые
высказывания?
a) «Простое высказывание — это базовый элемент языка, который
выражает утверждение или отрицание без внутренних логических
связок»
b) «Срочно примите меры по охране этого вида!»
c) «Почва — это живая система»
d) «Какое антропогенное воздействие наиболее опасно для
тундры?»

3. Повторяем изученный материал

2. Даны простыe высказывания:
P: «В регионе высокая плотность населения»;
Q: «В регионе развита промышленность»;
R: «Уровень загрязнения воды в регионе высок».
Сформулируйте сложное высказывание, описывающее ситуацию в
гипотетическом регионе, используя три простых высказывания и
логические связки.
Будет ли являться сложным высказыванием:
«Уровень загрязнения воды высок ИЛИ из-за высокой плотности
населения, ИЛИ из-за развитой промышленности»?

4. Повторяем изученный материал

3. Даны высказывания: А - "Петя едет в автобусе", В - "Петя читает
книгу", С - "Петя смотрит в окно".
Составить формулу алгебры сложного высказывания "Неверно,
что если Петя едет в автобусе, то он читает книгу или смотрит в
окно"
4. Географ формулирует: «Район считается засушливым, если
годовое количество осадков менее 200 мм или коэффициент
увлажнения меньше 0,3». Запишите формулу и определите, будет
ли район засушливым, если осадков 250 мм, а коэффициент
увлажнения 0,25.
5. Эколог делает запись: «Если продолжается сброс
промышленных отходов и не введены новые фильтры, то качество
воды ухудшится». Запишите это сложное высказывание в виде
логической формулы. В каком случае прогноз эколога окажется
ложным?

5. Повторяем изученный материал

6. Перечислите действия, необходимые для построения таблицы
истинности
7. Какие из следующих формул являются тавтологиями? (Отметьте
все верные)
a)(P → Q) → P
b)(P → Q) ∨ (Q → P)
c)P ∧ (P → Q) → Q

6.

ВВЕДЕНИЕ

7. Понятие предиката

Логика высказываний
(пропозициональная логика) оперирует
простейшими высказываниями, которые
могут быть или истинными, или
ложными.
В разговорном языке встречаются
более сложные повествовательные
предложения, истинность которых
может меняться при изменении
объектов, о которых идет речь.

8. Понятие предиката

В логике такие предложения, истинность
которых зависит от параметров,
обозначают с помощью предикатов.
"Предикат" с английского переводится как
сказуемое.

9. Понятие предиката

Формально предикат - функция,
аргументами которой могут быть
ПРОИЗВОЛЬНЫЕ ОБЪЕКТЫ из
некоторого множества, а значения
функции "истина" или "ложь".
Предикат можно рассматривать как
расширение понятия высказывания.

10.

Предложение, содержащее переменные, которые
при замене их на возможные значения становятся
высказываниями, называются предикатом или
высказывательной формой.

11. ПРИМЕР

предикат
"Икс любит кашу"
вместо неизвестного Икс могут быть
любой человек: либо Маша, либо Даша,
либо Саша...
Подстановка вместо Икс имени
конкретного человека превращает
предикат в обычное высказывание.
Предикат - это высказывание-функция,
значение (истина/ложь) которого зависит
от параметров

12.

"ВСЕ любят Игрека" - одноместный предикат.
"ВСЕ студенты 1 курса любят математическую логику" нульместный предикат, то есть высказывание (нет неизвестного).
Двухместный предикат Р(x,y) - функция двух переменных x и
y, определенная на множестве М=М1хМ2 и принимающая значения из
множества {1;0}.
"Икс любит Игрека" - двухместный предикат.

13.

14.

15.

16. РЕЗЮМИРУЕМ:

17.

• Субъект – это то, о чем что-то утверждается.
• Предикат – это то, что утверждается о субъекте.
• Логика предикатов – это расширение логики
высказываний за счет исполнения предикатов в
роли логических функций.
• Предикатом P x1 , x 2 ,..., x n называется функция,
определённая на множестве M и принимающая
значение «истина» или «ложь», то есть P : M n 1,0
• Множество M – контекст, или предметная область,
или область определения предиката.
• Множество всех x M , при которых P x 1,
называется множеством истинности предикатаP x
Ip x x M, P x 1

18. Операции логики предикатов

Предикаты при подстановке переменных
становятся высказываниями, поэтому с
предикатами можно производить все
логические операции.
Предикат Р(х), определенный на множество M
называется тождественно истинным, если
область определения предиката I p M , и
называется тождественно ложным, если
Ip

19. Конъюнкция

• Конъюнкцией двух предикатов P(x) и Q(x)
называется новый предикат P(x)^Q(x) ,
который принимает значение «истина» при
тех и только тех значениях xєM, при которых
каждый из предикатов принимает значение
«истина» и принимает значение «ложь» во
всех остальных случаях.

20. Дизъюнкция

• Дизъюнкцией двух предикатов P(x),Q(x)
называется новый предикат P(x)vQ(x) ,
который принимает значение «ложь», при
тех и только тех значениях xєM , при которых
каждый из предикатов принимает значение
«ложь» и принимает значение «истина» во
всех остальных случаях.

21. Отрицание

• Отрицанием предиката P(x) называется
новый предикат P(x), который принимает
значение «истина» при всех значениях xєM,
при которых P(x) принимает значение
«ложь» и наоборот.

22. Импликация

• Импликацией предикатов P(x) и Q(x)
называется новый предикат P(x)→Q(x) ,
который являются ложными при тех и только
тех значениях xєM , при которых P(x)
одновременно принимает значение
«истина», а Q(x) – значение «ложь», во
всех остальных случаях это «истина».

23. Эквиваленция

• Эквиваленцией предикатов P(x) и Q(x)
называется новый предикат P(x)↔Q(x) ,
который являются истинным при тех и
только тех значениях xєM, при которых
одновременно P(x) и Q(x) принимает
одинаковые значения значение
«истина» или «ложь», и ложным во всех
остальных случаях.

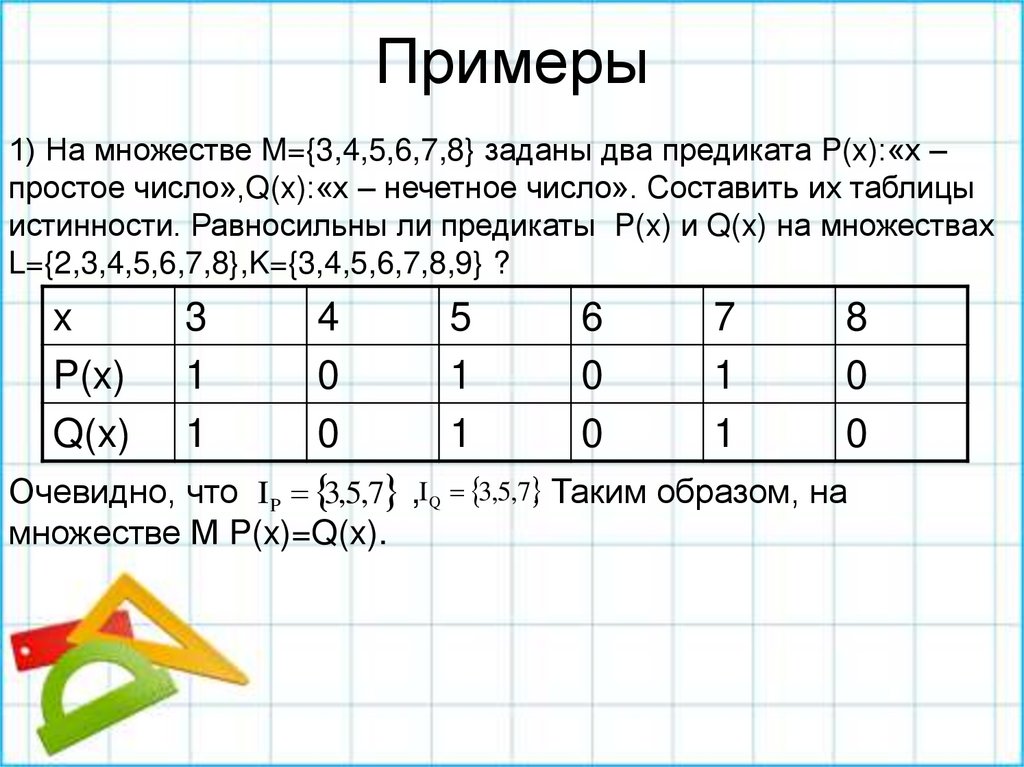
24. Примеры

1) На множестве M={3,4,5,6,7,8} заданы два предиката P(x):«х –
простое число»,Q(x):«х – нечетное число». Составить их таблицы
истинности. Равносильны ли предикаты P(x) и Q(x) на множествах
L={2,3,4,5,6,7,8},K={3,4,5,6,7,8,9} ?
x
P(x)
Q(x)
3
1
1
4
0
0
5
1
1
6
0
0
7
1
1
8
0
0
Очевидно, что IP 3,5,7 ,I Q 3,5,7 . Таким образом, на
множестве М P(x)=Q(x).

25. Примеры

• Найти область истинности предиката
0
1

26. Задача для самостоятельного решения в аудитории

Найти область истинности предиката:
P ( X ,Y ) = (( X + Y )) - делится на 3) → (( X + Y ) > 5),
где X = {2;5;6;8}, Y = {3;6;9};