Презентация Дробаха

1.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ЛНР
ЛУГАНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
ИМЕНИ ВЛАДИМИРА ДАЛЯ
Факультет естественных наук
Кафедра физики
Магистерская диссертация
Каналовая модель электрической дуги
и границы ее применимости
Студент группы ЕН – 171м
Дробаха Дмитрий Витальевич
Научный руководитель
Калюжный Геннадий Сергеевич,
к.ф.-м.н., доцент
Заведующий кафедрой
физики
Корсунов Константин Анатольевич,
д.т.н., профессор
Луганск 2019

2. ВВЕДЕНИЕ

Цель работы – расчет характеристик электрической дуги,
горящей в разрядной трубке, в рамках каналовой модели.
Задачи исследования:
- рассмотреть основные положения каналовой модели дуги;
- разработать алгоритм расчета характеристик дуги на основе
каналовой модели;
- написать программу, реализующую разработанный алгоритм;
- с помощью этой программы провести исследование характеристик
электрической дуги в разрядных трубках различного радиуса
методом вычислительного эксперимента.
Объект исследования - электрическая дуга, горящая в воздухе
в разрядной трубке.
Предмет исследования –расчет характеристик электрической
дуги,
таких
как
температура,
линейная
плотность
энерговыделения, напряженность электрического поля и размер
канала в рамках каналовой модели.

3.

Методы исследования – проведение вычислительного
эксперимента на основе математической модели дуги
(каналовая модель) с помощью системы компьютерной
математики Mathematica.
Новизна
полученных
результатов
заключается
в
разработке методики расчета характеристик электрической
дуги в рамках каналовой модели.
Практическая
ценность
полученных
результатов
заключается в том, что результаты работы могут быть
использованы для расчета характеристик электрической дуги
при решении различного рода физических и инженерных
задач.
Апробация
работы:
основные
результаты
работы
докладывались на университетской конференции студентов и
молодых ученых (Луганск, апрель 2019) и Международной
научно-практической конференции «Открытые физические
чтения» (Луганск, май 2019)

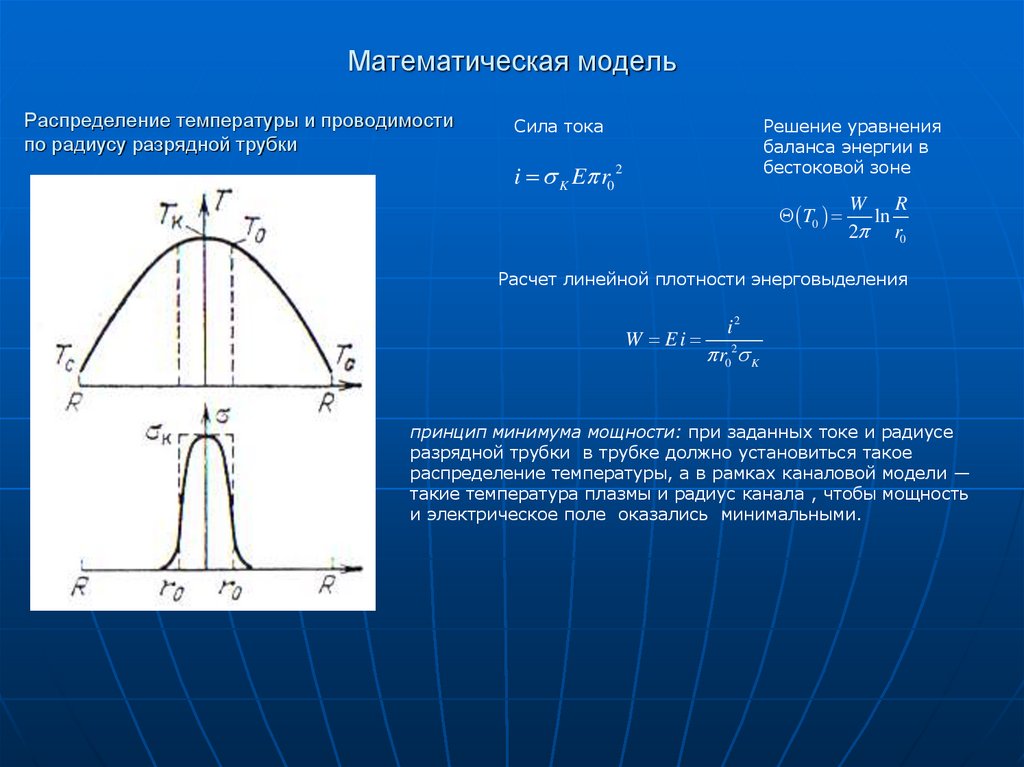
4. Математическая модель

Распределение температуры и проводимости
по радиусу разрядной трубки
Сила тока
Решение уравнения
баланса энергии в
бестоковой зоне
i K E r0 2
T0
W R
ln
2 r0
Расчет линейной плотности энерговыделения
W Ei
i2
r0 2 K
принцип минимума мощности: при заданных токе и радиусе
разрядной трубки в трубке должно установиться такое
распределение температуры, а в рамках каналовой модели —
такие температура плазмы и радиус канала , чтобы мощность
и электрическое поле оказались минимальными.

5. Алгоритм расчета

1. Задание величины силы тока и радиуса трубки R
2. Определение температуры границы канала как функции радиуса канала,
силы тока и радиуса трубки. Для этого необходимо численно решить
нелинейное уравнение
i2
R
T0 2
ln
2
2 r0 T0 k T0 r0
3. Определение значения радиуса канала, при котором достигается минимум функции
i2
W
r0 2 K T0 r0
4. По найденному значению радиуса канала определяем температуру на границе
канала с помощью функции, созданной на шаге 2.
5. Находим линейную плотность выделяемой мощности из соотношения
i2
i2
W Ei
r0 2 K r0 2 0
6. Находим напряженность электрического поля
E
W
i
7. Находим превышение температуры в центре канала над значением темепаратуры
на границе канала и температуру на оси канала
T
W
4 K
TK T0 T

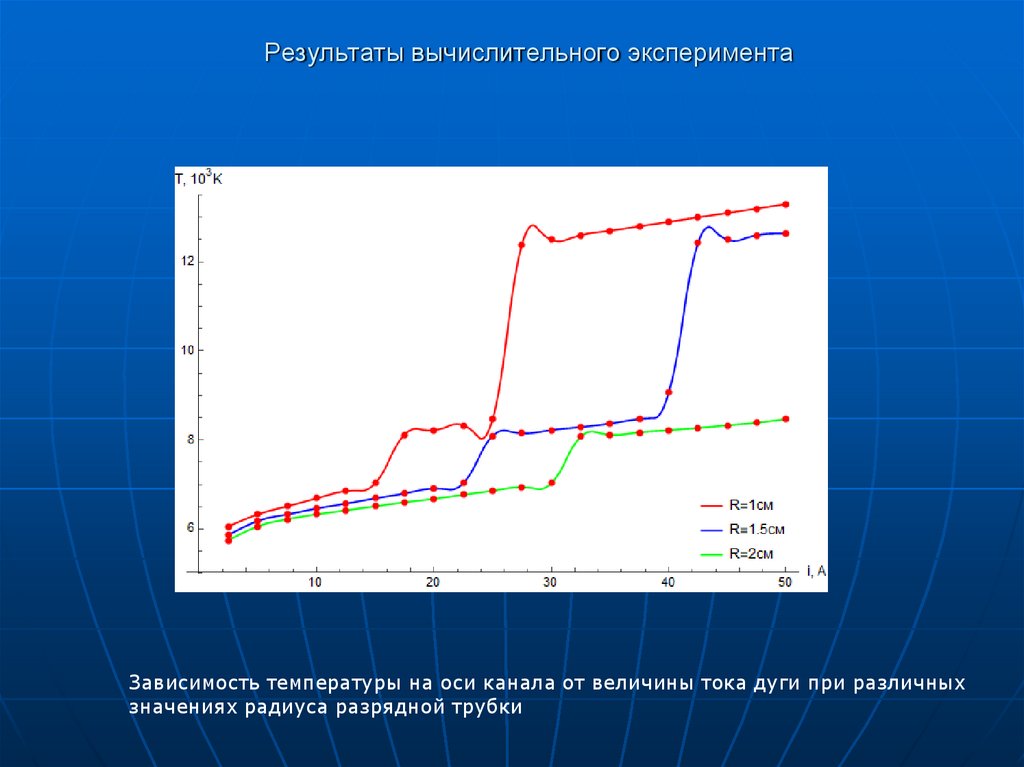
6. Результаты вычислительного эксперимента

Зависимость температуры на оси канала от величины тока дуги при различных
значениях радиуса разрядной трубки

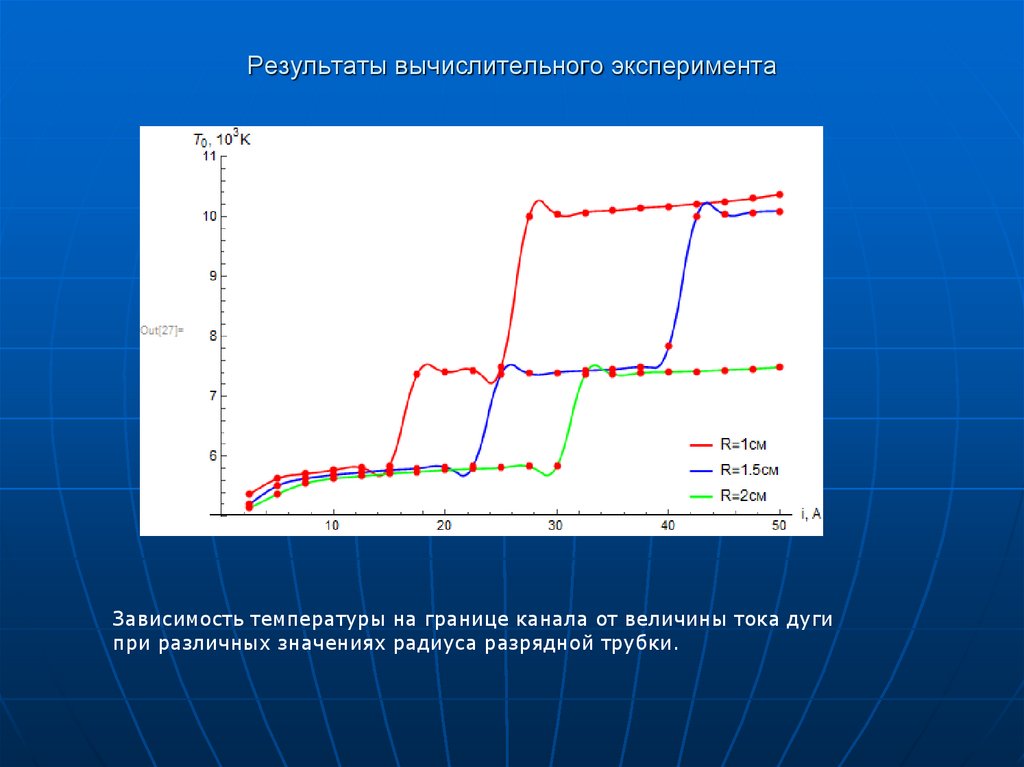
7. Результаты вычислительного эксперимента

Зависимость температуры на границе канала от величины тока дуги
при различных значениях радиуса разрядной трубки.

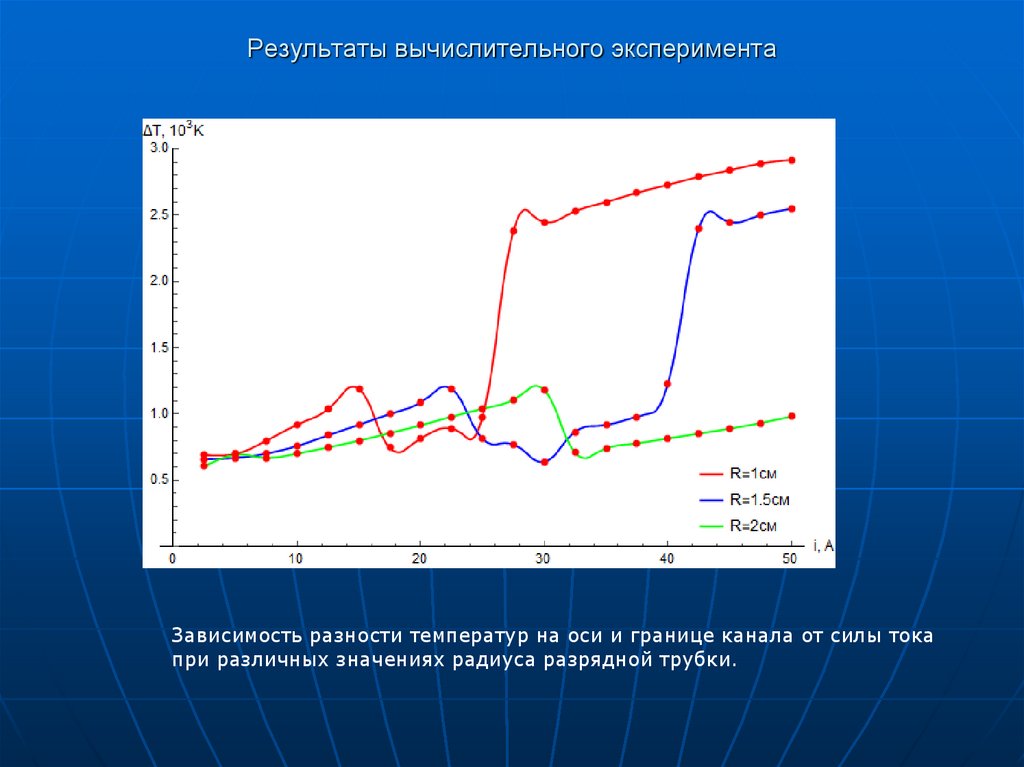
8. Результаты вычислительного эксперимента

Зависимость разности температур на оси и границе канала от силы тока
при различных значениях радиуса разрядной трубки.

9. Результаты вычислительного эксперимента

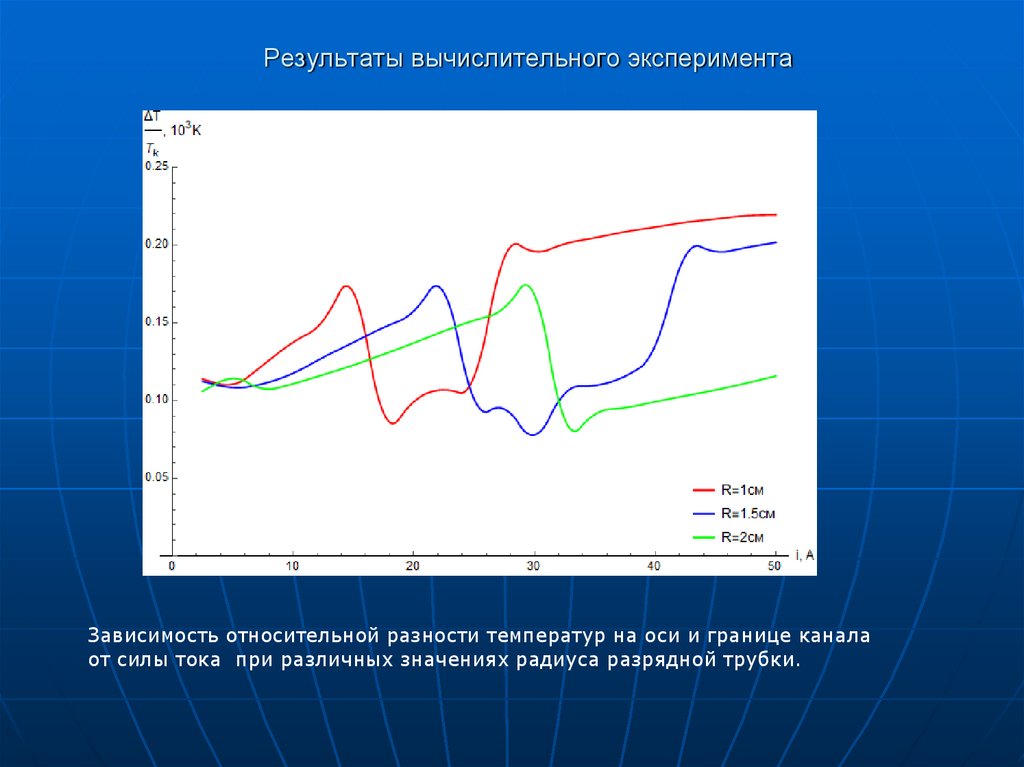
Зависимость относительной разности температур на оси и границе канала
от силы тока при различных значениях радиуса разрядной трубки.

10. Результаты вычислительного эксперимента

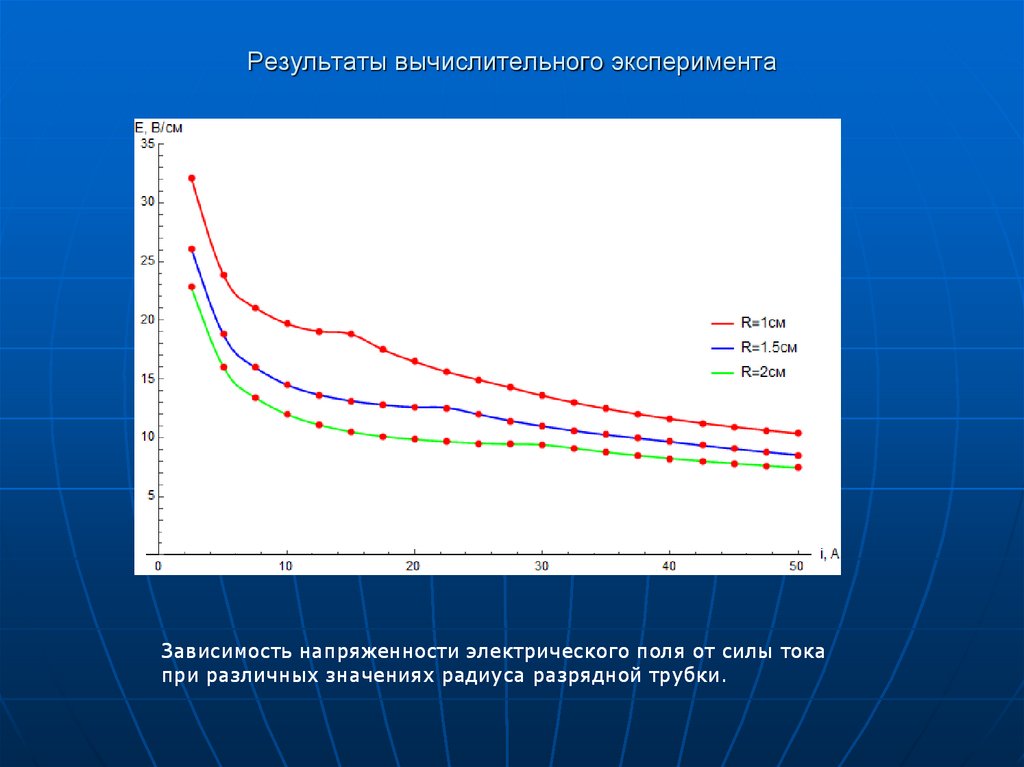
Зависимость напряженности электрического поля от силы тока
при различных значениях радиуса разрядной трубки.

11. Результаты вычислительного эксперимента

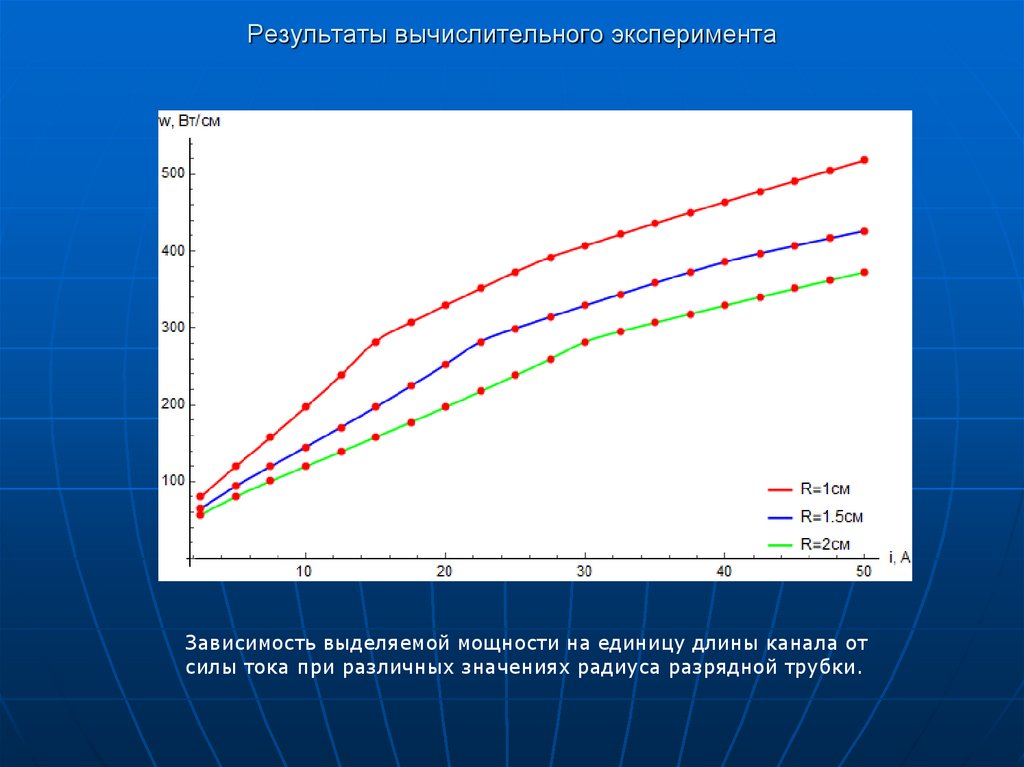
Зависимость выделяемой мощности на единицу длины канала от
силы тока при различных значениях радиуса разрядной трубки.

12.

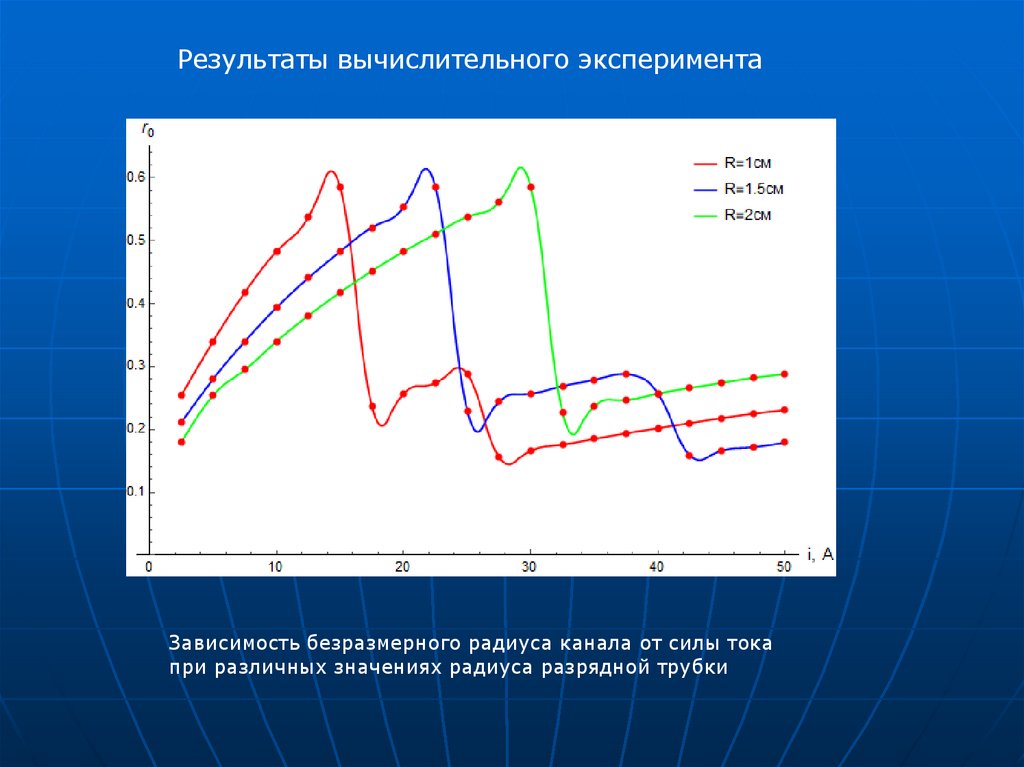
Результаты вычислительного эксперимента
Зависимость безразмерного радиуса канала от силы тока
при различных значениях радиуса разрядной трубки

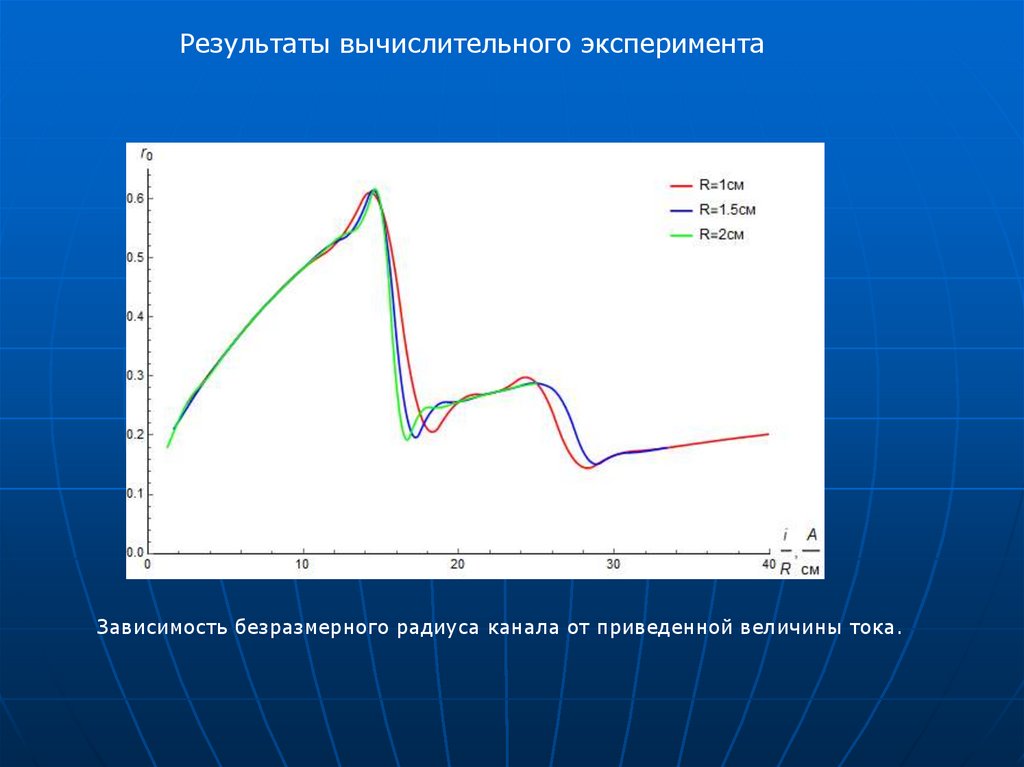
13.

Результаты вычислительного эксперимента
Зависимость безразмерного радиуса канала от приведенной величины тока.

14.

Заключение
Рассмотрена каналовая модель электрической дуги в разрядной
трубке.
Предложен алгоритм расчета характеристик дуги в рамках этой модели.
Создан блок программ, реализующий данный алгоритм. Программы
разработаны в среде системы компьютерной математики Mathematica с
широким привлечением численных методов.
Методом вычислительного эксперимента проведено исследование
характеристик
электрической
дуги.
Получены
зависимости
температуры, радиуса канала, линейной плотности выделяемой
мощности и напряженности электрического поля от тока дуги при
различных радиусах разрядной трубки.
Проведено обсуждение характера полученных зависимостей.
Показана справедливость закона подобия для столба электрической
дуги – характеристики дуги являются функциями приведенного тока i / R
Сделан предварительный вывод о границах применимости каналовой
модели: верхняя граница приведенного тока, до которой каналовая
модель адекватна, составляет i / R 15 А / см
Полученные результаты могут быть использованы в рамках курсов
«ЭВМ-эксперимент» и «Математическое моделирование физических
процессов и систем», которые читаются на кафедре физики.