Похожие презентации:
Лекции-3.7(55)
1. Лекция № 7 КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ. ВОЛНОВАЯ ФУНКЦИЯ. УРАВНЕНИЕ ШРЁДИНГЕРА
12. ВОПРОСЫ 23. Корпускулярно волновой дуализм. Гипотеза де Бройля. Опыт Дэвиссона и Джермера. Дифракция электронов и нейтронов.
24. Дифракция микрочастиц.Принцип неопределённости
Гейзенберга.
25. Задание микрочастиц. Волновая
функция. Принцип суперпозиции.
2
3. 26. Уравнение Шрёдингера. Уравнения Шрёдингера многомерное временное, стационарное, одномерное. Собственные значения энергии.
Частица в потенциальнойяме.
3
4.
45. 23. Корпускулярно волновой дуализм. Гипотеза де Бройля. Опыт Дэвиссона и Джермера. Дифракция электронов и нейтронов.
56. Корпускулярно-волновой дуализм Теория Бора оказалась недостаточной. Можно было описать атом водорода, но другие нет, даже атом
гелия.Возник вопрос: достаточно ли
представление электрона частицей с
определённой массой, скоростью и
координатой.
6
7. С другой стороны, у света была обнаружена двойственная природа – дуализм: волновая природа (интерференция, дифракция) и
корпускулярная (фотоэффект,явление Комптона). При возрастании
частоты света его волновые
свойства обнаружить все труднее и
свет приходится описывать как
корпускулу – частицу света – фотон.
7
8. Де Бройль предположил, что двойственная природа света характерна не только для света (поток фотонов), но и для всех
элементарных частиц: электронов,протонов, нейтронов и др.
8
9. Если импульс фотона pф = h/, имеет универсальный характер для любых волновых процессов, происходящих с частицами, то можно
Если импульс фотонаpф = h/ ,
имеет универсальный характер для
любых волновых процессов,
происходящих с частицами, то
можно найти длину волны частиц
(волну де Бройля)
= h/p = h/mʋ,
где m масса частицы; ʋ её
скорость (ʋ < c).
9
10. Если частица имеет кинетическую энергию Wk = mʋ2/2 = p2/(2m), то ее импульс Поэтому длина волны и частота частицы будут
Если частица имеет кинетическуюэнергию
Wk = mʋ2/2 = p2/(2m),
то ее импульс
p 2mWk
Поэтому длина волны и частота
частицы будут выражены
следующим образом
λ h
2mWk h mv
ω Wk 2 π Wk h
10
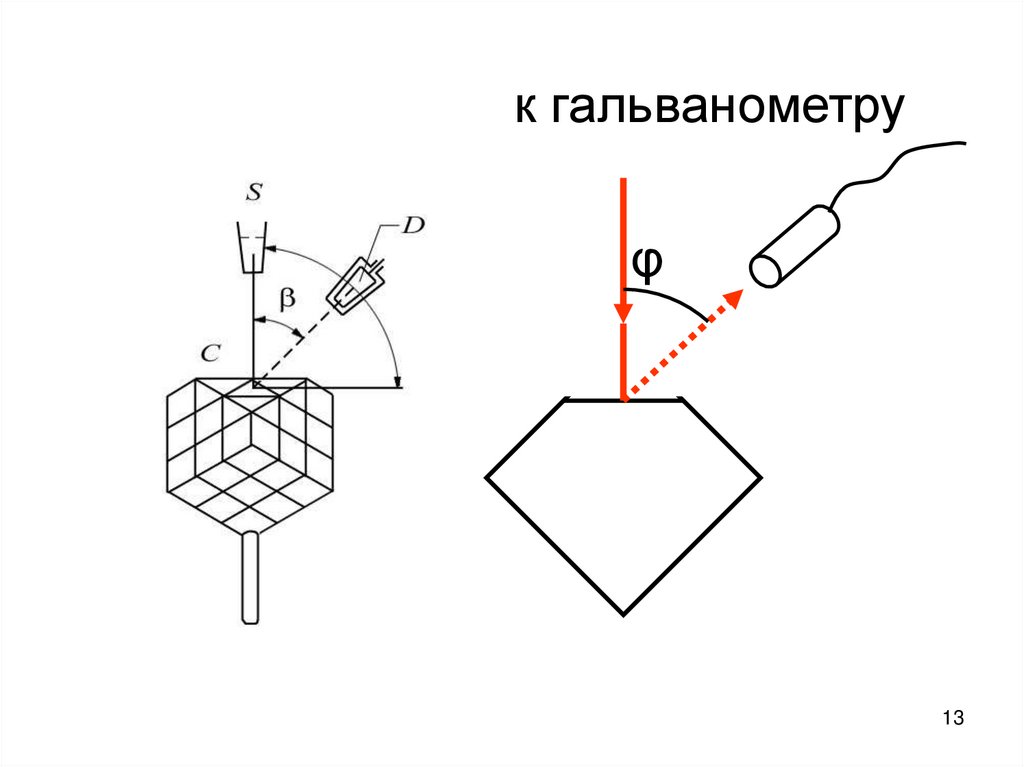
11. Экспериментальное подтверждение Опыт Дэвиссона и Джермера В 1927 году они исследовали отражение электронов от монокристалла
никеля.11
12. Отражённые электроны улавливались цилиндрическим электродом, присоединённом к гальванометру. Интенсивность отражённого пучка
оценивалась посиле тока, текущего через
гальванометр.
12
13.
к гальванометруφ
13
14.
I14
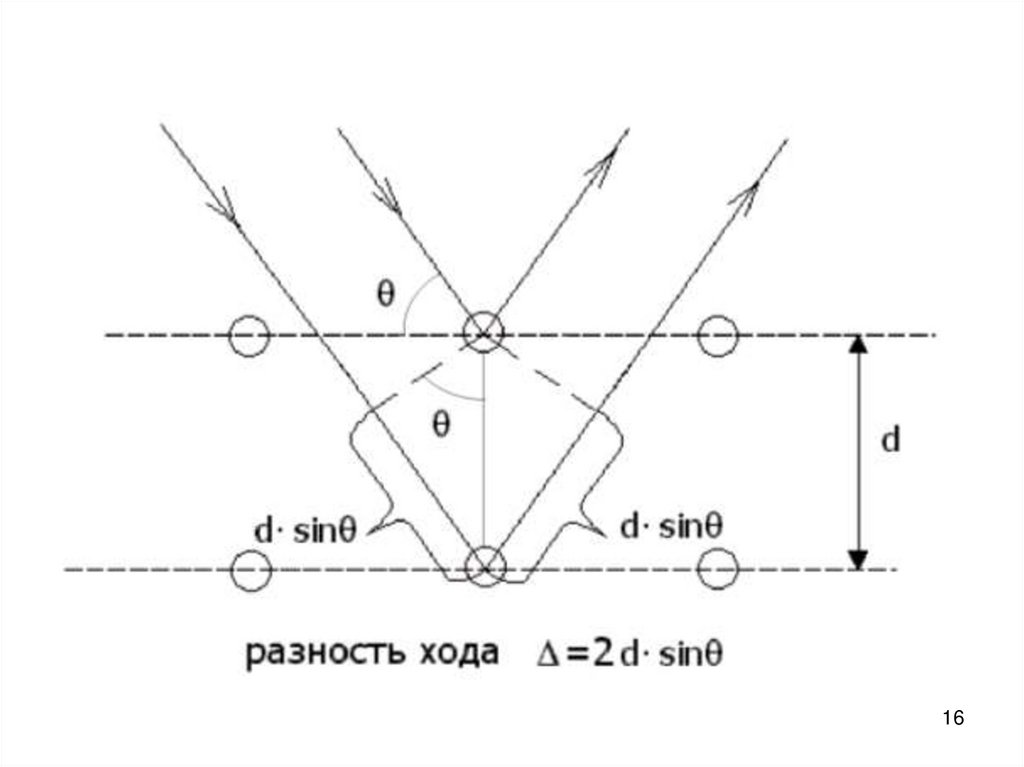
15. Напряжение, при котором ток максимален, 54 В, длина волны электрона 0,167 нм. Длина волны, отвечающая условию 2d sinφ = m
Напряжение, при котором токмаксимален, 54 В, длина волны
электрона 0,167 нм. Длина волны,
отвечающая условию
2d sinφ = m
(формула Брэгга, дифракция
рентгеновских лучей на атомах
кристаллов), равнялась
0,165 нм.
15
16.
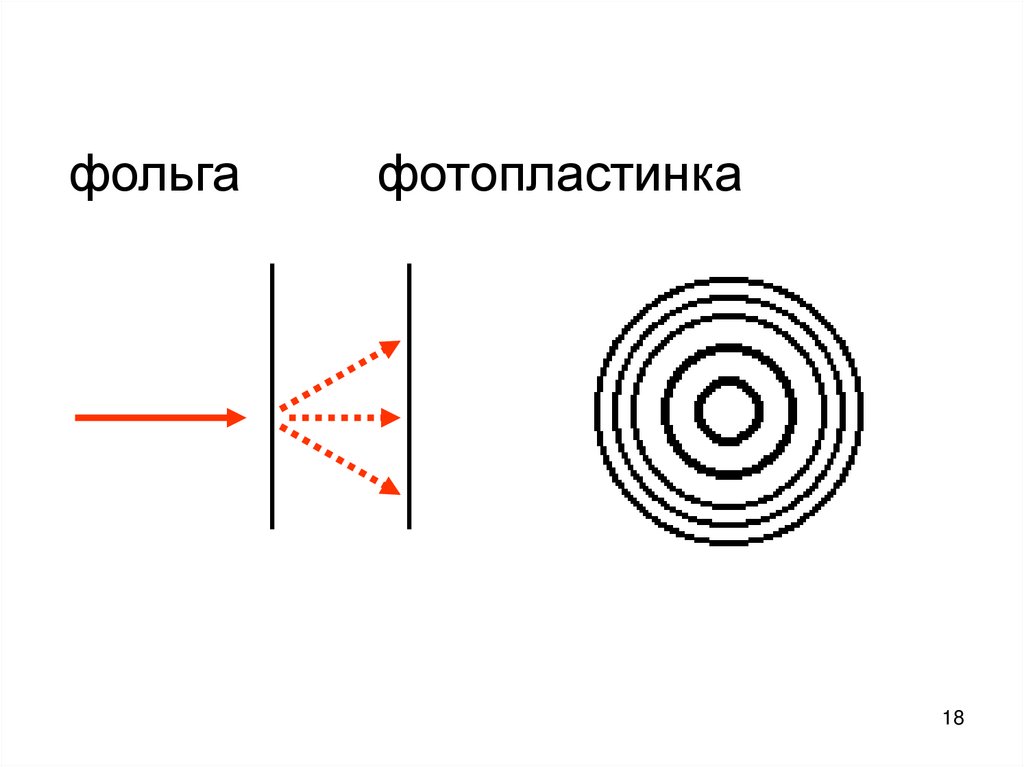
1617. Дифракция электронов и нейтронов В 1927 году Томсон, Тартаковский получили дифракцию электронов на золотой фольге.
1718.
фольгафотопластинка
18
19. Дифракция нейтронов на монокристалле NaCl
1920.
2021. 24. Дифракция микрочастиц. Принцип неопределённости Гейзенберга.
2122. Дифракция микрочастиц Микрочастицы – элементарные частицы (электроны, протоны, нейтроны, фотоны), а также сложные частицы
(атомы, молекулы, ядраатомов).
Поведение микрочастиц настолько
необычно, что их поведение
невозможно связать с обычным для
нас миром, что приходится
пользоваться абстракциями.
22
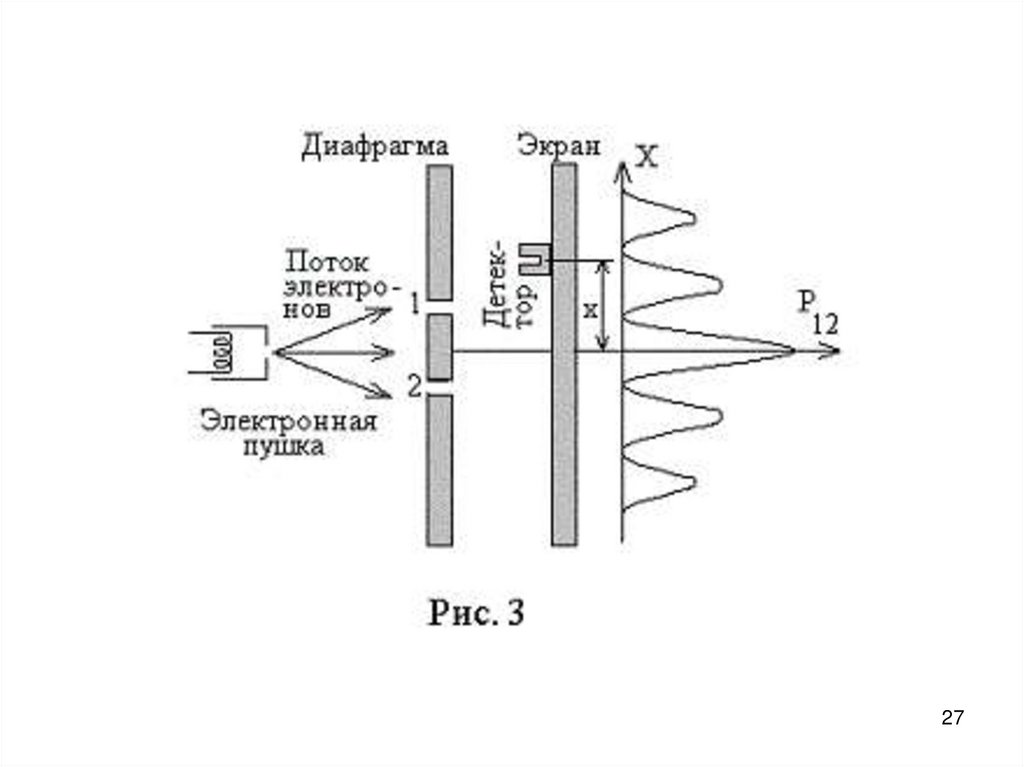
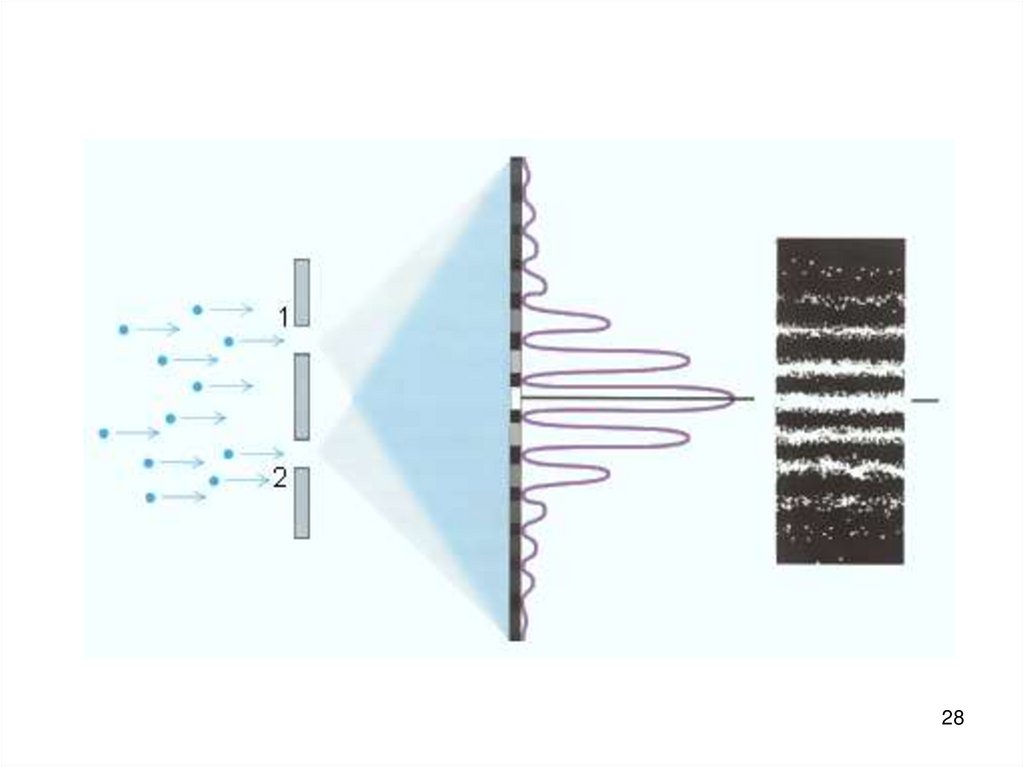
23. Проведём мысленный эксперимент, основанный на реальных (см. ранее описанные эффекты). Направим на преграду с двумя узкими
щелями параллельный пучокмоноэнергетических электронов. За
преградой поставим фотопластинку.
23
24. Если щели будут открыты по одной, то будут просто пятна, если обе – то увидим интерференционную картину. Это значит, что на
характердвижения электрона оказывают
влияние оба отверстия.
24
25. С классической точки зрения это трудно представить, ведь электрон – это целая, нераздельная частица, она может быть либо в 1-й,
либо во 2-й щели.Данный опыт подтверждает наличие
волновых свойств у электрона.
25
26.
2627.
2728.
2829. Принцип (соотношение) неопределённостей Гейзенберга Вернёмся к мысленному опыту. До отверстий мы знаем значение импульса
электрона p2 = E * 2m, ноне знаем через какую щель он
пройдёт. На фотопластинке можно
определить координату, но мы не
знаем как изменился импульс.
29
30. Данный вывод называется принципом неопределённости Гейзенберга и имеет строгую математическую формулировку: аналогично для
Данный вывод называетсяпринципом неопределённости
Гейзенберга и имеет строгую
математическую формулировку:
h
x px
4π
аналогично для энергии и времени:
h
E t
4π
30
31. Аналогичен принципу неопределённостей принцип дополнительности Бора: точное определение какой-либо величины приводит к потери
точности другойвеличины.
31
32. Иногда эти принципы интерпретируют следующим образом: воздействие измерительного прибора не позволяет точно определить
физические величины.Но это не так. Неопределённость
заключена в самой квантовой
природе микромира.
32
33.
3334. 25. Задание микрочастиц. Волновая функция. Принцип суперпозиции.
3435. Задание состояния микрочастиц Исходя из дуализма и принципа неопределённости, де Бройль предложил описывать частицу некоторой
волновой функцией(волной де Бройля):
r , t C exp i ωt k r
i
r , t C exp Et pr
35
36. Здесь E – полная энергия частицы, С – некоторая постоянная, i2 = (–1) – мнимая единица.
3637. Волновая функция не описывает положение частицы, она характеризует состояние частицы, через Ψ-функцию мы можем вычислить
вероятность нахождениячастицы в точке с координатами
(x, y, z, t).
37
38. «Размер» точки зададим как некоторую область объёмом dV В объёме V Ψ* – комплексно сопряжённое.
«Размер» точки зададим какнекоторую область объёмом dV
dW x, y, z, t dV dV
2
*
В объёме V
dW V , t dV dV
2
V
*
V
Ψ* – комплексно сопряжённое.
38
39. Пси функция должна удовлетворять условиям нормировки на бесконечности волновая функция стремится к нулю (Ψ(±∞) → 0).
Пси функция должна удовлетворятьусловиям нормировки
d
V
1
2
на бесконечности волновая функция
стремится к нулю (Ψ(±∞) → 0).
39
40. Принцип суперпозиции состояний: если какая-либо система способна находиться в состояниях как с волновой функцией Ψ1, так и с
функцией Ψ2, то она можетнаходиться и в состоянии с волновой
функцией:
Ψ = C1 Ψ1 + C2 Ψ2,
где C1 и C2 – любые числа, для
которых Ψ удовлетворяет условию
нормировки.
40
41.
4142. 26. Уравнение Шрёдингера. Уравнения Шрёдингера многомерное временное, стационарное, одномерное. Собственные значения энергии.
Частица в потенциальной яме.42
43. Уравнение Шрёдингера На основании идей де Бройля Шрёдингер получил уравнение, из решения которого получается вид Ψ функции
(временное уравнение Шрёдингера)h
h
i
2 Wp ( x, y, z, t ) ,
2π t
8π m
2
43
44. здесь i – мнимая единица; h – постоянная Планка; Wp(x, y, z, t) – потенциальная энергия частицы в силовом поле; m – масса
частицы;Ψ = Ψ(х, у, z, t) = Ψ(r, t) – волновая
функция частицы;
r = (х, у, z) – пространственная
координата и время t,
44
45. оператор Лапласа
2 2 2x
y
z
2
2
2
2
45
46. В одномерном случае уравнение принимает вид (одномерное уравнение Шрёдингера):
hh
i
W p ( x, y , z , t )
2
2π t
8π2 m x
2
2
46
47. Wp(x, y, z, t) – потенциальная энергия частицы в силовом поле – это функция координат и времени, градиент которой, взятый с
обратным знаком, определяет силу,действующую на частицу.
Если Wp не зависит от времени, то
она принимает смысл
потенциальной энергии.
47
48. Вид Ψ-функции определяется функцией Wp. Если Wp не зависит от времени, то получаем стационарное уравнение Шрёдингера:
8 m2 [W Wp ( x)] 0
2
x
h
2
2
48
49. где W = const – полная энергия частицы, Wp(x) – потенциальная энергия взаимодействия электрона и ядра, удаленные на расстояние
х.49
50. Уравнение Шрёдингера позволяет найти Ψ-функцию. Ψ-функция должна быть однозначной, непрерывной, конечной, должна иметь
непрерывную и конечнуюпроизводную.
Это всё стандартные условия.
50
51. В уравнении Шрёдингера энергия частицы W может принимать только определённые значения. Такие значения называются собственными.
Решения, соответствующиесобственным значениям W,
называются собственными
функциями,
а состояния – стационарными.
51
52. Совокупность собственных значений величины называется её спектром. Спектр может быть дискретным или сплошным.
5253. Пример. Частица в потенциальной яме (в потенциальном ящике). Примером движения электрона в потенциальном ящике является
движение коллективизированныхэлектронов в металлах.
53
54. В этом случае энергия электрона вне и внутри потенциального ящика имеет следующие значения: Wp = 0 при 0 x ℓ, Wp = при x
В этом случае энергия электрона внеи внутри потенциального ящика
имеет следующие значения:
Wp = 0 при 0 x ℓ,
Wp = при x 0 и x ℓ,
где ℓ – ширина потенциального
ящика.
54
55.
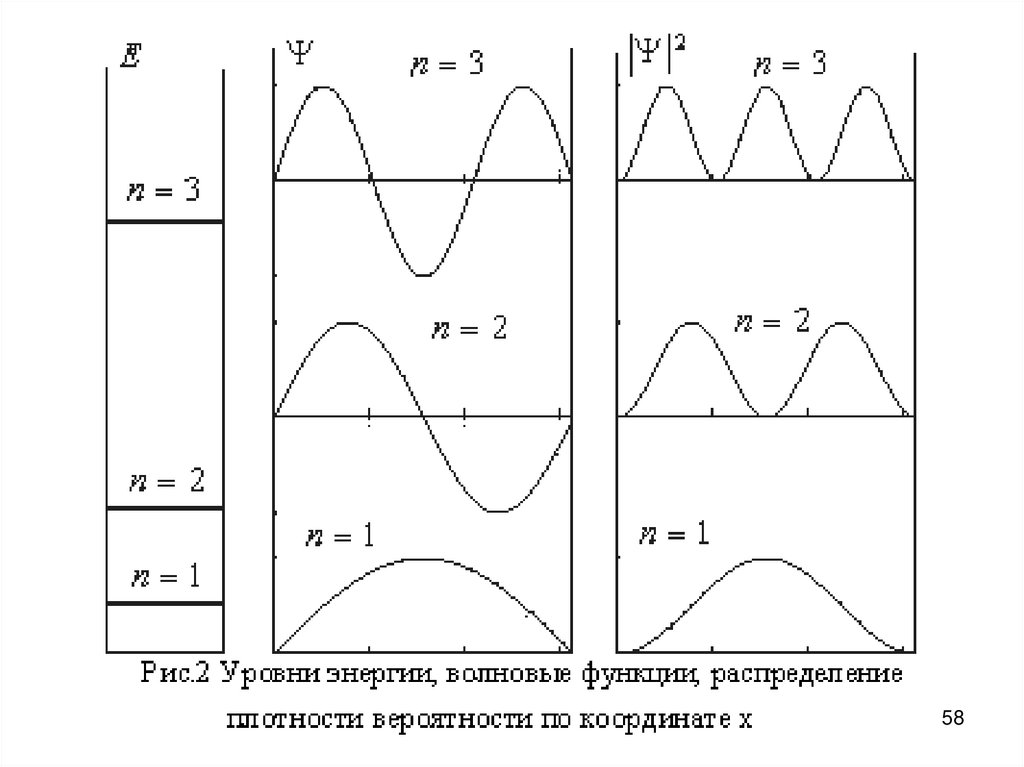
5556. Решая данную задачу с помощью одномерного стационарного уравнения Шрёдингера, находим, что на длине ℓ потенциального ящика
должно укладываться целое числоволн де Бройля.
И находим энергетический спектр
частицы в глубокой потенциальной
яме.
Wn = h2kn2/(8 2m) = h2n2/(8ℓ2m).
56
57. Энергетический спектр частицы в глубокой потенциальной яме дискретен и ограничен снизу. Следовательно, энергия электрона в
потенциальном ящике можетпринимать лишь ряд дискретных
собственных значений энергии Wn.
57
58.
5859. Это значит, что энергия электрона в потенциальном ящике является квантованной, а значения Wn называются уровнями энергии, где n
= 1, 2, 3, … главное квантовоечисло, определяющее вид волновой
функции и энергию частицы в
состоянии с этой волновой
функцией.
59















































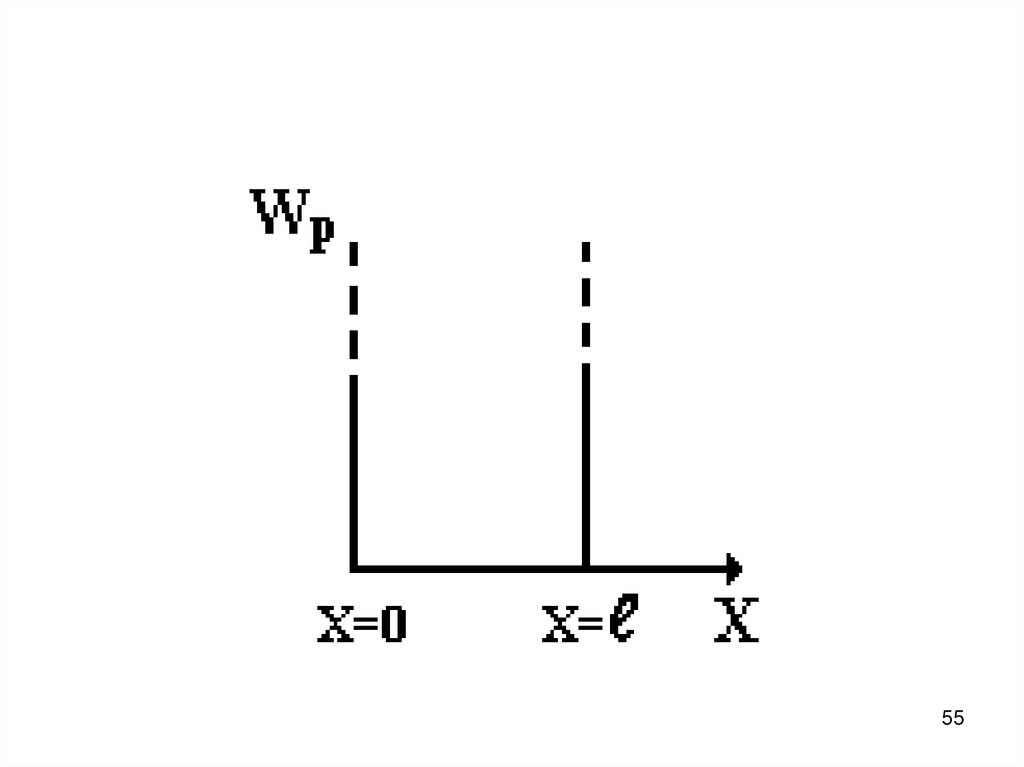



 Физика
Физика