Похожие презентации:
1. Метрология (1)
1. МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ, СЕРТИФИКАЦИЯ И УПРАВЛЕНИЕ КАЧЕСТВОМ
2. Литература
1. Сергеев А.Г., Латышев М.В, Терегия. В.В. Метрология,стандартизация, сертификация Учебное пособие. - М.: Логос. 2003.
2. Маллабоев У.М., Пилипец Л.В. Метрология, стандартизация и
сертификация: Методическое пособие. Тобольск: ТГСПА им. Д.И.
Менделеева, 2012. – 167 с.
3. Мурашкина Т.И., Мещеряков В.А., Бадеева Е.А. и др. Теория
измерений: учебное пособие.- М.: Высшая школа, 2007.
4. Сергеев, А.Г., Тегеря В.В. Метрология, стандартизация, сертификация
[Электронный ресурс]: учебник. –М.: Издательство Юрайт, ИД Юрайт,
2011.
5. Ахтулов А.Л., Ахтулова Л.Н., Смирнов С.И. Метрология,
стандартизация и сертификация [Электронный ресурс]: учебное
пособие. под ред. А. Л. Ахтулова. – Тюмень: ТюмГНГУ, 2011.
6. Андронова И.В., Невмержицкая Я.В. Стандартизация, метрология,
сертификация [Электронный ресурс]: учебник– Тюмень: ТюмГНГУ, 2011.
7. Лифиц И.М. Стандартизация, метрология и подтверждение
соответствия [Электронный ресурс]: учебник. – М.: Юрайт; ИД Юрайт,
2009. и др.
3.
ЛекцияСПИСОК СОКРАЩЕНИЙ
ФВ – физическая величина;
СИ – средство измерения;
ИВ – измерительная величина;
ВФВ – влияющая физическая величина;
ИП – измерительные приборы;
ИПр – измерительные преобразователи;
ИУ – измерительные устройства;
ИА – измерительная аппаратура;
ПИП – первичный измерительный преобразователь.
6
4.
стандартизацияк
а
ч
е
с
т
в
о
сертификация
метрология
Взаимосвязь дисциплин
5.
ЛекцияВведение
В современной рыночной экономике качество
выпускаемой продукции определяет
конкурентоспособность предприятия, его
жизнеспособность и устойчивое развитие.
Проблема качества является важнейшим
фактором повышения уровня жизни,
экономической, социальной и экологической
безопасности.
6
6.
ЛекцияКачество – это комплексное понятие,
характеризующее эффективность всех
сторон деятельности:
разработка стратегии,
организация производства,
маркетинг и др.
Важнейшей составляющей всей системы
качества является качество продукции.
6
7.
ЛекцияРассматривая метрологию, стандартизацию
и сертификацию можно сказать:
стандартизация нормирует качество;
метрология контролирует качество;
сертификация гарантирует качество
продукции, работ и услуг.
23
8.
ЛекцияДисциплина «Метрология, стандартизация
и сертификация» изучает принципы
создания изделий высокого качества, а
также методы и средства, обеспечивающие
контроль и гарантию качества,
поступающих потребителю изделий.
6
9.
ЛекцияОдна из основных функций государства и общества
– обеспечение права граждан на приобретение
товаров и услуг надлежащего качества и безопасных
для жизни и здоровья потребителей.
Метрология
Стандартизация
Сертификация
инструменты обеспечения
безопасности и качества
продукции, работ и услуг,
эффективности производства
Т.о., обеспечение качества товаров и
услуг как основная цель метрологии,
стандартизации, сертификации.
23
10.
ЛекцияМ
е
т
р
о
л
о
г
и
я
- деятельность,
по обеспечению
единства измерений
23
11. Лекция
Метрология – наука об измерениях, а измерения– один из важнейших путей познания.
Они играют огромную роль в
современном обществе.
Наука, промышленность, экономика и коммуникации
не могут существовать без измерений.
Практически нет ни одной сферы деятельности,
где бы интенсивно не использовались результаты
измерений, испытаний и контроля.
1
12.
ЛекцияС
т
а
н
д
а
р
т
и
з
а
ц
и
я
- деятельность,
устанавливающая
требования, нормы,
характеристики
к качеству
продукции или услуг
23
13. Лекция
Стандартизация изучает вопросыразработки и применения таких правил и
норм, которые отражают действие
общественных технико-экономических
законов, играют большую роль в развитии
промышленного производства.
Стандартизация имеет
непосредственное отношение к
совершенствованию управления
производством, повышению качества
всех видов товаров и услуг.
1
14.
ЛекцияС
е
р
т
и
ф
и
к
а
ц
и
я
- деятельность,
по установлению
соответствия продукции
или услуги определенным
требованиям и нормам
23
15. Лекция
Большое значение для регулированиямеханизмов рыночной экономики приобрела
сертификация.
Сертификация рассматривается как
официальное подтверждение соответствия
стандартам и во многом определяет
конкурентоспособность продукции.
1
16.
Лекцияосновная цель МСС:
В
Ы
В обеспечение качества
О
продукции, процесса
Д
или услуги
23
17.
ЛекцияКачество – совокупность
характеристик объекта,
относящихся к его способности
удовлетворять установленные
или предполагаемые
потребности.
23
18.
ЛекцияЗначение в системе качества
23
19.
ЛекцияОбъем изучения
23
20.
ЛекцияПервый принцип обеспечения
качества – «… потребитель
должен получить то, что он
хочет, когда он этого хочет и в
той форме, в какой он хочет» проф. Деминг Э.
23
21.
ЛекцияКачество
это не рацпредложение
и не лозунг,
это – образ жизни.
А. Фейгенбаум
(ученый в обл. экспертных систем)
23
22.
ЛекцияВ разделе «Основы метрологии»
рассматриваются:
ФЗ «Об обеспечении единства
измерений»;
Роль единства измерений в
обеспечении качества;
Основы метрологической
деятельности;
Поверка и калибровка СИ;
Государственный метрологический
контроль и надзор.
23
23.
ЛекцияВ разделе «Основы стандартизации»
рассматриваются:
ФЗ «О техническом регулировании»;
Роль стандартов и технических
регламентов в обеспечении качества;
Основы международной стандартизации;
Виды и категории НТД;
Государственный контроль и надзор в
области качества.
23
24.
ЛекцияВ разделе «Основы сертификации»
рассматриваются:
ФЗ «О техническом регулировании»
Системы сертификации;
Виды знаков соответствия и обращения
на рынке;
Роль сертификатов в обеспечении
качества;
Инспекционный контроль за
сертифицированной продукцией и
услугами.
23
25.
ЛекцияРоль МСС для решения задач
народного хозяйства:
Повышение качества
продукции, процессов и услуг
Обеспечение безопасности для
жизни и здоровья людей и
окружающей природной среды
Создание норм безопасности для
потенциально опасных машин,
оборудования, приборов.
Осуществление безопасной
утилизации производственных
и бытовых отходов
23
26.
ЛекцияЛюбой объект (предмет, процесс, явление)
можно охарактеризовать его свойствами или
качествами, которые проявляются в большей
или меньшей степени и, следовательно,
подвергаются количественной оценке.
В настоящее время хорошо известно
высказывание Ф. Энгельса
«Всякое качество имеет бесконечно
много количественных градаций».
Как же производится количественная
оценка этих свойств или качеств объекта?
Конечно, путем измерений
23
27.
ЛекцияЦелью изучения данной дисциплины
является формирование у студентов
знаний, умений и навыков в указанных
областях знаний, что подтверждается
выполнением РГР.
23
28. I. МЕТРОЛОГИЯ
ЛекцияI. МЕТРОЛОГИЯ
29. Лекция
1. Предмет, объект и задачиметрологии
С течением мировой истории человеку приходилось
измерять различные вещи, взвешивать продукты,
отсчитывать время, и т.д. Для этой цели
понадобилось создать целую систему различных
измерений, необходимую для вычисления объема,
веса, длины, времени и т.п.
Именно с помощью этих измерений происходит
формирование и управление различными
технологическими процессами, а также
контролирование качества выпускаемой продукции.
1
30. Лекция
Существует наука, систематизирующая иизучающая подобные единицы измерения, –
метрология (от греч. «metron» – мера,
«logos» – учение) .
Метрология – это наука об измерениях,
методах и средствах обеспечения
единства измерений и методах и средствах
обеспечения их требуемой точности.
1
31. Лекция
Бурное развитие метрологии неразрывно связанос развитием новых технологий.
Следует отметить и особое участие в создании
этой дисциплины Д.И. Менделеева (он занимался
метрологией с 1892 по 1907 г.г. когда он руководил
этой отраслью российской науки).
1
32. Лекция
Д. И. Менделеев:«… наука начинается … с тех пор,
как начинают измерять;
точная наука немыслима без меры»
1
33. Лекция
Метрология подразделяется на теоретическую,законодательную и практическую (рис. 1).
Теоретическая (фундаментальная) метрология
– предметом которого является разработка
фундаментальных основ метрологии;
Законодательная метрология – предметом
которого является установление обязательных
технических и юридических требований по
применению физических величин;
Практическая (прикладная) метрология –
предметом которой являются вопросы
практического применения разработок
теоретической метрологии и положений
законодательной метрологии.
1
34. Лекция
Рис. 1 – Структурнаясхема метрологии
1
35.
Лекции 1ЧТО ГЛАВНОЕ В
ПОВСЕДНЕВНОЙ
ДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА?
1. СПЕРВА – ТЕОРИЯ ВОПРОСА, ЗАТЕМ –
ПРАКТИКА
2. СПЕРВА – ПРАКТИКА, ЗАТЕМ – ТЕОРИЯ.
3
36.
Лекции« Теория - полководец,
практика - солдат, друг без друга
они существовать не могут»
Г. Галилей
4
37.
Лекции«Те, кто увлекается практикой,
не имея знаний, подобны морякам,
вступающим на корабль без руля и
компаса и никогда не знающим твердо,
куда они плывут.»
Леонардо да Винчи
5
38.
Лекции«Нет ничего более практичного,
чем хорошая теория».
Академик Б.С. Стечкин
6
39. Лекция
Методы метрологии широко используются всмежных отраслях знаний, таких как,
оценивание и контроль качества продукции,
сертификация промышленной продукции,
аттестация программ и алгоритмов
обработки данных и др.
1
40. Лекция
В нашей стране ежедневно проводят около 200 млрд.измерений. Доля затрат на измерения составляет от
10% до 15% затрат общественного труда, а в
отраслях промышленности, производящих сложную
технику, она достигает от 50 % до 70 %.
В развитых странах затраты на получение
достоверных результатов измерений заданной
точности достигают от 9 % до 12 % ВВП, в России эти
затраты составляют от 4 % до 5 % ВВП.
Эффект, получаемый в народном хозяйстве
благодаря применению средств измерений,
составляет примерно 8–10 руб. на 1 руб. затрат.
1
41. Лекция
Любая наука имеет свой объект, предмет иметоды исследования. Предмет любой науки
отвечает на вопрос ЧТО ей изучается.
Предметом метрологии является измерение
свойств объектов (длины, массы, плотности и
т.д.) и процессов (скорость протекания,
интенсивность протекания и др.) с заданной
точностью и достоверностью.
Объектом метрологии является физическая
величина (ФВ). Объект науки может быть общим
для ряда других наук.
2
42. Лекция
Следует различать объекты метрологии:1. единицы измерения величин;
2. средства измерений;
3. методики, используемые для
выполнения измерений и т. д.
2
43. Лекция
Важным понятием в метрологии являетсяединство измерений.
Понятие единство измерений характеризует
состояние измерений, когда их результаты
выражены в узаконенных единицах, а погрешности
известны и не выходят за установленные
пределы с заданной вероятностью.
Необходимость существования единства измерений
вызвана возможностью сопоставления
результатов различных измерений, которые были
проведены в различных районах, в различные
временные отрезки, а также с применением
разнообразных методов и средств измерения.
2
44.
ЛекцияВ связи с этим основными задачами
метрологии являются:
установление единиц физических величин,
государственных эталонов и образцовых средств
измерений;
разработка теории, новых методов средств
измерений и контроля;
обеспечение единства и необходимой точности
измерений;
разработка методов оценки погрешностей,
состояния средств измерения и контроля;
разработка методов передачи размеров единиц от
эталонов и образцовых средств измерений рабочим
средствам измерений.
3
45.
Лекция2. Основные понятия и определения метрологии
Мера – это средство измерения, предназначенное для
воспроизведения ф.в. заданного размера.
Физическая величина – это одно из свойств физического
объекта, общее в качественном отношении для многих
физических объектов, но в количественном отношении
индивидуальное для каждого физического объекта.
Физические величины делятся на:
а) измеряемые и б) оцениваемые.
Измеряемые физические величины могут быть выражены
количественно в установленных единицах измерения
(единицах физической величины).
Оцениваемые физические величины – это величины, для
которых единицы измерений не могут быть введены.
Их определяют при помощи установленных шкал.
4
46.
ЛекцияФизические величины классифицируются по следующим
видам явлений:
а) вещественные – они описывают физические и
физико-химические свойства веществ, материалов и
изделий из них;
б) энергетические – описывают энергетические
характеристики процессов преобразования, передачи и
поглощение (использование) энергии;
в) физические величины, характеризующие протекание
процессов во времени.
4
47.
ЛекцияЕдиницей физической величины – называют физическую
величину фиксированного размера, которой условно
присвоено числовое значение равное единице, и которое
применяется для количественного выражения
однородных с ней физических величин.
Различают основные и производные единицы физических
величин.
Для некоторых физических величин единицы
устанавливаются произвольно, такие единицы
физических величин называют основными.
Производные единицы физических величин получают по
формулам из основных единиц физических величин.
5
48.
ЛекцияСистема единиц физических величин – это совокупность
основных и производных единиц физических величин,
относящихся к некоторой системе величин.
В международной системе единиц СИ (Система
Интернациональная) принято семь основных единиц
физических величин:
единица времени – секунда (с),
единица длины – метр (м),
массы – килограмм (кг),
единица силы электрического тока – ампер (А),
термодинамической температуры – кельвин (К),
силы света – кандела (кд),
единица количества вещества – моль (моль).
5
49.
ЛекцияЭталон единицы физической величины – это средство
измерения, предназначенное для хранения и
воспроизведения единицы физической величины с
целью ее передачи другим средствам измерений данной
величины.
Понятие единство измерений характеризует
состояние измерений, когда их результаты выражены
в узаконенных единицах, а погрешности известны и
не выходят за установленные пределы с заданной
вероятностью.
Погрешность измерения – это отклонение результата
измерения от истинного значения измеряемой
величины.
5
50.
Лекция3. Объекты измерений
Объектом измерений являются физические
величины, то есть какие-либо свойства
физического объекта (предмета, процесса),
например длина, масса, время, температура и др.
В последнее десятилетие кроме физических
величин в прикладной метрологии начали
использоваться так называемые нефизические
величины.
Это связано с применением термина «измерение»
в экономике, информатике, управлении качеством,
и другие.
6
51.
ЛекцияБесконечное множество физических величин,
окружающих нас, обладает бесконечным
множеством различных качеств и свойств.
Свойства, для которых могут быть установлены
и воспроизведены градации определенного
размера, называются физическими величинами.
Физическая величина – одно из свойств физического
объекта (физической системы, явления или
процесса) общее в качественном отношении для
многих физических объектов, но в количественном
отношении индивидуальное для каждого из них.
6
52.
ЛекцияКачественная сторона понятия «физическая
величина» определяет род величины (длина как
характеристика протяженности вообще,
электрическое сопротивление как общее свойство
проводников электричества и т.п.), а
количественная – ее размер (длина конкретного
предмета, сопротивление конкретного
проводника).
Размер физической величины существует
объективно, независимо от того, знаем мы
его или не знаем.
6
53.
ЛекцияАнализ существующих величин
показывает, что они могут быть
разделены на два вида (рис. 2):
реальные,
идеальные.
6
54.
ЛекцияРис. 2 – Классификация величин
6
55.
ЛекцияК нефизическим величинам относят те,
которыми оперируют нефизические науки
(философия, социология, экономика
управления качеством, психология и т.д.).
Нефизическая величина – величина
нематериального размера, оцениваемая не
инструментальными методами, а также
величина размера нематериального объекта.
Нефизическими величинами оценивают ум,
знания, безопасность, привлекательность и
т.п.
6
56.
ЛекцияДля того, чтобы для каждого объекта можно было
установить различия в количественном содержании
свойства, отображаемого физической величиной, в
метрологии введены понятия ее размера и значения.
Размер физической величины – количественная
определенность физической величины,
присущая конкретному материальному объекту,
системе, явлению или процессу.
Значение физической величины – выражение
размера физической величины в виде некоторого
числа принятых для нее единиц.
6
57.
ЛекцияЕдиница измерения физической величины –
физическая величина фиксированного размера,
которой условно присвоено числовое значение,
равное единице, и применяемое для
количественного выражения однородных с ней
физических величин.
Выявляя общие метрологические особенности
отдельных групп физических величин, можно
предложить их классификацию по следующим
признакам (рис. 3):
6
58.
Лекция 3I
II
III
IV
I групп: по видам явлений;
II группа: по принадлежности к
различным группам физических
процессов;
Рис. 3 – Классификация
физических величин
III группа: по степени условной
независимости от других величин;
IV группа: по наличию размерности
6
физических величин.
59.
ЛекцияЦелью измерения и его конечным результатом
является нахождение значения физической
величины.
Для достижения этой цели в метрологии используют
понятия истинного и действительного значения
физической величины.
Нахождение истинного значения
измеряемой величины является
центральной проблемой
метрологии.
6
60.
ЛекцияИстинное значение физической величины – это
значение физической величины, которое
идеальным образом характеризует в
качественном и количественном отношении
соответствующую физическую величину.
Значение физической величины, полученное
экспериментальным путем и настолько близкое
к истинному значению, что в поставленной
измерительной задаче может быть использовано
вместо него, называется действительным
значением.
6
61.
ЛекцияОсновная физическая величина – условно
принятая физическая величина в качестве
независимой от других величин этой системы.
Производная физическая величина – физическая
величина определяемая через основные величины
этой системы.
Формализованным отражением качественного
различия измеряемых величин является их
размерность.
Основные величины длина (L), время (Т) и масса
(М) называются размерностями. Следовательно,
скорость имеет размерность L/T (или LT-1).
Мы будем использовать оба типа записи.
6
62.
ЛекцияРазмерность физической величины – выражение
в форме степенного одночлена, составленного из
произведений символов основных физических
величин в различных степенях:
dim X = LαM βT γ или dim X = MαLβT γ
L, M, T – размерности величин: длины, массы и
времени;
α, β, γ – показатели размерности физических
величин.
Каждый показатель размерности может быть
положительным или отрицательным, целым,
дробным или равным нулю.
Если все показатели размерности равны нулю,
то величина называется безразмерной.
6
63.
ЛекцияСогласно международному стандарту СИ (IS) –
размерность основных величин – длины, массы
и времени – обозначается соответствующими
буквами (см. табл. 1):
dim l = L; dim m = M; dim t = T.
6
64.
ЛекцияТаблица 1
Размерности некоторых физических величин,
выраженные через длину L, массу М и время Т
6
65.
Лекция4. Международная система единиц
физических величин
В 1791 г. Национальным собранием Франции была
принята первая в истории система единиц
физических величин. Она представляла собой
метрическую систему мер.
В нее входили: единицы длин, площадей,
объемов, вместимостей и веса.
А в их основу были положены две общеизвестные
ныне единицы: метр и килограмм.
6
66.
ЛекцияВ 1832 г. немецким математиком К. Гауссом была
разработана новейшая методика построения системы
единиц. В основу этой методику входить три основные
величины: массу, длину, время.
А в качестве основных единиц измерения данных
величин К. Гаусс взял миллиграмм, миллиметр и
секунду, поскольку все остальные единицы измерения
можно вычислить с помощью минимальных.
С развитием научно – технического прогресса
возникли еще ряд систем единиц физических величин,
основанием для которых служит принцип системы
Гаусса.
Все эти системы построены как метрические, однако
их отличием служат различные основные единицы.
6
67. Лекция
На современном этапе развития выделяют следующиеосновные системы единиц ФВ:
1) система СГС (1881 г.). Основными единицами СГС являются
следующие: сантиметр – единицы длины, грамм – единицы
массы, секунда – единицы времени;
2) система МКГСС (конец XIX в.), использующая первоначально
килограмм как единицу веса, а впоследствии как единицу силы,
что вызвало создание системы единиц физических величин,
основными единицами которой стали три физических единицы:
метр как единица длины, килограмм-сила как единица силы и
секунда как единица времени;
3) система МКСА (1901 г.), основы которой были созданы
итальянским ученым Дж. Джорджи, который предложил в качестве
единиц системы МКСА метр, килограмм, секунду и ампер.
4) система СИ (1960 г.). На XI Генеральной конференции по мерам
и весам была утверждена Международная система единиц (СИ).
В основе СИ лежат семь единиц, охватывающих следующие
области науки: механику, электричество, теплоту, оптику,
9
молекулярную физику, термодинамику и химию.
68.
ЛекцияЕдиницы длины, массы и времени системы МКС
совместно с единицей кельвин для температуры
и ампером для электрического тока образуют
Международную систему единиц, сокращенно СИ
(SI начальные буквы французского наименования
Systeme International).
В Российской Федерации использование
Международной системы единиц СИ (или МКС)
утверждено Государственным стандартом в 1982
году.
6
69.
ЛекцияПрименяемая в настоящий момент
Международная система единиц (СИ)
основана на семи основных единицах
происходит от французского наименования
«Systeme International (SI). СИ содержит семь
основных, две дополнительных, (табл. 1) а
также несколько внесистемных,
логарифмических единиц измерения.
6
70.
Таблица 1Основные и дополнительные единицы системы SI
Лекция
6
71.
ЛекцияL – длина. Метр – длина пути, которую проходит свет в
вакууме за 1/299 792 458 секунды*;
M – масса. Килограмм – масса, равная массе
международного прототипа килограмма**;
T – время. Секунда – продолжительность 9192631770
периодов излучения, соответствующего переходу
между двумя сверхтонкими уровнями основного
состояния атома цезия Cs-133 при отсутствии
возмущений со стороны внешних полей***;
I – сила электрического тока. Ампер – сила,
неизменяющегося тока, который при прохождении по
двум параллельным проводникам бесконечной длины
и ничтожно малой площади кругового поперечного
сечения, расположенным в вакууме на расстоянии 1 м
один от другого, создает на каждом участке проводника
длиной 1 м силу взаимодействия равную 2∙10-7 Н;
6
72.
Лекция* До недавнего времени международным эталоном
метра считалось расстояние между двумя штрихами
на стержне из платино-иридиевого сплава,
хранящемся в Международном бюро мер и весов во
Франции (г. Севр). Теперь эталон метра определяется
числом длин световой волны спектральной линии
изотопа криптон-86.
** Современный международный эталон килограмма
(кг) массы представляет собой цилиндр,
изготовленный из платино-иридиевого сплава; он, как
и прежний эталон длины, хранится в Международном
бюро мер и весов в г. Севр (Франция).
6
73.
Лекция*** В настоящее время наиболее точными считаются
часы, основанные на частоте излучения атомов
цезия-133. При этом секунда определяется как
интервал времени, на котором укладывается
9,19263177·109 периодов колебаний излучения,
испускаемого атомом цезия-133.
6
74.
ЛекцияΘ – термодинамическая температура. Кельвин –
1/273,16 часть термодинамической температуры
тройной точки воды;
N – количество вещества. Моль – количество
вещества системы, содержащее столько же
структурных элементов, сколько содержится
атомов в углероде C12 массой 0,012 кг;
J – сила света. Кандела – сила света в заданном
направлении источника, испускающего
монохроматическое излучение частотой 540∙1012 Гц,
энергетическая сила света которого в этом
направлении составляет 1/683 Вт/ср2).
6
75.
ЛекцияСложность приведенных формулировок отражает
развитие современной науки, позволяющей
представить основные единицы, с одной стороны,
как достоверные и точные, а с другой, как
объяснимые и понятные для всех стран мира.
Именно это и делает рассматриваемую систему
подлинно международной.
6
76.
ЛекцияВ системе СИ в 1960 г. введены две дополнительные
единицы для измерения плоского и телесного углов
– радиан и стерадиан.
Плоский угол. Радиан – угол между двумя
радиусами окружности, длина дуги между
которыми равна радиусу (1 рад. = 57°17'48'').
Телесный угол. Стерадиан – телесный угол с
вершиной в центре сферы, вырезающий на
поверхности сферы площадь, равную площади
квадрата со стороной, равной радиусу сферы.
6
77.
ЛекцияВсе остальные физические величины могут быть
получены как производные основных.
Например единица измерения силы – ньютон –
это производная единица, образованная
основными единицами – килограммом, метром и
секундой.
Используя второй закон Ньютона: (F = ma),
находим размерность единицы измерения силы:
6
78.
ЛекцияЕдиницы, не входящие в принятую систему носят
название внесистемных и делятся на четыре вида:
1. допускаемые наравне с единицами СИ (тонна,
минута, градус, секунда, литр и т.д.);
2. допускаемые к применению в специальных
областях (в астрономии – парсек, световой год; в
оптике – диоптрия; в физике – электрон–вольт и т.д.);
3. временно допускаемые к применению наравне с
единицами СИ (миля, карат и т. д.), но подлежащие
изъятию из обращения;
4. изъятые из употребления (миллиметр ртутного
столба, лошадиная сила и т.д.).
6
79.
ЛекцияЧтобы составить представление о
выполненном или предполагаемом
измерении, необходимо знать его
основные характеристики:
принцип измерения,
метод измерения,
погрешность измерения.
6
80.
ЛекцияПринцип измерения – совокупность физических
явлений, на которых основано измерение.
Метод измерения – совокупность приёмов
использования принципов и средств измерений.
Погрешность (или ошибка) измерения –
отклонение результаты измерения от
истинного значения измеряемой величины.
6
81.
Лекция5. Классификация измерений
I. Измерения классифицируются по нескольким
признакам, наиболее важные из которых
представлены в виде схемы на рис. 4.
По первому признаку измерения подразделяются на
статические, при которых измеряемая величина
(ИВ) остается постоянной во времени в процессе
измерения, и динамические, при которых ИВ
изменяется в процессе измерения.
II. Классификация по второму признаку является в
большей степени условной, однако широко
применяется в измерительной технике.
6
82.
ЛекцияРис. 4. Классификация измерений
23
83.
ЛекцияIII. По третьему признаку измерения подразделяются
на 3 класса:
1. Измерения максимально возможной точности, достижимой
при современном уровне техники. Это измерения, связанные
с созданием и воспроизведением эталонов.
2. Контрольно-поверочные измерения, погрешности которых
не должны превышать заданного значения. Такие измерения
осуществляются в основном государственными и
ведомственными метрологическими службами и
ремонтными организациями.
3. Технические измерения, в которых погрешность результата
определяется метрологическими характеристиками
средств измерения. Технические измерения являются
наиболее распространенными и выполняются во всех
отраслях хозяйства и науки (к ним относятся и
теплотехнические измерения).
6
84.
ЛекцияIV. С четвёртым признаком всё ясно.
Под наблюдением понимают экспериментальную
операцию, выполняемую в процессе измерения, в
результате которой получают одно значение из
серии значений величин, подлежащих совместной
обработке для получения результата измерений.
6
85.
ЛекцияV. По пятому признаку измерения подразделяются в
зависимости от значение из серии значений величин,
подлежащих совместной обработке для получения
результата измерений.
Прямыми называют измерения, при которых искомое
значение величины находят непосредственно из
опытных данных (напр.: измерение длины линейкой,
масса весами, температура термометром, давление).
Косвенными называют измерения, при которых
искомое значение величины находят на основании
известной зависимости между этой величиной и
величинами, измеренными прямым методом (напр.:
измерение расхода методом переменного перепада
давления, электрического сопротивления по падению
напряжения и силе тока и т.п).
6
86.
ЛекцияРис. 4. Классификация измерений
23
87.
ЛекцияСовокупными называют производимые одновременно
измерения нескольких одноимённых величин, при
которых искомые значения величины находят
решением системы уравнений, получаемых при
прямых измерениях различных сочетаний этих
величин или ряда других величин, функционально
связанных с измеряемыми.
Совместными называют проводимые одновременно
измерения двух или нескольких разноимённых
величин для нахождения зависимости между ними
(напр.: измерение тепловой энергии по температуре,
давлению и расходу теплоносителя, определение
удельного электрического сопротивления проводника
по его сопротивлению, длине и площади поперечного
сечения).
6
88.
ЛекцияИзмерение – это нахождение физической величины
(ФВ) опытным путем с помощью специальных
технических средств.
Измерительное преобразование – отражение
размера одной ФВ размером другой ФВ,
функционально с ней связанной.
Процесс решения любой задачи измерения включает в
себя три этапа:
подготовку,
проведение измерения (эксперимента),
обработку результатов.
Процесс измерения включает в себя ряд составных
элементов, которые показаны на рис. 5.
6
89.
ЛекцияРис. 5. Структурная схема процесса измерения: СИ – средство
измерения; М – мера; Y – результат измерения; X – измеряемая
величина; Z – влияющая физическая величина (ВФВ)
23
90.
ЛекцияОбъект измерения – это сложное явление или
процесс, характеризующийся множеством отдельных
ФВ (параметров), каждая из которых может быть
измерена в отдельности, но в реальных условиях
действует на измерительное устройство совместно со
всеми остальными параметрами.
В теплоэнергетике основными объектами измерения
являются котел, турбина и их вспомогательное
оборудование.
6
91. Лекция
Основным объектом в электроэнергетике являетсяэлектрическая система.
Электрическая ( или энергетическая) система (ЭС) – это
совокупность электрических станций, электрических
сетей и узлов потребления, объединенных единым
процессом производства, передачи и распределения
электрической энергии.
7
92. Лекция
793.
ЛекцияВ процессе измерения на СИ, оператора и объект
измерения воздействуют внешние факторы –
влияющие физические величины (ВФВ).
ВФВ называют ФВ, которая не измеряется данным СИ,
но оказывает влияние на результат измерения,
проведенным этим средством (температура окружающей
среды, атмосферное давление, влажность и т.п.).
СИ называется техническое средство (мера,
измерительный прибор или преобразователь,
измерительная система), используемое при измерениях
и имеющее нормированные метрологические
характеристики (класс точности, вариация и т.п.).
6
94.
ЛекцииЭлементы знаний
Физический объект (ФО)
частица, тело (вещество); поле.
Современная физика не делает
принципиальных различий между
веществом и полем.
Физическое явление (ФЯ)
взаимодействие ФО, изменение их
состояния
Физическая величина (ФВ)
характеристика ФО или ФЯ
Физический закон (ФЗ)
связь между ФВ
Научный факт (НФ)
экспериментальный факт
Элемент теории
гипотеза, постулат, теорема и т. п.
→ система знаний
4
95.
ЛекцииФО существуют;
ФЯ имеют место;
ФВ вводятся для описания ФО и ФЯ, имеют
размерность, бывают скалярные, векторные (в
рамках данного курса), могут быть чему-либо
равны или как-либо направлены, могут
изменяться, но не существуют и не участвуют в ФЯ;
ФЗ справедливы (или не справедливы) и имеют
границы применимости.
4
96.
ЛекцияМера – средство измерений, предназначенное для
воспроизведения физической величины заданного
размера.
Результат измерения – это значение физической
величины, найденное путем ее измерения.
Различают истинное и действительное значение
измеряемой величины.
Истинное значение ФВ – значение ФВ,
которое идеальным образом отражало бы в
качественном и количественном отношениях
соответствующее свойство объекта.
6
97.
ЛекцияВ философском аспекте истинное значение всегда
остается неизвестным, а совершенствование
измерений позволяет приближаться к истинному
значению физической величины (Tп.в. = 1000 °C =
99,9740 °C).
В метрологическом аспекте истинным значением
измеряемой величины называется её значение
свободное от погрешности измерения, т.е. не
содержащее погрешности.
Истинное значение измеряемой
величины практически получить
невозможно.
6
98.
ЛекцияЕсли погрешности минимально возможные,
которые можно получить при современном
уровне измерительной техники, то данный
результат измерений можно назвать
действительным значением ФВ.
Действительное значение ФВ – это значение
ФВ, найденное экспериментальным путем и
настолько приближающееся к истинному, что
для данной цели может быть использовано
вместо него.
6
99.
ЛекцияПоэтому, для оценки точности измерения в
практике принимается вместо истинного значения
измеряемой величины действительное значение
измеряемой величины, т.е. значение измеряемой
величины, полученное с наибольшей
точностью.
Его получают в результате измерения с
минимально допускаемой погрешностью, как
правило, с помощью рабочих эталонов.
6
100.
Лекция6. Виды и методы измерений
Прежде чем разбираться в сущности каких-либо
явлений, удобно их сначала упорядочить, т.е.
классифицировать.
Измерения можно классифицировать по различным
признакам:
а) в зависимости от способа получения измерительной
информации измерения разделяются на виды;
б) в зависимости от различия приемов использования
принципов и средств измерений измерения
производятся различными методами.
Рассмотрим сначала классификацию видов (а), а затем
методов измерений (б).
6
101.
Лекция6.1. Классификация видов измерений
Классификацию видов измерений можно проводить по
различным классификационным признакам, к которым
можно отнести следующее:
способ нахождения численного значения физической
величины,
число наблюдений,
характер зависимости измеряемой величины от
времени,
число измеряемых мгновенных значений в заданном
интервале времени,
условия, определяющие точность результатов,
способ выражения результатов измерения.
6
102.
ЛекцияПо способу нахождения численного
значения физической величины измерения
подразделяются на следующие виды:
прямые,
косвенные,
совокупные,
совместные.
6
103.
ЛекцияПрямым измерением называют измерение, при
котором значение измеряемой величины находят
непосредственно из опытных данных.
Прямые измерения выполняются при помощи средств,
предназначенных для измерения данных величин.
Числовое значение измеряемой величины
отсчитывается непосредственно по показанию
измерительного прибора.
Примеры прямых измерений:
измерение тока амперметром;
напряжения – вольтметром;
массы – на рычажных весах и др.
6
104.
ЛекцияЗависимость между измеряемой величиной X и
результатом измерения Y при прямом измерении
характеризуется уравнением:
X = Y,
т.е. значение измеряемой величины принимается равным
полученному результату.
К сожалению, прямое измерение не всегда можно провести.
Иногда нет под рукой соответствующего измерительного
прибора, или он неудовлетворителен по точности, или
даже вообще ещё не создан.
В этом случае приходится прибегать к косвенному
измерению.
6
105.
ЛекцияКосвенными измерениями называют такие измерения,
при которых значение искомой величины находят на
основании известной зависимости между этой
величиной и величинами, подвергаемыми прямым
измерениям.
При косвенных измерениях измеряют не собственно
определяемую величину, а другие величины,
функционально с ней связанные.
Значение измеряемой косвенным путем величины X
находят вычислением по формуле
X = F(Y1, Y2, … ,Yn),
Y1, Y2, … Yn – значения величин, полученных путем
прямых измерений.
6
106.
ЛекцияПримером косвенного измерения является определение
электрического сопротивления с помощью амперметра
и вольтметра.
Здесь путем прямых измерений находят значения
падения напряжения U на сопротивлении R и ток I через
него, а искомое сопротивление R находят по формуле
R = U/I.
Операцию вычисления измеряемой величины может
производить как человек, так и вычислительное
устройство, помещенное в прибор.
Прямые и косвенные измерения в настоящее время
широко используются в практике и являются наиболее
распространенными видами измерений.
6
107.
ЛекцияСовокупные измерения - это производимые
одновременно измерения нескольких одноименных
величин, при которых искомые значения величин
находят решением системы уравнений, получаемых при
прямых измерениях различных сочетаний этих величин.
Например, для определения значений сопротивлений
резисторов, соединенных треугольником (рис. 1),
измеряют сопротивления на каждой паре вершин
треугольника и получают систему уравнений:
R1 R 2 R3
R1 R 2 R3
R 2 R1 R 3
R 23
R1 R 2 R 3
R12
R31
Рис. 1.
R3 R1 R 2
R1 R 2 R3
6
108.
ЛекцияИз решения этой системы уравнений получают
значения сопротивлений
A
2 R23 R31 R12
A
R2
2 R31 R12 R 23
R1
.
где
R3
A
2 R12 R23 R31
A 4 R23 R31 R23 R31 R12
2
6
109.
ЛекцияСовместные измерения - это производимые
одновременно измерения двух или нескольких не
одноименных величин X1, X2,…, Xn, значения которых
находят решением системы уравнений
Fi(X1, X2, … ,Xn; Yi1, Yi2, … ,Yim) = 0,
i = 1, 2, …, m n; Yi1, Yi2, … ,Yim – результаты прямых или
косвенных измерений;
X1, X2, … ,Xn – значения искомых величин.
Например, индуктивность катушки
L = L0 (1 + 2 C L0),
L0 – индуктивность при частоте =2 f стремящейся к
нулю; С – межвитковая емкость.
Значения L0 и С нельзя найти прямыми или косвенными
измерениями.
6
110.
ЛекцияПоэтому в простейшем случае измеряют L1 при 1,
а затем L2 при 2 и составляют систему уравнений:
L1 = L0 (1 + 12 C L0),
L2 = L0 (1 + 22 C L0),
решая которую, находят искомые значения
индуктивности L0 и емкости С
L1 22 L2 21
L0
22 12
C
L2 L2 22 12
L L
1
2
2
2
2 2
1
Совокупные и совместные измерения это обобщение
косвенных измерений на случай нескольких величин.
Для повышения точности совокупных и совместных
измерений обеспечивают условие m ≥ n, т.е. число
уравнений должно быть больше или равно числу
искомых величин.
6
111.
ЛекцияПо числу наблюдений измерения подразделяются на:
обыкновенные измерения – измерения,
выполняемые с однократным наблюдением;
статистические измерения – измерения с
многократными наблюдениями.
Наблюдение при измерении – экспериментальная
операция, выполняемая в процессе измерений, в
результате которой получают одно значение из
группы значений величин, подлежащих совместной
обработке для получения результатов измерений.
Результат наблюдения – результат величины,
получаемый при отдельном наблюдении.
6
112.
ЛекцияПо характеру зависимости измеряемой величины от
времени измерения разделяются на:
статические, при которых измеряемая величина
остается постоянной во времени в процессе
измерения;
динамические, при которых измеряемая величина
изменяется в процессе измерения и является
непостоянной во времени.
А для оценки точности результатов динамических
измерений необходимо знание динамических
свойств средств измерений.
6
113.
ЛекцияПо числу измеряемых мгновенных значений в
заданном интервалы времени измерения
подразделяются на дискретные и непрерывные
(аналоговые).
Дискретные измерения – измерения, при
которых на заданном интервале времени число
измеряемых мгновенных значений конечно.
Непрерывные (аналоговые) измерения –
измерения, при которых на заданном интервале
времени число измеряемых мгновенных значений
бесконечно.
6
114.
ЛекцияПо условиям, определяющим точность
результатов, измерения бывают
максимально возможной точности, достигаемой
при существующем уровне техники;
контрольно-поверочные, погрешность которых
не должна превышать некоторое заданное
значение;
технические измерения, в которых погрешность
результата определяется характеристиками
средств измерений.
6
115.
ЛекцияПо способу выражения результатов измерения
различают - абсолютные и относительные
измерения.
Абсолютные измерения – измерения, основанные
на прямых измерениях одной или нескольких
основных величин и (или) использовании значений
физических констант.
Относительные измерения – измерение
отношения величины к одноименной величине,
играющей роль единицы, или измерения величины
по отношению к одноименной величине,
принимаемой за исходную.
6
116.
Лекция6.2. Методы измерений
и их классификация
Прямые измерения являются наиболее
распространенными и служат основой для
более сложных видов измерений.
Различают 2 метода прямых измерений:
метод непосредственной оценки;
метод сравнения с мерой.
Мера – средство измерений, предназначенное
для воспроизведения физической величины
заданного размера. Напр.: гиря – мера массы.
6
117.
ЛекцияРис. 6.2.1 Классификация методов измерения
23
118.
ЛекцияМетод непосредственной оценки – метод измерений, в
котором значение величины определяют
непосредственно по отсчетному устройству ИП
прямого действия, заранее градуированного в
единицах измеряемой величины.
Этот метод является наиболее простым и поэтому
широко применяется при измерении различных величин,
например:
измерение веса тела на пружинных весах,
измерение силы электрического тока стрелочным
амперметром,
измерение разности фаз цифровым фазометром и
т.д.
6
119.
ЛекцияФункциональная схема измерения методом
непосредственной оценки приведена на рис. 1
Рис. 1 Метод непосредственной оценки (см. след. слайд)
Мерой в приборах непосредственной оценки служат
деления шкалы отсчетного устройства. Они поставлены
не произвольно, а на основании градуировки прибора.
Т.о, деления шкалы отсчетного устройства являются как
бы заменителем (отпечатком) значения реальной
физической величины и поэтому могут быть
использованы непосредственно для нахождения
значений измеряемых прибором величин.
6
120.
ЛекцияБлок-схема экспериментальной
установки для исследования
диэлектрической проницаемости
ЖК в диапазоне частот 10 Гц –
110 МГц.
1 – измерительная ячейка;
2 – постоянный магнит;
3 – низкочастотный измеритель
полных сопротивлений (ВМ-507);
4 – измеритель импеданса и
передач ВЧ (ВМ-538);
5,6,7,8 – универсальные
цифровые вольтметры для
измерения импеданса (5,7) и
сдвиг фазы (6,8);
9 – цифровой частотомер;
10 – держательный столик;
11 – термостатирующий сосуд;
12 – термостат;
13 – холодильный агрегат
6
121.
ЛекцияКонструкция измерительной
ячейки.
1 – тефлоновый держатель
кюветы;
2 – коаксиальный разъем;
3 – винты;
4 – внешние цилиндрические
электроды;
5 – внутренний электрод;
6 – кварцевые изолирующие
прокладки;
7 – кварцевая кювета.
6
122.
ЛекцияНизкочастотный измеритель полных сопротивлений
(ВМ-507) обеспечивает измерение импеданса Z от 1 Ом до
10 МОм и сдвига фаз φ от – 90° до 90° в диапазоне частот
5,0 Гц ÷ 5·105 Гц.
Мост ВМ-538 позволяет измерять полное сопротивление
в диапазоне от 1 Ом до 105 Ом и сдвиг фаз φ от 0° до 360° в
интервале частот 5·105 ÷ 1,1·108 Гц.
6
123.
ЛекцияВсе приборы непосредственной оценки фактически
реализуют принцип сравнения с физическими
величинами.
Но это сравнение разновременное и осуществляется с
помощью промежуточного средства - делений шкалы
отсчетного устройства.
6
124.
ЛекцияМетод сравнения с мерой – метод измерения, в
котором измеряемую величину сравнивают с
величиной, воспроизводимой мерой.
Эти методы по сравнению с методом
непосредственной оценки более точны.
Метод сравнения с мерой подразделяют на
нулевой и дифференциальный в зависимости от
наличия или отсутствия при сравнении разности
между измеряемой величиной и величиной,
воспроизводимой мерой.
6
125.
ЛекцияРис. 6.2.1 Классификация методов измерения
23
126.
Лекция 3Нулевой метод – это метод сравнения с мерой, в
котором результирующий эффект воздействия
измеряемой величины и меры на прибор сравнения
доводят до нуля.
К приборам, принцип работы которых основан на
нулевом (компенсационном) методе относятся
автоматические потенциометры, уравновешенные
мосты, равноплечные весы и др.
Функциональная схема нулевого метода измерения
приведена на рис. 2.
6
127.
Лекция 3Рис. 2 Нулевой метод измерения
Здесь измеряемая величина X и мера X0 воздействуют
на два входа измерительного прибора сравнения.
Результирующий эффект воздействия определяется
разностью этих величин, т.е.
ε = X – X0 .
6
128.
Лекция 3Изменяя величину, воспроизводимую мерой можно
довести величину ε до 0. Это обстоятельство
отмечается индикатором нуля.
Если ε = 0, то Х = Х0, результат измерения Y есть
полученное значение меры, т.е. Y = X0 .
Поскольку на индикатор нуля воздействует разность
величин, то его предел измерения может быть выбран
меньшим, а чувствительность большей, чем у прибора
для измерения X методом непосредственной оценки.
6
129.
Лекция 3Точность индикации равенства двух величин может
быть весьма большой. А это ведет к повышению
точности измерения.
Погрешность измерения нулевым методом
определяется погрешностью меры и погрешностью
индикации нуля.
Нулевой метод измерения требует обязательного
применения многозначных мер.
Точность таких мер всегда хуже однозначных мер.
6
130.
Лекция 3Дифференциальный метод – это метод сравнения
с мерой, в котором на ИП измеряемая величина
сравнивается с однородной величиной, имеющей
известное значение, незначительно отличающееся
от значения измеряемой величины, и при котором
измеряется разность между этими двумя
величинами (газоанализаторы, неуравновешенные
мосты).
На рис. 3 показана функциональная схема
дифференциального метода.
6
131.
Лекция 3Рис. 3 Дифференциальный метод измерения
Здесь мера имеет постоянное значение Х0, разность
измеряемой величины Х и меры Х0, т.е. ε = Х - Х0, не
равна нулю и измеряется измерительным прибором.
Результат измерения находятся как
Y = X0 + ε.
6
132.
Лекция 3Здесь измерительный прибор измеряет не всю величину
Х, а только ее часть ε позволяет уменьшить влияние на
результат измерения погрешности измерительного
прибора, причем влияние погрешности измерительного
прибора тем меньше, чем меньше разность ε.
Действительно, при измерении напряжения U = 97 В
вольтметром непосредственной оценки с пределом
измерения 100 В и допущенной относительной
погрешности измерения этого напряжения 1 % мы
получаем абсолютную погрешность измерения ∆1=
97 0,01 = 0,97 1 В.
6
133.
Лекция 3Если же мы будем измерять это напряжение
дифференциальным методом с использованием
образцового источника напряжения U0 = 100 В, то
разность напряжений U - U0 = (97 - 100) В = -3 В мы можем
измерить вольтметром с пределом измерения всего 3 В.
Пусть относительная погрешность измерения этого
напряжения будет также равна 1 %.
Это дает абсолютную погрешность измерения
напряжения 3 В, равную 2 = 3 0,01 = 0,03 В.
6
134.
Лекция 3Если эту погрешность привести к измеряемому
напряжению U, мы получим относительную
погрешность измерения напряжения, равную
2/U = 0,03/97 0,0003 (0,03 %), т.е. приблизительно в 30
раз меньше, чем при измерении напряжения U методом
непосредственной оценки.
Это увеличение точности измерения произошло
потому, что в первом случае прибором была измерена
почти вся величина с относительной погрешностью
в 1 %, а во втором случае измеряется не вся величина,
а только ее 1/30 часть.
6
135.
Лекция 3В этих расчетах не учитывалась погрешность меры,
которая полностью входит в результат измерения.
Следовательно, при малых разностных величинах
точность измерения дифференциальным методом
приближается к точности измерения нулевым
методом и определяется лишь погрешностью меры.
Кроме того, дифференциальный метод не требует
меры переменной величины.
В приведенном примере измерения напряжения
дифференциальным методом использовалось
непосредственное сравнение.
6
136.
ЛекцияКак в нулевом, так и в дифференциальном
методе могут быть выделены методы:
противопоставления,
замещения,
совпадения.
6
137.
ЛекцияМетод противопоставления – метод сравнения с
мерой, в котором измеряемая величина и величина,
воспроизводимая мерой, одновременно воздействуют
на прибор сравнения, с помощью которого
устанавливается соотношение между этими
величинами.
Примером этого метода является взвешивание груза на
равноплечих весах с помещением измеряемой массы и
уравновешивающих ее гирь на двух чашках весов и с
полным уравновешиванием весов.
При этом измеряемая масса определяется как сумма
массы гирь, ее уравновешивающих, и показания по
шкале весов.
6
138.
ЛекцияМетод противопоставления позволяет значительно
уменьшить воздействие на результат измерений
влияющих величин, поскольку последние более или
менее одинаково искажают сигналы, как в цепи
преобразования измеряемой величины, так и в цепи
преобразования величины, воспроизводимой мерой.
Отсчетное устройство прибора сравнения реагирует
на разность сигналов, вследствие чего эти искажения
в некоторой степени компенсируют друг друга.
Этот метод также применяют при измерении ЭДС,
напряжения, тока и сопротивления.
6
139.
ЛекцияМетод замещения есть метод сравнения с
мерой, в котором измеряемую величину замещают
мерой с известным значением величины.
Функциональная схема метода замещения
изображена на рис. 4.
Измеряемая
величина
X
Y1
Измерительный
прибор
Мера
X0
Результат
измерения
Y
Отсчет
Рис. 4 Метод замещения
6
140.
ЛекцияВ нем используется измерительный прибор
непосредственной оценки.
Техника измерения состоит в следующем (рис. 4).
Сначала на вход измерительного прибора подают
измеряемую величину Х и отмечают показания прибора
(отсчет) Y1.
После этого вместо измеряемой величины на тот же
самый вход (это очень существенно) прибора подают
величину Х0, воспроизводимую мерой.
В этом случае показание прибора становится равным Y2.
Изменяя величину, воспроизводимую мерой, добиваются
равенства показаний, т.е. Y1 = Y2.
При этом можно утверждать, что Х = Х0 независимо от
погрешности измерительного прибора.
6
141.
ЛекцияДействительно, в первом случае получаем Y1= X + ∆1, где
∆1 - погрешность измерительного прибора при получении
счета Y1.
При воздействии на прибор меры
Y2 = X + ∆2,
∆2 - погрешность измерительного прибора при получении
счета Y2.
Поскольку мы добиваемся одинаковых показаний (Y1=Y2),
а интервал времени между двумя измерениями невелик,
то на одной и той же отметке шкалы прибора
погрешность одинакова, т.е. ∆1 = ∆2 .
Следовательно, из равенства Y1=Y2 или X+∆1=X+∆2
вытекает, что Х=Х0.
6
142.
ЛекцияИсключение погрешности измерительного прибора
из результата измерений является новым
достоинством метода замещения.
Т.о., методом замещения можно осуществить точное
измерение, имея прибор с большой погрешностью.
Нетрудно сообразить, что точность измерения
методом замещения определяется погрешностью
меры.
Правда, при более строгом подходе к методу
замещения следует учитывать два обстоятельства.
6
143.
ЛекцияВо-первых, здесь сравнение разновременное, а за
время между двумя измерениями погрешность
измерительного прибора может несколько измениться,
так что равенство ∆1=∆2 несколько нарушится.
Теперь становится ясно, почему измеряемая величина и
мера должны подаваться на один и тот же вход
прибора.
Это, прежде всего, связано с тем, что погрешность
измерительного прибора на разных входах даже при
одинаковых показаниях может быть разной!
6
144.
ЛекцияВо-вторых, метод замещения сводится к получению
одинаковых показаний прибора.
Само равенство показаний может быть установлено
с конечной точностью.
А это также ведет к погрешности измерения.
Точность установления равенства показаний будет
больше в приборе, обладающем большей
чувствительностью.
6
145.
ЛекцияСледовательно, при измерении методом замещения
можно использовать пусть не точный, но зато
чувствительный и быстродействующий прибор.
Тогда остаточная погрешность, обусловленная
измерительным прибором, будет невелика.
Метод замещения является самым точным из всех
известных методов и обычно используется для
проведения наиболее точных измерений.
6
146.
ЛекцияМетод совпадений (или метод нониуса) представляет
собой метод сравнения с мерой, в котором разность
между измеряемой величиной и величиной,
воспроизводимой мерой, измеряют, используя
совпадение отметок шкал или периодических
сигналов.
Этот метод применяется в тех случаях, когда
измеряемая величина меньше цены деления заданной
меры.
При этом применяются две меры с разными ценами
деления, которые отличаются на размер оцениваемого
разряда отсчетов.
6
147.
ЛекцияПусть имеем одну калиброванную меру с ценой
деления xk1 и измеряемую величину x, которая
меньше цены деления. В этом случае используют
вторую меру с ценой деления xk2.
Т.о., если чувствительность необходимо увеличить
в п раз, то соотношение между ними будет иметь вид
xk2 = xk1 (1 - 1/n).
В частности, при n = 10, xk2 = 0,9 xk1.
Измеряемую величину x устанавливают между
нулевыми отметками мер и находят число Nx, равное
номеру совпавших делений мер (рис. 5).
6
148.
Лекция0
1
2
3
4
5
6
Xk1
7
8
9
10
Первая мера со
ступенями xk1
Nx
0
1
X
2
3
4
Xk2
5 6
7
8
9
10
Вторая мера со
ступенями k2
Рис. 5 Нониусный метод измерения
В этом случае справедливо соотношение
Nx xk1 = x + Nx xk2 ,
откуда
x = Nx ( xk1 - xk2) = Nx ( xk1 - 0,9 xk1) = Nx
0,1 xk1
6
149.
ЛекцияПримером измерения методом совпадения может
служить измерение длины детали с помощью
штангенциркуля с нониусом или стрелочные весы.
Другим примером может служить - измерение
частоты вращения детали с помощью мигающей
лампы стробоскопа: наблюдая положение метки на
вращающейся детали в моменты вспышек лампы, по
частоте вспышек и смещению метки определяют
частоту вращения детали.
6
150.
ЛекцияШтангенциркуль – универсальный инструмент,
предназначенный для высокоточных измерений
наружных и внутренних размеров, а также глубин
отверстий.
Представляет собой две измерительные поверхности,
между которыми устанавливается размер.
Одна из поверхностей инструмента, базовая, составляет
единое целое со штангой-линейкой.
Другая поверхность соединяется с двигающейся по
линейке рамкой.
На линейке нанесены деления, а на рамке установлен
или выгравирован нониус.
6
151.
ЛекцияПринцип нониуса впервые был изобретен Абу Али
ибн Синой.
Современная конструкция шкалы была предложена
французским математиком П. Вернье в 1631 году, в
честь которого ее называют также «верньер».
Название «нониус» это приспособление получило в
честь португальского математика П. Нуниша (1502 –
1578), который изобрел прибор другой конструкции,
но использующий тот же принцип.
6
152.
ЛекцияВ целях повышения надежности штангенинструмент
изготавливается из материалов с высокой
износостойкостью и не подвергающихся коррозии,
для чего используются закаленные стали,
хромирование и армирование рабочих поверхностей
твердым сплавом.
Иногда штангенинструмент, предназначенный для
грубых измерений, изготавливают из пластмассы.
6
153.
Лекция1. штанга;
2. подвижная рамка;
3. шкала штанги;
4. губки для внутренних
измерений;
5. губки для наружных
измерений;
6. линейка глубиномера;
7. нониус;
8. винт для зажима рамки.
6
154.
ЛекцияЦелое число миллиметров у штангенинструментов
отсчитывается по шкале штанги слева направо
нулевым штрихом нониуса.
Шкала нониуса.
Нониус длиной 19 мм разделен на
10 частей.
Одно деление нониуса составляет
19/10 = 1,9 мм, что на 0,1 мм меньше
целого числа миллиметров.
Перед началом измерений штангенциркулем надо
осмотреть его и проверить на точность.
Для этого надо совместить губки инструмента.
При этом нулевые риски обеих шкал должны совпасть.
Одновременно должен совместиться десятый штрих
нониуса с девятнадцатым штрихом миллиметровой
шкалы.
6
155.
ЛекцияНониус
На рисунке 13 нониус (нижняя шкала) показывает 7
целых 6 десятых деления основной (верхней) шкалы.
Целая часть обычно определяется по показаниям
нулевого деления нониуса, а дробная часть
определяется по номеру того деления нониуса,
которое точно совпадает с делением основной
шкалы (обведено красным пунктиром).
6
156.
Лекция6
157.
ЛекцияМикрометр – специальный измерительный прибор,
предназначенный для высокоточных измерений
линейных размеров контактным методом.
В роли преобразовательного механизма микрометры
используют микропару (винт и гайку), позволяющую
добиваться высокой точности.
6
158.
Лекция1. Корпусом инструмента служит
скоба 1, в которую запрессованы с
одной стороны пятка 2, с другой стебель 5, на котором закреплена
микрогайка и нанесена продольная
шкала.
Одной измерительной поверхностью
является торец микрометрического
винта 3, выдвигающегося из стебля,
второй - торец пятки 2.
Микровинт связан с корпусом барабана 6, имеющим на
конусном конце круговую шкалу.
Заканчивается барабан резьбой, на которую
навинчивается гайка 9, являющаяся корпусом механизма
трещетки. Для ограничения измерительного усилия
микрометр снабжен трещоткой.
6
159.
ЛекцияОсновное назначение - трещетки
обеспечивать постоянство
измерительного усилия за счет
храповика 7 и подпружиненного
стержня 8.
Микрометр снабжен устройством 4,
позволяющим стопорить микровинт
и гайкой 10 для регулировки зазора
в паре микровинт - микрогайка
Чтобы приблизить микровинт к пятке, вращают
барабан трещотку по часовой стрелке (от себя), а для
обратного движения микровинта барабан вращают
против часовой стрелки (на себя). Закрепляют
микровинт в требуемом положении стопором.
6
160.
ЛекцияЦена деления шкалы стебля равна 0,5 мм, а шкалы
барабана – 0,01 мм.
Шаг резьбы микропары (микровинт и микрогайка) Р
равен 0,5 мм.
На барабане нанесено 50 делений.
Если повернуть барабан на одно деление его шкалы,
то торец микровинта переместится относительно пятки
на 0,01 мм (P / n = 0,5 / 50 = 0,01мм), где n число делений
круговой шкалы.
Микровинт связан с барабаном 6, который на конусном
конце имеет круговую шкалу с числом делений n = 50.
Учитывая, что шаг резьбы винтовой пары S = 0,5 мм,
цена деления круговой шкалы (нониуса) микрометра
«C» равна:
C = S / n = 0,5 / 50 = 0,01 мм.
6
161.
ЛекцияРазмер измеряемой детали с точностью до 0,5 мм
отсчитывают по шкале стебля указателем, которым
является скошенный край барабана.
Сотые доли миллиметра отсчитывают по круговой шкале
барабана, указателем которой является продольный штрих
на стебле микрометра.
Погрешность измерения зависит от пределов измерения
микрометра и составляет:
от 3 мкм для микрометров с пределами измерения 0 - 25 мм,
до 50 мкм для микрометров с пределами измерения 400-500
мм.
6
162.
ЛекцияОпределяющим признаком методов сравнения
является то, что в процессе измерения происходит
сравнение двух однородных величин - известной
(воспроизводимой мерой) и измеряемой.
При измерениях методами сравнения используются
реальные физические меры, а не их «отпечатки».
Сравнение может быть одновременным и
разновременным.
При одновременном сравнении мера и измеряемая
величина воздействуют на измерительный прибор
одновременно, а при разновременным - воздействие
измеряемой величины и меры на измерительный
прибор разнесено во времени.
6
163.
ЛекцияКроме того, сравнение может быть непосредственным
и опосредованным.
При непосредственном сравнении измеряемая
величина и мера непосредственно воздействуют на
устройство сравнения, а при опосредованном
сравнении – через другие величины, однозначно
связанные с известной и измеряемой величинами.
Одновременное сравнение осуществляется обычно
методами противопоставления, нулевым,
дифференциальным и совпадения, а разновременное –
методом замещения.
6
164.
ЛекцияОбобщение методов измерения
Рассмотренная классификация методов измерений
изображена на рис. 6.
Рассмотренные методы определяют принципы
построения измерительных приборов.
Их не следует путать с методикой измерения и
алгоритмом измерения.
Методика выполнения измерений – установленная
совокупность операций и правил при измерении,
выполнение которых обеспечивает получение
результатов с гарантированной точностью в
соответствии с принятым методом.
6
165.
ЛекцияМЕТОДЫ ИЗМЕРЕНИЯ
Методы непосредственной оценки
Методы сравнения с мерой
Методы одновременного
сравнения
Методы разновременного
сравнения
Противопоставления
Дифференциальный
Совпадений
Нулевой
Непосредственное
сравнение
Замещений
Опосредованное
сравнение
Рис. 6 Классификация методов измерений
6
166.
ЛекцияИзмерения должны осуществляться в соответствии с
аттестованными в установленном порядке
методиками.
Порядок разработки и аттестации методик
выполнения измерений определяется Госстандартом
России.
Алгоритм измерения – точное предписание о
выполнении в определенном порядке совокупности
операций, обеспечивающих измерение значения
физической величины.
6
167.
Лекция7. Погрешности измерений
Важным показателем измерения является их точность,
которая представляет собой ту степень близости итогов
измерения к некоторому действительному значению,
которая используется для качественного сравнения
измерительных операций.
Поэтому, как известно, истинного значения измеряемой
величины получить невозможно и на практике приходится
пользоваться ее действительным значением.
В качестве количественной оценки, как правило,
используется погрешность измерений (разность между
полученным и действительным значением измеряемой
величины) ±∆.
Причем чем погрешность меньше, тем считается выше
точность.
6
168.
ЛекцияСогласно закону теории погрешностей, если
необходимо повысить точность результата (при
исключенной систематической погрешности) в 2 раза,
то число измерений необходимо увеличить в 4 раза;
если требуется увеличить точность в 3 раза, то
число измерений увеличивают в 9 раз и т. д.
Процесс оценки погрешности измерений считается
одним из важнейших мероприятий в вопросе
обеспечения единства измерений.
6
169.
ЛекцияВиды погрешностей
Выделяют следующие виды погрешностей:
1) абсолютная погрешность;
2) относительна погрешность;
3) приведенная погрешность;
4) основная погрешность;
5) дополнительная погрешность;
6) систематическая погрешность;
7) случайная погрешность;
8) инструментальная погрешность;
6
170.
Лекция9) методическая погрешность;
10) личная погрешность;
11) статическая погрешность;
12) динамическая погрешность;
13) погрешность отсчитывания;
14) мультипликативная погрешность;
15) аддитивная погрешность;
16) промахи и грубые погрешности.
6
171.
ЛекцияПогрешности измерений классифицируются по
следующим признакам.
1,2. По способу математического выражения погрешности
делятся на абсолютные погрешности и относительные
погрешности.
4,5. По характеру зависимости погрешности от влияющих
величин погрешности делятся на основные и
дополнительные.
6,7. По характеру появления погрешности делятся на
систематические погрешности и случайные погрешности.
11,12. По взаимодействию изменений во времени и входной
величины погрешности делятся на статические
погрешности и динамические погрешности.
14,15. По характеру зависимости погрешности от входной
величины погрешности делятся на аддитивные и
мультипликативные.
6
172.
Лекция1. Абсолютная погрешность – это значение,
вычисляемое как разность между значением величины,
полученным в процессе измерений, и настоящим
(действительным) значением данной величины.
2. Относительная погрешность – это число,
отражающее степень точности измерения.
3. Приведенная погрешность – это значение,
вычисляемое как отношение значения абсолютной
погрешности к номинальному значению.
6
173.
Лекция4. Основная погрешность – это погрешность,
полученная в нормальных условиях эксплуатации
средства измерений (при нормальных значениях
влияющих величин).
5. Дополнительная погрешность – это погрешность,
которая возникает в условиях несоответствия
значений влияющих величин их нормальным значениям,
или если влияющая величина переходит границы
области нормальных значений.
6
174.
Лекция6, 7. По признаку зависимости от причин возникновения,
характера и условий появления принято выражать
погрешность измерения ∆ суммой двух составляющих,
называемых случайной (ψ) и систематической (θ)
погрешностями измерений:
±∆ = ψ + θ
6
175.
ЛекцияРис. 7. Классификация погрешностей измерения
23
176.
ЛекцияСлучайная погрешность измерения –
составляющая погрешности измерения,
изменяющаяся случайным образом при
повторных измерениях одной и той же
величины.
Она не может быть исключена из результата
измерений. Однако проведением ряда повторных
измерений с использованием для их обработки
методов математической статистики определяют
значение измеряемой величины со случайной
погрешностью.
6
177.
ЛекцияОжидаемая случайная погрешность – это
погрешность, которая получается в результате
специально созданных условий измерения,
характеризующихся тем, что интенсивность
всех действующих факторов доводится до
некоторого уровня, обеспечивающего более или
менее равное влияние на формирование
погрешности.
Грубой случайной погрешностью называют
погрешность измерения, существенно
превышающую ожидаемую при данных условиях.
Причинами грубых погрешностей могут являться
неисправность СИ, резкое изменение условий
измерений и влияющих величин.
6
178.
ЛекцияПромах – погрешность измерения, которая явно
и резко искажает результат.
Промах является случайной субъективной ошибкой.
Их появления – следствие неправильных действий
экспериментатора, неисправности СИ или
непредвиденных изменений ситуации измерений.
Грубые погрешности и промахи обычно
исключаются из экспериментальных
данных, подлежащих обработке.
6
179.
ЛекцияСистематическая погрешность –
составляющая погрешности измерения,
остающаяся постоянной или закономерно
изменяющаяся при повторных измерениях
одной и той же величины.
Выявление и оценка систематической
погрешности является наиболее трудным
моментом любого измерения.
Обнаруженная и оцененная систематическая
погрешность исключается из результата
измерения введением поправки.
6
180.
ЛекцияРис. 7. Классификация погрешностей измерения
23
181.
ЛекцияПогрешность метода измерений – обусловлена
несовершенством метода измерений.
Инструментальная погрешность измерения –
зависит от погрешности применяемых СИ и
состоит из трёх составляющих (погрешность
конструкции, технологическая, старения).
Погрешность установки – является следствием
неправильности монтажа средств измерения.
Погрешность от влияющих величин – является
следствием воздействия на объект и СИ внешних
факторов (тепловых и воздушных потоков,
магнитных, электрических и других полей,
атмосферного давления, влажности воздуха и т.п.).
6
182.
ЛекцияПо характеру проявления погрешности делятся
на постоянные и переменные погрешности.
Постоянные погрешности – не изменяют
своего значения при повторных измерениях.
Напр.: неправильная установка начала
отсчёта и т.п.
Переменные погрешности – при повторных
измерениях могут принимать разные
значения.
Причина их появления – действие внешних
факторов и особенности СИ.
6
183.
ЛекцияОбе составляющие погрешности измерения (и случайная, и
систематическая) проявляются одновременно.
Причем значение случайной погрешности не известно
заранее, поскольку оно может возникать из-за целого ряда
неуточненных факторов.
Данный вид погрешности нельзя исключить полностью,
однако их влияние можно несколько уменьшить,
обрабатывая результаты измерений.
Систематическая погрешность, и в этом ее особенность,
если сравнивать ее со случайной погрешностью, которая
выявляется вне зависимости от своих источников,
рассматривается по составляющим в связи с источниками
возникновения.
6
184.
ЛекцияВышеперечисленные погрешности могут
иметь место, как при статических, так и
при динамических измерениях.
Погрешности, возникающие при этих
измерениях, принято называть
статическими и динамическими.
6
185.
Лекция11. Статическая погрешность – это погрешность,
которая возникает в процессе измерения
постоянной (не изменяющейся во времени)
величины.
12. Динамическая погрешность – это погрешность,
численное значение которой вычисляется как
разность между погрешностью, возникающей при
измерении непостоянной (переменной во времени)
величины, и статической погрешностью
(погрешностью значения измеряемой величины в
определенный момент времени).
6
186.
Лекция13. Погрешность отсчитывания – это погрешность,
возникающая из-за неточного определения долей
деления шкалы измерения.
14. Мультипликативная погрешность – это
погрешность, изменяющаяся вместе с изменением
значений величины, подвергающейся измерениям.
15 Аддитивная погрешность – это погрешность,
возникающая по причине суммирования численных
значений и не зависящая от значения измеряемой
величины, взятого по модулю (абсолютного).
6
187.
ЛекцияАбсолютной аддитивной погрешности не связано со
значением измеряемой величины и чувствительностью
средства измерений. Абсолютные аддитивные
погрешности неизменны на всем диапазоне измерений.
Значения мультипликативных погрешностей
изменяются пропорционально изменениям значений
измеряемой величины. Значения мультипликативных
погрешностей также пропорциональны
чувствительности средства измерений.
6
188.
ЛекцияНапример, на высоких частотах электрического поля
(выше 10 МГц) из-за паразитной параллельной емкости
или последовательной индуктивности возникает
большая погрешность.
В этом случае появляется необходимость дополнительной
градуировки прибора. Поэтому ВЧ измерителей (ИП) для
измерения ε и tgδ нужно прокалибровать одновременно по
емкости и проводимости на дискретных частотах (напр.:
10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 МГц.
В качестве эталонов можно использовать тефлоновые
конденсаторы емкостью от 20 пкФ до 250 пкФ.
Параллельно конденсатору подключались без
индуктивные сопротивления с проводимостью в
диапазоне 10-4 - 2∙10-2 См.
Емкость тефлоновых конденсаторов нужно заранее
определить при помощи цифрового моста переменного
6
тока на частотах 103 - 104 Гц.
189.
Лекция8. Основные сведения о
средствах измерений
(СИ)
6
190.
Лекция8.1. Классификация средств измерений и
их метрологические характеристики
Измерения производят с помощью средств
измерений.
Средство измерений (СИ) – техническое
средство, предназначенное для измерений,
имеющее нормированные метрологические
характеристики, воспроизводящее и (или)
хранящее единицу физической величины, размер
которой принимают неизменным (в пределах
установленной погрешности) в течение
известного интервала времени.
6
191.
ЛекцияВ метрологии средства измерений
принято классифицировать по:
1. Виду;
2. Метрологическому назначению.
1. Различают следующие виды СИ:
меры,
измерительные устройства,
измерительные установки,
измерительные системы (рис. 8).
6
192.
ЛекцияРис. 8. Классификация средств измерений
23
193.
ЛекцияМера физической величины
Мера физической величины – средство
измерений, предназначенное для
воспроизведения и (или) хранения физической
величины одного или нескольких заданных
размеров, значения которых выражены в
установленных единицах и известны с
необходимой точностью.
Пример: Мерой является резистор,
воспроизводящий сопротивление определенного
размера с известной погрешностью.
6
194.
ЛекцияРазличают следующие разновидности мер:
однозначная мера – мера, воспроизводящая физическую
величину одного размера (например, гиря 1 кг);
многозначная мера – мера, воспроизводящая физическую
величину разных размеров (например, штриховая мера
длины);
набор мер – комплект мер разного размера одной и той же
физической величины, предназначенных для применения
на практике, как в отдельности, так и в различных
сочетаниях (например, набор концевых мер длины);
магазин мер – набор мер, конструктивно объединенных в
единое устройство, в котором имеются приспособления
для их соединения в различных комбинациях (например,
магазин электрических сопротивлений).
6
195.
ЛекцияОпределение сопротивления проводника мостиком Уитсона.
магазин
электрических
сопротивлений
6
196.
ЛекцияТ.о., мера – СИ, предназначенное для воспроизведения
и хранения физической величины одного или
нескольких заданных размеров.
Самым многочисленным видом средств измерений
являются измерительные устройства (ИУ),
применяемые самостоятельно или в составе
измерительных установок и измерительных систем.
В зависимости от формы представления сигнала
измерительной информации ИУ подразделяют на:
измерительные приборы (ИП);
измерительные преобразователи (ИПр).
6
197.
ЛекцияРис. 8. Классификация средств измерений
23
198.
ЛекцияИзмерительный прибор – СИ, предназначенное для
получения значений измеряемой физической величины
в установленном диапазоне и с установленной
погрешностью.
Измерительный прибор (ИП) вырабатывает сигналы
измерительной информации в форме доступной для
непосредственного восприятия наблюдателем, например,
в виде отсчета на аналоговом или цифровом отсчетном
устройстве.
Аналоговый ИП – ИП, показания которого являются
непрерывной функцией измеряемой величины.
Цифровой ИП – ИП, автоматически вырабатывающий
дискретные сигналы измерительной информации,
показания которого представлены в цифровой форме.
6
199.
ЛекцияРис. 8. Классификация средств измерений
23
200.
ЛекцияПо способу индикации значений измеряемой величины
измерительные приборы разделяют на показывающие
и регистрирующие.
По действию измерительные приборы разделяют на
интегрирующие и суммирующие.
Интегрирующие приборы – приборы, показания
которых определяются интегралом по времени или
по другой независимой переменной от измеряемой
величины.
Суммирующие приборы – приборы, дающие показания
мгновенных значений измеряемой величины.
6
201.
ЛекцияИзмерительный прибор (ИП) различают
также:
приборы прямого действия и приборы
сравнения,
аналоговые и цифровые приборы,
самопишущие и печатающие приборы.
6
202.
ЛекцияРис. 8. Классификация средств измерений
23
203.
ЛекцияПриборами прямого действия называют приборы,
которые осуществляют одно или несколько
преобразований сигнала измерительной информации в
одном направлении.
Приборами сравнения называют приборы, в которых
наряду с цепью прямого преобразования имеется цепь
обратного преобразования сигнала измерительной
информации.
В таких приборах происходит сравнение измеряемой
величины с известной величиной, однородной с
измеряемой величиной.
6
204.
ЛекцияАналоговыми измерительными приборами называют
приборы, показания которых являются непрерывной
функцией измеряемой величины.
Пример – Прибор с отсчетным устройством
в виде стрелки и шкалы.
Цифровыми измерительными приборами называют
приборы, автоматически вырабатывающие
дискретный (кодированный) сигнал измерительной
информации и дающие показания в цифровой форме.
6
205.
ЛекцияИзмерительный преобразователь (ИПр)– СИ,
предназначенное для выработки сигнала
измерительной информации в форме, удобной для
дальнейшего преобразования, обработки и хранения,
но не поддающийся непосредственному восприятию
наблюдателю.
ИПр либо входит в состав какого-либо измерительного
прибора (измерительной установки, измерительной
системы и др.), или применяется вместе с каким-либо
средством измерений.
По характеру преобразования ИПр различают:
аналоговые,
цифро-аналоговые,
аналого-цифровые преобразователи.
6
206.
ЛекцияРис. 8. Классификация средств измерений
23
207.
ЛекцияПо месту в измерительной цепи различают первичные и
промежуточные преобразователи.
Выделяют также масштабные и передающие
преобразователи.
Примеры – Термопара в термоэлектрическом термометре,
измерительный трансформатор тока.
Первичный измерительный преобразователь – ИПр, на
который непосредственно воздействует измеряемая
физическая величина, т.е. первый преобразователь в
измерительной цепи измерительного прибора
(установки, системы).
В одном средстве измерений может быть несколько
первичных преобразователей.
6
208.
ЛекцияДатчик - конструктивно обособленный первичный
преобразователь, от которого поступают измерительные
сигналы (он «дает» информацию).
Датчик может быть вынесен на значительное расстояние
от средства измерений, принимающего его сигналы.
В области измерений ионизирующих излучений
применяют термин детектор.
Пример – Датчики запущенного метеорологического
радиозонда передают измерительную информацию о
температуре, давлении, влажности и других параметрах
атмосферы.
6
209.
ЛекцияМасштабный ИПр предназначен для изменения
измеряемой величины в заданное число раз (усилитель).
Функциональный ИПр предназначен для формирования
сигнала измерительной информации, связанного с
измеряемой величиной некоторой заданной функцией.
Измерительная информация представляется ИПр
обычно в виде сигналов постоянного или переменного
тока или напряжения, последовательности
прямоугольных импульсов, давления сжатого воздуха
или жидкости и т.п.
6
210.
ЛекцияРис. 8. Классификация средств измерений
23
211.
ЛекцияИзмерительная установка – совокупность
функционально объединенных мер, ИП, ИПр и других
устройств, предназначенная для измерений одной или
нескольких физических величин и расположенная в
одном месте (или предназначенных для выработки
сигналов измерительной информации в форме,
удобной для непосредственного восприятия
наблюдателем).
Измерительную установку, применяемую для поверки,
называют поверочной установкой.
Измерительную установку, входящую в состав эталона,
называют эталонной установкой.
Некоторые большие измерительные установки называют
измерительными машинами.
6
212.
ЛекцияПримеры:
1. Установка для измерений удельного сопротивления
электротехнических материалов.
2. Установка для испытаний магнитных материалов.
Измерительная машина – измерительная установка
крупных размеров, предназначенная для точных
измерений физических величин, характеризующих
изделие.
Примеры.
1. Силоизмерительная машина.
2. Машина для измерения больших длин в промышленном
производстве.
3. Делительная машина.
4. Координатно-измерительная машина.
6
213.
ЛекцияИзмерительная система – совокупность
функционально объединенных мер, ИП, ИПр, ЭВМ и
других технических средств, размещенных в разных
точках контролируемого объекта и соединенных
между собой каналами связи с целью измерений одной
или нескольких физических величин, свойственных
этому объекту, и выработки измерительных
сигналов в разных целях (или предназначенная для
выработки сигнала измерительной информации в
форме, удобной для автоматической обработки,
передачи и (или) использования в автоматических
системах управления, а также в форме удобной для
восприятия наблюдателем).
6
214.
ЛекцияРис. 8. Классификация средств измерений
23
215.
ЛекцияВ зависимости от назначения измерительные системы
(ИС) разделяют на:
измерительные информационные,
измерительные контролирующие,
измерительные управляющие системы и др.
ИС, перестраиваемую в зависимости от изменения
измерительной задачи, называют гибкой измерительной
системой (ГИС).
Примеры.
ИС теплоэлектростанции, позволяющая получать
измерительную информацию о ряде физических величин
в разных энергоблоках. Она может содержать сотни
измерительных каналов.
6
216.
ЛекцияРадионавигационная система для определения
местоположения различных объектов, состоящая из
ряда измерительно-вычислительных комплексов,
разнесенных в пространстве на значительное
расстояние друг от друга.
В последние годы получили распространение
измерительно-вычислительные комплексы (ИВК).
ИВК это функционально объединенная совокупность
средств измерений, ЭВМ и вспомогательных
устройств, предназначенная для выполнения в составе
измерительной системы конкретной измерительной
задачи.
ИВК является разновидностью измерительноинформационных систем.
6
217.
ЛекцияРис. 8. Классификация средств измерений
23
218.
Лекция2. Все средства измерений по выполняемым
метрологическим функциям делят на:
рабочие эталоны,
рабочие средства измерений.
6
219.
ЛекцияЭталон – это устройство, обеспечивающее
воспроизведение и хранение единиц с целью
передачи информации о ее размере СИ,
выполненное по особой спецификации и
официально утвержденное в установленном
порядке в качестве эталона.
6
220.
ЛекцияРабочий эталон – эталон, предназначенный для
передачи размера единицы рабочим средствам
измерений.
Термин рабочий эталон заменил собой термин
образцовое средство измерений, что сделано в
целях упорядочения терминологии и приближения ее
к международной.
При необходимости рабочие эталоны подразделяют
на разряды (1-й, 2-й, ..., n-й).
В этом случае передачу размера единицы
осуществляют через цепочку соподчиненных по
разрядам рабочих эталонов.
При этом от последнего рабочего эталона в этой
цепочке размер единицы передают рабочему
6
средству измерений.
221.
ЛекцияРис. 9. Обобщенная
поверочная схема
23
222.
ЛекцияВсе вопросы, связанные с хранением, применением
и созданием эталонов, а также контроль за их
состоянием, решаются по единым правилам,
установленным ГОСТом «ГСИ. Эталоны единиц
физических величин.
Основные положения» и ГОСТом «ГСИ. Эталоны
единиц физических величин. Порядок разработки и
утверждения, регистрации, хранения и применения».
Классифицируются эталоны по принципу
подчиненности.
По этому параметри эталоны бывают:
1) первичные;
2) вторичные.
14
223.
Лекция1. Первичный эталон должен служить целям
обеспечения воспроизведения, хранения единицы
и передачи размеров с максимальной точностью,
которую можно получить в данной сфере
измерений.
Их утверждают ГОСТом в виде государственных
эталонов и придает данным эталонам силы закона.
На Гос. комитет по стандартам возложена
обязанность создавать, утверждать, хранить и
применять государственные эталоны.
14
224.
Лекция2. Вторичный эталон воспроизводит единицу
при особенных условиях, заменяя при этих
условиях первичный эталон.
Он создается и утверждается для целей обеспечения
минимального износа государственного эталона.
Вторичные эталоны создают, утверждают,
хранят и применяют министерства и ведомства.
14
225.
ЛекцияГосударственный эталон
Первичный (или специальный) эталон
Эталон копия
Эталон сравнения
РЭ
Эталон свидетель
Вторичные эталоны
РЭ 1-го разряда
Рабочие эталоны (РЭ)
РЭ 2-го разряда
РЭ 4-го разряда
РСИ
РСИ
РСИ
РСИ
РСИ
Рис. 9.1. Классификация эталонов по подчиненности
РЭ – рабочий эталон; РСИ – рабочее средство измерений.
15
226.
ЛекцияВторичные эталоны могут делиться по признаку назначения.
Так, выделяют:
1) эталоны – копии, предназначенные для передачи
размеров единиц рабочим эталонам;
2) эталоны – сравнения, предназначенных для проверки
невредимости государственного эталона, а также для
целей его заменяя при условии его порчи или утраты;
3) эталоны – свидетели, предназначенные для сличения
эталонов, которые по ряду различных причин не
подлежат непосредственному сличению друг с другом;
4) рабочие эталоны, которые воспроизводят единицу от
вторичных эталонов и служат для передачи размера
эталону более низкого разряда.
14
227.
ЛекцияЭталонная база Российской Федерации имеет в своем
составе 114 государственных эталонов и более 250
вторичных эталонов единиц различных ФВ, в том числе
первичные государственные эталоны метра,
килограмма и секунды.
Точность последних эталонов особенно важна, так как
эти единицы участвуют в образовании производных
единиц всех научных направлений.
В отличие от первичных эталонов, рабочие эталоны не
обязательно уникальные, специально изготовляемые СИ.
16
228.
ЛекцияГосударственный эталон
Первичный (или специальный) эталон
Эталон копия
Эталон сравнения
РЭ
Эталон свидетель
Вторичные эталоны
РЭ 1-го разряда
Рабочие эталоны (РЭ)
РЭ 2-го разряда
РЭ 4-го разряда
РСИ
РСИ
РСИ
РСИ
РСИ
Рис. 9.1. Классификация эталонов по подчиненности
РЭ – рабочий эталон; РСИ – рабочее средство измерений.
15
229.
ЛекцияВ качестве рабочих эталонов допускается
использование следующих СИ:
выпускаемых по стандарту или техническим
условиям на СИ конкретного типа
(стандартизованные рабочие эталоны –
поверочные установки);
импортируемых из-за границы партиями или
единичными экземплярами;
не стандартизованных, т. е. изготовленных
единичными экземплярами;
индивидуально собранных из СИ, которые
выпускаются по стандарту или техническим
условиям в качестве рабочих СИ широкого
назначения.
16
230.
ЛекцияРабочее средство измерения – СИ
предназначенное для измерений, не связанных с
передачей размера единиц другим средствам
измерений
Рабочий эталон – средство, предназначенное для
поверки (калибровки) по ним рабочих СИ и
утвержденное в качестве рабочего эталона.
6
231.
ЛекцияГосударственный эталон
Первичный (или специальный) эталон
Эталон копия
Эталон сравнения
РЭ
Эталон свидетель
Вторичные эталоны
РЭ 1-го разряда
Рабочие эталоны (РЭ)
РЭ 2-го разряда
РЭ 4-го разряда
РСИ
РСИ
РСИ
РСИ
РСИ
Рис. 9.1. Классификация эталонов по подчиненности
РЭ – рабочий эталон; РСИ – рабочее средство измерений.
15
232.
ЛекцияЗакон РФ об обеспечении единства
измерений трактует понятие поверки и
калибровки СИ следующим образом.
6
233.
ЛекцияПоверка СИ – совокупность операций,
выполняемых органами государственной
метрологической службы с целью определения и
подтверждения соответствия метрологических
характеристик СИ установленным техническим
требованиям.
6
234.
ЛекцияКалибровка СИ – совокупность операций,
выполняемых с целью определения и
подтверждения действительных значений
метрологических характеристик и пригодности к
применению СИ, не подлежащих государственному
метрологическому контролю и надзору.
6
235.
ЛекцияМетрологические характеристики
средств измерения
При использовании средств измерений важно
знать степень соответствия информации о
измеряемой величине, содержащейся в выходном
сигнале, ее истинному значению.
С этой целью для каждого средства измерений
вводятся и нормируются определенные
метрологические характеристики (МХ).
6
236.
ЛекцияМетрологические характеристики – это
характеристики свойств средства измерений,
влияющие на результат измерений и на его
погрешности.
Для каждого типа средств измерений устанавливают
свои метрологические характеристики.
Метрологические характеристики, устанавливаемые
нормативно-техническими документами, называют
нормируемыми метрологическими характеристиками,
а определяемые экспериментально –
действительными метрологическими
характеристиками.
6
237.
ЛекцияНоменклатура метрологических характеристик,
правила выбора комплексов нормируемых
метрологических характеристик для средств
измерений и способы их нормирования
определяются стандартом ГОСТ 8.009-84 ГСИ.
«Нормируемые метрологические характеристики
средств измерений».
6
238.
ЛекцияМетрологические характеристики средств
измерений включают:
функцию преобразования (градуировочная
или статическая характеристика),
чувствительность,
порог чувствительности,
диапазон измерений,
область рабочих частот,
статические и динамические погрешности,
собственную мощность потребления.
6
239.
ЛекцияФункция преобразования средства измерений
Функция преобразования средства измерений –
Y = F(X) – это функциональная зависимость между
информативными параметрами выходного Y и
входного X сигналов.
Идеальная функция преобразования – линейная
зависимость.
Эта зависимость может быть представлена в виде
формулы, таблицы или графика.
6
240.
ЛекцияЧувствительность
Чувствительность – важная характеристика
средства измерений. Она характеризует способность
прибора реагировать на изменение входного
сигнала.
Чувствительность – свойство средства
измерений, определяемое отношением изменения
выходного сигнала этого средства к вызывающему
его изменению измеряемой величины.
Чувствительность определяется из функции
преобразования.
Различают абсолютную и относительную
чувствительность.
6
241.
ЛекцияАбсолютную чувствительность определяют по
формуле
S = ∆y/∆x,
относительную чувствительность определяют по
формуле
S0 = ∆y/(∆x/x),
∆y – изменение сигнала на выходе,
х – измеряемая величина,
∆x – изменение измеряемой величины.
В общем случае
y dy
S lim
x 0 x
dx
6
242.
ЛекцияПри линейной функции преобразования
S
Y
const
X
При нелинейной функции преобразования
чувствительность зависит от измеряемой величины x.
У средств измерения при постоянной чувствительности
шкала равномерная, т.е. длина всех делений шкалы
одинакова.
Величина равная обратной величине чувствительности
является постоянной прибора
с = 1/S.
6
243.
ЛекцияПорог чувствительности средства измерений
Порог чувствительности средства измерений –
характеристика средства измерений в виде
наименьшего значения изменения физической
величины, начиная с которого может
осуществляться ее измерение данным средством.
Если самое незначительное изменение массы,
которое вызывает перемещение стрелки весов,
составляет 10 мг, то порог чувствительности весов
равен 10 мг.
Порог чувствительности не следует путать с
чувствительностью средства измерения.
Он выражается в единицах входной величины.
6
244.
ЛекцияДиапазон измерений средства измерений
Диапазон измерений средства измерений – область
значений величины, в пределах которой
нормированы допускаемые пределы погрешности
средства измерений.
Значения величины, ограничивающие диапазон
измерений снизу и сверху (слева и справа),
называют соответственно нижним пределом
измерений Хн или верхним пределом измерений Хк.
Различают полный и
рабочий диапазон
измерений (рис. 10).
Рис.10
6
245.
ЛекцияПолный диапазон – диапазон, в котором относительная
погрешность средства измерений не превышает 100 %.
Он ограничен снизу порогом чувствительности ∆0, а
сверху – верхним пределом измерений Хк
Рабочий диапазон – диапазон, в
котором относительная
погрешность не превышает
заранее заданного значения δзад.
Рис.10
Диапазон измерений может состоять из нескольких
поддиапазонов с разными погрешностями.
Диапазон измерений следует отличать от
диапазона показаний.
6
246.
ЛекцияДиапазон показаний средства измерений – область
значений шкалы прибора, ограниченная начальным и
конечным значениями шкалы.
Показание средства измерений – значение величины
или число на показывающем устройстве средства
измерений.
Вариация показаний измерительного прибора –
разность показаний прибора в одной и той же точке
диапазона измерений при плавном подходе к этой
точке со стороны меньших и больших значений
измеряемой величины.
Вариация показаний измерительного прибора
приближенно равна удвоенной погрешности от
трения в опорах.
6
247.
ЛекцияОбласть рабочих частот
Область рабочих частот – полоса частот, в
пределах которой погрешность прибора, вызванная
изменением частоты, не превышает допустимого
предела.
Характеристики, влияющие на собственную
мощность потребления
Характеристики, влияющие на собственную мощность
потребления – это характеристики средств
измерений, отражающие их способность влиять на
инструментальную составляющую погрешности
вследствие взаимодействия средства измерений с
любым из подключенных к его входу или выходу
компонентов, например объектом измерений и др.
6
248.
ЛекцияПотребление энергии средством измерений от объекта
измерения или от предвключенного прибора приводит к
изменению значения измеряемой величины, и,
следовательно, к появлению погрешности.
Для оценки влияния средства измерения на режим работы
объекта измерений указывают входное полное
сопротивление или входной импеданс Zвх.
Входное сопротивление влияет на мощность,
потребляемую от объекта измерения средством измерения.
Для оценки допустимой нагрузки на средство измерения
указывают выходное полное сопротивление или выходной
импеданс Zвых.
Чем меньше Zвых, тем больше допускаемая нагрузка на
средство измерения.
6
249.
Лекция8.2. Статические характеристики и другие
параметры измерительных устройств
Поверка и калибровка всех измерительных
устройств связаны с определением их реальных
статических характеристик, под которыми
понимается зависимость выходной величины
от входной.
В общем случае режим работы ИУ, при котором
значение входного Х и выходного Y сигналов не
изменяются, называют статическим.
6
250.
ЛекцияСтатической характеристикой ИУ
называют функциональную зависимость
выходного сигнала Y от входного Х в
статическом режиме работы ИУ.
Статическая характеристика описывается
в общем случае некоторым уравнением
преобразования:
Y = f (X).
На рис. 10.1 приведены различные
статические характеристики ИУ.
6
251.
ЛекцияРис. 10.1 Статические
характеристики ИУ
Основное требование,
предъявляемо к статической
характеристике ИУ, сводится к
получению линейной зависимости
между выходной и входной
величинами.
При нелинейной (1) статической
характеристике
чувствительность будет
различной в разных точках, а
шкала неравномерной.
Приборы с линейной (2) или
пропорциональной (3)
статической характеристикой
имеют неизменную в точке
чувствительность и
равномерную шкалу.
6
252.
ЛекцияУ измерительных преобразователей (ИПр)
статическая характеристика, как правило,
является линейной:
Y = к∙Х,
к – коэффициент преобразования (в АСУ –
коэффициент передачи), определяемый как
отношение сигнала на выходе измерительного
преобразователя, к вызывающему его сигналу
на входе измерительного преобразователя.
6
253.
ЛекцияКроме статической характеристики для
определения метрологических свойств ИУ
используется ряд параметров и понятий.
Диапазон показаний – область значений
шкалы, ограниченная конечным Хк и
начальным значением шкалы Хн (рис.11).
Диапазон измерений (рабочая часть шкалы) –
область значений измеряемой величины, для
которой нормированы допускаемые
погрешности ИП (иногда указанные диапазоны
могут совпадать).
6
254.
ЛекцияХк
Хн
Рис. 11. Схема отсчетного устройства ИП
6
255.
ЛекцияДля количественной оценки влияния на выходной
сигнал ИУ входного сигнала в произвольной точке
статической характеристики служит предел
отношения приращения ∆Y выходного сигнала к
приращению ∆Х входного сигнала, когда ∆Х→0, т.е.
производная в выбранной точке:
Этот параметр называют чувствительностью ИП.
Графически чувствительность определяется
тангенсом угла наклона α касательной, проведенной
к выбранной точке А статической характеристики
(рис. 10.1).
6
256.
ЛекцияРис. 10.1 Статические характеристики ИУ
6
257.
ЛекцияЦена деления однозначно связана с числом делений
«n» шкалы ИП. Число делений связано с допускаемой
погрешностью ИП, обычно представляемой его
классом точности К.
Число делений ИП, как правило, в первом
приближении определяется из соотношения:
Под порогом чувствительности (К) понимают то
наименьшее значение входного сигнала, которое
вызывает уверенно фиксируемое изменение
выходного сигнала.
6
258.
Лекция8.3. Погрешности измерительных
устройств
Инструментальная погрешность
(погрешность измерительного устройства)
имеет определяющее значение для наиболее
распространенных технических измерений.
На рис. 12 приведена классификация
погрешностей ИУ по ряду признаков.
6
259.
ЛекцияРис. 12. классификация погрешностей измерительных
устройств
6
260.
ЛекцияОсновной погрешностью ИУ называют погрешность,
которая получается при использовании его в
нормальных условиях.
Как правило, за нормальные условия принимают
температуру окружающей среды равную t = (20±2) °C;
атмосферное давление равное Р = 760 мм. рт. ст.;
заданное напряжение питания;
нормальное рабочее положение и т.д.
Нормальные условия применения указываются в
стандартах или технических условиях на ИУ.
Дополнительной погрешностью ИУ называют
изменение его погрешности, вызванной отклонением
одной из влияющих физических величин от ее
нормативного значения или выходом ее за пределы
нормальной области значений.
6
261.
ЛекцияВ зависимости от формы представления
погрешности ИУ подразделяются на:
абсолютные,
относительные,
приведенные.
6
262.
ЛекцияАбсолютной погрешностью измерительного
прибора ∆ называют разность показаний
прибора ХП и действительного значения ХД
измеряемой величины:
±∆ = ХП – ХД,
ХП = ХН; Х1, Х2, … Хm … ХК – показания прибора.
Действительное значение ХД определяется с
помощью рабочих эталонов или по номинальным
статическим характеристикам ИУ.
6
263.
ЛекцияОтносительной погрешностью ИП называют
отношение абсолютной погрешности ИП к
действительному значению измеряемой величины.
Она выражается в %:
Так как абсолютная погрешность ±∆<< ХД, ХД ≈ ХП,
то относительную погрешность можно рассчитать
и по формуле:
6
264.
ЛекцияПриведенной погрешностью ИП называют
отношение абсолютной погрешности ИП к
нормирующему значению ХN.
Приведенную погрешность также выражают в
процентах:
Нормирующее значение ХN – условно принятое
значение, которое чаще всего равно диапазону
показаний ИП ХN = ХК – ХН.
6
265.
ЛекцияСуть погрешности в зависимости
от формы представления для
измерительных преобразователей
(ИПр) та же, что и для ИП.
6
266.
ЛекцияДля рассмотрения зависимости погрешности ИУ от
значения измеряемой величины используются понятия
номинальной и реальной функции преобразования ИУ.
Номинальной (идеальной) функцией преобразования
называют функцию преобразования, которая
приписана ИУ данного типа, указана в его паспорте и
используется при выполнении измерений и проверке
(калибровке).
Реальной функцией преобразования называют ту
функцию преобразования, которой обладает
конкретный экземпляр ИУ данного типа.
Из-за несовершенства технологии они, как правило,
отличаются друг от друга.
6
267.
ЛекцияПо принципу отклонения реальной
характеристики от номинальной
погрешности принято разделять на:
аддитивную,
мультипликативную,
гистерезисную.
6
268.
ЛекцияРис. 12. классификация погрешностей измерительных
устройств
6
269.
ЛекцияАддитивной или погрешностью нуля ИУ,
называют погрешность, которая остается
постоянной при всех значениях измеряемой
величины *.
В этом случае (рис. 12, а) реальная функция
преобразования Y = fР(Х) несколько смещена
относительно номинальной Y = fН(Х), т.е., выходной
сигал ИУ для всех значений измеряемой величины Х
будет больше (или меньше) на одну и ту же
величину, чем он должен быть, в соответствии с
номинальной функцией преобразования.
* устраняется с помощью корректора нуля прибора.
6
270.
ЛекцияРис. 12. Реальные и номинальные функции
преобразования ИУ
6
271.
ЛекцияСистематическая аддитивная погрешность
устраняется с помощью специального корректора
нуля.
Случайную аддитивную погрешность исключить из
результата измерения нельзя, но можно определить
некоторую полосу, ширина которой остается
постоянной при всех значения измеряемой величины
(рис. 12, а).
Возникновение случайной аддитивной погрешности
вызывается трением в опорах, контактными
сопротивлениями, дрейфом нуля, шумом и фоном
измерительного устройства и др.
6
272.
ЛекцияМультипликативной или погрешностью
чувствительности ИУ называют погрешность,
которая линейно возрастает (или убывает) с
увеличением измеряемой величины.
Графически появление мультипликативной
погрешности интерпретируется (рис. 12 б),
поворотом реальной функции преобразования
Y = fр(Х) относительно номинальной Y = fН(Х).
6
273.
ЛекцияРис. 12. Реальные и номинальные функции
преобразования ИУ
6
274.
ЛекцияПричиной возникновения случайной
мультипликативной погрешности является
изменение коэффициента преобразования
отдельных элементов и узлов ИУ.
Если мультипликативная погрешность
является случайной, то реальная функция
преобразования Y = fр(Х) представляет полосой,
ширина которой с увеличением измеряемой
величины увеличивается (рис. 12 б).
6
275.
ЛекцияНаиболее существенной и трудно устранимой
систематической погрешностью ИУ является
погрешность гистерезиса или погрешность
обратного хода, выражающаяся в несовпадении
(рис. 12, в) реальной функции преобразования ИУ
при увеличении (прямой ход) или уменьшении
(обратный ход) измеряемой величины.
Причинами гистерезиса могут быть люфт и сухое
трение в механических передающих элементах,
внутреннее трение в металлах пружин, явление
упругого последействия в упругих чувствительных
элементах, явление поляризации в электрических
элементах и т.п.
6
276.
ЛекцияРис. 12. Реальные и номинальные функции
преобразования ИУ
6
277.
Лекция8.4. Нормирование метрологических
характеристик ИУ
Статические и динамические характеристики, а также
погрешности ИУ принято называть метрологическими
характеристиками, так как они влияют на точность
измерений проводимых с помощью этих ИУ.
ИУ допускает применению в том случае, когда
нормированы их метрологических характеристики.
Сведения о метрологических характеристиках
приводятся в технической документации на ИУ.
Посредством нормирования метрологических
характеристик ИУ обеспечивается взаимозаменяемость
ИУ и единство измерений в государственном
масштабе.
6
278.
ЛекцияНормируются следующие метрологические
характеристики ИУ.
1. Характеристики, предназначенные для
определения результата измерений:
функция преобразования,
коэффициент преобразования,
цена деления,
чувствительность,
диапазон измерений,
верхний и нижний пределы измерений,
диапазон показаний,
конечные и начальные значения шкалы.
6
279.
Лекция2. Характеристики погрешности:
систематическая погрешность,
случайная погрешность,
динамическая погрешность,
мультипликативная погрешность,
аддитивная погрешность,
абсолютная, относительная и
приведенная погрешность,
основная погрешность и вариация.
Разность показаний ИП в одной и той же точке при прямом
и обратном ходе указателя называется вариацией.
6
280.
Лекция3. Характеристики чувствительности к
влияющим величинам:
изменение показаний,
изменение коэффициента преобразования,
функция влияния,
дополнительная погрешность, иногда
размах.
6
281.
ЛекцияРеальные значения метрологических
характеристик ИУ определяются при их
выпуске, а затем периодически проверяются
в процессе эксплуатации, т.е. ИУ проходят
через определенный промежуток времени
поверку или калибровку.
При отклонении хотя бы одной
метрологической характеристики от
нормы ИУ ремонтируют или бракуют.
6
282.
ЛекцияОсновная погрешность измерительного
устройства нормируется путем установления
предела допускаемой основной соответственно
абсолютной, относительной или приведенной
погрешности:
Значение предела допускаемой основной абсолютной,
относительной или приведенной погрешностей
определяется из ряда предпочтительных чисел:
(1; 1,5; 2; 2,5; 4; 5; 6)∙10п,
где n = +1, 0, –1, –2 и т. д.
6
283.
ЛекцияОбобщенной метрологической характеристикой
ИУ является класс точности
Класс точности ИУ – это обобщенная
характеристика, определяемая пределами
допускаемых основных и дополнительных
погрешностей, а также другими свойствами
ИУ, отражающими уровень их точности, при
нормальных условиях эксплуатации, значения
которых устанавливается в стандартах на
отдельные виды ИУ.
6
284.
ЛекцияКласс точности ИУ характеризует
предел допускаемой основной
абсолютной, приведенной или
относительной погрешности, но не
характеризует точность измерения.
6
285.
Лекция8.5. Структурные схемы
измерительных устройств
Составление структурных схем необходимо для
анализа работы измерительных устройств, для
выяснения принципа действия и для синтеза
построения измерительных устройств из отдельных
измерительных преобразователей.
Существует множество разновидностей измерительных
устройств (ИУ).
Все они состоят из простейших измерительных
преобразователей (ИПр), число которых ограничено
несколькими десятками.
Комбинируя их в разнообразном сочетании, можно
создавать различную измерительную аппаратуру (ИА).
6
286.
ЛекцияВсе устройства в зависимости от
соединения ИПр можно разделить на:
устройство прямого преобразования;
устройство уравновешивающего
преобразования.
6
287.
ЛекцияУстройство прямого преобразования характеризуется
тем, что преобразования выполняются последовательно
одно за другим в одном (прямом), направлении от
входной величины Х через посредство измерительных
преобразователей (П), включенных последовательно, к
выходной величине Y.
Рис. 13 Измерительное устройство прямого
преобразования
6
288.
ЛекцияУстройство уравновешивающего (компенсирующего)
преобразования характеризуется тем, что
используется две цепи преобразования (прямая и
обратная) роли которых различны.
Рис. 14. Измерительное устройство
уравновешивающего преобразования
6
289.
ЛекцияОбратная цепь преобразует выходную величину Y
в величину Хос, однородную по своей физической
природе с выходной величиной Х, полностью или
частично ее уравновешивающую.
В результате чего на вход П1 поступает величина
∆Х = Х - Хос, которая в свою очередь прямой цепью
преобразуется в выходную величину Y.
6
290.
Лекция9. Схемы измерительных систем и их
метрологические характеристики
Для производства измерений на реальных
объектах ИУ располагаются в различных
точках пространства и соединяются между
собой соответствующими линиями связи.
При измерении на расстоянии используются
дистанционные измерительные системы, в
которых расстояния между отдельными
измерительными устройствами достигают
нескольких десятков и даже сотен метров.
6
291.
ЛекцияВ общем случае структурную схему измерительной
системы, можно представить в виде последовательной
цепи (или последовательное соединение ) нескольких
ИУ (преобразователей) рис.15.
Рис. 15. Структурные схемы измерительных систем
6
292.
ЛекцияВ зависимости от типа измеряемой физической
величины, принципа действия первичный
измерительный преобразователь (ПИПр) и
расстояния, на которое необходимо передать
информацию, в состав измерительной системы могут
быть включены:
ПИПр – первичный измерительный
преобразователь (1);
ППр – промежуточный преобразователь (2);
ФПр – функциональный преобразователь (3).
6
293.
ЛекцияИнформация поступает по соответствующим каналам
связи на измерительный прибор (ИП) 4, который
выдает информацию в форме удобной для
восприятия человеком.
Многие электронные измерительные приборы в своем
составе содержат передающий преобразователь,
предназначенный для передачи информации об
измеренном параметре на другой измерительный
прибор, ВМ или в схему АСУ и т. п.
6
294.
ЛекцияРис. 15. Структурные схемы измерительных систем
6
295.
ЛекцияИзмерительные преобразователи (ИПр) и некоторые
каналы связи входящие в ИС, имеют нормированные
метрологические характеристики.
Обычно эта информация предоставляется в виде
предела допускаемой основной приведенной
(абсолютной, относительной) погрешности.
Поэтому для приближенной оценки приведенной
погрешности ИС из n включенных последовательно
преобразователей с линейными функциями
преобразования можно использовать уравнение:
γi – предел основной допускаемой приведенной
погрешности i-го преобразователя ИС.
6
296.
ЛекцияДля получения более реальной погрешности ИС
рекомендуется суммирование допускаемых
приведенных погрешностей ИУ входящих в ИС
производить вероятностным методом, т.е. по
уравнению:
γ1, γ2, ...., γn – предел допускаемой основной
приведенной погрешности i-го преобразователя или
канала связи.
6
297.
Лекция10. Оценка точности результата наблюдения
Для оценки точности результата наблюдения служит
среднее квадратическое отклонение результата
наблюдения σn. Квадрат этой величины, т.е. σn 2
называется рассеянием или дисперсией результата
наблюдения и обозначается обычно символом D.
Число наблюдений можно найти только приближенное
значение σхi или оценку этого отклонения по формуле:
n – число наблюдений;
xi – значение величины, полученное при i-м наблюдении;
– результат измерения (среднее арифметическое значение).
6
298.
ЛекцияДля получения полного представления о точности
и надежности оценки случайного отклонения
результата наблюдения должны быть указаны:
1. доверительные границы,
2. доверительный интервал,
3. доверительная вероятность.
6
299.
Лекция1. При известном σхi доверительные границы
указывают следующим образом:
нижняя граница –σхi или
, верхняя граница
+σхi или
(сокращено ±σхi ;
), за
пределы которых с вероятностью Р = 0,683 (или
68.3%) не выйдут значения случайных отклонений
или результатов отдельных наблюдений xi
ряда измерений.
2. Доверительный интервал выражается в виде:
3. В инженерной практике предпочтение отдается
доверительной вероятности Рд = 0,95 или 0,9973.
6
300.
Лекция11. Оценка точности результата
измерения
Для оценки достоверности результата измерения,
принимаемого равным среднему арифметическому
значению , применяют показатель точности,
аналогичный показателю точности результата
наблюдения.
При этом согласно теории погрешностей оценка среднего
квадратического отклонения результата измерения
в
раз меньше оценки среднего квадратического
отклонения результата наблюдения σхi (см. параг. 10).
6
301.
ЛекцияТ.о., при числе измерений n оценка среднего
квадратического отклонения результата
измерения (среднего арифметического) будет равна:
– среднее квадратическое отклонение результата
измерения (среднего арифметического).
6
302.
ЛекцияПри известном
доверительные границы
указывают следующим образом:
нижняя граница – - или
,
верхняя граница +
или
(сокращено
), за пределы которых с вероятностью
0,683 не выйдут погрешности результата измерения
или среднее арифметическое значение .
Доверительный интервал результата измерения
выражается в виде:
или
6
303.
Лекция12. Оценка точности результата измерения
при малом числе наблюдений
На практике в большинстве случаев число
измерений не превышает 15 – 20 отдельных
наблюдений.
Для оценки точности результата измерения
при малом числе наблюдений (n ≤ 20) и условии,
что распределение погрешностей отдельных
измерений следуют, нормальному закону
пользуются tр - таблицей основанной на
распределении Стьюдента.
6
304.
ЛекцияРаспределение Стьюдента учитывает то,
что при малом числе наблюдений и при
одинаковой доверительной вероятности
получается уменьшенное значение
средней квадратической погрешности по
сравнению с погрешностью при n
наблюдениях.
6
305.
ЛекцияПри практическом применении распределения
Стьюдента погрешность среднего
арифметического значения при n ≤ 20 и
заданной доверительной вероятности Рд
определяется из значений σхi или
по
выражению:
6
306.
ЛекцияТаблица 1
Значения tр и
в зависимости от
доверительной вероятности Рд и k = n - 1
6
307.
Лекция, принимаемого как окончательный результат
измерения, указываются доверительные
границы и доверительный интервал при
выбранной доверительной вероятности.
Доверительные границы
, нижняя
,
верхняя
.
Доверительный интервал
определяется по формуле
и выражается в единицах определяемой величины.
6
308.
ЛекцияПример: Произведено 12 измерений ТЭДС
термоэлектрическим преобразованием градуировки
(с НСХ – номинальная статическая характеристика)
ПП (платинородий – платина).
Условия измерения: температура рабочего спая
равна 419,58 0С, а свободных концов 0 0С.
Результаты измерений не содержат систематической
погрешности.
Базовые значения результатов измерений,
случайные погрешности результатов наблюдений
и их квадраты приведены в табл. 2.
Определить действительное значение ТЭДС и
температуры, доверительные границы и интервал
при доверительной вероятности 0,95.
6
309.
ЛекцияТаблица 1.3
Данные измерения ТЭДС при t = 419,58 0С и to = 0 0С, случайные
погрешности результатов наблюдений и их квадраты
6
310.
ЛекцияОпределим средне арифметическое значение
Средние квадратические отклонения результатов
наблюдения и измерения:
Истинное значение ТЭДС Х можно приближенно
положить равным среднеарифметическому значению
ТЭДС
6
311.
ЛекцияДля оценки достоверности этого равенства задана
доверительная вероятность Р = 0,95.
Найдем доверительные границы, соответствующие
этой вероятности.
По табл. 2 для Р = 0,95 и k = n – 1 = 11 находим tр = 2,2.
Согласно выражению
получим:
6
312.
ЛекцияВ соответствии с вероятностью 0,95 мы можем
утверждать, что истинное значение ТЭДС
заключено между доверительными границами:
или
т.е. результат измерения с вероятностью 95%
попадёт в эти границы.
6
313.
Лекция13. Правовые основы метрологии
Главным законодательным актом,
обеспечивающим единство измерений, является
Закон РФ «Об обеспечении единства измерений».
Этот Закон направлен на защиту прав граждан и их
интересов, а также на защиту интересов экономики
страны от отрицательных последствий
недостоверных результатов измерений.
Единство измерений – характеристика качества
измерений.
Она заключается в том, что результаты измерений
выражаются в установленных единицах, чьи
размеры равны размерам воспроизводимых величин
(с учетом погрешностей).
6
314.
ЛекцияЗакон определяет:
1. Основные метрологические понятия;
2. Компетенцию Госстандарта России в обеспечении
единства измерений;
3. Единицы ФВ, государственные эталоны, средства
и методики измерений;
4. Компетенцию и структуру государственной
метрологической службы;
5. Метрологические службы государственных
органов управления предприятий и организаций;
6
315.
Лекция6. Сферы распространения и виды государственного
метрологического контроля и надзора;
7. Права, обязанности и ответственность
государственных инспекторов по обеспечению
единства измерений;
8. Закон определяет условия испытаний средств
измерения;
9. Требования к выполнению измерений по
аттестованным методикам;
6
316.
Лекция10. Основные положения калибровки и сертификации
средств измерения;
11. Лицензирование деятельности организаций и
физических лиц по изготовлению, ремонту,
продаже и прокату средств измерений;
12. Источники финансирования работ по
обеспечению единства измерений;
13. Ответственность за нарушение положений этого
закона.
6
317.
ЛекцияКроме того, законом об «Обеспечении единства
измерений» определяются сферы деятельности,
в которых соблюдение метрологических
требований, обязательно и на которые
распространяется государственный
метрологический надзор:
6
318.
Лекцияздравоохранение, ветеринария, охрана окружающей
среды и обеспечение безопасности труда,
испытания и контроль качества продукции с целью
определения соответствия обязательным
требованием государственного стандарта РФ,
обеспечение обороны страны – на обязательную
сертификацию продукции и услуг,
на торговые операции и взаимные расчеты между
покупателем и продавцом, в том числе на операции
с применением игровых автоматов –
государственные учетные операции,
6
319.
Лекцияизмерения, проводимые по поручениям органов
суда, прокуратуры и государственных органов
управления РФ,
на продукцию, поставляемую по контрактам для
государственных нужд,
на геодезические и гидрометрические измерения –
на банковские, налоговые, таможенные и почтовые
операции,
на регистрацию национальных и международных
рекордов.
6
320.
ЛекцияГосударственная система обеспечения единства
измерений состоит из нормативных документов,
устанавливающих правила и требования на
достижение и поддержание единства измерений
в РФ при требуемой точности.
6
321.
Лекция14. Метрологические службы,
обеспечивающие единство измерений
Государственная метрологическая служба несет
ответственность за метрологическое обеспечение в
стране на межотраслевом уровне и осуществляет
государственный контроль и надзор в
определенных законом сферах.
6
322.
ЛекцияВ состав государственной метрологической службы
входят:
1. Государственные научные метрологические
центры – органы государственной метрологической
службы на территориях республик, областей,
автономных округов, автономных областей, а
также государственные метрологические службы
городов Москвы и Санкт-Петербурга.
6
323.
ЛекцияГосударственные научные метрологические
центры являются хранителями государственных
эталонов.
Они проводят исследования в области теории
измерений, а также в области применения
принципов и методов высокоточных измерений;
занимаются разработкой научно-методических
основ совершенствования Российской системы
измерений;
разрабатывают нормативные документы по
обеспечению единства измерений.
6
324.
Лекция2. Государственная служба времени, частоты и
определения параметров вращения Земли.
Государственная служба времени, частоты
занимается межрегиональной и межотраслевой
координацией работ по обеспечению единства
измерений времени и частот, а также по
определению параметров частот вращения Земли.
Также она занимается хранением и передачей
размеров единиц времени, шкал атомного
всемирного и координатного времени, координат
полюсов Земли.
Измерительную информацию этой службы используют
службы навигации и управления судами, самолетами
и спутниками, а также единая измерительная служба
России.
6
325.
Лекция3. Государственная служба стандартных образцов
состава и свойств веществ и материалов
Государственная служба стандартных образцов
состава и свойств веществ и материала организует
создание и применение эталонных образцов, состава
и свойств веществ и материалов (металлов,
сплавов, медицинских продуктов, минерального
сырья, почв и т.д.).
Служба также разрабатывает средства сравнения
стандартных образцов с характеристиками
веществ и материалов, которые производятся
промышленными, сельскохозяйственными и др.
предприятиями для их идентификации и контроля.
6
326.
Лекция4. Государственная служба стандартных
справочных данных о физических константах и
свойствах веществ и материалов
Государственная служба стандартных справочных
данных о физических константах и свойствах веществ
и материалов обеспечивает разработку
достоверных данных о физических константах, о
свойствах веществ и материалах, а также о
свойствах минерального сырья.
Потребителями такой информации являются
организации создающие новую технику к точности
характеристик, которой предъявляют особо высокое
требование.
6
327.
Лекция15. Передача размеров единиц
физических величин
Передача размеров единиц физических величин –
это приведение размеров единицы физической
величины хранимой поверяемым средством
измерения к размеру единицы ф.в., хранимой и
воспроизводимой эталоном, осуществляемое при
их поверке или калибровке.
Размер передается от более точных средств
измерений к менее точным.
Суть поверки и калибровки средств измерений
заключается в нахождении погрешности средства
измерения и установлении его пригодности к
использованию.
6
328.
ЛекцияПоверка средств измерений – это совокупность
операций, выполняемых государственной
метрологической службой с целью определения и
подтверждения соответствия средств измерений
установленным техническим требованиям.
Поверка носит обязательный характер, и
проводиться в отношении средств измерений,
которые применяются в установленных законом
сферах (здравоохранение, охрана окружающей
среды, обеспечение обороноспособности страны и
т.д.).
6
329.
ЛекцияКалибровка средств измерений – это комплекс
операций, осуществляемых с целью определения и
подтверждения действительных характеристик
средств измерения и пригодности к применению
этих средств измерений (неподлежащие
государственному контролю и надзору).
Калибровка носит добровольный характер.
Сопоставление государственного эталона,
вторичного эталона и рабочих средств измерений
определено государственной поверочной схемой.
Поверочная схема – документ, устанавливающий
средства (с помощью чего), методы (каким образом) и
точность передачи размеров единиц от
государственного эталона к рабочим средствам
измерения.
6
330.
ЛекцияВиды поверок средств измерения
В РФ применяются следующие виды поверки средств
измерения:
а) первичная поверка, ей подлежат средства
измерений при выпуске из производства после
ремонта, а также средства измерений, ввозимые по
импорту.
б) периодическая поверка, такой поверке подлежат
средства измерения, находящиеся в эксплуатации или
на хранении.
в) внеочередная поверка, осуществляется при
эксплуатации и хранении в следующих случаях:
– повреждение поверительного клейма;
6
331.
Лекция– утрата свидетельства о поверке;
– ввод в эксплуатацию средства измерения,
длительное время находящегося на хранении
(длительность определяется государственной
метрологической службой);
– неудовлетворительная работа прибора.
г) инспекционная поверка, ее проводят для
подтверждения пригодности к применению средств
измерений. При проведении государственного
метрологического надзора,
д) экспертная поверка, производиться при
возникновении спорных вопросов по метрологическим
характеристикам средств измерений, их исправности и
пригодности к применению.
6
332.
Лекция16. Государственный метрологический
контроль и надзор за средствами измерения
Государственный метрологический контроль и
надзор – это деятельность, осуществляемая
органами государственной метрологической
службы по проверке юридических лиц на
соответствие Закону «Об обеспечении единства
измерений» и требованиям государственных
стандартов и другим нормативным документам
в области метрологии.
6
333.
ЛекцияГосударственный метрологический контроль
осуществляется путем:
калибровки средств измерений,
надзор за состоянием и применением средств
измерений, за выполнением методик измерений и
контроль мер применяемых при калибровке
(контроль эталонов),
выдача обязательных предписаний с целью
устранения нарушений метрологических правил и
норм,
проверка своевременности представления средств
измерений на испытания для утверждения типа
средств измерений, а также на поверку или
калибровку.
6
334.
ЛекцияГосударственный метрологический контроль
включает:
1 Утверждение типа средств измерений необходимо
для постановки на производство и выпусков в
обращение новых типов средств измерений или при
их ввозе по импорту.
Процедура утверждения типа предусматривает
обязательные испытания средств измерений.
Принятие решения об утверждении типа, ее
государственную регистрацию и выдачу
сертификата об утверждении типа средства
измерения.
На средство измерения утвержденного типа
наноситься специальное клеймо.
6
335.
Лекция2. Поверка средств измерения, в том числе эталонов
осуществляется органами государственного
метрологического контроля и надзора РФ. В отличие
от процедуры утверждения типа средства
измерения, в котором участвует только одно
средство измерения представляющее тип, поверке
подлежит каждое средство измерения.
3. Согласно закону об обеспечении единства
измерений деятельность по изготовлению,
ремонту, продаже и прокату средств измерений
должна подвергаться лицензированию органами
государственной метрологической службы.
6
336.
ЛекцияЛицензия – это документально оформленное
решение, выдаваемое органами ГМС юридическому
или физическому лицу на осуществление
деятельности по изготовлению, ремонту,
продаже и прокату средств измерения.
По настоящему законодательству лицензия
выдается не более чем на 5 лет.
6
337.
ЛекцияГосударственный метрологический надзор
производится на предприятиях и в организациях
независимо от подчиненности и форм собственности
в виде проверок соблюдения норм в соответствии
с Законом «Об обеспечении единства измерений».
6
338.
ЛекцияГосударственный метрологический надзор следит:
за выпуском, состоянием и применением средств
измерения,
за аттестованными методиками измерений,
за эталонами единиц ФВ,
за соблюдением правил и норм, касающихся
метрологии на предприятиях,
за количеством отчуждаемых товаров,
за количеством фасованных товаров в упаковках
любого вида при их фасовке и продаже.
6
339.
ЛекцияПроверки, проводимые органами государственной
метрологической службы, могут быть: плановыми,
внеплановыми, повторными.
Плановая проверка не реже одного раза в 3 года.
Внеплановые проверки производятся по
инициативе потребителей (общество защиты прав
потребителей, налоговой инспекцией).
Повторная проверка осуществляется для контроля
выполнения предписаний выданных органами
государственной метрологической службы.
При этом срок проведения повторных проверок
указан в предписании.
6
340.
Лекция6
341.
Лекция6



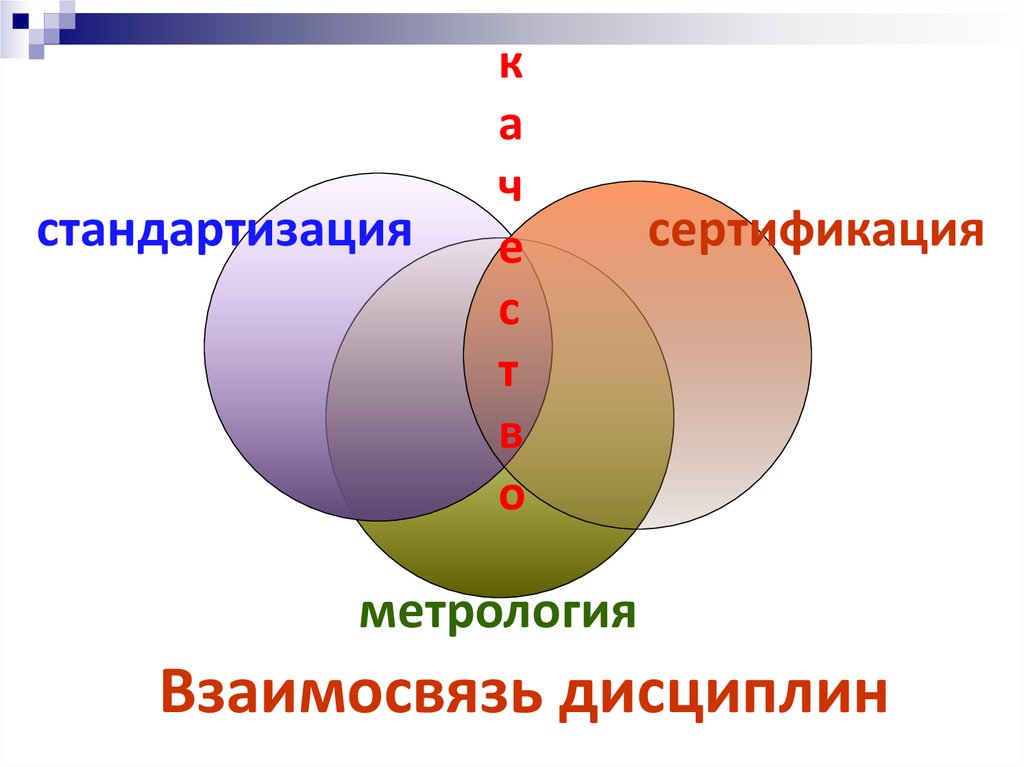




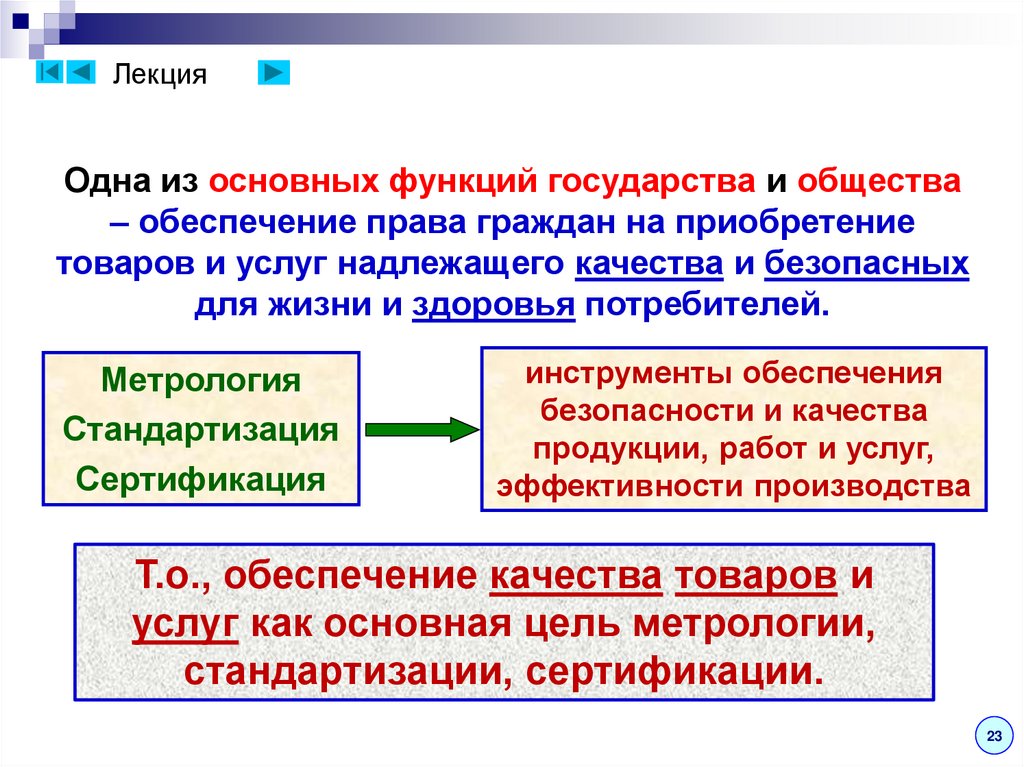








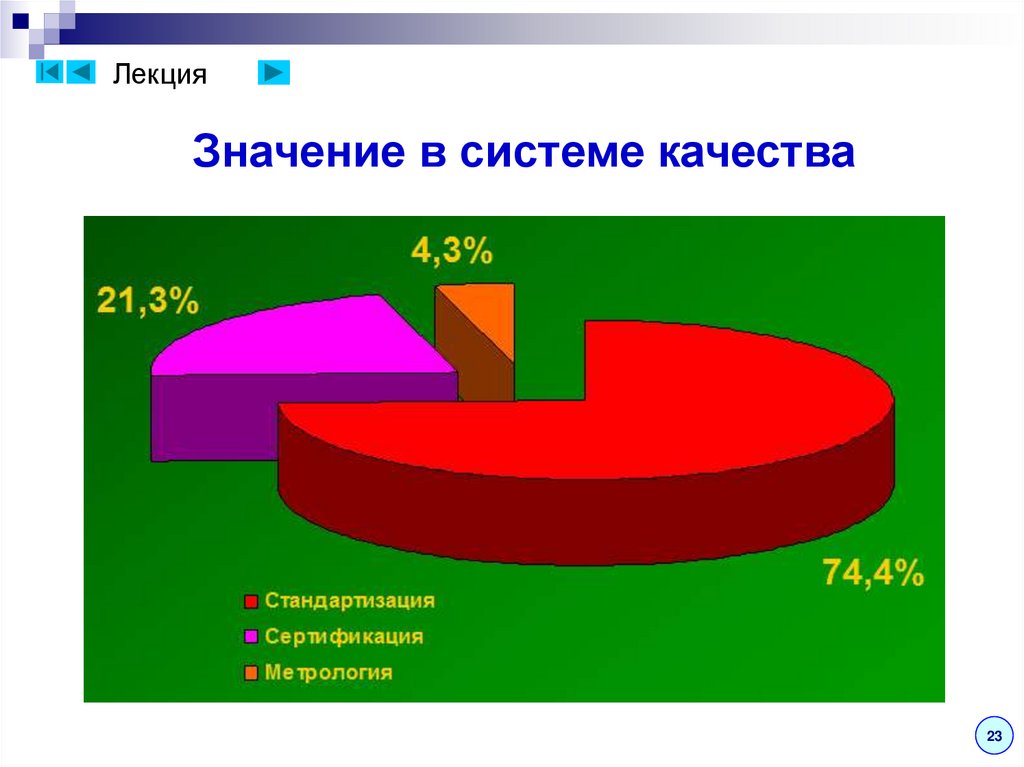
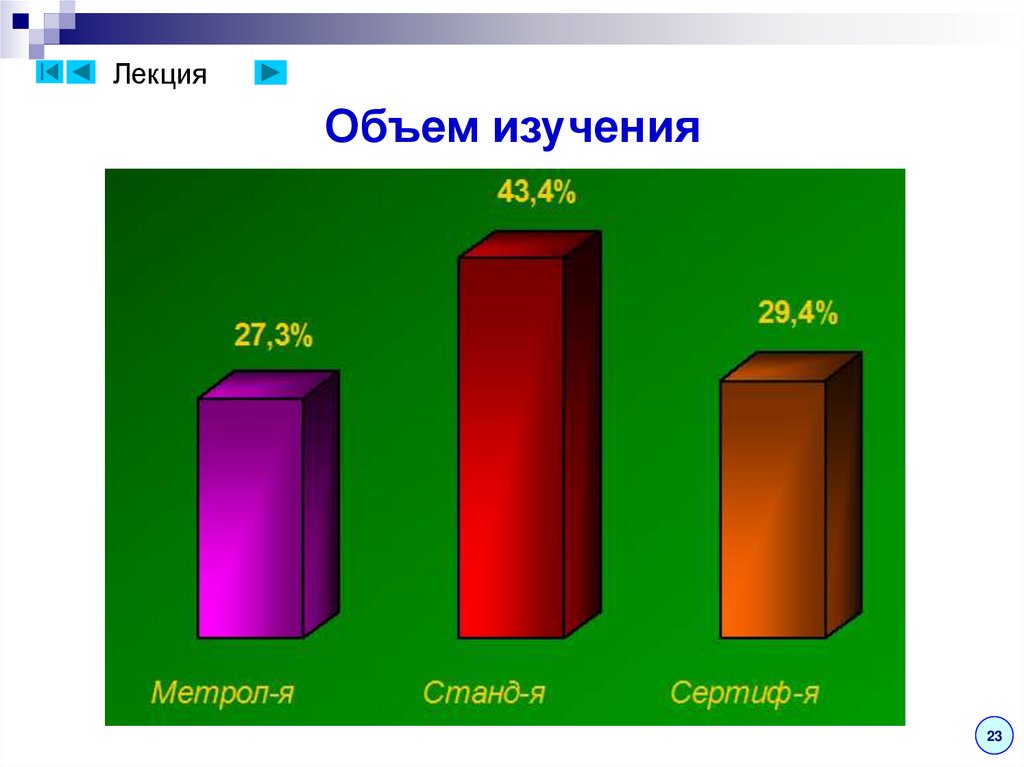










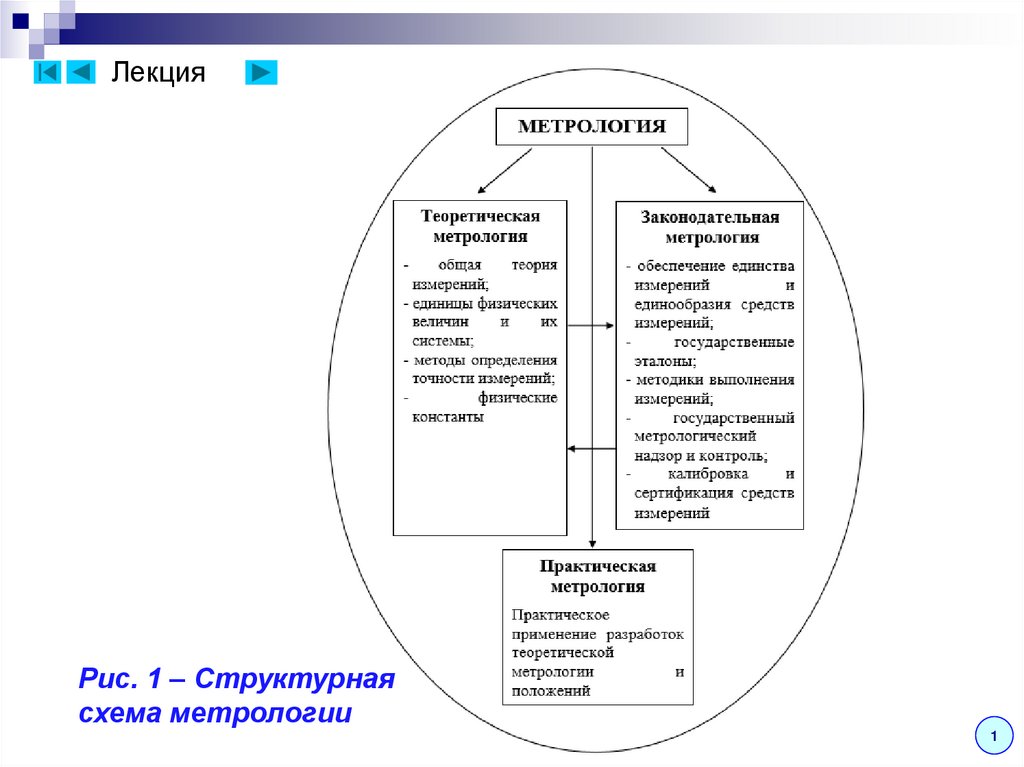
















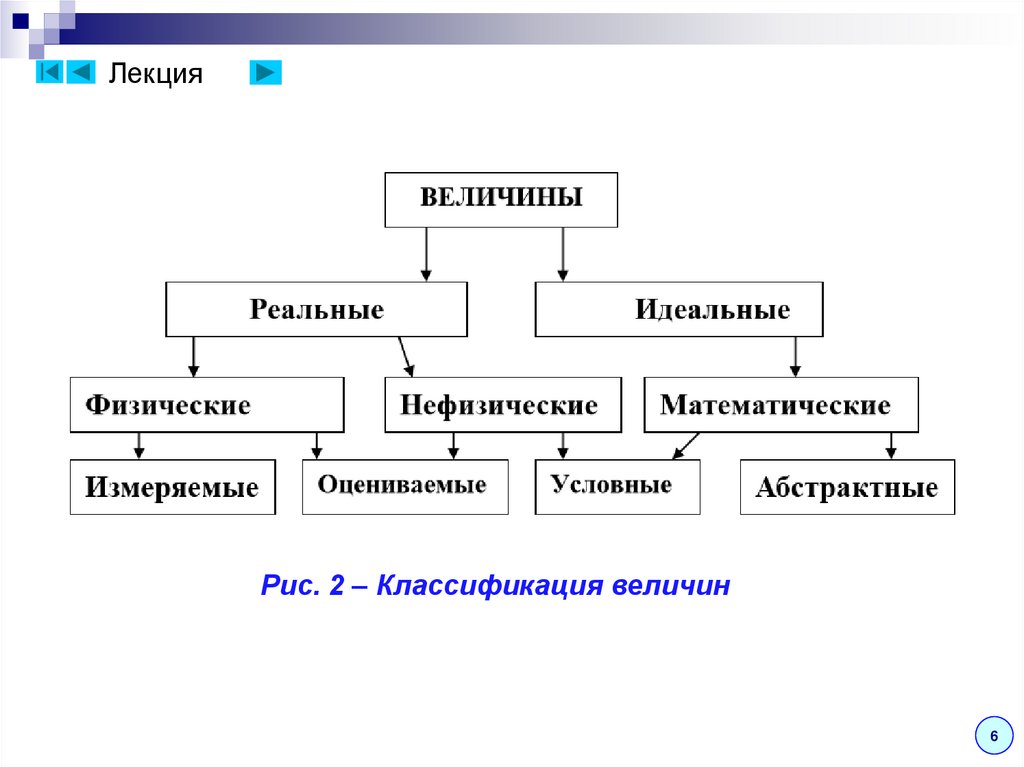



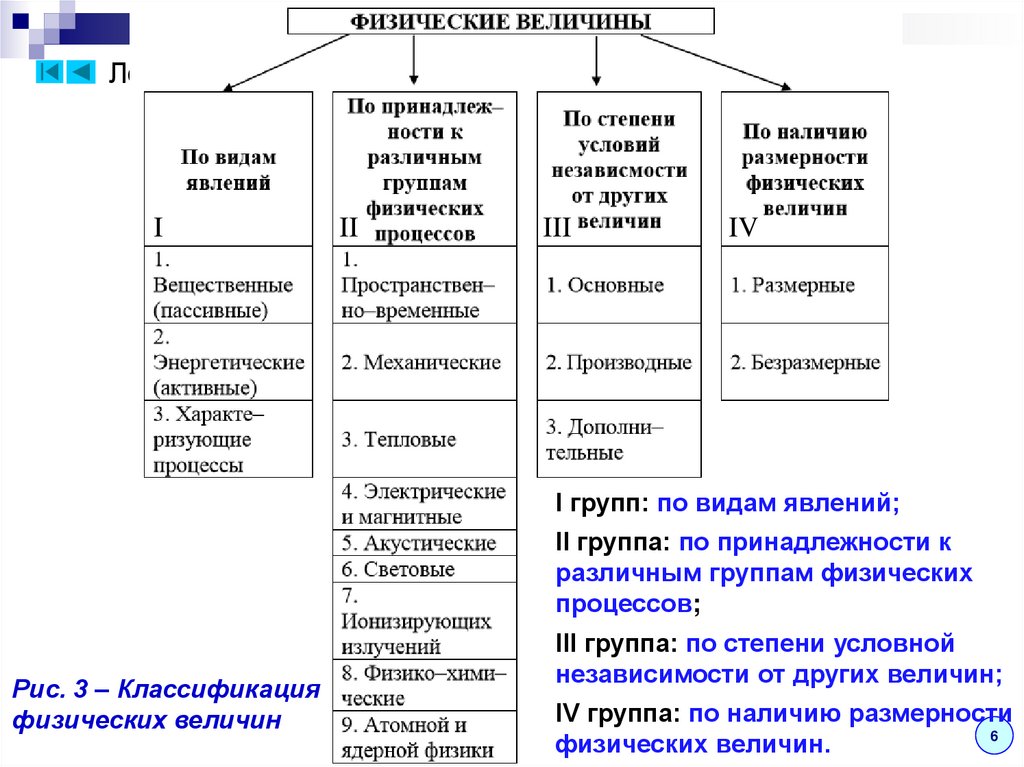

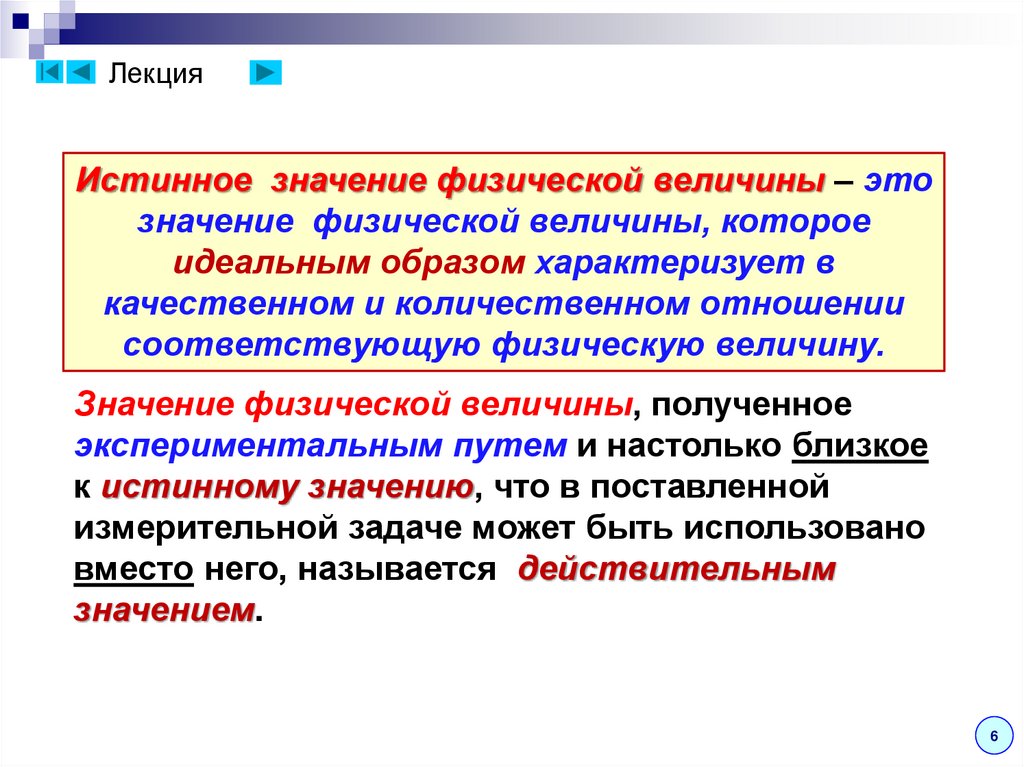





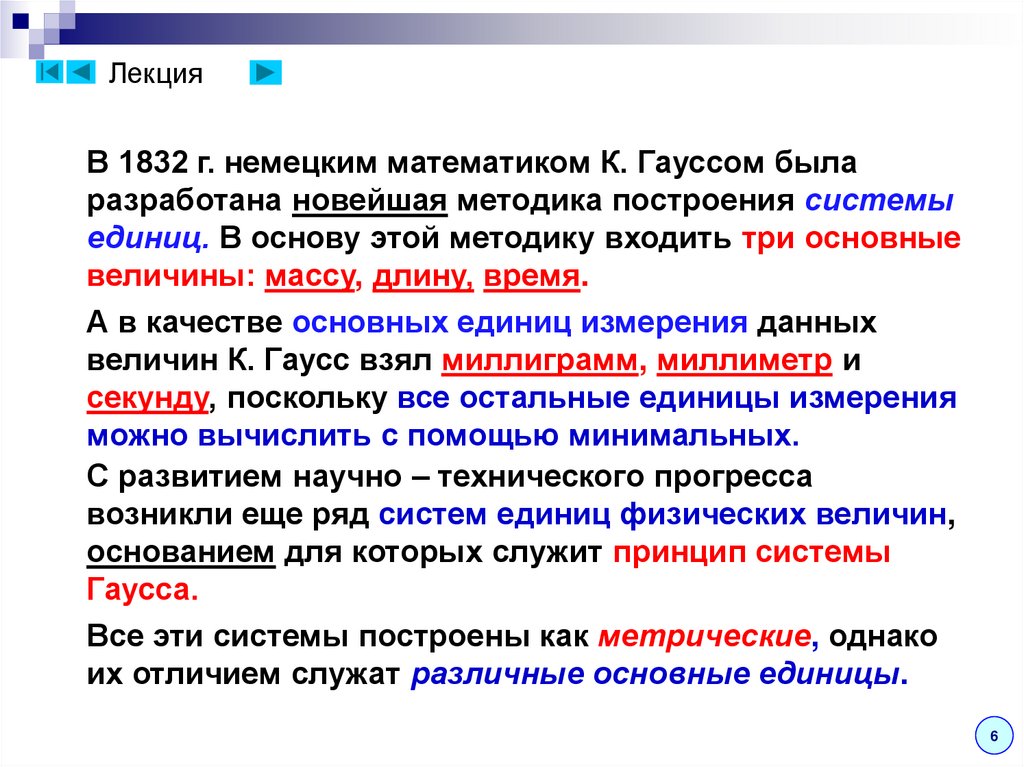



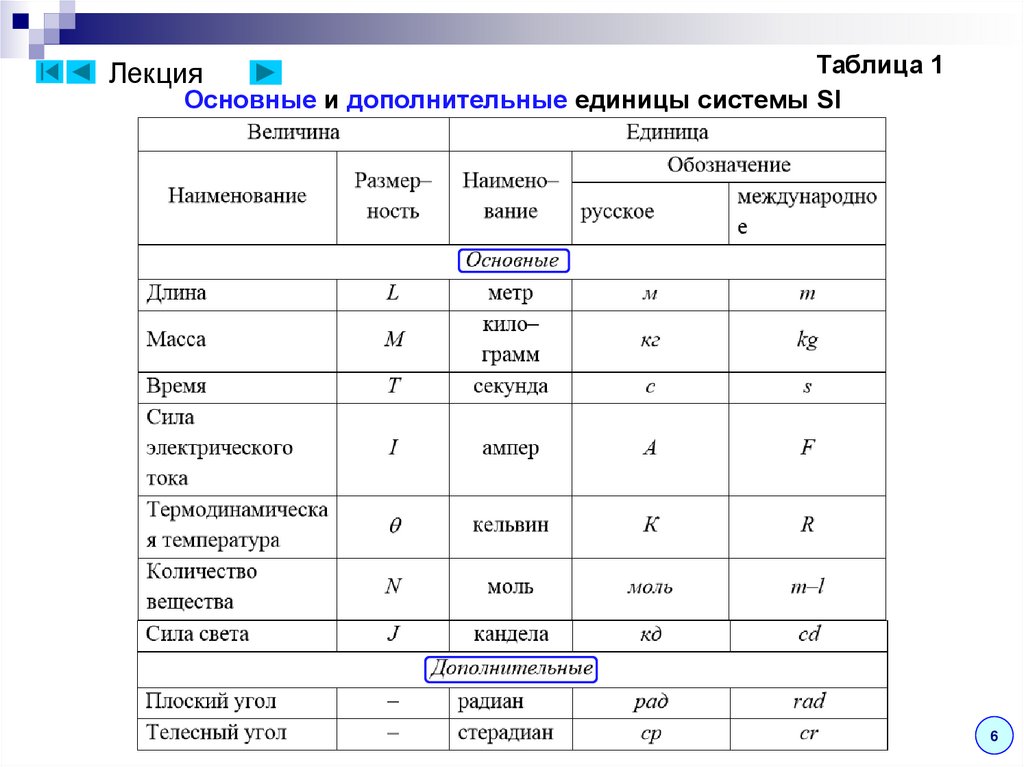



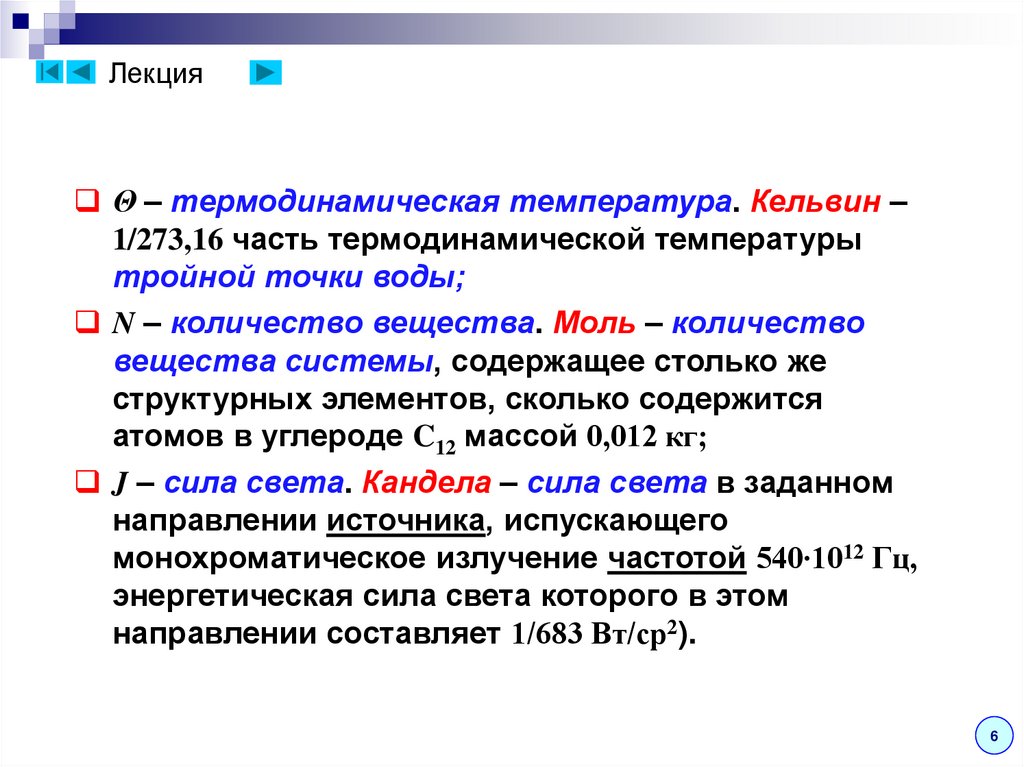







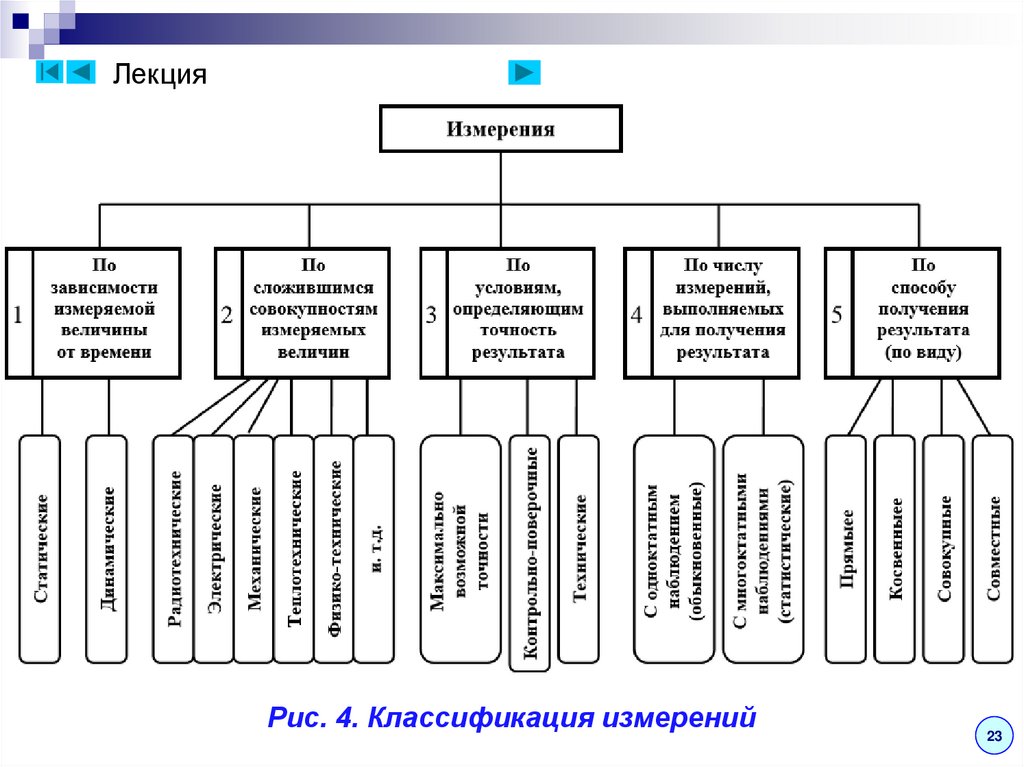
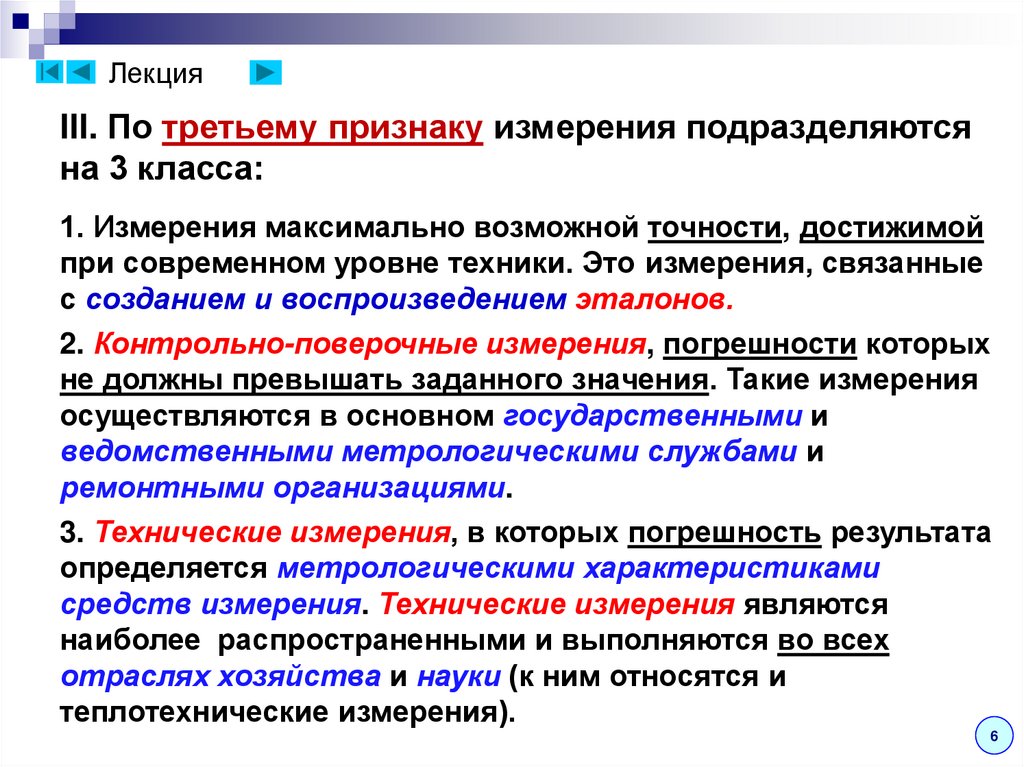


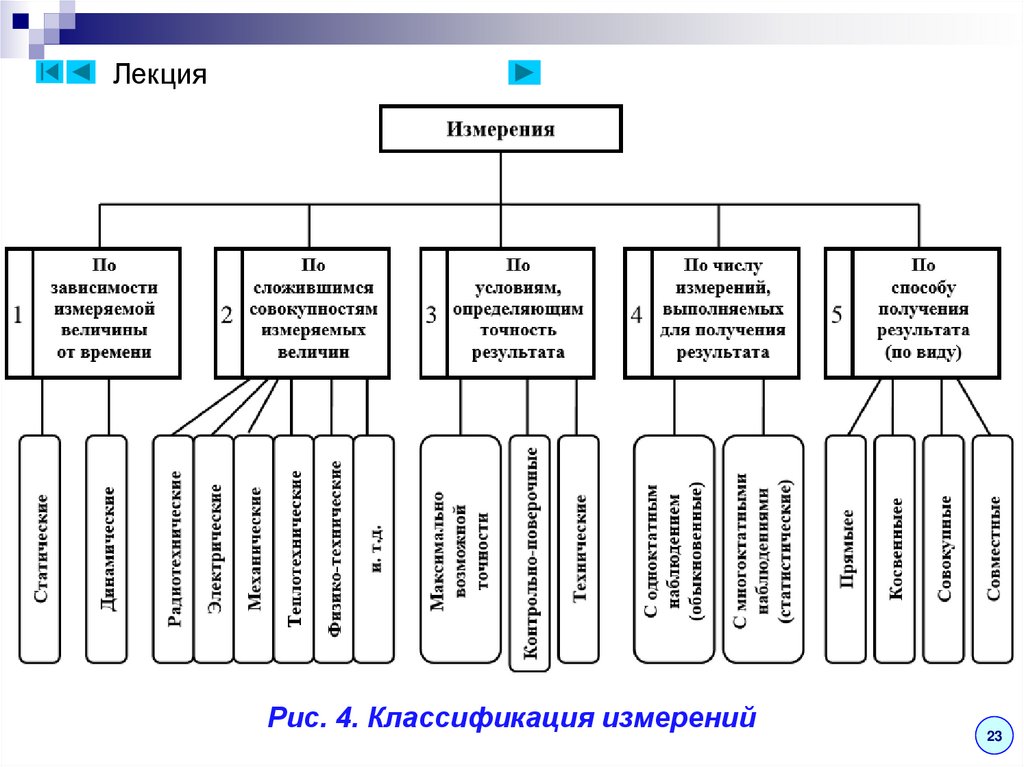


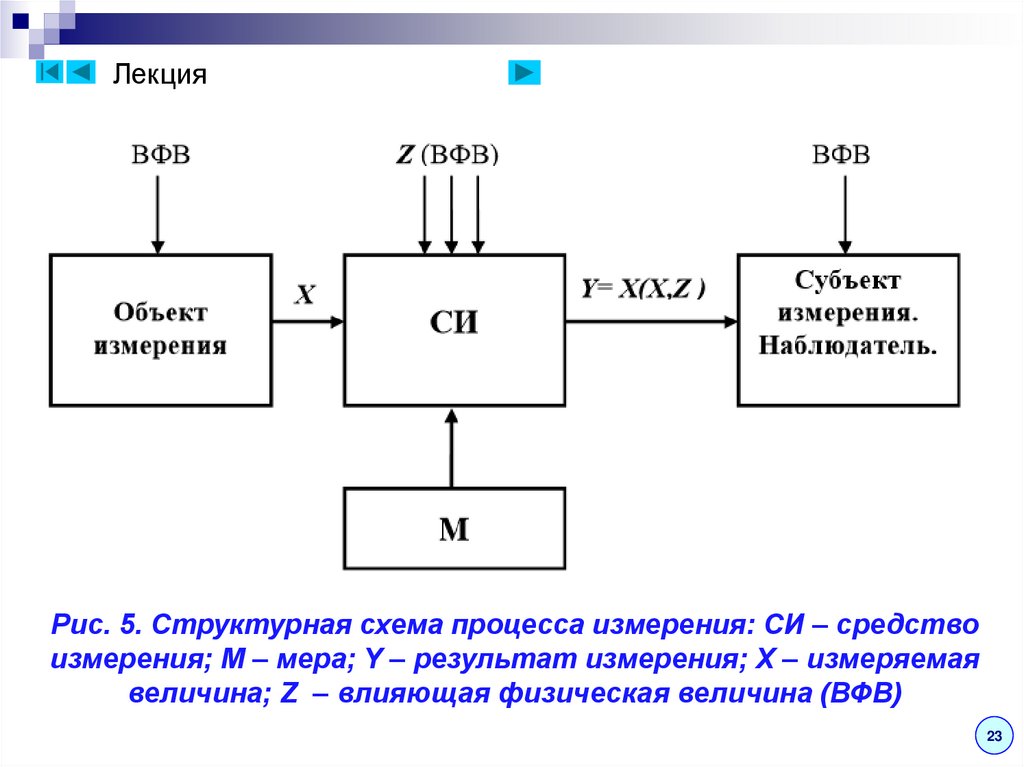
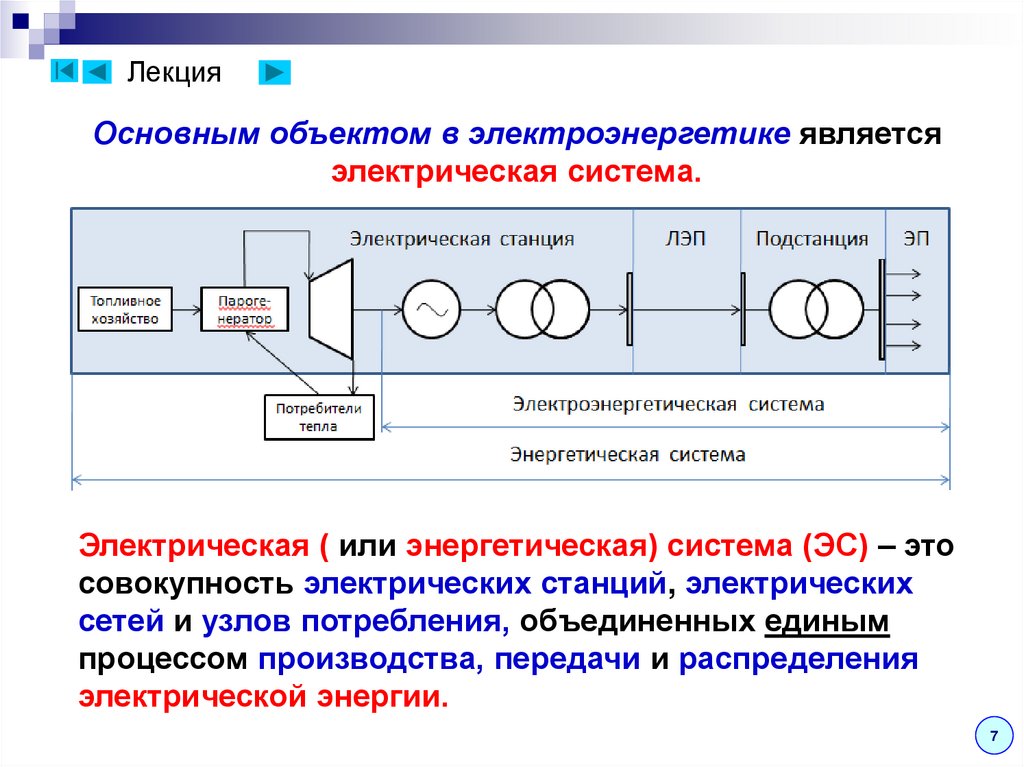
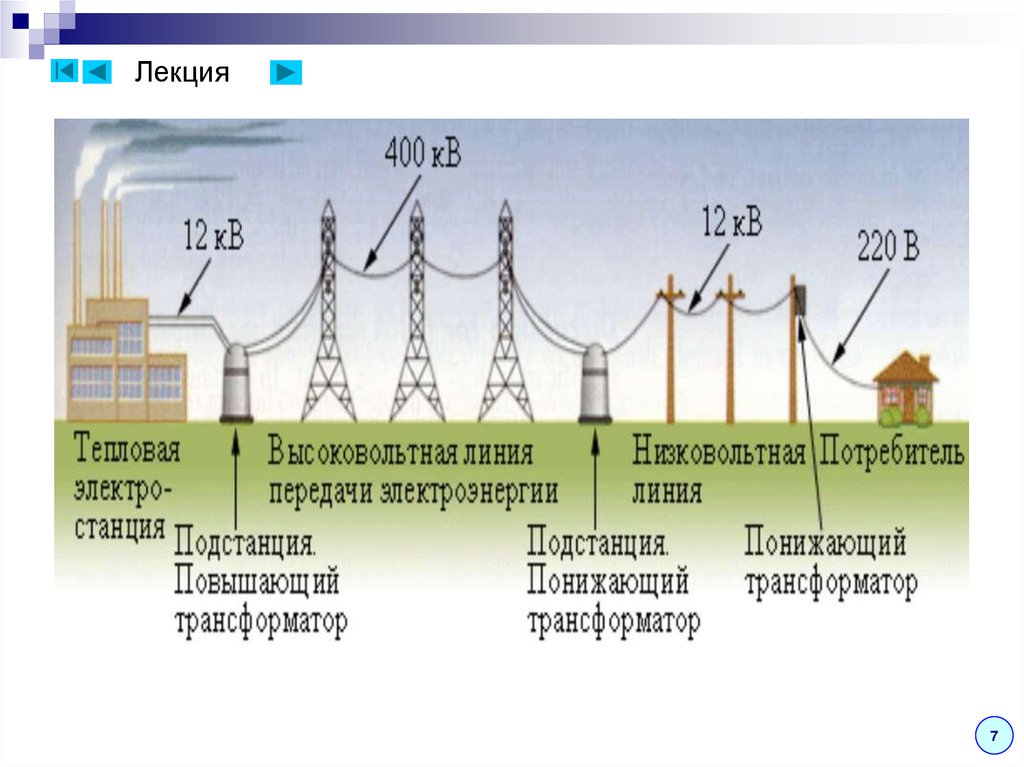


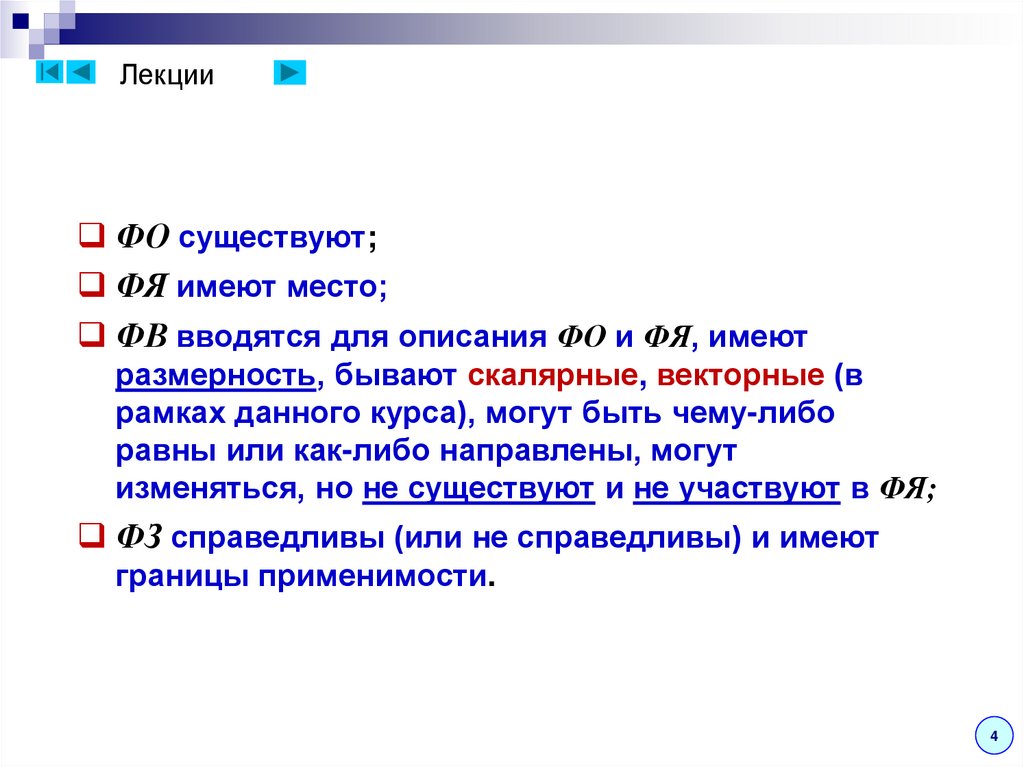













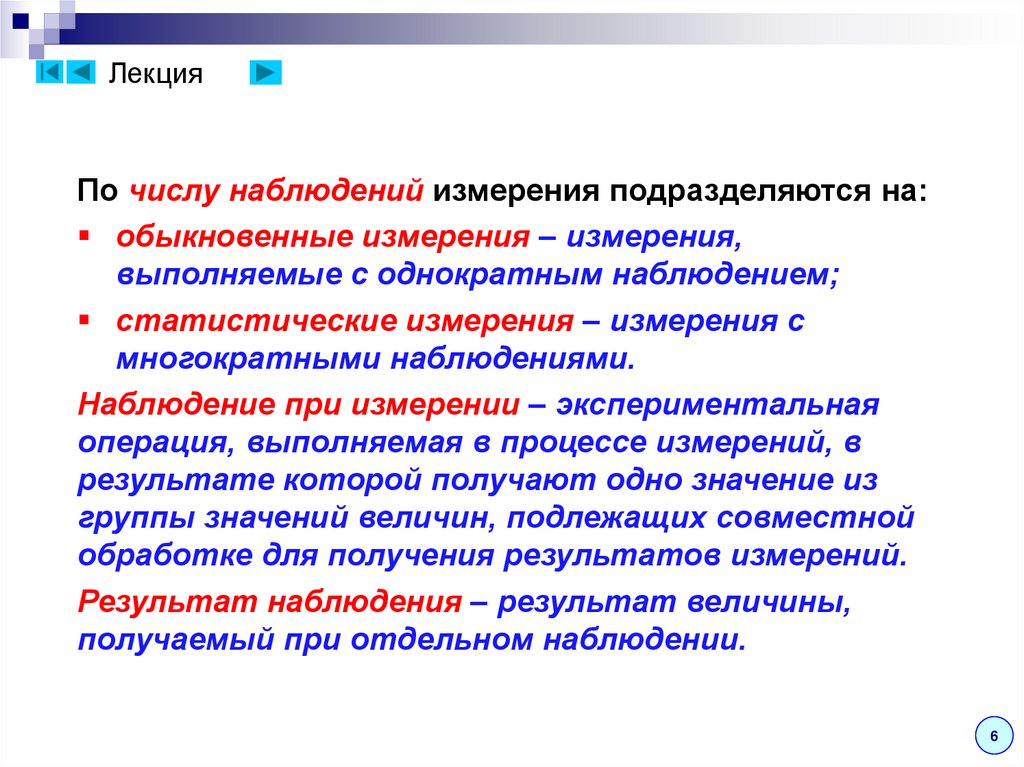
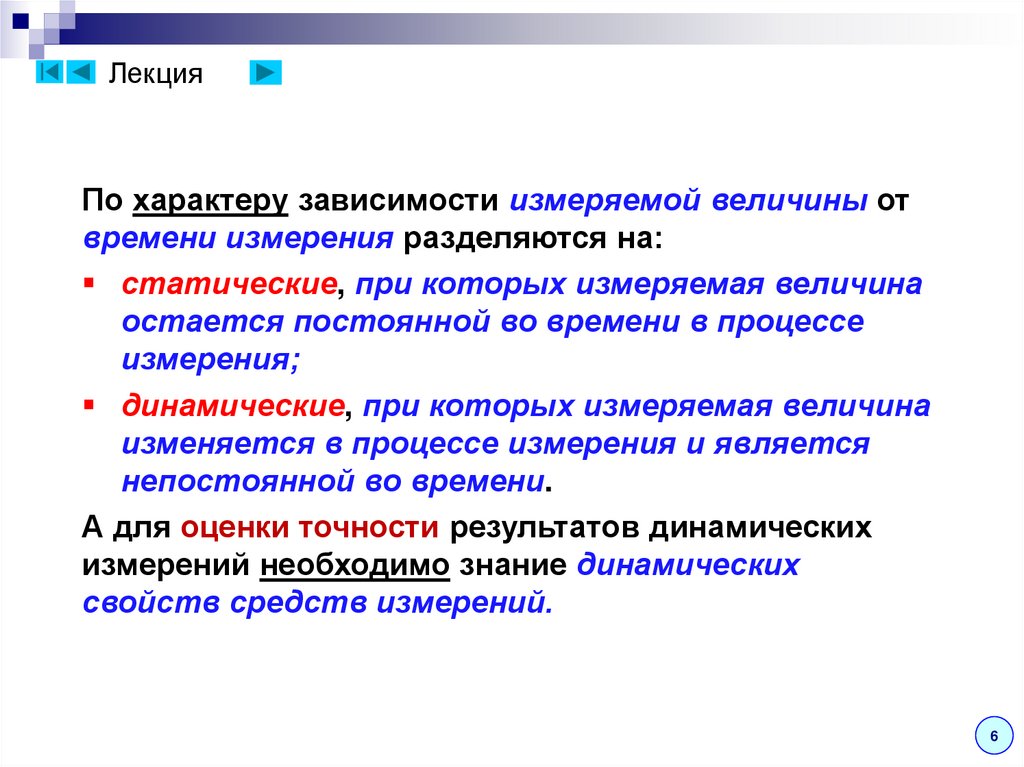

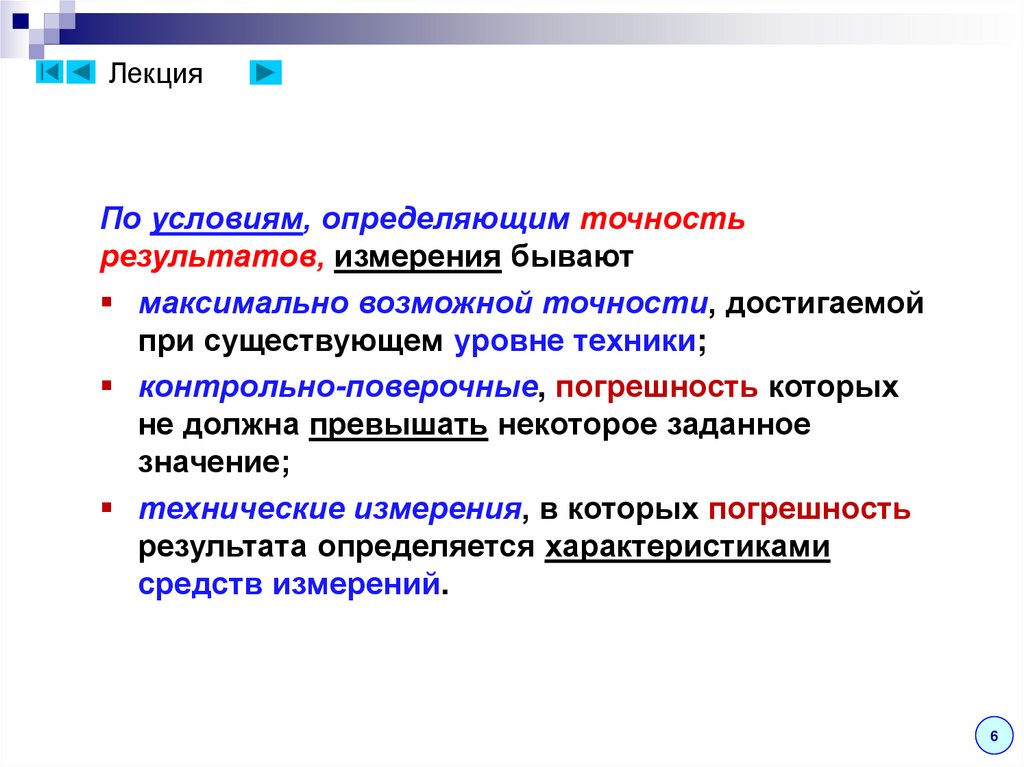


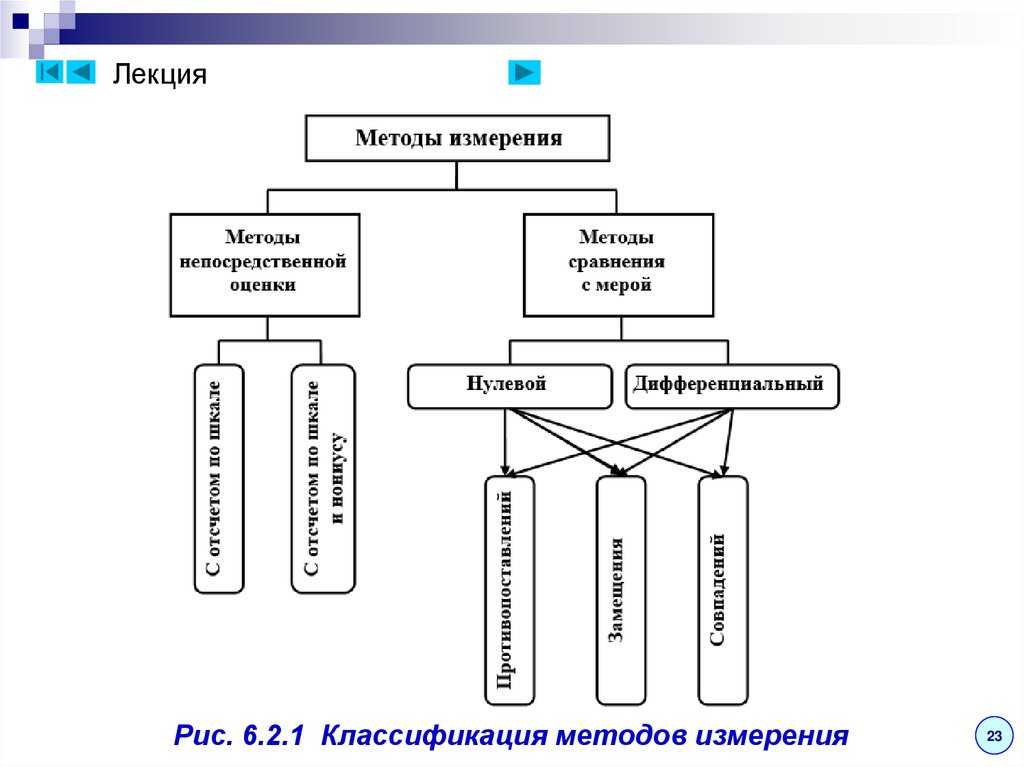

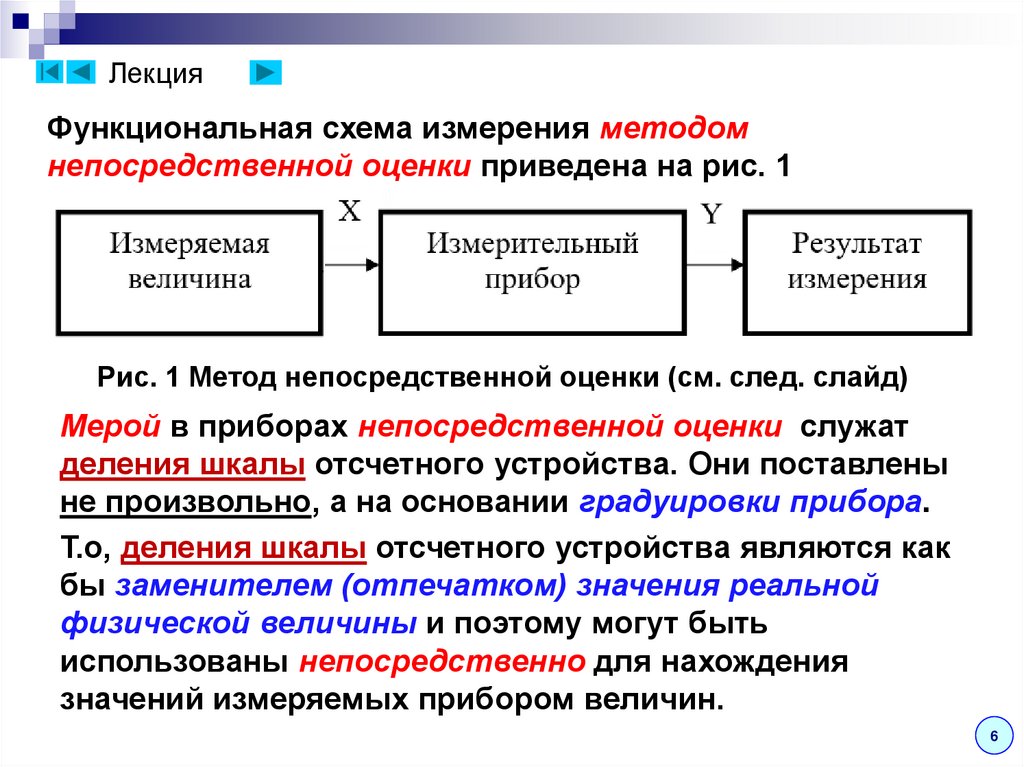
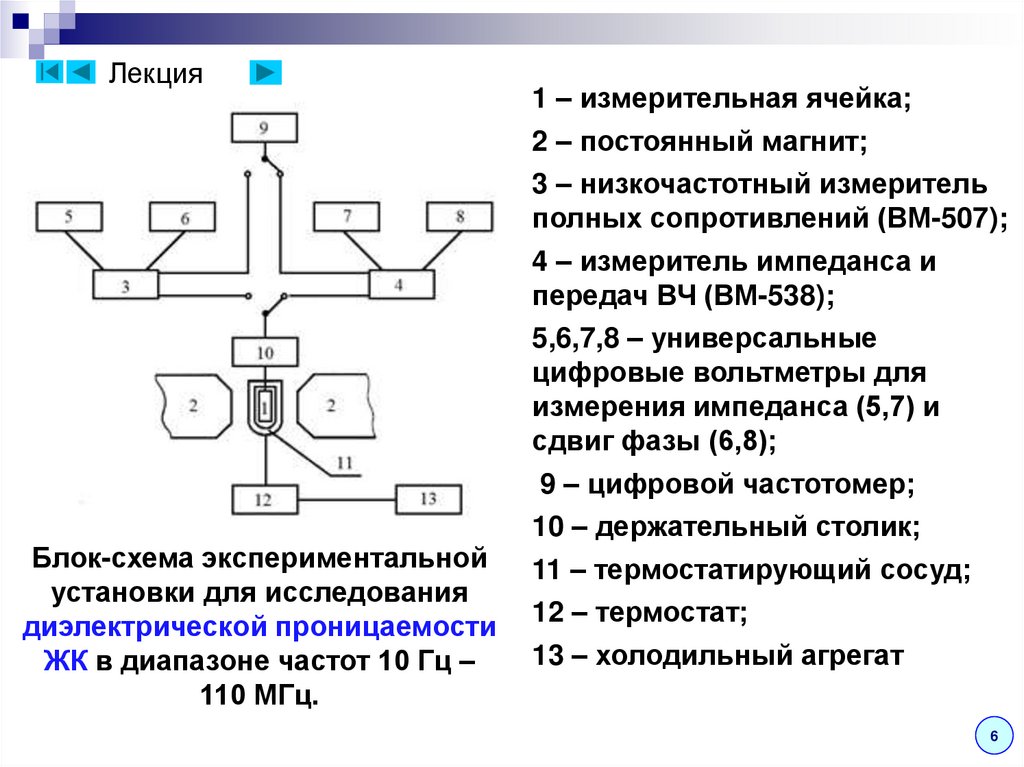
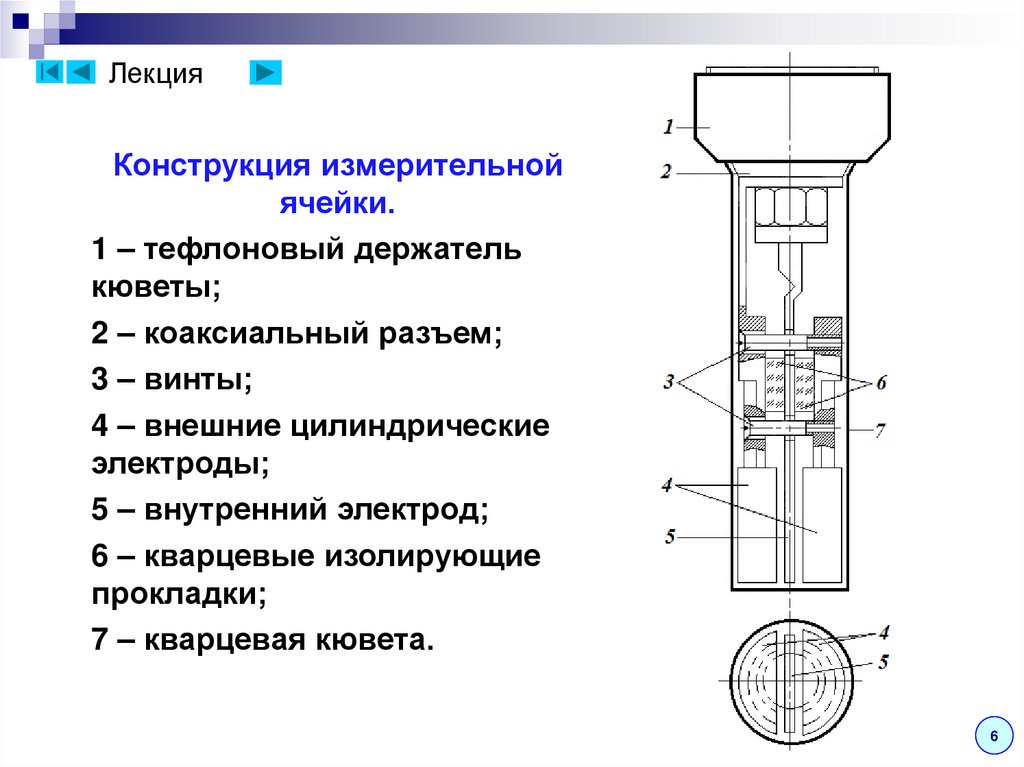

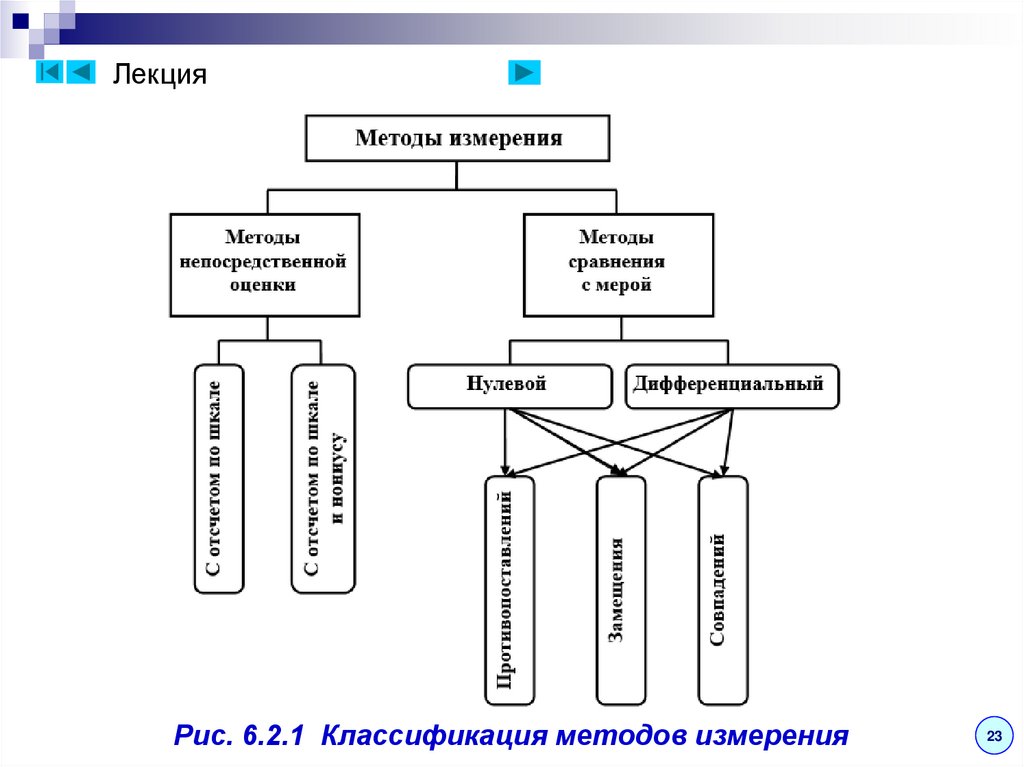

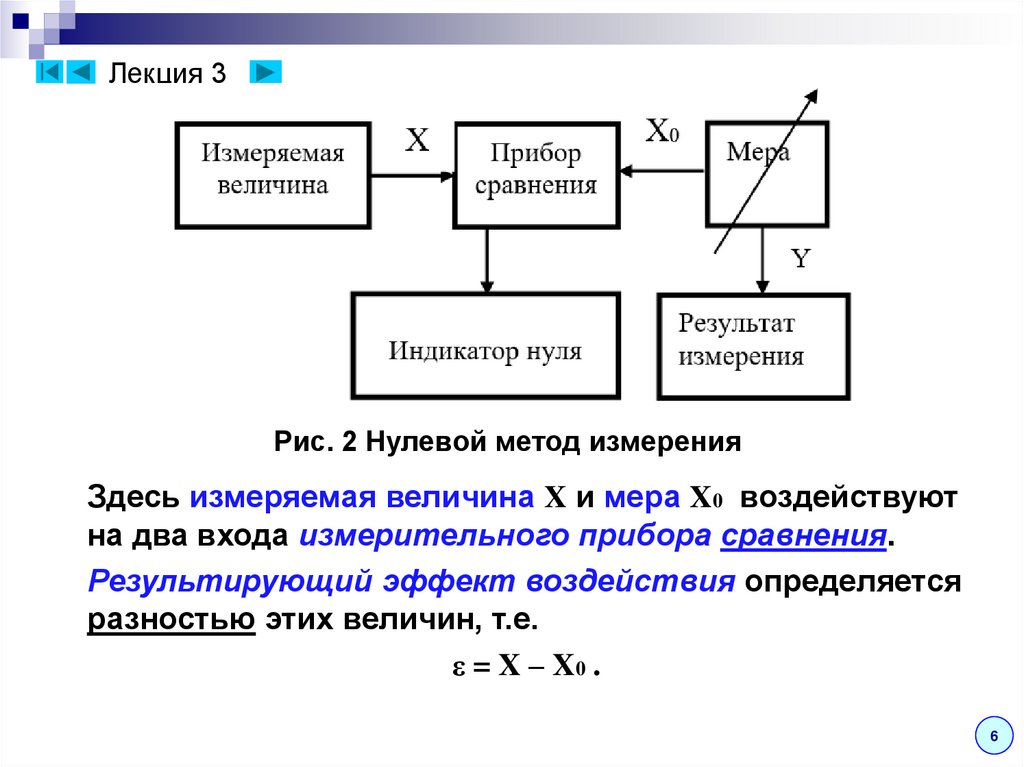


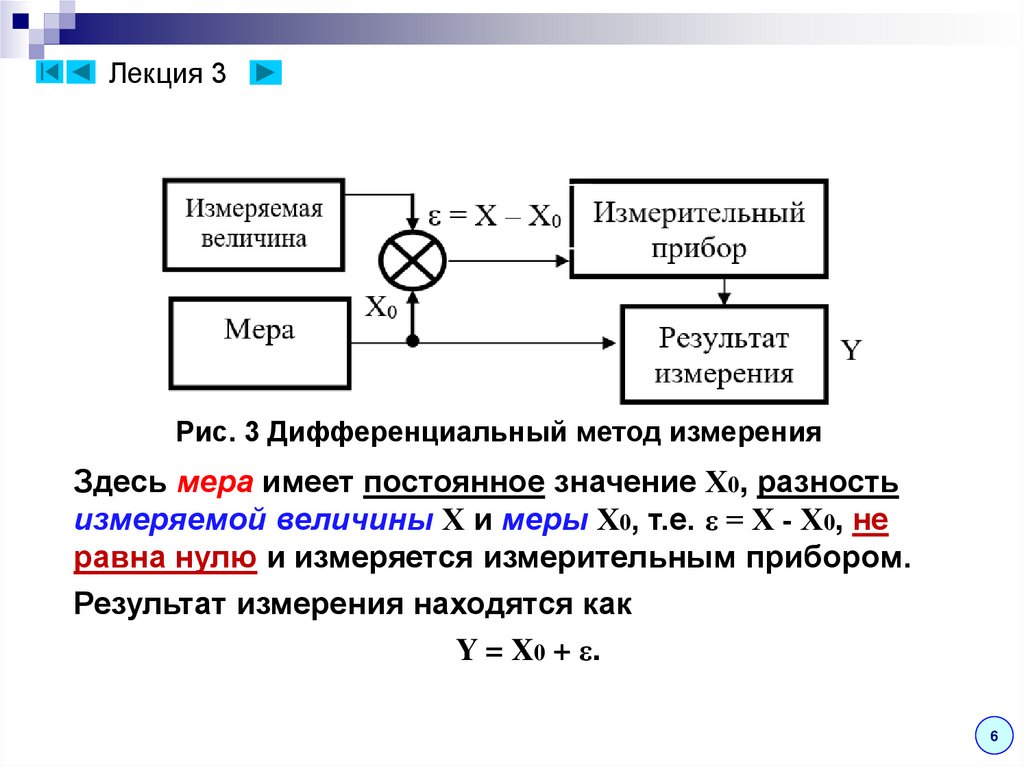






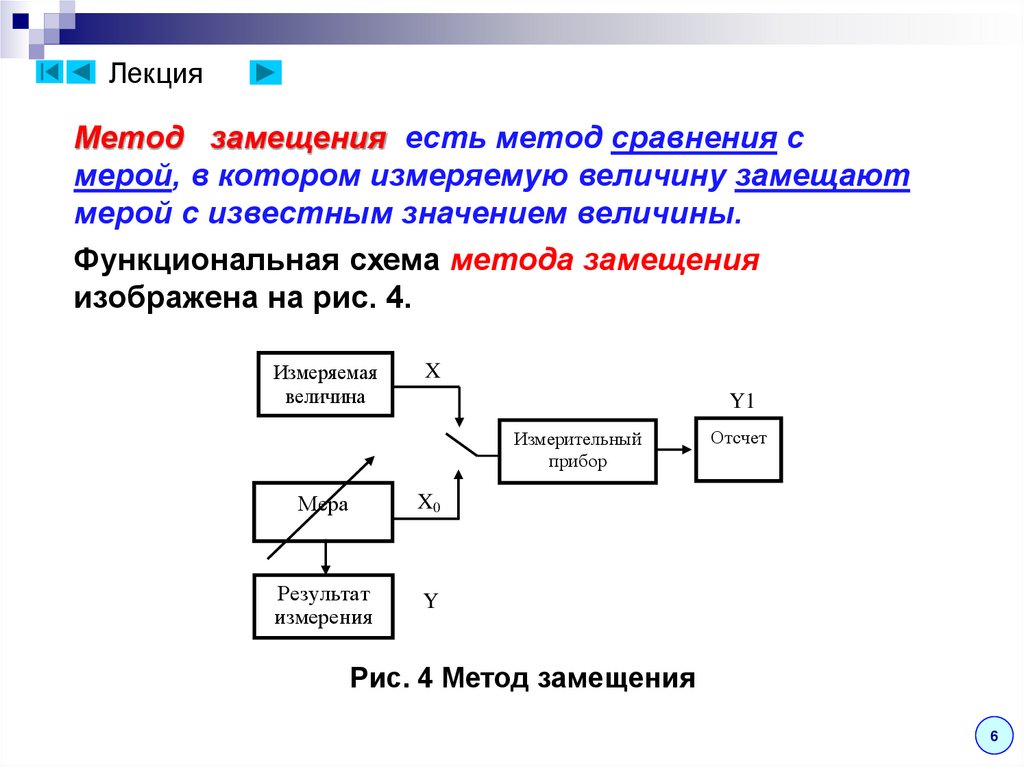
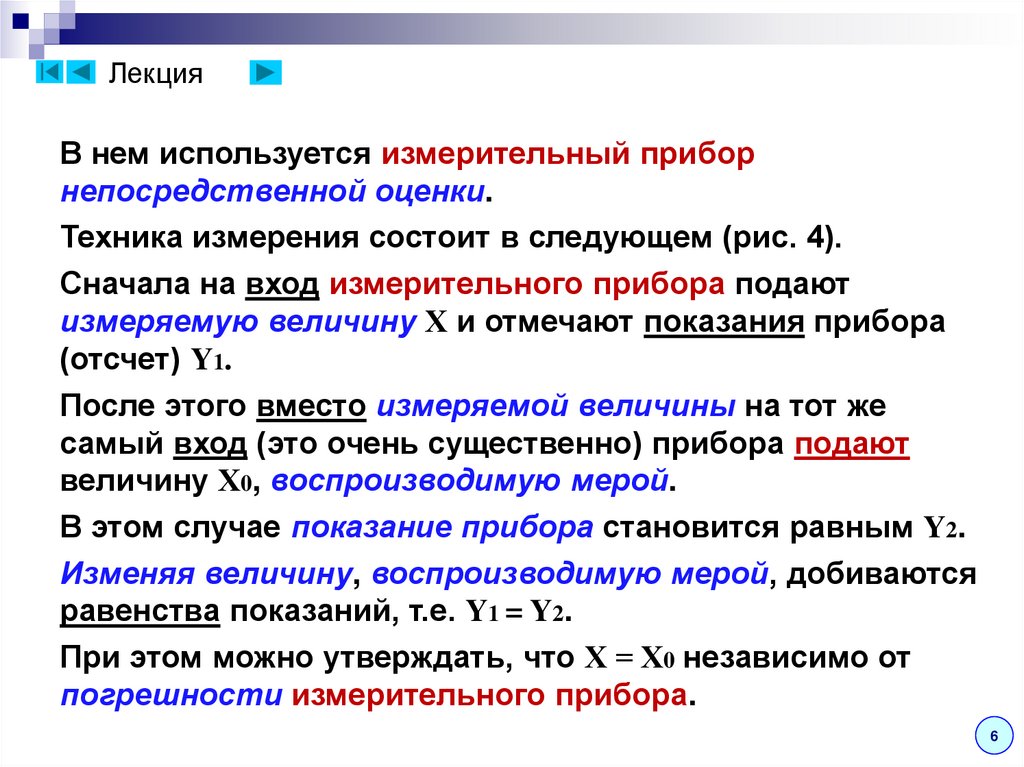










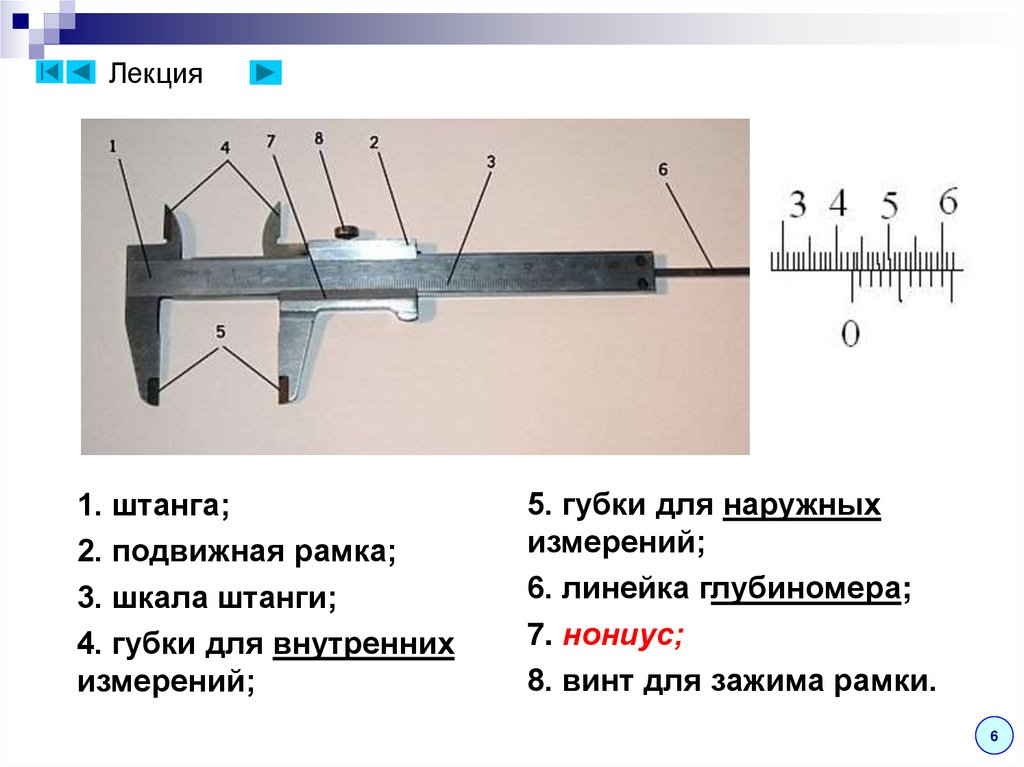

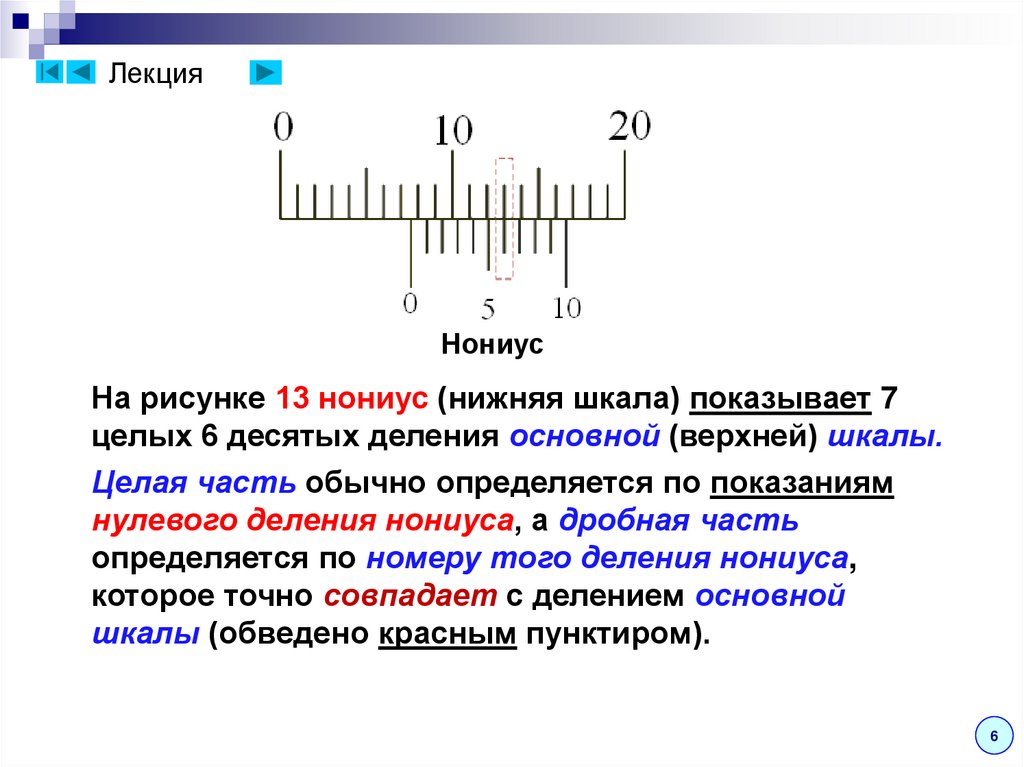









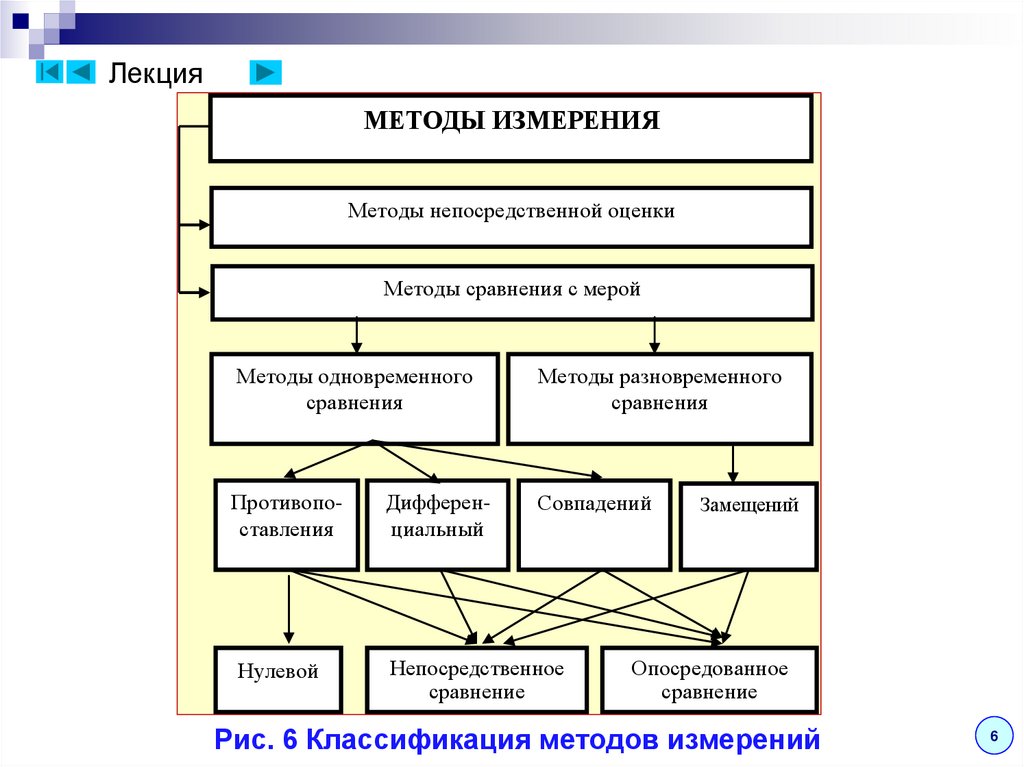







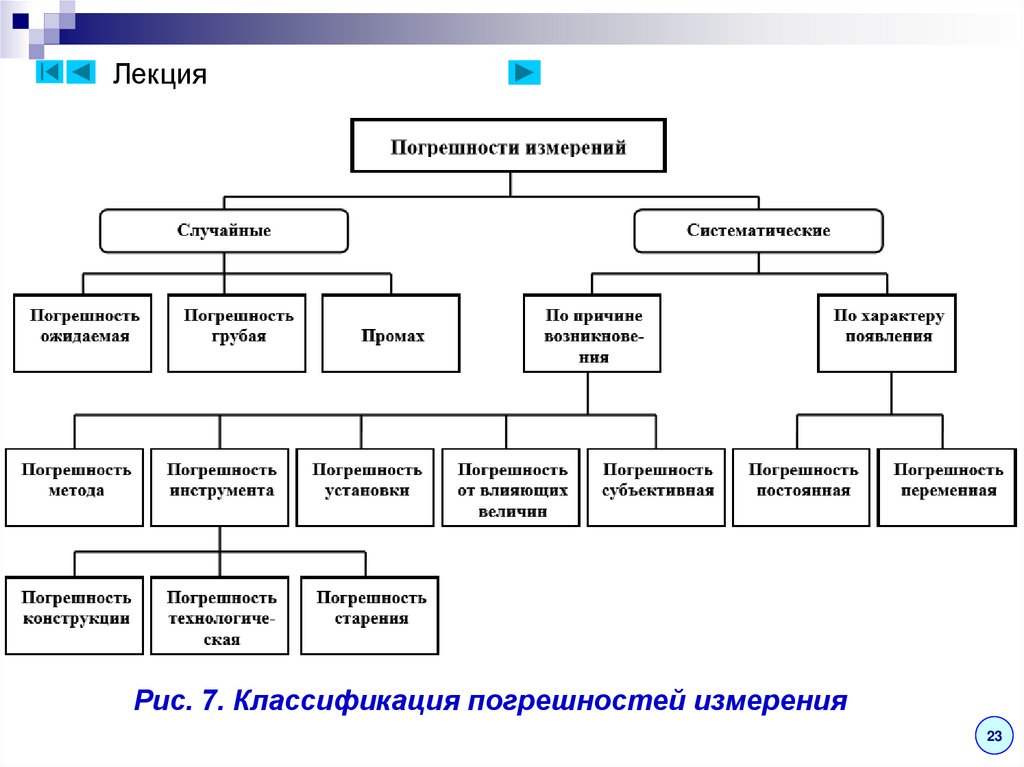


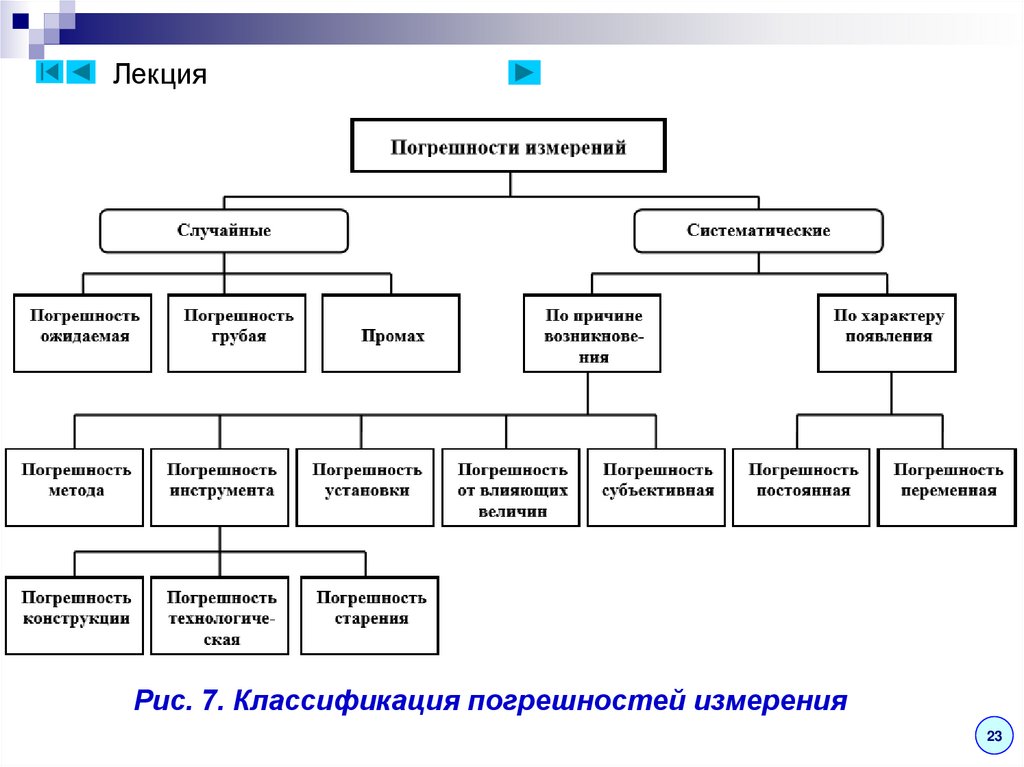











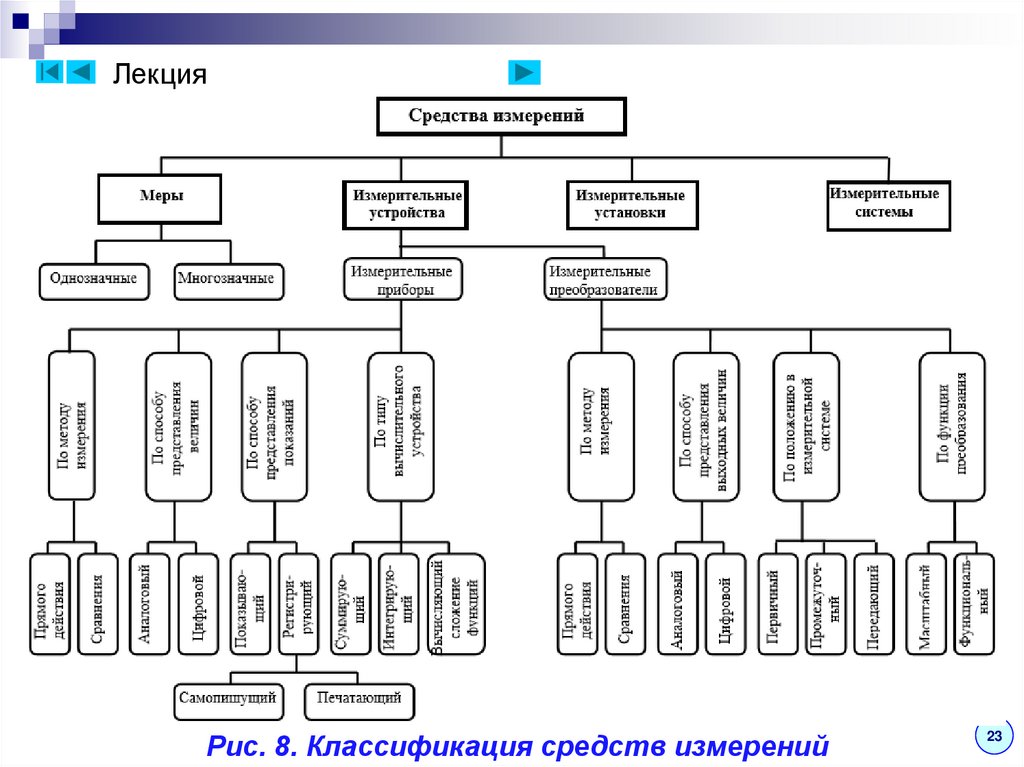

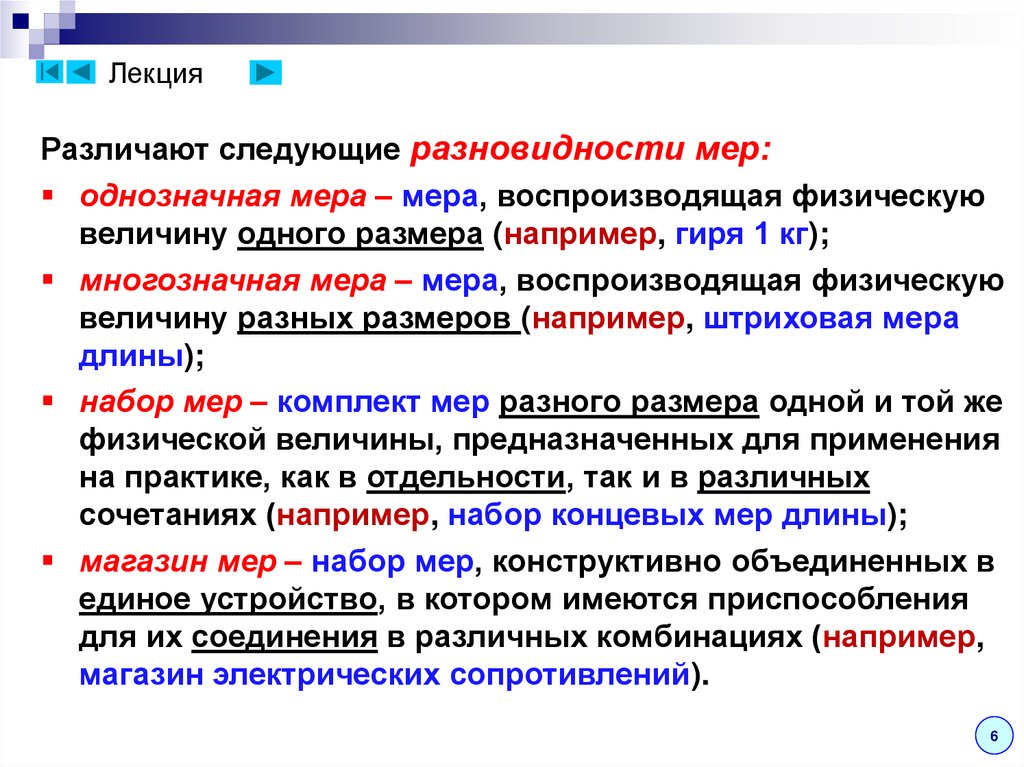
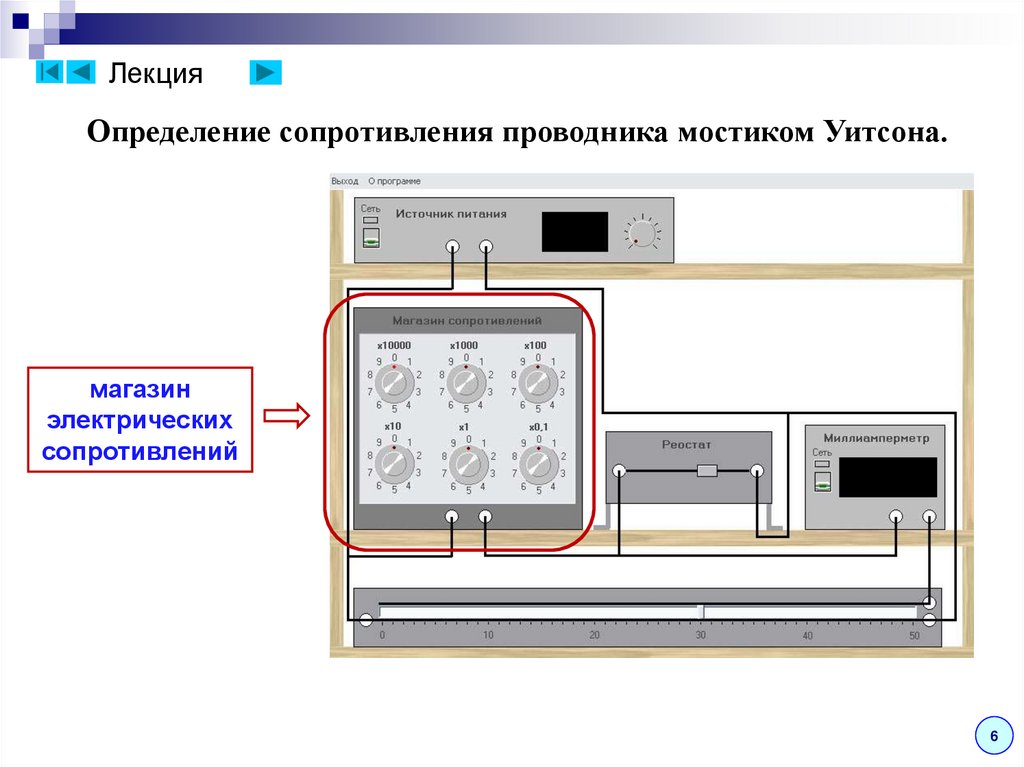
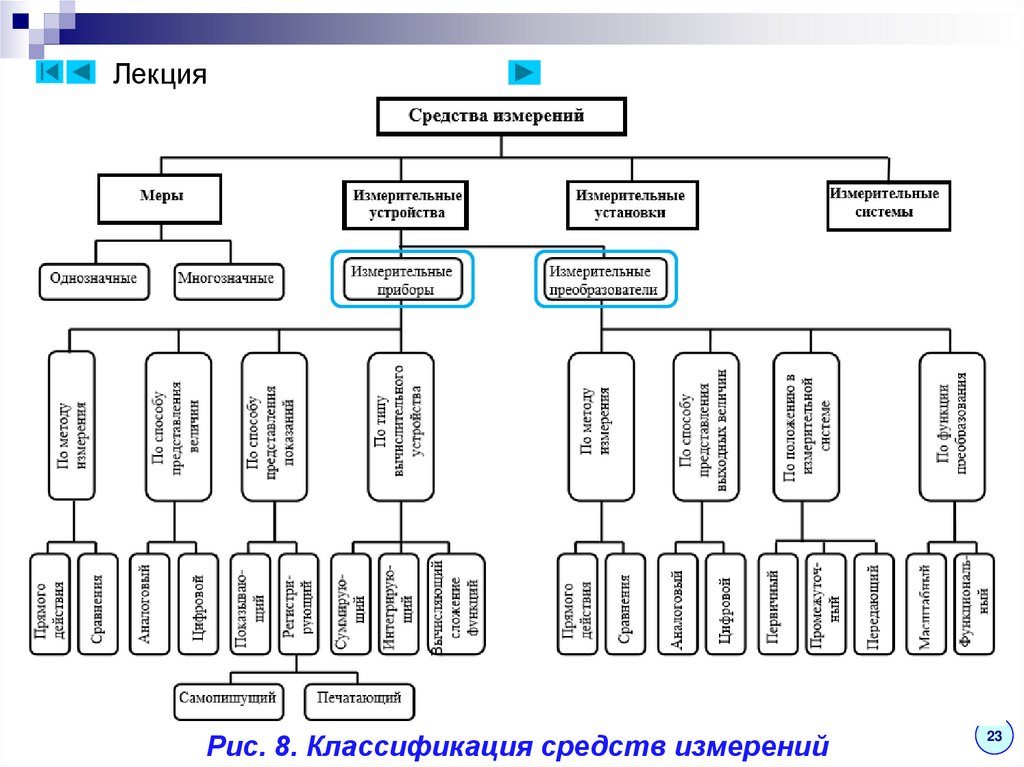

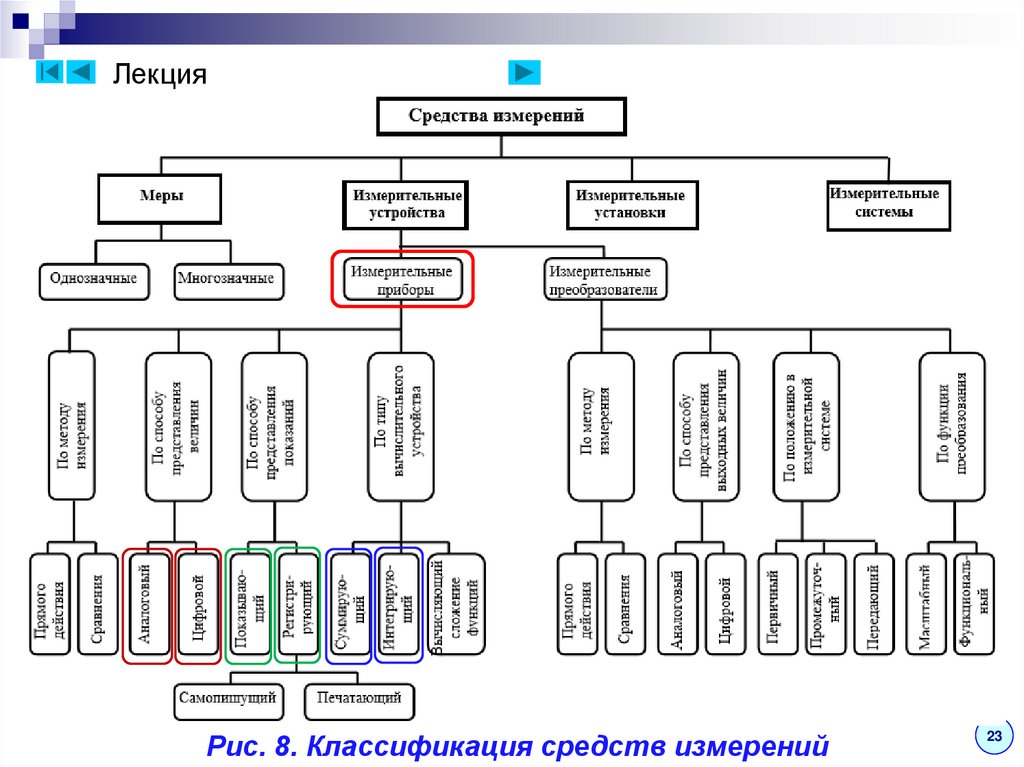

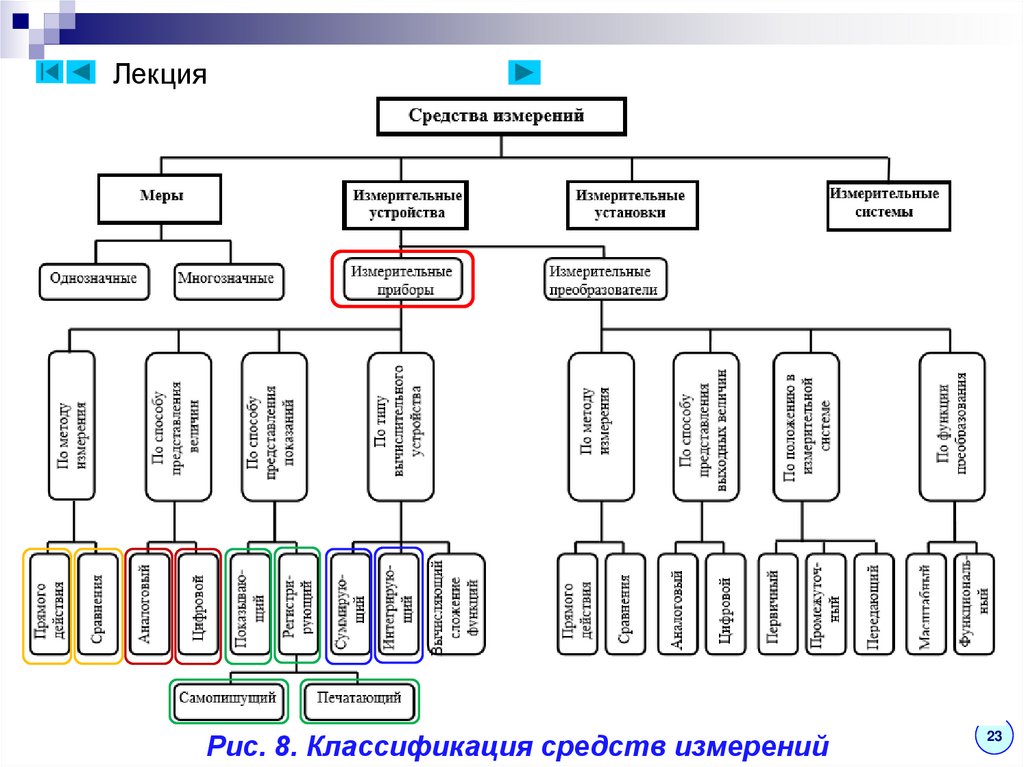
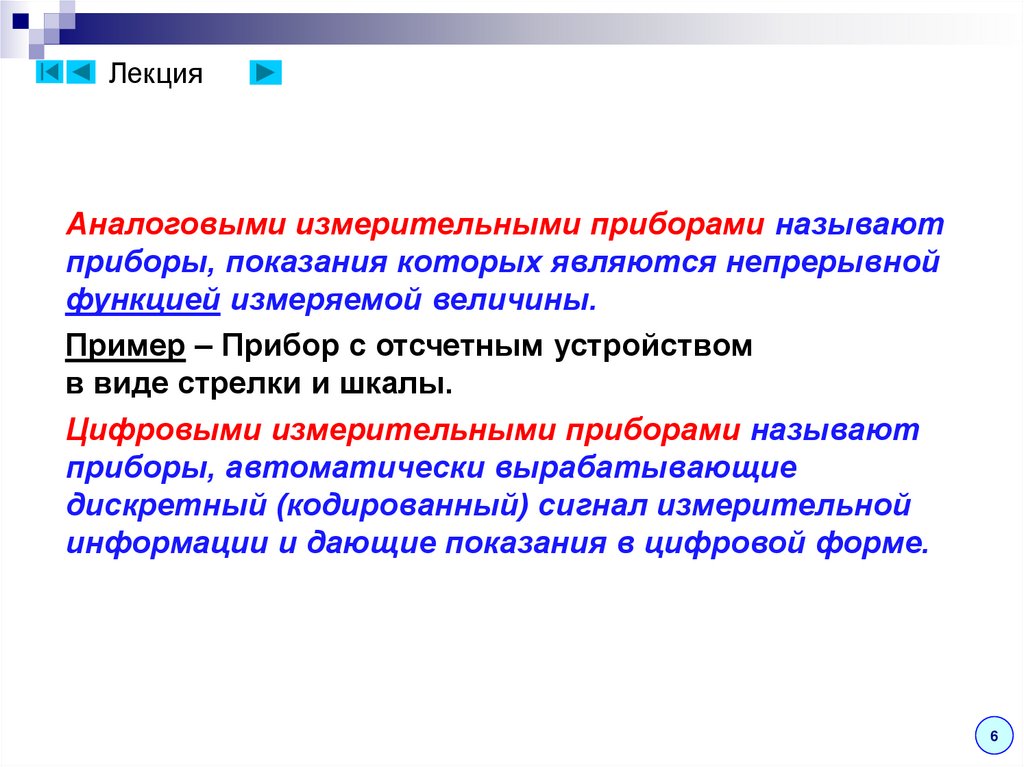
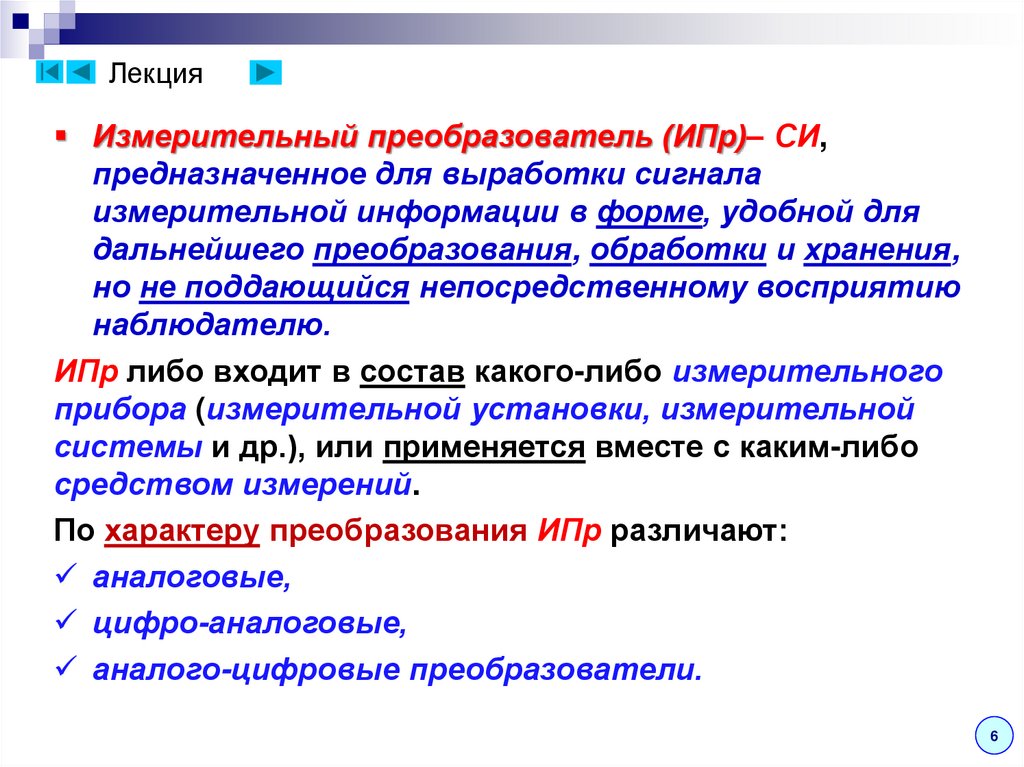
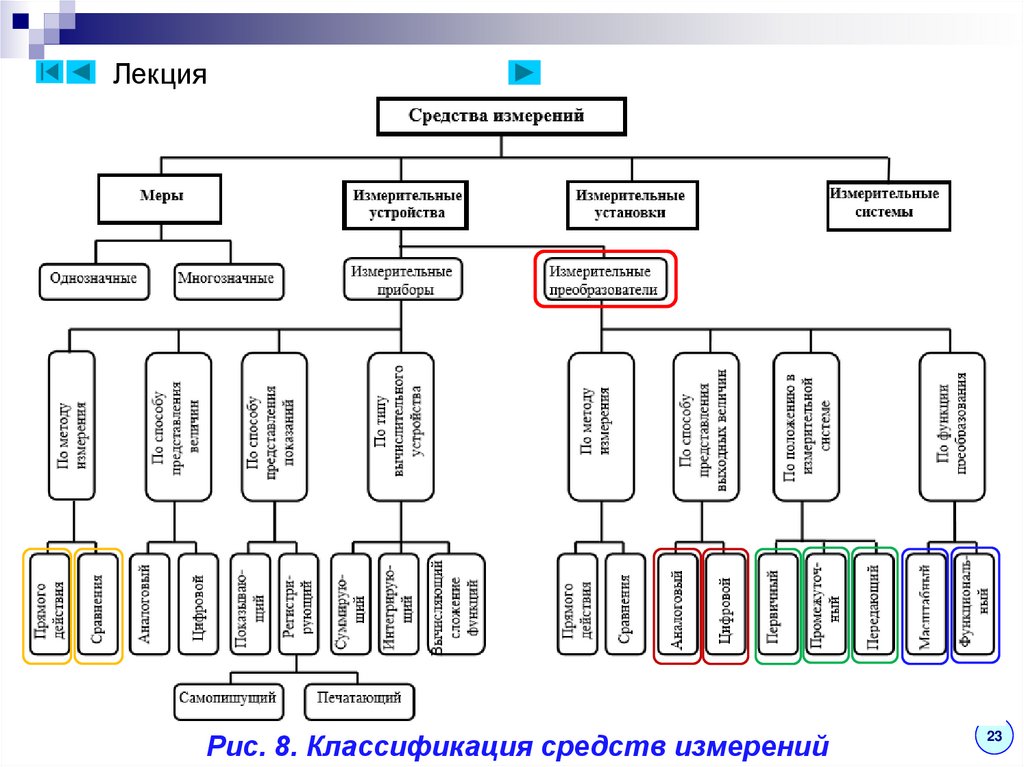


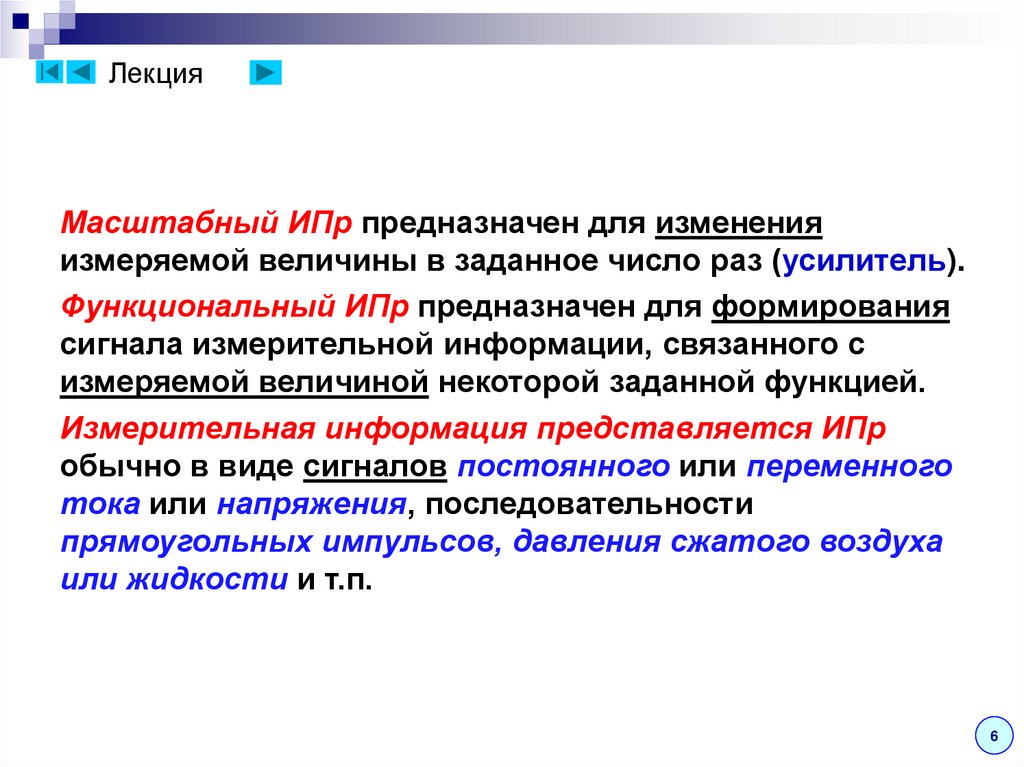
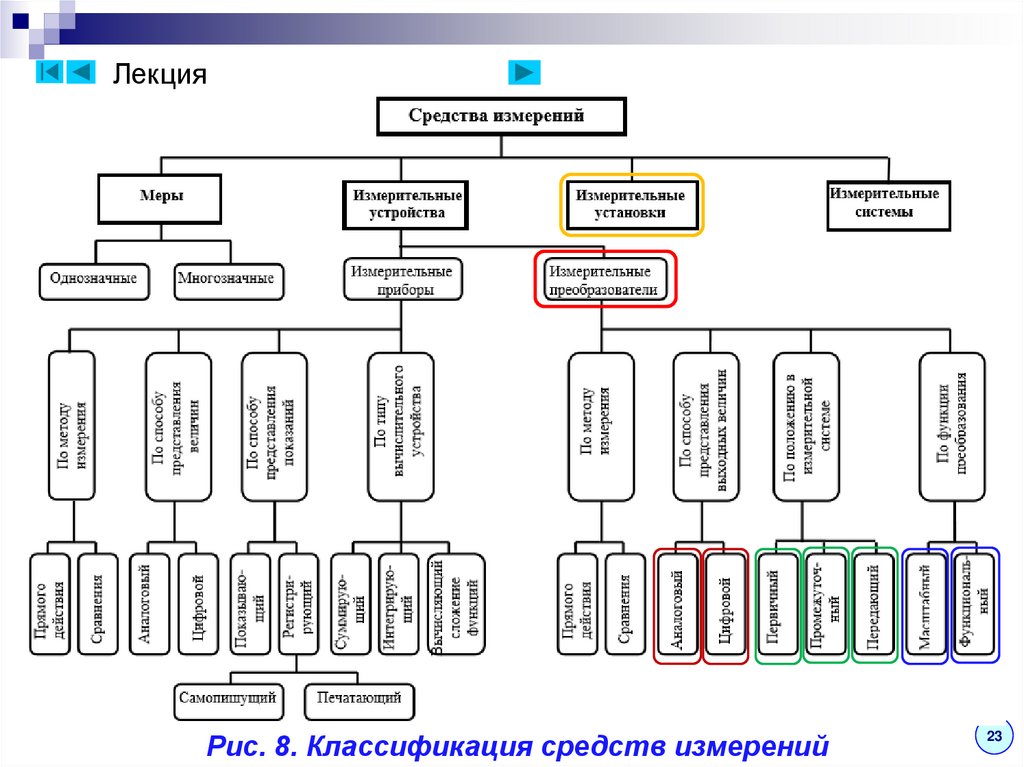


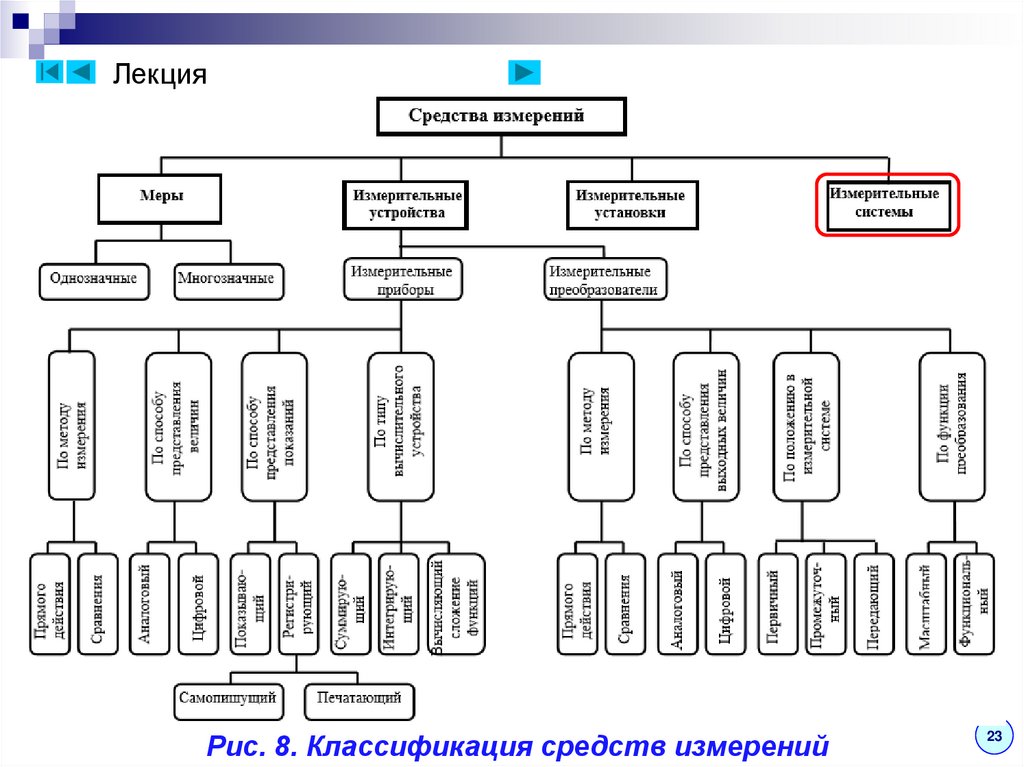


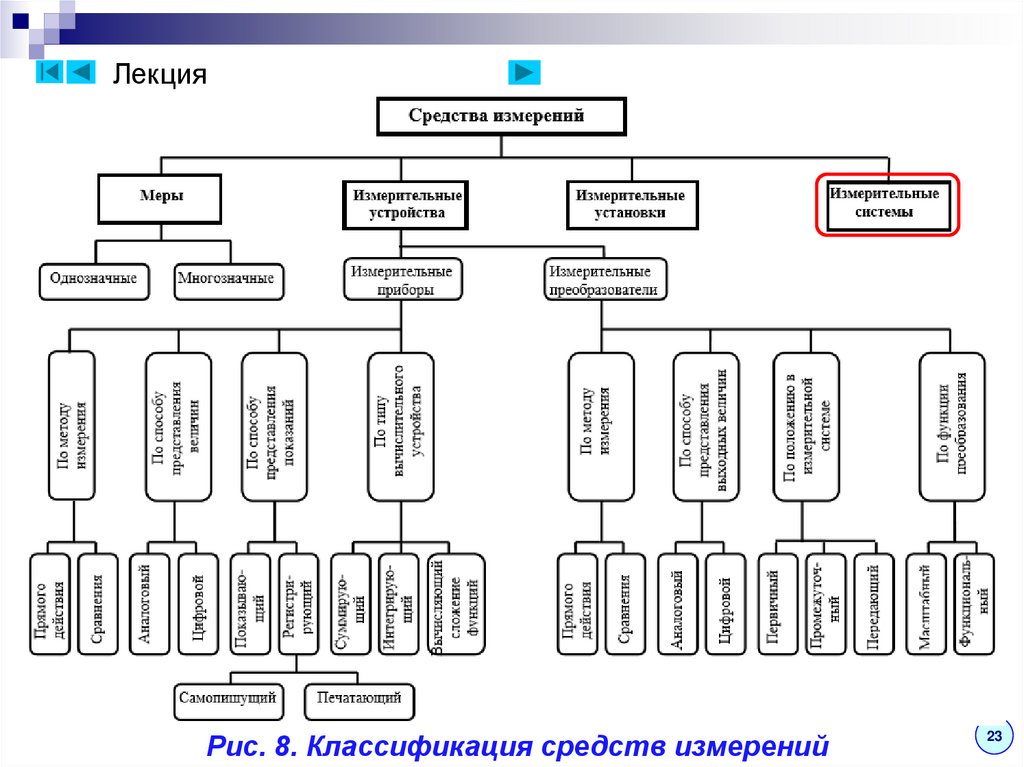


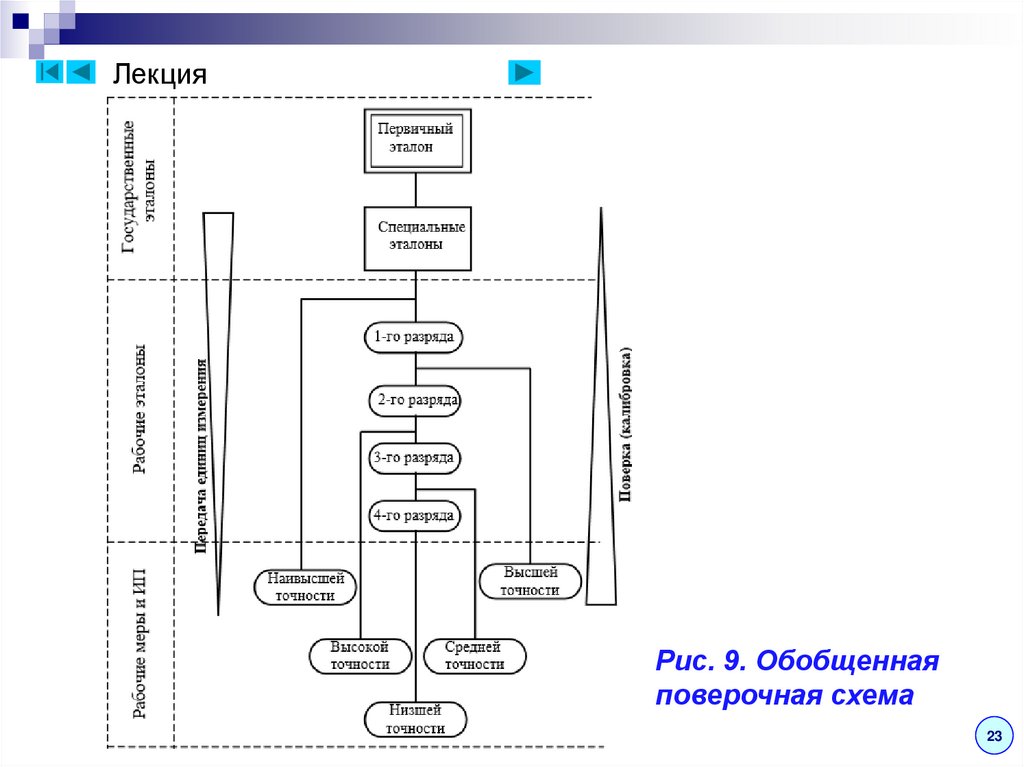

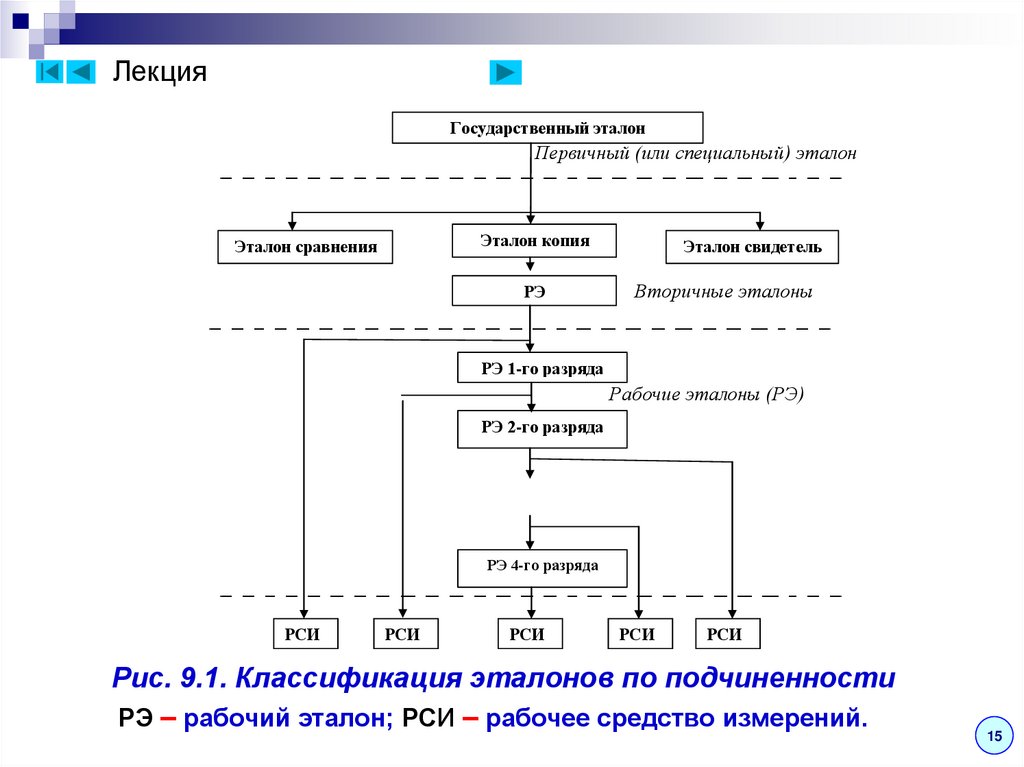

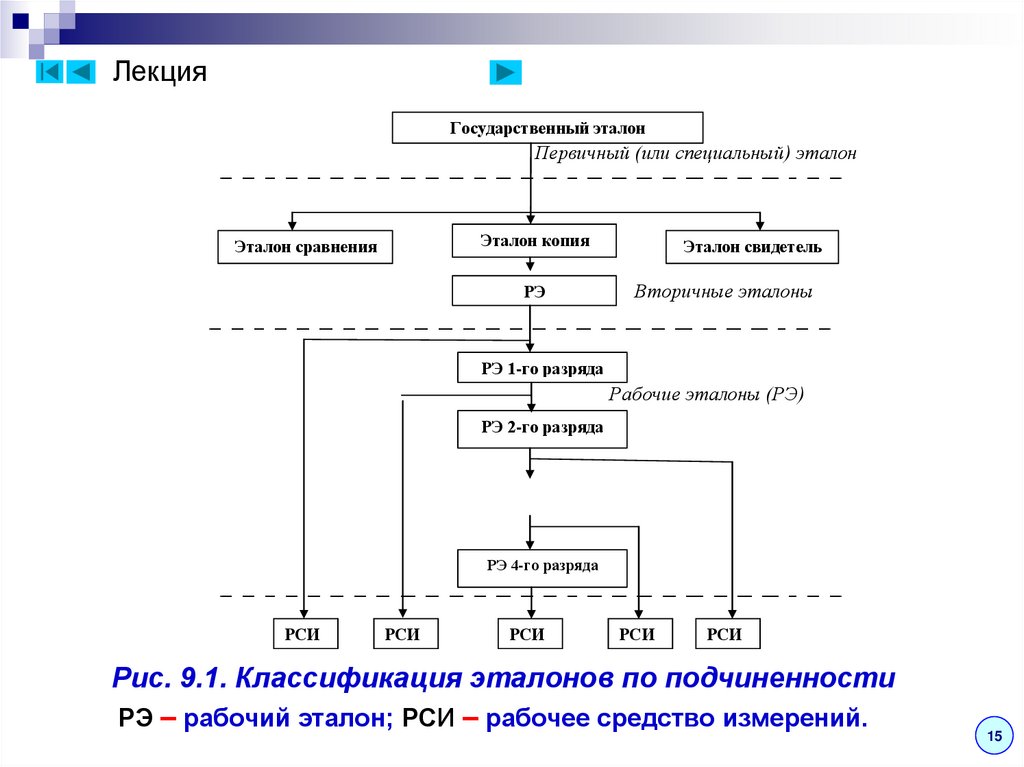


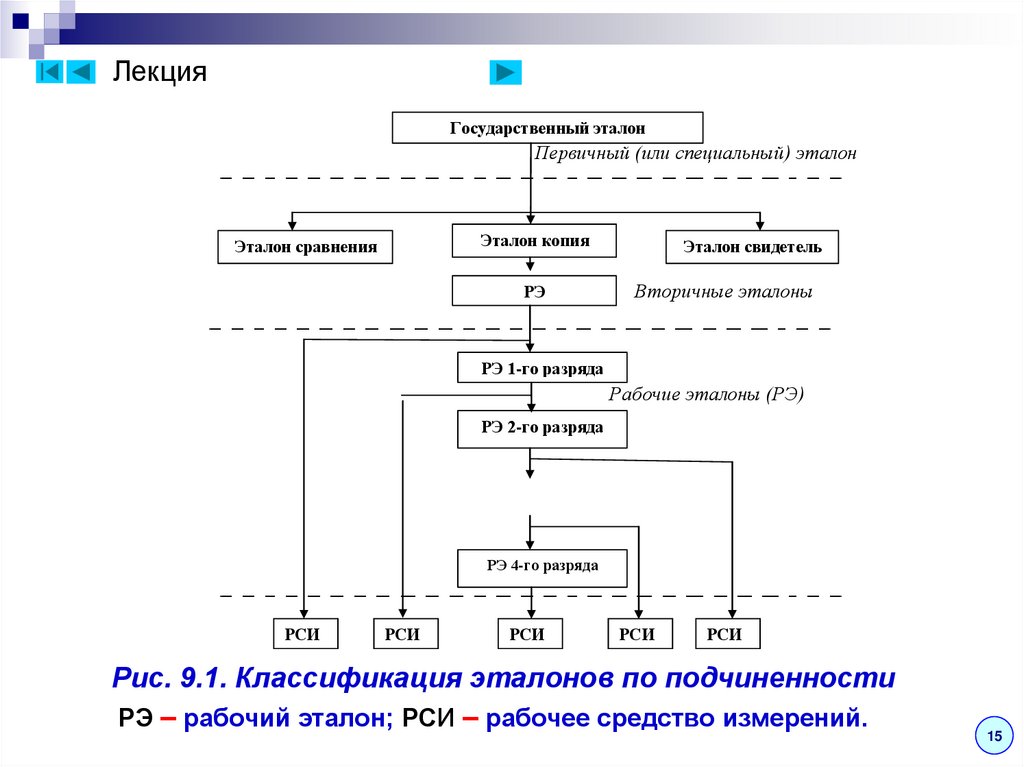

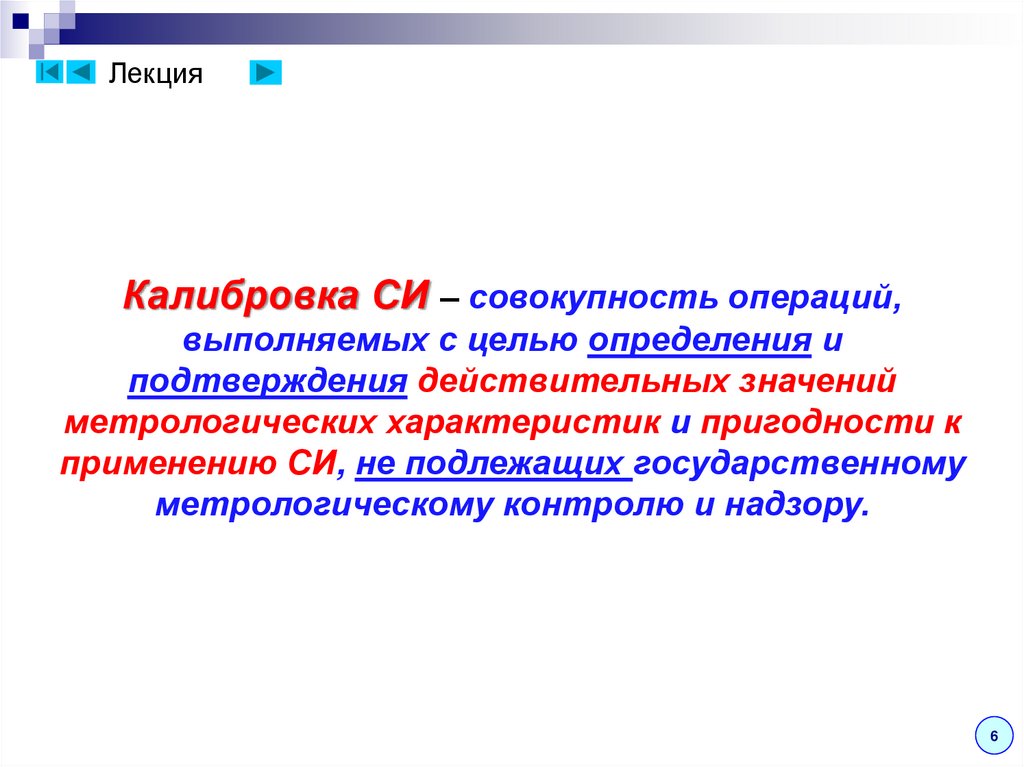

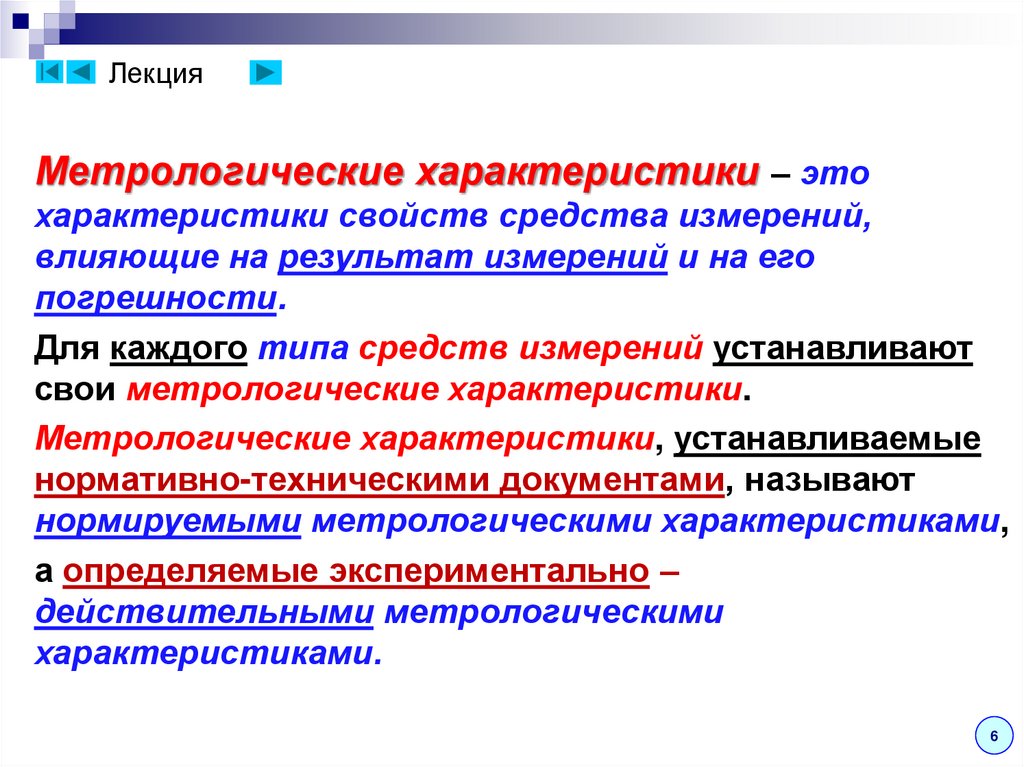



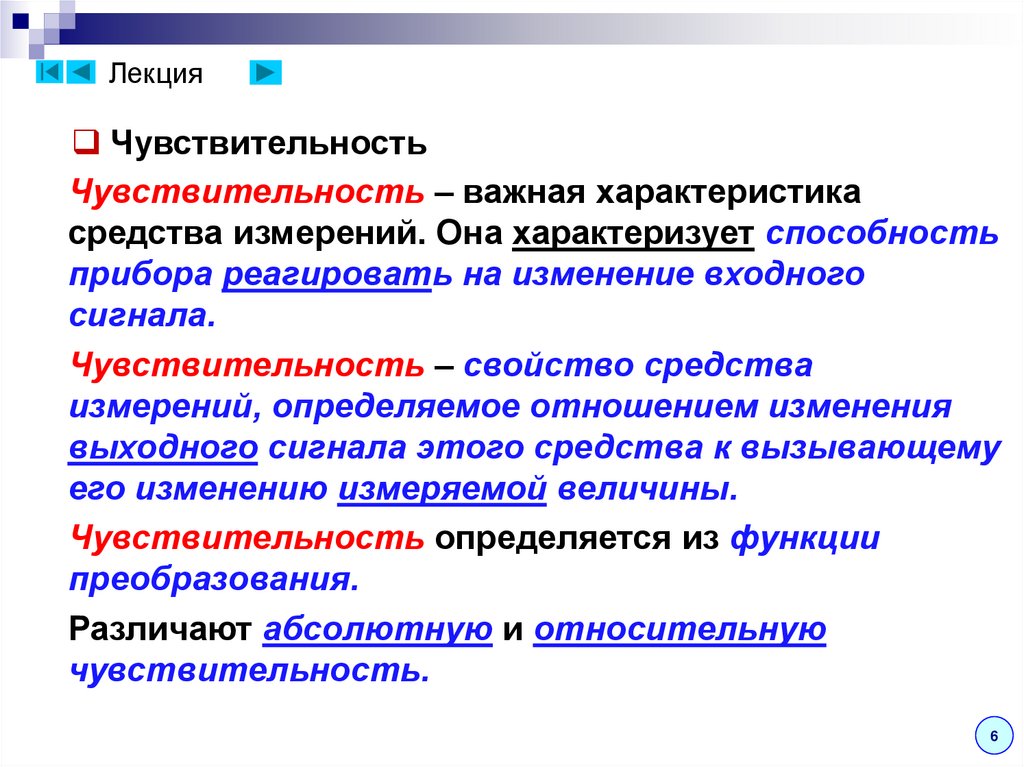

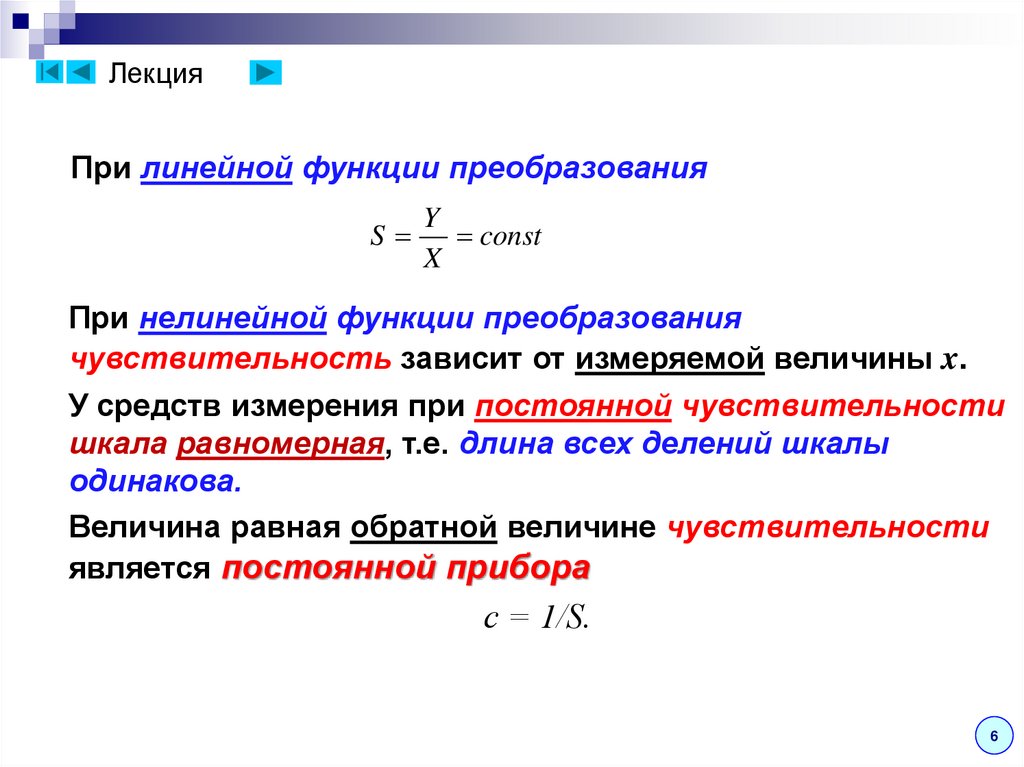
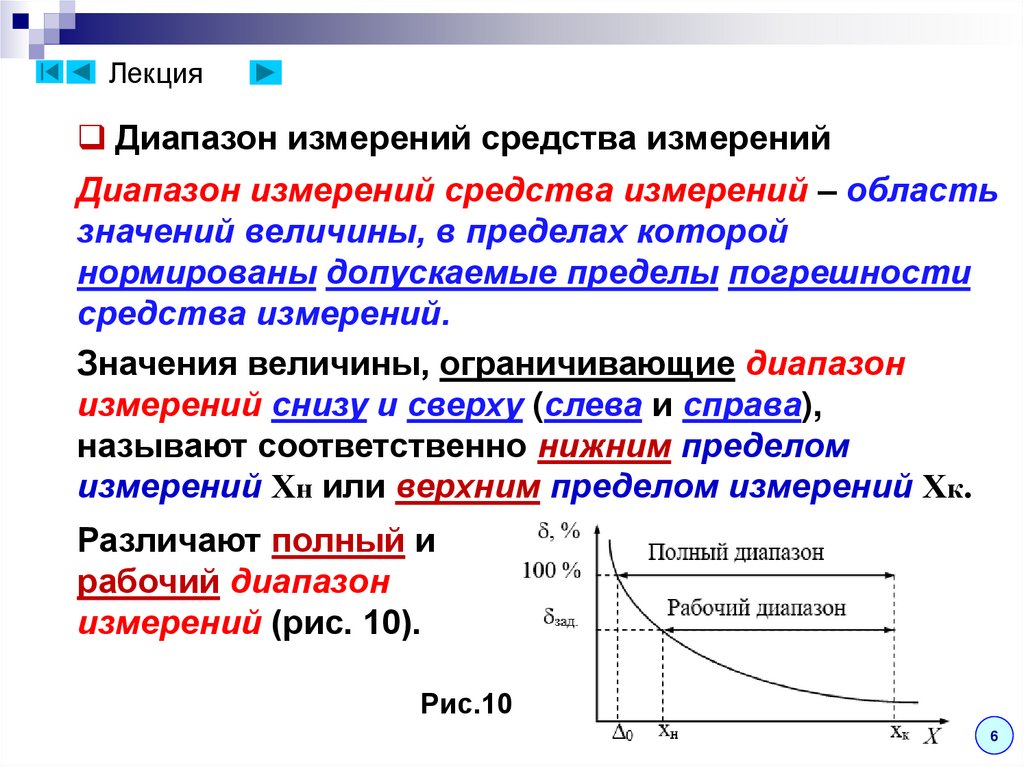


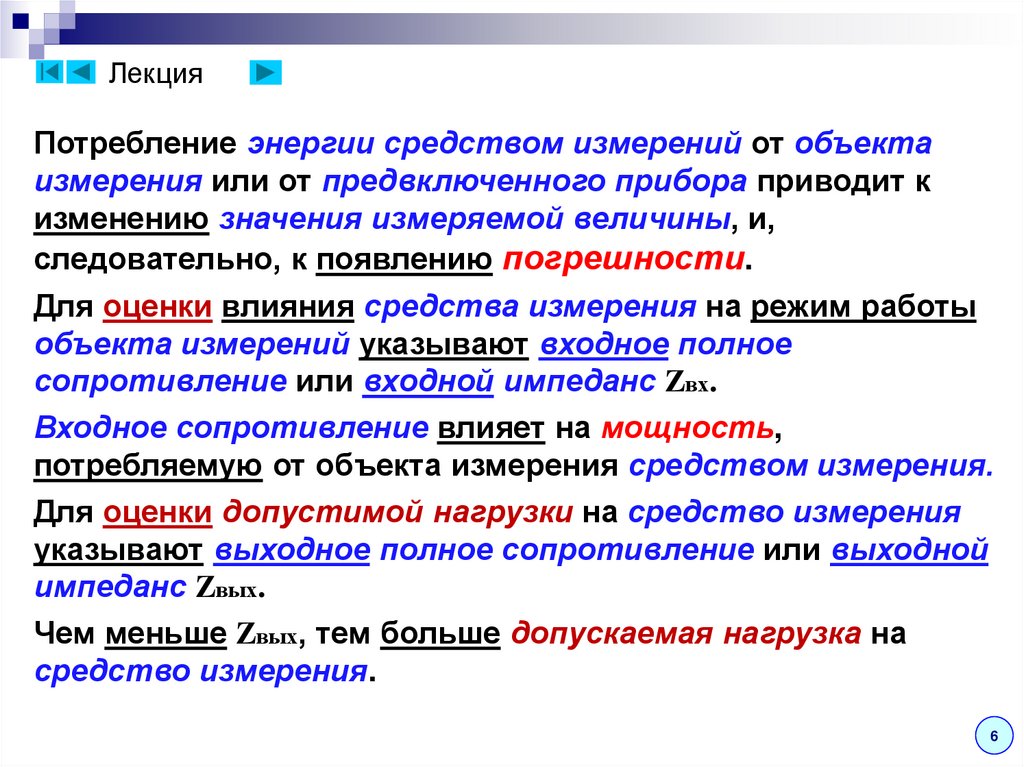





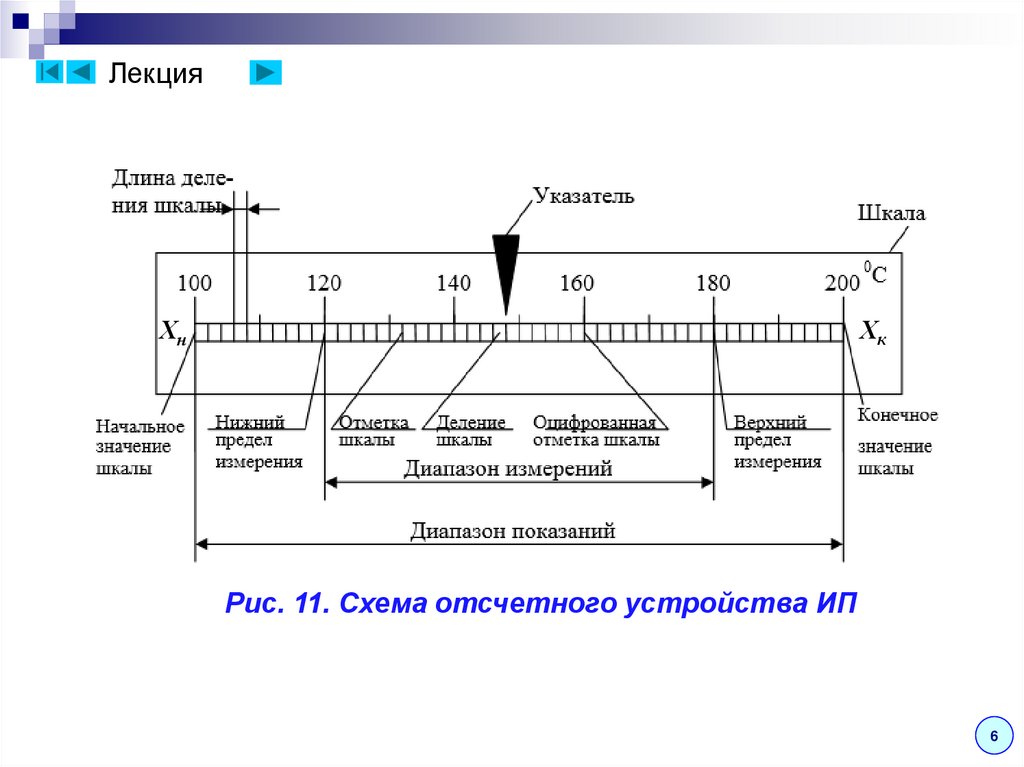

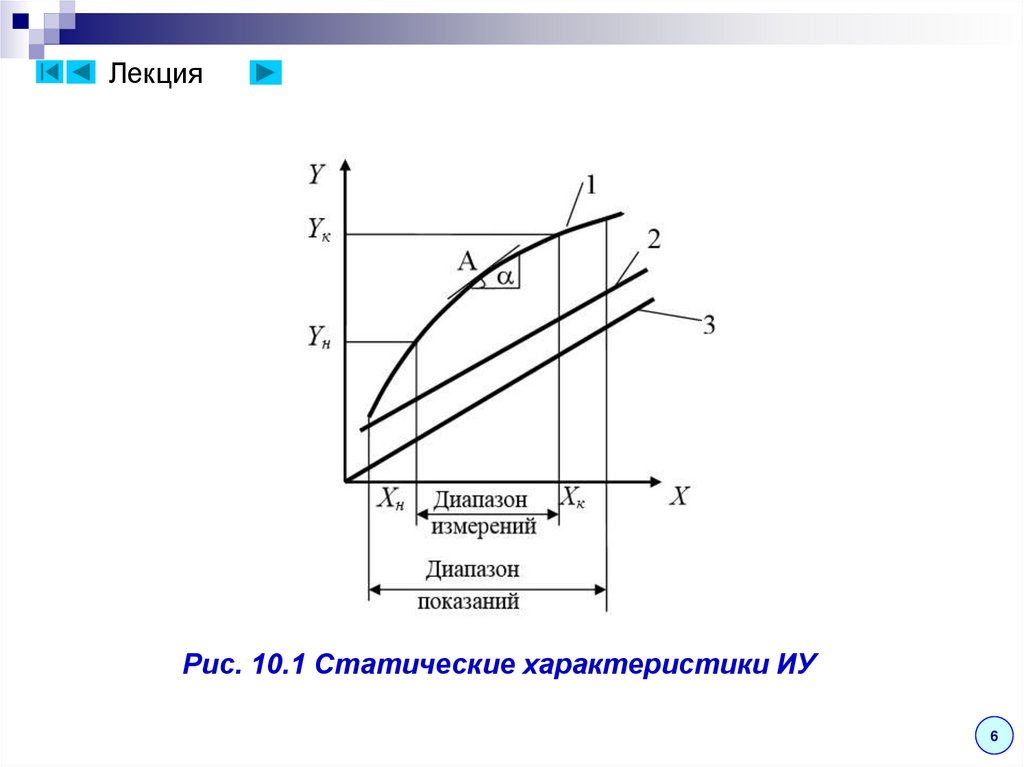


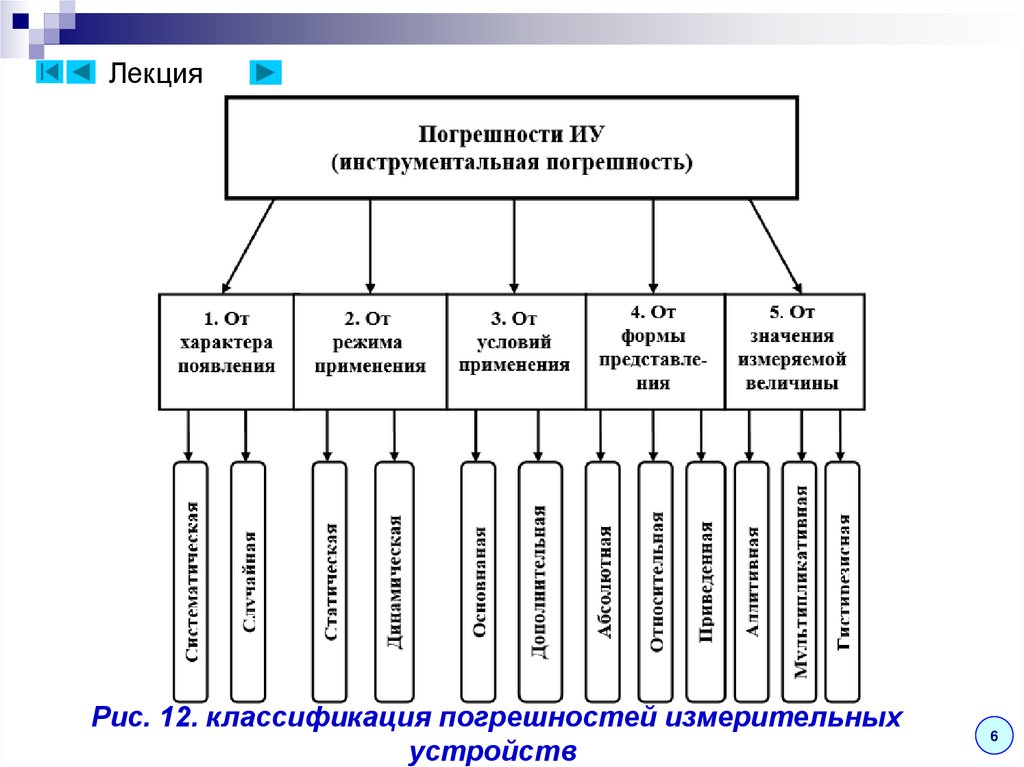

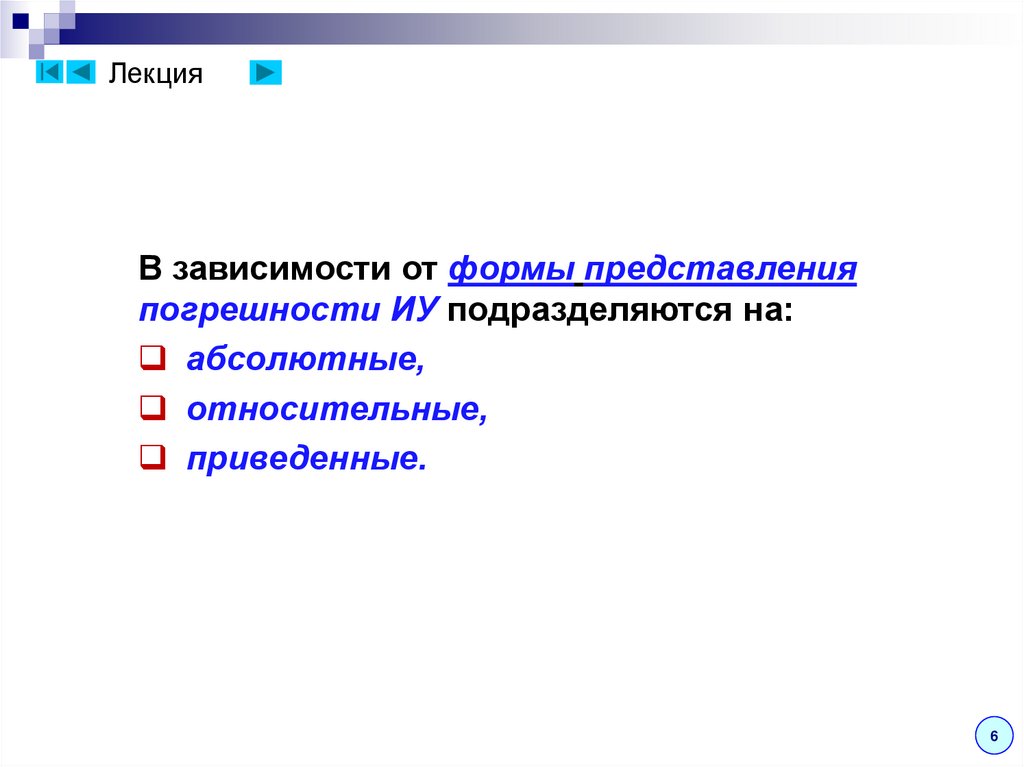





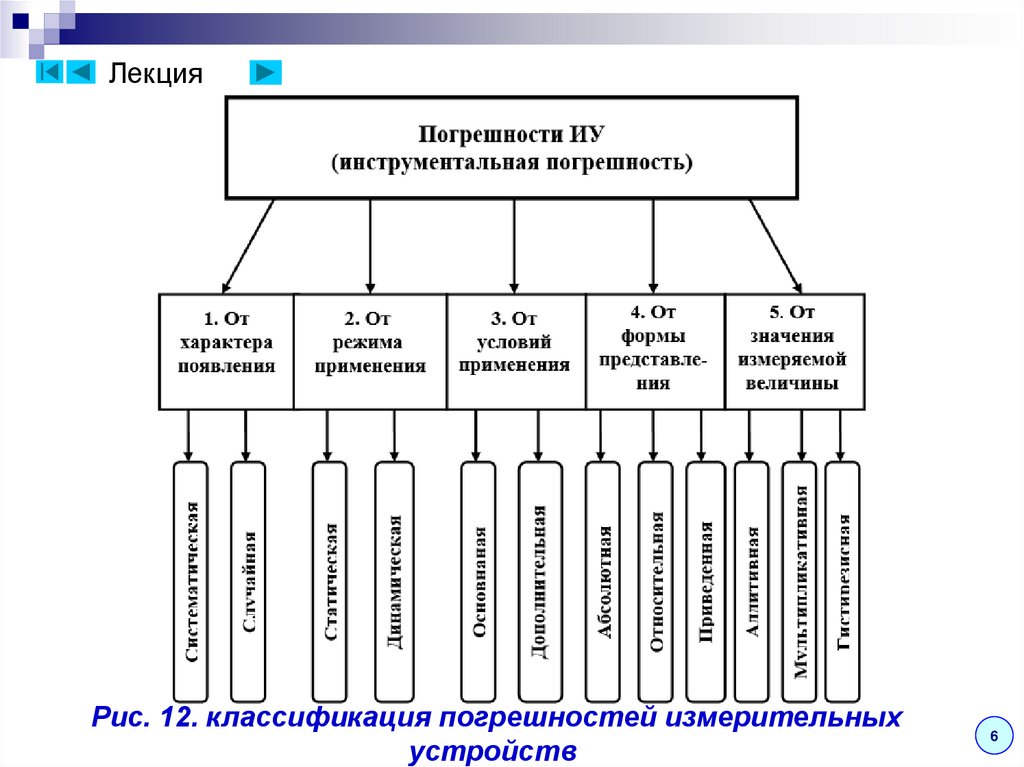
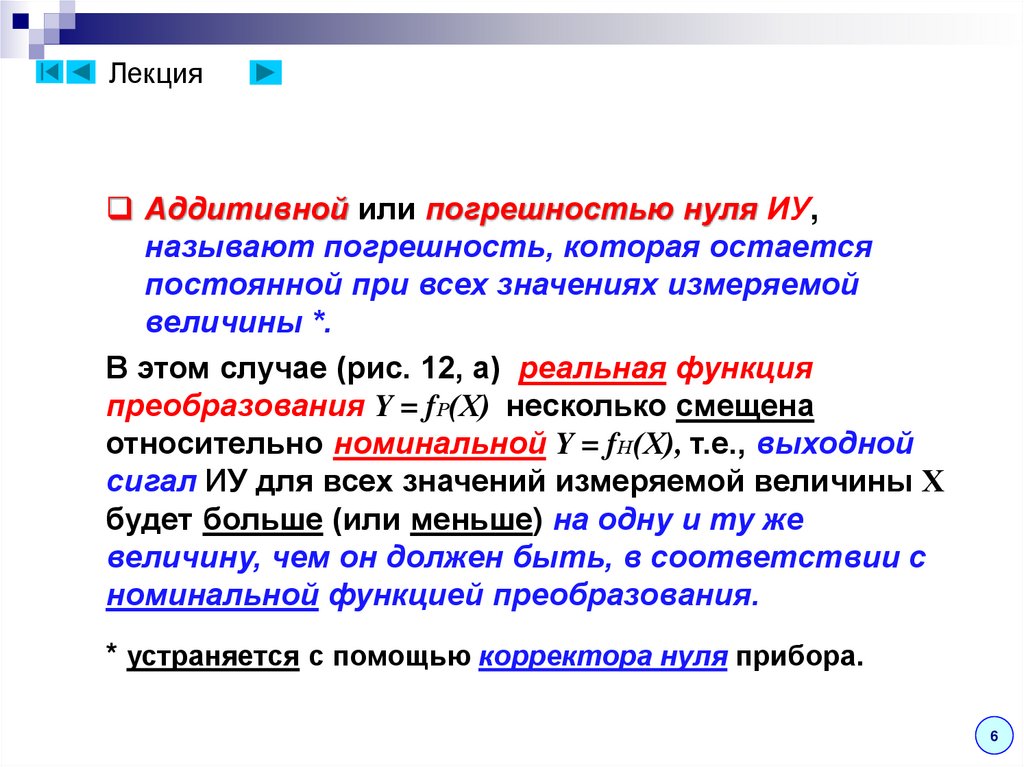
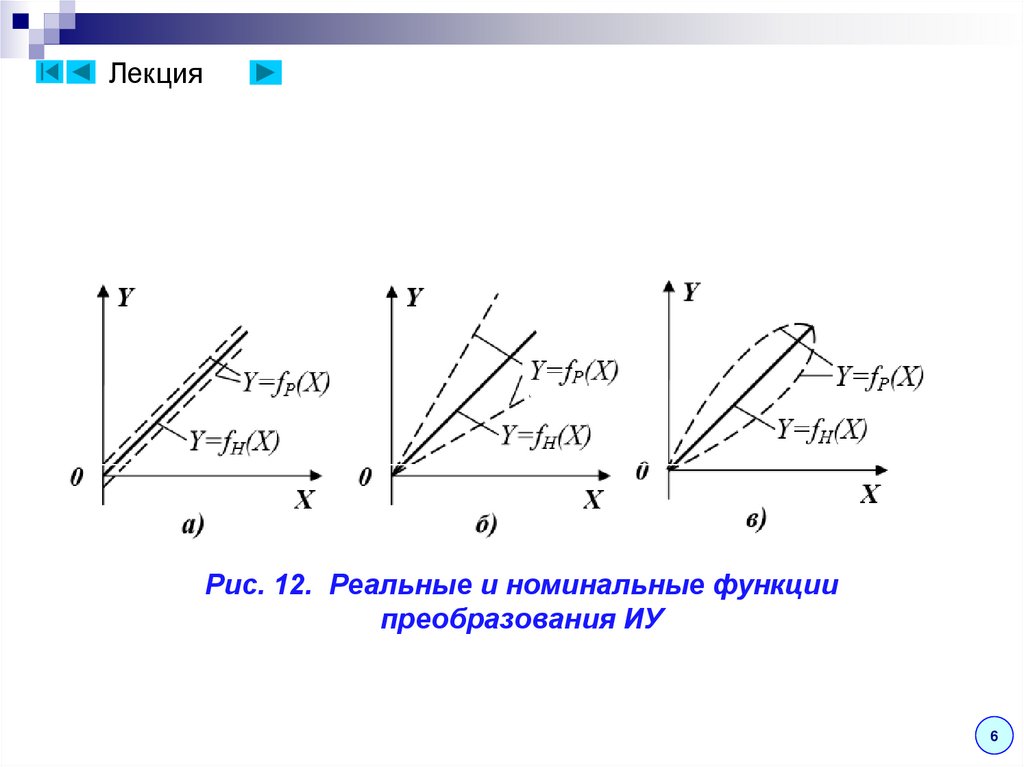

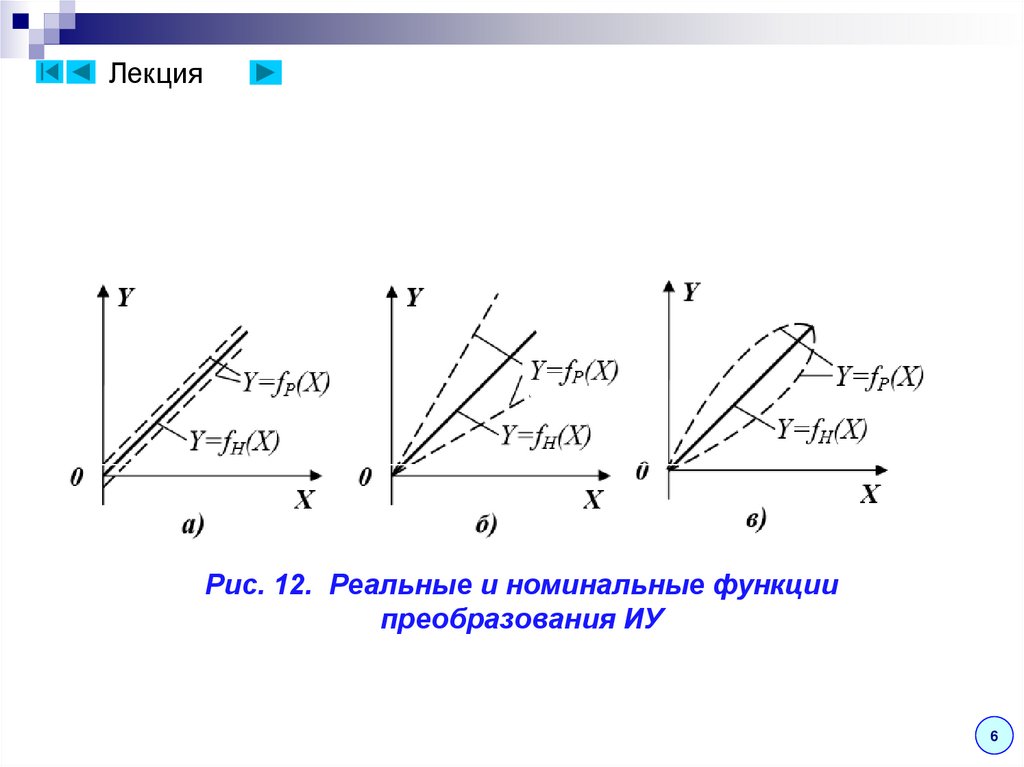


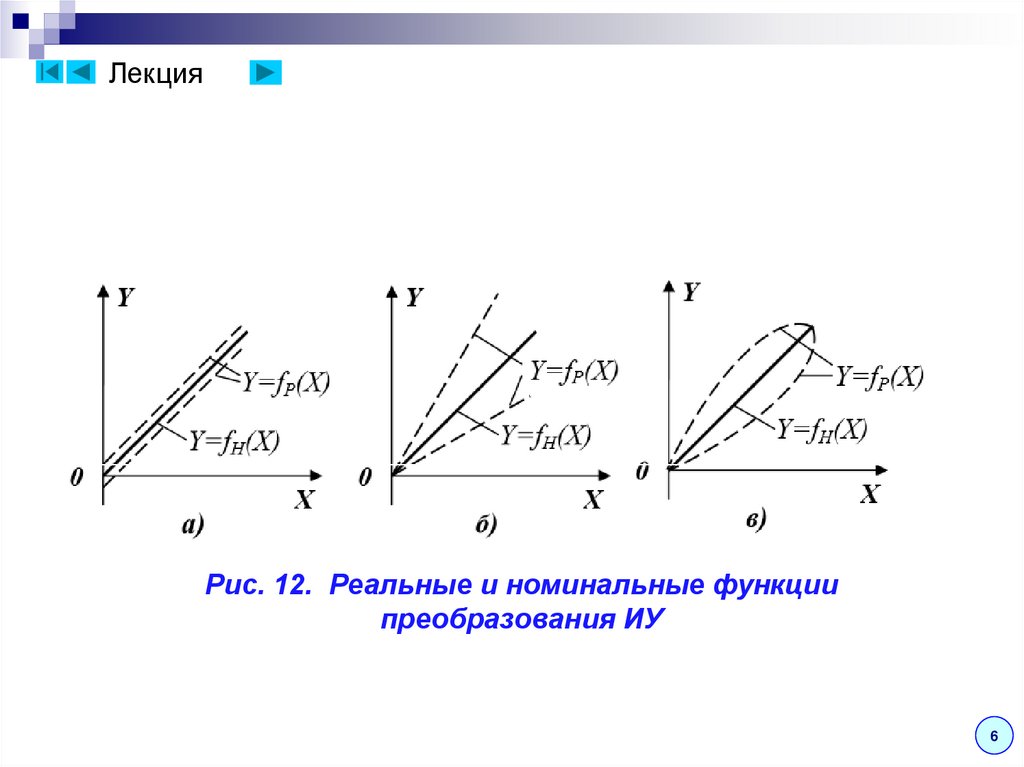








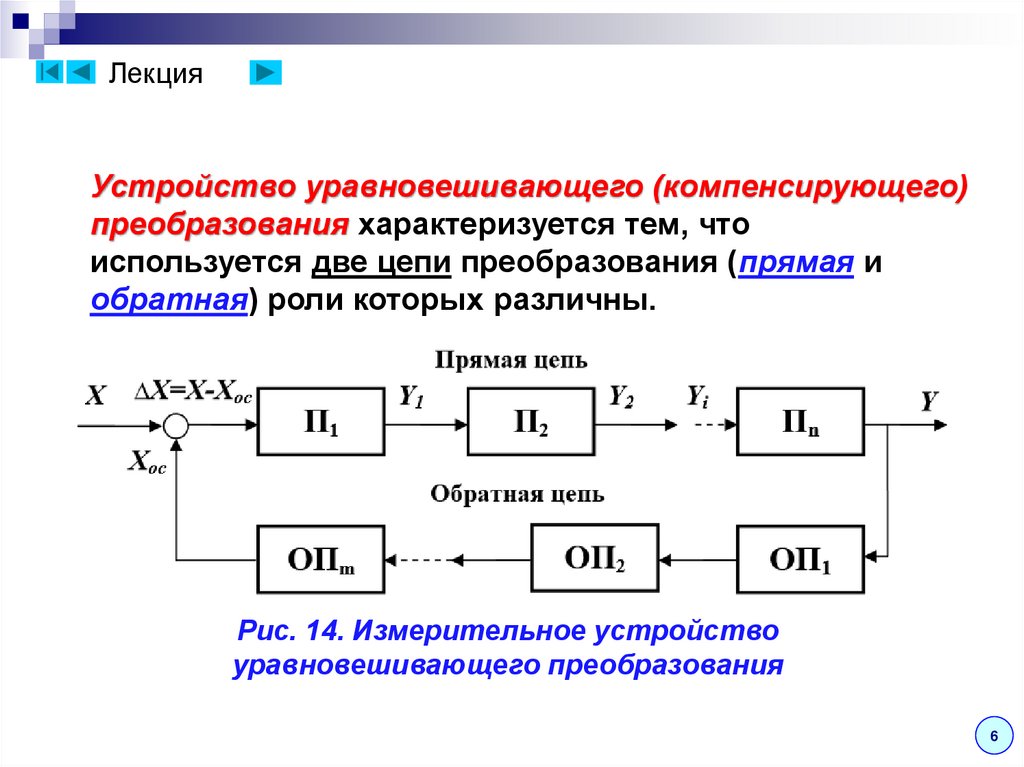


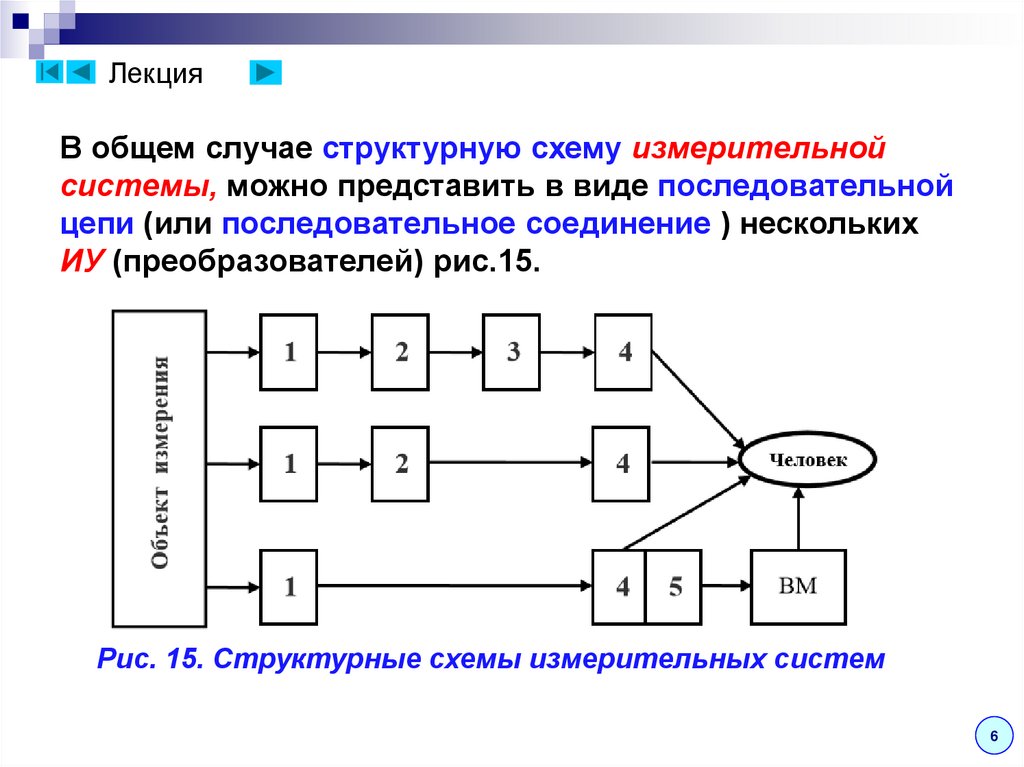


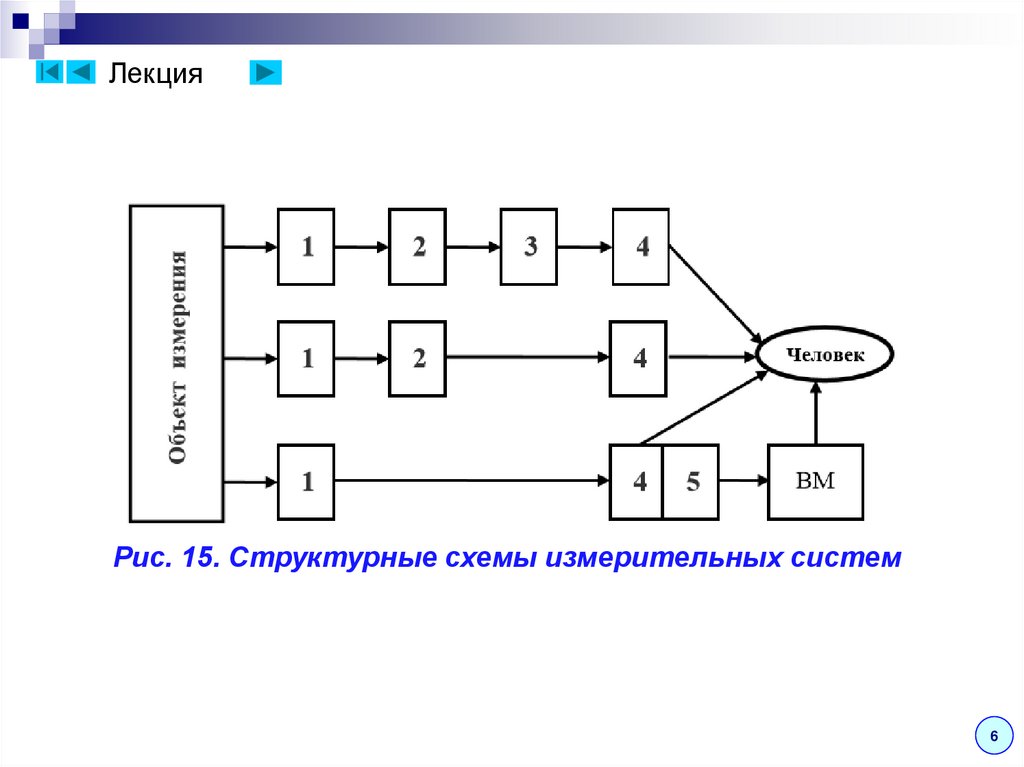



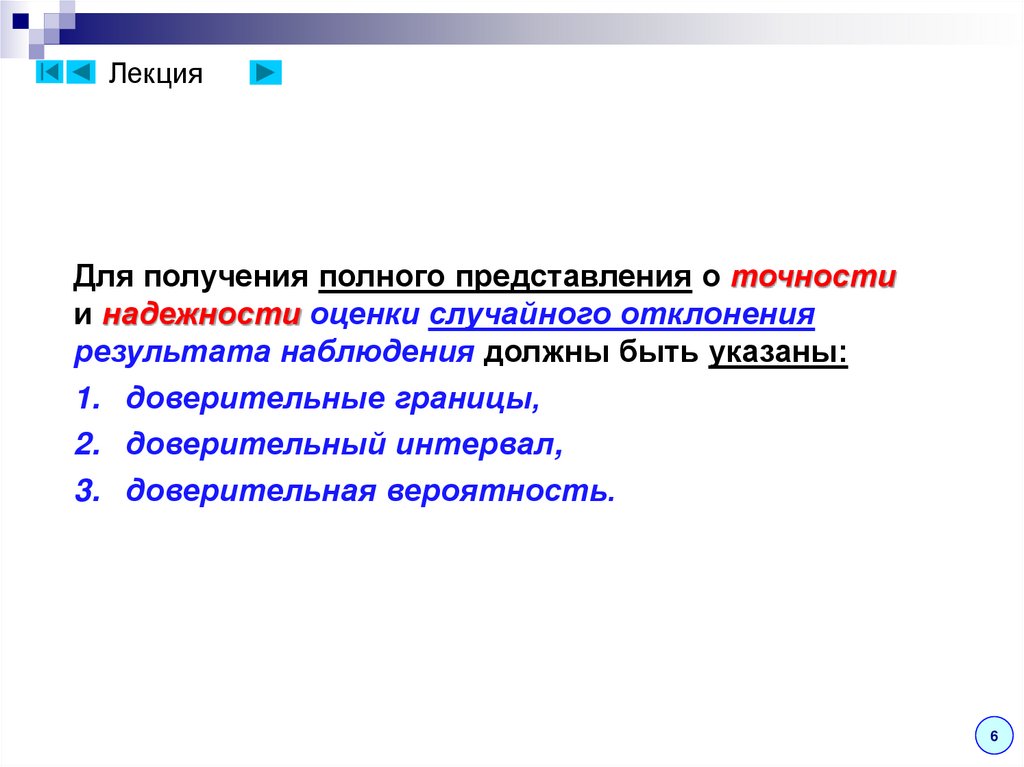







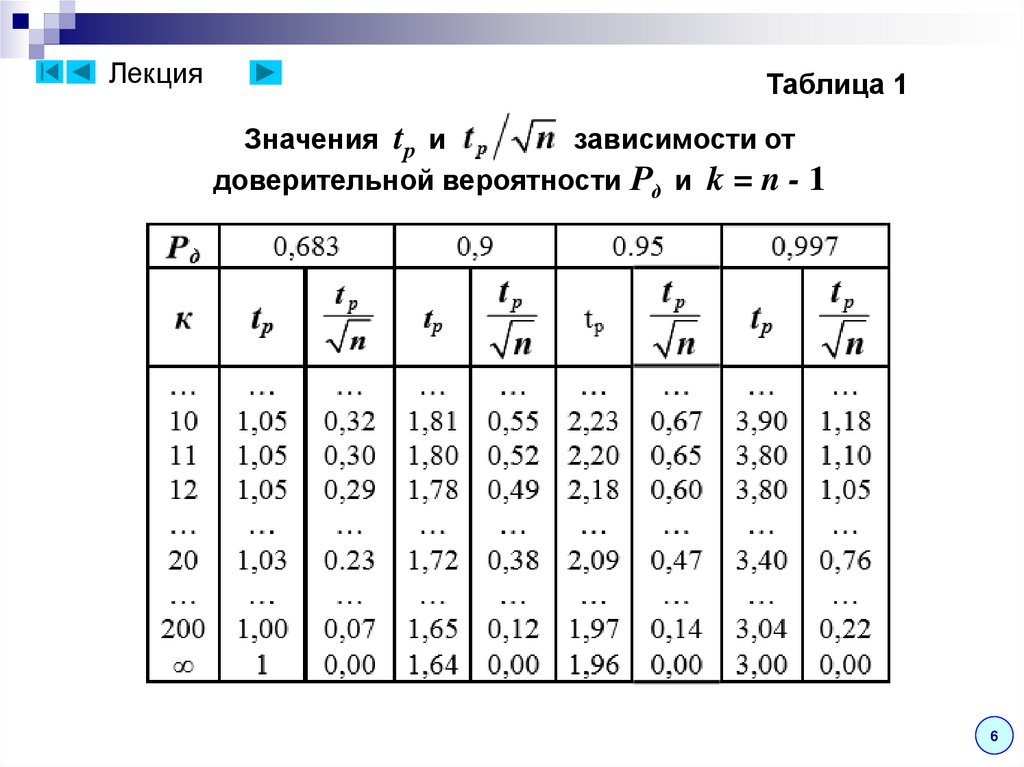


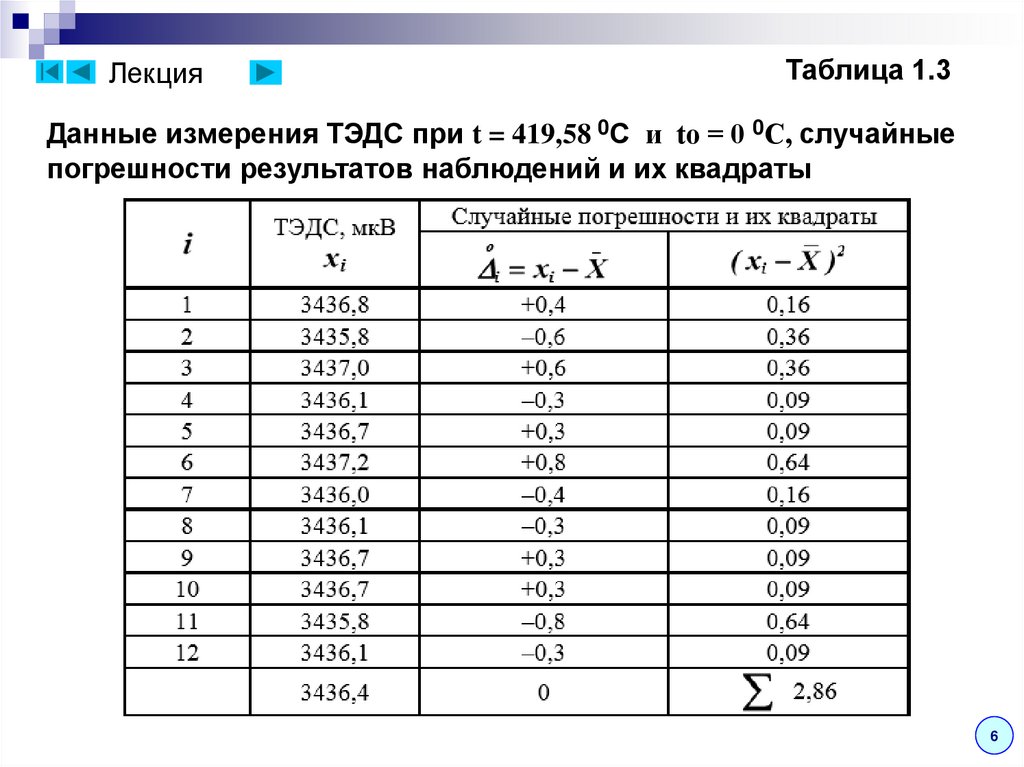



























 Математика
Математика








