5. Системы счисления

1. Системы счисления

2.

I. Системы счисления.
II. Перевод чисел из одной системы счисления в другую
1.Перевод из десятичной системы
а) целое число
б) правильная десятичная дробь
в) вещественное число.
2. Перевод в десятичную систему
3. Перевод из двоичной в восьмеричную и шестнадцатеричную
системы.
4. Перевод из восьмеричной и шестнадцатеричной системы в
двоичную
5. Перевод из восьмеричной в шестнадцатеричную систему и обратно.
III. Арифметические операции в позиционных системах счисления
1. сложение
2. вычитание
3. умножение
4. деление
Выход
2

3. Системы счисления

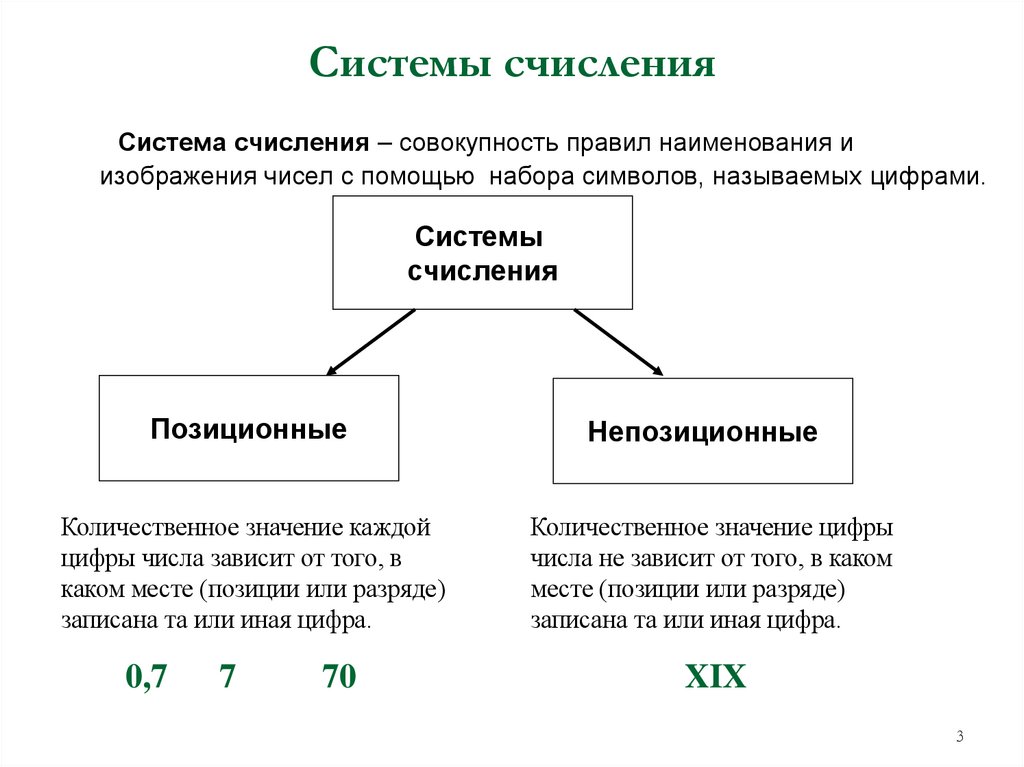
Система счисления – совокупность правил наименования и
изображения чисел с помощью набора символов, называемых цифрами.
Системы
счисления
Позиционные
Непозиционные
Количественное значение каждой
цифры числа зависит от того, в
каком месте (позиции или разряде)
записана та или иная цифра.
Количественное значение цифры
числа не зависит от того, в каком
месте (позиции или разряде)
записана та или иная цифра.
0,7
7
70
XIX
3

4. Непозиционные системы счисления

Система римских цифр, основанная на употреблении латинских букв для
десятичных разрядов
I = 1, X = 10, С = 100, М = 1 000
и их половин
V = 5, L = 50, D = 500.
Если большая цифра записана
перед меньшей , их складывают:
Если меньшая цифра записана
перед большей – из большей
вычитают меньшую:
4

5. Непозиционные системы счисления

Цифры V, L,D – не повторяются, I, X, C, M – могут повторно
использоваться до 3-х раз
5

6. Непозиционные системы счисления

Число в системе римских чисел записывается по схеме
«тысячи — сотни — десятки — единицы».
Пример. Записать число 1974 в системе римских цифр.
Решение. Выпишем тысячи, сотни, десятки и единицы:
1 000 — M;
900 — CM;
70 — LXX;
4 — IV.
1974 =MCMLXXIV
6

7. Непозиционные системы счисления

Сложение и вычитание
Сложить два римских числа достаточно просто.
Например: XIX+XXVI=XXXV
Сложение выполняется в следующей последовательности:
а) IX+VI=XV (I после V "уничтожает" I перед X);
б) X+XX=XXX (при добавлении еще одного X, получаем XXXX, или XL).
Сложность вычитания римских чисел приблизительно такая же.
Например, для вычитания из 500 числа 263 уменьшаемое число необходимо
для начала разложить на более мелкие составляющие, а затем сократить
повторяющиеся в уменьшаемом и вычитаемом знаки:
D−CCLXIII=CCCCLXXXXVIIIII−CCLXIII=CCXXXVII
500-263 = 100+100+100+100+50+10+10+10+10+5+1+1+1+1)-263
Умножение.
С умножением дело обстояло гораздо сложнее.
Допустим, требовалось умножить 126 на 37.
CXXVI⋅XXXVII
Приходилось умножать множимое на каждую цифру множителя отдельно, а
затем складывать все произведения. Такая техника выполнения умножения
аналогична умножению многочленов.
7

8. Недостатки непозиционных систем счисления

сложность представления больших чисел
(больше 10 000);
сложность выполнения арифметических
операций над числами, записанными с
помощью этих систем счисления.
8

9. Позиционные системы счисления

Первая позиционная система счисления была придумана еще в
Древнем
Вавилоне,
причем
вавилонская
нумерация
была
шестидесятеричная, т.е. в ней использовалось шестьдесят цифр!
В XIX веке довольно широкое
двенадцатеричная система счисления.
распространение
получила
В настоящее время наиболее распространены десятичная,
двоичная, восьмеричная и шестнадцатеричная системы счисления.
9

10. Основание системы счисления

Количество различных символов, используемых для изображения
числа в позиционных системах счисления, называется основанием
системы счисления.
Позиции цифр называются разрядами.
Основание системы счисления показывает во сколько раз изменяется
количественное значение цифры при перемещении её на соседнюю
позицию
За основание системы можно принять любое натуральное число не
менее 2.
10

11. Основание системы счисления

Компьютеры используют двоичную систему, так как
• для её реализации нужны технические устройства с двумя
устойчивыми состояниями,
• представление информации с помощью только двух состояний
надежно и помехоустойчиво,
• возможно применение аппарата булевой алгебры для выполнения
логических преобразований,
• двоичная арифметика намного проще десятичной
Помимо двоичной системы специально для работы с вычислительной
техникой были разработаны восьмеричная и шестнадцатеричная
системы счисления. Данные системы счислений легко переводятся в
двоичный код и в тоже время проще для восприятия человеком.
Двоичная, восьмеричная и шестнадцатеричная системы считаются
машинными.
11

12. Основание системы счисления

Система счисления
Основание
Алфавит цифр
Десятичная
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двоичная
2
0, 1
Восьмеричная
8
0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
12

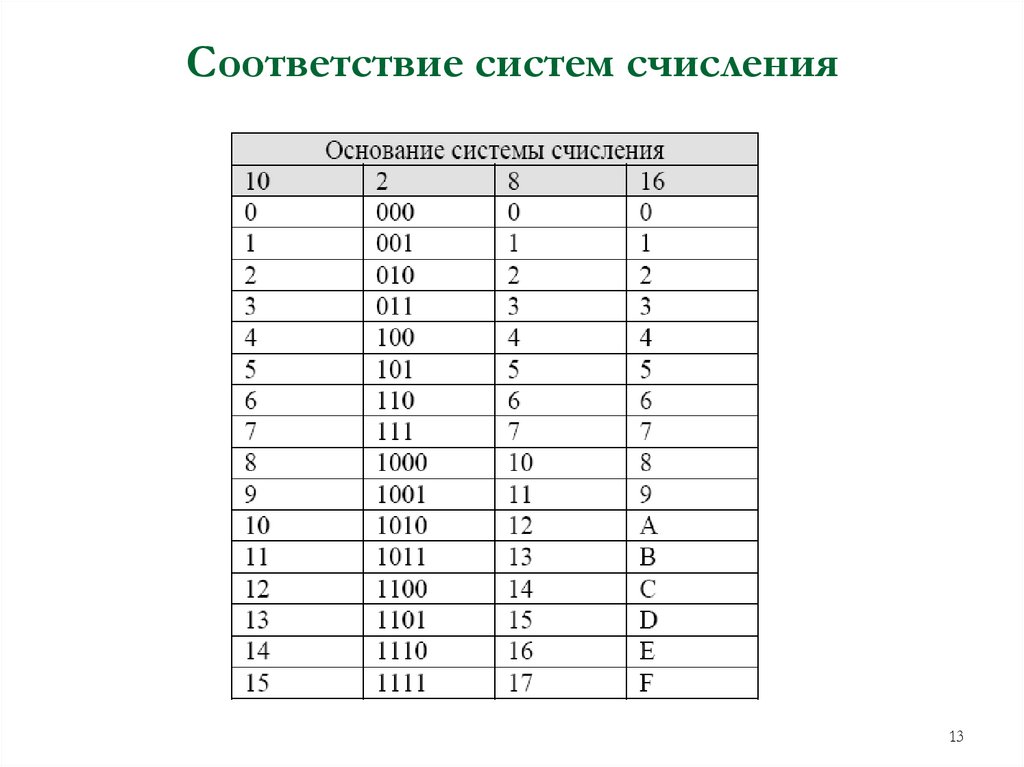
13. Соответствие систем счисления

13

14. Развернутая форма записи числа Aq в системе с основанием q

Cокращённая форма записи числа Aq в системе счисления с основанием q
Aq= an-1an-2 … a1a0, a-1… a-m,
где ai – цифры системы счисления, n и m –число целых и дробных
разрядов соответственно
Развернутая форма записи числа Aq в системе с основанием q
Aq=an-1qn-1+an-2qn-2+…+a1q1+a0q0+a-1q-1+…+a-mq-m ,
где ai – цифры системы счисления, n и m –число целых и дробных
разрядов соответственно
14

15.

3247810=3*10000+2*1000+4*100+7*10+8=
3*104+2*103+4*102+7*101+8*100
26,38710=2*101+6*100+3*10-1+8*10-2+7*10-3
101101, 0112=1*10101+0*10100+1*1011+1*1010+
+0*101+1*100+0*10-1+1*10-10+1*10-11
15FC16=1*103+5*102+F*101+C
!!! В любой системе счисление ее основание записывается как 10
В меню
15

16. Перевод целых чисел из десятичной системы счисления

Алгоритм перевода:
1. Основание новой системы счисления выразить в десятичной и все
последующие действия производить в десятичной системе счисления.
2. Последовательно делить с остатком данное число и получаемые
целые частные на основание новой системы счисления до тех пор,
пока частное не станет равно нулю.
3. Полученные остатки выразить цифрами алфавита новой системы
счисления
4. Записать число в новой системе счисления из полученных остатков,
начиная с последнего.
16

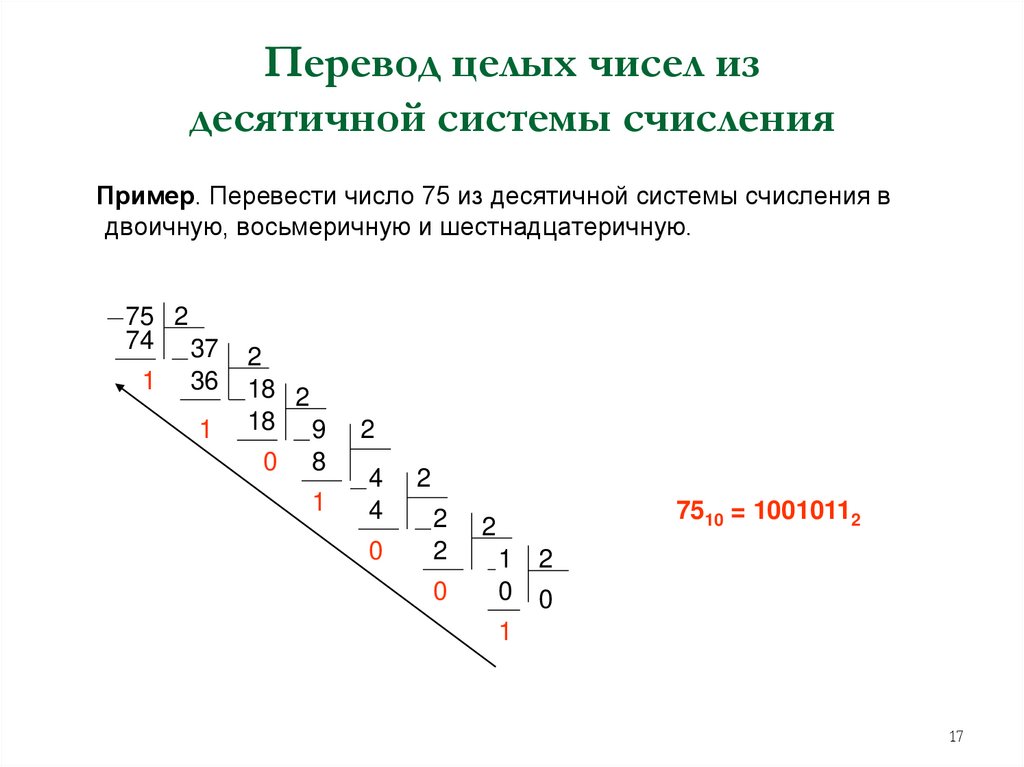
17. Перевод целых чисел из десятичной системы счисления

Пример. Перевести число 75 из десятичной системы счисления в
двоичную, восьмеричную и шестнадцатеричную.
75 2
74 37
1 36
1
2
18 2
18 9
0 8
1
2
4
4
0
2
2
2
0
7510 = 10010112
2
1
0
2
0
1
17

18. Перевод целых чисел из десятичной системы счисления

Пример. Перевести число 75 из десятичной системы счисления в
двоичную, восьмеричную и шестнадцатеричную.
75 8
72 9
3 8
1
8
1
0
75 16
64 4
11 0
8
0
16
0
4
1
7510 = 1138
В меню
7510 = 4B16
18

19. Перевод правильной десятичной дроби из десятичной системы счисления

Алгоритм перевода:
1. Основание новой системы счисления выразить в десятичной и все
последующие действия производить в десятичной системе счисления
2. Последовательно умножать десятичную дробь и получаемые дробные
части произведений на основание новой системы счисления до тех
пор, пока дробная часть не станет равна нулю или не будет достигнута
необходимая точность перевода.
3. Полученные целые части произведений выразить цифрами алфавита
новой системы счисления.
4. Записать дробную часть числа в новой системе счисления начиная с
целой части первого произведения.
19

20. Перевод правильной десятичной дроби из десятичной системы счисления

Пример. Перевести число 0,1875 из десятичной системы в счисления в
двоичную, восьмеричную и шестнадцатеричную.
0,1875
2
0,3750
2
0,7500
2
0,1875
8
1,5000
8
4,0000
0,1875
16
1,1250
1,875
3,0000
1,5000
2
1,0000
0,187510 = 0,00112
0,187510 = 0,148
0,187510 = 0,316
20

21. Перевод правильной десятичной дроби из десятичной системы счисления

Пример. Перевести число 0,35 из десятичной системы в счисления в
двоичную, восьмеричную и шестнадцатеричную.
0,35
2
0,70
2
1,40
2
0,80
2
0,35
8
2,80
8
0,35
16
5,60
16
6,40
8
9,60
3,20
1,60
2
1,20
0,3510 0,010112
В меню
0,3510 0,2638
0,3510 0,5916
21

22. Перевод вещественных чисел из десятичной системы счисления

При переводе смешанных дробей отдельно по
своим правилам переводятся целая и дробные части,
результаты перевода разделяются запятой.
22

23. Перевод вещественных чисел из десятичной системы счисления

Пример. Перевести число 68,74 из десятичной системы в счисления в
двоичную, восьмеричную и шестнадцатеричную
68 2
68 34
0 34
0
2
17 2
16 8
1 8
0
0,74
2
1,48
2
2
4
4
0
0,96
2
2
2
2
0
1,92
2
2
1
0
2
0
1
68,7410 = 1000100,101112
1,84
2
1,68
23

24. Перевод вещественных чисел из десятичной системы счисления

Пример. Перевести число 68,74 из десятичной системы в счисления в
двоичную, восьмеричную и шестнадцатеричную
68 8
64 8
4 8
0
8
1
0
0,74
8
5,92
8
8
0
7,36
8
1
2,88
68,7410 = 104,5728
24

25. Перевод вещественных чисел из десятичной системы счисления

Пример. Перевести число 68,74 из десятичной системы в счисления в
двоичную, восьмеричную и шестнадцатеричную
68 16
64 4
4 0
16
0
4
0,74
16
11,84
16
13,44
68,7410 = 44,BD8
В меню
25

26. Перевод чисел в десятичную систему счисления

При переводе числа из системы счисления с основанием q в десятичную
надо представить это число в виде суммы произведений степеней
основания его системы счисления на соответствующие цифры числа
an-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m
и выполнить арифметические вычисления.
q-основание системы счисления, представленное в десятичной системе
26

27. Перевод чисел в десятичную систему счисления

Пример. Перевести число 1011,1 из двоичной системы счисления в
десятичную.
разряды
число
3 2 1 0 -1
1 0 1 1, 12 = 1∙23 + 0∙22 + 1∙21 + 1∙20 + 1∙2-1 = 11,510
Пример. Перевести число 276,8 из восьмеричной системы счисления в
десятичную.
разряды
2 1 0 -1
число
2 7 6, 58
= 2∙82 + 7∙81 + 6∙80 + 5∙8-1 = 190,62510
Пример. Перевести число 1F3 из шестнадцатеричной системы
счисления в десятичную.
разряды
число
2 1 0
1 F 316 = 1∙162 + 15∙161 + 3∙160 = 49910
В меню
27

28. Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную

Для перехода от двоичной к восьмеричной/шестнадцатеричной системе
счисления поступают следующим образом: двигаясь от запятой влево и
вправо, разбивают двоичное число на триады/тетрады, дополняя при
необходимости нулями крайние левую и правую группы. Затем каждую
триаду/тетраду заменяют соответствующей
восьмеричной/шестнадцатеричной цифрой.
Пример
01 0 1 0 1 0 0 1,1 0 1 1 1 0 2 = 251,658
2
5
1
5
6
1 0 1 0 1 0 0 1,1 0 1 1 1 000 2 = A9,B816
A
В меню
9
B
8
Таблица соответствия
28

29. Перевод из восьмеричной и шестнадцатеричной системы счисления в двоичную

Заменить каждую цифру восьмеричного/шестнадцатеричного числа
эквивалентной ей двоичной триадой/тетрадой .
Пример. Перевести число 527,18 в двоичную систему счисления.
527,18 = 101 010 111, 001 2
5
2
7
1
Пример. Перевести число 1A3,F16 в двоичную систему счисления.
1A3,F16 = 0001 1010 0011, 1111 2
1
В меню
A
3
Таблица соответствия
F
29

30. Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно

При переходе из восьмеричной системы счисления в
шестнадцатеричную и обратно, необходим промежуточный перевод
чисел в двоичную систему.
Пример. Число 1ЕС416 перевести в восьмеричную систему счисления
Пример. Число 75368 перевести в шестнадцатеричную систему счисления.
Таблица соответствия
В меню
30

31. Арифметические операции в позиционных системах счисления

Над числами, записанными в любой системе счисления, можно
производить различные арифметические операции.
Особый
интерес
вызывает
операция
сложения,
т.к.
арифметическое устройство ЭВМ может только складывать числа.
Все остальные арифметические операции заменяются сложением.
Например, вычитание – это сложение положительного и
отрицательного
числа,
умножение
–
это
многократно
повторяющееся сложение, деление – это произведение числителя
и знаменателя в -1 степени.
31

32. Арифметические операции в позиционных системах счисления

Правила выполнения основных арифметических операций в любой
позиционной системе счисления подчиняются тем же законам, что и в
десятичной системе.
При сложении цифры суммируются по разрядам, и если при этом
возникает переполнение разряда, то производится перенос в старший
разряд. Переполнение разряда наступает тогда, когда величина числа
в нем становится равной или большей основания системы счисления.
При вычитании из меньшей цифры большей в старшем разряде
занимается единица, которая при переходе в младший разряд будет
равна основанию системы счисления
32

33. Арифметические операции в позиционных системах счисления

Если при умножении однозначных чисел возникает переполнение
разряда, то в старший разряд переносится число, кратное основанию
системы счисления. При умножении многозначных чисел в различных
позиционных системах применяется алгоритм перемножения чисел в
столбик, но при этом результаты умножения и сложения
записываются с учетом основания системы счисления.
Деление в любой позиционной системе производится по тем же
правилам, как и деление углом в десятичной системе, то есть
сводится к операциям умножения и вычитания.
33

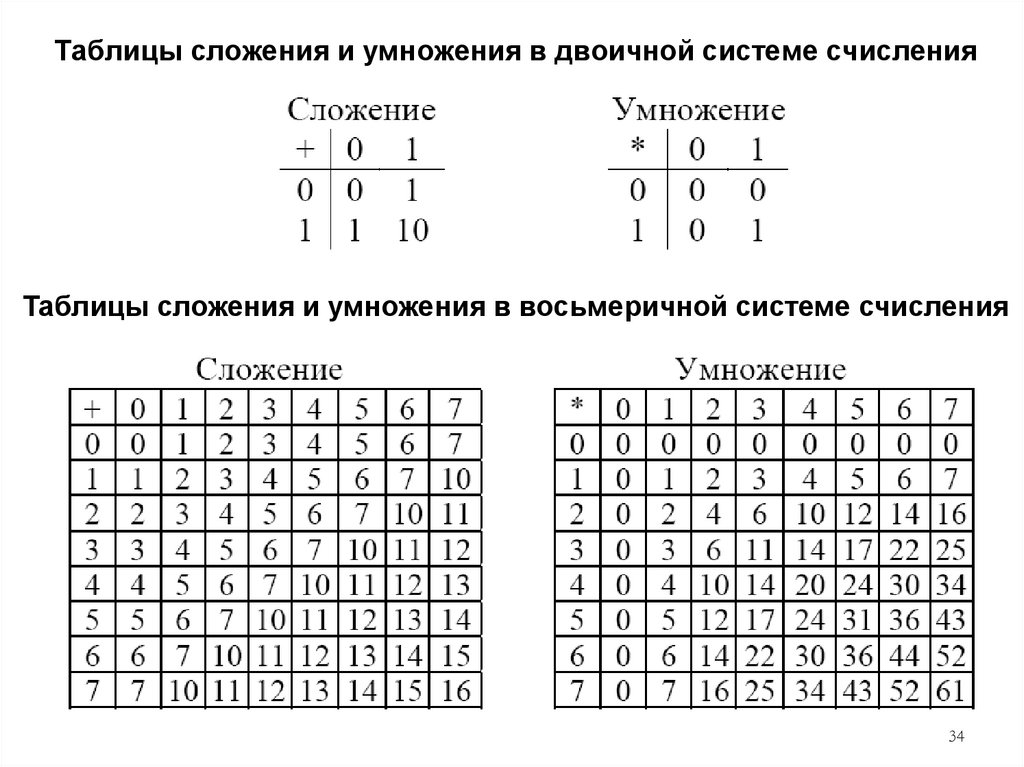
34.

Таблицы сложения и умножения в двоичной системе счисления
Таблицы сложения и умножения в восьмеричной системе счисления
34

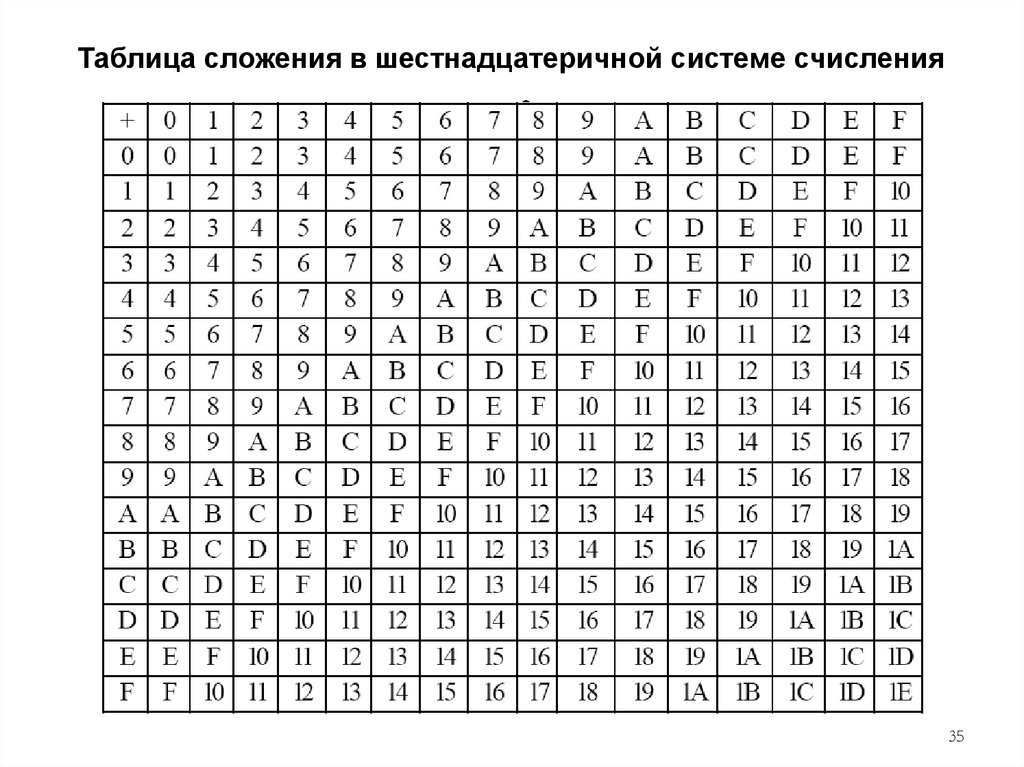
35.

Таблица сложения в шестнадцатеричной системе счисления
35

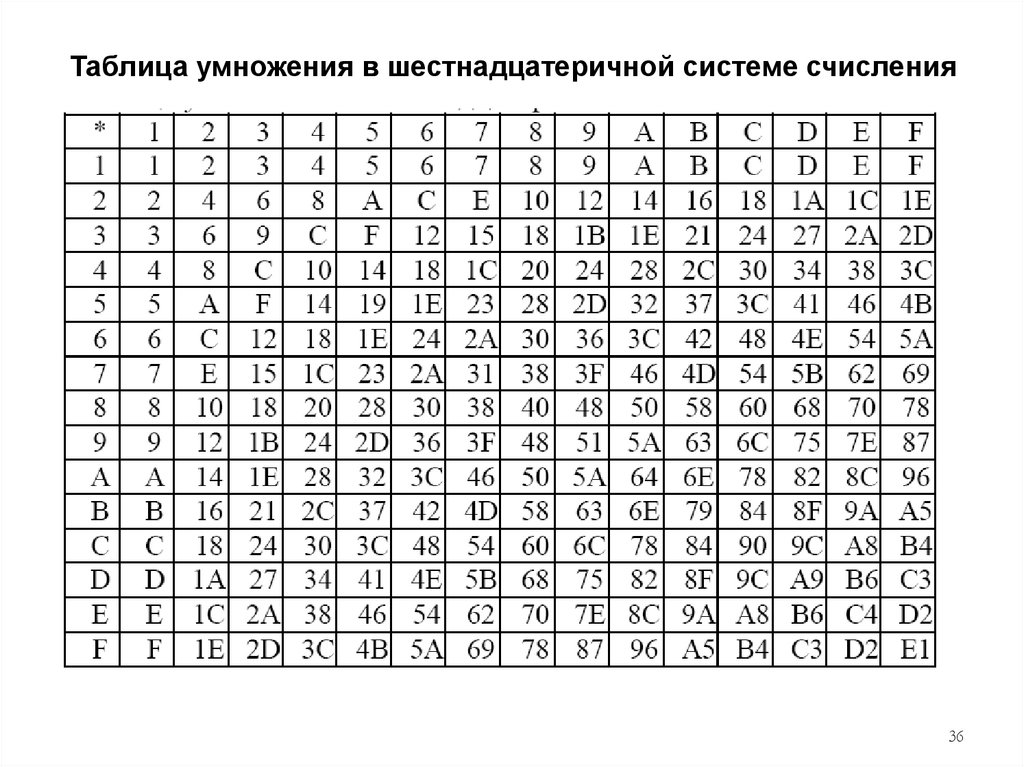
36.

Таблица умножения в шестнадцатеричной системе счисления
36

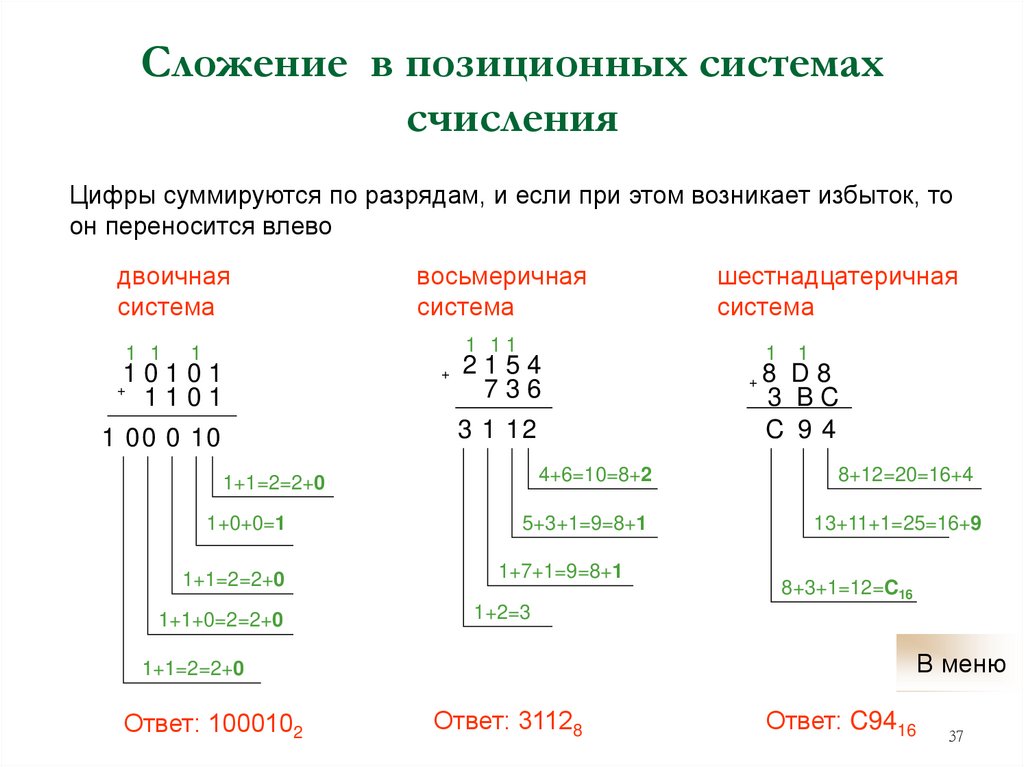
37. Сложение в позиционных системах счисления

Цифры суммируются по разрядам, и если при этом возникает избыток, то
он переносится влево
двоичная
система
1 1
восьмеричная
система
шестнадцатеричная
система
1 11
1
10101
1101
+
+
2154
736
3 1 12
1 00 0 10
1+1=2=2+0
1+1+0=2=2+0
+
1
8 D8
3 BC
C 94
4+6=10=8+2
8+12=20=16+4
5+3+1=9=8+1
13+11+1=25=16+9
1+1=2=2+0
1+0+0=1
1
1+7+1=9=8+1
8+3+1=12=C16
1+2=3
В меню
1+1=2=2+0
Ответ: 1000102
Ответ: 31128
Ответ: C9416
37

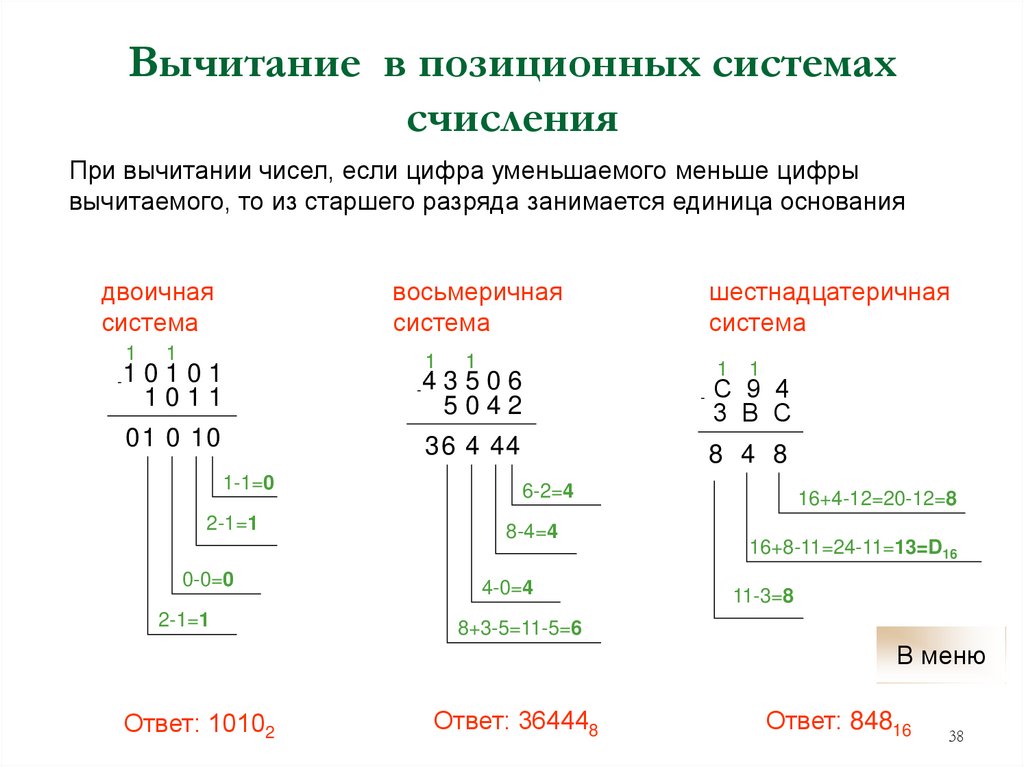
38. Вычитание в позиционных системах счисления

При вычитании чисел, если цифра уменьшаемого меньше цифры
вычитаемого, то из старшего разряда занимается единица основания
двоичная
система
1
восьмеричная
система
1
1
-1 0 1 0 1
1011
-
01 0 10
1
1
43506
5042
2-1=1
0-0=0
2-1=1
1
- С 9 4
3 В С
36 4 44
1-1=0
шестнадцатеричная
система
8 4 8
6-2=4
8-4=4
4-0=4
16+4-12=20-12=8
16+8-11=24-11=13=D16
11-3=8
8+3-5=11-5=6
В меню
Ответ: 10102
Ответ: 364448
Ответ: 84816
38

39. Умножение в позиционных системах счисления

При умножении многозначных чисел в различных позиционных системах
применяется алгоритм перемножения чисел в столбик, но при этом
результаты умножения и сложения записываются с учетом основания
системы счисления
двоичная
система
восьмеричная
система
2 2
4
1
х1 1 0 1 1
1101
1
11 1 1 0 1 1
1 1 1 0 1 1
11011
101011111
1+1+1=3=2+1
х1 6 3
63
15 3 1
1262
3∙3=9=8+1
1 3 3 56∙3=18=16+2=8∙2+2
1
6∙3+1=19=16+3=2∙8+3
6∙6+2=38=32+6=4∙8+6
1∙3+2=5
6+5=11=8+3
6∙1+4=10=8+2
1+1+1=3=2+1
В меню
1+1=2=2+0
Ответ: 1010111112
Ответ: 133518
39

40. Деление в позиционных системах счисления

Деление в любой позиционной системе производится по тем же правилам,
как и деление углом в десятичной системе. При этом необходимо
учитывать основание системы счисления.
двоичная
система
восьмеричная
система
100011
1110
1110
1 0 ,1
1 11 0
1110
0
Ответ: 10,12
13351
1262
163
63
5 31
531
0
Ответ: 638
В меню
40