3. Проекция вектора скорости на оси координат

4. Ускорение. Нормальное и тангенциальное ускорения

5.1. Поступательное движение твердого тела

5.2. Вращательное движение вокруг неподвижной оси

490.03K

Категория:

Физика

Похожие презентации:

Кинематика движения материальной точки

Кинематика движения материальной точки. Тема 2

Кинематика движения материальной точки

Кинематика движения материальной точки (лекция 1)

Физические основы механики. Тема 2. Кинематика движения материальной точки

Кинематика движения материальной точки (лекция № 2)

Кинематика движения материальной точки (тема 2)

Кинематика движения материальной точки

Кинематика движения материальной точки. Тема 2

Лекция дистанционное

1. ФИЗИКА

Лектор: Гребенщиков Максим
Леонидович
Кафедра физики
(корпус 14, каб. 342)

2.

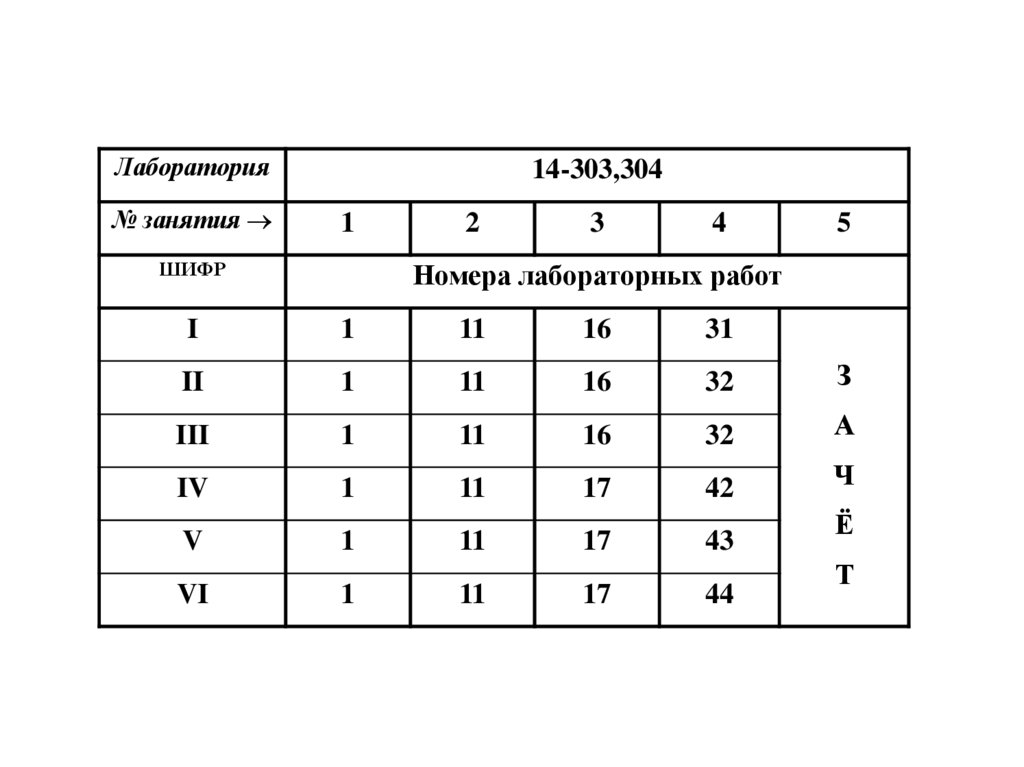
Лаборатория
№ занятия
14-303,304
1
ШИФР
2
3
4
5
Номера лабораторных работ
I
1
11
16
31
II
1
11
16
32
З
III
1
11
16
32
А
IV
1
11
17
42
Ч
V
1
11
17
43
VI
1
11
17
44
Ё
Т

3. Самостоятельная работа

• Подготовка к лабораторным работам
• Выполнение домашнего задания по
практике

4. ЛИТЕРАТУРА

• УЧЕБНИК: Трофимова Т. И. Курс физики:
учебное пособие для вузов . Москва:
Академия, 2007.- 560 с.
• ЗАДАЧНИК: Чертов А.Г., Воробьев А. А.
Задачник по физике. Москва. Высшая школа.
2007.
• ДОПОЛНИТЕЛЬНЫЙ УЧЕБНИК: Суслопаров
А.М., Василевский Л.С. Механика.
Молекулярная физика и термодинамика.
Учебное пособие. Киров. ОАО « Дом печатиВятка» 2008

5. Экзамен

Для допуска к экзамену необходимо:
Выполнение контрольной работы на
положительную отметку
Выполнение всех лабораторных работ
(теоретических и практических заданий)
Отсутствие задолженностей по домашним
заданиям

6. ФИЗИКА

Физика - наука изучающая общие
свойства и законы движения
вещества и поля
академик А. Ф. Иоффе

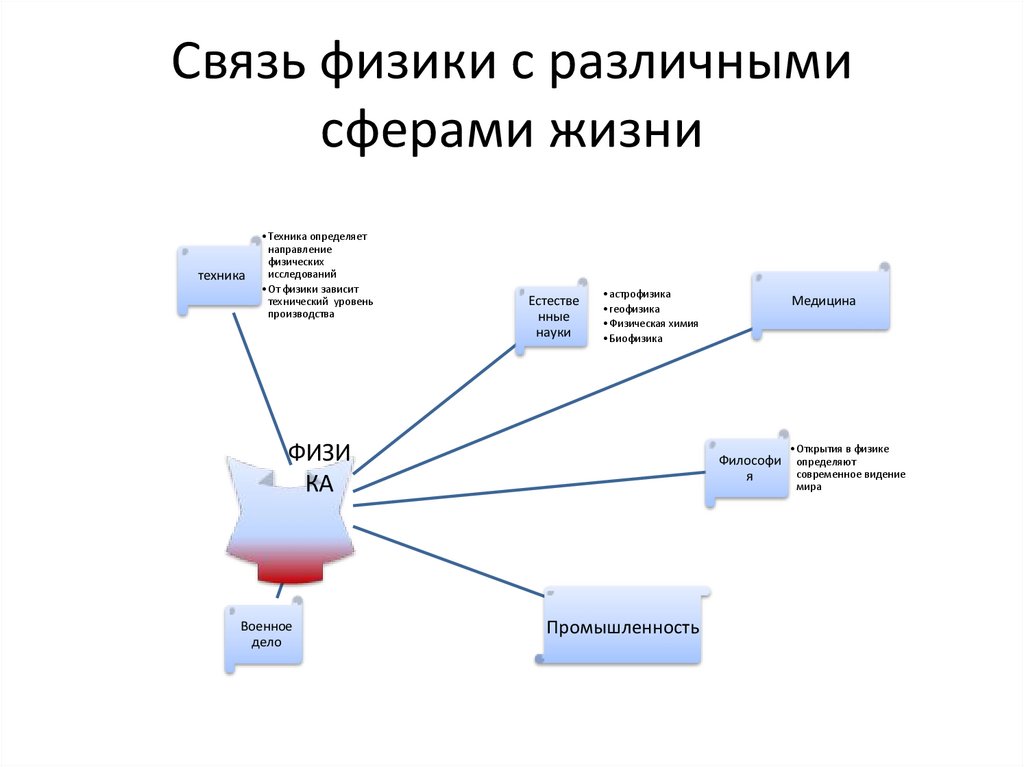
7. Связь физики с различными сферами жизни

техника
•Техника определяет
направление
физических
исследований
•От физики зависит
технический уровень
производства
Естестве
нные
науки
•астрофизика
•геофизика
•Физическая химия
•Биофизика
ФИЗИ
КА
Военное
дело
Медицина
Философи
я
Промышленность
•Открытия в физике
определяют
современное видение
мира

8. Измерения. Единицы физических величин

9. опыт

Основной метод исследования в физике,
основанное на практике чуственно-эмпирическое познание объективной действительности, то есть наблюдение исследуемых
явлений в точно учитываемых условиях,
позволяющих следить за ходом явлений и
многократно воспроизводить его при
повторении этих условий.

10.

• ГИПОТЕЗА – научное предположение выдвигаемое для объяснения какого-либо явления и
требующее проверки на опыте и теоретического
обоснования чтобы стать достоверной теорией.
• ФИЗИЧЕСКИЕ ЗАКОНЫ - устойчивые, повторяющиеся физические закономерности, существующие в природе.
• ИЗМЕРЕНИЯ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ – действие выполняемое с помощью средств измерений, для нахождения значений этих величин в
принятых единицах.

11. Система Интернациональная (СИ)

МЕТР (м)
КИЛОГРАММ (кг)
СЕКУНДА (с)
АМПЕР (А)
КЕЛЬВИН (К)
МОЛЬ (моль)
КАНДЕЛЛА ( кд)
РАДИАН (рад),СТЕРАДИАН (ср)дополнительные единицы измерения

12.

• МЕТР- длина равная 1650763,73 длины волны в
вакууме излучения, соответствующему переходу между уровнями 2 р₁₀ и 5d₅ атома криптона
Kr-86
• КИЛОГРАММ-масса равная массе международного прототипа килограмма (платино-иридиевого цилиндра, хранящегося в международном
бюро мер и весов (Франция) )
• СЕКУНДА- время равное 9192631770 периодам
излучения, соответствующего переходу между
двумя сверхтонкими уровнями основного состояния атома цезия Cs-133

13.

• АМПЕР- сила неизменяющегося тока, который при
прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенного в
вакууме на расстоянии 1 м один от другого, создаёт между проводниками силу равную 2∙10⁻⁷ Н на
каждый метр длины.
• КЕЛЬВИН - 1/273,16 часть термодинамической
температуры тройной точки воды.
• МОЛЬ- количество вещества системы содержащей
столько же структурных элементов, сколько атомов
содержится в нуклиде углерода ¹²С массой 0.012 кг.

14.

• КАНДЕЛЛА- сила света в заданном направ-лении
источника, испускающего монохро-матическое
излучение частотой 540∙10¹² Гц, энергетическая
сила света которого в этом направлении
составляет 1/683 Вт/ср.
Дополнительные единицы измерения
• РАДИАН –угол между двумя радиусами окружности, длина дуги между которыми рав-на
радиусу окружности (1 рад≈57,2957⁰).
• СТЕРАДИАН- телесный угол с вершиной в центре
сферы, вырезающий на поверхности сферы
площадь, равную площади квадрата со
стороной равной радиусу сферы.

15. Производные единицы измерения

Для установления произвольных единиц измерения используют физические законы,
связывающие их с основными единицами.
v=s/t
[ м/с]
Размерность физической величины- её выражение в основных единицах измерения.
Например размерность силы (через 2 закон
Ньютона): F=ma
dim F=MLT⁻²
Н = кг*м/с²

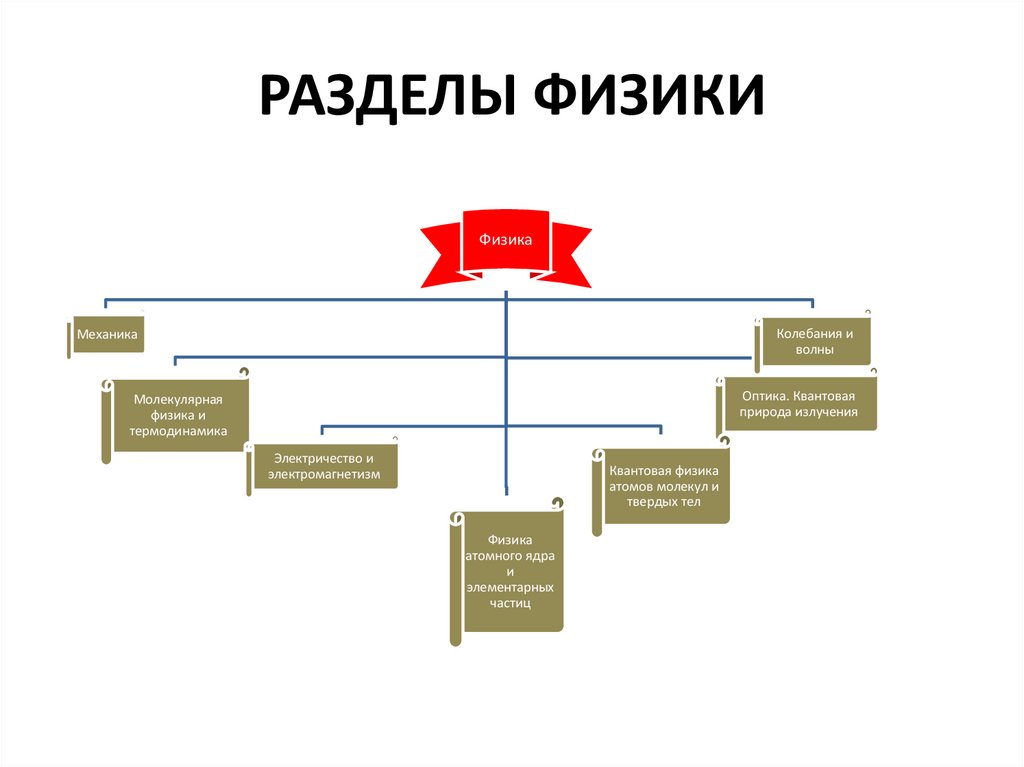
16. РАЗДЕЛЫ ФИЗИКИ

Физика
Колебания и
волны
Механика
Оптика. Квантовая
природа излучения
Молекулярная
физика и
термодинамика
Электричество и
электромагнетизм
Квантовая физика
атомов молекул и
твердых тел
Физика
атомного ядра
и
элементарных
частиц

17. МЕХАНИКА

Часть физики, которая изучает закономерности механического движения и причины вызывающие или
изменяющие это движение.

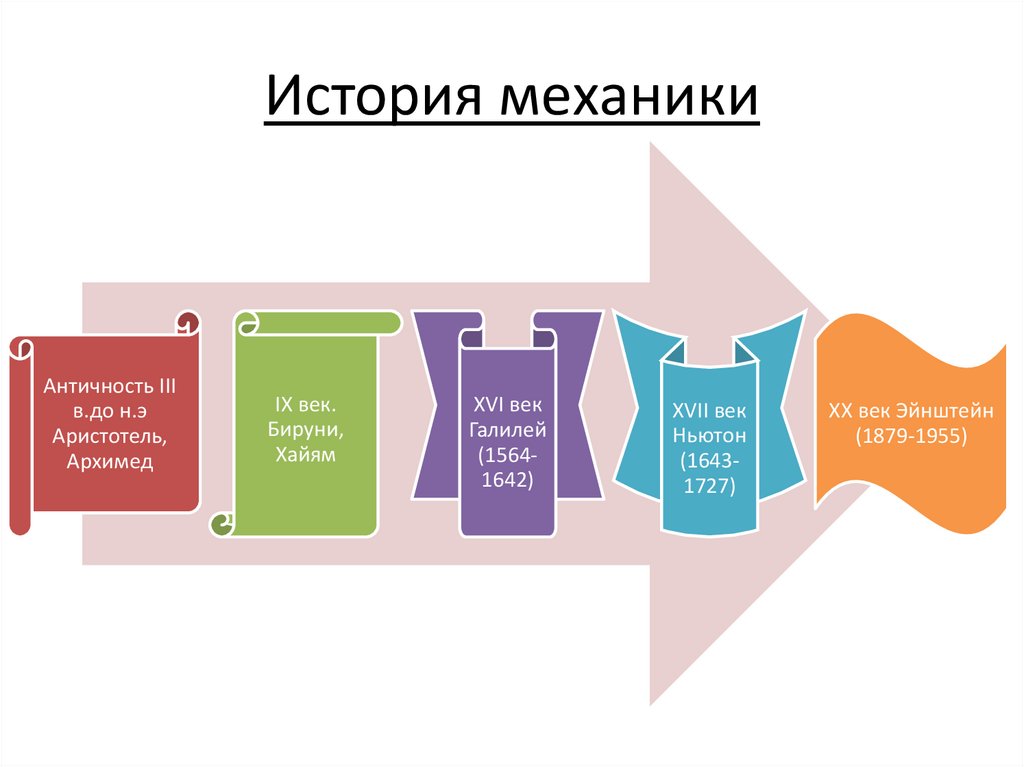
18. История механики

Античность III
в.до н.э
Аристотель,
Архимед
IX век.
Бируни,
Хайям
XVI век
Галилей
(15641642)
XVII век
Ньютон
(16431727)
XX век Эйнштейн
(1879-1955)

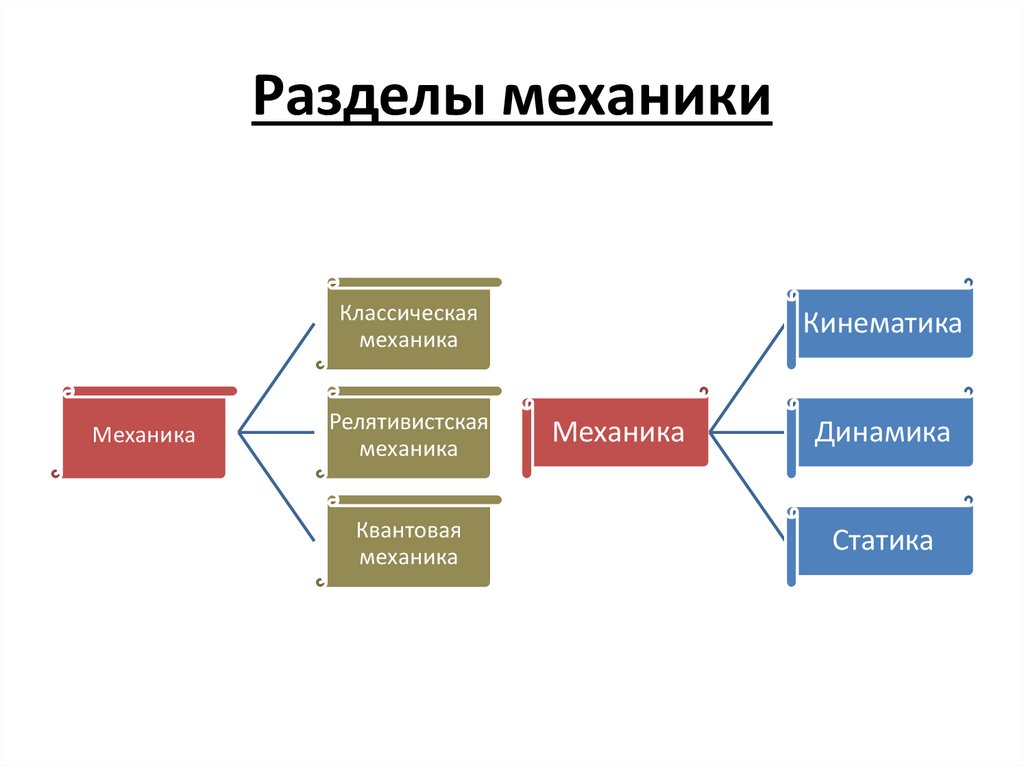
19. Разделы механики

Классическая
механика
Механика
Релятивистская
механика
Квантовая
механика
Кинематика
Механика
Динамика
Статика

20.

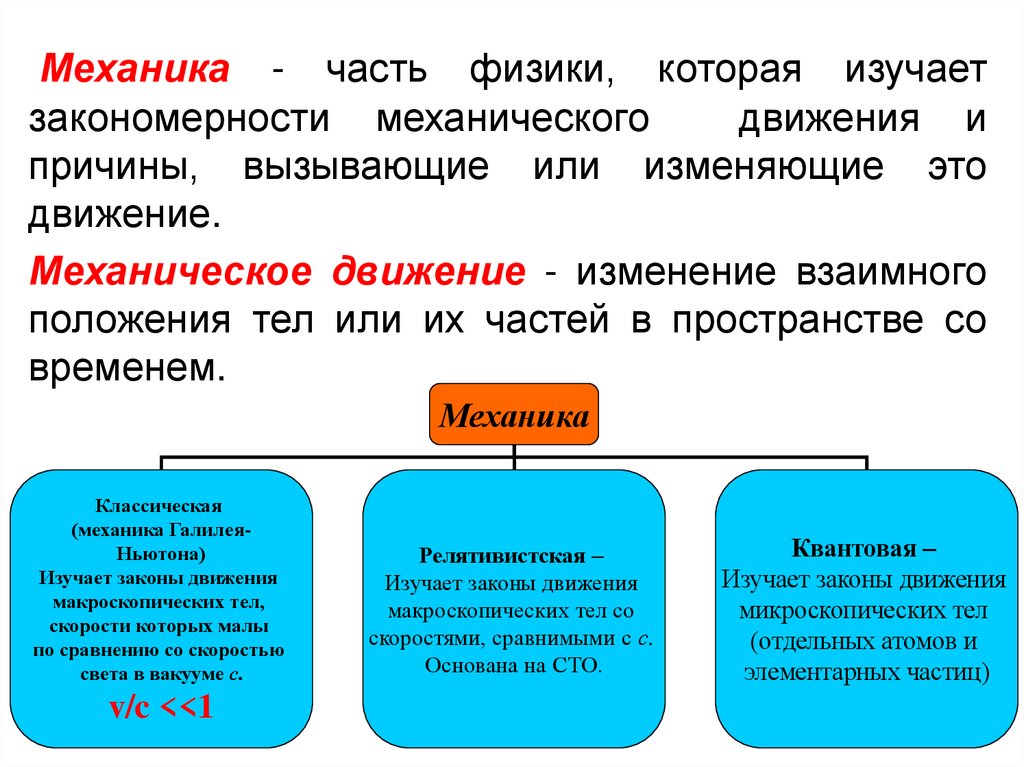
Механика - часть физики, которая изучает
закономерности механического
движения и
причины, вызывающие или изменяющие это
движение.
Механическое движение - изменение взаимного
положения тел или их частей в пространстве со
временем.
Механика
Классическая
(механика ГалилеяНьютона)
Изучает законы движения
макроскопических тел,
скорости которых малы
по сравнению со скоростью
света в вакууме с.
v/c <<1
Релятивистская –
Изучает законы движения
макроскопических тел со
скоростями, сравнимыми с с.
Основана на СТО.
Квантовая –
Изучает законы движения
микроскопических тел
(отдельных атомов и
элементарных частиц)

21.

Кинематика (от греческого слова kinema –
движение) – раздел механики, в котором изучаются геометрические свойства движения тел без
учета их массы и действующих на них сил.
Динамика (от греческого dynamis – сила)
изучает движения тел в связи с теми причинами,
которые обуславливают это движение.
Статика (от греческого statike – равновесие) изучает условия равновесия тел.
Поскольку равновесие – есть частный случай
движения, законы статики являются естественным
следствием законов динамики и в данном курсе не
21
изучается.

22. КИНЕМАТИКА

23. ФИЗИЧЕСКИЕ МОДЕЛИ

• Материальная точка - тело обладающее массой, разме-
рами которого в данной задаче можно пренебречь.
• Макроскопическое тело (система тел) - тело (систе-
ма тел), которое можно разбить на малые взаимодействующие между собой части, каждая из которых может
рассматриваться как материальная точка.
• Абсолютно твёрдое тело - тело, которое не при каких условиях не может деформироваться , и расстояние
между двумя любыми точками этого тела всегда постоянно.

24. ДВИЖЕНИЕ

• Поступательное движение - движение при
котором любая прямая, жестко связанная с
движущимся телом, остается параллельной
своему первоначальному положению.
• Вращательное движение - движение при
котором все точки тела движутся по
окружностям, центры которой лежат на
одной оси.

25. Система отсчета, тело отсчета

Всякое движение относительно,
поэтому
для
описания
движения
необходимо условиться,
относительно
какого другого тела будет отсчитываться
перемещение данного тела. Выбранное
для этой цели тело называют телом
отсчета.
Практически, для описания движения
приходится связывать с телом отсчета
систему
координат
(декартова,
сферическая, цилиндрическая и т.д.).
25

26.

Система отсчета – совокупность системы координат и часов,
связанных с телом по отношению к
которому изучается движение.
Движения тела, как и материи, вообще
не
может
быть
вне
времени
и
пространства. Материя, пространство и
время неразрывно связаны между собой
(нет пространства без материи и времени и
наоборот).
26

27.

Пространство трехмерно,
поэтому
«естественной»
системой координат является,
декартова или прямоугольная
система координат, которой мы в
основном и будем пользоваться.
В
декартовой
системе
координат, положение точки А в
данный момент времени по
отношению к этой системе характеризуется тремя координатами
r
x, y, z или радиус-вектором
прове-денным
из
начала
координат в данную точку
27

28.

Рисунок 2.1
При движении материальной точки её
координаты
с
течением
времени
изменяются.
В общем случае её движение
определяется
скалярными
или
28
векторными уравнениями:

29.

Кинематические уравнения движения
материальной точки:
x x(t ),
y y (t ),
z z (t ).
r x i y j zk
Эти уравнения эквивалентны векторному уравнению
где х, у, z – проекции радиус-вектора r на
оси координат, а i, j, k – единичные
векторы (орты), направленные по
соответствующим осям, причем
k i , j , i j , k , j k, i

30.

Число
независимых
координат,
полностью
определяющих
положение
точки
в
пространстве,
называется
числом степеней свободы i
Если материальная точка движется в
пространстве, то она имеет три степени
свободы i=3 (координаты х, у, z). Если она
движется на плоскости – две степени
свободы i=2. Если вдоль линии – одна
степень свободы i=1.
30

31. Кинематика материальной точки

1. Путь, перемещение
Положение точки А в пространстве
можно задать с помощью радиус-вектора r1
проведенного из точки отсчета О или начала
координат
31

32.

При движении точки А из точки 1 в точку 2 её радиусвектор
изменяется и по величине, и по направлению,
т.е. r зависит от времени t.
Геометрическое
место точек
концов r называется траекторией точки.
Длина траектории есть путь Δs. Если
точка движется по прямой, то приращение r
32
равно пути s.

33.

Пусть за время t точка
переместилась из точки 1 в точку 2.
r
Вектор перемещения
приращение r1
за время t
r r2 r1 x x0 i y y0 j z z0 k;
Δ r Δx i Δy j Δzk
А
есть
(1)
(2)
Модуль вектора:
Δ r Δx Δy Δz .
2
2
2
(3)

34.

2. Скорость
34

35. Скорость

Средний
вектор
скорости
определяется как отношение вектора
перемещения r ко времени t, за
которое это перемещение произошло
Δr
Δt
Вектор r
совпадает с
направлением
вектора υ
35

36.

Мгновенная скорость в точке 1:
Δr dr
lim .
Δt dt
Δt 0
Модуль вектора скорости
dr
.
dt
Мгновенная скорость -вектор скорости
в данный момент
времени
равен
первой
производной от r по времени и направлен
по касательной к траектории в данной
36
точке в сторону движения точки А.

37.

При t 0 т.е. на
бесконечно малом
участке траектории
S = r (перемещение
совпадает с траекторией)
В этом случае
мгновенную скорость
можно выразить через
скалярную величину –
путь:
Δs ds
υ lim
;
Δt 0
Δt dt
ds
или υ .
dt
Так вычислять скорость проще, т.к. S – скаляр
37

38.

Обратное действие – интегрирование
ds υdt – площадь бесконечно узкого
прямоугольника. Чтобы вычислить весь
путь S за время t, надо сложить площади
всех прямоугольников.
38

39.

t
S υdt.
0
Геометрический смысл этого интеграла в
том, что площадь под кривой (t ) есть
39
путь тела за время t.

40.

Принцип
независимости
движения
(действия сил)
Если материальная точка участвует в нескольких движениях,
то ее результирующее
перемещение d r равно векторной сумме
перемещений, обусловленных каждым из этих
движений в отдельности:
d r d r d r ... d r d r d r ,
n
1
2
i
n
i 1
i
40

41.

Так как
Тогда
dr
dt
2
i
n
...
1
.
n
i 1
i
Таким образом, скорость тоже подчиняется принципу независимости движения.
В дальнейшем мы подробнее рассмотрим
принцип независимости действия сил.
41

42.

В физике существует общий принцип,
который называется
принцип суперпозиции
результирующий эффект сложного
процесса взаимодействия представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности, при условии, что последние
взаимно не влияют друг на друга.
Принцип суперпозиции играет большую
роль во многих разделах физики и техники.
42

43. 3. Проекция вектора скорости на оси координат

В векторной форме уравнения записываются
легко и кратко. Но для практических вычислений
нужно знать проекции вектора на оси координат
выбранной системы отсчета.
Положение точки А
задается
радиус-вектором r .
Спроецируем вектор r
на оси – x, y, z.
43

44.

Понятно, что х, y, z зависят от времени t,
т.е. x(t), y(t), z(t). Зная зависимость этих
координат от времени (закон движения
точки) можно найти в каждый момент
времени скорость точки.
Проекция вектора скорости
на ось x равна:
dx
dt
x
44

45.

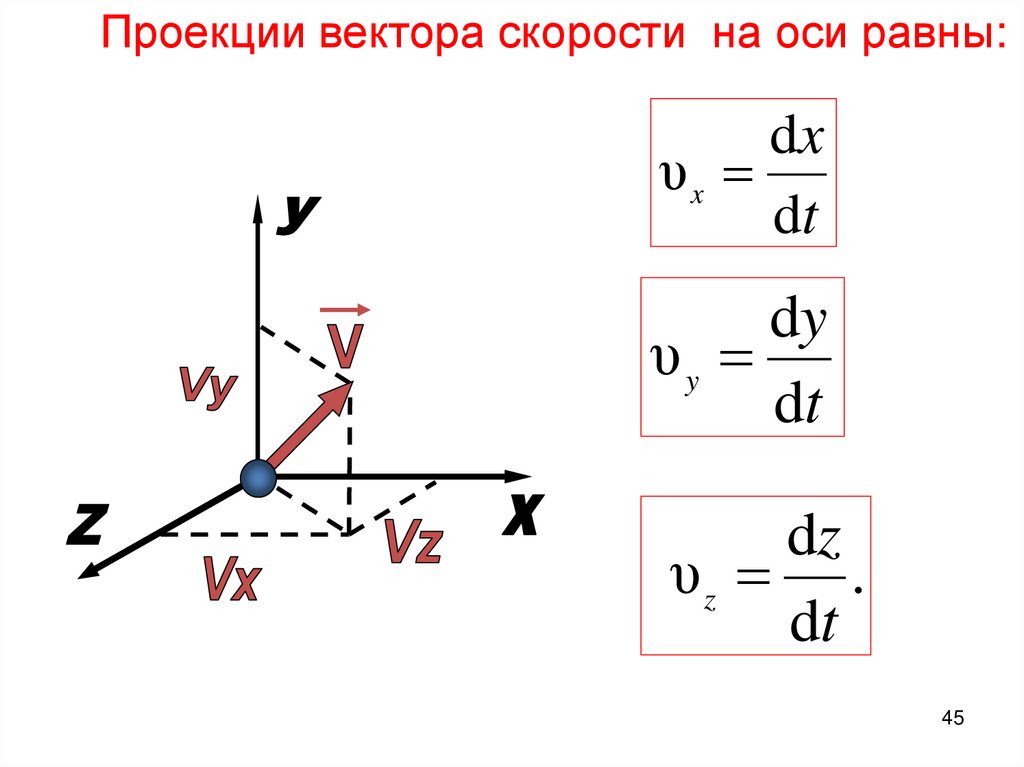
Проекции вектора скорости на оси равны:
dx
υx
dt
dy
υy
dt
dz
υz .
dt
45

46.

Так как вектор, то
dx dy dz
υ υ x i υ y j υz k i j k,
dt
dt
dt
где i, j, k единичные векторы – орты.
υ x i y j z k
Модуль вектора скорости:
2
2
x
y
2
z
46

47. 4. Ускорение. Нормальное и тангенциальное ускорения

В произвольном случае движения скорость не
остается постоянной. Быстрота изменения
скорости по величине и направлению
характеризуются ускорением:
d
a
dt
Ускорение величина векторная.
(4.1)
При криволинейном движении
изменяется и по
времени, и по направлению. В какую сторону? С какой
скоростью? Из выражения (4.1) на эти вопросы не 47
ответишь.

48.

Введем единичный вектор τ (см. рисунок),
связанный с точкой 1 и направленный по
касательной
движения точки 1
к траектории
(векторы и τ в точке 1 совпадают).
Тогда можно записать:
τ,
– модуль вектора
где
скорости.
Рисунок
48

49.

Найдем общее ускорение (как производную):
dτ
d d
a
τ a a .
dt dt
dt
n
(4.2)
Получили два слагаемых ускорения:
a – тангенциальное ускорение,
совпадающее
с направлени
ем
в данной точке.
a – нормальное
n
ускорение или
центростремительное.
49

50.

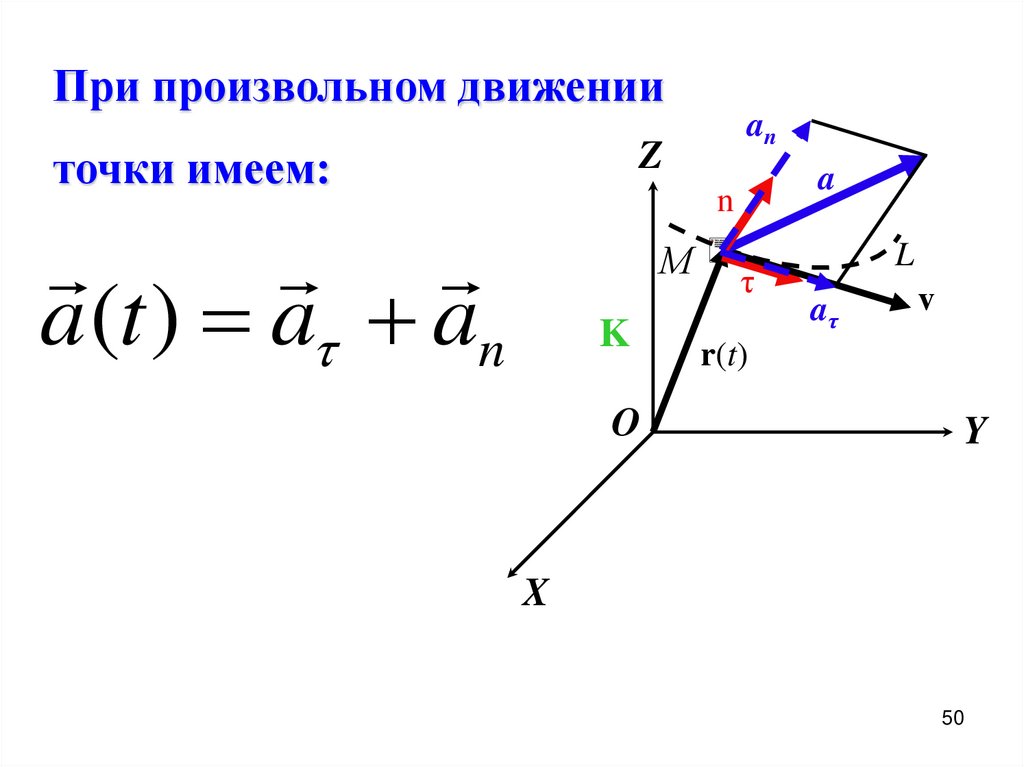
При произвольном движении
an
Z
точки имеем:
a
n
a (t ) a an
М
K
O
τ
L
aτ
v
r(t)
Y
X
50

51.

d
a
τ
dt
или по модулю
τ
dυ
aτ
dt
-показывает изменение вектора скорости
по величине:
d
0
- если
то a направлено
в ту же сторону, что и
dt
вектор т.е. ускоренное движение;
d
- если
0
dt
d
0
- при
dt
то a направлено
в противоположную
сторону , т.е. замедленное движение;
то aτ 0, const – движение
постоянной по модулю скоростью.
51

52.

Нормальное ускорение
υ
показывает быстроту
a n,
изменения направления
r
вектора скорости
Модуль нормального ускорения: a a
.
r
2
n
2
n
n
Центростремительным
называют
ускорение – когда движение происходит по
окружности. А когда движение происходит по
произвольной кривой – говорят, нормальное
ускорение, перпендикулярное к касательной в
52
любой точке траектории.

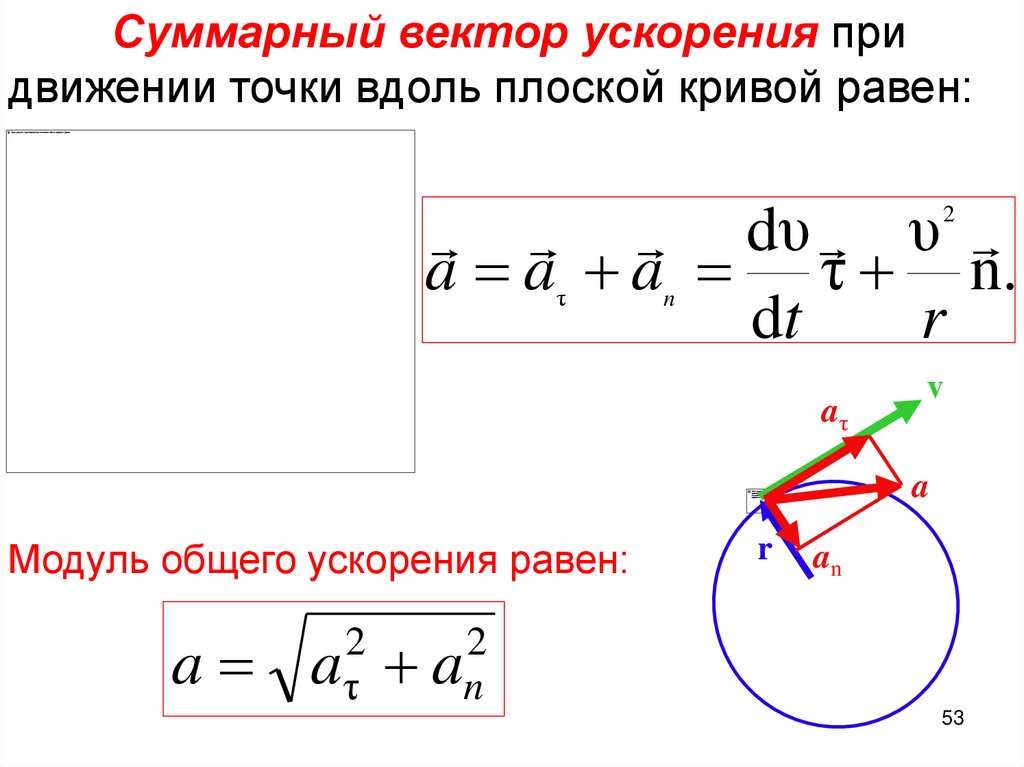
53.

Суммарный вектор ускорения при
движении точки вдоль плоской кривой равен:
dυ υ
a a a τ n.
dt
r
2
τ
n
aτ
v
a
Модуль общего ускорения равен:
a
r
an
2
2
aτ an
53

54.

Рассмотрим
несколько
(частных) случаев:
предельных
a 0; an 0 – равномерное прямоли
нейное движение;
a const; an 0 – равноускоренное
прямолинейное движение;
a 0; a const – равномерное движение
n
по окружности.
54

55.

Вспомним несколько полезных формул
(прямая задача кинематики) :
t
s υdt υt
При равномерном движении
0
При движении с постоянным ускорением
2
at
S υ 0t
.
2
υ υ0 at
55

56.

Обратная
задача
кинематики
заключается в том, что по известному
значению ускорения a(t) найти скорость точки
и восстановить траекторию движения r(t).
d (t )
a(t )
,
dt
По определению
отсюда
t2
(t ) (t ) a(t )dt
0
t1
dr
или, так как (t )
,
dt
Следовательно
t2
r (t ) r (t ) (t )dt.
0
t1

57. 5. Кинематика твердого тела

Различают пять видов движения твердого
тела:
- поступательное;
- вращательное вокруг неподвижной оси;
- плоское;
- вокруг неподвижной точки;
- свободное.
Поступательное движение и вращательное движение вокруг оси – основные
виды движения твердого тела.
Остальные виды движения твердого тела можно
свести к одному их этих основных видов или к57 их
совокупности.

58. 5.1. Поступательное движение твердого тела

Поступательное движение – это такое
движение твердого тела, при котором любая
прямая,
связанная
с
телом,
остается
параллельной своему начальному положению и при
этом, все точки твердого тела совершают
равные перемещения.
Скорости и ускорения всех точек твердого тела
в данный момент времени t одинаковы. Это
позволяет
свести
изучение
поступательного
движения твердого тела к изучению движения
отдельной точки, т.е. к задаче кинематики
материальной точки, подробно рассмотренной в
58
прошлом разделе.

59.

Рис. 1
Рис. 2
При вращательном движении все точки тела
движутся по окружностям, центры которых лежат на
одной и той же прямой OO' , называемой осью
вращения (рисунок 2).
Из определения вращательного движения ясно,
что
понятие
вращательного
движения
для
59
материальной точки неприемлемо.

60. 5.2. Вращательное движение вокруг неподвижной оси

Движение твердого тела, при котором две
его точки О и О' остаются неподвижными,
называется вращательным движением вокруг
неподвижной оси, а неподвижную прямую ОО'
называют осью вращения.
Пусть абсолютно твердое
тело вращается вокруг
неподвижной оси ОО'
Рисунок 3
60

61.

Проследим за некоторой точкой М этого
твердого тела. За время dt
точка М совершает
элементарное перемещение
При том же самом угле поворота dφ другая
точка, отстоящая от оси на большее или меньшее
расстояния,
совершает
другое
перемещение.
Следовательно, ни само перемещение некоторой
точки твердого тела,
dr
ни первая производная
2
dr
ни вторая производная
dt
dt
2
не могут служить
характеристикой движения
всего твердого тела.
61

62.

Угол поворота dφ характеризует перемещения всего тела за время dt (угловой путь)
Удобно ввести dφ – вектор элементарного
поворота тела, численно равный dφ и направленный
вдоль оси вращения ОО' так, чтобы глядя вдоль
вектора dφ мы видели вращение по часовой стрелке
(направление вектора dφ
и направление вращения связаны
правилом буравчика).
Элементарные
повороты
удовлетворяют обычному правилу сложения векторов:
dφ dφ dφ .
1
2
62