Презентация лекции

1. Дискретная математика

К.т.н., доцент Макареня Сергей Николаевич
доцент кафедры ИСиТ
МИДО БНТУ
makarenya@bntu.by
+375 29 562 82 95

2. Введение

Дискретная математика (дискретный анализ) – раздел математики, который
занимается изучением свойств объектов конечного характера.
В отличие от дискретной математики классическая математика в основном
занимается изучением свойств объектов непрерывного характера. Важными
отличиями разделов дискретной математики от классических разделов
непрерывной математики являются отсутствие понятия непрерывности и
предела последовательности.
К разделам дискретной математики обычно относят:
математическую логику,
теорию алгоритмов,
булеву алгебру,
теорию конечных автоматов,
теорию дискретных групп,
теорию графов,
комбинаторику,
теорию чисел и еще много других разделов

3. Введение

Элементы дискретной математики возникли в глубокой
древности. Развиваясь параллельно с другими разделами
математики, они в значительной мере являлись их составной
частью.
Типичными для того периода были задачами, связанные со
свойствами целых чисел и приведшие затем к созданию теории
чисел. К их числу могут быть отнесены задача отыскания
алгоритма сложения и умножения натуральных чисел у древних
египтян (2-е тыс. до н.э.), задачи о суммировании и делимости
натуральных чисел в пифагорейской школе (6 в. до н.э.).
Позже (17-18 вв.) в основном в связи с игровыми задачами
появились элементы комбинаторного характера и дискретной
теории вероятностей (Б. Паскаль, П.Ферма и др.).
Стремление к строгости математических рассуждений привели к
одного важного раздела – математической логики (19-20 вв.).
Однако наибольшего развития дискретная математика достигла в
связи с запросами практики, приведшими к появлению новой
науки – кибернетики (20 в.).

4. 1. Теория множеств

5. Понятие множества. Принадлежность множеству, элементы множества

Понятие множества относится к элементарным (не определяемым
через другие понятия) понятиям математики.
Г. Кантору (основатель теории множеств) принадлежит следующая
формулировка понятия множества: «Множество — это объединение
определённых, различных объектов, называемых элементами
множества, в единое целое».
Объекты, образующие некоторое множество, называются его
элементами. Принадлежность некоторого элемента x множеству
A обозначается как x A — «x есть элемент множества A» или «x
принадлежит множеству A».
Непринадлежность некоторого элемента а множеству М обозначается в
виде: а М.
Множества принято обозначать заглавными буквами латинского
алфавита, а элементы множеств — строчными буквами.

6. Пустое множество. Подмножество

Пустым множеством называется множество, не содержащее ни одного
элемента. Пустое множество обозначают символом .
Пустое множество является подмножеством любого множества.
Множество A называется подмножеством множества B, если
любой элемент, принадлежащий A, также принадлежит B. Это
записывается в виде отношения включения: A B. Таким образом,
(A B) (x A x B). Множество B, в свою очередь, называется
надмножеством множества A, что записывается в виде отношения
обратного включения: B A. (Иногда, говорят, что множество В
содержит, или покрывает, множество А).

7. Пустое множество. Подмножество

Множество А называют собственным (строгим, истинным) подмножеством
множества В, если А является подмножеством В, но не равно ему
(A B) и А В) и обозначается: A B ( - знак строгого включения в отличие
от знака нестрогого включения).
Пример:
1.
Если A – множество всех людей, B – мужчин, то B A;
2.
Множество четных чисел является собственным подмножеством множества
натуральных чисел;
3.
Множество A = {1, 2, 3, 4, 5} является подмножеством (но не собственным)
множества B = {x / x N, 0 < x < 6}.
Обычно в конкретных рассуждениях элементы всех множеств берутся из
некоторого одного, достаточно широкого множества, своего для каждого
случая, которое называется универсальным множеством (универсумом).
Универсальное множество обычно обозначается U (от англ. universe, universal
set), реже E.

8. Мощность множества

Мощность множества можно рассматривать как числовую характеристику
(метрику) любого множества.
Мощностью некоторого конечного множества А является число его
элементов. Мощность множества А принято обозначать |А|, например,
мощность множества А={a, b, c} равна |А|=3. Мощность пустого множества
равна нулю: | |=0.
Множества, имеющие конечное число элементов и, соответственно,
конечное значение мощности, называются конечными, а множества с
бесконечным числом элементов и, соответственно, с бесконечной
мощностью — бесконечными.
Множества, обладающие одинаковым значением мощности, называются
равномощными. Понятие равномощности распространяется и на
бесконечные множества.

9. Счётные и несчётные множества

Бесконечные множества разделяются на счётные и несчётные.
Бесконечное множество называется счётным, если его элементы можно
пронумеровать; в противном случае, бесконечное множество называется
несчётным.
Простейшим примером счётного множества является множество всех
натуральных чисел, в связи с чем можно дать другое определение счётного
множества: множество называется счётным, если оно равномощно
множеству натуральных чисел, т.е. его можно представить в виде {x0, x1, x2,
…}, где хi — элемент множества, однозначно соответствующий его номеру i.
Простейший пример несчётного множества — множество действительных
чисел. Другими примерами счётных множеств являются множества целых и
рациональных чисел, а примером несчётного множества — множество
комплексных чисел.
Любое подмножество счётного множества является либо конечным, либо
счётным, иначе говоря, каждое бесконечное подмножество счётного
множества также является счётным.
Объединение конечного числа счётных множеств также является счётным
множеством.

10. Способы задания множеств

Задание множеств списком предполагает перечисление элементов. Например,
множество А состоит из букв a, b, c, d : A={a, b, c, d} или множество L
включает цифры 0, 2, 3, 4: L={0, 2, 3, 4}.
Задание множеств порождающей процедурой означает описание
характеристических свойств элементов множества: X = { x | H (x) }, т. е.
множество X содержит такие элементы x, которые обладают свойством H (x).
Например: B = { b | b = / 2 k , k N }, N — множество всех натуральных
чисел.
Задание множества описанием свойств элементов. Например, M — это
множество чисел, являющихся степенями двойки.
К описанию свойств естественно предъявить требования точности и
недвусмысленности.
Графическое задание множеств осуществляют с помощью диаграмм ЭйлераВенна. Построение диаграммы заключается в изображении большого
прямоугольника, представляющего универсальное множество U, а внутри его
— кругов, представляющих рассматриваемые множества.

11. Диаграммы Эйлера-Венна

Построение диаграммы заключается в изображении большого
прямоугольника, представляющего универсальное множество U, а внутри
его — кругов, представляющих рассматриваемые множества.
Точки, лежащие внутри различных областей диаграммы, могут
рассматриваться как элементы соответствующих множеств. Имея
построенную диаграмму, можно заштриховать определенные области для
обозначения вновь образованных множеств.
U
A
B
Пример диаграммы Эйлера-Венна

12. Равенство множеств

Множество A равно множеству B, если A и B включены друг в друга или,
иначе, между ними существует отношение взаимного включения: A=B
(A B) и (B A).
Вторая часть равенства указывает на наиболее типичный метод
доказательства равенства множеств A и B, который заключается в
доказательстве сначала утверждения А В, а затем В А.
Равные множества содержат одинаковые элементы, причем порядок
элементов в множествах не существенен:
A={1, 2, 3} и В={3, 2, 1} A=B.

13. Операции над множествами. Объединение множеств

Объединением множеств А и В называется множество, состоящее из всех
тех элементов, которые принадлежат хотя бы одному из множеств А, В
(рис. 4): A B = {x | x A или x B}.
U
A
B
Пример 1.
А={a,b,c}, B={b,c,d}, C={c,d,e}.
A B={a,b,c,d}; A C={a,b,c,d,e}; B C={b,c,d,e}; A B C={a,b,c,d,e}.

14. Операции над множествами. Пересечение множеств

Пересечением множеств А и В называется множество, состоящее из всех тех и
только тех элементов, которые принадлежат одновременно как множеству А,
так и множеству В:
A B = {x | x A и x B}.
U
A
B
Пример 2.
А={a,b,c}, B={b,c,d}, C={c,d,e}.
А В={b,c}; A C={c}; B C={c,d}; A B C={c}.

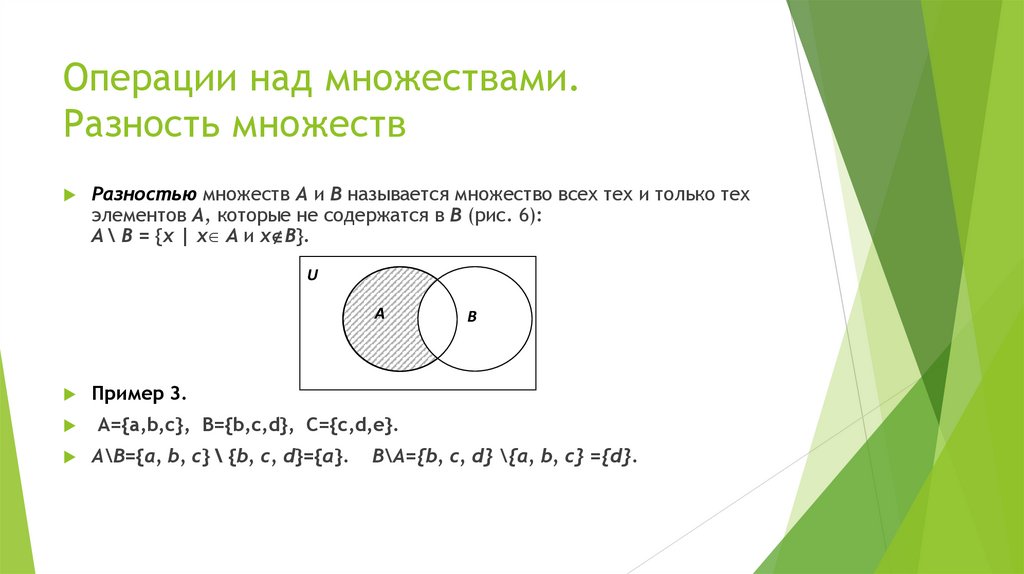
15. Операции над множествами. Разность множеств

Разностью множеств А и В называется множество всех тех и только тех
элементов А, которые не содержатся в В (рис. 6):
A \ B = {x | x A и x B}.
U
A
Пример 3.
А={a,b,c}, B={b,c,d}, C={c,d,e}.
А\В={а, b, c} \ {b, c, d}={a}.
B
В\А={b, c, d} \{а, b, c} ={d}.

16. Операции над множествами. Симметрическая разность множеств

Симметрической разностью множеств А и В называется множество, состоящее из
элементов, которые принадлежат либо только множеству А, либо только множеству В
(рис. 7). Симметрическую разность обозначают как AΔB, A – B или A B:
AΔB = {x | (x A и x B) или ( x В и x А)}.
Таким образом, симметрическая разность множеств A и B представляет собой
объединение разностей (относительных дополнений) этих множеств: AΔB = (A \ B) (B \
A).
Пример 4 А={a,b,c}, B={b,c,d}, C={c,d,e}.
AΔB ={a} {d}={a,d}.

17. Операции над множествами. Дополнение множества

Дополнением (абсолютным) множества А называется множество всех тех
элементов х универсального множества U, которые не принадлежат
множеству А.
Дополнение множества А обозначается:
С учетом введенной операции дополнения, разность множеств А и В можно
представить в виде:
U
A

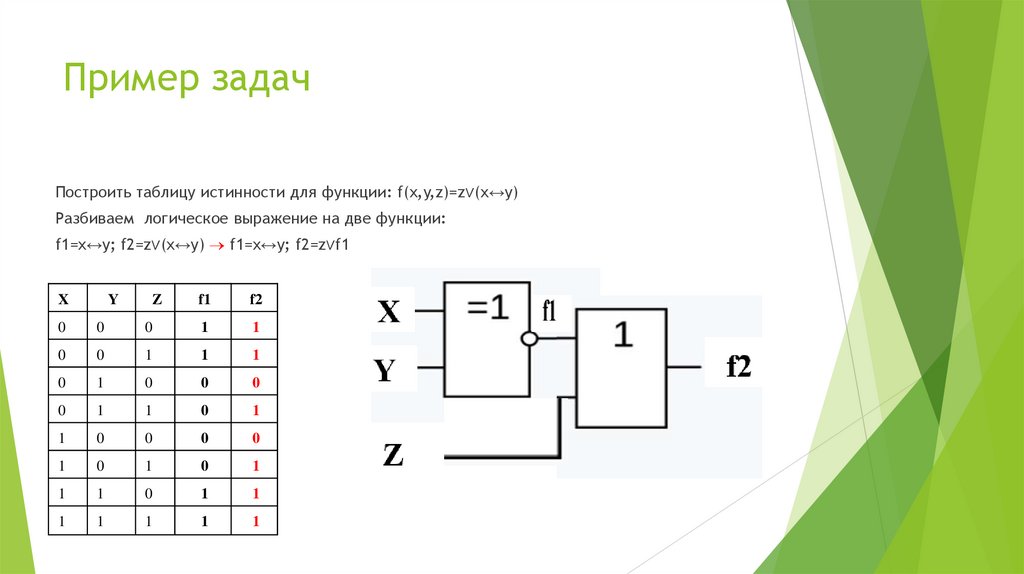
18. Пример задач

1.Перечислить все элементы следующих множеств (ℕ – множество
натуральных чисел: 1, 2, 3…):{x ∈ ℕ|3x + 4 < 31} ∩{x ∈ ℕ|x > 5}
{x ∈ ℕ|3x + 4 < 31} 3x + 4 < 31 3х<27 x<9 {1, 2, 3, 4, 5, 6, 7, 8}
{x ∈ ℕ|x > 5} {6, 7, 8, 9, 10, …}
{1, 2, 3, 4, 5, 6, 7, 8} ∩{6, 7, 8, 9, 10, …} = {6, 7, 8}
2. Перечислить все элементы следующих множеств (ℕ2 – множество пар
натуральных чисел, например (1, 1), (2, 5), (4,2): {(x, y) ∈ ℕ 2|x ≤ 3, y < 3}
х={1,2, 3}; у={1,2} (1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2)

19. 2. Математическая логика

Основоположником логики как науки является древнегреческий
философ и ученый Аристотель (384–322 гг. до н. э.), который впервые
разработал теорию логического вывода одних утверждений из
других.
Применение в логике математических методов связывается с именем
немецкого математика Г. Лейбница (1646–1716 гг.), который
предложил заменить логические рассуждения вычислениями,
подобно тому, как это делается в математике.
Математическая логика как наука начинается с работ английского
математика Джорджа Буля (1815 – 1864 гг.), труды которого положили
начало алгебры логики, основными элементами которой являются
двоичные переменные, принимающие значение 1 и 0 или «истина» и
«ложь», и операции над ними (Создание математической логики и
Булевой алгебры).

20. Высказывания

Высказыванием называется всякое повествовательное предложение, о
котором в данной ситуации можно сказать, истинно оно или ложно.
Высказывания обозначаются прописными буквами латинского алфавита:
А, В, С, … .
Поставим в соответствие высказыванию логическую переменную х,
которая принимает значение 1, если высказывание истинно, и 0, если
высказывание ложно.

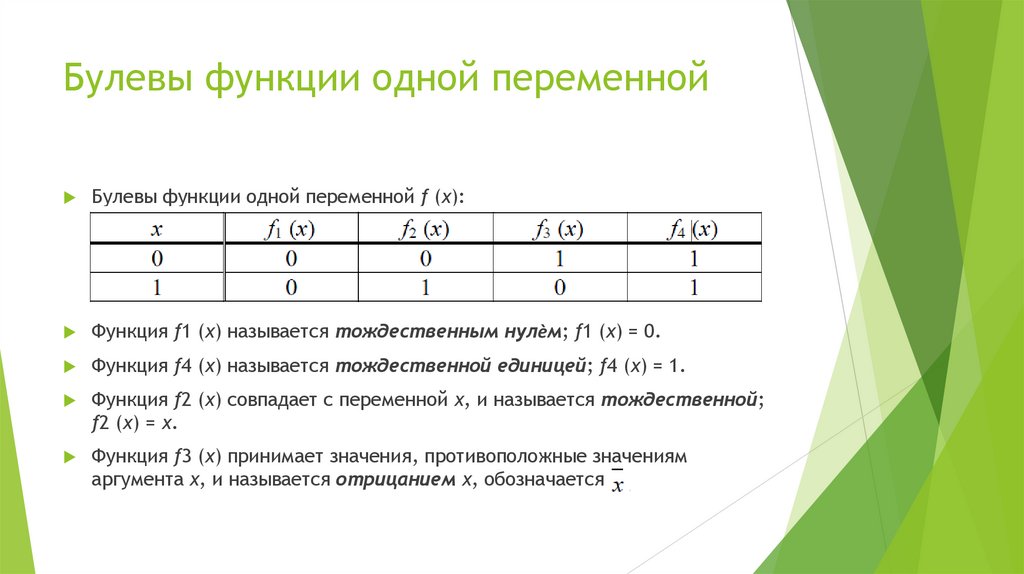
21. Логические операции

Логические операции — это операции над высказываниями, при которых
истинностные значения составных высказываний определяются только
истинностными значениями исходных высказываний, а не их смыслом.
Логические операции удобно задавать с помощью таблиц истинности, где
перечисляются все возможные наборы значений составляющих
высказываний и соответствующее каждому такому набору значение
составного высказывания.
Наборы из единиц и нулей расположены в порядке возрастания.

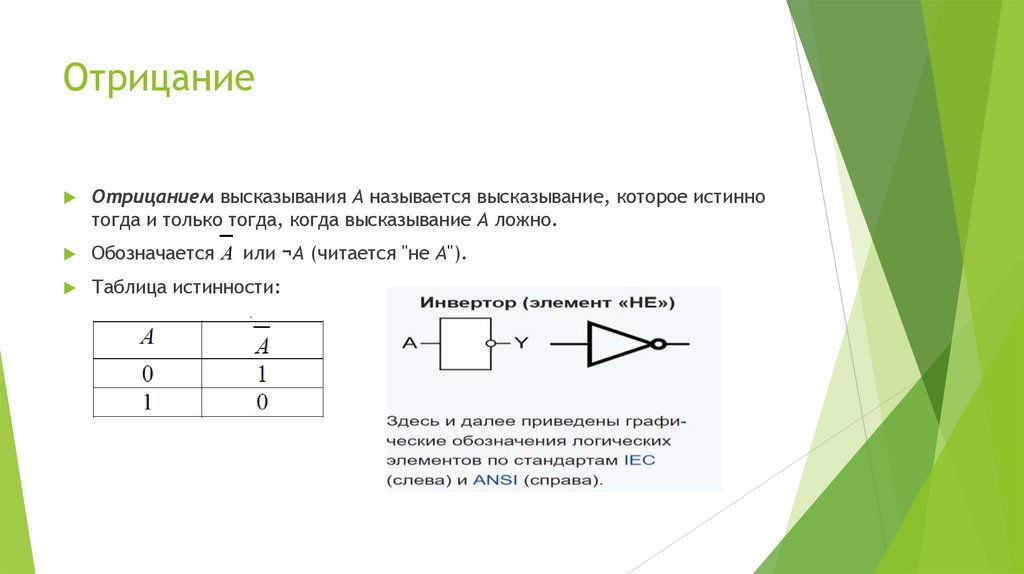
22. Отрицание

Отрицанием высказывания А называется высказывание, которое истинно
тогда и только тогда, когда высказывание А ложно.
Обозначается
Таблица истинности:
или ¬А (читается "не А").

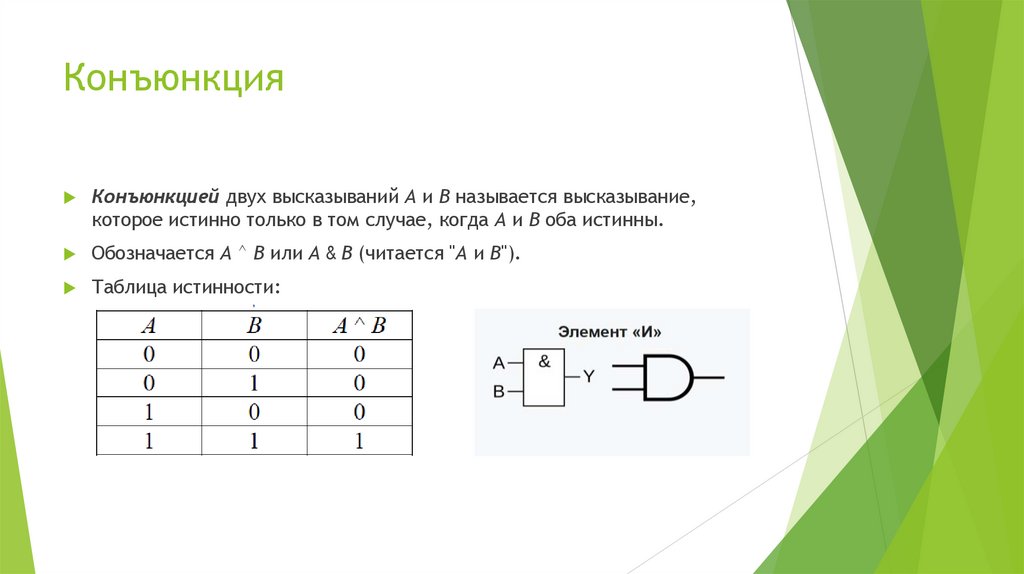
23. Конъюнкция

Конъюнкцией двух высказываний А и В называется высказывание,
которое истинно только в том случае, когда А и В оба истинны.
Обозначается А ^ В или А & В (читается "А и В").
Таблица истинности:

24. Дизъюнкция

Дизъюнкцией двух высказываний А и В называется высказывание,
которое истинно, когда хотя бы одно из них истинно.
Обозначается
Таблица истинности:
(читается "А или В").

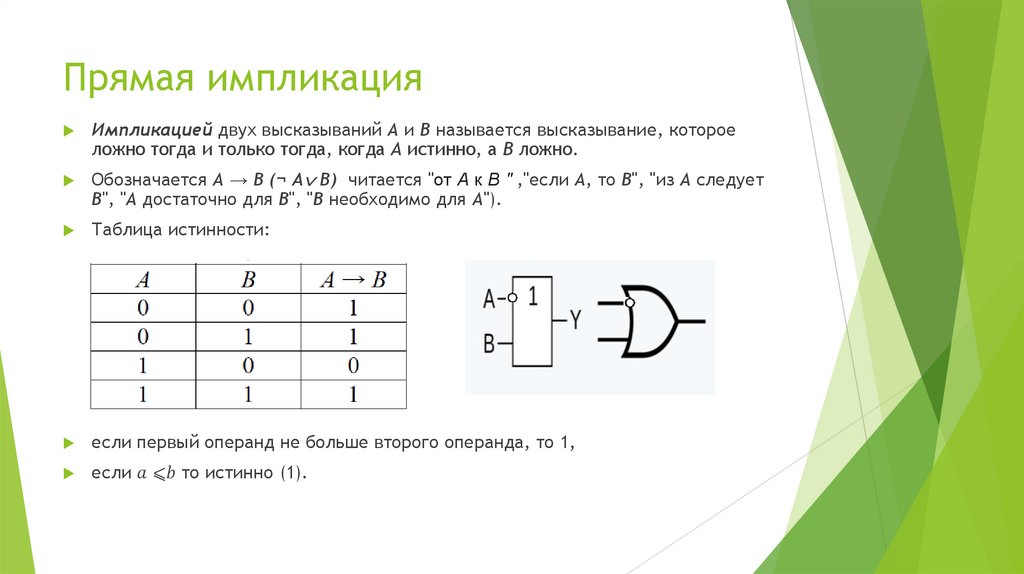
25. Прямая импликация

Импликацией двух высказываний А и В называется высказывание, которое
ложно тогда и только тогда, когда А истинно, а В ложно.
Обозначается А → В (¬ А В) читается "от А к В " ,"если А, то В", "из А следует
В", "А достаточно для В", "В необходимо для А").
Таблица истинности:
если первый операнд не больше второго операнда, то 1,
если