7_Логические модели представления знаний (часть 1)

1. Логические модели представления знаний

1

2. 1. Формальные и семиотические системы

2

3. Формальная система

В основе всех логических моделей представления знаний лежит
понятие формальной системы (теории), задаваемой:
А - алфавит (множество базовых элементов),
F –множество формул,
В - множество аксиом,
R- множество правил вывода.
• А - алфавит (множество базовых элементов (конечное или
счётное)) состоит из элементов, которые не могут быть расщеплены
на более мелкие элементы. Из них строятся остальные производные
элементы формальной системы.
Примеры: алфавит некоторого языка, набор десятичных цифр,
набор деталей детского конструктора.
• F – множество формул, которые строятся из А и называются
правильно построенными совокупностями (ППС) или правильно
построенными формулами (ППФ).
Примеры: слова и фразы языка, записи чисел в десятичной
системе, различные конструкции, собранные из исходных деталей
конструктора.
3

4.

• Множество аксиом В образует любое множество
ППС. На это множество не накладывают никаких
специальных
ограничений.
В
формальных
системах ничего не говорится об истинности или
ложности ППС. Поэтому аксиомы ППС здесь
также не ассоциируются с чем-то абсолютно
истинным (как, например, в геометрии).
• Правила вывода R служат для того, чтобы с их
помощью из множества аксиом можно было
получать (выводить) другие ППС, которые не
входят в начале в множество B.
Множество, получаемое после применения
семантических правил к аксиомам называется
множеством выводимых совокупностей (ВС).
4

5.

• Формальная система, для которой существует конструктивная
процедура, дающая однозначный ответ на вопрос – принадлежит ли
данная ППС множеству ВС, называется разрешимой формальной
системой.
Пример:
• Детские кубики, содержащие 6 кубиков (базовых элементов –
множество А).
• Множество формул (ППС) F, такие, в которых все шесть кубиков
выложены в виде прямоугольника 3 х 2 или 2 х 3.
• Множество аксиом B совпадает с такой совокупностью кубиков,
которая соответствует одной из приложенных картинок.
• Множество правил вывода R дают возможность из одной
исходной картинки (аксиомы) получать (выводить) новые.
Для данной системы существует конструктивная процедура
определения всех семантических правильных совокупностей (МВС),
так как эта процедура содержится в наборе 6 картинок, прилагаемых
к игре.
Следовательно, систему игры в кубики можно считать
разрешимой формальной системой.
5

6.

Когда формальная система используется
для описания некоторого объекта реального
мира, и происходящих в нём процессов
(пример с кубиками), элементы множеств А,
F, B, R приобретают некоторый определенный
смысл. Этот процесс называется внешней
интерпретацией формальной системы.
В формальных системах множества А, F, B,
R остаются неизменными.
Для описания сложных явлений реального
мира, постоянно находящихся в динамике,
такая модель оказывается в ряде случаев
слишком бедной, неадекватной.
6

7. Семиотическая система

Семиотическая система – формальная
система, где множества А, F, B, R могут
изменяться.
C=
,
где
- правила
изменения множеств A, F, B, R
соответственно, М – формальная
система, С – семиотическая система.
7

8.

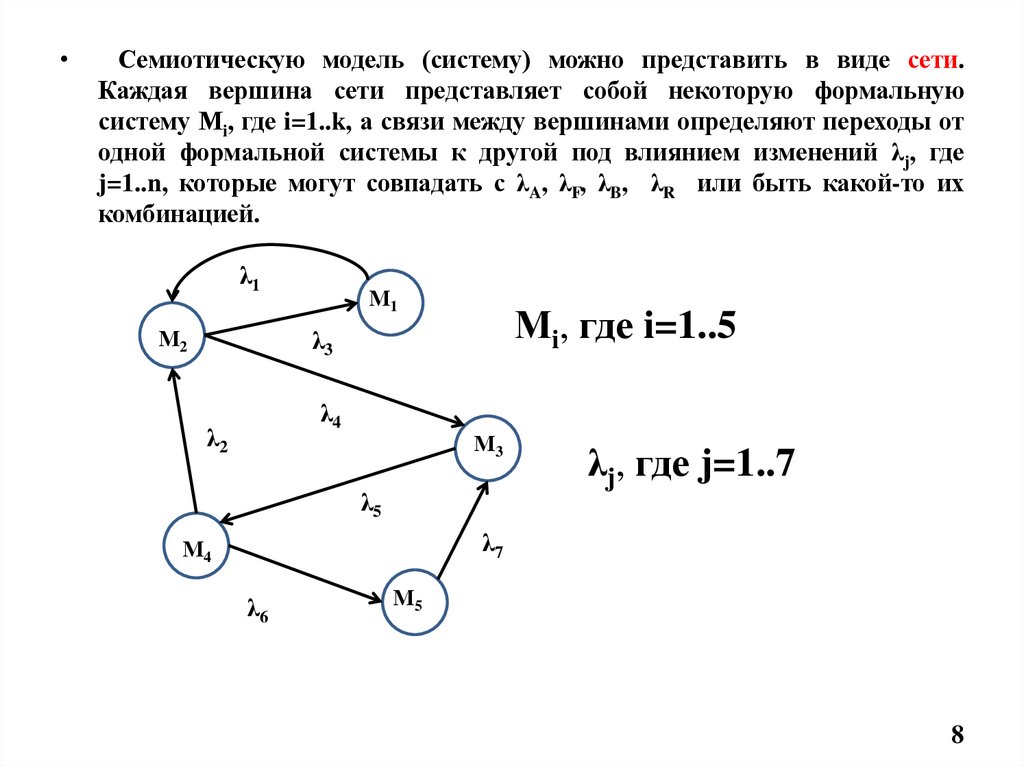
Семиотическую модель (систему) можно представить в виде сети.
Каждая вершина сети представляет собой некоторую формальную
систему Мi, где i=1..k, а связи между вершинами определяют переходы от
одной формальной системы к другой под влиянием изменений λj, где
j=1..n, которые могут совпадать с λA, λF, λB, λR или быть какой-то их
комбинацией.
λ1
М2
М1
Мi, где i=1..5
λ3
λ4
λ2
М3
λ5
λj, где j=1..7
λ7
М4
λ6
М5
8

9. Семиотическая (знаковая) система

• Человек окружен знаковыми системами, его
деятельность пронизана ими. Он постоянно творит такие
системы.
Пример: колода игральных карт, являющаяся
некоторой семиотической системой, и, договариваясь с
партнёрами о множествах A, F, B, R, можно придумать
большое множество карточных игр.
• Чрезвычайно сложной семиотической системой
является естественный язык. Для естественного языка
характерно, что его элементы многозначны и в ряде
случаев их значение можно установить лишь на основе
анализа всей фразы и ситуации, в которой она
произнесена.
9

10. 2. Поиск решений в предикатных моделях знаний. Дедуктивная система принятия решений

10

11.

Пропозициональная формула является общезначимой или
тавтологией, если она принимает значение Истина для любой
интерпретации.
А V ¬A = И
Пропозициональная формула является противоречием, если она
имеет значение ложь во всех интерпретациях .
А& ¬ А = Л
¬ (¬ А) = A
¬ (A&B)= ¬ A V ¬B закон де Моргана
A→B = ¬A∨B
Теорема дедукции – основная теорема логического вывода.
Формула G является логическим следствием формул F1, F2,…,
Fn тогда и только тогда, когда формула
F1 & F2 &…& Fn →G является тавтологией.
Следствие из теоремы дедукции:
ППФ G является логическим следствием ППФ F1, F2,…, Fn тогда
и только тогда, когда формула F1 & F2 …& Fn & ¬ G является
противоречием.
11

12.

Ǝx
–
квантор
существования
(существует такой x)
Ɐx – квантор всеобщности (для всех x)
¬ ƎxP(x)= Ɐx(¬P(x))
=
- силлогизм modus ponens
(правило заключения)
12

13.

• На языке предикатов знания о некоторой предметной
области записываются в виде совокупности ППФ, которые
образуют некоторую базу знаний.
• Запрос к этой базе знаний также формулируется в виде
ППФ, которая называется целевой ППФ.
• Принятие решения по данному запросу при этом сводится к
выяснению вопроса логического следования целевой ППФ из
множества ППФ, входящих в базу знаний.
• Данная задача называется задачей доказательства теорем,
а система, решающая данную задачу называется дедуктивной
системой принятия решений.
Дедуктивные системы являются основой построения
интеллектуальных ИПС, которые в отличии от обычных ИПС
обладают способностью выводить новые факты, не
содержащиеся в явном виде в базе знаний.
13

14.

• На языке предикатов знания о некоторой предметной
области записываются в виде совокупности ППФ, которые
образуют некоторую базу знаний.
• Запрос к этой базе знаний также формулируется в виде
ППФ, которая называется целевой ППФ.
• Принятие решения по данному запросу при этом сводится к
выяснению вопроса логического следования целевой ППФ из
множества ППФ, входящих в базу знаний.
• Данная задача называется задачей доказательства теорем,
а система, решающая данную задачу, называется дедуктивной
системой принятия решений.
Дедуктивные системы являются основой построения
интеллектуальных ИПС, которые в отличии от обычных ИПС
обладают способностью выводить новые факты, не
содержащиеся в явном виде в базе знаний.
14

15. Автоматизация логического вывода

Согласно теореме дедукции выяснение
вопроса логического следования ППФ G из
множества ППФ F1,…,Fn равносильно
доказательству общезначимости
ППФ F1 & F2 & …& Fn G
или противоречивости
ППФ F1 & F2 & … & Fn & ¬ G
(следствие
основной
теоремы
логического вывода).
15

16.

В 1936 г. американский ученый-математик Алонзо
Чёрч доказал, что не существует эффективной
разрешающей процедуры, позволяющей установить
общезначимость формулы в исчислении предикатов 1-го
порядка. По этой причине исчисление предикатов
называли неразрешимой формальной теорией.
Алонзо Чёрч
14.06.1903 – 11.08.1995
16

17.

Результаты Чёрча о неразрешимости исчисления предикатов
оттеснили работы французского математика Эрбрана, который
предложил механическую процедуру дедуктивного вывода,
позволяющую доказать общезначимость формулы исчисления
предикатов, если она является таковой на самом деле. Поэтому
исчисление предикатов 1-го порядка называют полуразрешимым.
Жак Эрбран
12.02.1908 – 27.07.1931
17

18.

Работы в области автоматизации вывода показали, что на ЭВМ
проще доказывать не общезначимость некоторой формулы, а
противоречивость её отрицания. В 1965 г. английским логиком Дж.
Робинсоном был предложен принцип резолюции и на основе него
разработан эффективный метод автоматического вывода, в основе
которого лежал приём доказательства противоречивости отрицания
исходной формулы. В дальнейшем он был усовершенствован.
Джон Алан Робинсон
1930 – 05.08.2016
Процедуры опровержения - процедуры, связанные
с
автоматизацией логического вывода, основываются не на
доказательстве общезначимости формулы, а на доказательстве ее
противоречивости.
18

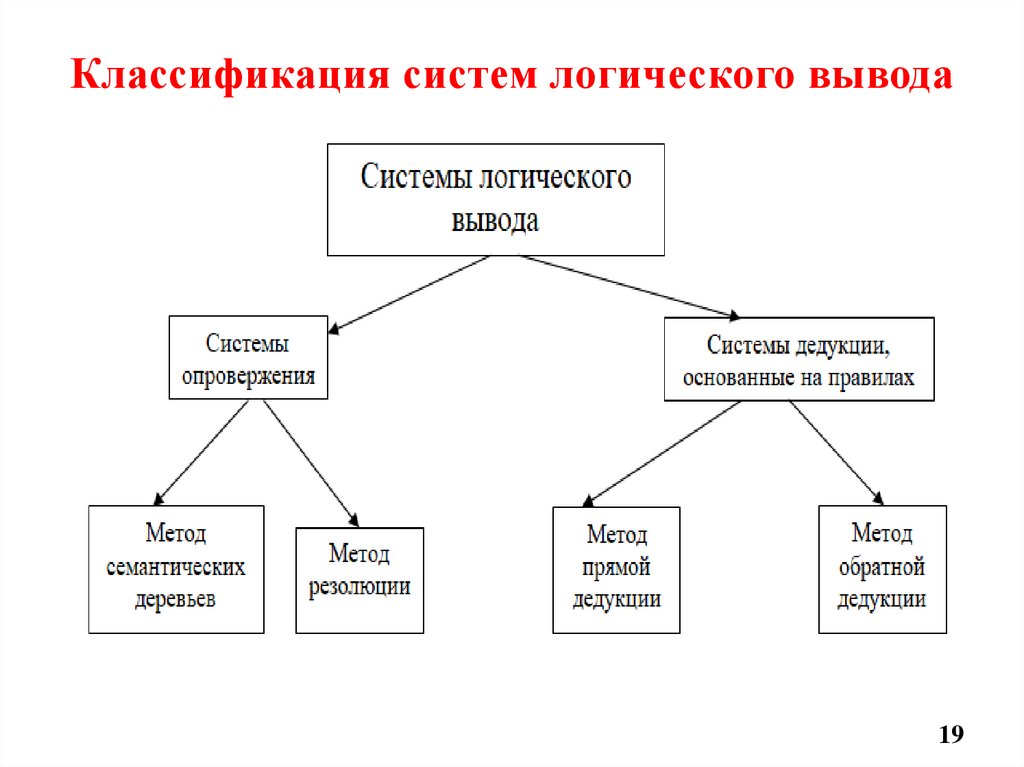
19. Классификация систем логического вывода

19

20. Универсум Эрбрана

Для того, чтобы доказать противоречивость множества E
предложений (т.е. противоречивость их конъюнкции),
необходимо доказать, что не существует интерпретации, при
которой все предложения истинны. Осуществить перебор всех
возможных интерпретаций практически невозможно.
Однако, как было показано Эрбраном, существует такое
подмножество Н множества возможных интерпретаций, для
которого множество E является противоречивым тогда и
только тогда, когда оно противоречиво для всего множества
возможных интерпретаций. Потому можно ограничиться
перебором лишь в этом подмножестве Н. Данное подмножество
называется универсумом Эрбрана и определяется следующим
образом.
20

21. Универсум Эрбрана

Пусть множество Н0 – множество константных букв,
встречающихся в множестве предложений E. Если в E нет
константных букв, то в Н0 включается некоторая
произвольная константная буква, скажем а. Для i>0 Нi есть
Нi-1, объединенное со всеми элементами (термами)
fi(t1,…,tn), образованными функциональными буквами fi из E и
элементами tj, j=1,…,n из Нi-1. Множество Hi называется i–м
уровнем универсума Эрбрана, а сам универсум есть
Н=Н∞
Пример.
E= { P(x) V Q(a) V ¬ P(f(x)); ¬ Q(b) V P(g(x)) }
H0 = {a, b};
H1 = { a, b, f(a), f(b), g(a), g(b) };
H2 = { a, b, f(a), f(b), g(a), g(b), f(f(a)), f(f(b)), f(g(a)), f(g(b)),
g(f(a)), g(f(b)), g(g(a)), g(g(b)) }
21

22. Эрбрановская база

Эрбрановской
базой
множества
предложений E называется множество всех
константных частных случаев атомных
формул, получающихся заменой всех их
переменных членами универсума Эрбрана.
Для предыдущего примера эрбрановская
база имеет вид:
{ P(a), Q(a), P(b), Q(b), P(f(a)), Q(f(a)),
P(g(a)), Q(g(a)), P(f(f(a))), P(f(f(b))), P(f(g(a))),
P(f(g(b))), P(g(f(a))), P(g(f(b))), P(g(g(a))),
P(g(g(b))), Q(f(f(a))), Q(f(f(b))), Q(f(g(a))),
Q(f(g(b))), Q( g(f(a))), Q(g(f(b))), Q(g(g(a))),
Q(g(g(b)))}
22

23. Семантические деревья 

Семантические деревья
Одним из методов доказательства противоречивости множества
E предложений является метод семантических деревьев. Суть
данного метода состоит в построении семантического дерева,
позволяющего
перебрать
все
возможные
интерпретации
предложений из E, заданные на универсуме Эрбрана.
Так как множество константных случаев атомных формул,
входящих в предложения из E, определяется эрбрановской базой, то
формирование различных интерпретаций осуществляется путем
приписывания элементам эрбрановской базы значений TRUE или
FALSE.
Графически этот процесс изображается в виде семантического
бинарного дерева, каждое ребро которого представляет собой
решение, принятое относительно значения одного из элементов
эрбрановской базы. Условимся записывать рядом с ребром, где
элементу приписывается значение ТRUE, сам этот элемент, а рядом с
ребром, где элементу приписывается значение FALSE, - его
23
отрицание.

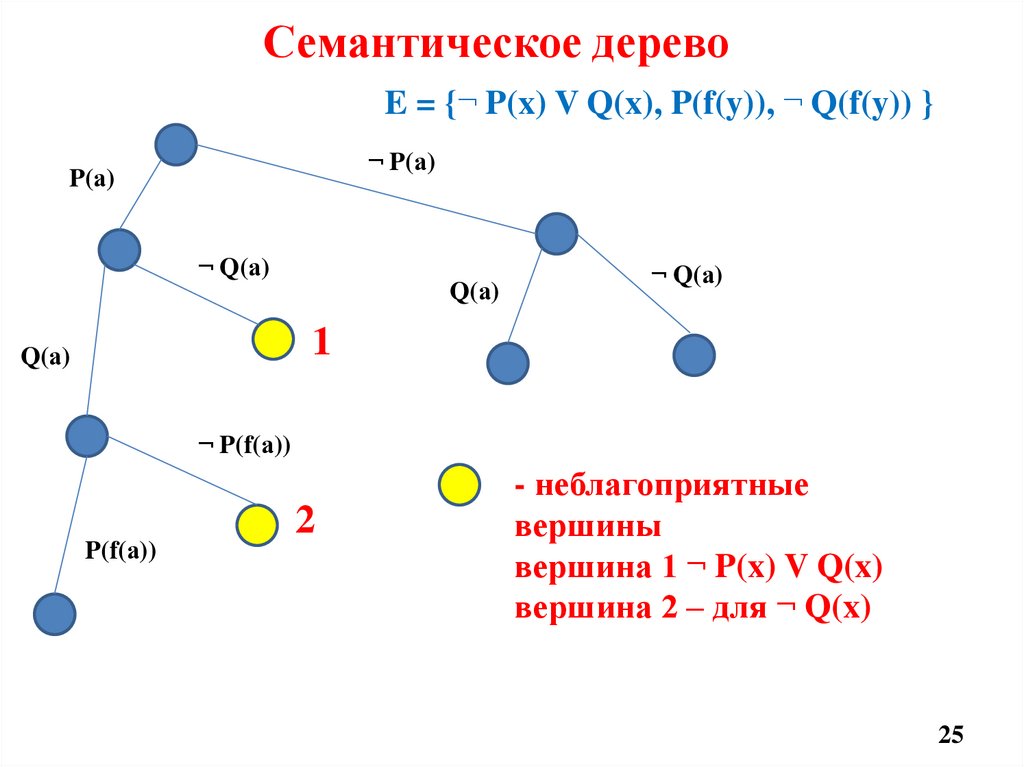
24. Семантическое дерево

Построим семантическое дерево для
противоречивого множества предложений
E = {¬ P(x) V Q(x), P(f(y)), ¬ Q(f(y)) },
универсумом Эрбрана здесь будет
множество
H = { a, f(a), f(f(a)), f(f(f(a))), …},
а эрбрановскую базу можно упорядочить
так
{ P(a), Q(a), P(f(a)), Q(f(a)), P(f(f(a))),…}.
24

25. Семантическое дерево

E = {¬ P(x) V Q(x), P(f(y)), ¬ Q(f(y)) }
¬ P(а)
P(а)
¬ Q(а)
Q(а)
¬ Q(а)
1
Q(а)
¬ P(f(а))
P(f(а))
2
- неблагоприятные
вершины
вершина 1 ¬ P(x) V Q(x)
вершина 2 – для ¬ Q(x)
25

26.

Так как эрбрановская база неограниченна, то
результирующее семантическое дерево, очевидно,
будет бесконечным.
Если множество предложений действительно
противоречиво, то оказывается возможным, не
просматривая
дерево
неограниченно
вниз,
установить, что определенные интерпретации не
удовлетворяют тем или иным предложениям.
Вершины дерева, в которых этот факт установлен,
называются неблагоприятными вершинами для того
или иного предложения.
Если множество предложений противоречиво, то
каждый путь в дереве в конце концов должен
оборваться.
26

27. Недостатки метода семантических деревьев

Чрезвычайно
быстрое
разрастание
семантического
дерева, требующее выполнения
все большего объема вычислений.
27