Похожие презентации:
8_Логические модели представления знаний(ч2)
1. Логические модели представления знаний (часть 2)
12. 2. Метод резолюции
23. Основные понятия
Подстановка – замена переменных в некоторомвыражении на термы. Любую подстановку можно
представить в виде множества упорядоченных пар
S = {t1 / v1 ,…, tn / vn },
где пара ti / vi означает, что в некотором выражении
каждое вхождение переменой vi заменяется на терм ti, не
содержащий эту переменную.
Примеры
y=sin(2x)
Подстановка S1 = {z/2x}
y s1 =sin(z)
P[x, f(y), b]
Подстановка S1 = {z/x, w/y}
P[x, f(y), b] s1 = P[z, f(w), b]
3
4. Основные понятия
Унификация – применение подстановки S кмножеству {Fi} выражений с целью приведения их к
одному и тому же виду. Если такая подстановка S
существует, т.е. F1S = F2S = F3S= …, то S называется
унификатором для {Fi} , а само множество {Fi} –
унифицируемым.
Пример
{Fi} = {P[x, f(y), b]; P[x, f(b), b] }
S = {a/x, b/y} дает P[a, f(b), b] S
Хотя подстановка S = {a/x, b/y} является
унификатором для нашего множества, она не является
простейшим
унификатором.
Действительно,
для
унификации достаточно было бы применить подстановку
S = {b/y}.
4
5. Основные понятия
Наиболееобщим
(простейшим)
унификатором
(НОУ)
называется
унификатор g, обладающий тем свойством,
что если S есть любой унификатор для {Fi},
то существует некоторая подстановка S’
такая, что {Fi} S = {Fi} gS’
5
6. Основные понятия
Алгоритмунификации
находит
НОУ
для
унифицируемого множества {Fi} выражений или сообщает о
неудаче, если множество не унифицируемо.
1. Положить к=0 и S0 = {} – пустая подстановка.
2. Если {Fi} не является одноэлементным множеством, то
перейти к этапу 3, иначе S=Sk и закончить работу.
3. Все выражения Fi просматривать одновременно слева
направо до тех пор, пока не обнаружатся различные термы. Из
этих термов образовать множество рассогласования. Если в
этом множестве есть два элемента tk и vk , где tk – терм, а vk переменная, не входящая в tk, то сформировать
модифицированную подстановку Sk+1 = {Sk, tk / vk }, и перейти к
шагу 2. В противном случае – неудача (закончить работу).
6
7. Пример
{Fi} = {P(x, z, v ), P(x, f(y), y), P(x, z, b)}№
п/п
k
Множество
рассогласования
Подстановка
Sk
Результат
{Fi}
{}
0
1
{z, f(y)}
{f(y)/z}
{P(x, f(y),v ); P(x, f(y), y); P(x, f(y), b)}
2
{v , y, b}
{f(y)/z, y/v }
{P(x, f(y), y); P(x, f(y), b)}
3
{y, b}
{f(y/z), y/v , b/y}
{P(x, f(b), b)}
Останов
произошел
т.к.
результат
стал
одноэлементным
множеством,
а
НОУ
является
подстановка
g={f(y/z), y/v , b/y}.
7
8. Основные понятия
Резолюция – правило вывода, которое можетприменяться
к
определенному
классу
ППФпредложениям. Процесс резолюции, если он приложим,
применяется к двум родительским предложениям и
порождает третье, выводимое из этих двух, предложение.
Пусть исходные предложения задаются в виде {Li}и
{Mi}. Предположим, что существуют {li} ⸦ {Li}и {mi} ⸦
{Mi} такие, что {li}=¬{mi}, и для {li} { mi} существует НОУ
g. Тогда говорят, что два предложения {Li}и {Mi}
разрешаются и, что новое предложение
rij ={{Li} – {li}}g {{Mi} – {mi}}g
называется их резольвентой.
8
9. Процедура доказательства теорем методом резолюции
В типичной задаче на доказательствотеорем есть множество F ППФ, исходя из
которого необходимо доказать некоторую
ППФ G. Эта задача сводится к задаче
доказательства противоречивости множества
{F U (¬ G)} или, что то же самое,
противоречивости ППФ F1&…&Fn& ¬ G.
Выявление
факта
противоречивости
некоторого
множества
предложений
называют процедурой опровержения.
.
9
10. Процедура опровержения методом резолюции
Процедура опровержения методом резолюции состоит изследующих шагов:
1. Образовать множество предложений
E = {F U {¬ G}}.
2. Выбрать два разрешимых предложения ci = {{Li} – {li}}g и
cj = {{Mi} – {mi}}g в множестве E и вычислить резольвенту rij для ci и
c j.
3. Если rij является пустым предложением (NIL-пустое
множество), то теорема доказана, иначе включить rij в множество E и
перейти к шагу 2.
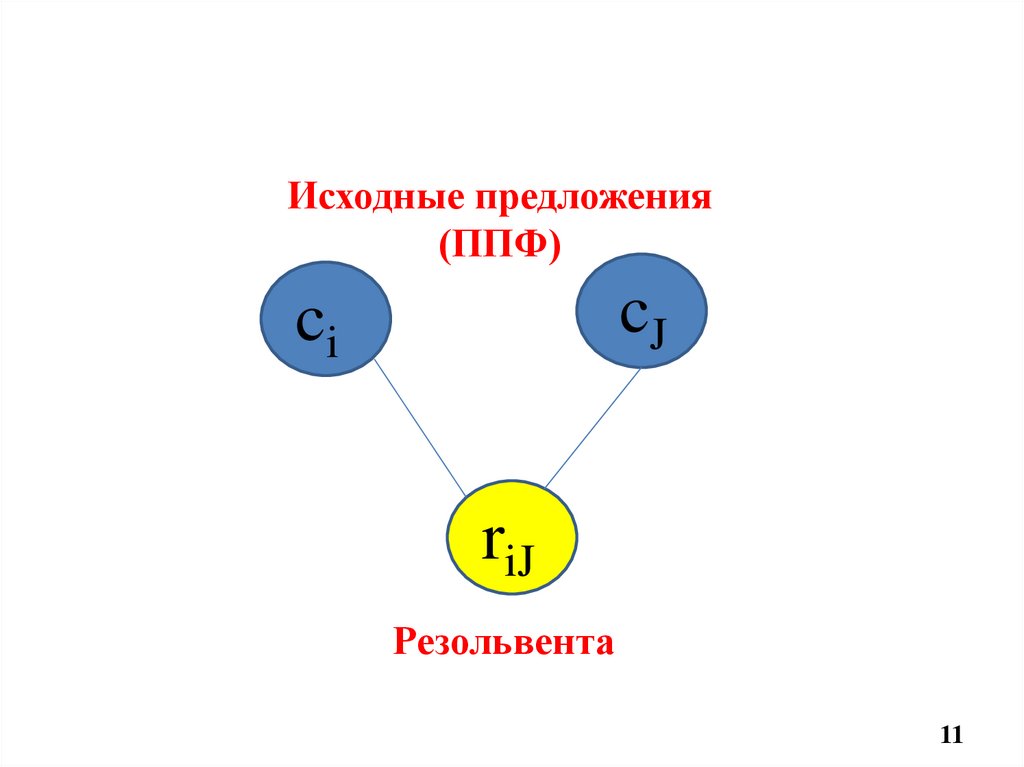
Чтобы следить за тем, какие резолюции были выбраны, процесс
доказательства можно изображать в виде графа. Вершины этого графа
помечены предложениями. Когда два предложения ci и cj создают
резольвенту rij, то они образуют новую вершину rij, причем ребра связывают
ее с вершинами ci и cj.
Таким образом, опровержение на основе резолюции может быть
представлено некоторым деревом опровержения, корневая вершина
которого помечена предложением NIL (пустым множеством).
10
11.
Исходные предложения(ППФ)
cJ
ci
riJ
Резольвента
11










 Математика
Математика








