Issledovanie_na_monoton

1. Исследование функций на монотонность

2.

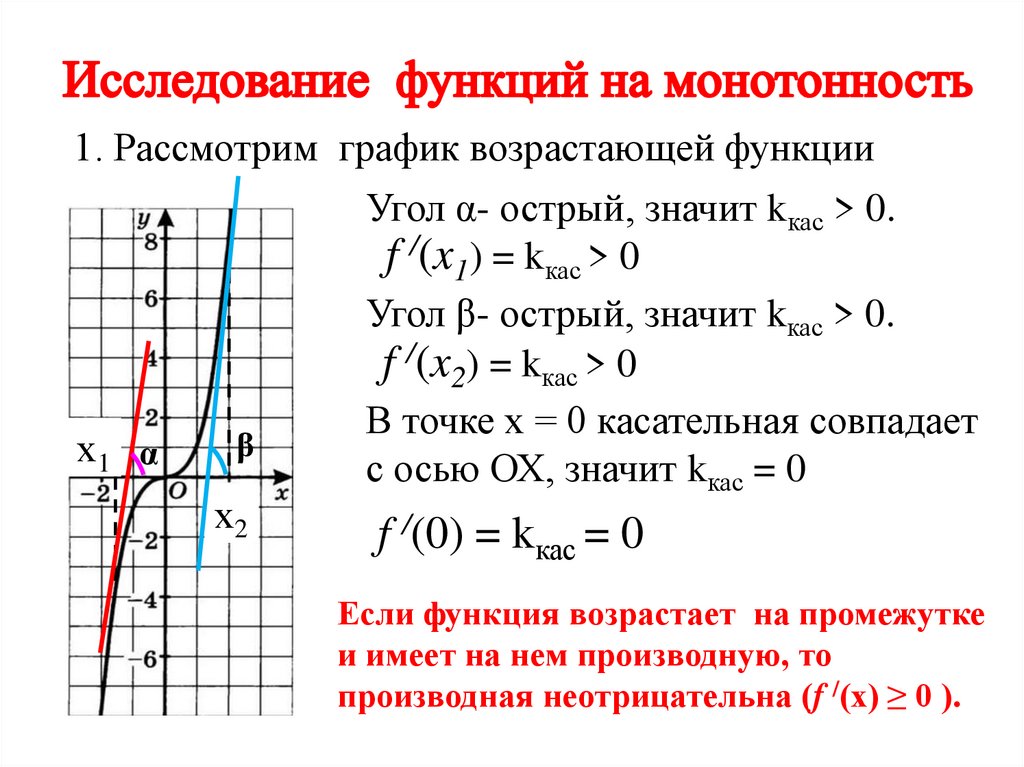
1. Рассмотрим график возрастающей функции
х1 α
β
х2
Угол α- острый, значит kкас > 0.
f /(x1) = kкас > 0
Угол β- острый, значит kкас > 0.
f /(x2) = kкас > 0
В точке х = 0 касательная совпадает
с осью ОХ, значит kкас = 0
f /(0) = kкас = 0
Если функция возрастает на промежутке
и имеет на нем производную, то
производная неотрицательна (f /(x) ≥ 0 ).

3.

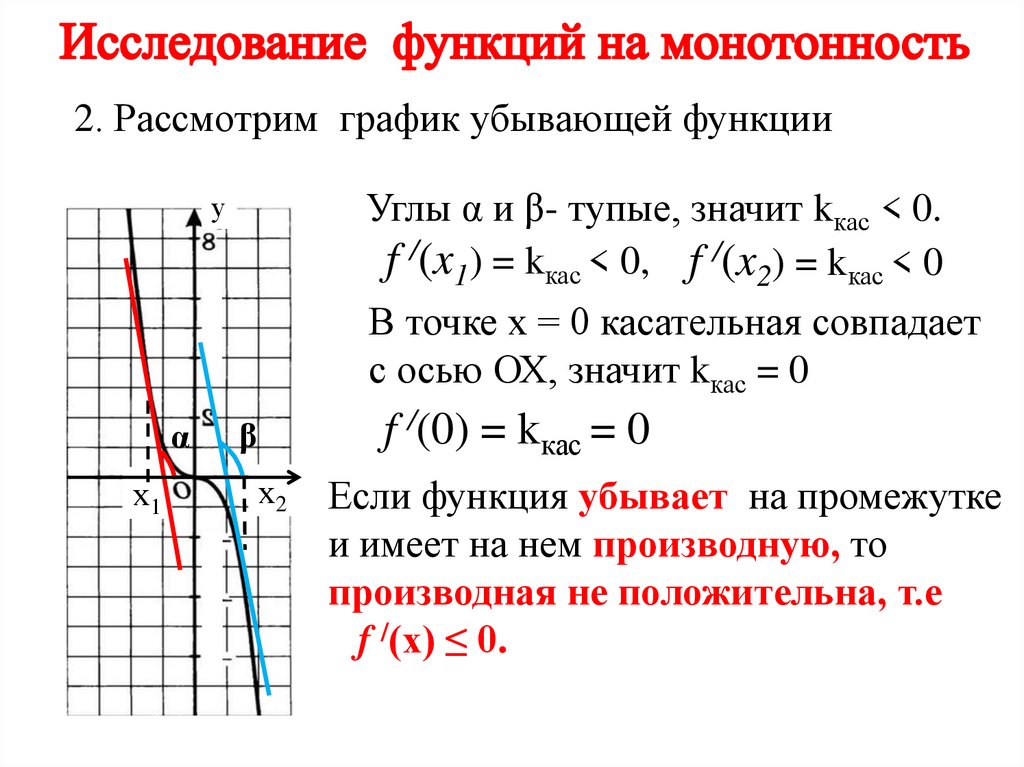
2. Рассмотрим график убывающей функции
Углы α и β- тупые, значит kкас < 0.
f /(x1) = kкас < 0, f /(x2) = kкас < 0
у
В точке х = 0 касательная совпадает
с осью ОХ, значит kкас = 0
α
х1
f /(0) = kкас = 0
β
х2
Если функция убывает на промежутке
и имеет на нем производную, то
производная не положительна, т.е
f /(x) ≤ 0.

4. Обратные утверждения

Теорема 1
Если во всех точках открытого промежутка Х
выполняется неравенство f /(x) ≥ 0 (f /(х) = 0 либо
не выполняется, либо выполняется лишь в
конечном множестве точек), то функция у= f(x)
возрастает на промежутке Х.

5. Обратные утверждения

Теорема 2
Если во всех точках открытого промежутка Х
выполняется неравенство f /(x) ≤ 0 (f /(х) = 0 либо
не выполняется, либо выполняется лишь в
конечном множестве точек), то функция у= f(x)
убывает на промежутке Х.

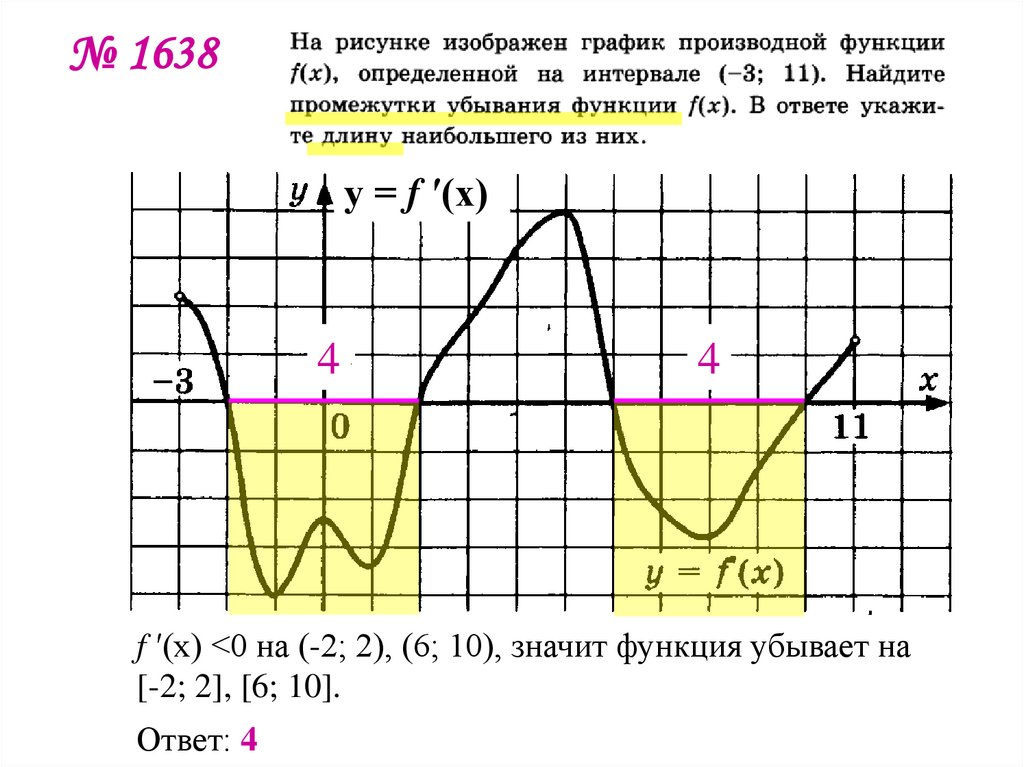
6. № 1638

у = f ′(x)
4
4
f ′(x) <0 на (-2; 2), (6; 10), значит функция убывает на
[-2; 2], [6; 10].
Ответ: 4

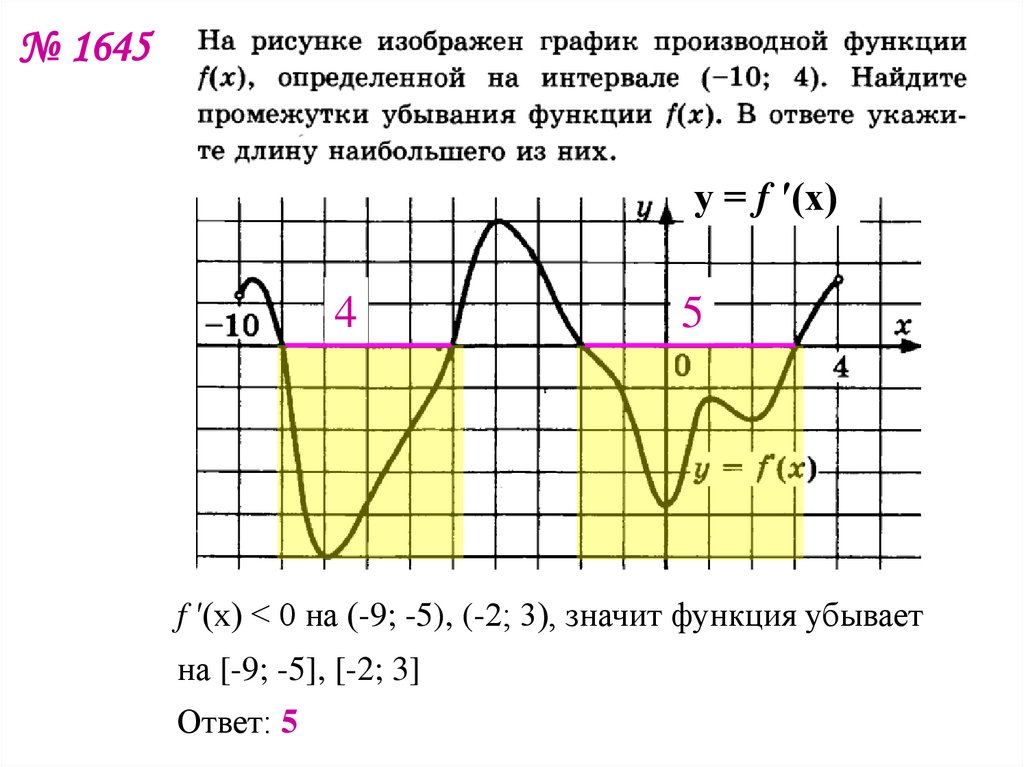
7. № 1645

у = f ′(x)
4
5
f ′(x) < 0 на (-9; -5), (-2; 3), значит функция убывает
на [-9; -5], [-2; 3]
Ответ: 5

8.

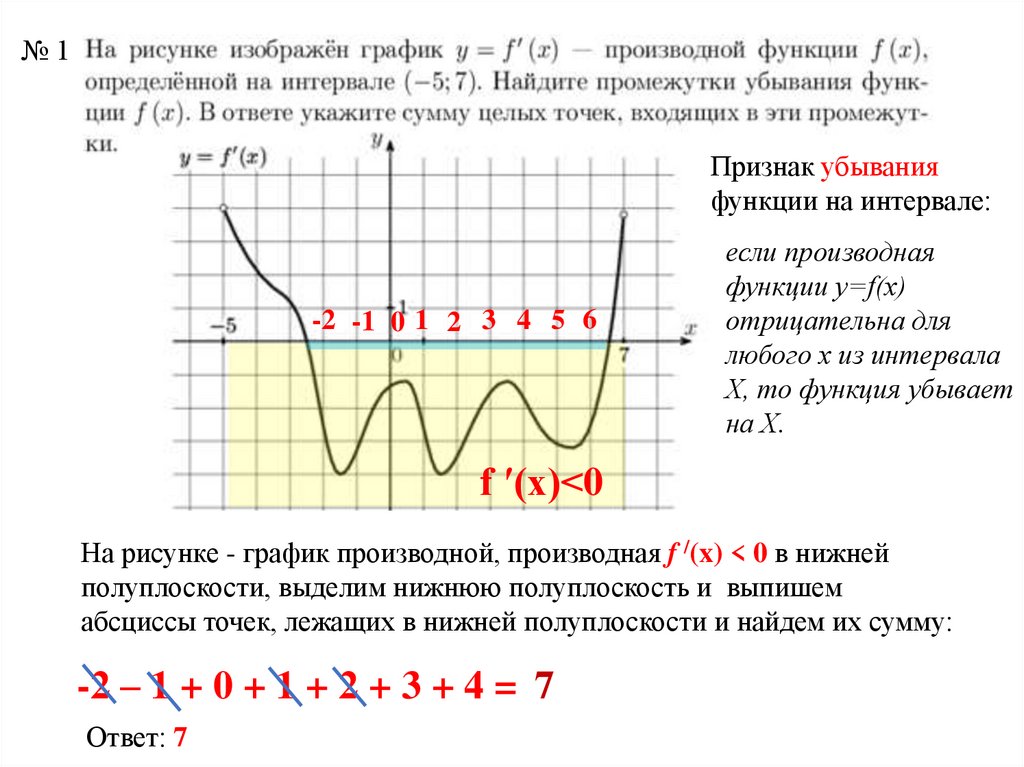
№1
Признак убывания
функции на интервале:
-2 -1 0 1 2 3 4 5 6
если производная
функции y=f(x)
отрицательна для
любого x из интервала
X, то функция убывает
на X.
f ′(x)<0
На рисунке - график производной, производная f /(x) < 0 в нижней
полуплоскости, выделим нижнюю полуплоскость и выпишем
абсциссы точек, лежащих в нижней полуплоскости и найдем их сумму:
-2 – 1 + 0 + 1 + 2 + 3 + 4 = 7
Ответ: 7

9.

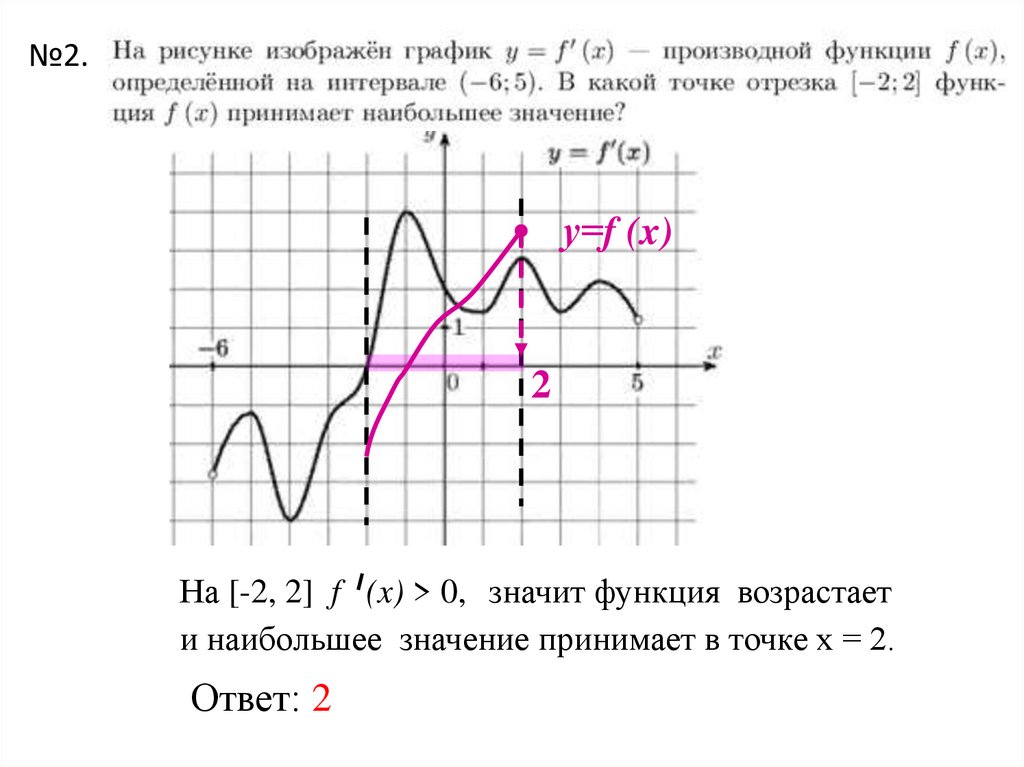
№2.
у=f (x)
2
На [-2, 2] f (x) > 0, значит функция возрастает
и наибольшее значение принимает в точке х = 2.
Ответ: 2

10.

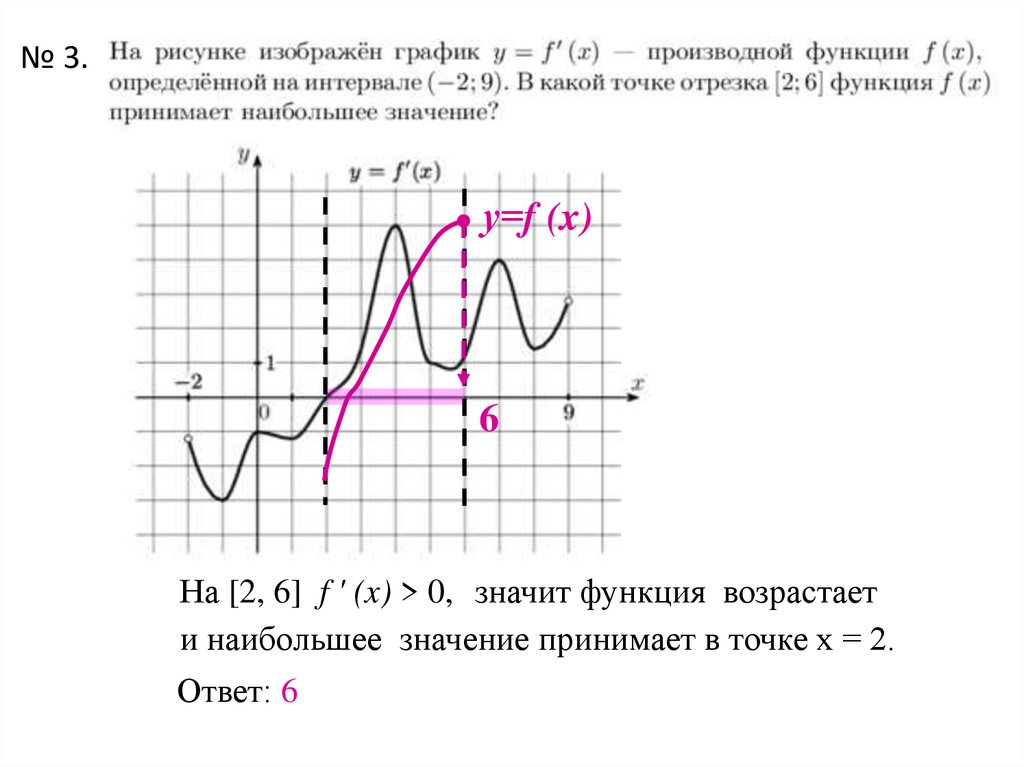
№ 3.
у=f (x)
6
На [2, 6] f ' (x) > 0, значит функция возрастает
и наибольшее значение принимает в точке х = 2.
Ответ: 6

11.

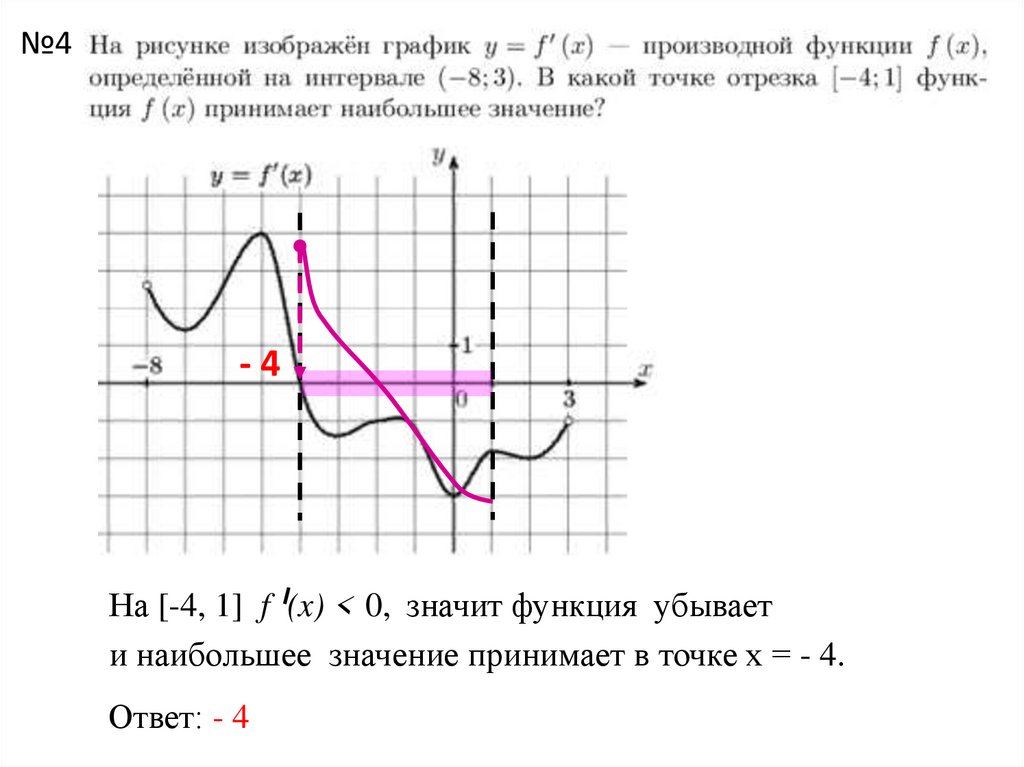
№4
-4
На [-4, 1] f (x) < 0, значит функция убывает
и наибольшее значение принимает в точке х = - 4.
Ответ: - 4

12.

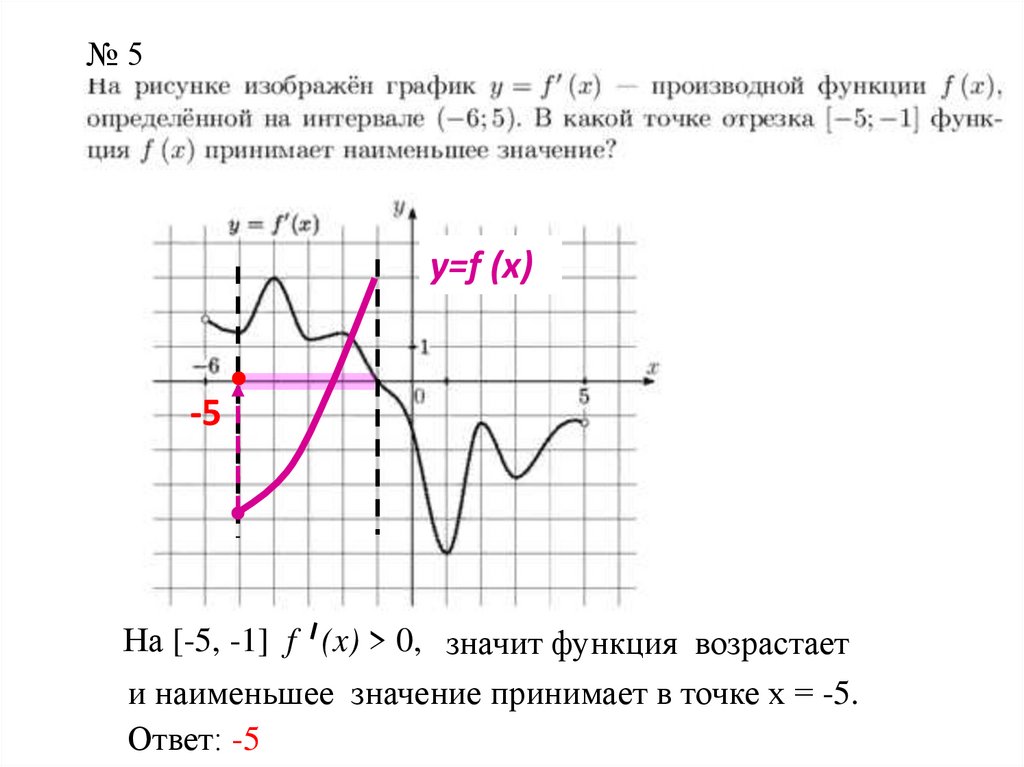
№5
у=f (x)
-5
На [-5, -1] f (x) > 0, значит функция возрастает
и наименьшее значение принимает в точке х = -5.
Ответ: -5

13.

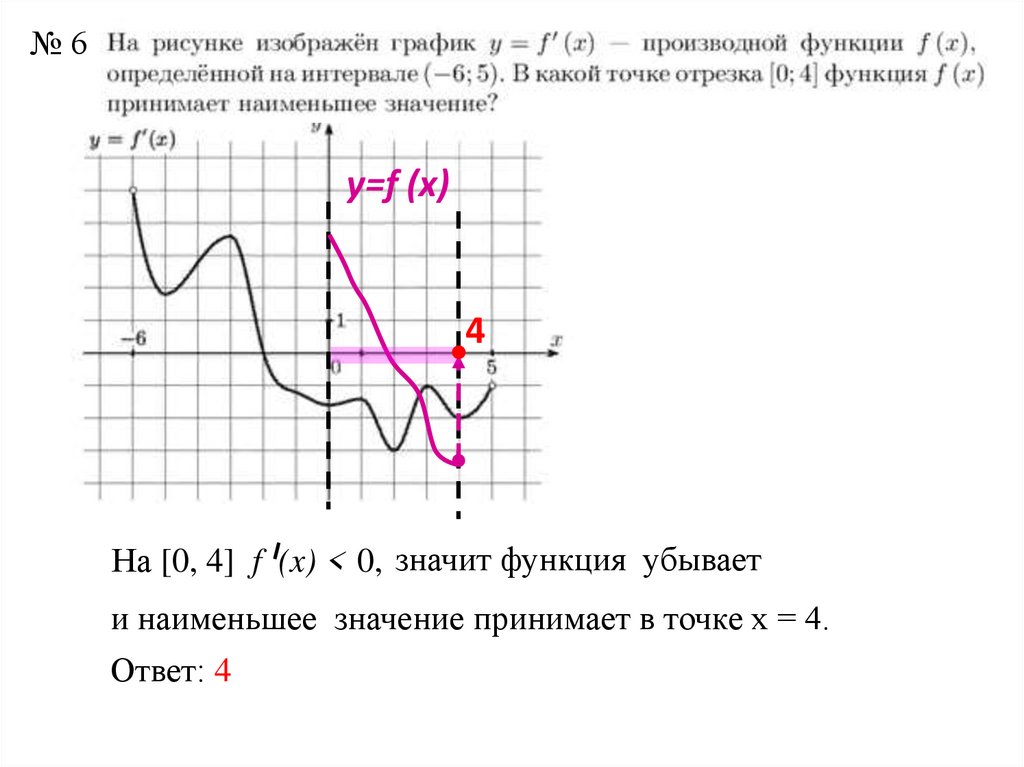
№6
у=f (x)
4
На [0, 4] f (x) < 0, значит функция убывает
и наименьшее значение принимает в точке х = 4.
Ответ: 4

14.

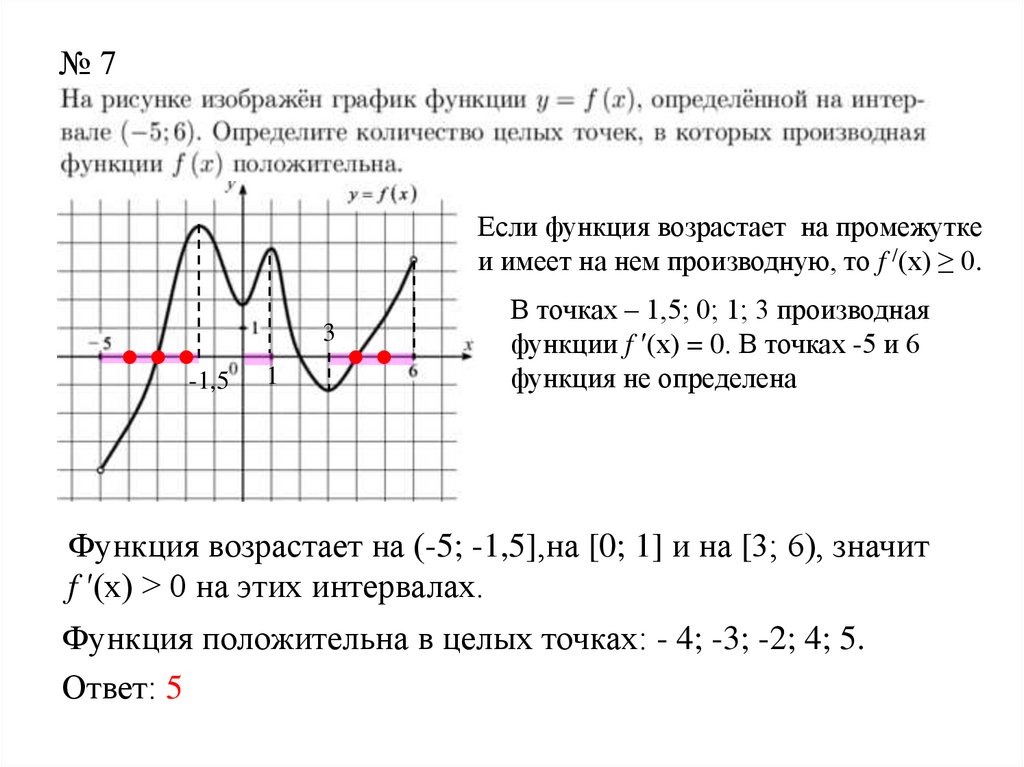
№7
Если функция возрастает на промежутке
и имеет на нем производную, то f /(x) ≥ 0.
3
-1,5
1
В точках – 1,5; 0; 1; 3 производная
функции f ′(x) = 0. В точках -5 и 6
функция не определена
Функция возрастает на (-5; -1,5],на [0; 1] и на [3; 6), значит
f ′(x) > 0 на этих интервалах.
Функция положительна в целых точках: - 4; -3; -2; 4; 5.
Ответ: 5

15.

№8
4
-4
1
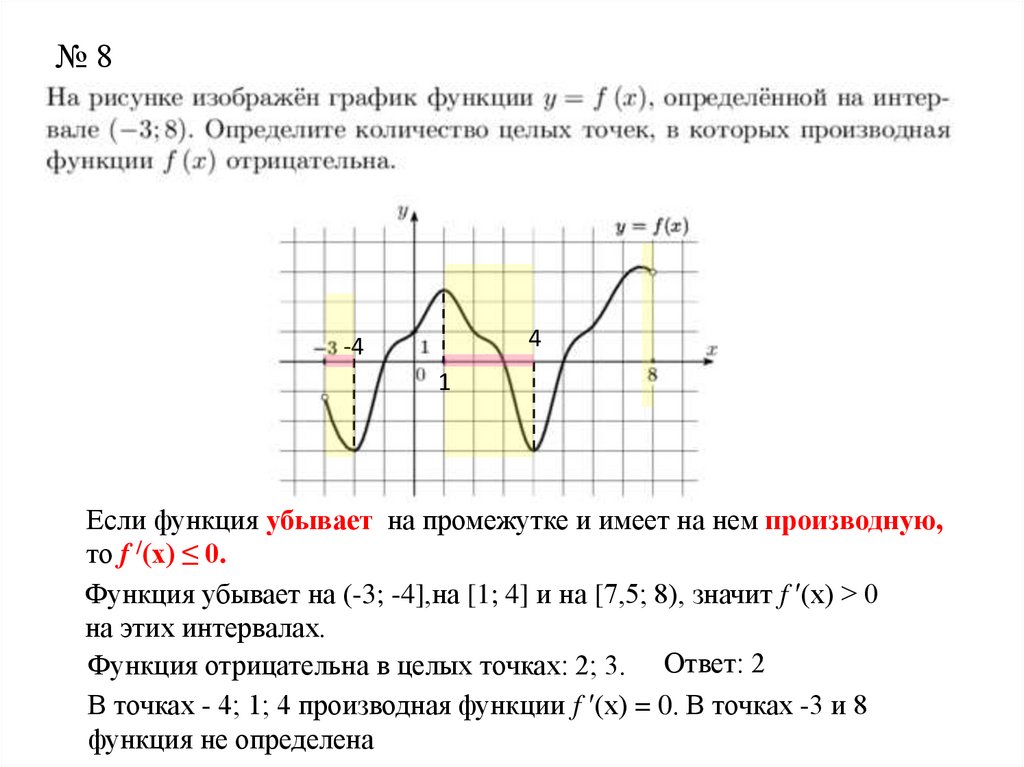
Если функция убывает на промежутке и имеет на нем производную,
то f /(x) ≤ 0.
Функция убывает на (-3; -4],на [1; 4] и на [7,5; 8), значит f ′(x) > 0
на этих интервалах.
Функция отрицательна в целых точках: 2; 3. Ответ: 2
В точках - 4; 1; 4 производная функции f ′(x) = 0. В точках -3 и 8
функция не определена

16.

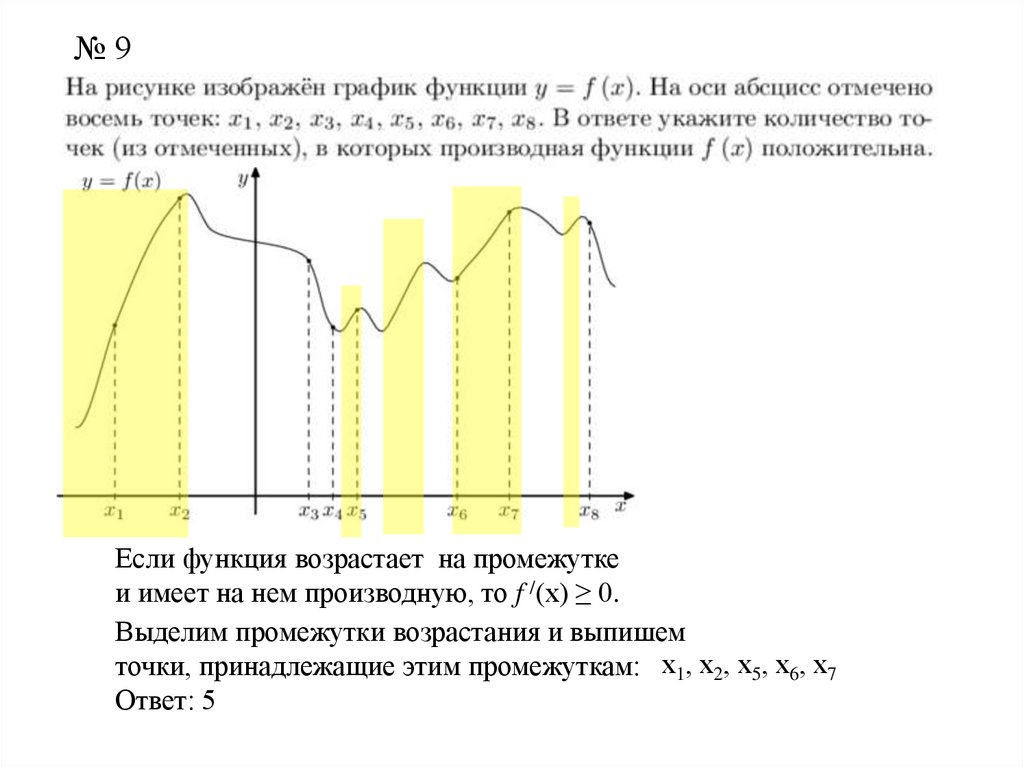
№9
Если функция возрастает на промежутке
и имеет на нем производную, то f /(x) ≥ 0.
Выделим промежутки возрастания и выпишем
точки, принадлежащие этим промежуткам: х1, х2, х5, х6, х7
Ответ: 5

17.

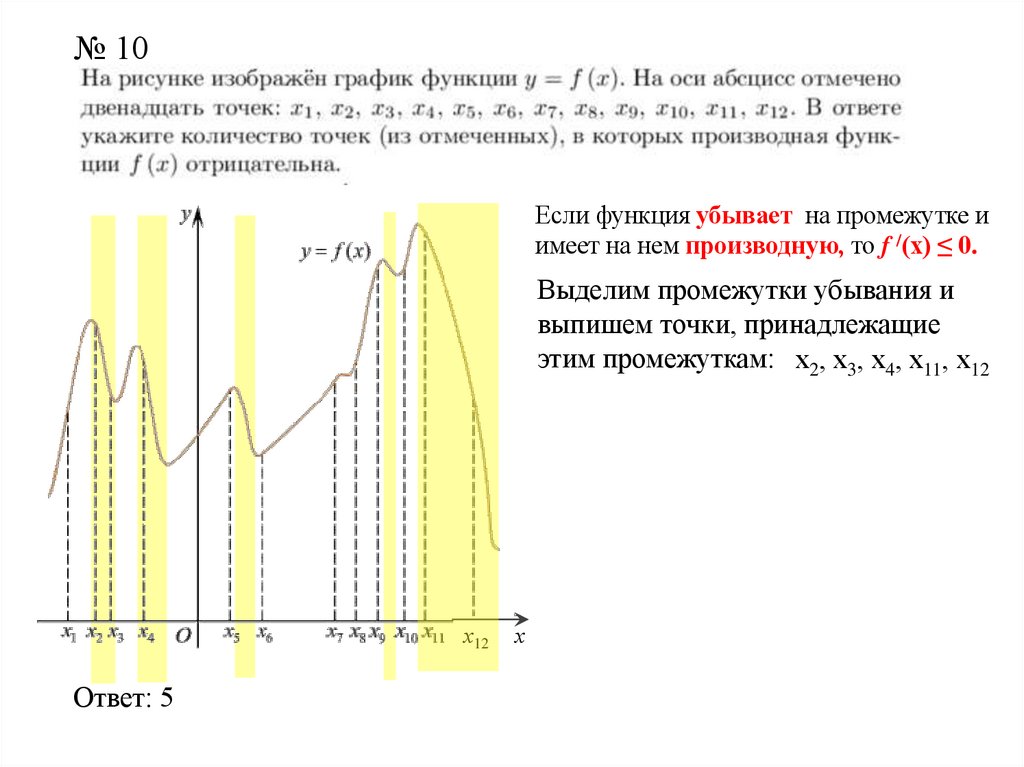
№ 10
Если функция убывает на промежутке и
имеет на нем производную, то f /(x) ≤ 0.
Выделим промежутки убывания и
выпишем точки, принадлежащие
этим промежуткам: х2, х3, х4, х11, х12
х12
Ответ: 5
х

18.

№ 11
Если во всех точках открытого
промежутка Х выполняется неравенство
f /(x) ≥ 0 (f /(х) = 0 либо не выполняется,
либо выполняется лишь в конечном
множестве точек), то функция у= f(x)
возрастает на промежутке Х.
На рисунке - график производной, производная f /(x) ≥ 0 в верхней
полуплоскости, выделим верхнюю полуплоскость и выпишем
абсциссы точек, лежащих в верхней полуплоскости: х4, х5, х6.
Ответ: 3

19.

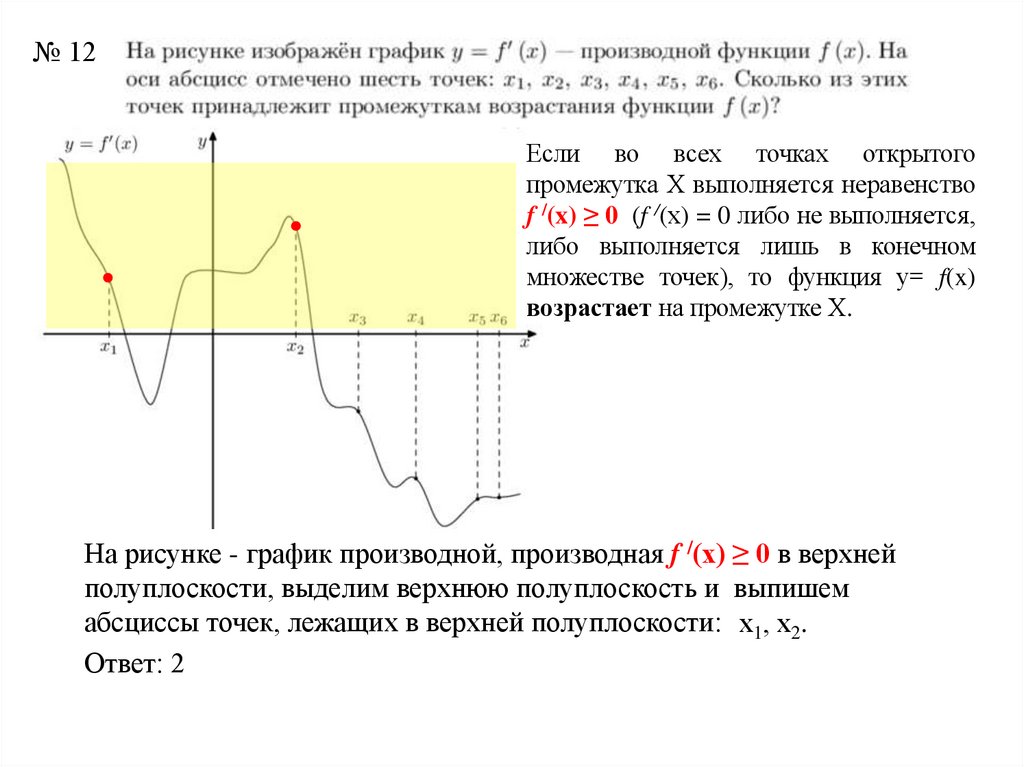
№ 12
Если во всех точках открытого
промежутка Х выполняется неравенство
f /(x) ≥ 0 (f /(х) = 0 либо не выполняется,
либо выполняется лишь в конечном
множестве точек), то функция у= f(x)
возрастает на промежутке Х.
На рисунке - график производной, производная f /(x) ≥ 0 в верхней
полуплоскости, выделим верхнюю полуплоскость и выпишем
абсциссы точек, лежащих в верхней полуплоскости: х1, х2.
Ответ: 2

20.

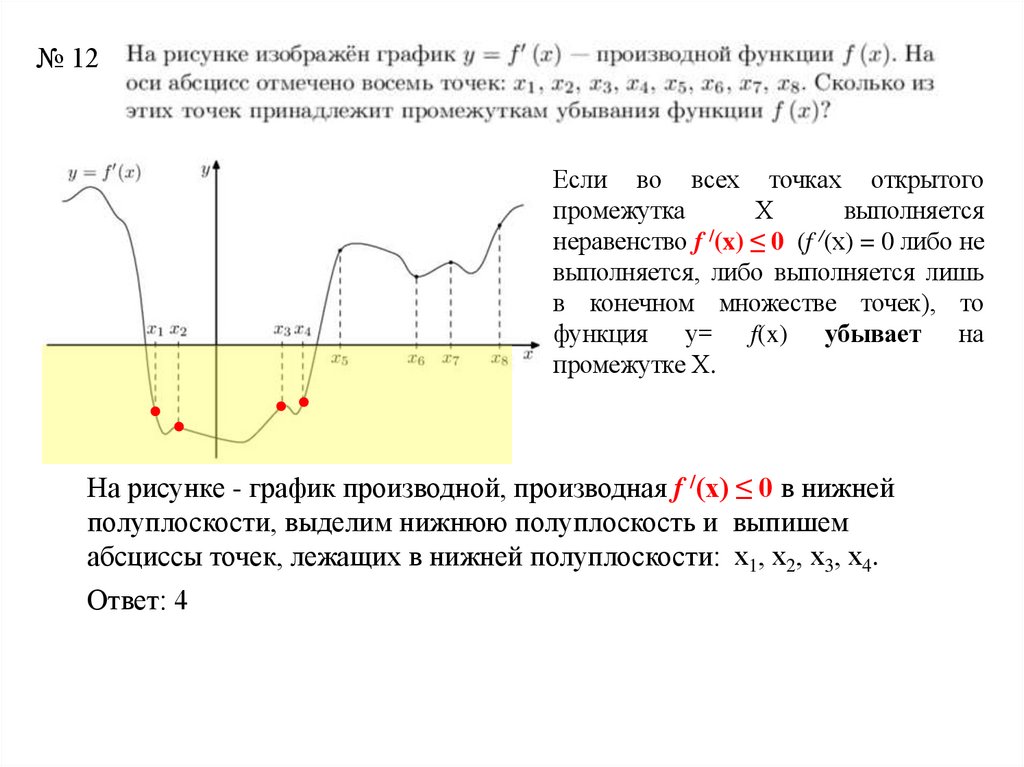
№ 12
Если во всех точках открытого
промежутка
Х
выполняется
неравенство f /(x) ≤ 0 (f /(х) = 0 либо не
выполняется, либо выполняется лишь
в конечном множестве точек), то
функция у= f(x) убывает на
промежутке Х.
На рисунке - график производной, производная f /(x) ≤ 0 в нижней
полуплоскости, выделим нижнюю полуплоскость и выпишем
абсциссы точек, лежащих в нижней полуплоскости: х1, х2, х3, х4.
Ответ: 4