Похожие презентации:
Shortest Paths
1. Shortest Paths
1. Dijkstra’s algorithm.2. The Bellman-Ford algorithm.
3. The Floyd-Warshall algorithm.
2.
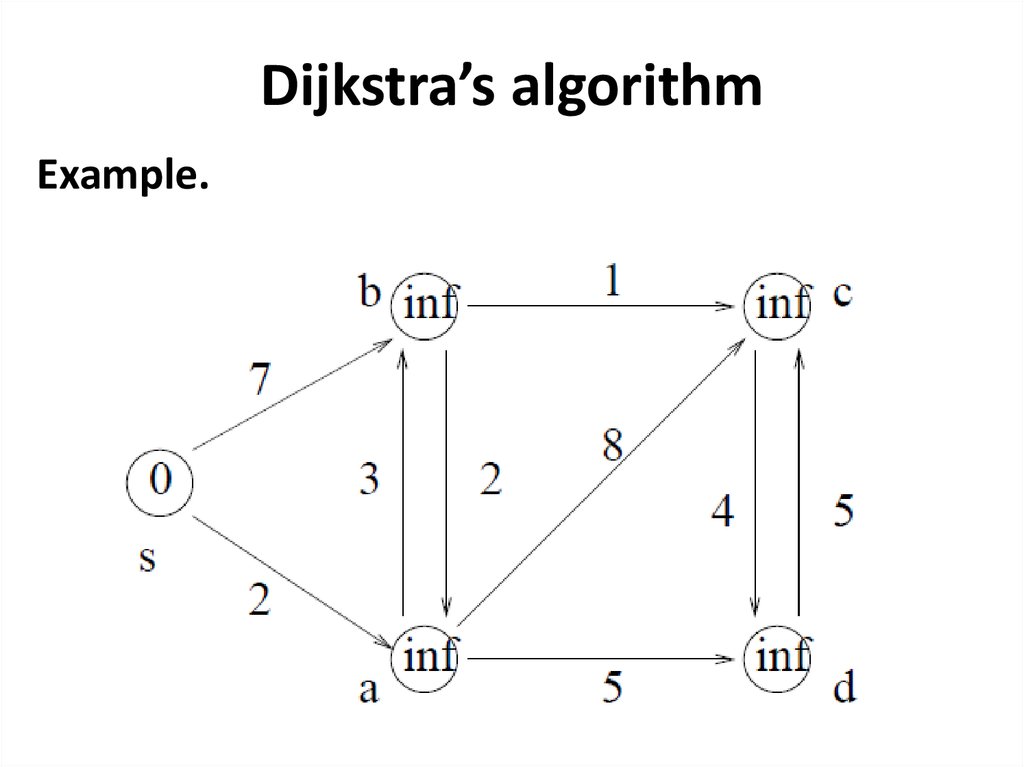
Dijkstra’s algorithmare given:
source vertex s;
the weight weight (u, v) of each edge (u, v);
to calculate:
for each vertex v the shortest-path weight sp(s, v);
=> shortest[v]
the vertex preceding v;=> pred[v]
3.
Dijkstra’s algorithm4.
Dijkstra’s algorithmthe situation at time 0
shortest[s]= 0
5.
Dijkstra’s algorithmat time 4
shortest[y]= 4, pred[y]= s
6.
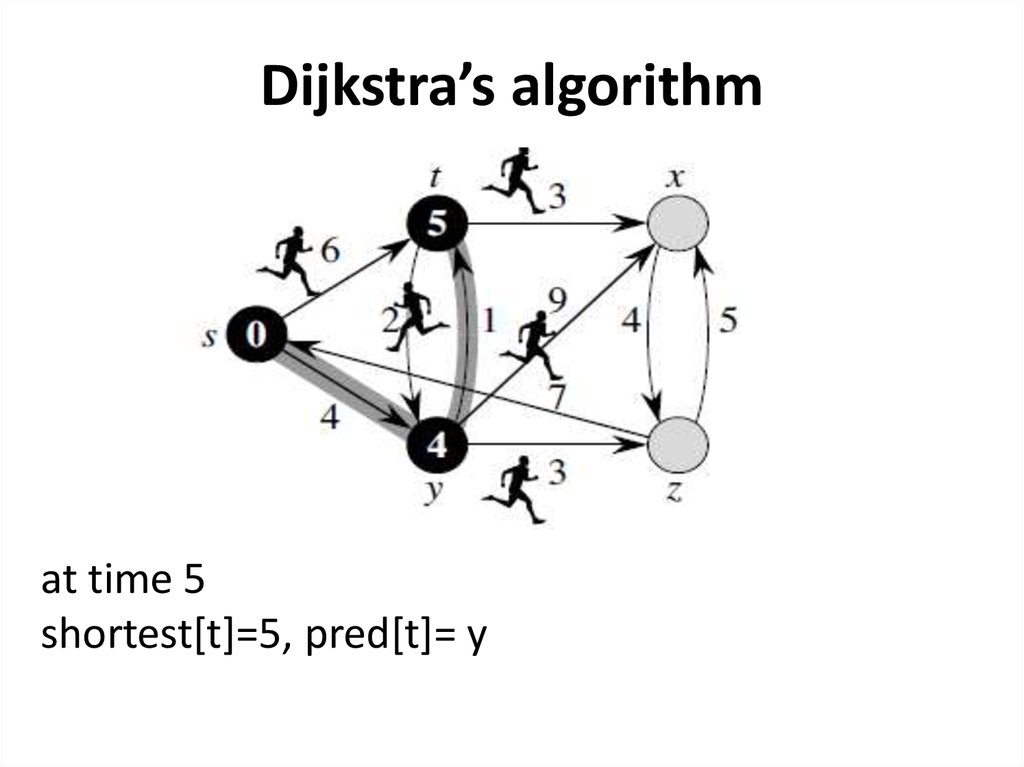
Dijkstra’s algorithmat time 5
shortest[t]=5, pred[t]= y
7.
Dijkstra’s algorithmat time 7
shortest[z]=7, pred[z]= y
8.
Dijkstra’s algorithmat time 8
shortest[x]=8, pred[x]=t
9.
Dijkstra’s algorithmDijkstra’s algorithm works a little differently. It
treats all edges the same.
Dijkstra’s algorithm works by calling the RELAX
procedure once for each edge.
10.
11.
Dijkstra’s algorithmA set Q is a set of vertices for which the final
shortest and pred values are not yet known.
All vertices not in Q have their final shortest and
pred values.
In the step 1 shortest[s] = 0, shortest[v] = ∞ for all
other vertices, and pred[v] = NULL for all vertices.
12.
Dijkstra’s algorithmA set Q is a set of vertices for which the final
shortest and pred values are not yet known.
All vertices not in Q have their final shortest and
pred values.
In the step 1 shortest[s] = 0, shortest[v] = ∞ for all
other vertices, and pred[v] = NULL for all vertices.
Algorithm repeatedly finds the vertex u in set Q
with the lowest shortest value, removes that
vertex from Q, and relaxes all the edges leaving u.
13.
Dijkstra’s algorithmQuestion 1: How does the algorithm find new
paths and do the relaxation?
Question 2: In which order does the algorithm
process the vertices one by one?
14.
Dijkstra’s algorithmAnswer to Question 1: How does the algorithm
find new paths and do the relaxation?
Finding new paths. When processing a vertex u,
the algorithm will examine all vertices v from array
of vertices of adjacent of u (v∈








































 Математика
Математика








