ОКИ 1 семестр Лекция_1 (1)

1.

Кафедра стандартизации и метрологии
Курс
Основы компьютерного
инжиниринга
Лектор: доцент, канд. техн. наук
Поликарпов Юрий Васильевич

2.

Образование
Уфимский авиационный институт, Механико-технологический факультет,
специальность Технология машиностроения, станки и инструменты
Аспирантура Московского авиационного института по специальности
Прикладная геометрия и инженерная графика
Достижения
Поликарпов Юрий
Васильевич
Доцент кафедры
стандартизации и метрологии
• Кандидат технических наук
• Доцент
• Область научных интересов – математическое моделирование
сложных технических поверхностей, твердотельное и
поверхностное моделирование изделий авиа- и машиностроения

3. Основные учебники

Гордон В. О. Курс начертательной геометрии: [учебное пособие для
студентов высших технических учебных заведений] - Москва:
Высшая школа, 2009 - 272 с.
Левицкий В. С. Машиностроительное черчение и автоматизация
выполнения чертежей: учебник для бакалавров - Москва: Юрайт,
2014 - 435 с.
Поликарпов Ю. В. Основы компьютерной графики: [учебное
пособие] / Ю. В. Поликарпов, М. А. Семашко; Уфимский
государственный авиационный технический университет (УГАТУ) Уфа: УГАТУ, 2014 - 72 с.
© Поликарпов Ю.В.
3

4. Лекция № 1. Проекции и их свойства

1. Задачи дисциплины.
2. Единая система конструкторской документации.
3. Основные правила оформления чертежей:
форматы, масштабы, линии чертежа, шрифты
чертежные, основные надписи, простановка
размеров, сопряжения.
4. Центральная проекция и её свойства.
5. Параллельная проекция и её свойства.
6. Аксонометрическая проекция и её свойства.
7. История развития геометрии.
(Гордон §§ 1,2, 71-75; Левицкий 1.6, 2.1-2.5, 3.15, 5.8, 5.9)
© Поликарпов Ю.В..
4

5. 1. Задачи дисциплины

Основы компьютерного инжиниринга - область знаний,
обеспечивающая
возможность
общения
между
собой
технических специалистов на специальном графическом языке. В
этом языке в качестве слов используются только линии и точки,
из которых образуются элементы всякого изображения на
чертежах.
В настоящее время чертежи широко используются во всех
областях науки и техники.
© Поликарпов Ю.В..
5

6. Задачи дисциплины

«Чертеж является языком техники», – говорил один из
создателей начертательной геометрии французский ученый и
инженер Гаспар Монж (1746-1818). Причем этот язык является
интернациональным, он понятен любому технически грамотному
специалисту, независимо от того, на каком языке он говорит. А
для того, чтобы язык техники был и для вас понятен, нужно
сначала изучить грамматику этого языка. Этим вы и будете
заниматься в процессе изучения нашей дисциплины. Мы
познакомим вас с существующими правилами выполнения и
оформления чертежей любых изделий общего машиностроения.
© Поликарпов Ю.В..
6

7. Задачи дисциплины

Основные задачи курса «Основы компьютерного инжиниринга»:
1) ознакомить студентов с существующими способами построения
чертежей пространственных предметов на плоскости;
2) научить студентов способам задания и изображения на чертежах
геометрических объектов (точек, прямых, кривых линий, плоскостей,
поверхностей), из которых формируются внешние и внутренние формы
изделий общего машиностроения;
3) познакомить студентов с существующими правилами выполнения и
оформления чертежей любых изделий общего машиностроения;
4) научить студентов основным приемам построения конструкторской
документации на проектируемое изделие с помощью систем автоматизированного проектирования;
5) научить студентов читать и понимать готовые чертежи.
© Поликарпов Ю.В..
7

8. Задачи дисциплины

Дисциплина «Основы компьютерного инжиниринга» включает следующие
разделы:
• элементы начертательной геометрии,
• машиностроительное черчение,
• основы компьютерной графики.
Дисциплина поможет изучить пространственные формы изделий общего
машиностроения и соответствующие геометрические закономерности при
помощи чертежей этих изделий. Чертеж при этом является инструментом, с
помощью которого осуществляется непосредственное изучение геометрических
форм предметов и решаются пространственные задачи. Однако, не всякое
изображение предмета на листе бумаги позволяет точно определить его
геометрическую форму.
© Поликарпов Ю.В..
8

9. Задачи дисциплины

Для того, чтобы чертеж был геометрически равноценным
изображаемому предмету (а только в этом случае можно изучать сам
предмет по его чертежу), он должен быть построен при помощи метода
проецирования (от латинского слова рrоjесеrе – бросать вперед).
Поэтому чертежи, применяемые в технике, носят название
проекционных чертежей.
Среди требований, предъявляемых к чертежам, наиболее существенными являются:
наглядность (давать пространственное представление изображаемого
предмета);
обратимость (по нему можно однозначно воспроизвести форму и
размеры изображаемого предмета).
© Поликарпов Ю.В..
9

10. Задачи дисциплины

Необходимо отметить, что основы компьютерного инжиниринга
входит в число фундаментальных дисциплин, составляющих основу высшего технического образования. Без знаний, полученных
при изучении этой дисциплины, невозможно успешное освоение
специальных дисциплин на следующих курсах обучения.
© Поликарпов Ю.В..
10

11. 2. Единая система конструкторской документации

В Российской Федерации комплекс государственных
стандартов, устанавливающих взаимосвязанные нормы и
правила по разработке, оформлению и обращению
конструкторской документации, разрабатываемой и
применяемой на всех стадиях жизненного цикла изделия
(при
проектировании,
изготовлении,
эксплуатации,
ремонте, утилизации) называется единой системой
конструкторской документации (ЕСКД).
© Поликарпов Ю.В..
11

12. Единая система конструкторской документации

Система построения обозначений государственных стандартов:
ГОСТ 2.301 – 68*
Внесены изменения
Год регистрации (до 2000 года, после 4 цифры)
Порядковый номер стандарта в группе
Номер группы стандартов
Класс (2 – номер комплекса стандартов ЕСКД)
Государственный стандарт
© Поликарпов Ю.В..
12

13. Единая система конструкторской документации

Стандарты ЕСКД распределяются по классификационным группам:
0. Общие положения;
1. Основные положения;
2. Классификация и обозначение изделий и конструкторских документов;
3. Общие правила выполнения чертежей;
4. Правила выполнения чертежей различных изделий;
5. Правила изменения и обращения конструкторской документации;
6. Правила выполнения эксплуатационной и ремонтной документации;
7. Правила выполнения схем;
8. Правила выполнения документов при макетном методе проектирования;
9. Прочие стандарты.
© Поликарпов Ю.В.
13

14. 3. Общие правила оформления чертежей: форматы (ГОСТ 2.301-68)

Форматом называется размер листа бумаги, на котором
выполняется чертеж. Форматы листов определяются размерами
внешней рамки, выполненной тонкой линией.
Формат с размерами сторон 1189х841 мм, площадь которого
равна 1м2 (а соотношение сторон 1: 2) называют основным и
обозначают А0. Более мелкие форматы получаются путем
деления на две равные части длинной стороны формата. Их тоже
называют основными.
© Поликарпов Ю.В..
14

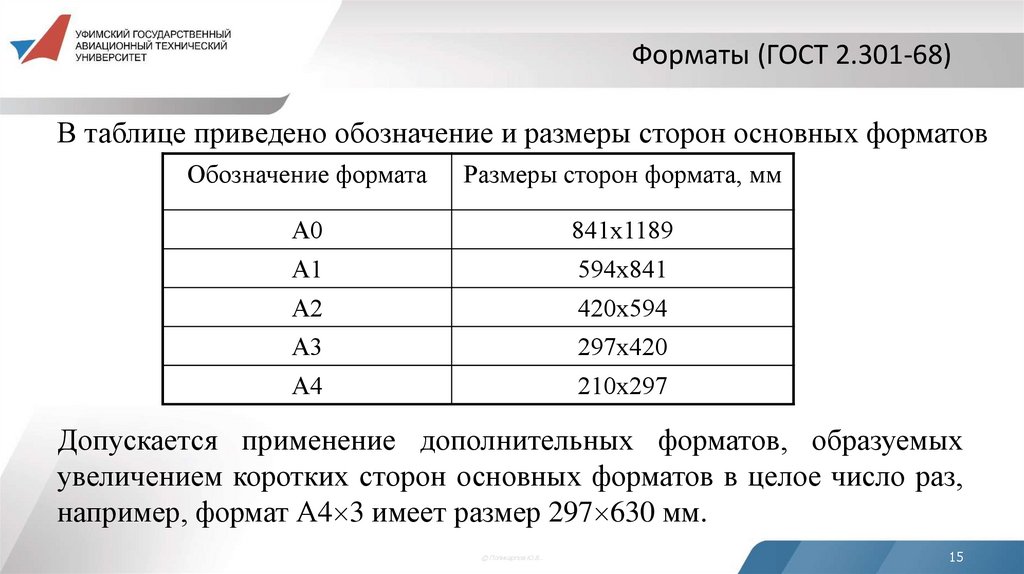
15. Форматы (ГОСТ 2.301-68)

В таблице приведено обозначение и размеры сторон основных форматов
Обозначение формата
Размеры сторон формата, мм
А0
841х1189
А1
594х841
А2
420х594
А3
297х420
А4
210х297
Допускается применение дополнительных форматов, образуемых
увеличением коротких сторон основных форматов в целое число раз,
например, формат А4 3 имеет размер 297 630 мм.
© Поликарпов Ю.В..
15

16. Форматы (ГОСТ 2.301-68)

А4
А3
© Поликарпов Ю.В..
16

17. Масштабы (ГОСТ 2.302-68)

Масштабом называется отношение линейных pазмеpов
изображения предмета к его действительным размерам. Масштаб
чертежей в зависимости от сложности и величины изображаемых
изделий выбирается из следующего ряда таблицы:
Масштабы уменьшения 1:2, 1:2,5; 1:4, 1:5, 1:10, 1:15, 1:20, 1:25, 1:40, 1:50,
1:75, 1:100, 1:200, 1:400, 1:500, 1:800, 1:1000
Натуральная величина
1:1
Масштабы увеличения
2:1, 2,5:1, 4:1, 5:1, 10:1, 20:1, 40:1, 50:1, 100:1
Масштаб, указываемый в основной надписи чертежа или рядом с
изображением, обозначают без буквы М, например, 1:1; 2:1.
© Поликарпов Ю.В..
17

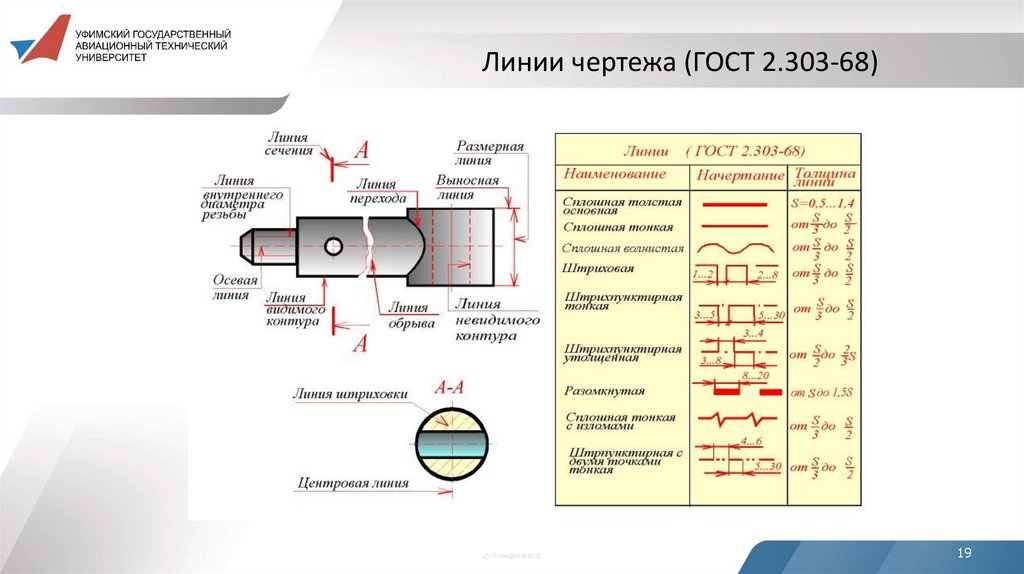
18. Линии чертежа (ГОСТ 2.303-68)

Для изображения предметов на чертежах ГОСТ 2.303-68
устанавливает начертания и основные назначения линий.
Толщина S сплошной толстой основной линии должна
быть в пределах от 0,5 до 1,4 мм в зависимости от величины
и сложности изображения, а также от формата чертежа.
Толщина линий должна быть одинаковой для всех
изображений на данном чертеже.
© Поликарпов Ю.В..
18

19. Линии чертежа (ГОСТ 2.303-68)

© Поликарпов Ю.В.
19

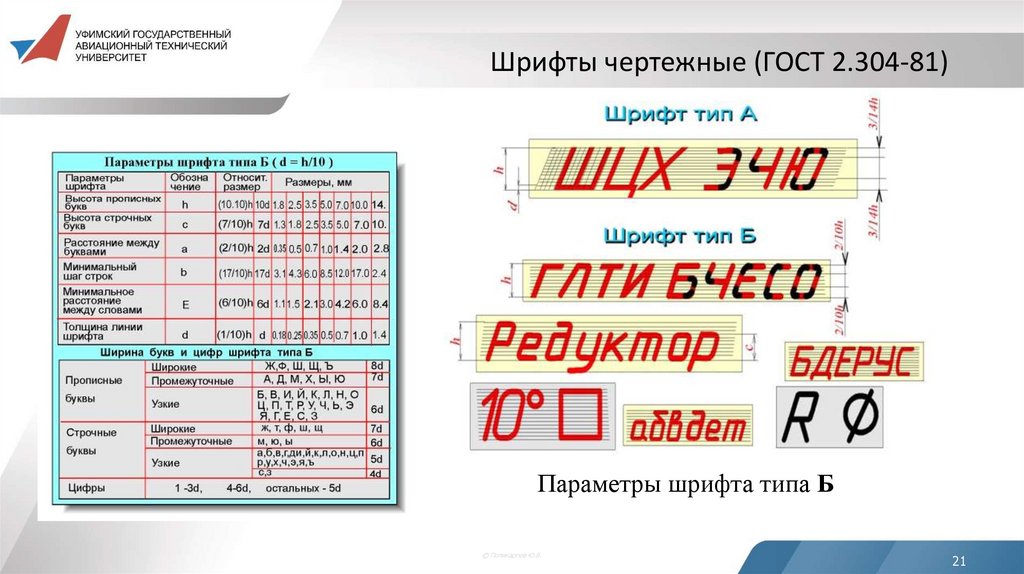
20.

Шрифты чертежные (ГОСТ 2.304-81)
Надписи на чертежах выполняют стандартным шрифтом согласно
ГОСТ 2.304-81. Основным параметром шрифта является его размер
h - высота прописных букв в миллиметрах, измеренная по
перпендикуляру к основанию строки. Стандартом установлены
следующие pазмеpы шрифта:
1,8; 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40.
Стандартом установлены 2 типа шрифта: тип А (d = h/14) и тип Б
(d = h/10), каждый из которых можно выполнить или без наклона,
или с наклоном 75 градусов к основанию строки.
© Поликарпов Ю.В..
20

21. Шрифты чертежные (ГОСТ 2.304-81)

Параметры шрифта типа Б
© Поликарпов Ю.В.
21

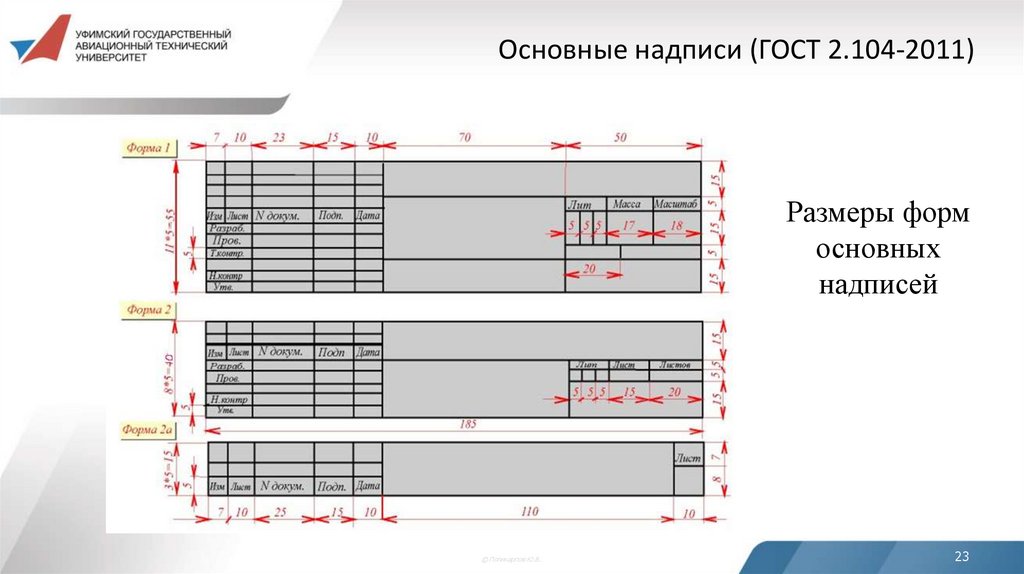
22.

Основные надписи (ГОСТ 2.104-2011)
ГОСТ 2.104-2011 устанавливает три формы основных надписей
для применения в конструкторских документах. Основные надписи
располагаются в правом нижнем углу конструкторских документов
по короткой или длинной сторонам, кроме формата А4, у которого
основная надпись располагается только по короткой стороне:
форма 1 – основная надпись для графических конструкторских
документов высотой 55 мм;
форма 2 – основная надпись для первого листа текстовых
конструкторских документов высотой 40 мм;
форма 2а – основная надпись для последующих листов текстовых
конструкторских документов высотой 15 мм.
© Поликарпов Ю.В..
22

23.

Основные надписи (ГОСТ 2.104-2011)
Размеры форм
основных
надписей
© Поликарпов Ю.В..
23

24.

А4
А3
© Поликарпов Ю.В..
24

25.

Нанесение размеров
Простановка размеров – одна из наиболее ответственных стадий
при изготовлении чертежа. Правила нанесения размеров на чертежах и
других технических документах установлены ГОСТ 2.307-68.
Размером называется числовое значение линейной величины
(длины, диаметра и др.) или угла в единицах измерения. Линейные
размеры на машиностроительных чертежах указывают в миллиметрах,
без обозначения единицы измерения, угловые – в градусах, минутах,
секундах.
25
© Поликарпов Ю.В..

26.

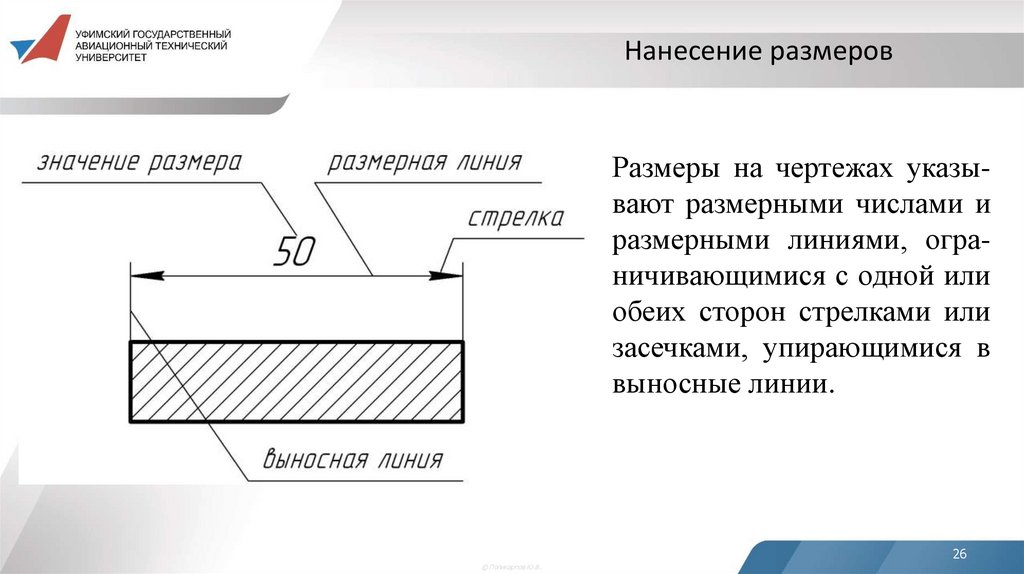
Нанесение размеров
Размеры на чертежах указывают размерными числами и
размерными линиями, ограничивающимися с одной или
обеих сторон стрелками или
засечками, упирающимися в
выносные линии.
26
© Поликарпов Ю.В..

27.

Нанесение размеров
Размерные линии проводят параллельно
отрезку, размер которого указывают, а
выносные линии – перпендикулярно размерным. Величина стрелок зависит от толщины
линий видимого контура (для учебных
чертежей рекомендуется 3…5 мм). Угол
стрелки – 20 градусов.
© Поликарпов Ю.В..
27

28.

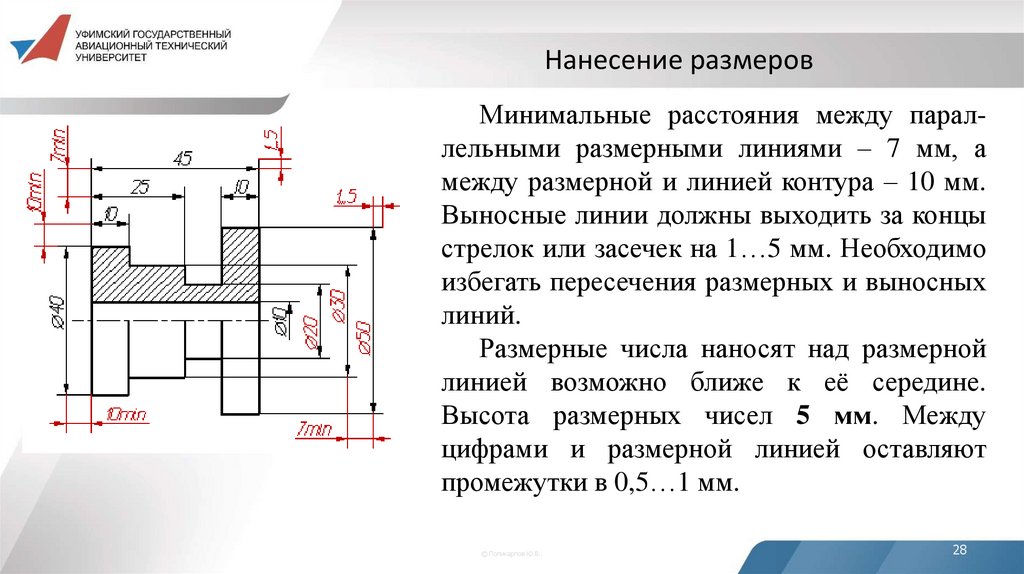
Нанесение размеров
Минимальные расстояния между параллельными размерными линиями – 7 мм, а
между размерной и линией контура – 10 мм.
Выносные линии должны выходить за концы
стрелок или засечек на 1…5 мм. Необходимо
избегать пересечения размерных и выносных
линий.
Размерные числа наносят над размерной
линией возможно ближе к её середине.
Высота размерных чисел 5 мм. Между
цифрами и размерной линией оставляют
промежутки в 0,5…1 мм.
© Поликарпов Ю.В..
28

29.

Сопряжения
Сопряжением называется плавный переход одной линии в другую.
Общую точку обеих линий (точку стыка линий) называют точкой
сопряжения.
Условием плавного перехода является наличие в точке сопряжения
общей касательной к обеим линиям.
t
s2
s1
Правила построения сопряжений изучить самостоятельно по учебнику
Левицкого раздел 3.15
© Поликарпов Ю.В..
29

30.

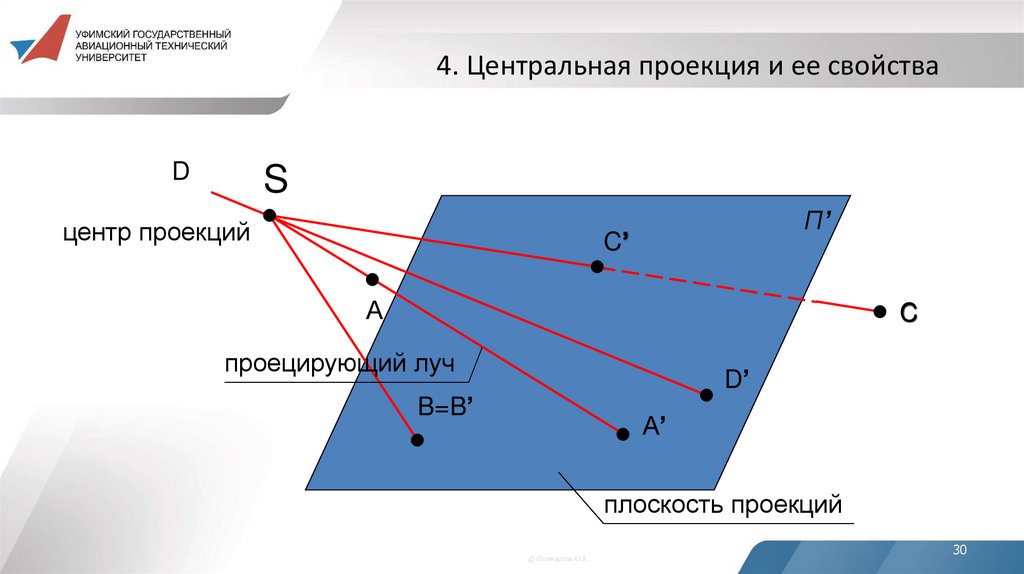
4. Центральная проекция и ее свойства
D
S
центр проекций
П’
C’
А
C
проецирующий луч
D’
B=B’
А’
плоскость проекций
© Поликарпов Ю.В..
30

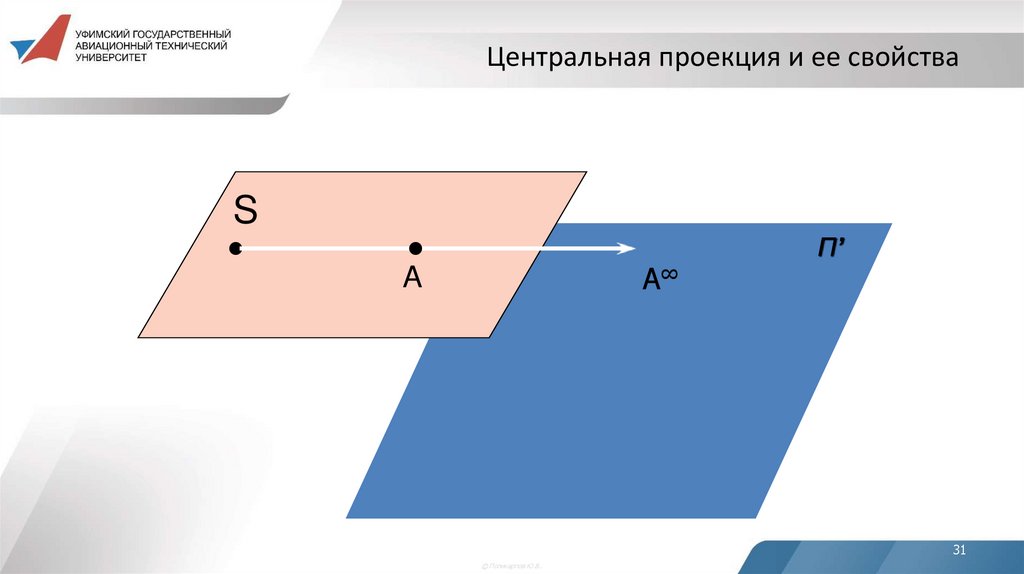
31.

Центральная проекция и ее свойства
S
А∞
A
П’
31
© Поликарпов Ю.В..

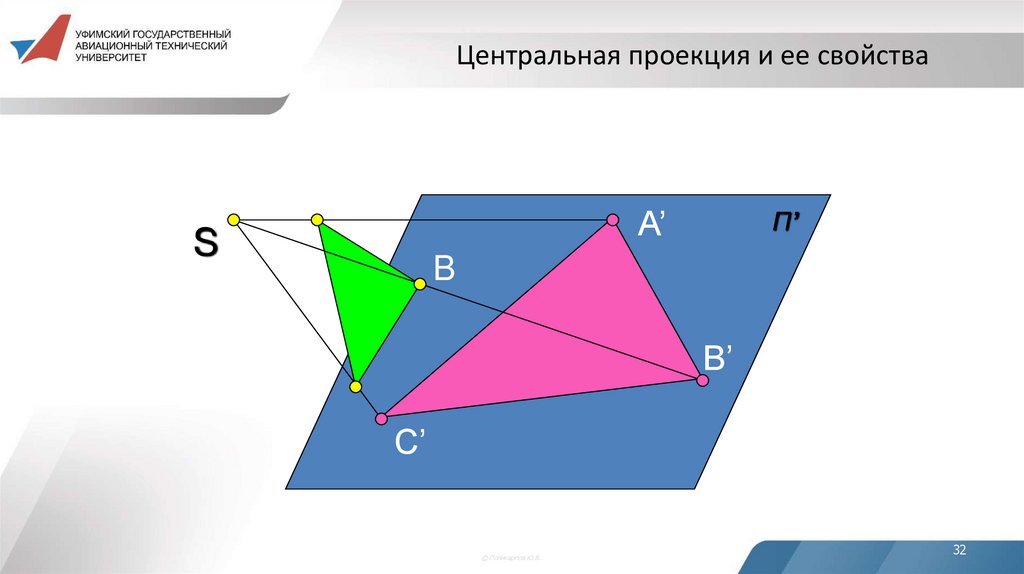
32. Центральная проекция и ее свойства

A
A’
S
П’
B
B’
C
C’
© Поликарпов Ю.В..
32

33. Свойства центральной проекции

1. Проекцией точки является точка.
2. Проекцией прямой линии является прямая линия.
3. Проекцией точки, лежащей на некоторой прямой,
является точка, лежащая на проекции этой прямой.
© Поликарпов Ю.В..
33

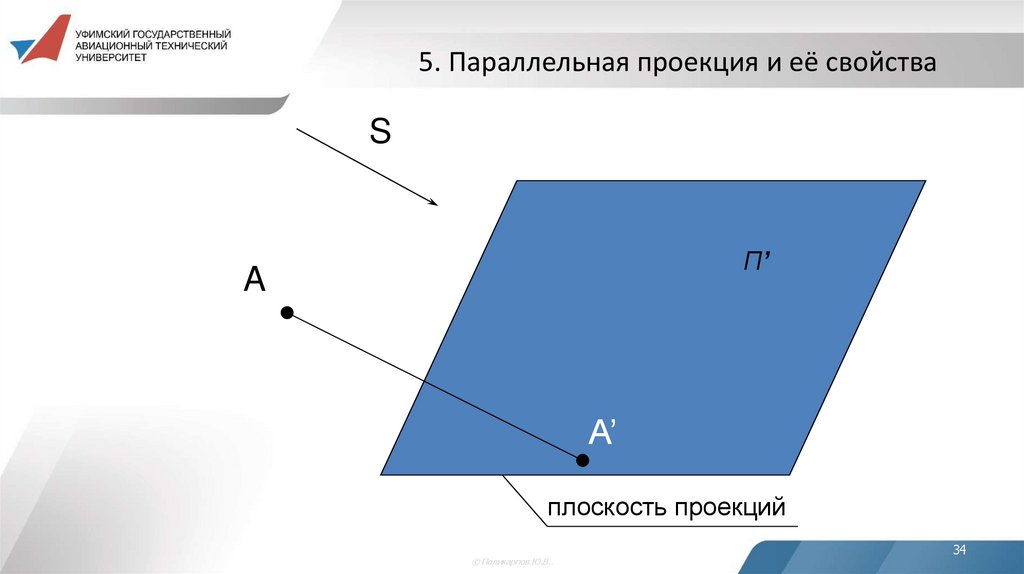
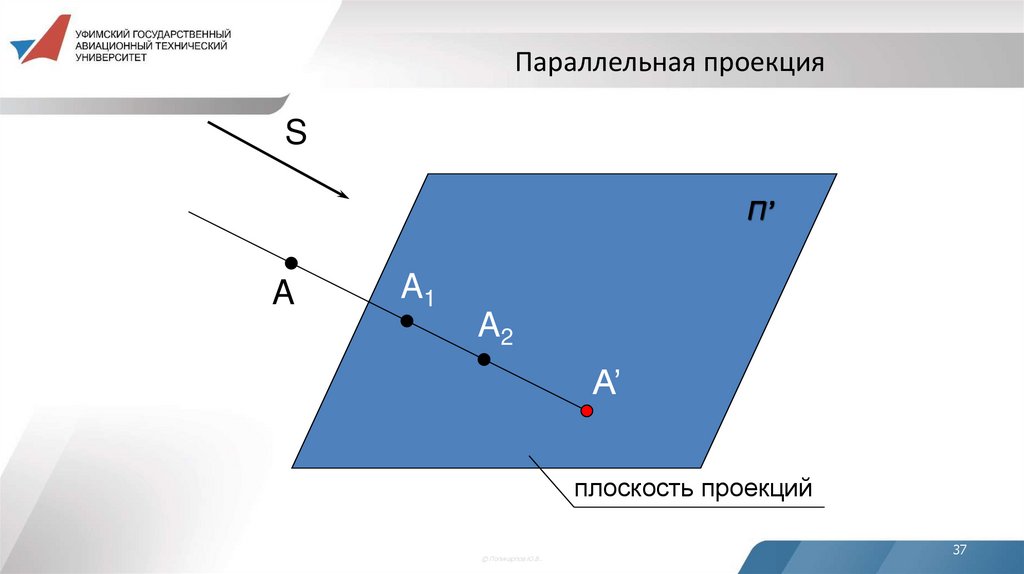
34. 5. Параллельная проекция и её свойства

S
П’
A
A’
плоскость проекций
© Поликарпов Ю.В..
34

35. Свойства параллельной проекции

Параллельная проекция кроме трёх свойств центральной
проекции обладает также еще следующими свойствами.
4. Проекциями параллельных прямых являются параллельные
прямые.
5. Отношение проекций отрезков, лежащих на параллельных
прямых или на одной и той же прямой, равно отношению самих
отрезков.
6. Проекция фигуры не меняется при параллельном переносе
плоскости проекций.
© Поликарпов Ю.В..
35

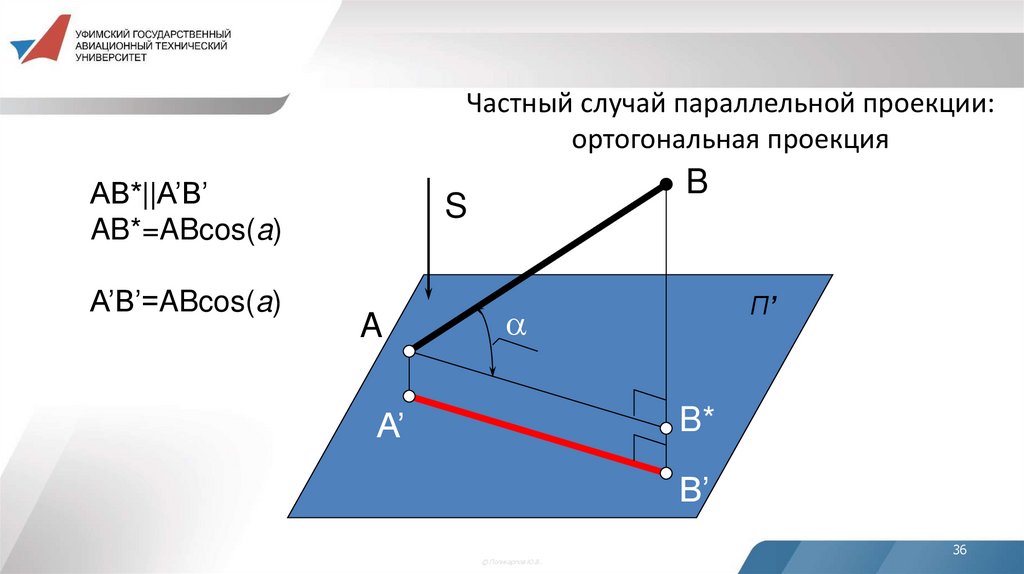
36. Частный случай параллельной проекции: ортогональная проекция

AB*||A’B’
AB*=ABcos(a)
A’B’=ABcos(a)
B
S
A
П’
B*
A’
B’
36
© Поликарпов Ю.В..

37. Параллельная проекция

S
П’
A
A1
A2
A’
плоскость проекций
© Поликарпов Ю.В..
37

38. 6. Аксонометрическая проекция и её свойства

Название аксонометрическая происходит от древнегреческих слов
аксон – ось и метрио – измеряю. Метод аксонометрического
проецирования состоит в том, что данная фигура вместе с осями
прямоугольных координат, к которым она отнесена в пространстве,
проецируется на некоторую плоскость проекций, называемую
аксонометрической плоскостью проекций или картинной плоскостью.
В зависимости от вида проецирования аксонометрическая проекция
называется центральной – используется центральное проецирование; и
параллельной – используется параллельное проецирование.
В последнем случае аксонометрическая проекция может быть косоугольной (при косоугольном проецировании) и ортогональной или
прямоугольной (при ортогональном проецировании).
© Поликарпов Ю.В..
38

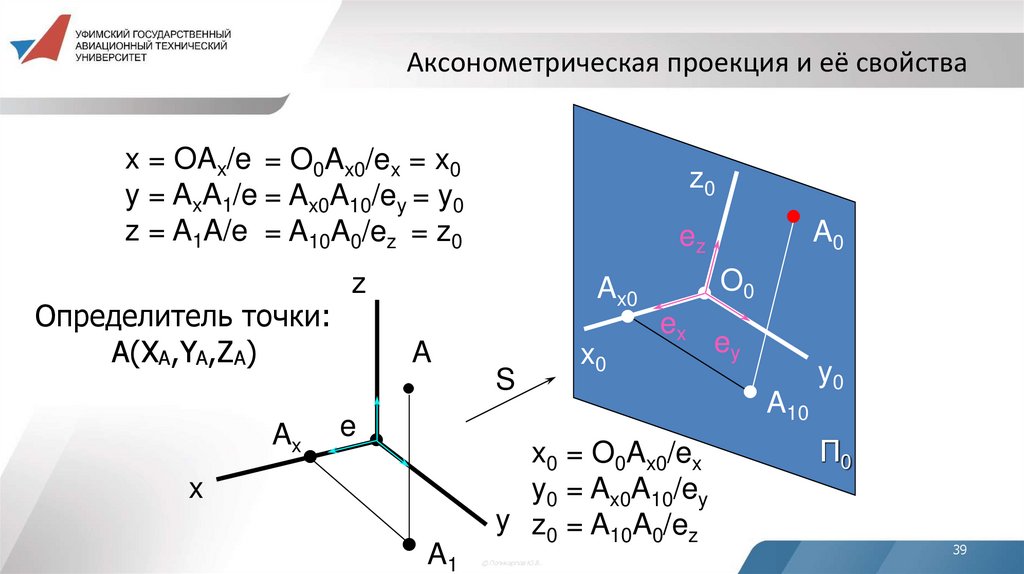
39. Аксонометрическая проекция и её свойства

x = OAx/e = O0Ax0/ex = x0
y = AxA1/e = Ax0A10/ey = y0
z = A1A/e = A10A0/ez = z0
Определитель точки:
A(XA,YA,ZA)
Ax
x
z0
z
O0
Ax0
A
e
O
A1
A0
ez
S
x0
ex
x0 = O0Ax0/ex
y0 = Ax0A10/ey
y z0 = A10A0/ez
© Поликарпов Ю.В..
ey
A10
y0
П0
39

40. Аксонометрическая проекция и её свойства

Основное
свойство
аксонометрических
проекций:
аксонометрические координаты точек, измеренные
аксонометрическими масштабами, численно равны
натуральным.
Для удобства построения аксонометрических чертежей
используют
показатели
искажения
отношение
аксонометрического
масштаба
к
соответствующему
натуральному масштабу:
k = ex / e ; m = ey / e ; n = ez / e .
© Поликарпов Ю.В..
40

41. Аксонометрическая проекция и её свойства

Если все три коэффициента искажения равны между собой,
аксонометрическая проекция называется изометрической. Если
равны между собой любые два коэффициента искажения,
проекция называется диметрической. Если все коэффициенты
различны – триметрической.
При построении аксонометрических проекций обычно
пользуются некоторыми величинами, пропорциональными
коэффициентам искажения. Эти величины называются
приведенными коэффициентами искажения.
© Поликарпов Ю.В.
41

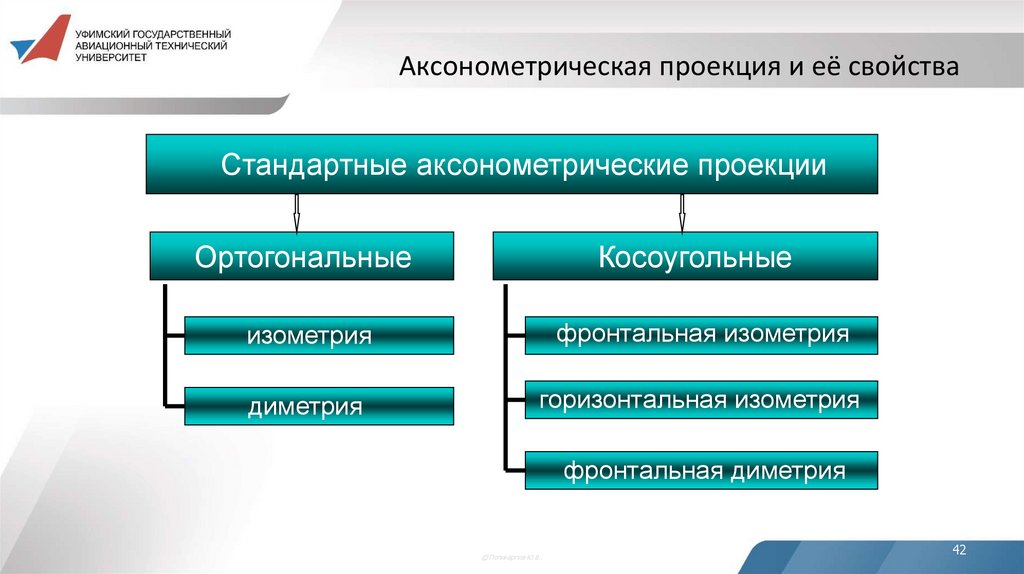
42. Аксонометрическая проекция и её свойства

Стандартные аксонометрические проекции
Ортогональные
Косоугольные
изометрия
фронтальная изометрия
диметрия
горизонтальная изометрия
фронтальная диметрия
© Поликарпов Ю.В..
42

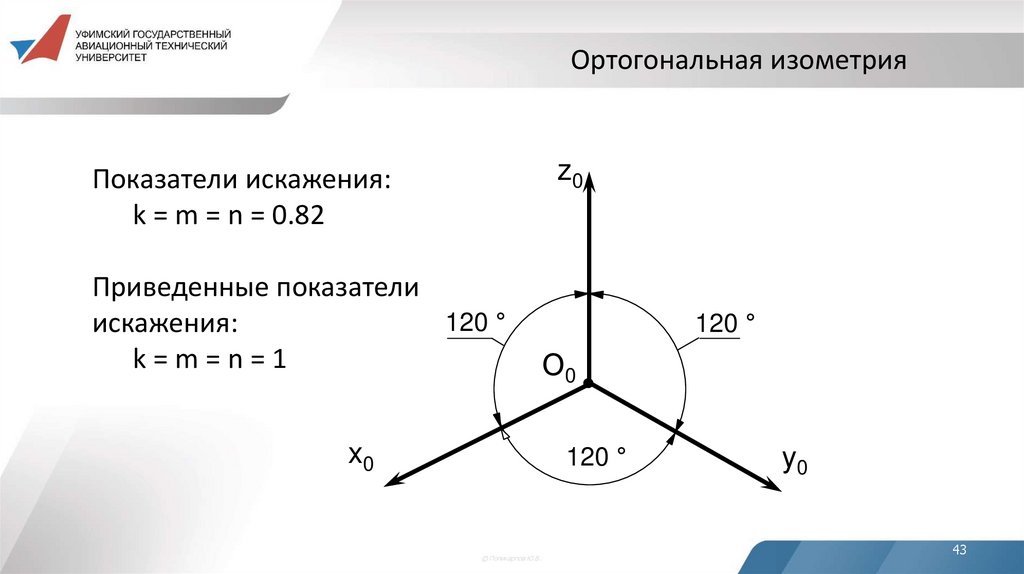
43. Ортогональная изометрия

z0
Показатели искажения:
k = m = n = 0.82
Приведенные показатели
120 °
искажения:
k=m=n=1
120 °
О0
x0
120 °
© Поликарпов Ю.В..
y0
43

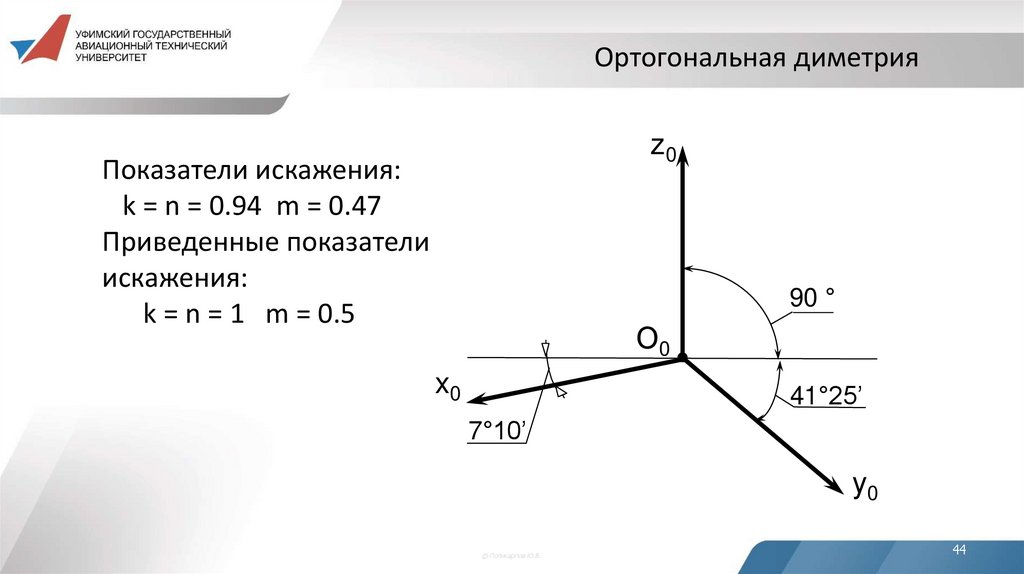
44. Ортогональная диметрия

z0
Показатели искажения:
k = n = 0.94 m = 0.47
Приведенные показатели
искажения:
k = n = 1 m = 0.5
90 °
О0
x0
41°25’
7°10’
y0
© Поликарпов Ю.В..
44

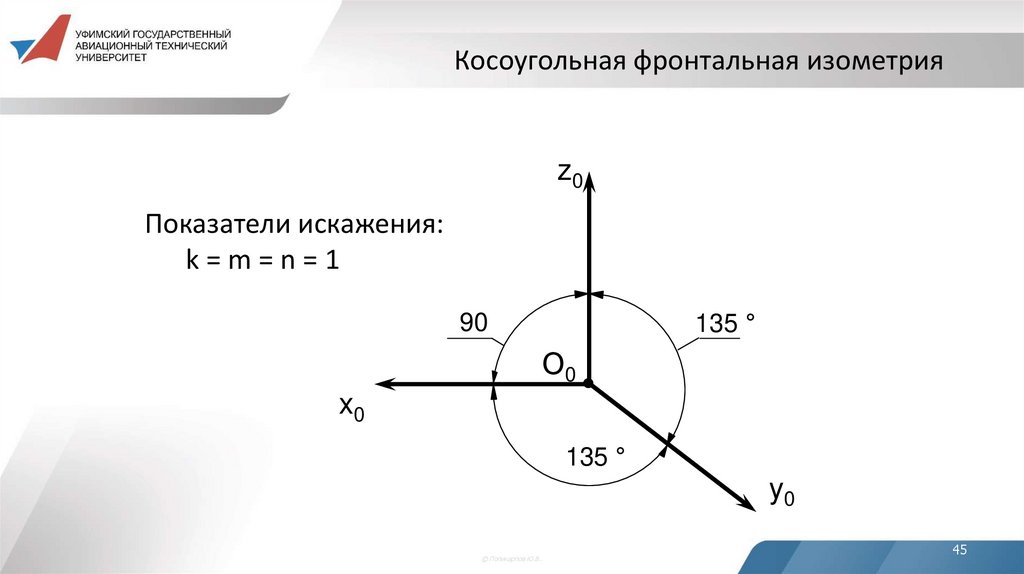
45. Косоугольная фронтальная изометрия

z0
Показатели искажения:
k=m=n=1
90 °
135 °
О0
x0
135 °
y0
© Поликарпов Ю.В..
45

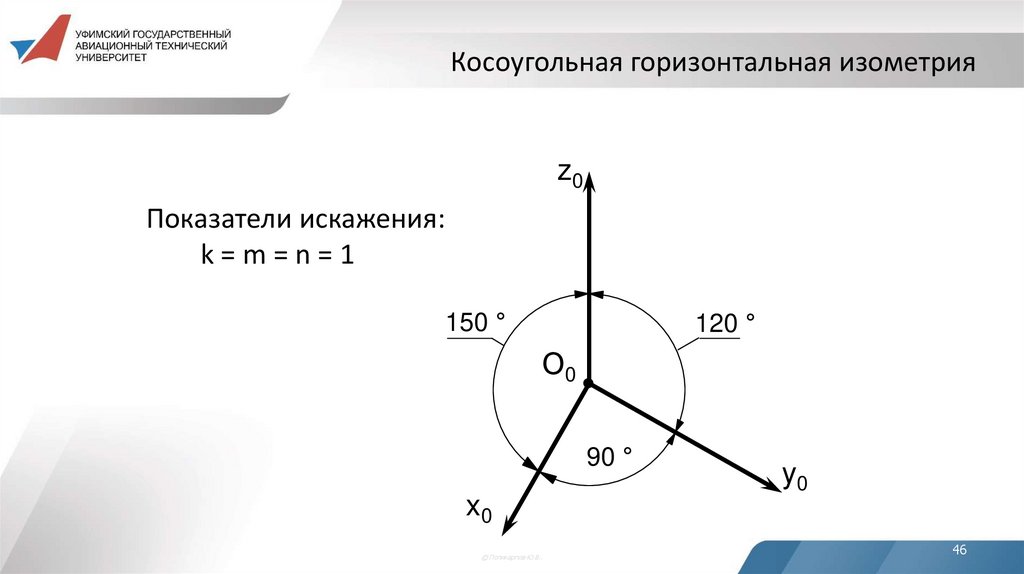
46. Косоугольная горизонтальная изометрия

z0
Показатели искажения:
k=m=n=1
150 °
120 °
О0
90 °
x0
© Поликарпов Ю.В..
y0
46

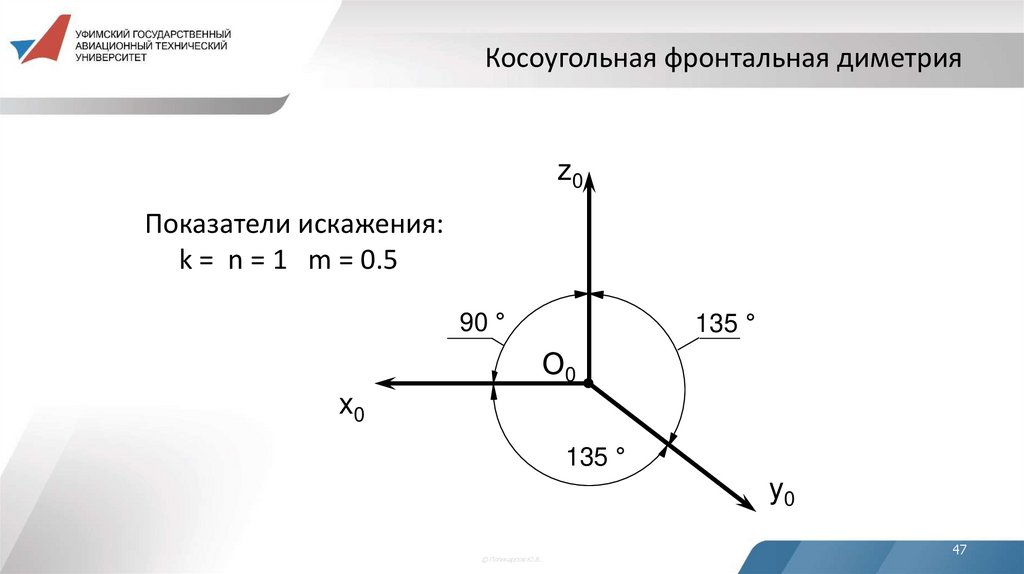
47. Косоугольная фронтальная диметрия

z0
Показатели искажения:
k = n = 1 m = 0.5
90 °
135 °
О0
x0
135 °
y0
© Поликарпов Ю.В..
47

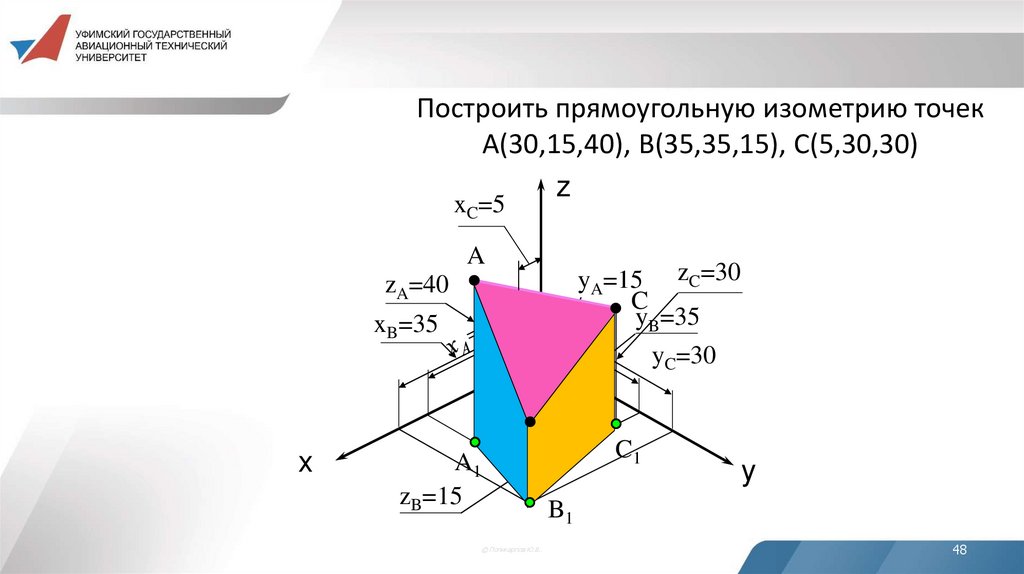
48. Построить прямоугольную изометрию точек А(30,15,40), В(35,35,15), С(5,30,30)

z
xC=5
A
zA=40
xB=35
О
yA=15 zC=30
C
yB=35
yC=30
B
x
C1
A1
zB=15
y
B1
© Поликарпов Ю.В..
48

49. 7. История развития геометрии

Основные закономерности и свойства пространства, составляющие содержание элементарной геометрии, излагались еще до
нашей эры в трудах греческих геометров. Особенно большое
значение имели работы Эвклида, жившего в III веке до нашей эры.
В своих «Началах» Эвклид изложил элементарную геометрию,
которая получила название эвклидова геометрия. В основу своей
геометрии Эвклид положил систему постулатов, на которых
строится эта наука.
© Поликарпов Ю.В..
49

50.

История развития геометрии
Постулат означает требование. Эвклид так и пишет: «Нужно потребовать:
1) чтобы от каждой точки к каждой точке можно было провести прямую
линию;
2) чтобы ограниченную прямую линию можно было непрерывно
продолжить по прямой;
3) чтобы из любого центра любым радиусом можно было описать
окружность;
4) чтобы все прямые углы были друг другу равны;
5) чтобы всякий раз, как прямая, пересекая две прямые, образует с ними
внутренние односторонние углы, составляющие вместе меньше двух прямых,
эти прямые при неограниченном продолжении пересекались с той стороны, с
которой эти углы составляют меньше двух прямых.
© Поликарпов Ю.В..
50

51.

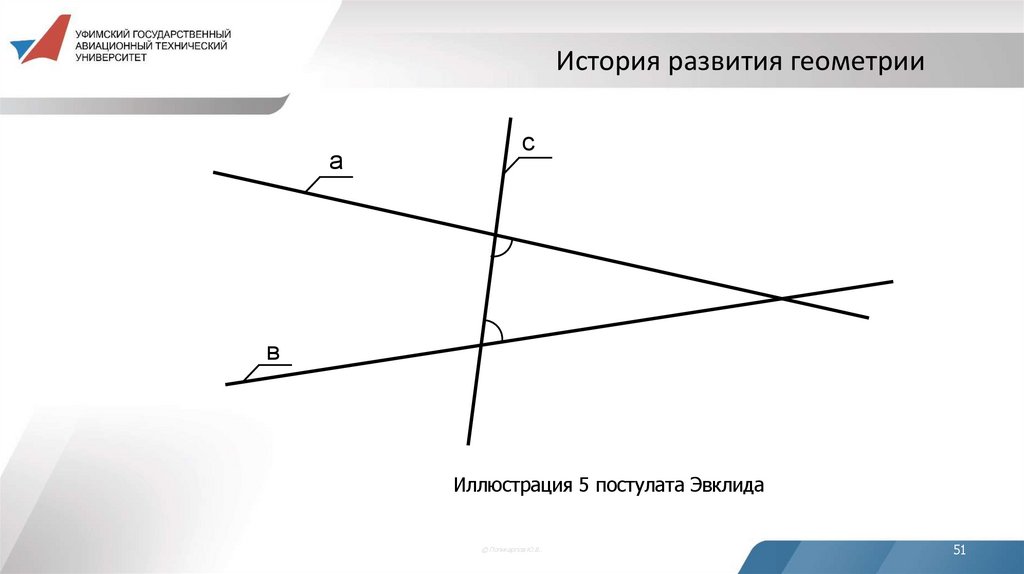
История развития геометрии
а
с
в
Иллюстрация 5 постулата Эвклида
© Поликарпов Ю.В..
51

52.

История развития геометрии
Пятый постулат, называемый как постулат о параллельных прямых,
гораздо сложнее первых четырех. Он скорее похож на теорему, которая
нуждается в доказательстве. Эвклид отводил пятому постулату особое
место среди его аксиом. Изложение материала он разбил на две части.
Сначала Эвклид рассматривает теоремы, которые можно доказать, не
прибегая к помощи пятого постулата. Эта часть теперь называется
абсолютной геометрией. Затем сгруппированы все теоремы, которые
доказываются только на основе пятого постулата. Эту часть и называют
собственно эвклидовой геометрией.
Многие математики последующих веков, считая пятый постулат
теоремой, пытались его доказать. Однако в течение 2000 лет им этого
сделать не удалось. Кроме новых формулировок пятого постулата, других
успехов не было.
52
© Поликарпов Ю.В..

53.

История развития геометрии
Так продолжалось до 11 февраля 1826 года, когда на
заседании Ученого Совета Казанского университета профессор
Николай Иванович Лобачевский (1792-1856) сообщил о создании
им новой геометрии, построенной на отрицании пятого
постулата Эвклида. Свою геометрию Лобачевский назвал
воображаемой или пангеометрией.
© Поликарпов Ю.В..
53

54.

История развития геометрии
В противоположность постулату Эвклида, Лобачевский в основу
построения теории параллельных линий положил следующую аксиому:
«Через точку, не лежащую на данной прямой, можно провести в
плоскости, определяемой этой точкой и прямой, более одной прямой, не
пересекающей данную прямую».
Отвергнув обязательность пятого постулата, Лобачевский расстался с
привычным пространством эвклидовой геометрии и открыл существование
пространства с особыми свойствами, совершенно не похожего на привычное
нам пространство, в котором протекает вся наша жизнь. Смоделировать
плоскость Лобачевского на эвклидовой плоскости невозможно. Поэтому выполнить чертеж, иллюстрирующий аксиому параллельности Лобачевского,
можно лишь условно.
54
© Поликарпов Ю.В..

55.

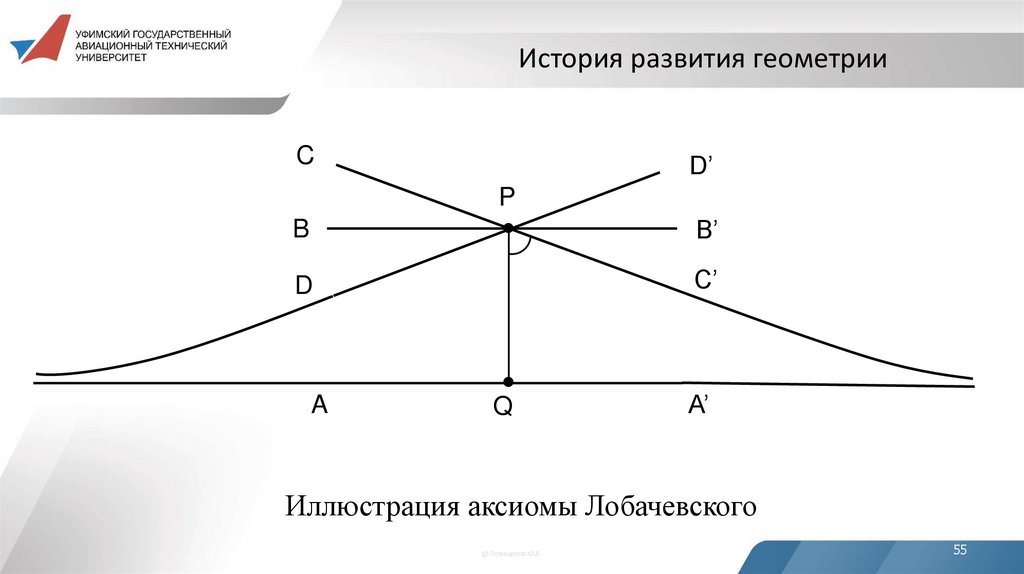
История развития геометрии
C
D’
P
B
B’
D
C’
A
Q
A’
Иллюстрация аксиомы Лобачевского
© Поликарпов Ю.В..
55

56.

История развития геометрии
Таким образом, Лобачевский постулировал, что через каждую
точку на плоскости в его новом пространстве проходят две прямые,
параллельные данной прямой. Заменив своим постулатом пятый
постулат Эвклида, но сохранив в неприкосновенности все остальные,
Лобачевский на этой основе построил новую геометрию открытого
им пространства, не содержащую никаких противоречий.
© Поликарпов Ю.В..
56

57.

История развития геометрии
В эвклидовой плоскости угол между перпендикуляром и параллелью
всегда равен 90°. На плоскости Лобачевского угол между
перпендикуляром и каждой из двух параллелей к прямой всегда будет
меньше 90°. Более того, величина этого угла параллельности, как его
называет Лобачевский, непостоянна: она меняется в зависимости от
длины перпендикуляра, опущенного из точки на первоначальную прямую.
Когда длина перпендикуляра стремится к нулю, угол параллельности
стремится к 90°, а когда перпендикуляр растет до бесконечности, этот
угол становится равным нулю, т.е. величина угла зависит от отношения
отрезка PQ к некоторому другому постоянному отрезку, являющемся
радиусом кривизны пространства Лобачевского.
© Поликарпов Ю.В..
57

58.

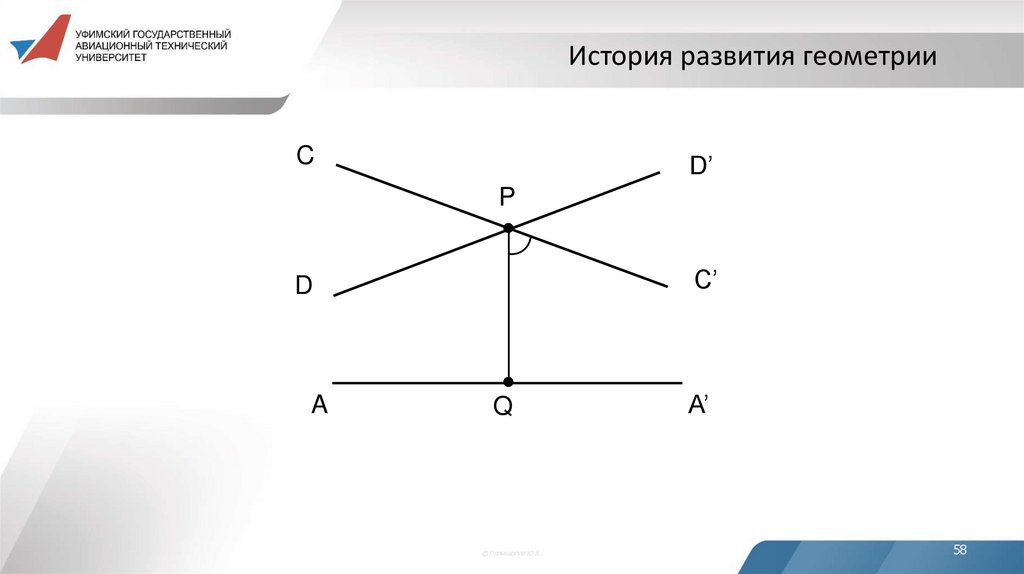
История развития геометрии
C
D’
P
C’
D
A
Q
© Поликарпов Ю.В..
A’
58

59.

История развития геометрии
На плоскости Лобачевского сумма углов треугольника не
постоянна. Она зависит от длины сторон треугольника. Чем
больше стороны, тем меньше сумма углов. В пределе, при
бесконечном возрастании всех трех сторон, сумма углов будет
стремиться к нулю. А так как углы зависят от длины сторон,
значит, никаких подобных фигур существовать не может.
© Поликарпов Ю.В..
59

60.

История развития геометрии
Итак, пространство Лобачевского обладает кривизной. Лобачевский
показал, что теоретически радиус кривизны пространства может иметь
любые значения и каждому из них будет соответствовать свое
искривленное пространство. Вопрос о степени искривления реального
пространства Вселенной лежит уже вне геометрии, его могут решить
только физика и астрономия. В частном случае, когда радиус кривизны
становится равным бесконечности, пространство Лобачевского
переходит в пространство Эвклида - плоское, нулевой кривизны.
Лобачевский подчеркивал, что его геометрия может быть только
геометрией
огромных
пространств,
гигантских
межзвездных
расстояний, геометрией Вселенной.
© Поликарпов Ю.В..
60

61.

История развития геометрии
Новая глава в истории неэвклидовой геометрии связана с именем
Бернгарда Римана (1826-1866), который дал новое, расширенное
понятие пространства. Он определил его как непрерывную
совокупность любых однородных объектов. Он показал, что, опираясь
на законы математики и логики, можно конструировать различные nмерные пространства, каждому из которых соответствует своя
геометрия. Тем самым Риман открыл существование гигантского
множества пространств. Риман дал основные идеи геометрий
различных n-мерных пространств без детальной их разработки.
Совокупность этих геометрий называют римановой геометрией в
широком смысле слова.
© Поликарпов Ю.В..
61

62.

История развития геометрии
Однако он также обобщил и разработал еще глубже геометрию
трехмерного пространства с постоянной кривизной. Эвклидово
пространство с нулевой кривизной Риман считал частным случаем
пространств с постоянной кривизной. Пространство с постоянной
отрицательной кривизной открыл Лобачевский. Риман исследовал и
описал пространство с постоянной положительной кривизной,
детально разработал геометрию такого пространства, которая и
называется геометрией Римана.
© Поликарпов Ю.В..
62

63.

История развития геометрии
Приведем основные положения геометрии Римана. Главной
особенностью пространства с положительной кривизной
является то, что это пространство замкнутое, как замкнуты
сферические и эллиптические поверхности. Под прямой Риман
понимает линию, являющуюся кратчайшей между двумя
точками. Все прямые пространства - замкнутые линии.
Параллельных прямых в геометрии Римана нет. Любые две
прямые обязательно пересекаются в двух точках (аналогично
меридианам на глобусе). Сумма углов треугольника больше
180°. В геометрии Римана возможен треугольник, у которого все
три угла прямые.
© Поликарпов Ю.В..
63

64.

История развития геометрии
Предположения Лобачевского и Римана об искривлении пространства
подтвердил известный физик Альберт Эйнштейн, разработавший в 1915
году общую теорию относительности. Он доказал, что наше пространство
обладает кривизной. Когда Эйнштейна спросили, что его побудило на эти
исследования, он ответил – геометрия Лобачевского, с которой он
познакомился и она оставила неизгладимые впечатления. Но Эйнштейн не
определил знак кривизны нашего пространства. Это сумел предсказать
советский астрофизик Александр Фридман, разработавший в 1923 году
теорию нестационарной Вселенной. Он показал, что в настоящий момент
наша вселенная должна иметь отрицательную кривизну. Американский
астроном Эдвин Хаббл в 1929 году на основании астрономических
наблюдений подтвердил это предположение.
© Поликарпов Ю.В..
64

65.

История развития геометрии
В заключение приведем по еще одному названию
рассмотренных геометрий. Геометрию Лобачевского (пространства
с отрицательной кривизной) называют гиперболической,
геометрию Римана (пространства с положительной кривизной) эллиптической, а геометрию Эвклида (пространства с нулевой
кривизной) - параболической.
© Поликарпов Ю.В..
65

66.

Заключение
Итак, изучив данную тему, вы:
познакомились с предметом и методом современной инженерной
графики;
узнали о ЕСКД и основных правилах оформления чертежей;
изучили центральную, параллельную и ортогональную проекции и
их свойства;
познакомились с аксонометрической проекцией и её свойствами;
научились строить точки и прямые линии в аксонометрической
проекции;
совершили небольшой экскурс в историю развития геометрии.
© Поликарпов Ю.В..
66

67.

СПАСИБО ЗА ВНИМАНИЕ!
Поликарпов Ю.В.
https://www.ugatu.su/
450008, Республика Башкортостан,
г. Уфа, ул. К. Маркса, д. 12
+ 7 (987) 254-38-29
info@ugatu.su
67