ege27_2025 (1)

1. Решение задач ЕГЭ Задача 27 (40 минут)

К.Ю. Поляков
Решение задач ЕГЭ
Задача 27
(40 минут)
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

2. Пособие «Решаем задачи ЕГЭ на Python»

Задача 27 ЕГЭ по информатике
2
Пособие «Решаем задачи ЕГЭ на Python»
Поляков К. Ю., 100 баллов по информатике. Решаем задачи ЕГЭ
на языке Python. 4-е изд. М. : Лаборатория знаний, 2025.
Для: учеников на 80+,
учителей, репетиторов.
(почти) все задания
обсуждение
варианты решения
новое 27-е задание
+ задание 24
+ regex
+ задание 26
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

3. Постановка задачи

Задача 27 ЕГЭ по информатике
3
Постановка задачи
(Демо-2025) Учёный решил провести кластеризацию
полученных точек, являющихся изображениями звёзд, то есть
разбить их множество на N непересекающихся непустых
подмножеств (кластеров), таких что точки
каждого подмножества лежат внутри прямоугольника со
сторонами длиной H и W, причём эти прямоугольники между
собой не пересекаются. Для
каждого файла определите
координаты центра каждого
кластера, затем вычислите Px –
среднее арифметическое
абсцисс центров кластеров, и
Py – среднее арифметическое
ординат центров кластеров.
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

4. Две подзадачи

Задача 27 ЕГЭ по информатике
4
Две подзадачи
1) разбить точки на кластеры
– вручную или автоматически?
– правильно ли разбили?
– укладываемся по времени?
2) найти центр каждого кластера
– укладываемся по времени?
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

5. Уменьшение количества точек (Р7)

Задача 27 ЕГЭ по информатике
6
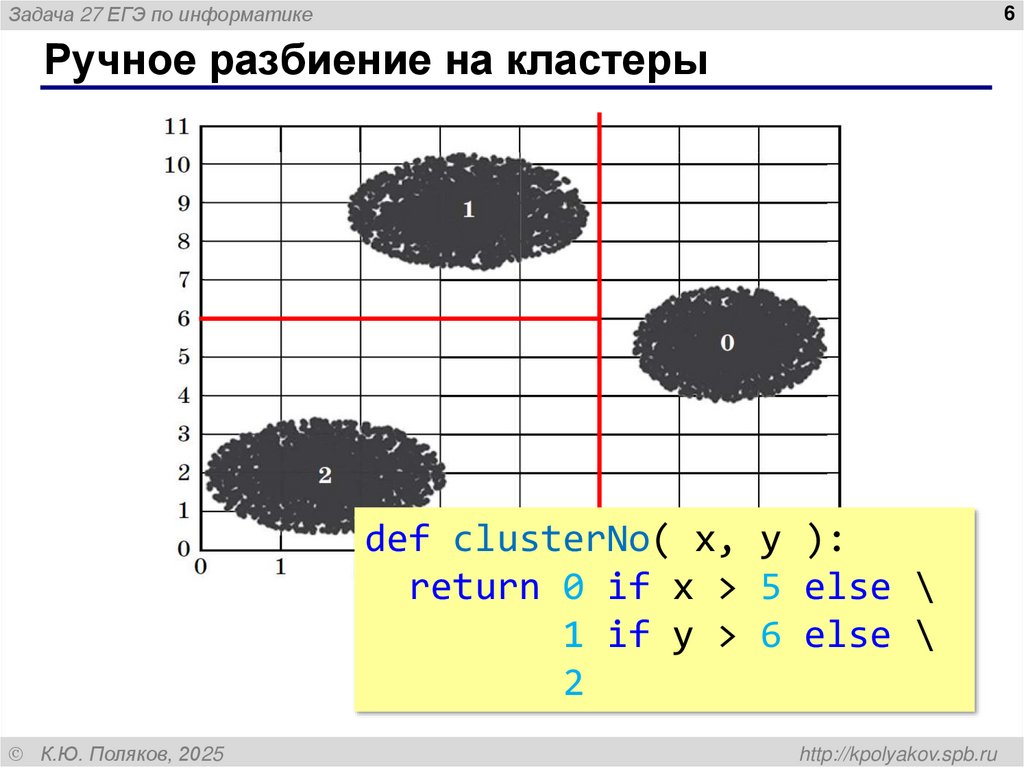
Ручное разбиение на кластеры
def clusterNo( x, y ):
return 0 if x > 5 else \
1 if y > 6 else \
2
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

6. Ручное разбиение на кластеры

Задача 27 ЕГЭ по информатике
7
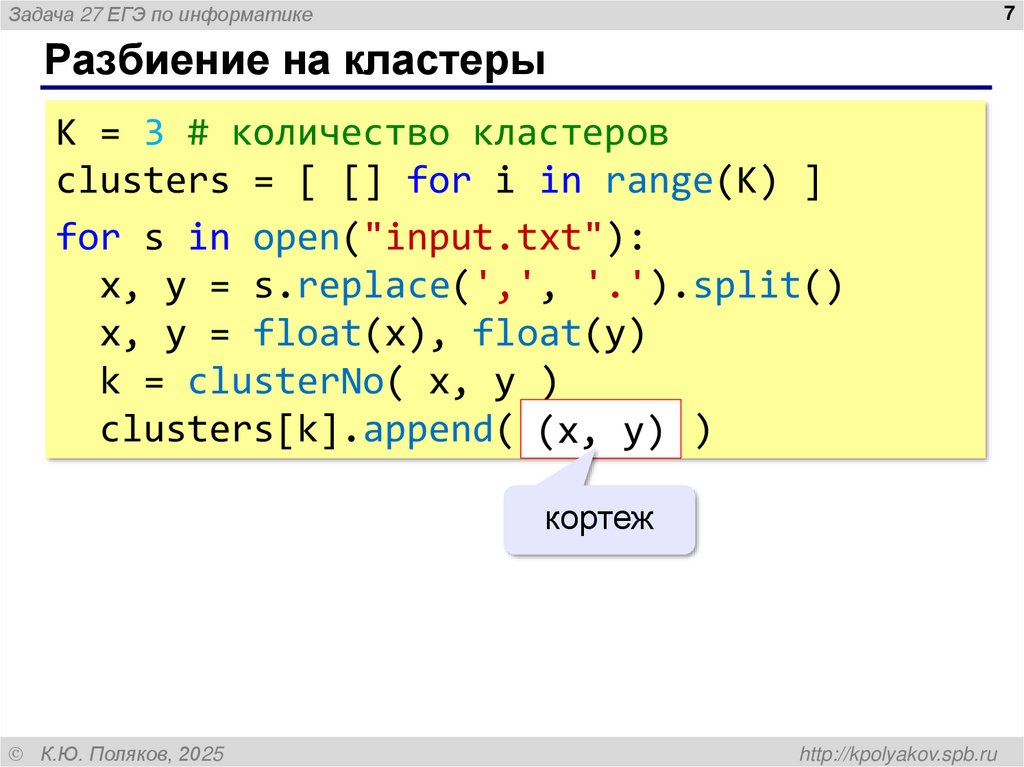
Разбиение на кластеры
K = 3 # количество кластеров
clusters = [ [] for i in range(K) ]
for s in open("input.txt"):
x, y = s.replace(',', '.').split()
x, y = float(x), float(y)
k = clusterNo( x, y )
clusters[k].append( (x, y) )
кортеж
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

7. Разбиение на кластеры

Задача 27 ЕГЭ по информатике
8
Расстояние между точками
def dist( p1, p2 ):
return ((p2[0]-p1[0])**2 +
(p2[1]-p1[1])**2)**0.5
или так
from math import dist
! Ускорение в 2-3 раза!
O(N)
! Минимизация по сумме квадратов
расстояний может дать другой результат!
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

8. Расстояние между точками

Задача 27 ЕГЭ по информатике
9
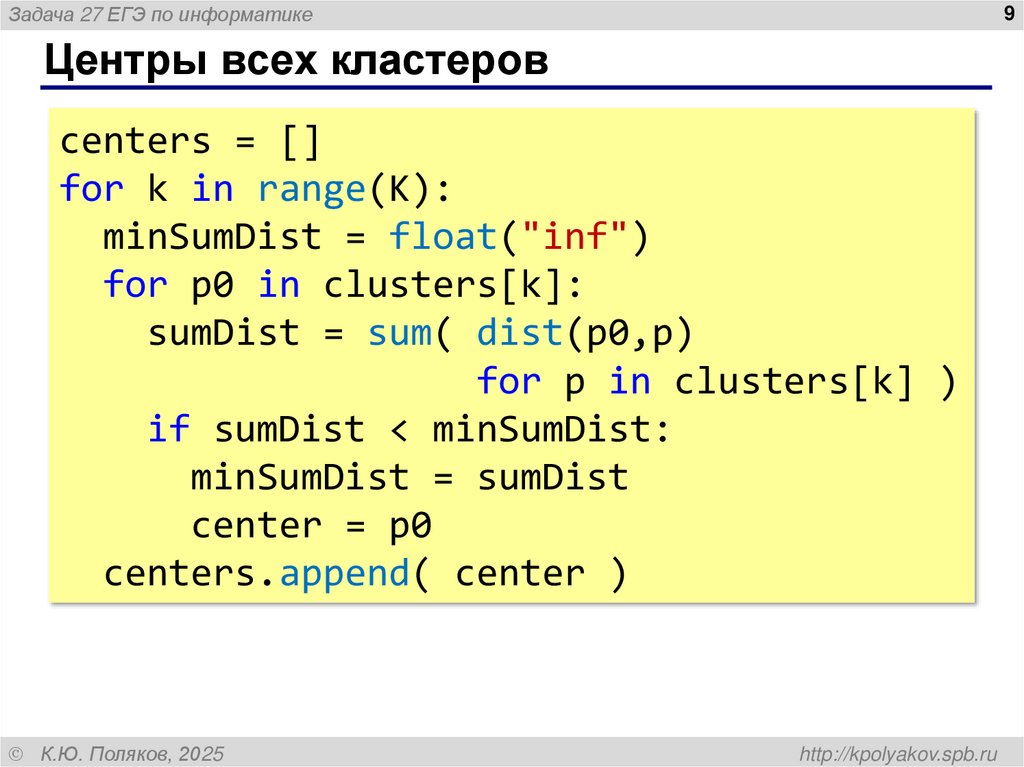
Центры всех кластеров
centers = []
for k in range(K):
minSumDist = float("inf")
for p0 in clusters[k]:
sumDist = sum( dist(p0,p)
for p in clusters[k] )
if sumDist < minSumDist:
minSumDist = sumDist
center = p0
centers.append( center )
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

9. Центры всех кластеров

Задача 27 ЕГЭ по информатике
10
Центр кластера – функция
def getCenter( cluster ):
minSumDist = float("inf")
for p0 in cluster:
sumDist = sum( dist(p0,p)
for p in cluster )
if sumDist < minSumDist:
minSumDist = sumDist
center = p0
return center
centers = [ getCenter(cluster)
for cluster in clusters ]
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

10. Центр кластера – функция

Задача 27 ЕГЭ по информатике
11
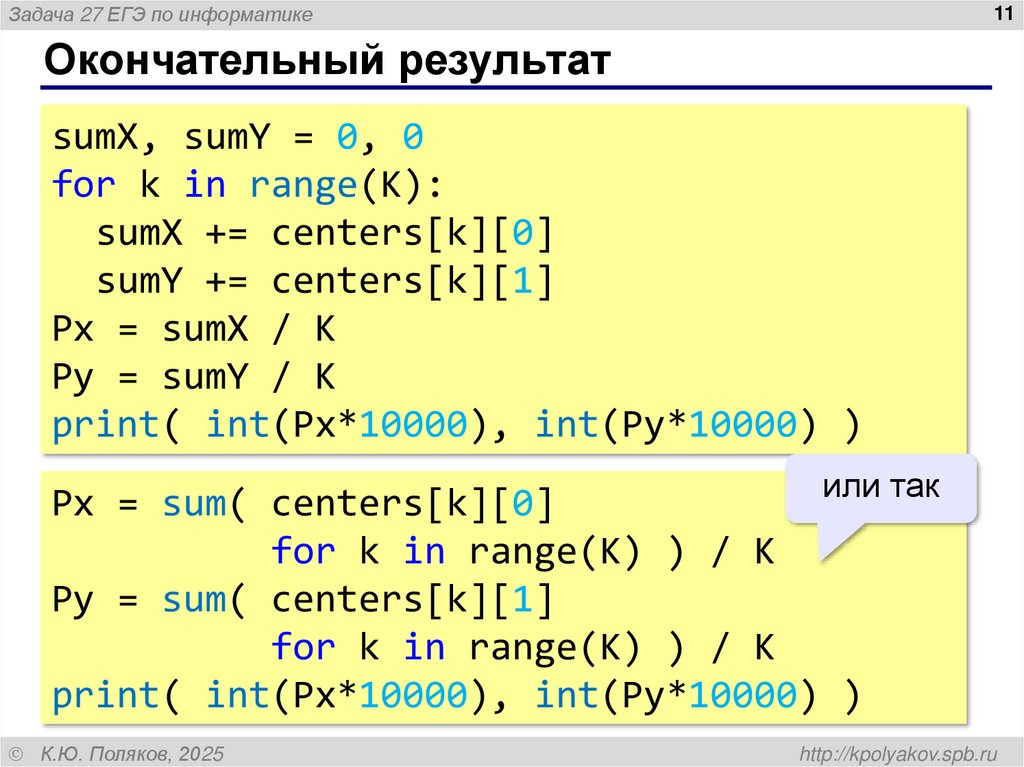
Окончательный результат
sumX, sumY = 0, 0
for k in range(K):
sumX += centers[k][0]
sumY += centers[k][1]
Px = sumX / K
Py = sumY / K
print( int(Px*10000), int(Py*10000) )
или так
Px = sum( centers[k][0]
for k in range(K) ) / K
Py = sum( centers[k][1]
for k in range(K) ) / K
print( int(Px*10000), int(Py*10000) )
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

11. Окончательный результат

Задача 27 ЕГЭ по информатике
12
Ускорение – искать около средней точки
Средняя точка (центроид)
N = len(cluster)
cx = sum( p[0] for p in cluster ) / N
cy = sum( p[1] for p in cluster ) / N
pMid = (cx, cy)
Точки в -окрестности
delta = 0.2
ptsNearCenter = [p for p in cluster
if dist(pMid,p) < delta ]
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

12. Ускорение – искать около средней точки

Задача 27 ЕГЭ по информатике
13
Поиск в окрестности средней точки
def getCenter( cluster ):
N = len(cluster)
pMid = ...
delta = 0.2
ptsNearCenter = ...
minSumDist = float("inf")
for p0 in ptsNearCenter:
sumDist = sum( dist(p0,p)
for p in cluster )
if sumDist < minSumDist:
minSumDist = sumDist
center = p0
return center
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

13. Поиск в окрестности средней точки

Задача 27 ЕГЭ по информатике
14
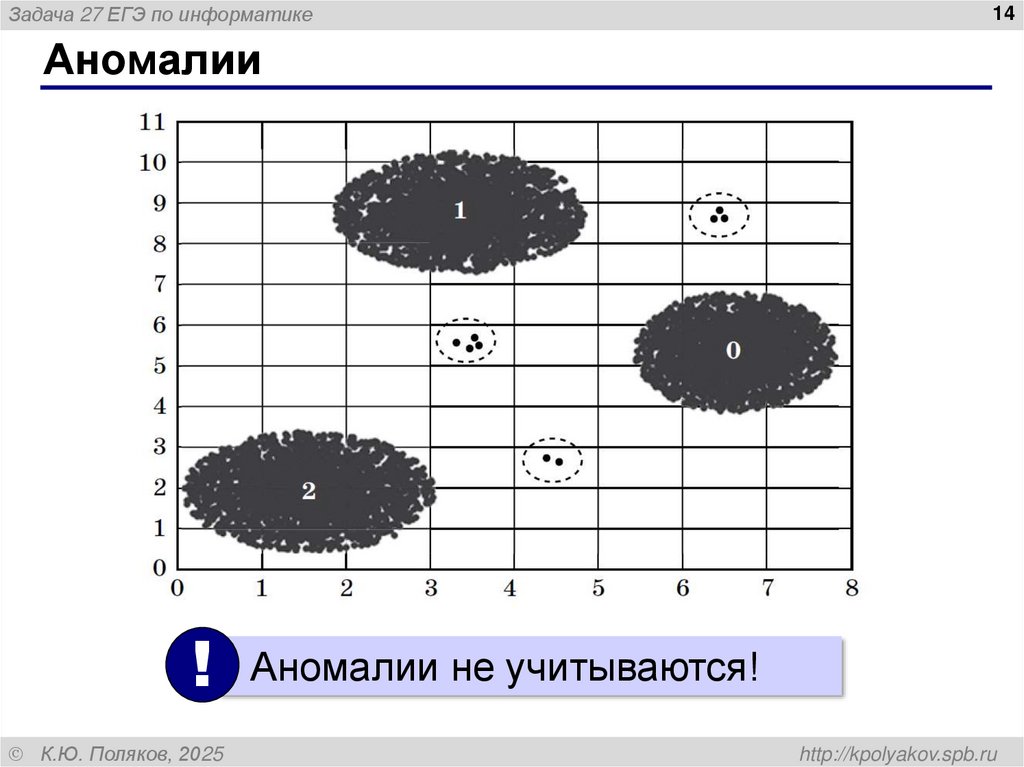
Аномалии
! Аномалии не учитываются!
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

14. Аномалии

Задача 27 ЕГЭ по информатике
15
Отсечение аномалий
def clusterNo( x, y ):
return 0 if x > 5 and y < 7 else \
1 if x < 5 and y > 6 else \
2 if x < 4 and y < 4 else \
-1 # аномалия
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

15. Отсечение аномалий

Задача 27 ЕГЭ по информатике
16
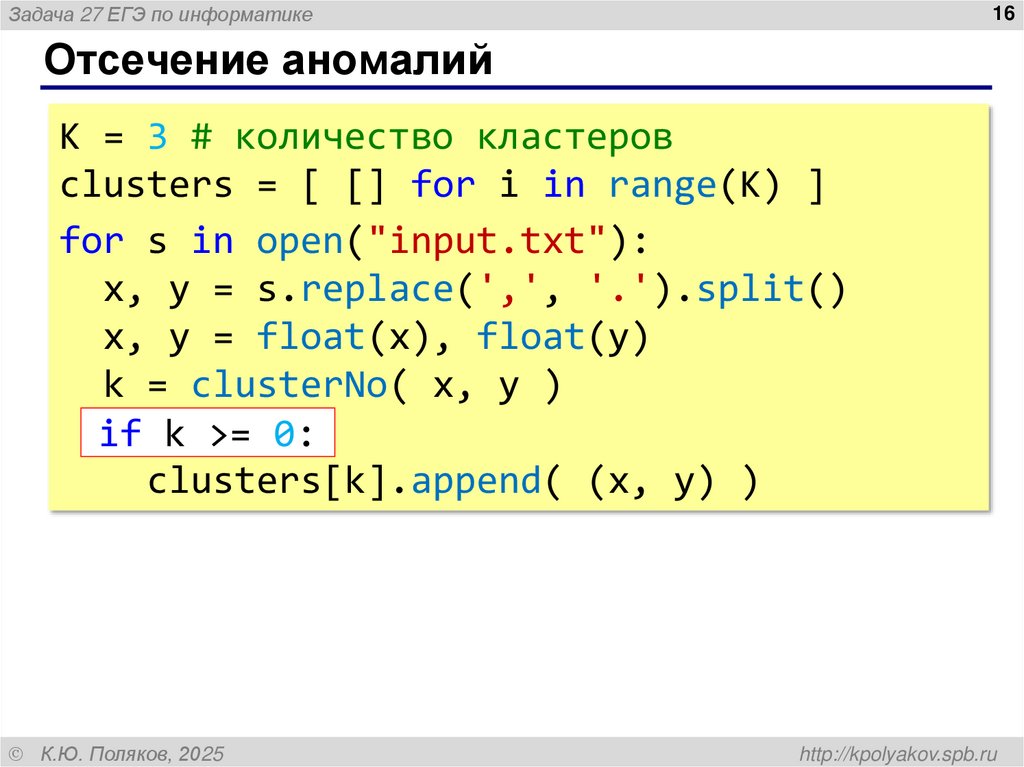
Отсечение аномалий
K = 3 # количество кластеров
clusters = [ [] for i in range(K) ]
for s in open("input.txt"):
x, y = s.replace(',', '.').split()
x, y = float(x), float(y)
k = clusterNo( x, y )
if kk >=
>= 0:
0:
if
clusters[k].append( (x, y) )
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

16. Отсечение аномалий

Задача 27 ЕГЭ по информатике
17
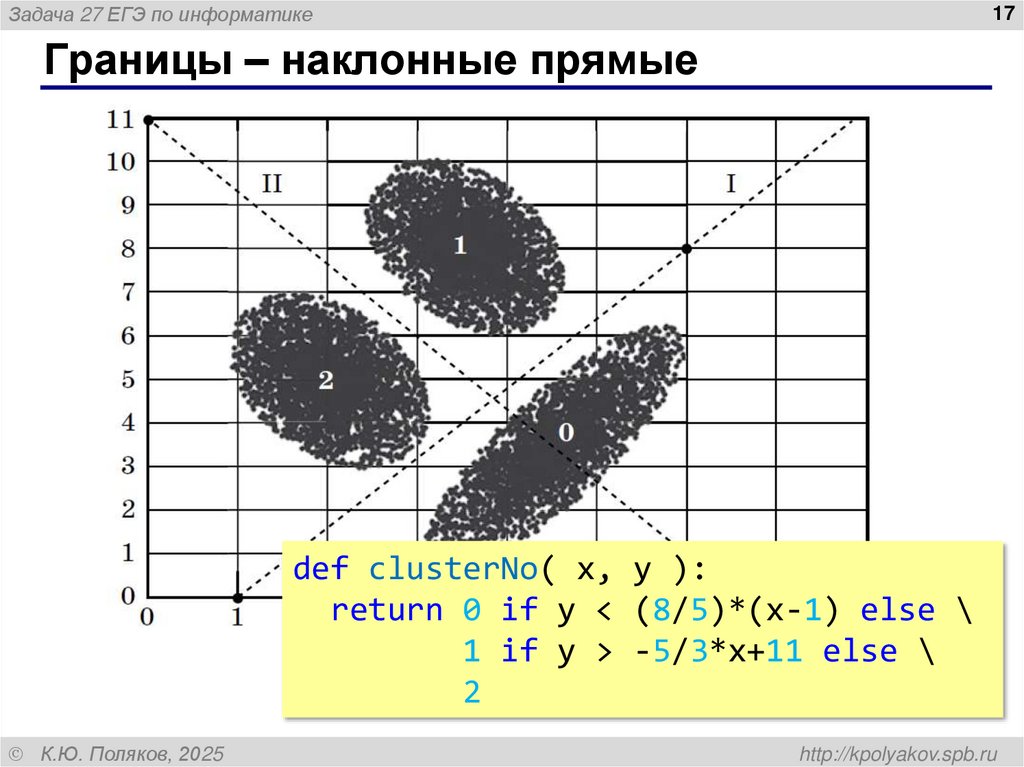
Границы – наклонные прямые
def clusterNo( x, y ):
return 0 if y < (8/5)*(x-1) else \
1 if y > -5/3*x+11 else \
2
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

17. Границы – наклонные прямые

Задача 27 ЕГЭ по информатике
18
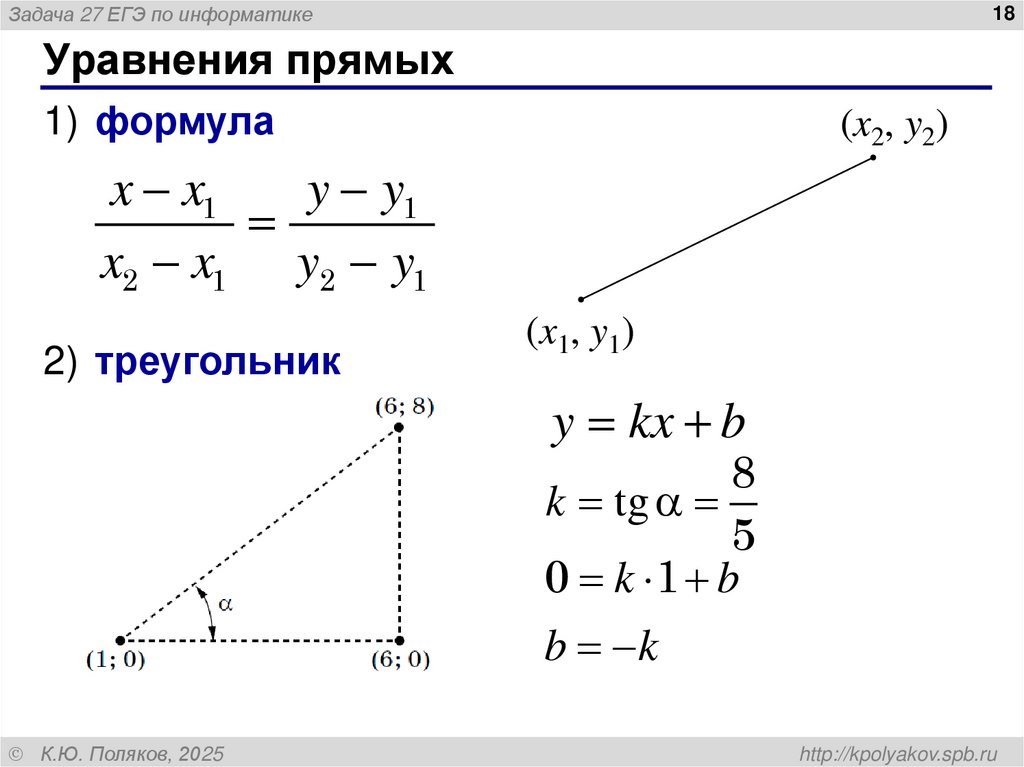
Уравнения прямых
1) формула
(x2, y2)
x x1
y y1
x2 x1 y2 y1
2) треугольник
(x1, y1)
y kx b
8
k tg
5
0 k 1 b
b k
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

18. Уравнения прямых

Задача 27 ЕГЭ по информатике
19
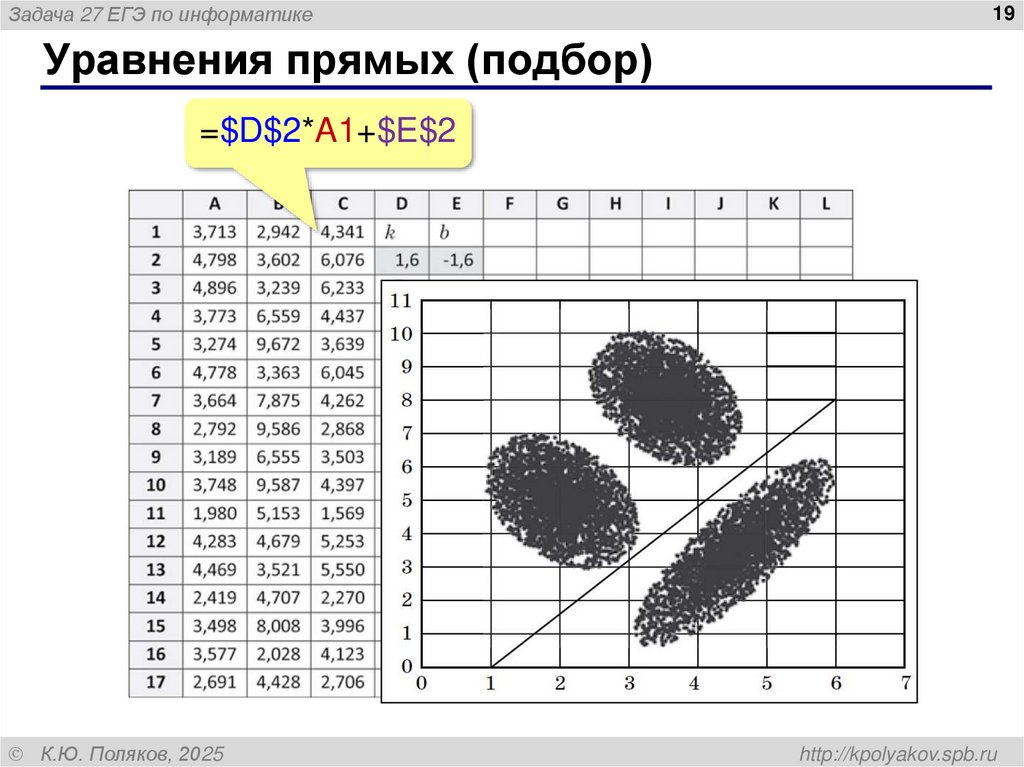
Уравнения прямых (подбор)
=$D$2*A1+$E$2
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

19. Уравнения прямых (подбор)

Задача 27 ЕГЭ по информатике
20
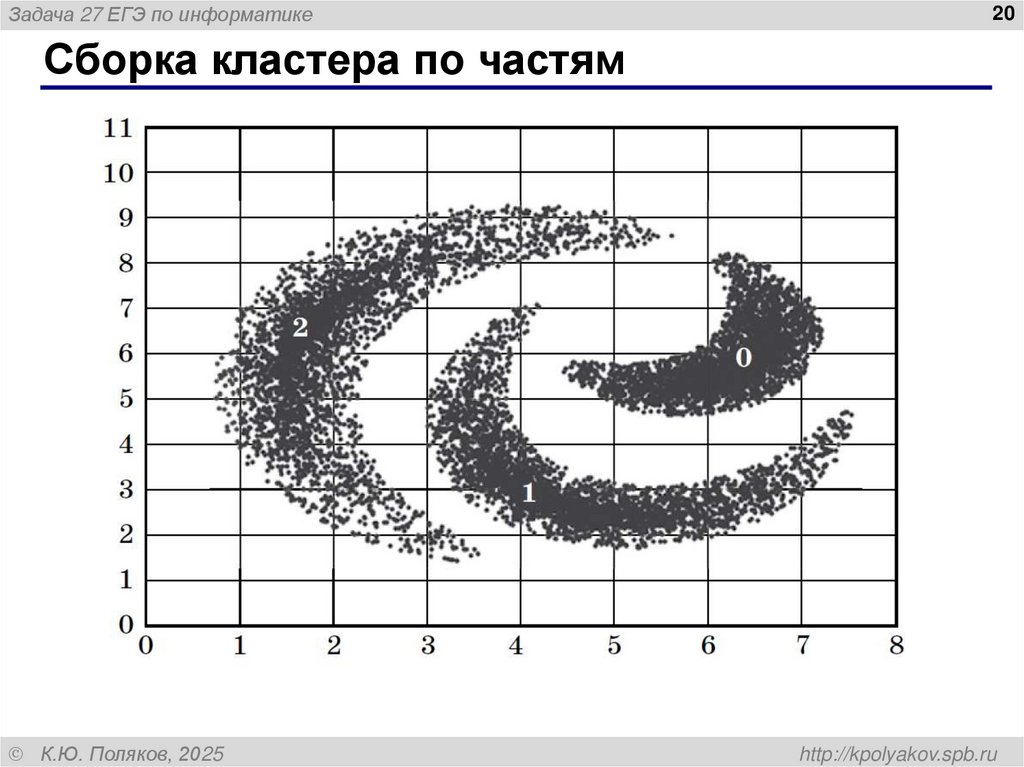
Сборка кластера по частям
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

20. Сборка кластера по частям

Задача 27 ЕГЭ по информатике
21
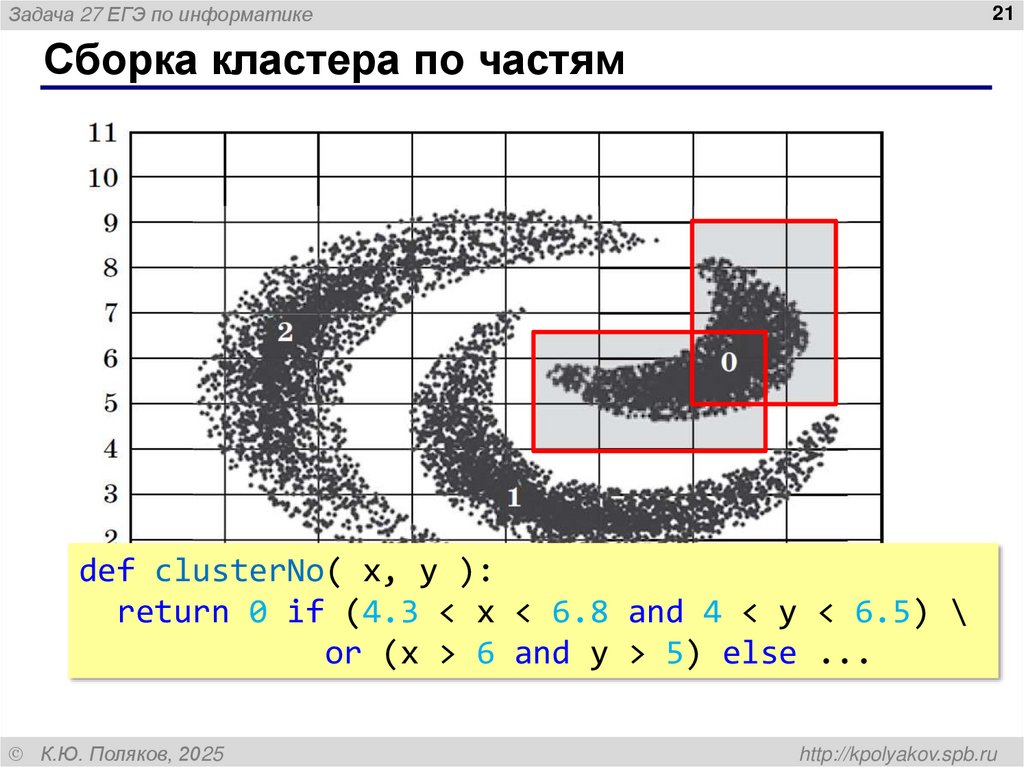
Сборка кластера по частям
def clusterNo( x, y ):
return 0 if (4.3 < x < 6.8 and 4 < y < 6.5) \
or (x > 6 and y > 5) else ...
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

21. Сборка кластера по частям

Задача 27 ЕГЭ по информатике
22
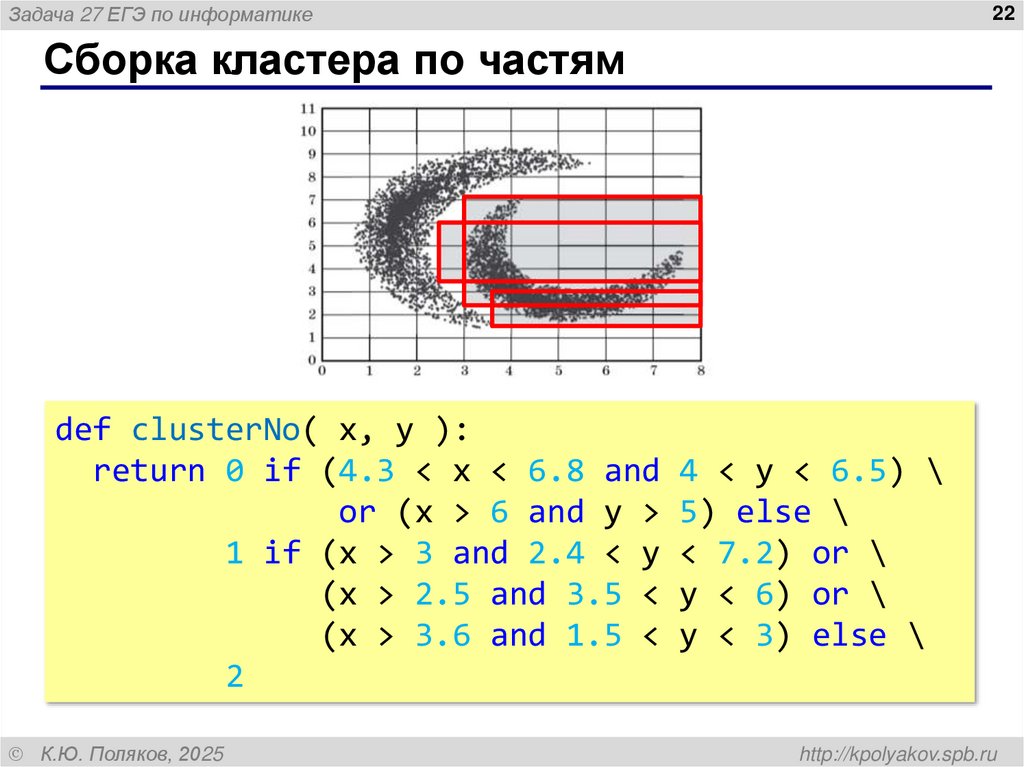
Сборка кластера по частям
def clusterNo( x, y ):
return 0 if (4.3 < x < 6.8 and 4 < y < 6.5) \
or (x > 6 and y > 5) else \
1 if (x > 3 and 2.4 < y < 7.2) or \
(x > 2.5 and 3.5 < y < 6) or \
(x > 3.6 and 1.5 < y < 3) else \
2
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

22. Сборка кластера по частям

Задача 27 ЕГЭ по информатике
23
Визуализация (Черепаха)
from turtle import *
tracer(0); penup(); hideturtle()
colors = ["red", "green", "blue"]
scale, shiftX, shiftY = 50, 200, 250
for k, cluster in enumerate(clusters):
for x, y in cluster:
goto( x*scale-shiftX, y*scale-shiftY )
dot( 3, colors[k] )
done()
А. Богданов
Солвер всех прототипов новых 27х на кластеризацию
https://vkvideo.ru/video-142628541_456239405
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

23. Визуализация (Черепаха)

Задача 27 ЕГЭ по информатике
24
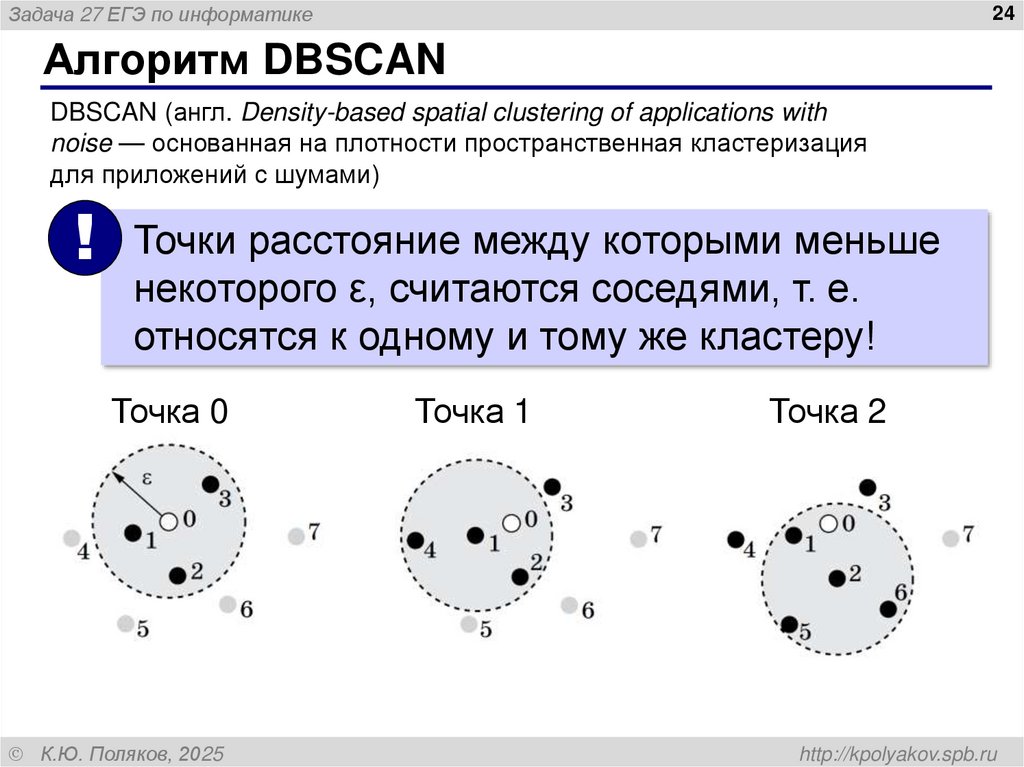
Алгоритм DBSCAN
DBSCAN (англ. Density-based spatial clustering of applications with
noise — основанная на плотности пространственная кластеризация
для приложений с шумами)
! Точки расстояние между которыми меньше
некоторого ε, считаются соседями, т. е.
относятся к одному и тому же кластеру!
Точка 0
К.Ю. Поляков, 2025
Точка 1
Точка 2
http://kpolyakov.spb.ru

24. Алгоритм DBSCAN

Задача 27 ЕГЭ по информатике
25
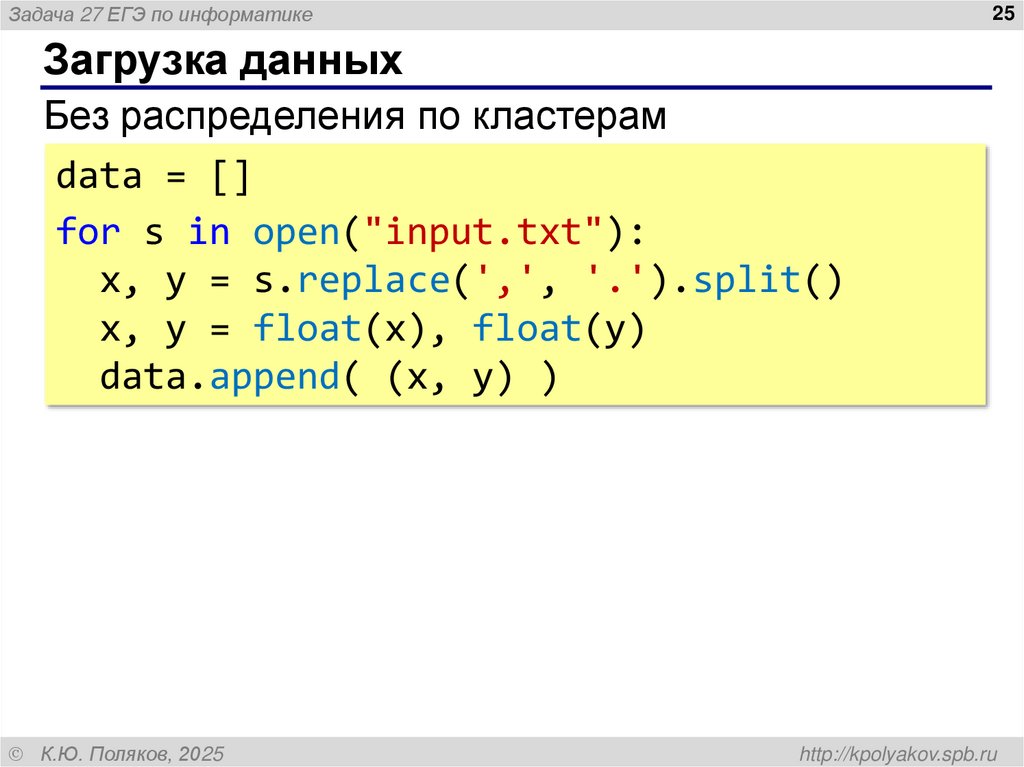
Загрузка данных
Без распределения по кластерам
data = []
for s in open("input.txt"):
x, y = s.replace(',', '.').split()
x, y = float(x), float(y)
data.append( (x, y) )
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

25. Загрузка данных

Задача 27 ЕГЭ по информатике
26
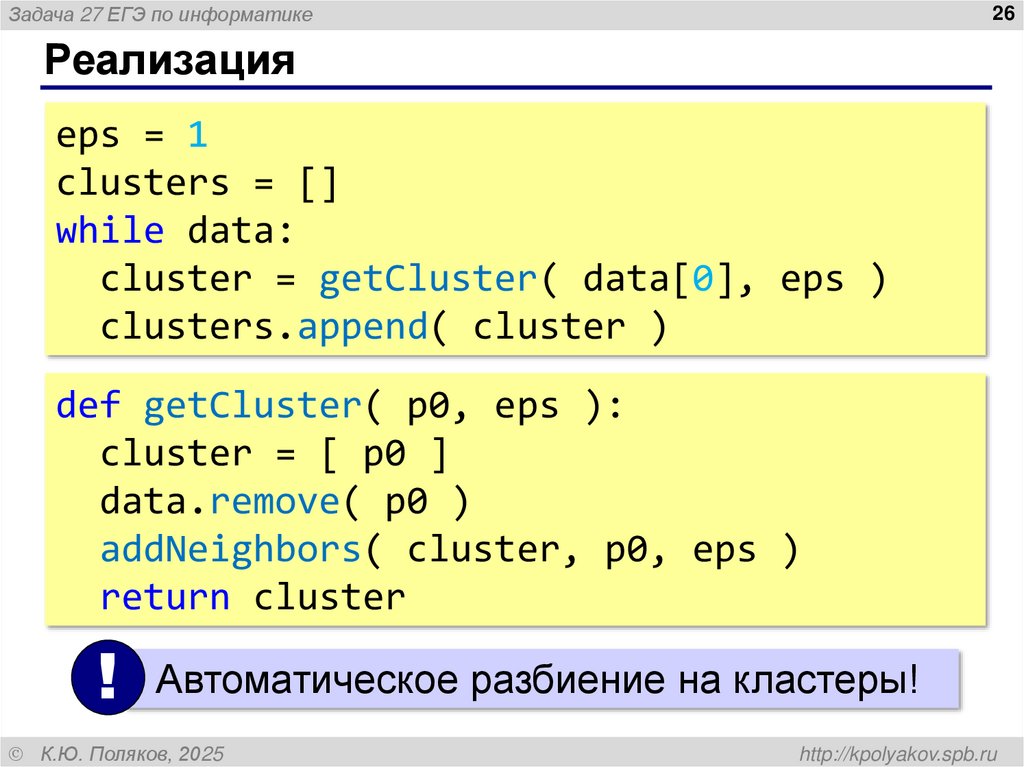
Реализация
eps = 1
clusters = []
while data:
cluster = getCluster( data[0], eps )
clusters.append( cluster )
def getCluster( p0, eps ):
cluster = [ p0 ]
data.remove( p0 )
addNeighbors( cluster, p0, eps )
return cluster
! Автоматическое разбиение на кластеры!
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

26. Реализация

Задача 27 ЕГЭ по информатике
27
Рекурсивный вариант
def addNeighbors( cluster, p0, eps ):
neighbors = [ p for p in data
if dist(p, p0) < eps ]
cluster += neighbors
for p in neighbors:
data.remove( p )
for p in neighbors:
addNeighbors( cluster, p, eps )
p0
К.Ю. Поляков, 2025
p
это «соседи
соседей»
http://kpolyakov.spb.ru

27. Рекурсивный вариант

Задача 27 ЕГЭ по информатике
28
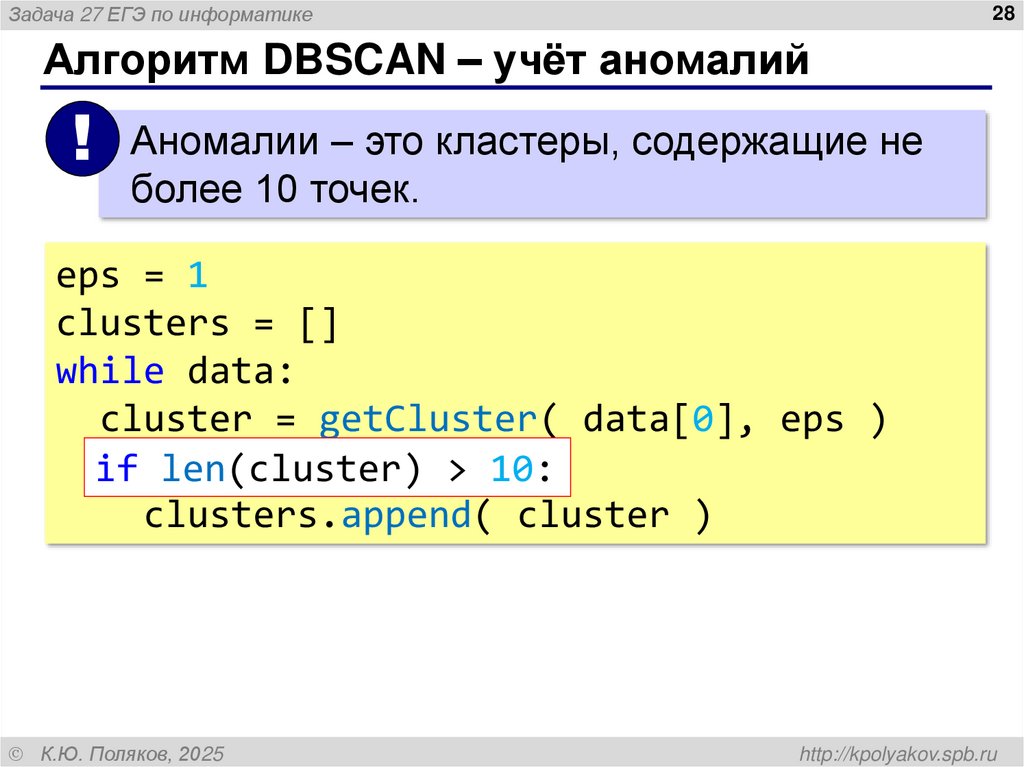
Алгоритм DBSCAN – учёт аномалий
! Аномалии – это кластеры, содержащие не
более 10 точек.
eps = 1
clusters = []
while data:
cluster = getCluster( data[0], eps )
if len(cluster)
len(cluster) >> 10:
10:
if
clusters.append( cluster )
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

28. Алгоритм DBSCAN – учёт аномалий

Задача 27 ЕГЭ по информатике
29
Алгоритм DBSCAN без рекурсии
def getCluster( p0, eps ):
cluster = [ p0 ]
data.remove( p0 )
for p in cluster:
cluster:
neighbors = [ n for n in data
if dist(n, p) < eps ]
cluster += neighbors
for n in neighbors:
data.remove( n )
return cluster
Л. Шастин
Задание 27 — Метод DBSCAN
https://youtu.be/TjZtxwkVoWU
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

29. Алгоритм DBSCAN без рекурсии

Задача 27 ЕГЭ по информатике
30
Кластеризация слиянием
Для каждой точки p определяются все кластеры из
списка clusters, в которых есть точки, соседние с p; эти
кластеры объединяются в один кластер совместно с
точкой p.
В. Лашин
Самое простое решение 27 задания —
кластеризация слиянием
https://youtu.be/VliZSipTrwE
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

30. Кластеризация слиянием

Задача 27 ЕГЭ по информатике
31
Кластеризация слиянием
eps = 1
новый кластер из
clusters = []
одной точки
for p0 in data:
срез
clusters.append( [p0] )
(копия)
for cluster in clusters[:-1]:
кроме
if any( dist(p0,p) < eps
последнего
for p in cluster ):
clusters[-1] += cluster
clusters.remove( cluster )
В. Лашин
Самое простое решение 27 задания —
кластеризация слиянием
https://youtu.be/VliZSipTrwE
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

31. Кластеризация слиянием

Задача 27 ЕГЭ по информатике
32
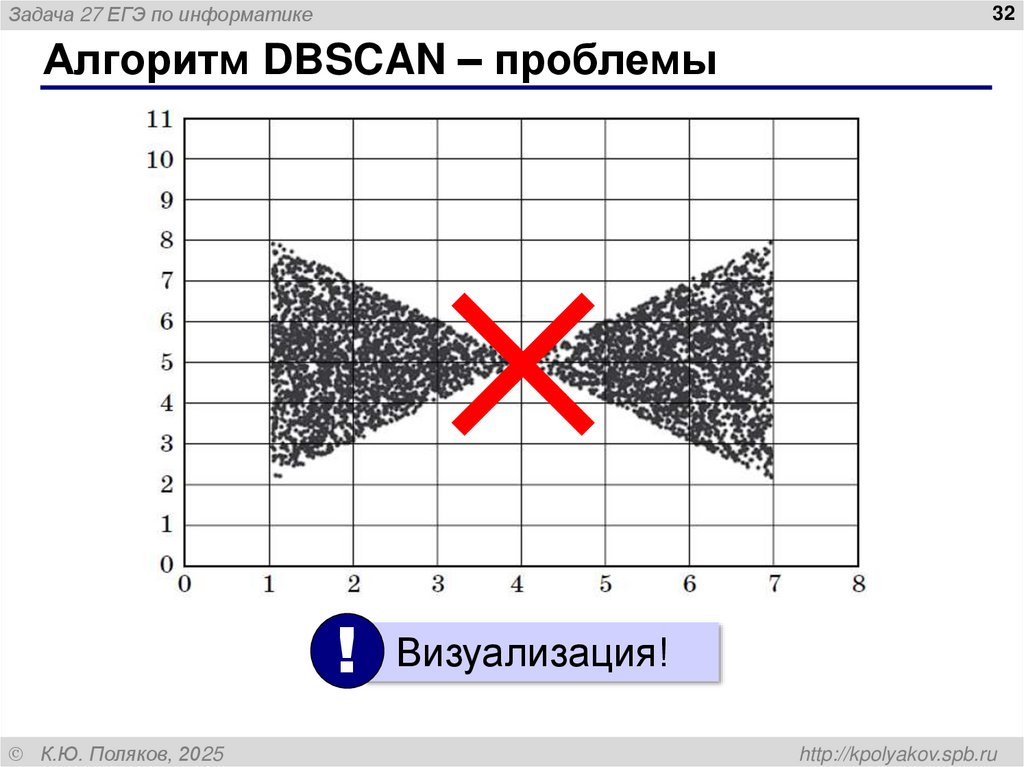
Алгоритм DBSCAN – проблемы
! Визуализация!
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

32. Алгоритм DBSCAN – проблемы

Задача 27 ЕГЭ по информатике
33
Метод k-средних
Метод k-медоидов – выбрать точку данных,
суммарное расстояние от которой до всех остальных
точек кластера минимально.
Шаг 1. Выбрать K точек — временные центры кластеров.
Шаг 2. Каждую точку данных связать с ближайшим
центром (разделение на кластеры).
Шаг 3. Для каждого кластера найти новый центр —
точку кластера, суммарное расстояние от которой до
всех остальных точек этого кластера минимально.
Шаг 4. Если центры кластеров изменились, перейти к
шагу 2, иначе завершить работу алгоритма.
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

33. Метод k-средних

Задача 27 ЕГЭ по информатике
34
Метод k-медоидов
K = 3 # количество кластеров
centers = [(6.5, 5), (3.5, 9), (1.5, 2)]
oldCenters = []
while centers != oldCenters:
oldCenters = centers
clusters = [ [] for i in range(K) ]
for p in data:
distToCenters = [ dist(p,center)
for center in centers ]
k = distToCenters.index(
min(distToCenters) )
clusters[k].append( p )
centers = [ getCenter(cluster)
for cluster in clusters ]
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

34. Метод k-медоидов

Задача 27 ЕГЭ по информатике
35
Метод k-медоидов: проблемы
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

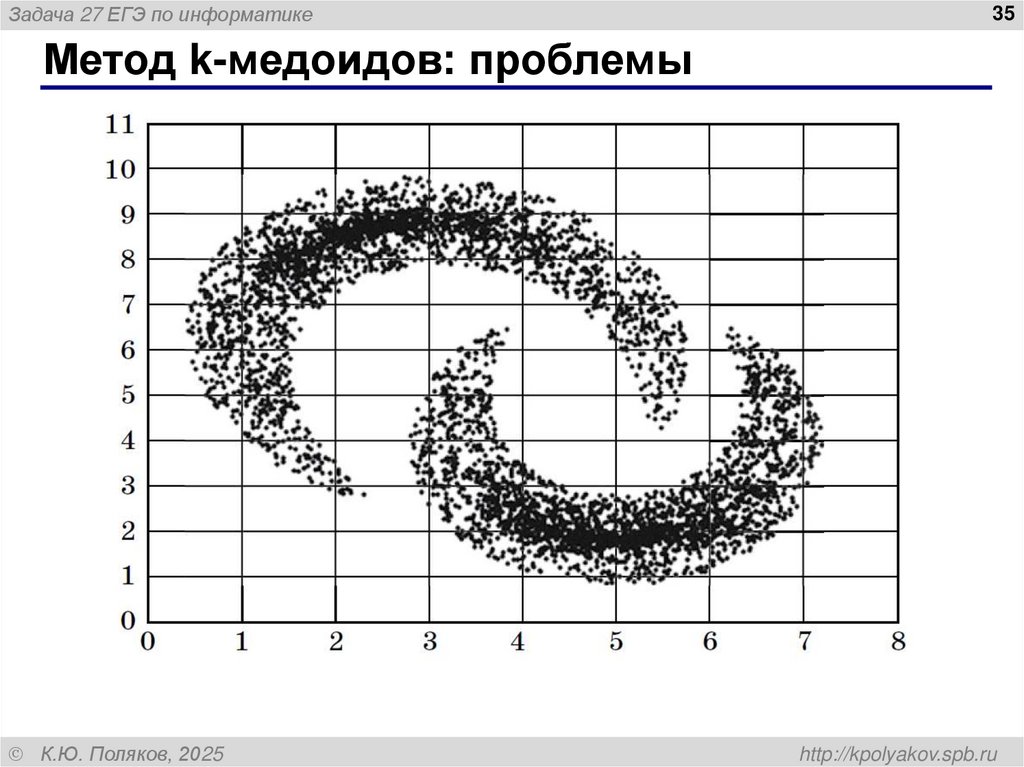
35. Метод k-медоидов: проблемы

Задача 27 ЕГЭ по информатике
36
Метод k-медоидов: проблемы
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

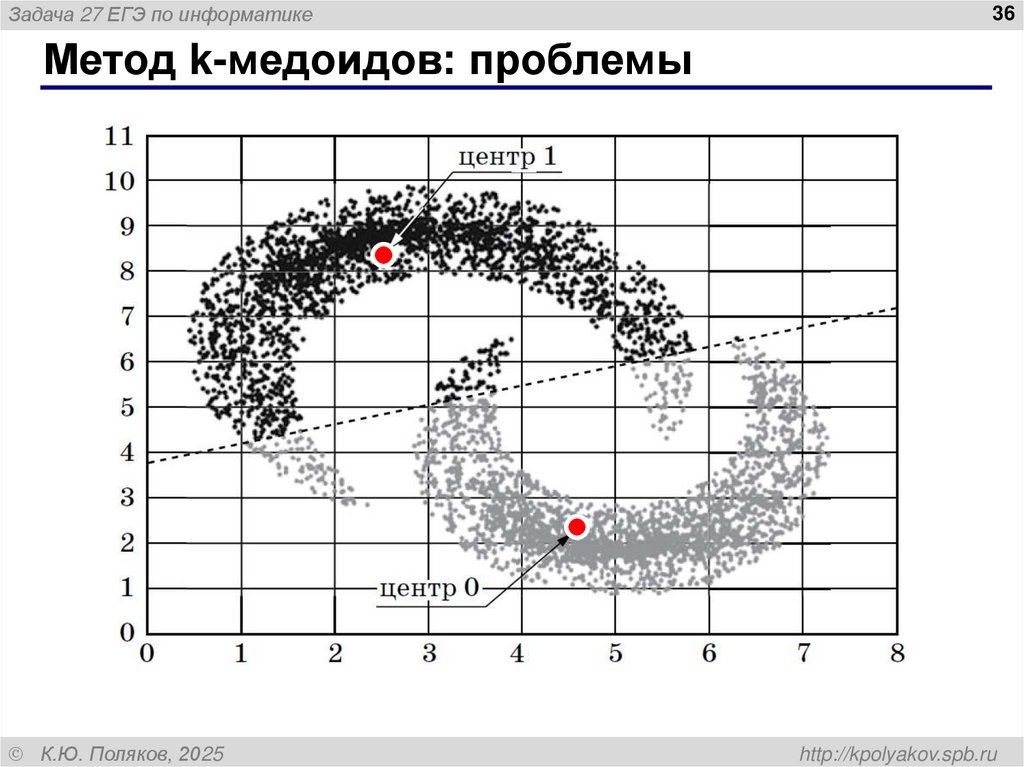
36. Метод k-медоидов: проблемы

Задача 27 ЕГЭ по информатике
37
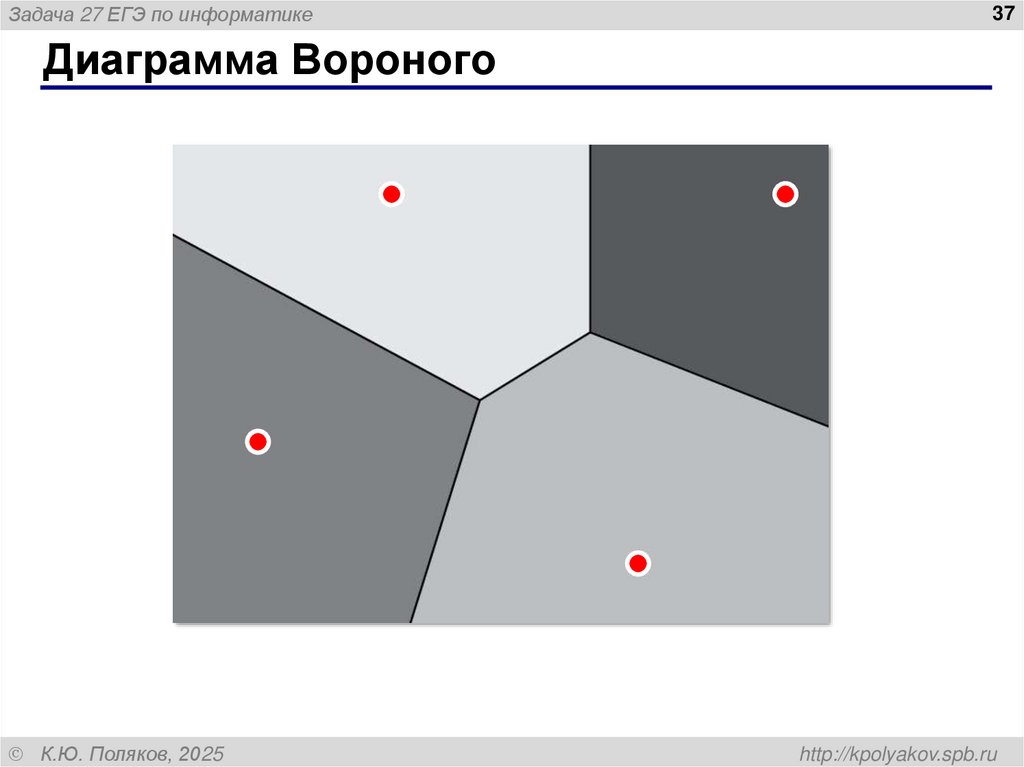
Диаграмма Вороного
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

37. Диаграмма Вороного

Задача 27 ЕГЭ по информатике
38
Возможные проблемы
Алгоритм DBSCAN
• два кластера расположены близко друг к
другу
Метод k-средних
• кластеры сложной формы
• кластеры разного размера
• задачи с аномалиями
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

38. Возможные проблемы

Задача 27 ЕГЭ по информатике
39
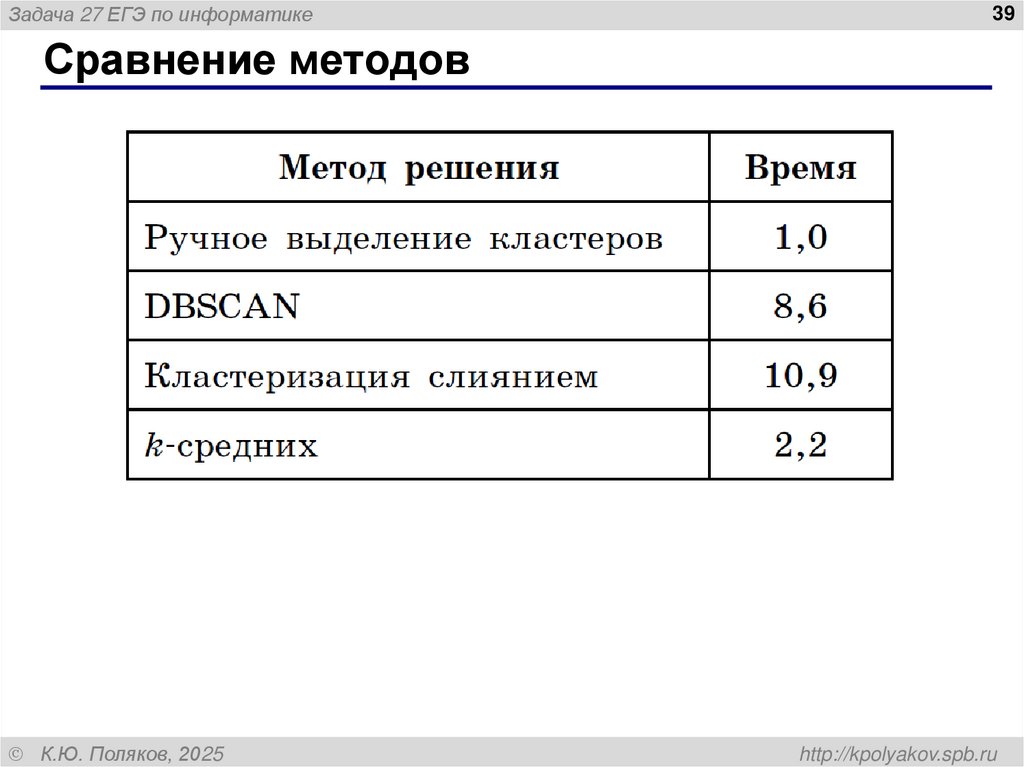
Сравнение методов
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

39. Сравнение методов

Задача 27 ЕГЭ по информатике
40
Решение в электронных таблицах
1) Выделить точки каждого кластера на отдельный
лист.
2) В каждом кластере для каждой точки найти
сумму расстояний до остальных точек этого же
кластера.
! Формулы для работы с массивами!
3) Отсортировать точки по сумме расстояний;
первая строка – центр.
4) Вычислить средние значения координат
центров.
И. Воропаев
Решение № 27 в Excel. Способ от PRO100 ЕГЭ
https://vkvideo.ru/video-205997912_456239251
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

40. Решение в электронных таблицах

Задача 27 ЕГЭ по информатике
41
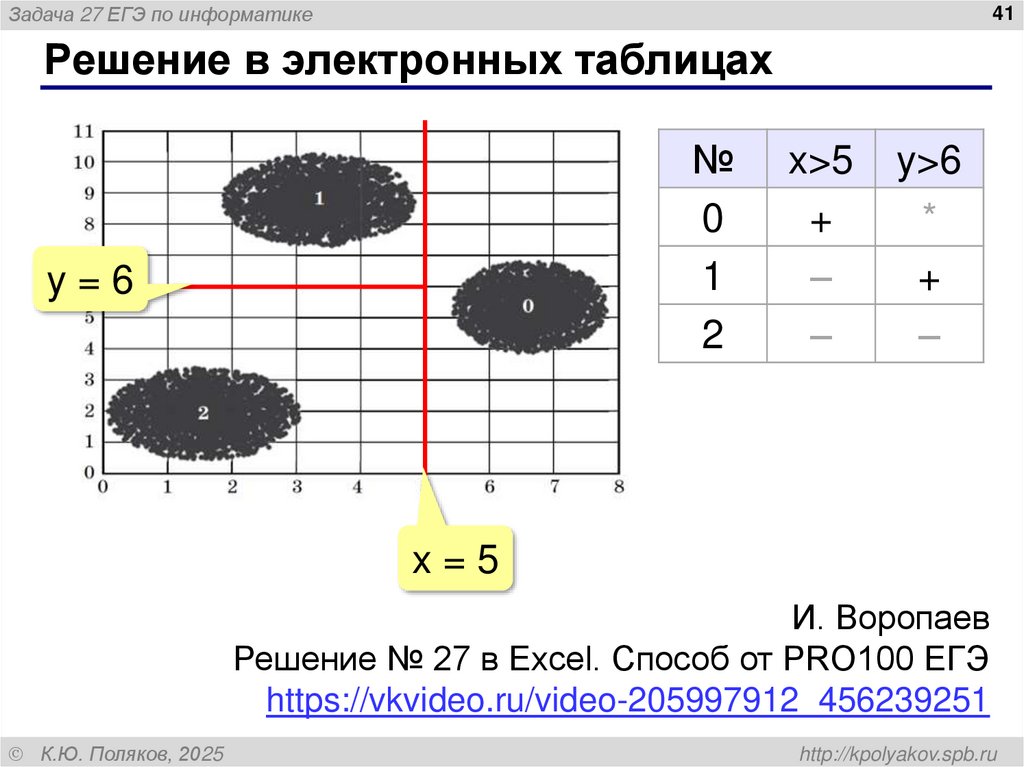
Решение в электронных таблицах
№
0
1
2
y=6
x>5
+
–
–
y>6
*
+
–
x=5
И. Воропаев
Решение № 27 в Excel. Способ от PRO100 ЕГЭ
https://vkvideo.ru/video-205997912_456239251
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

41. Решение в электронных таблицах

Задача 27 ЕГЭ по информатике
42
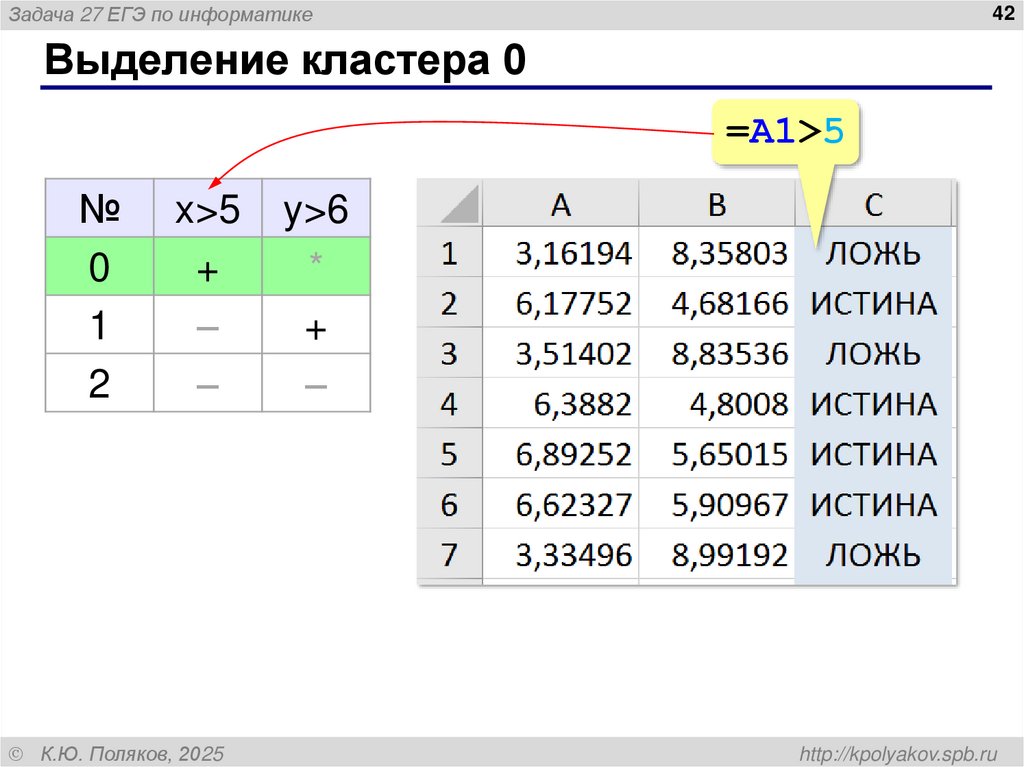
Выделение кластера 0
=A1>5
№
0
1
2
x>5
+
–
–
К.Ю. Поляков, 2025
y>6
*
+
–
http://kpolyakov.spb.ru

42. Выделение кластера 0

Задача 27 ЕГЭ по информатике
43
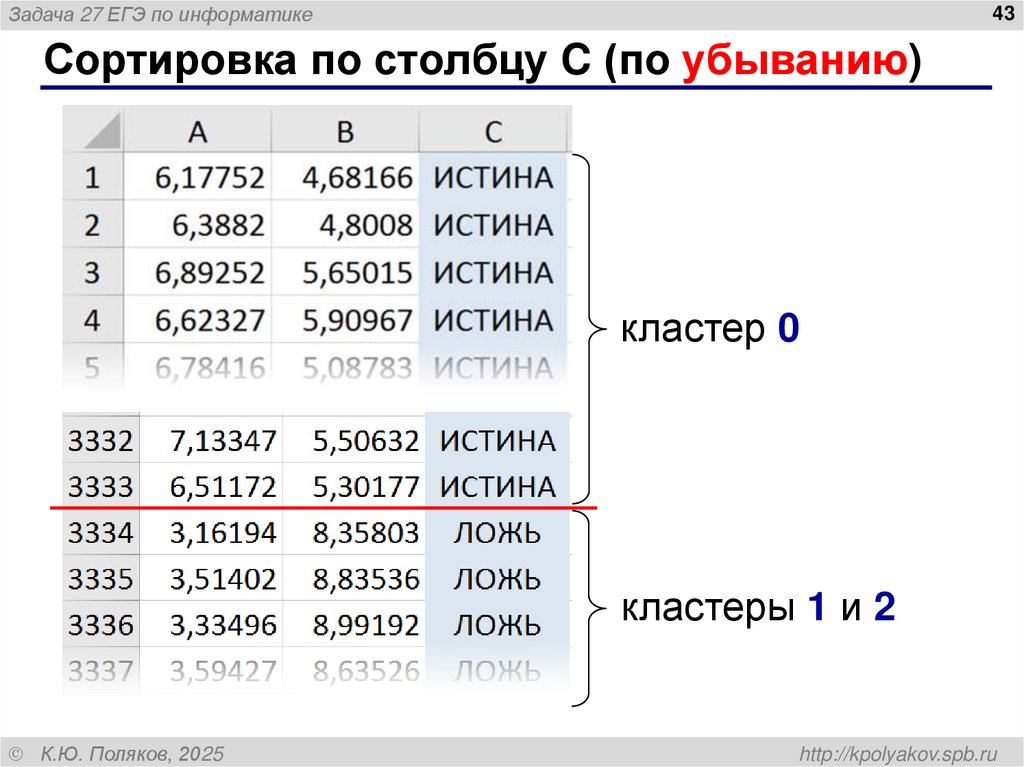
Сортировка по столбцу C (по убыванию)
кластер 0
кластеры 1 и 2
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

43. Сортировка по столбцу C (по убыванию)

Задача 27 ЕГЭ по информатике
44
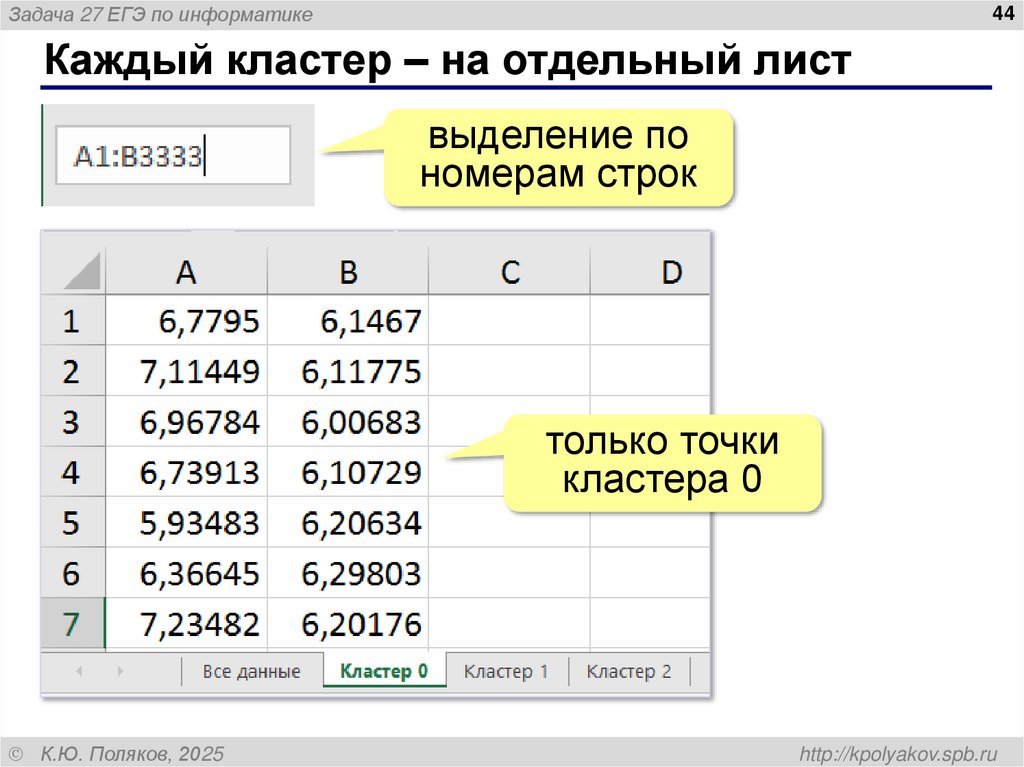
Каждый кластер – на отдельный лист
выделение по
номерам строк
только точки
кластера 0
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

44. Каждый кластер – на отдельный лист

Задача 27 ЕГЭ по информатике
45
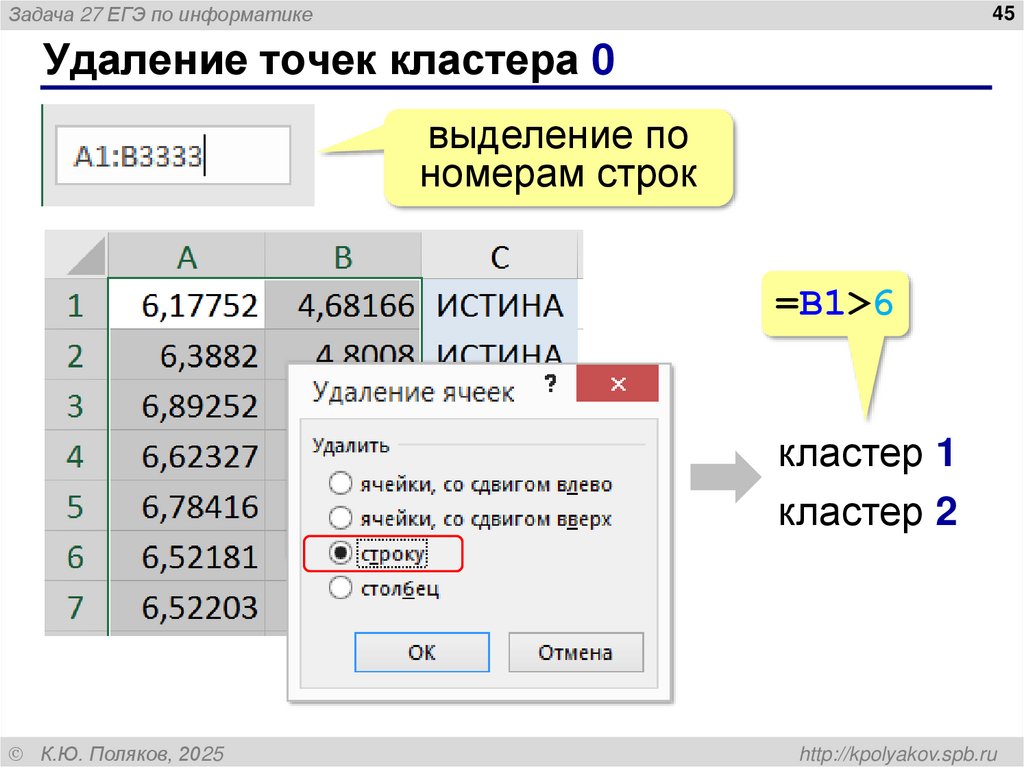
Удаление точек кластера 0
выделение по
номерам строк
=B1>6
кластер 1
кластер 2
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

45. Удаление точек кластера 0

Задача 27 ЕГЭ по информатике
46
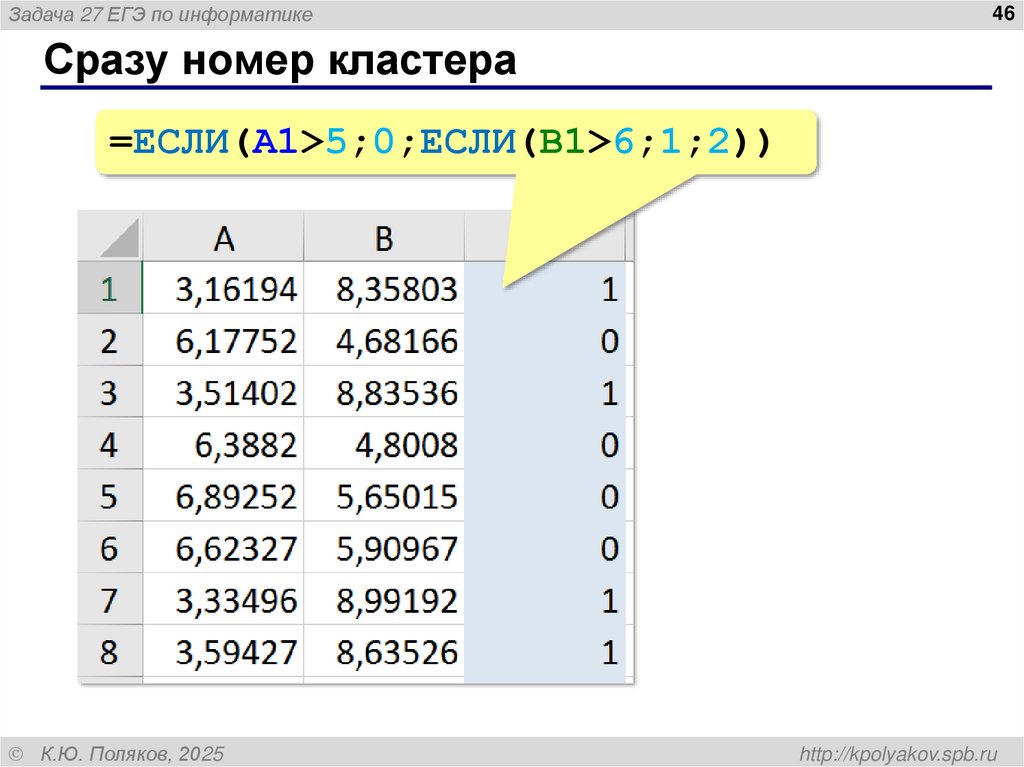
Сразу номер кластера
=ЕСЛИ(A1>5;0;ЕСЛИ(B1>6;1;2))
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

46. Сразу номер кластера

Задача 27 ЕГЭ по информатике
47
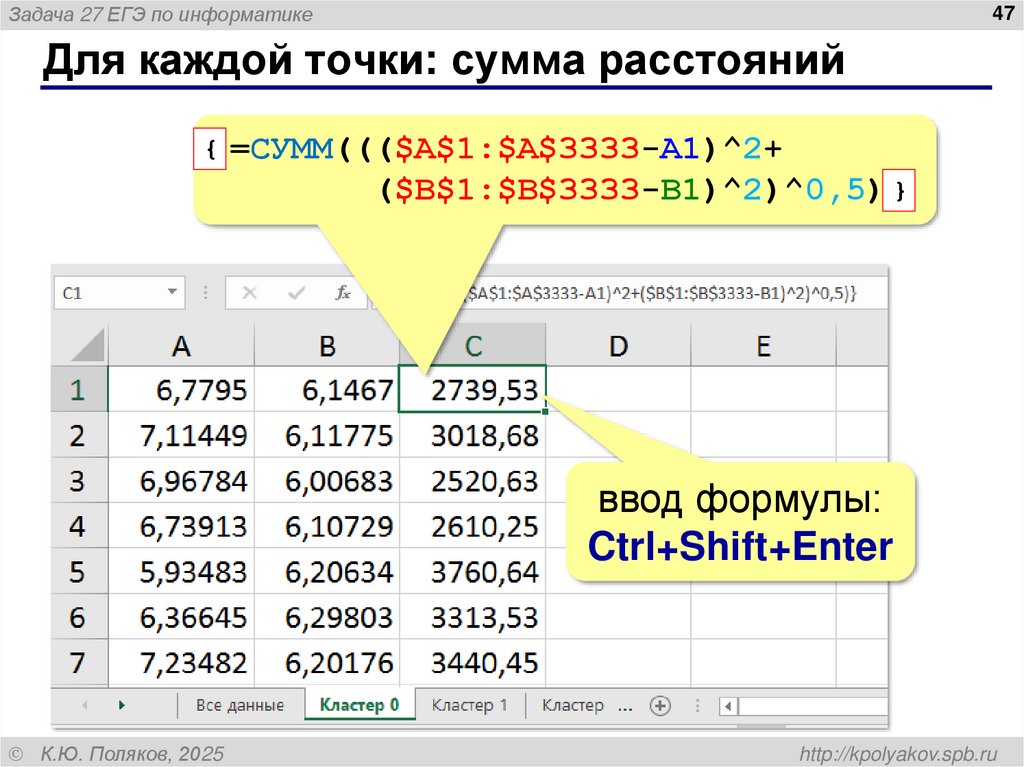
Для каждой точки: сумма расстояний
{ =СУММ((($A$1:$A$3333-A1)^2+
($B$1:$B$3333-B1)^2)^0,5) }
ввод формулы:
Ctrl+Shift+Enter
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

47. Для каждой точки: сумма расстояний

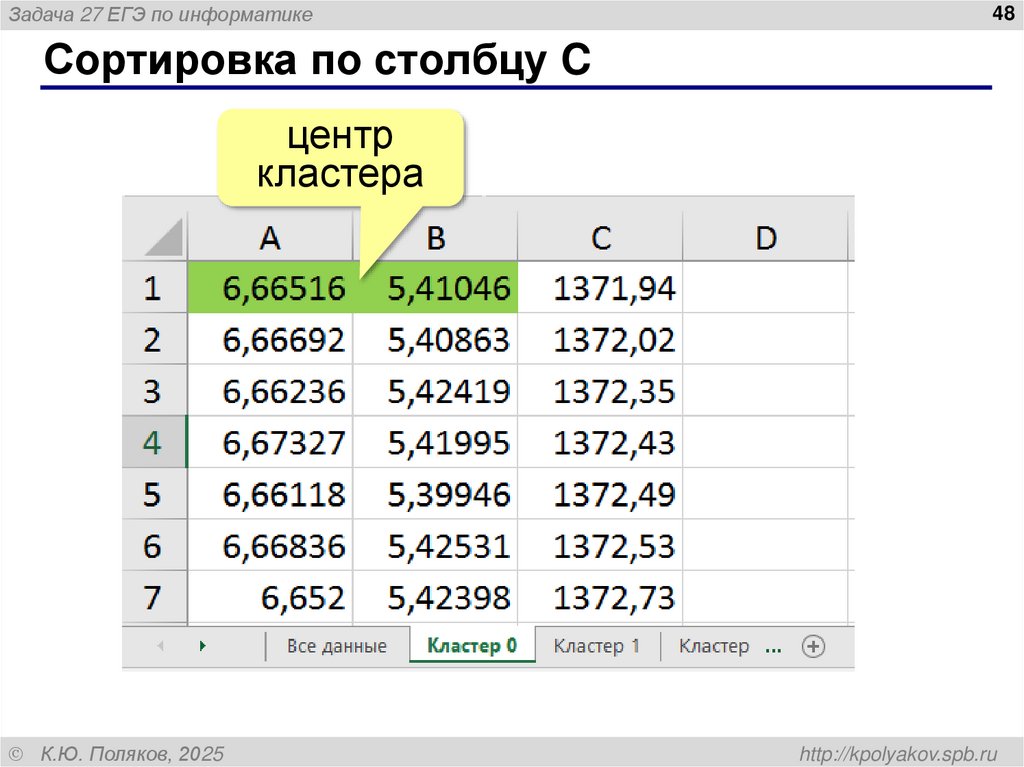
Задача 27 ЕГЭ по информатике
48
Сортировка по столбцу C
центр
кластера
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

48. Сортировка по столбцу C

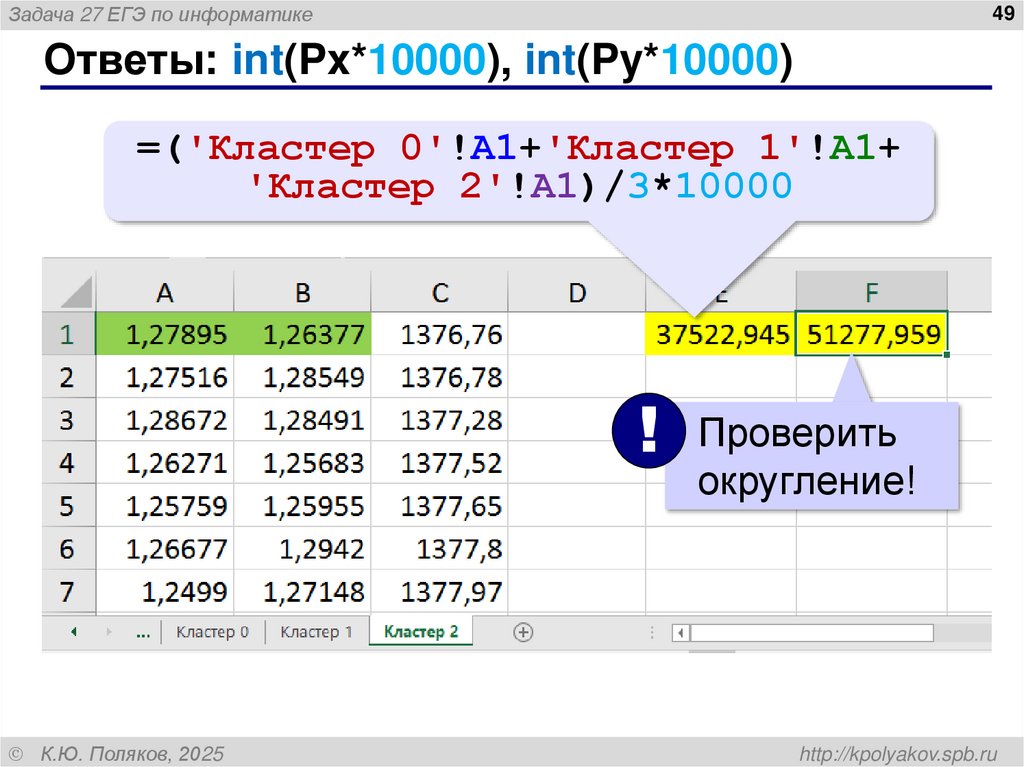
Задача 27 ЕГЭ по информатике
49
Ответы: int(Px*10000), int(Py*10000)
=('Кластер 0'!A1+'Кластер 1'!A1+
'Кластер 2'!A1)/3*10000
! Проверить
округление!
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

49. Ответы: int(Px*10000), int(Py*10000)

Задача 27 ЕГЭ по информатике
50
Демо-2026
Для файла А определите координаты центра
каждого кластера, затем найдите два числа:
Px – минимальную из абсцисс центров кластеров и
Py – минимальную из ординат центров кластеров.
Для файла Б определите координаты центра
каждого кластера, затем найдите два числа:
Q1 – расстояние между центрами кластеров с
минимальным и максимальным количеством точек и
Q2 – максимальное расстояние от центра кластера
до точки этого же кластера среди всех кластеров.
Гарантируется, что во всех кластерах количество
точек различно.
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

50. Демо-2026

Задача 27 ЕГЭ по информатике
51
Вычисление Q1
Q1 – расстояние между центрами кластеров с
минимальным и максимальным количеством точек
... # распределение по кластерам
clusters.sort(
key=lambda cls: len(cls) )
... # поиск координат центров
Q1 = dist( centers[0], centers[2] )
print( int(Q1*10_000) )
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

51. Вычисление Q1

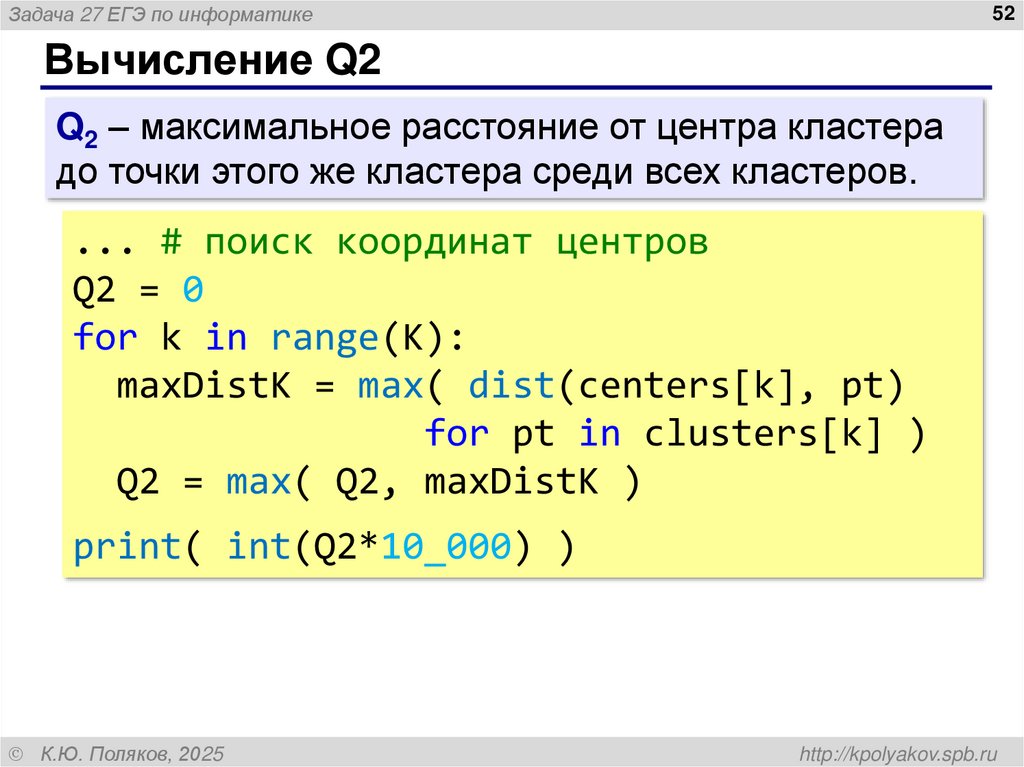
Задача 27 ЕГЭ по информатике
52
Вычисление Q2
Q2 – максимальное расстояние от центра кластера
до точки этого же кластера среди всех кластеров.
... # поиск координат центров
Q2 = 0
for k in range(K):
maxDistK = max( dist(centers[k], pt)
for pt in clusters[k] )
Q2 = max( Q2, maxDistK )
print( int(Q2*10_000) )
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

52. Вычисление Q2

Задача 27 ЕГЭ по информатике
53
Возможные варианты вопросов
(А. Кабанов) Диаметром кластера D назовём
максимальное расстояние между двумя точками в
кластере.
def diameter( cluster ):
можно
D = 0
оптимизировать!
for p1 in cluster:
for p2 in cluster:
D = max( D, dist(p1,p2) )
return D
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

53. Возможные варианты вопросов

Задача 27 ЕГЭ по информатике
54
Возможные варианты вопросов
(А. Кабанов) Средним расстоянием назовём среднее
арифметическое расстояние между всеми парами
различных точек в кластере.
def averageDist( cluster ):
sumDist = count = 0
for p1 in cluster:
for p2 in cluster:
if p1
p1 !=
!= p2:
p2:
if
sumDist += dist(p1,p2)
count += 1
return sumDist / count
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

54. Возможные варианты вопросов

Задача 27 ЕГЭ по информатике
55
Возможные варианты вопросов
(А. Кабанов) Точкой наведения назовём точку, в
единичной окрестности которой находится наибольшее
количество точек кластера. Если таких точек несколько,
то выбирается точка с наибольшей координатой x.
def targetPoint( cluster ):
count = []
for p0 in cluster:
k = sum( 1 for p in cluster
if dist(p,p0) <= 1 )
count.append( (k, p0[0], p0) )
return max(count)[2]
max(x) при
одинаковых k
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

55. Возможные варианты вопросов

Задача 27 ЕГЭ по информатике
56
Возможные варианты вопросов
(А. Кабанов) Изолированной точкой назовём точку, в
единичной окрестности которой находится наименьшее
количество точек кластера. Если таких точек несколько,
то выбирается точка с наибольшей координатой y.
def isolatedPoint( cluster ):
count = []
for p0 in cluster:
k = sum( 1 for p in cluster
if dist(p,p0) <= 1 )
count.append( (k, -p0[1]
-p0[1], p0) )
return min(count)[2]
max(y) при
одинаковых k
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

56. Возможные варианты вопросов

Задача 27 ЕГЭ по информатике
57
Возможные варианты вопросов
(В. Лашин) Диагональю кластера назовём отрезок
наибольшей длины, соединяющий две точки этого
кластера.
def diag( cluster ):
maxDist = 0
for p1 in cluster:
for p2 in cluster:
if dist(p1, p2) > maxDist:
maxDist = dist(p1, p2)
points = (p1, p2)
return points
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

57. Возможные варианты вопросов

Задача 27 ЕГЭ по информатике
58
Возможные варианты вопросов
(В. Лашин) Крайней точкой кластера назовём такую
точку, что расстояние от неё до ближайшей точки другого
кластера минимально.
def shortest(cluster1, cluster2):
distances = []
for p1 in cluster1:
for p2 in cluster2:
d = dist(p1, p2)
distances.append( (d, (p1, p2) ) )
return min(distances)[1]
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

58. Возможные варианты вопросов

Задача 27 ЕГЭ по информатике
59
Возможные варианты вопросов
(В. Лашин) X-медианой кластера назовём такую
абсциссу точки кластера, что в этом кластере количество
точек с абсциссами, меньшими x-медианы, равно
количеству точек с абсциссами, большими x-медианы.
def xMedian(cluster):
for p1 in cluster:
count = 0
предполагаем,
что такая точка
for p2 in cluster:
есть!
if p2[0] > p1[0]:
count += 1
if count == len(cluster) // 2:
return p1[0]
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

59. Возможные варианты вопросов

Задача 27 ЕГЭ по информатике
60
Возможные варианты вопросов
(В. Лашин) Центроидом кластера назовём точку (не
обязательно принадлежащую кластеру!), абсцисса и
ордината которой – средние арифметические абсцисс и
ординат всех точек кластера, соответственно.
def centroid( cluster ):
N = len(cluster)
return (
sum( p[0] for p in cluster ) / N,
sum( p[1] for p in cluster ) / N )
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru

60. Возможные варианты вопросов

Задача 27 ЕГЭ по информатике
61
Конец фильма
ПОЛЯКОВ Константин Юрьевич
д. т. н., учитель информатики
г. Санкт-Петербург
kpolyakov@mail.ru
К.Ю. Поляков, 2025
http://kpolyakov.spb.ru