Preemstvennost-DOO-i-NOO-v-formirovanii-predstavlenij-o-chasti-i-celom-v-matematike (1)

1.

Преемственность ДОО и НОО в
формировании представлений о части
и целом в математике
«Актуальные вопросы математического образования»
Автор: Тараповская Юлия

2.

ЦЕЛЬ И ЗАДАЧИ
Обеспечение плавного перехода от наглядно-действенного опыта к
осознанным математическим действиям
Цель заключается в обосновании и демонстрации практических приемов, которые помогают детям плавно перейти от нагляднодейственного опыта в дошкольном образовании к осознанным математическим действиям в начальной школе. Этот переход
критически важен для формирования прочных математических представлений.
1
2
3
Анализ основ
Сопоставление ФГОС
Разработка методик
Теоретический анализ проблемы
Сравнение требований ФГОС ДО и
Создание авторских методик для ДОО и
преемственности.
ФГОС НОО.
НОО.

3.

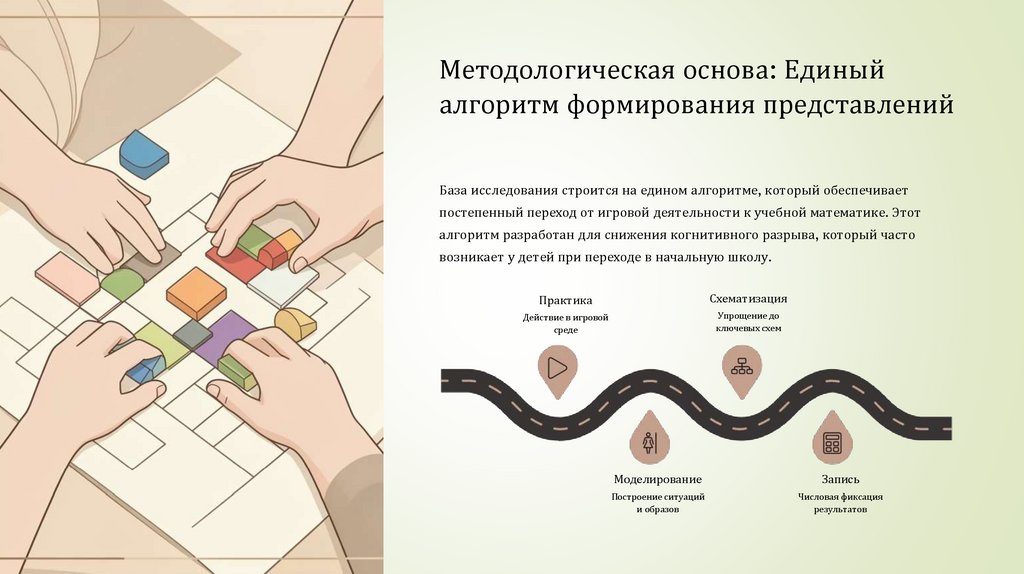
Методологическая основа: Единый
алгоритм формирования представлений
База исследования строится на едином алгоритме, который обеспечивает
постепенный переход от игровой деятельности к учебной математике. Этот
алгоритм разработан для снижения когнитивного разрыва, который часто
возникает у детей при переходе в начальную школу.
Практика
Схематизация
Действие в игровой
среде
Упрощение до
ключевых схем
Моделирование
Запись
Построение ситуаций
и образов
Числовая фиксация
результатов

4.

МЕТОДИКИ В ДОО
Формирование представления о части и целом
В дошкольном образовании используются три ключевые методики, которые помогают детям на чувственном уровне освоить понятия «часть»
и «целое». Эти методики используют наглядные материалы и игровую форму для формирования базовых математических представлений.
1. «Целое в
действии»
2. «Собери по
условию»
Деление яблока или
Сборка целого из
картонной полоски на 2-3
разрезных кругов и
Сравнение частей с
части и последующее
полосок разных форм.
использованием
восстановление целого.
Задания направлены на
визуальных мерок и
Развивает чувственное
развитие анализа, синтеза
рамок, без числовой
понимание делимости,
и зрительного
записи. Закладывает
равных и неравных
сопоставления.
основу для понимания
частей.
3. «Равные и
неравные части»
доли и равенства частей.

5.

МЕТОДИКИ В НОО
Осознанные математические действия
В начальной школе мы переходим к более абстрактным методам, которые помогают младшим школьникам осознанно работать с
математическими концепциями, связывая их с полученным ранее наглядным опытом.
1. «От предмета к модели»
2. «От модели к числу»
3. «Одна ситуация — разные
представления»
Перевод наглядных моделей в
Разложение целого на равные части
схематические изображения, развивая
(например, 12 предметов), формируя
Умение переводить информацию между
понимание соответствия между
связь наглядной ситуации с числовыми
предметной, графической и числовой
предметом и схемой.
выражениями.
формами, развивая гибкость мышления.

6.

Роль речевого сопровождения в
обучении математике
Речевое сопровождение является ключевым компонентом всех наших методик.
Оно превращает пассивные манипуляции с предметами в осмысленные
математические действия и способствует формированию понятийного аппарата у
детей.
«Когда ребенок проговаривает свои действия, он не только объясняет их
другим, но и осмысливает их сам, строя внутреннюю логику процесса.»
Наводящие вопросы педагога: Стимулируют детей к размышлению и поиску
решений.
Требование объяснить действия: Помогает детям структурировать свои
мысли и выражать их словесно.
Аргументация выбора: Развивает критическое мышление и умение
обосновывать свою точку зрения.

7.

Материально-методическая база: Простота и доступность
Для реализации методик используются простые, доступные материалы, которые легко найти и изготовить. Это
позволяет быстро и эффективно интегрировать их в образовательный процесс, не требуя значительных затрат.
• Разрезные круги и полоски
• Пуговицы, камушки, счётные предметы
• Листы с разметкой
• Простые рамки-мерки
Особенности: Доступность, минимальные затраты, возможность быстрой демонстрации (5–7 минут).

8.

ОЖИДАЕМЫЕ ОБРАЗОВАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ
Формирование прочных математических представлений
Применение предложенных методик ведет к конкретным образовательным результатам, которые готовят детей к успешному освоению
математики на следующих этапах обучения.
В ДОО
В НОО
Осознанные манипуляции с частями
Построение схем
Устные объяснения действий
Числовая запись отношений
Понимание равных и неравных частей
Готовность к изучению дробей и состава числа

9.

Практическая значимость: От
преемственности к уверенности
Исследование имеет большое практическое значение, поскольку он направлен на решение
одной из ключевых проблем образования — обеспечение плавного и эффективного перехода
детей между дошкольным и начальным уровнями обучения.
• Преемственность ДОО и НОО
Обеспечивает плавный переход и снижает разрыв в обучении.
• Снижение учебной тревожности
Дети чувствуют себя более уверенно в новой образовательной среде.
• Повышение уверенности
Укрепляет самооценку детей в математических способностях.
• Устойчивые математические представления
Формирует прочную базу для дальнейшего изучения математики.
Методики легко внедряются в образовательный процесс и могут быть адаптированы под
индивидуальные особенности и уровень развития детей.

10.

Заключение: К целостному
математическому мышлению
Предложенные приемы и методики демонстрируют свою эффективность в
формировании целостного математического мышления у детей. Они просты в
реализации и создают прочную основу для дальнейшего успешного обучения.
Простота в реализации: Методики легко адаптируются и не требуют сложных
ресурсов.
Плавный переход: Обеспечивают непрерывность от практики к абстракции.
Целостное мышление: Развивают глубокое понимание математических
концепций.
Спасибо за внимание!