CM_Logique1(1)

1. Outils mathématiques pour Informatique

UTC 501
Outils
mathématiques
pour Informatique

2. Objectifs de ce cours

•Se familiariser avec les concepts
fondamentaux de la logique
mathématique, incluant la théorie
des ensembles.
•Apprendre à maîtriser les
propositions et les prédicats en
mathématiques.
•Découvrir les tables de vérité.
•Acquérir la capacité de manipuler les
connecteurs logiques et les
quantificateurs en mathématiques.

3. Contenu pédagogique

Voilà ce que nous l’allons aborder :
Présentation et Historique de la
Logique Mathématique
Les Propositions : Définition, tables
de vérité et connecteurs binaires
Les Quantificateurs usuels et leurs
propriétés
Le Langage ensembliste : Cadre
d’étude, vocabulaire de la Théorie
des Ensembles, les symboles et
leurs propriétés

4. Présentation et Historique de la Logique Mathématique

5. Pourquoi La Logique ?

Présentation et Historique de la Logique Mathématique
Pourquoi La Logique ?
•Philosophie: fondement du
raisonnement déductif
•Mathématique: la logique
comme fondation des preuves
mathématiques
•Informatique: nos dispositifs
informatiques sont des circuits
logiques

6. Qu’ est-ce que la Logique ?

Présentation et Historique de la Logique Mathématique
Qu’ est-ce que la Logique ?
Étude des principes des raisonnements
corrects
• Ce qui est « logique » dans le langage courant
n’est pas forcément « logique » selon la
logique
Dans le langage courant :
• « logique » = « qui fait sens »
• En logique : « logique » = « qui est
nécessairement vrai »

7. (Contre-)exemples

Présentation et Historique de la Logique Mathématique
(Contre-)exemples
• « Je suis enseignant-chercheur et comme j’aime bien la
logique et que je l’utilise dans le cadre de mes travaux
de recherche, il est logique que j’enseigne la logique ! »
• Pas logique ! Cela fait sens mais ce n’est pas
nécessairement vrai qu’on enseigne ce que l’on aime
utiliser.
• « Vous êtes étudiants à l’école des mines, par
conséquent, vous avez logiquement des droits. »
• Pas logique ! Cela fait sens car tout être humain a des
droits, mais cela pourrait être différent.
• « Nécessairement vrai » signifie « vrai dans toutes les
situations imaginables, réelles ou inventées »
• « Si je suis enseignant et je suis chercheur, alors je suis
enseignant »
• Logique ! Cela est nécessairement vrai

8. Logiques formelles

Présentation et Historique de la Logique Mathématique
Logiques formelles
Pour formaliser les raisonnements logiques, on utilise un
langage formel (une logique formelle).
Il existe de nombreuses logiques formelles, mais on n’en
verra uniquement deux (les plus connues) :
La logique propositionnelle
La logique des prédicats (aussi appelée logique du
premier ordre)
Une logique (formelle) est caractérisée par :
Sa syntaxe (comment on écrit)
Sa sémantique (comment on interprète)

9. Plusieurs logiques

Présentation et Historique de la Logique Mathématique
Plusieurs logiques
CURRY
HOWARD
Logique
CHURCH-TURIN
HILBERT
BOOLE
FREGE
LEIBNIZ
Chronologie

10. Quelques données d’Histoire

Présentation et Historique de la Logique Mathématique
Quelques données d’Histoire
LEIBNIZ : Notation mathématique moderne
BOOLE (XXème siècle) : Logique mathématique avec calcul
de vérité
FREGE (Début XXème.) : extension tenant compte de la
notion de variable Systèmes logiques formalisés
HILBERT (1900) : 23 problèmes non résolus
Nombreux travaux en logique : Axiomes de Peano en
arithmétique, Théorie des ensembles, Théorie des modèles
CHURCH , TURING (années 30) : Algorithmique
Lambda-Calcul et Machine de Turing : Naissance du premier
langage de programmation
CURRY-HOWARD : Correspondance entre preuves formelles
et Lambda-Calcul

11. notions abordées dans ce cours

Eléments
Ensembles
Appartenance
Symboles et lettres, qui assemblés selon certaines
règles, forment les propositions
Connecteurs et Nouvelles Propositions
Combinaisons de propositions
Construction de Raisonnements

12. Les Propositions

Elles font apparaitre un nouvel alphabet et des
règles de formation, pour donner naissance à un
langage formel…

13. Contenu

Les Propositions
Contenu
Voici les chapitres que nous allons aborder :
Définitions
Tables de Vérité
Négation d’une proposition
Connecteurs Binaires
Propriétés

14. Définitions

Les Propositions
Définitions
Exemple introductif…
Considérons les 3 énoncés suivants, concernant des
nombres ou des faits :
A : 210 = 1024
B:5<4
C : “3 est un nombre impair”
Le contenu de A est vrai, celui de B est faux et celui de C est
vrai.
A, B et C sont trois exemples de propositions arithmétiques

15. Définitions

Les Propositions
Définitions
Proposition : On appelle proposition
tout énoncé dont on peut dire sans
ambiguïté s'il est vrai ou s'il est faux.

16. Tables de Vérité

Les Propositions
Tables de Vérité
Plaçons nous dans un cadre général…
P
Notons P une proposition
Soit P est vraie : elle sera
alors notée V
Soit P est fausse : elle sera
alors notée F
V
F
Autre notation :
P
1 pour Vrai
1
0 pour Faux
0

17. Négation d’une Proposition

Les Propositions
Négation d’une Proposition
Négation d’une Proposition :
On appelle négation de la proposition P la
proposition Q telle que
Q est fausse si et seulement si P est vraie.

18. Négation d’une Proposition

Les Propositions
Négation d’une Proposition
Reprenons les exemples précédents
A : 210 = 1024
(V)
Négation : 210 1024 (F)
B:5<4
Négation : 5 ≥ 4
(F)
(V)
C : “3 est un nombre impair” (V)
Négation : “3 n’est pas un nombre impair” (F)

19. Négation d’une Proposition

Les Propositions
Négation d’une Proposition
Plus Généralement,
A toute proposition P, on peut associer une nouvelle
proposition, notée
P ou encore P
dont la valeur de vérité est donnée dans la table de vérité
ci-dessous
P est la négation de P
est le connecteur négation
P
P
On notera encore
V
F
F
V
Q P P
« non P » , ou “P barre”

20. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Où comment relier deux propositions…
La négation est un connecteur unaire
Connecteur Binaire : permet de relier deux
propositions pour former une nouvelle proposition.
Connecteurs Binaires usuels :
La Conjonction
La Disjonction
L’Implication
L’Equivalence

21. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Conjonction de deux propositions : Connecteur logique ET
Conjonction :
On appelle conjonction des propositions
P et Q, et l'on note
P Q

22. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Conjonction de deux propositions : Connecteur logique ET
Conjonction (Suite) :
Cette nouvelle proposition est vraie
si et seulement si
P et Q sont vraies simultanément.

23. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Conjonction de deux propositions : Connecteur logique ET
A tout couple de propositions (P,Q), la conjonction ‘’ET’’
associe la proposition
P Q
dont la valeur de vérité est donnée dans la table ci-contre :
P
Q
P Q
P
Q
P Q
V
V
V
1
1
1
V
F
F
1
0
0
F
V
F
0
1
0
F
F
F
0
0
0

24. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Disjonction de deux propositions : Connecteur logique OU
Disjonction :
On appelle disjonction des propositions
P et Q, (Dit “P ou Q”)
la nouvelle proposition qui est vraie
si et seulement si l’une au moins des 2
propositions est vraie.
“P ou Q”:Nouvelle Proposition notée P Q

25. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Disjonction de deux propositions : Connecteur logique OU
A tout couple de propositions (P,Q), la disjonction “OU”
associe la proposition P Q
dont la valeur de vérité est donnée dans la table ci-contre :
P
Q
P Q
P
Q
P Q
V
V
V
1
0
1
V
F
V
1
1
1
F
V
V
0
1
1
F
F
F
0
0
0

26. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Reprenons les propositions des exemples précédents
A : 210 = 1024
(V)
B:5<4
(F)
C : “3 est un nombre impair” (V)
Première application :
A B : (210 = 1024) (5 < 4)
(210 = 1024) ET (5 < 4)
Est une proposition fausse car B est fausse.
A C : (210 = 1024) (3 est un nombre impair)
(210 = 1024) ET (3 est un nombre impair)
Est une proposition vraie car A est vraie et C est vraie.

27. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Reprenons les propositions des exemples précédents
A : 210 = 1024
(V)
B:5<4
(F)
C : “3 est un nombre impair” (V)
Seconde application :
A B : (210 = 1024) (5 < 4)
(210 = 1024) OU (5 < 4)
Est une proposition vraie car A est vraie.
A C : (210 = 1024) (3 est un nombre impair)
(210 = 1024) OU (3 est un nombre impair)
Est une proposition vraie. (A et C sont vraies).

28. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Implication : Connecteur logique (Si…..alors…)
Implication :
A tout couple de propositions (P,Q),
l’implication associe une nouvelle
proposition :
P Q
“Si P, alors Q”, notée
qui n'est fausse que dans le seul cas où
la proposition P est vraie
et la proposition Q fausse.

29. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Implication
La valeur de vérité du connecteur “implication” est donnée
dans la table ci-contre :
P
Q
P Q
P
Q
P Q
V
V
V
1
1
1
V
F
F
1
0
0
P Q
F
V
V
0
1
1
F
F
V
0
0
1

30. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Reprenons les exemples précédents
A B : (210 = 1024) (5 < 4)
est une proposition fausse car A est vraie et B est fausse.
A C : (210 = 1024) (3 est un nombre impair)
Est une proposition vraie car A est vraie et C est vraie.
Il ne faut cependant pas chercher un lien de cause à
effet entre 210 = 1024, et “3 est un nombre impair” .
Ici, on a introduit l’implication, c'est-à-dire le connecteur
indépendamment du contenu des propositions situées
de part et d’autres du symbole .

31.

V V V Si je travaille, alors je réussis. Je travaille, et je
réussis. (Vrai)
V F F Si je travaille, alors je réussis. Je travaille, mais je ne
réussis pas. (Faux)
F V V Si je travaille, alors je réussis. Je ne travaille pas,
mais je réussis quand même. (Vrai)
F F V Si je travaille, alors je réussis. Je ne travaille pas, et
je ne réussis pas. (Vrai)

32. Logique propositionnelle : exemples

• Les propositions servent à représenter des
affirmations qui peuvent être vraies ou fausses :
• A : « Il y a une éclipse de Soleil »
• B : « On a trouvé un vaccin contre le SARSCoV-2 »
• C : « Les étudiants ont eu leur diplôme »
• Par soucis de concision, on utilise une lettre
pour représenter une proposition. On essaie de
détailler le plus possible les propositions :
• Ne pas écrire : D : « Les étudiants ont eu leur
diplôme et sont contents »
• Écrire plutôt : E : « Les étudiants ont eu leur
diplôme » et F : « Les étudiants sont contents »

33. Questions et Exercices

Exercices 1 à 6

34. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Equivalence : Connecteur logique
qui se traduit par
“si et seulement si” ou “est équivalent à”
Equivalence :
Soient P et Q deux propositions.
La proposition “P est équivalente à Q”,
notée P Q
(lue “P si et seulement si Q”)
n’est vraie que si l’on a simultanément
P Q et Q P

35. Connecteurs Binaires

Les Propositions
Connecteurs Binaires
Equivalence :
La valeur de vérité du connecteur “équivalence” est donnée
dans la table ci-contre :
P
Q
P Q
Q P
P Q et
Q P
V
V
V
V
V
V
V
F
F
V
F
F
F
V
V
F
F
F
F
F
V
V
V
V
P Q

36. Propriétés

Les Propositions
Propriétés
Les premières propriétés de ces connecteurs sont :
La Commutativité de “et” et “ou”
La Double distributivité
La Complémentarité
L’implication et l’équivalence
La négation de propositions
“connectées”

37. Propriétés

Les Propositions
Propriétés
La commutativité
Pour toutes propositions P et Q
P Q Q P
P Q Q P

38. Propriétés

Les Propositions
Propriétés
La double distributivité
Pour toutes propositions P,Q et R
P (Q R) (P Q) (P R)
P (Q R) (P Q) (P R)
(Mêmes tables de vérité)

39. Propriétés

Les Propositions
Propriétés
La complémentarité :
Pour toute proposition P
P ( P) est toujours vraie
P ( P) est une proposition toujours fausse

40. Propriétés

Les Propositions
Propriétés
L’implication et l’équivalence “imbriquées” :
Pour toutes propositions P et Q
P Q P Q
P Q P Q Q P
P Q Q P

41. Propriétés

Les Propositions
Propriétés
La négation d’une proposition avec connecteurs :
Pour toutes propositions P et Q
( P) P
P Q P Q
P Q P Q

42. Propriétés

Les Propositions
Propriétés
La négation d’une proposition avec connecteurs :
Autrement dit, en français :
non(nonP) est la proposition P
non(P et Q) est la proposition
((nonP)ou(nonQ))
non (P ou Q) est la proposition
((nonP)et(nonQ))

43.

Les Propositions
Définitions
• Une tautologie est une formule qui est
satisfaite par toute interprétation.
• Une contradiction est une formule qui n’est
satisfaite par aucune interprétation.
• Une formule est satisfiable s’il existe une
interprétation qui la satisfait.
• Une formule φ est conséquence logique
d’une formule ψ si toutes les interprétations qui
satisfont ψ satisfont aussi φ.
• Une formule φ est logiquement équivalente à
une formule ψ ssi φ est conséquence logique
de ψ et ψ est conséquence logique de φ.

44.

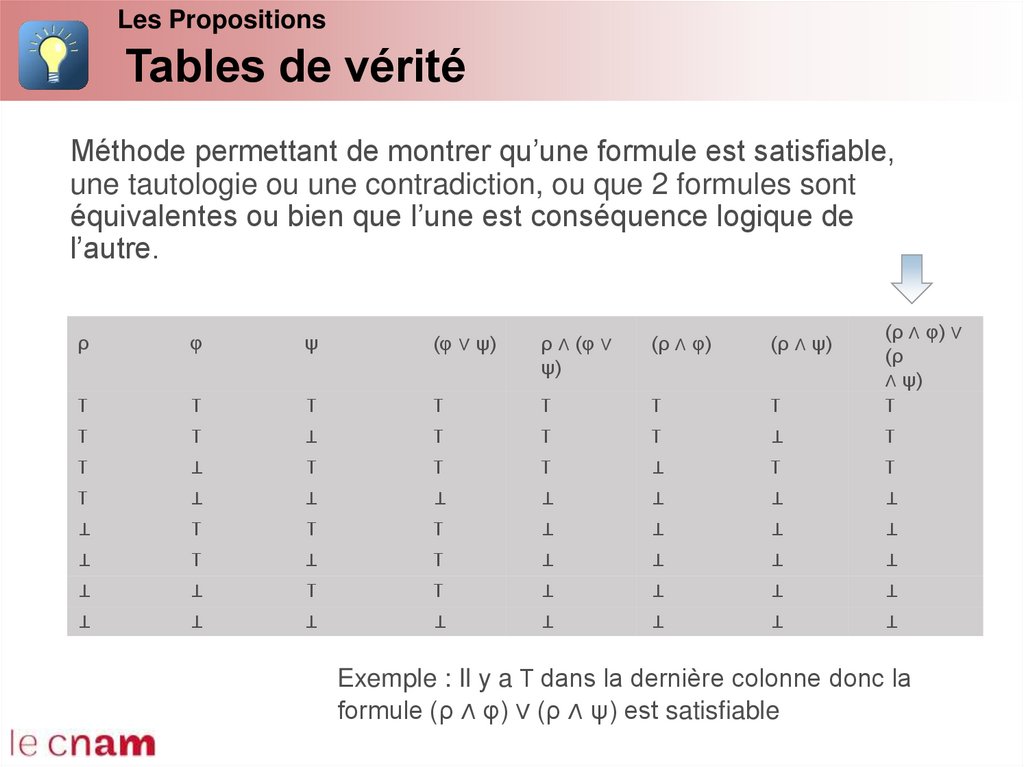
Les Propositions
Tables de vérité
Méthode permettant de montrer qu’une formule est satisfiable,
une tautologie ou une contradiction, ou que 2 formules sont
équivalentes ou bien que l’une est conséquence logique de
l’autre.
ρ
φ
ψ
(φ ∨ ψ)
ρ ∧ (φ ∨
ψ)
(ρ ∧ φ)
(ρ ∧ ψ)