Тема 10. Граф. Весовая матрица графа. Длина пути м

1.

Граф. Весовая матрица графа.
Длина пути между вершинами графа.
Вычисление количества путей в направленном
ациклическом графе.

2.

Понятие графа.
Ориентированный и неориентированный граф
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
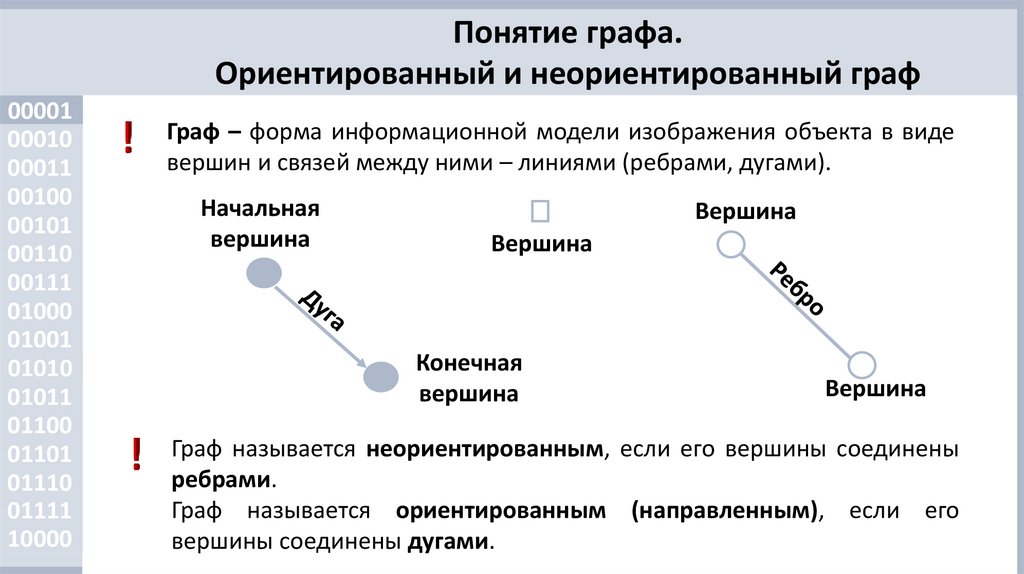
Граф – форма информационной модели изображения объекта в виде
вершин и связей между ними – линиями (ребрами, дугами).
Начальная
вершина
Вершина
Вершина
Конечная
вершина
Вершина
Граф называется неориентированным, если его вершины соединены
ребрами.
Граф называется ориентированным (направленным), если его
вершины соединены дугами.

3.

Путь. Связный граф
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
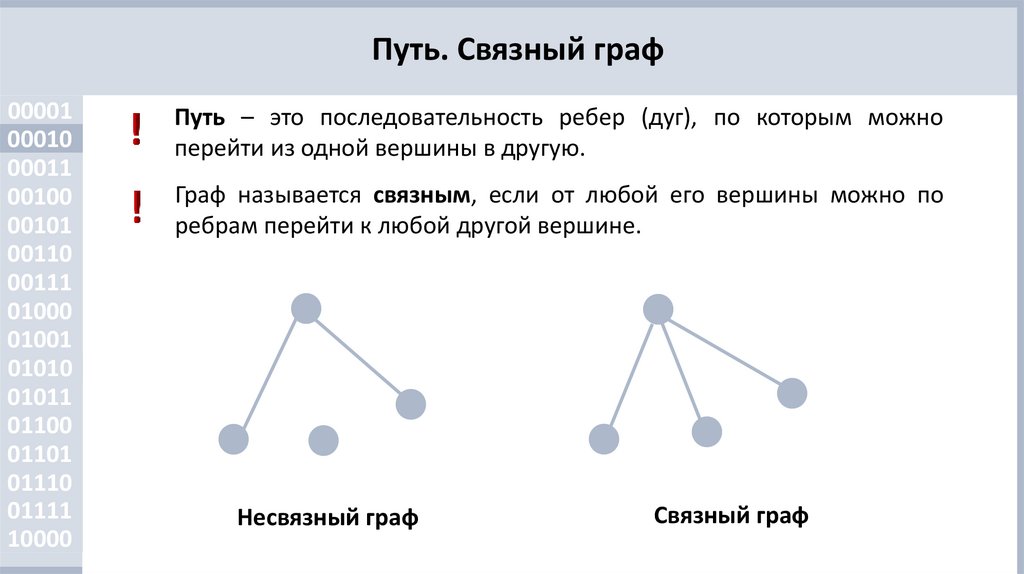
Путь – это последовательность ребер (дуг), по которым можно
перейти из одной вершины в другую.
Граф называется связным, если от любой его вершины можно по
ребрам перейти к любой другой вершине.
Несвязный граф
Связный граф

4.

Цепь. Цикл. Сеть.
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
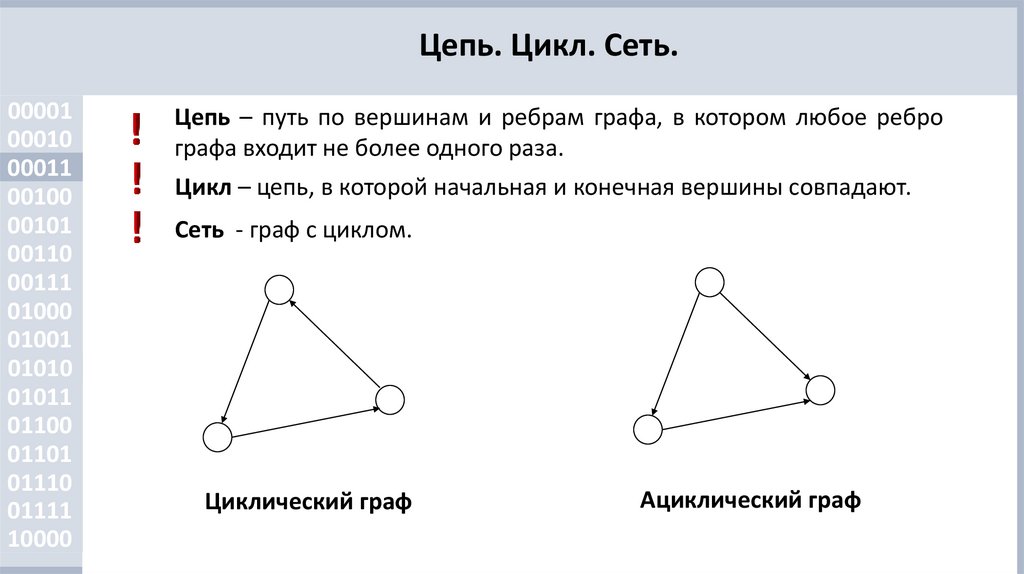
Цепь – путь по вершинам и ребрам графа, в котором любое ребро
графа входит не более одного раза.
Цикл – цепь, в которой начальная и конечная вершины совпадают.
Сеть - граф с циклом.
Циклический граф
Ациклический граф

5.

Четные и нечетные вершины графа
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
Четная вершина – вершина, из которой выходит четное число ребер
(имеет четную степень).
Нечетная вершина - вершина, из которой выходит нечетное число
ребер (имеет нечетную степень).
Если у графа все вершины четные, то его можно обойти, не отрывая
карандаш от бумаги; начинать можно в любой вершине.
Если у графа две вершины нечетные, то его можно обойти, не
отрывая карандаш от бумаги; начинать надо в одной из нечетных
вершин, а закончить – в другой.
Если у графа более двух вершин нечетные, то такой граф нельзя
обойти, не отрывая карандаш от бумаги.

6.

Взвешенный граф. Вес ребра
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
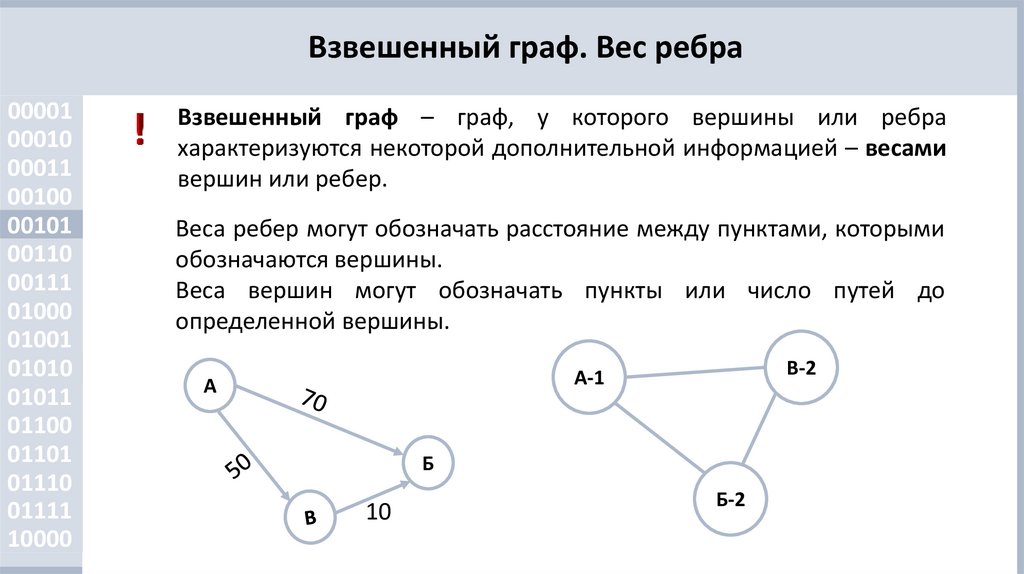
Взвешенный граф – граф, у которого вершины или ребра
характеризуются некоторой дополнительной информацией – весами
вершин или ребер.
Веса ребер могут обозначать расстояние между пунктами, которыми
обозначаются вершины.
Веса вершин могут обозначать пункты или число путей до
определенной вершины.
В-2
А-1
А
Б
10
Б-2

7.

Весовая матрица графа
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
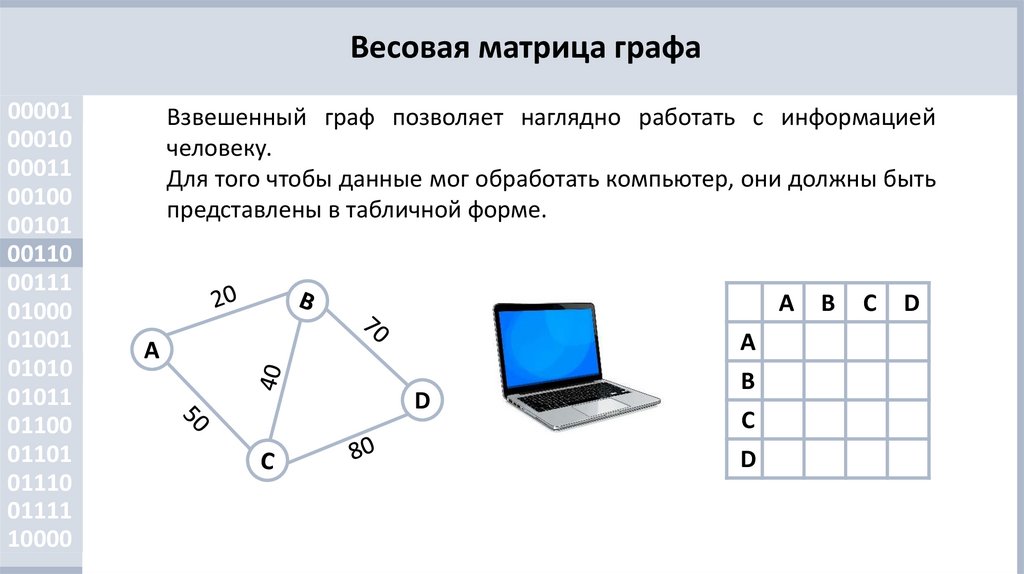
Взвешенный граф позволяет наглядно работать с информацией
человеку.
Для того чтобы данные мог обработать компьютер, они должны быть
представлены в табличной форме.
A
A
А
D
B
C
D
B
C
D

8.

Создание весовой матрицы графа
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
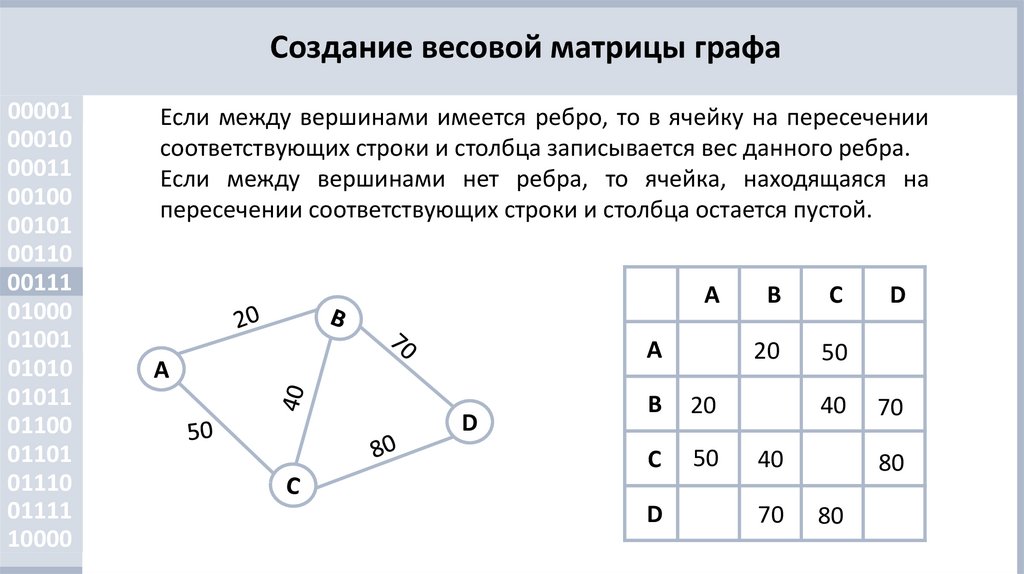
Если между вершинами имеется ребро, то в ячейку на пересечении
соответствующих строки и столбца записывается вес данного ребра.
Если между вершинами нет ребра, то ячейка, находящаяся на
пересечении соответствующих строки и столбца остается пустой.
A
A
А
D
B
20
C
50
D
B
C
20
50
40
40
70
D
70
80
80

9.

Поиск оптимального пути в графе
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
Для решения некоторых задач бывает удобно по имеющейся весовой
матрице строить граф. При этом одной и той же таблице могут
соответствовать графы, внешне не похожие друг на друга.
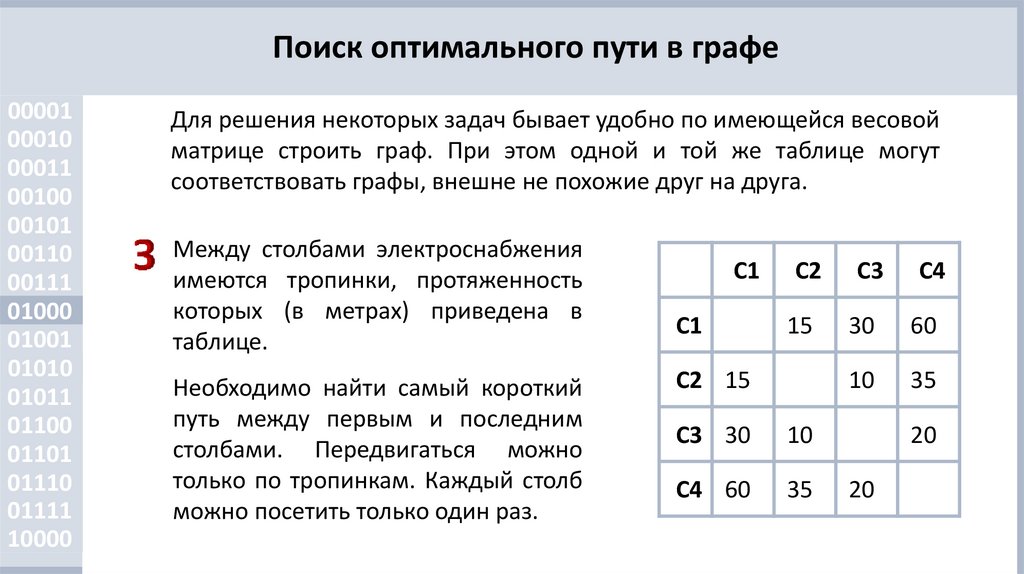
Между столбами электроснабжения
имеются тропинки, протяженность
которых (в метрах) приведена в
таблице.
Необходимо найти самый короткий
путь между первым и последним
столбами. Передвигаться можно
только по тропинкам. Каждый столб
можно посетить только один раз.
С1
С1
С2
С3
С4
15
30
60
10
35
С2 15
С3 30
10
С4 60
35
20
20

10.

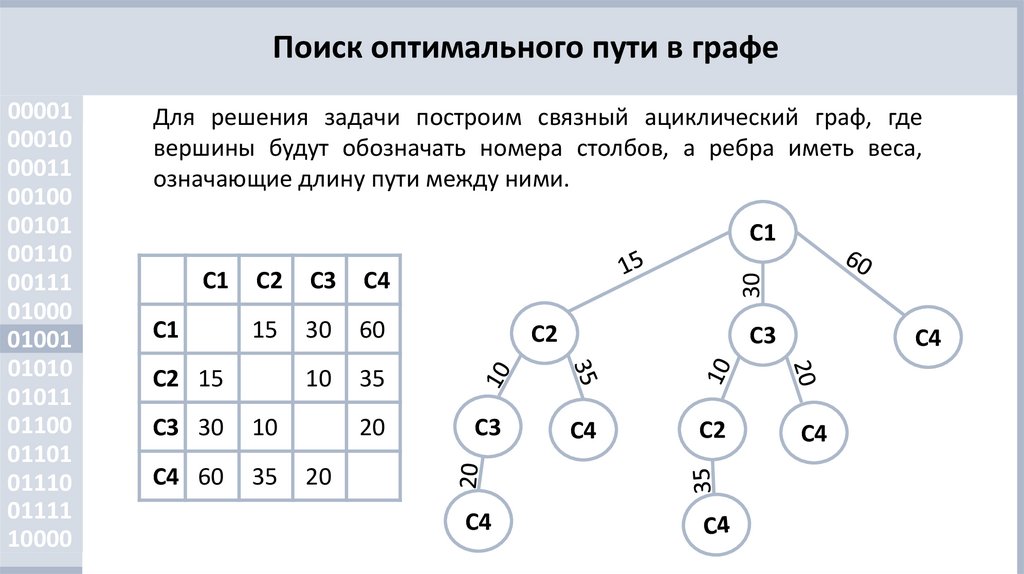
Поиск оптимального пути в графе
Для решения задачи построим связный ациклический граф, где
вершины будут обозначать номера столбов, а ребра иметь веса,
означающие длину пути между ними.
С1
С1
С1
С2
С3
С4
15
30
60
10
35
С2 15
С3 30
10
С4 60
35
20
30
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
С2
С3
20
С4
С3
С4
С2
С4
С4

11.

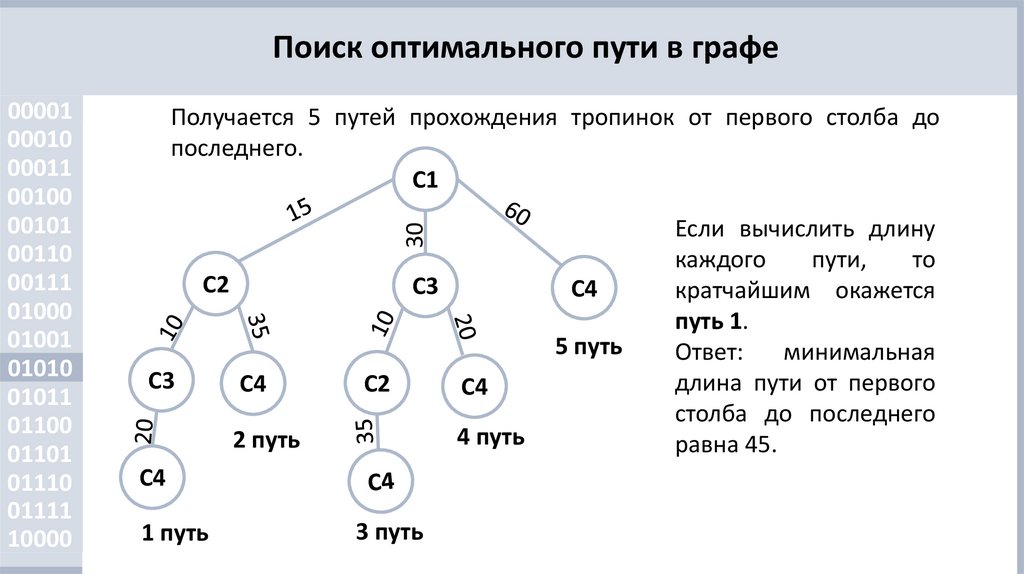
Поиск оптимального пути в графе
Получается 5 путей прохождения тропинок от первого столба до
последнего.
С1
30
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
С2
С3
С4
5 путь
С3
С4
С2
4 путь
2 путь
С4
1 путь
С4
3 путь
Если вычислить длину
каждого
пути,
то
кратчайшим окажется
путь 1.
Ответ:
минимальная
длина пути от первого
столба до последнего
равна 45.

12.

Источник и сток в ориентированном графе
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
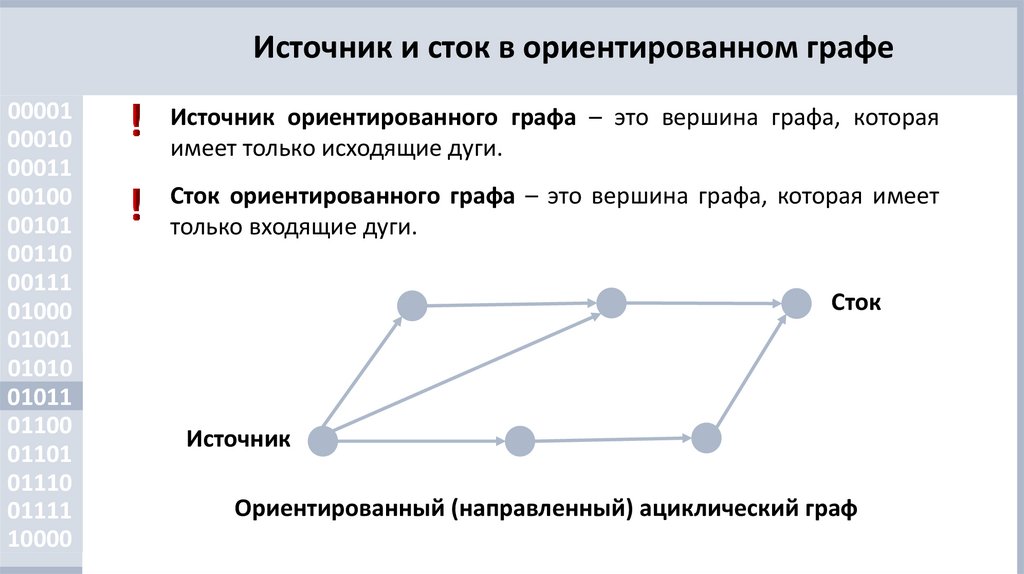
Источник ориентированного графа – это вершина графа, которая
имеет только исходящие дуги.
Сток ориентированного графа – это вершина графа, которая имеет
только входящие дуги.
Сток
Источник
Ориентированный (направленный) ациклический граф

13.

Вычисление количества путей в направленном
ациклическом графе
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
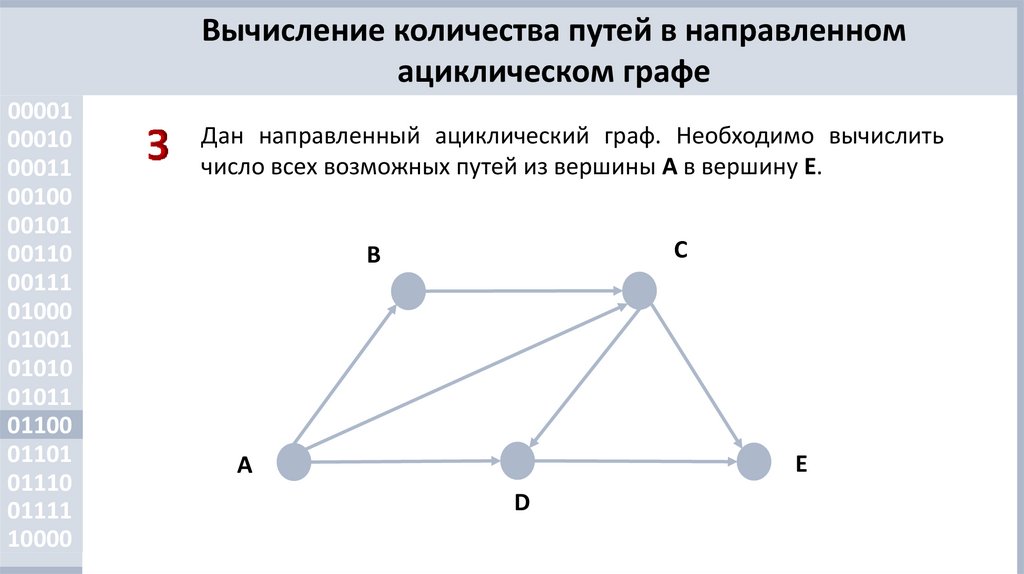
Дан направленный ациклический граф. Необходимо вычислить
число всех возможных путей из вершины А в вершину E.
C
B
E
A
D

14.

Вычисление количества путей в направленном
ациклическом графе
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
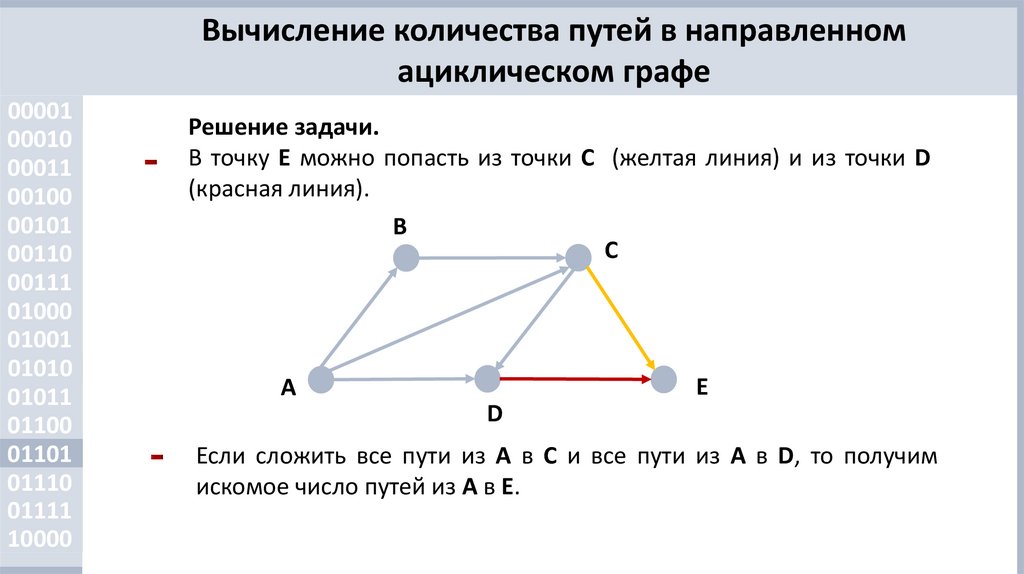
Решение задачи.
В точку E можно попасть из точки C (желтая линия) и из точки D
(красная линия).
B
C
E
A
D
Если сложить все пути из A в C и все пути из A в D, то получим
искомое число путей из A в E.

15.

Вычисление количества путей в направленном
ациклическом графе
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
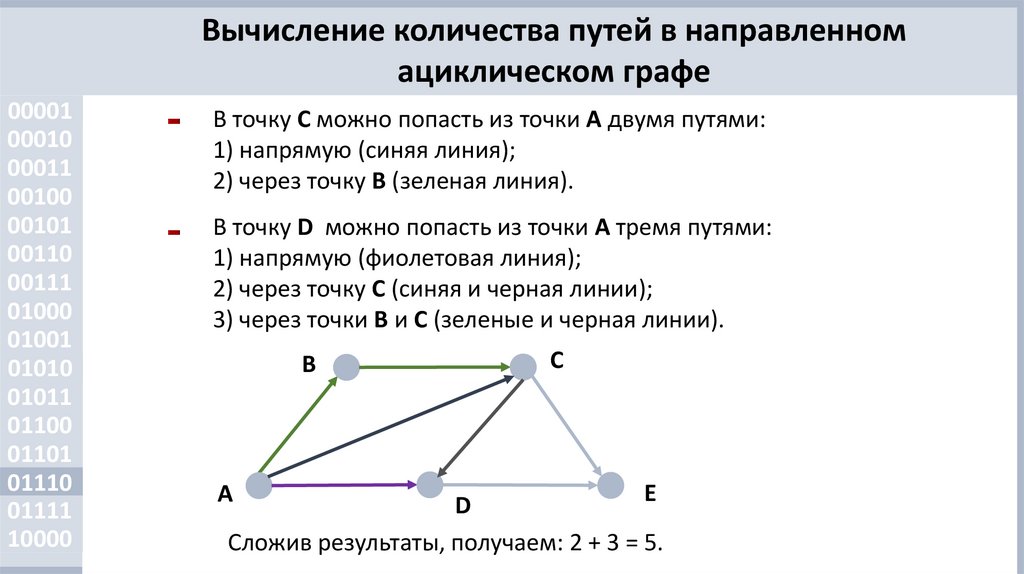
В точку С можно попасть из точки А двумя путями:
1) напрямую (синяя линия);
2) через точку B (зеленая линия).
В точку D можно попасть из точки A тремя путями:
1) напрямую (фиолетовая линия);
2) через точку C (синяя и черная линии);
3) через точки В и С (зеленые и черная линии).
B
C
E
D
Сложив результаты, получаем: 2 + 3 = 5.
A

16.

Наглядное представление решения задачи
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
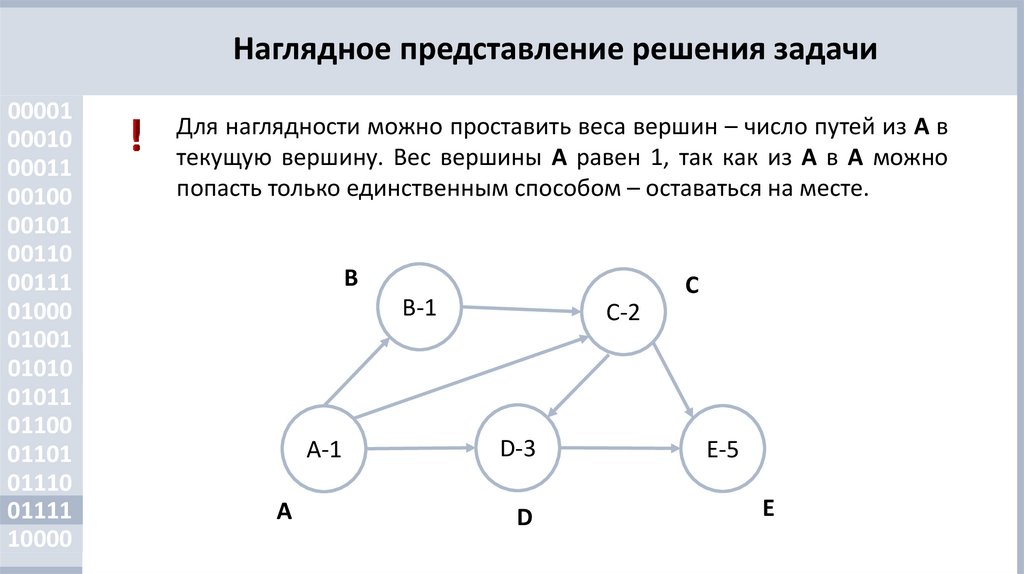
Для наглядности можно проставить веса вершин – число путей из A в
текущую вершину. Вес вершины A равен 1, так как из A в A можно
попасть только единственным способом – оставаться на месте.
B
C
B-1
A-1
A
C-2
D-3
D
E-5
E

17.

Применение графов в общественной жизни
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
Графы как информационные модели широко применяются не только
в науках для отражения связей между явлениями и объектами
окружающего мира, но и в различных сферах жизни общества.
Например, при проектировании городских кварталов дома,
сооружения обозначаются вершинами, а дороги, линии
электропередач, инженерные сети – ребрами графа. По таким
моделям можно планировать оптимальные транспортные маршруты,
расположение автобусных остановок, торговых точек, социально
значимых организаций (детские сады, школы и т.п.).
Благодарю за внимание!