Графы 7 класс

1.

Медиана
Размах
Среднее
арифметическое
Описательная
статистика
Примеры
Диаграммы
Представление
данных
Случайная
изменчивость
Таблицы
Частоты
значений
Случайные
события
Графы
Вероятности
и частоты
Монета и
игральная
кость
Гистограммы
Графы
Пути
в графе
Степень
вершин

2. ГРАФЫ.

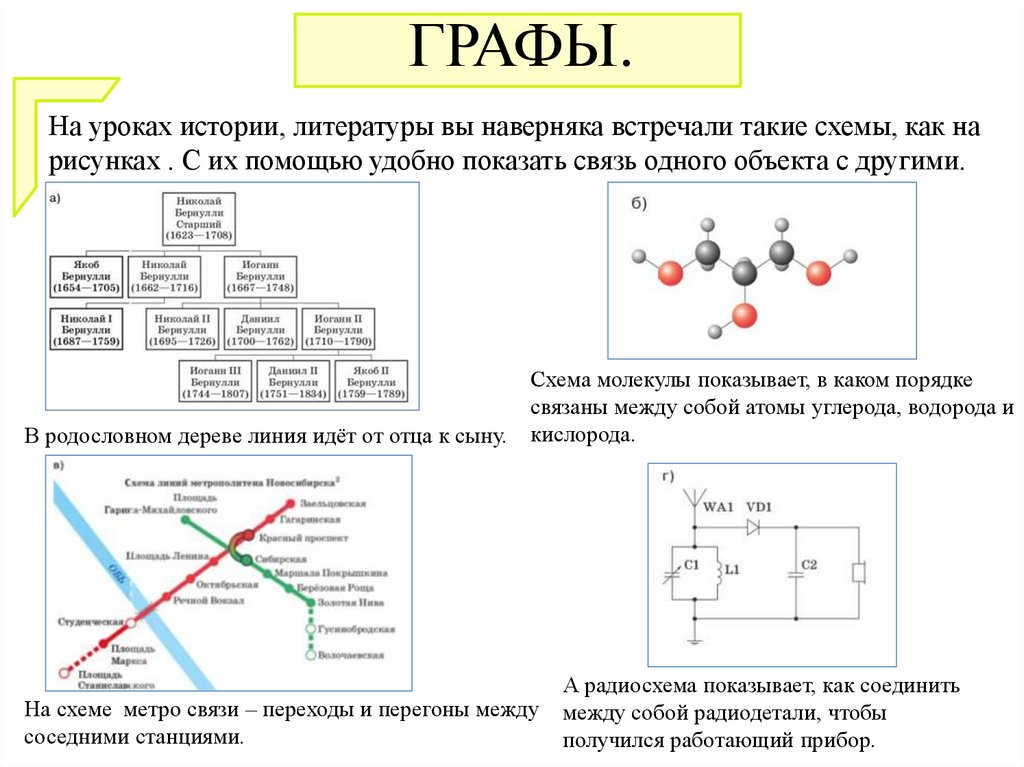
На уроках истории, литературы вы наверняка встречали такие схемы, как на
рисунках . С их помощью удобно показать связь одного объекта с другими.
В родословном дереве линия идёт от отца к сыну.
Схема молекулы показывает, в каком порядке
связаны между собой атомы углерода, водорода и
кислорода.
На схеме метро связи – переходы и перегоны между
соседними станциями.
А радиосхема показывает, как соединить
между собой радиодетали, чтобы
получился работающий прибор.

3.

ГРАФЫ.
У всех этих схем есть общее – они показывают связи между отдельными
элементами.
Для изображения и изучения связей между различными объектами –
предметами или понятиями – в математике применяется граф.
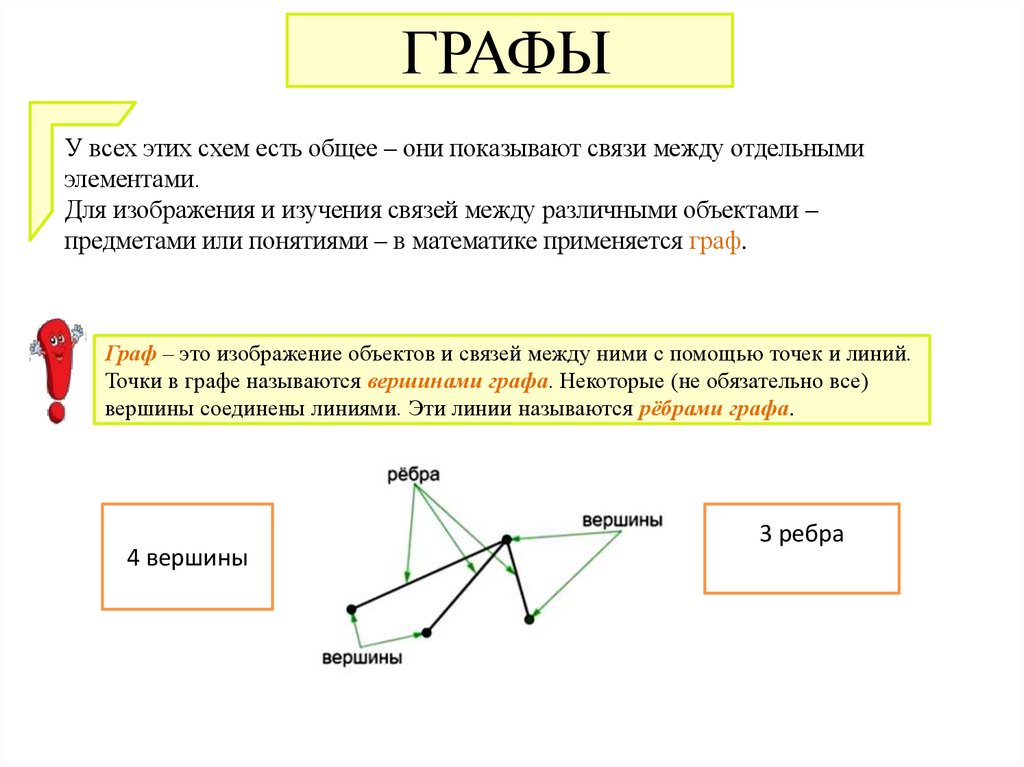
Граф – это изображение объектов и связей между ними с помощью точек и линий.
Точки в графе называются вершинами графа. Некоторые (не обязательно все)
вершины соединены линиями. Эти линии называются рёбрами графа.
4 вершины
3 ребра

4.

ВЕРШИНЫ. РЕБРА.
• Рёбра можно изобразить дугами или отрезками.
• Каждое ребро соединяют две вершины.
• Вершину, из которой не выходит ни одно ребро, называют изолированной.
• Каждая вершина в графе должна быть явно отмечена.
• На рисунке рёбра могут пересекаться, но точка пересечения не является
вершиной графа. Это две нитки: одна пересекает другую, но узелка в точке
пересечения нет.

5.

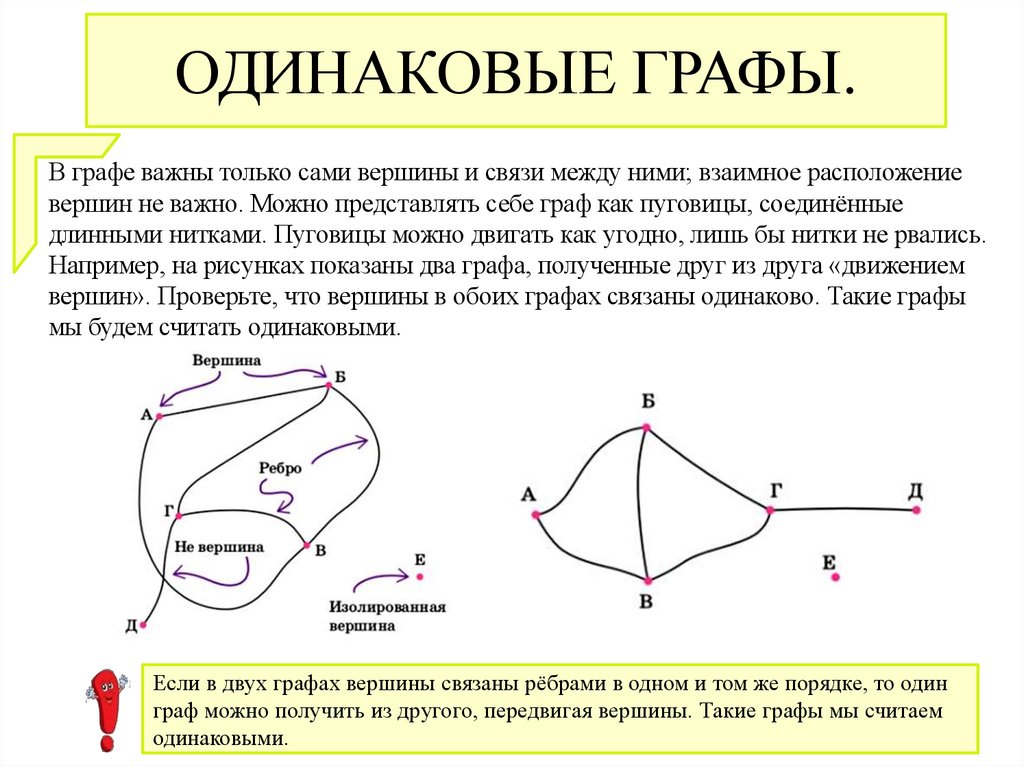
ОДИНАКОВЫЕ ГРАФЫ.
В графе важны только сами вершины и связи между ними; взаимное расположение
вершин не важно. Можно представлять себе граф как пуговицы, соединённые
длинными нитками. Пуговицы можно двигать как угодно, лишь бы нитки не рвались.
Например, на рисунках показаны два графа, полученные друг из друга «движением
вершин». Проверьте, что вершины в обоих графах связаны одинаково. Такие графы
мы будем считать одинаковыми.
Если в двух графах вершины связаны рёбрами в одном и том же порядке, то один
граф можно получить из другого, передвигая вершины. Такие графы мы считаем
одинаковыми.

6.

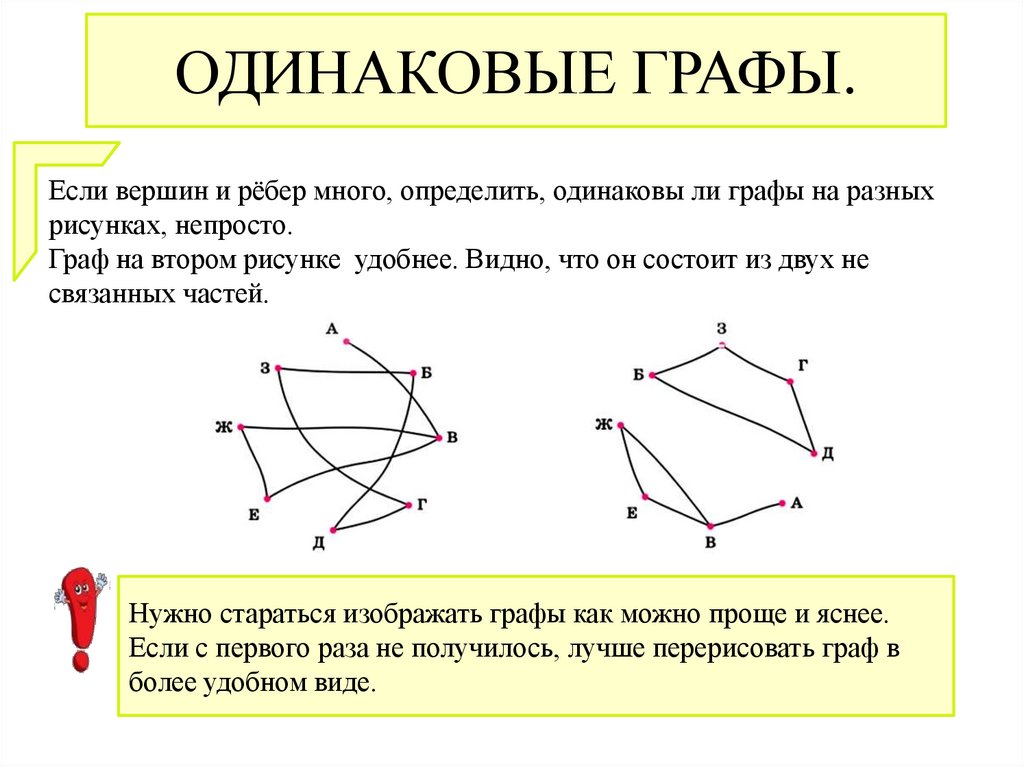
ОДИНАКОВЫЕ ГРАФЫ.
Если вершин и рёбер много, определить, одинаковы ли графы на разных
рисунках, непросто.
Граф на втором рисунке удобнее. Видно, что он состоит из двух не
связанных частей.
Нужно стараться изображать графы как можно проще и яснее.
Если с первого раза не получилось, лучше перерисовать граф в
более удобном виде.

7. ОТВЕТЬТЕ НА ВОПРОСЫ:

1. Вспомните, где вам встречались графы.
2. Как называются линии, связывающие вершины графа?
3. Как можно проверить, одинаковы два графа или нет?

8. Определи по рисунку, сколько вершин и ребер имеет граф.

.
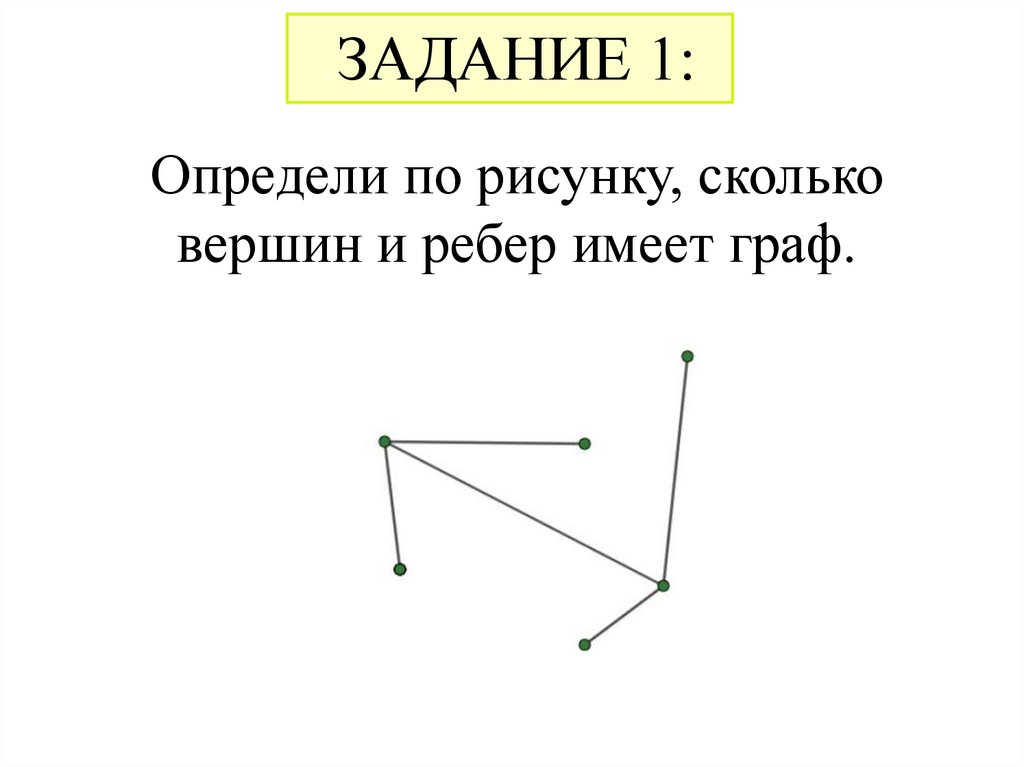
ЗАДАНИЕ 1:
Определи по рисунку, сколько
вершин и ребер имеет граф.

9.

.
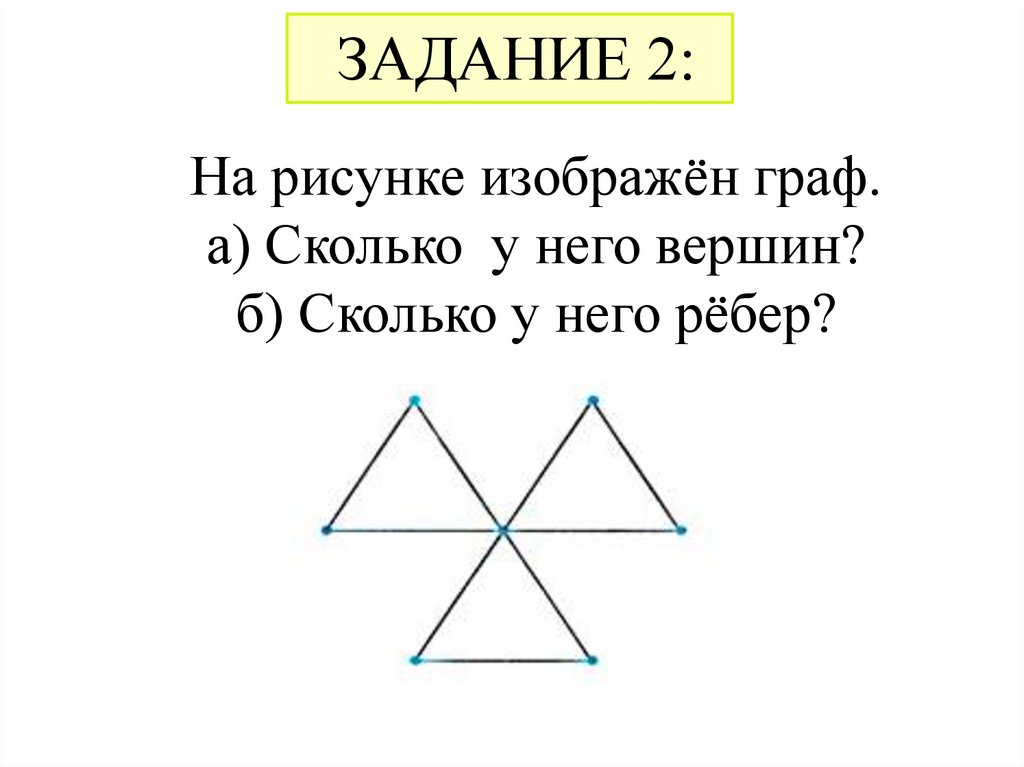
ЗАДАНИЕ 2:
На рисунке изображён граф.
а) Сколько у него вершин?
б) Сколько у него рёбер?

10.

.
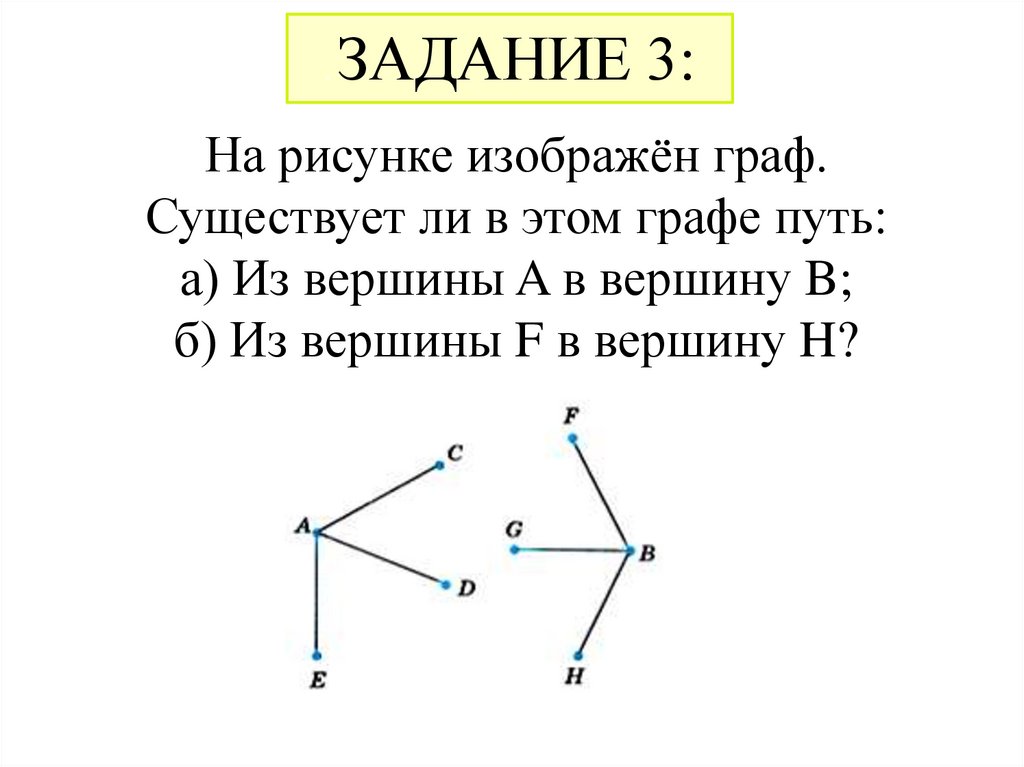
ЗАДАНИЕ 3:
На рисунке изображён граф.
Существует ли в этом графе путь:
а) Из вершины A в вершину B;
б) Из вершины F в вершину H?

11.

.
ЗАДАНИЕ 4:
С помощью построения графа
ответь на вопрос задачи.
Ребята, которые дружат, могут помочь друг
другу с подготовкой к контрольной работе.
Известно, что Михаил дружит с Димой и
Никитой, Варвара – с Димой и Валей,
Алексей – с Жорой и Олегом, Ксения – с
Олегом. Может ли Михаил помочь Олегу
подготовиться к контрольной работе?

12.

.
ЗАДАНИЕ 5:
В таблице показаны внутрироссийские рейсы авиакомпании «Аврора»:
а) Постройте граф, в котором вершины соответствуют городам, и две вершины связаны
ребром, только если между соответствующими городами имеется авиарейс
авиакомпании «Аврора».
б) Есть ли в построенном графе цикл? Если есть, выделите рёбра цикла жирной линией.
Путь от одной вершины до другой – цепочка,
соединяющая эти вершины.
Кратчайший путь – путь, в котором
наименьшее возможное число рёбер.
Длина пути – количество рёбер в этом пути.
Связный граф – граф, в котором существует
путь из любой вершины в любую другую
вершину.

13.

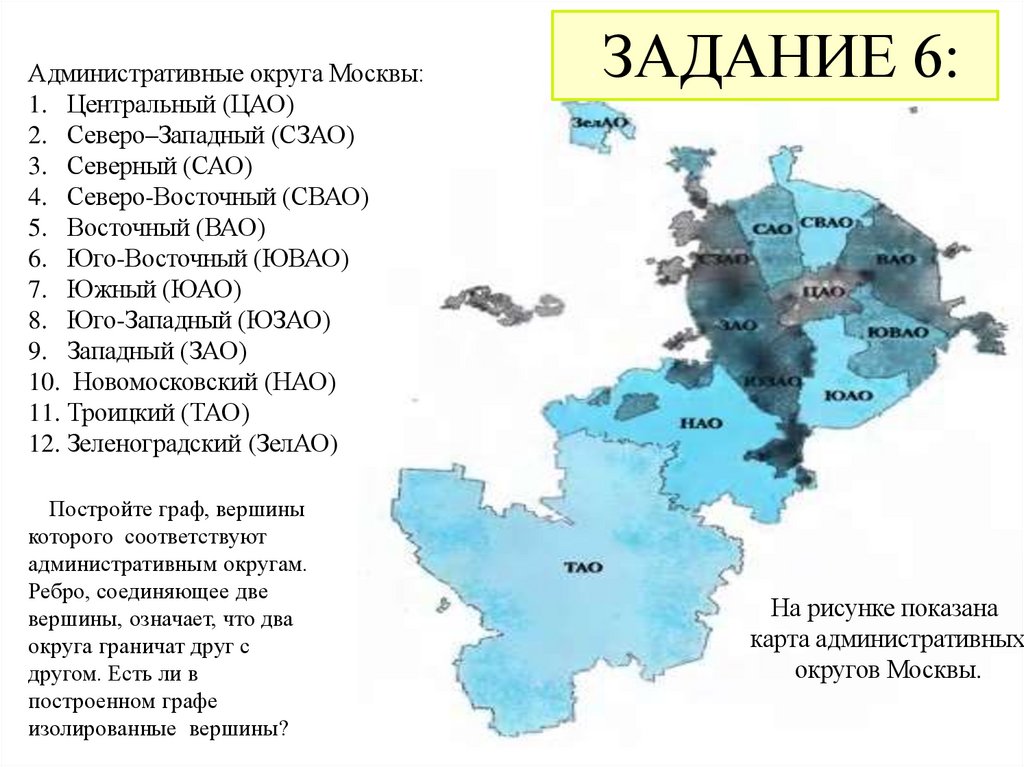
Административные округа Москвы:
1. Центральный (ЦАО)
2. Северо–Западный (СЗАО)
3. Северный (САО)
4. Северо-Восточный (СВАО)
5. Восточный (ВАО)
6. Юго-Восточный (ЮВАО)
7. Южный (ЮАО)
8. Юго-Западный (ЮЗАО)
9. Западный (ЗАО)
10. Новомосковский (НАО)
11. Троицкий (ТАО)
12. Зеленоградский (ЗелАО)
Постройте граф, вершины
которого соответствуют
административным округам.
Ребро, соединяющее две
вершины, означает, что два
округа граничат друг с
другом. Есть ли в
построенном графе
изолированные вершины?
.
ЗАДАНИЕ 6:
На рисунке показана
карта административных
округов Москвы.

14.

.
ЗАДАНИЕ 7:
Даны числовые множества:
A = {1, 7}, B = {2, 4, 6}, C = {1, 6, 7},
D = {0, 2, 8}, E = {0, 1, 6, 7}, F = {5, 6, 7, 8},
G = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, H = {0, 2, 4, 6, 8}.
Постройте граф, вершины которого соответствуют
множествам.
Две вершины будут соединены ребром при условии, что:
а) одно из соответствующих множеств является
подмножеством другого;
б) соответствующие множества имеют непустое пересечение (у
них есть хотя бы один общий элемент).

15. Ответы:

1
Вершин 6, ребер 5.
2
Вершин 7, ребер 9.
3
А)нет; б) да.
4
Нет
5
Цикл В-Ю-Х

16.

Медиана
Размах
Среднее
арифметическое
Описательная
статистика
Примеры
Диаграммы
Представление
данных
Случайная
изменчивость
Таблицы
Частоты
значений
Случайные
события
Графы
Вероятности
и частоты
Монета и
игральная
кость
Гистограммы
Графы
Пути
в графе
Степень
вершин