Похожие презентации:
Основные определения метрологии. Меры и эталоны
1. Санкт-Петербургский горный университет
Метрология и стандартизацияЛекции 1-2
«Основные определения метрологии.
Меры и эталоны»
Ассистент Епифанцев К.В.
2.
МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ, СЕРТИФИКАЦИЯ(технические специальности)
Сергеев А.Г., Крохин В.В. Метрология. – М.: Логос, 2001
Сергеев А.Г., Латышев М.В. Сертификация. – М.: Логос,
2000 (Общие принципы)
Бурдун Г.Д., Марков Б.Н. Основы метрологии. – М.: Изд-во
стандартов, 1975. (Кроме системы СИ)
Метрология, стандартизация, сертификация и
электроизмерительная техника/Под ред. К.К.Кима. – СПб.:
Питер, 2006. (Все разделы)
Тартаковский Д.Ф., Ястребов А.С. Метрология,
стандартизация и технические средства измерений. – М.:
Высшая школа, 2003. (Введение в метрологию).
Кузнецов В.А., Ялунина Г.А. Основы метрологии: Учебное
пособие – М.: Изд-во стандартов,1995.
3.
Тартаковский Д.Ф. Измерительная информация всистеме доказательств – СПб.: Издательство
“Юридический центр Пресс”, 2003. (Метрология).
Яблонский О.П., Иванова В.А. Основы стандартизации,
метрологии, сертификации. – Ростов-на-дону: Феникс,
2004. (Без метрологии)
Басаков М.И. Основы стандартизации, метрологии,
сертификации (на основе Федерального закона “О
техническом регулировании”). Конспект лекций. –
Ростов н/д: Феникс, 2005. (Федеральный закон)
Метрология и радиоизмерения./ Под ред. проф.
В.И.Нефедова. – М.: Высш. шк., 2003. (Основы
метрологии)
Панфилов В.А. Электрические измерения. – М.:
Академия, 2006. (метрология)
4.
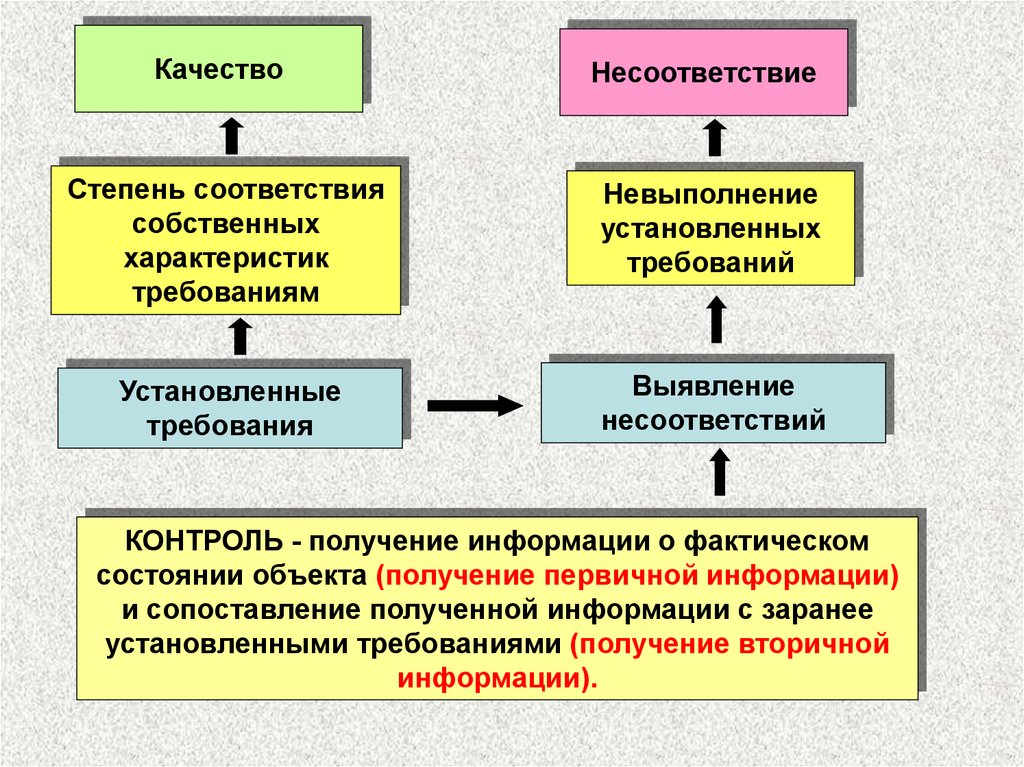
Успешность работы любой организации во многомопределяется качеством продукции (работ, услуг).
Методы обеспечения качества базируются на
триаде – метрология, стандартизация, сертификация
(подтверждение соответствия).
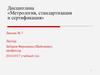
О качестве объекта судят по тому, насколько он удовлетворяет
установленным требованиям. Невыполнение установленных
требований является несоответствием.
Для выявления несоответствий сопоставляют информацию о
фактическом состоянии объекта (первичная информация) и
информацию о заранее установленных требованиях – получают
вторичную информацию
Достоверность вторичной информации зависит от качества
первичной количественной информации, получаемой при
помощи измерений, т.е. от эффективности метрологической
службы.
5.
КачествоНесоответствие
Степень соответствия
собственных
характеристик
требованиям
Невыполнение
установленных
требований
Установленные
требования
Выявление
несоответствий
КОНТРОЛЬ - получение информации о фактическом
состоянии объекта (получение первичной информации)
и сопоставление полученной информации с заранее
установленными требованиями (получение вторичной
информации).
6.
Получение количественной(измерительной) информации,
необходимой для установления
требований
Метрология
КАЧЕСТВО
получение информации о
фактическом состоянии объекта
(получение первичной
информации)
Стандартизация
Установленные
требования
Сертификация
(подтверждение соответствия)
сопоставление полученной информации с заранее
установленными требованиями (получение вторичной
информации)
7.
метрологиястандарт
метрон - мера,
измерение;
логос - наука
ста-стоять,
устанавливать;
нд-соединительный
суффикс;
Арт-искусство
наука об
измерениях
Искусство
устанавливать
Стандартизация направлена на оптимизацию и упорядоченность
деятельности на научной основе
сертификация
серти-верно;
фацио-делать
сделано верно
8. МЕТРОЛОГИЯ
МЕТРОЛОГИЯ – Наука об измерениях, методах исредствах обеспечения их единства и способах
достижения требуемой точности.
(РМГ 29-99. Метрология. Основные термины и
определения).
Измерение;
Обеспечение единства;
Точность.
9.
Из опыта известно, что ни одно измерение, как бы тщательнооно ни проводилось, не может дать абсолютно точный
результат, вследствие чего часто говорят о наличии ошибок,
погрешностей,
неопределенности
при
проведении
измерительного эксперимента
ПРИМЕР 1. Имеются две электрические цепи. В первой
протекает электрический ток I1, а во второй – I2. Показания
первого амперметра составило 1А, а второго 1,02А. Значит ли
это, что сила тока в первой цепи меньше, чем во второй?
А1
I1
А2
I2
10.
Из технической документации – в первом случае значение силыэлектрического тока при показании 1 А находится в пределах от 0,98 А до
1,02 А, а во втором при показании 1,02 А – в пределах от 0,97 А до 1,07 А.
В отличие от показаний приборов, истинные значения силы тока
находятся в неизвестной точке внутри интервалов, поэтому сила тока во
второй цепи может быть меньше.
1,02
0,98
0,95
1
1,05
0,97
I1, А
0,95
1,02
1
1,07
1,05
I2, А
Необходимо ответить на вопрос. Как получить информацию,
необходимую для формирования интервала до того, как она
будет занесена в ТД на измерительный прибор?
11.
ПРИМЕР 2. (Дж. Тейлор)Плотнику для того, чтобы установить дверь,
необходимо измерить высоту дверного
проема.
Проведя измерения “на глаз”, он может
определить, что высота проема находится в
пределах от 205 см до 215 см.
Применяя рулетку, он может
получить результат – от 211,2 см до
211,3 см. Применяя более точную
рулетку, улучшив условия
измерений, можно сократить
интервал до долей миллиметра.
12.
Лазерный интерферометр,фото с сайта NIST
Американские физики научились ошибаться на
стомиллиардную долю метра
Используя лазерный интерферометр можно сократить интервал
до долей микрометра, но определить высоту проема
ТОЧНО ПО- ПРЕЖНЕМУ ОКАЖЕТСЯ НЕВОЗМОЖНО.
Выясниться, что высота проема меняется в различных точках, высота
зависит от температуры, слоя пыли, само понятие плоскость исчезает.
Это значит, что такой величины, как высота дверного проема нет.
Это проблема порогового несоответствия – модель
объекта и измерительная задача должны находиться
в определенном соответствии.
13.
ПРИМЕР 3. (Дж. Тейлор)Определить, изготовлена корона из золота или более дешевого
сплава??
Дано: золото = 15,5 г/см3
сплав = 13,8 г/см3
Результаты двух экспертов:
Измеренная величина
эксперт А
эксперт В
15
13.9
13.5-16.5
13.7-14.1
Наилучшая оценка для
корона
Вероятный интервал
корона
Кроме того, что эксперт А не решил задачу, необходимо ответить на
вопросы:
ЧТО ТАКОЕ НАИЛУЧШАЯ ОЦЕНКА И ИМЕЕТ ЛИ ОНА СМЫСЛ?
ЧТО ТАКОЕ ВЕРОЯТНЫЙ ИНТЕРВАЛ И КАК ЕГО ПОЛУЧИТЬ?
14.
ПРИМЕР 4. (Тартаковский Д.Ф.)Результаты измерений используются при принятии решений. Пусть
измерениями в рамках судебно-медицинской экспертизы (СМЭ)
установлено, что содержание алкоголя в крови потерпевшего составляет
2,9 %о (%о – промилле – тысячная доля). В руководстве по СМЭ
приведены следующие данные
1,5-2,5 %о – опьянение средней тяжести
2,5-3,0 %о – сильное опьянение
3,0-5,0 %о – тяжелое отравление
Если оценка точности измерений не указана, то может быть сделан вывод о
состоянии сильного опьянения.
На самом деле возможны (часто таковы СИ) отклонения до 20% от
полученного результата. А это значит, что при полученном интервале
2,32 – 3,48 %о, возможны все три вывода.
Точность, с которой проводятся измерения, должна дать возможность
сделать правильный вывод. Первичная информация, полученная при
измерении с недостаточной точностью, не позволяет сделать
правильные выводы (к вопросу о получении вторичной информации).
15.
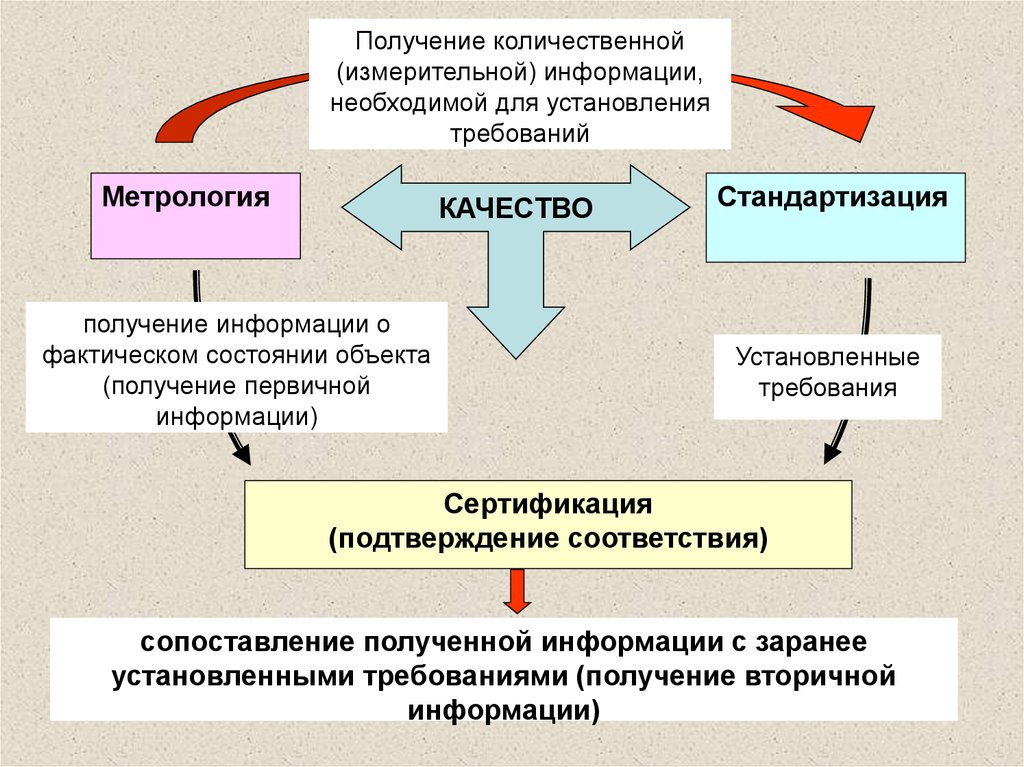
Объекты познанияидеальные
материальны
е
познавательная деятельность
количество
качество
эксперимент
теория
с применением
технических
средств
без применения
технических
средств
переработка, передача, хранение количественной
информации и ее использование
16.
Методами количественного анализа служат теория и эксперимент.В свою очередь, экспериментальные исследования могут
выполняться с применением и без применения технических
средств (инструментов).
Полученная тем или иным путем количественная информация о
свойствах и явлениях окружающего мира перерабатывается и
хранится в устройствах и системах информатики.
Наука о получении количественной информации опытным путем
называется МЕТРОЛОГИЕЙ.
Опытным путем, т.е. экспериментально, количественная
информация получается при помощи измерений. Таким образом,
МЕТРОЛОГИЯ – НАУКА О ПОЛУЧЕНИИ ИЗМЕРИТЕЛЬНОЙ
ИНФОРМАЦИИ.
Другие определения будут рассмотрены при дальнейшем изучении
дисциплины
17.
Возмущающиевоздействия
Цель (задача) измерения
Модель
возмущающих
воздействий
Априорная информация
Модель объекта
исследований
Объект
исследований
модель ФВ
Анализ
полученной
измерительной
информации,
решение
обратной
измерительной
задачи,
принятие
решений
Модель
Входного
воздействия
ФВ
Метод
измерений
Входное
воздействие
СИ
Модель СИ
Отклик
(выходной
сигнал)
Метрологические
характеристики СИ
Модель
отклика
Модель результатов
измерений
Результаты
измерений
алгоритм обработки результатов измерений
Обработка результатов измерений и оценка их точности
18.
ПОДРАЗДЕЛЕНИЕ ВЕЛИЧИНВеличины
Материального
мира
Физические
(применяемые в
физике, химии,
биологии, технических
науках и др.)
измеряемые
Идеальных
моделей реальности
Нефизические
(применяемые в
психологии,
социологии,
экономике и т.д.)
оцениваемые
Математические
(применяемые в
математике)
вычисляемые
В рамках данного курса рассматриваются только
физические величины
19. Физическая величина
• Общепринятыеили
установленные
законодательным путем характеристики (меры)
различных свойств, общих в качественном
отношении для многих физических объектов
(физических
систем,
их
состояний
и
происходящих
в
них
процессов),
но
в
количественном отношении
индивидуальных
для каждого из них, называются физическими
величинами.
20. Примеры ФВ
ОбъектСвойство
Характеристика
(мера)
Окружающее
пространство
Протяженность
Длина
События и явления
реального мира
Длительность
Время
Сохранение
состояния покоя
или равномерного
прямолинейного
движения
Инертность
Масса
21. Связь между физическими величинами
Между измеряемыми физическими величинамисуществуют связи и зависимости, выражаемые
математическими соотношениями и формулами.
Эти формулы и соотношения могут отражать:
законы природы
Пример - второй закон Ньютона
F = m·a
или могут быть определениями некоторых
физических величин.
Пример - Определение плотности по формуле = m/V
.
В подобных зависимостях одни величины выступают
как основные, а другие - как производные от них.
22. КАЧЕСТВЕННАЯ ХАРАКТЕРИСТИКА ИЗМЕРЯЕМЫХ ВЕЛИЧИН
Формализованным отражением качественного различияизмеряемых величин является их размерность.
Для
основных
величин
Для
производных
величин
dim l = L -размерность длины
dim m = M - размерность массы
dim t = T – размерность времени
и т.д.
Q = AB dim Q = dim A dim B;
Q = A / B dim Q = dim A / dim B;
Q = An dim Q = (dim A)n
23. ОСНОВНЫЕ ПРАВИЛА ПРИ ОПРЕДЕЛЕНИИ РАЗМЕРНОСТИ
1. dim Q = L M T .2. Размерности левой и правой частей уравнения
должны быть одинаковы.
3. Алгебраически суммироваться могут только
величины, имеющие одинаковые размерности.
4. Алгебра размерностей мультипликативна
Теория размерностей повсеместно применяется
для оперативной проверки правильности формул.
24. Пример применения теории размерностей
Пусть дана зависимостьVt = Vо + at2 / 2
Проведем проверку на основе алгебры
размерностей:
LT-1 = LT-1 + LT-2T2;
LT-1 = LT-1 + L ?????
Vt = Vо + at / 2
25.
КОЛИЧЕСТВЕННАЯ ХАРАКТЕРИСТИКАИЗМЕРЯЕМЫХ ВЕЛИЧИН
Любое свойство может проявляться в большей или
меньшей
степени,
т.е.
имеет
количественную
характеристику.
Количественной
характеристикой
любой физической величины, характеризующей то или
иное свойство, служит РАЗМЕР, хотя не принято
говорить “размер длины”, “размер массы” т.п. Принято
говорить просто “длина”, “масса”.
Размер является объективной количественной оценкой,
не зависящей от выбора единиц измерений. Например,
1000 мм, 10 см, 1 м – варианты представления одного и
того же размера.
26.
АКСИОМЫ МЕТРОЛОГИИПервая: измерение есть ни что иное как сравнение
одного размера с другим.
Вторая: результат измерения без округления
является случайным
Третья: без априорной информации измерение
невозможно.
Примечание:
Априорная информация –до проведения измерения.
Апостериорная информация – после измерения.
27. Первая аксиома относится к процедуре измерения и говорит о том, что сравнение размеров опытным путем является единственным способом получ
Первая аксиома относится к процедуре измерения иговорит о том, что сравнение размеров опытным путем
является единственным способом получения
измерительной информации
Получение информации о размере физической
величины является содержанием любого измерения.
Степень нагретости
1
2
3
4
5
6
7
8
9
10
11
Протяженность интервала
Опорные (реперные) точки
Шкала порядка
28.
0Q2
Q1
100
оС
32
180
0
оF
Q1 = Qo + q1[Q]
оF/оС
Q2 = Qo + q2[Q]
tC = (tF - 32)5/9.
= 100/180 = 5/9
Q1 - Q2 = (q1- q2)[Q]
Шкала интервалов
29.
К273,16 (273,15)
Значение физической величины – выражение размера
физической величины в
виде некоторого числа
принятых для нее единиц
Q = q[Q]
q – числовое значение
[Q] – размер, принятый за
единицу
Пример:
U = 120 B
([Q] B)
q1[Q1]= q2[Q2]
ШКАЛА ОТНОШЕНИЙ
30.
Обобщим варианты сравнения между собой двухразмеров Qi и Qj
Первый, самый простой, наименее информативен
Qi Qj ;
Qi Qj ;
Qi = Qj
Второй, более информативен
Qi - Qj = QiQj
Третий, самый информативный
Qi /Qj = xij
31.
21
mN
m2
3
q
m1
m2
=
M
+
M
+
M
1. Первое изделие тяжелее второго.
2. Весы приводятся в состояние равновесия, определяется разность m1 - m2.
3. Весы приводятся в состояние равновесия, m1 = q [M]
32.
Виды измерительных шкал1. Шкала порядка: Измерения проводятся путем сравнения
по принципу “больше-меньше”.
Объекты расставляют в порядке возрастания или
уменьшения какого-либо свойства. Такую расстановку
называют ранжированием.
2. Шкала интервалов:
Особенностью шкалы интервалов является возможность
выбора положения нулевого отсчета (по усмотрению
исследователя).
Пример применения шкалы интервалов – измерения времени.
3. Шкала отношений:
Размер измеряемой величины определяется по отношению
к известному размеру, который обычно принимается за
единицу.
33.
Статья 2.Основные понятия п.8
Измерение – совокупность операций, выполняемых для
определения количественного значения величины.
РМГ 29-99. Метрология. Основные термины и определения
Измерение физической величины – совокупность операций по
применению технического средства, хранящего единицу
физической величины, обеспечивающих нахождение
соотношения (в явном или неявном виде) измеряемой величины
с ее единицей и получение значения этой величины.
34.
Можно ли предположить такую фразу:“Температура воздуха на улице 120 0С. Выходя на улицу
необходимо одеть шубу.”
Такого не может быть, при такой температуре окружающего
воздуха человек вообще не может выжить
Этот подход правомерен с точки зрения существующей шкалы Цельсия
??
0
100
120
Но во времена самого Цельсия было по-другому
35.
ЦЕЛЬСИЙ, АНДЕРС (Celsius, Anders)(1701–1744), шведский астроном и физик
Позже шведский биолог
К.ЛИННЕЙ «перевернул»
эту шкалу, приняв за 0°
температуру
таяния
льда.
В 1733 Цельсий обнародовал данные
наблюдений северного сияния, полученных
им самим и другими астрономами в период
с 1716 по 1732. В 1733 принимал участие в
экспедиции, целью которой была проверка
гипотезы И.Ньютона о том, что Земля
сплющена у полюсов. В 1742 опубликовал
работу с описанием стоградусной шкалы
термометра, в которой температура кипения
воды
при
нормальном
атмосферном
давлении была принята за 0°, а температура
таяния льда принята за 100°
Так что известная нам шкала на самом
деле должна была бы называться
шкалой Цельсия-Линнея
36.
Известно выражение “От горшка два вершка”.О каком росте идет речь, если известно, что вершок =
1/16 аршина, ¼ четверти и в современных единицах
равен 4,44см. ?
Понятно, что человек, не может иметь рост около 9 см.
Тогда вопрос в том, какова высота горшка, т.е. какой размер
принят за условный 0 ?
На Руси до XVIII века это был рост человека около 1,51м, т.е. рост
измеряли “поверх двух аршин”. Поэтому и рост был не 34 вершка, а
только 2 вершка.
Рост в
Вершках
1
Рост в метрах
1,47 1,56 1,65 1,73 1,82 1,87 2,09
3
5
7
9
10
15
37.
В рассказе И.С.Тургенева "Муму" обогатыре дворнике Герасиме
говорится, что он был "мужчина
двенадцати вершков роста". Какого
роста был Герасим?
В старину (а фактически до 1925 года) рост
человека определялся в вершках свыше
обязательных для нормального человека 2
аршин (1,42 м). Известно, что 1 вершок
приблизительно равен 4,45 см, таким образом,
рост Герасима достигал ?? м.
Примерно 1,95 м
38. СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН И ИХ ЕДИНИЦ
Совокупность ФВ, образованных в соответствии спринятыми принципами, когда одни величины
принимаются за независимые, а другие являются их
функциями (производные физические величины),
называется системой физических величин.
Совокупность единиц основных и производных величин
называется системой единиц.
Единица ФВ - размер физической величины, которому
приписывается числовое значение, равное 1
39. ПРАВИЛА КОНСТРУИРОВАНИЯ СИСТЕМ ЕДИНИЦ
1. выбираются основные физические величины;2. устанавливаются единицы основных физических
величин;
3. устанавливаются единицы производных физических
величин.
Выбор единиц основных ФВ осуществляется произвольно,
исходя из удобства применения на практике.
В общем случае единицы производных величин выражаются
через единицы основных величин в виде
[Q] = k[A] [B] [...] ... ,
При k=1 система согласованная (когерентная)
40.
Пример. Если в скорости равномерного движения v = l/tскорость v выразить в километрах в час, длину пути l – в
метрах, а время t – в секундах, то получим
v = vкм/ч км/ч, l = lм м, t = tс с,
v КМ / Ч
км l М м
ч
tС с
v КМ / Ч
ч м lМ
с км t С
41.
учитывая, что 1 ч = 3600 с и 1 км = 1000 м, получимследующее уравнение связи между числовыми
значениями:
vкм/ч = 3,6 lм / tc
таким образом, выражая скорость в километрах в час,
длину пути - в метрах, время – в секундах, получим
уравнения связи с числовым коэффициентом 3,6. Если
выразить скорость в милях в час, длину пути – в ярдах,
время – в секундах, то уравнение между числовыми
значениями примет вид
vмиль/ч = 2,045 lярд / tc
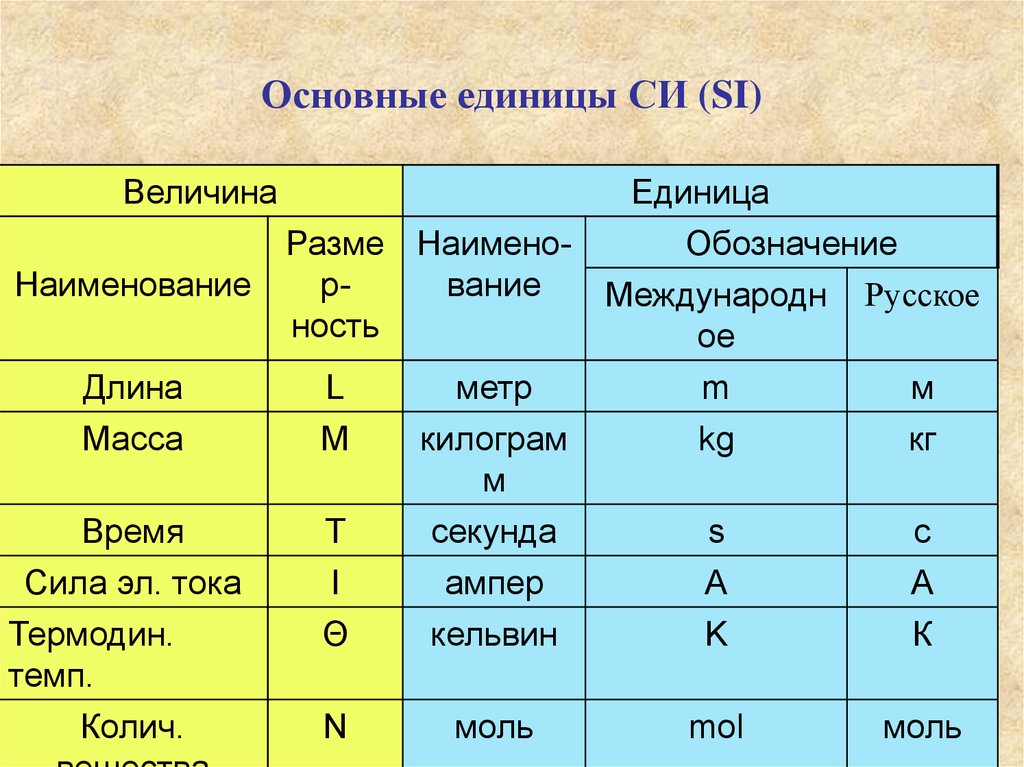
42. Основные единицы СИ (SI)
ВеличинаНаименование
Единица
Разме НаименоОбозначение
рвание
Международн Русское
ность
ое
Длина
L
метр
m
м
Масса
M
kg
кг
Время
Сила эл. тока
Термодин.
темп.
Колич.
T
I
Θ
килограм
м
секунда
ампер
кельвин
s
A
K
с
А
К
моль
mol
моль
N
43. Определения основных единиц СИ
Метр – длина пути, проходимого светом в вакууме заинтервал времени 1/299792458 c.
Килограмм – единица массы, равная массе международного
прототипа килограмма (хранится в МБМВ).
Секунда – это длительность 9192631770 периодов излучения,
соответствующего переходу между двумя сверхтонкими
уровнями основного состояния атома цезия – 133.
Ампер – сила неизменяющегося тока, который при
прохождении по двум параллельным прямолинейным
проводникам бесконечной длины и ничтожно малой площади
кругового поперечного сечения, расположенным в вакууме на
расстоянии 1м один от другого, вызвал бы на каждом участке
проводника длиной 1м силу взаимодействия, равную 2 10-7 Н.
44.
Кельвин – единица термодинамической температуры равная1/273,16 части термодинамической температуры тройной точки
воды.
Примечание Допускается применение градуса Цельсия
По размеру 1 оС = 1 К.
Кандела – сила света в заданном направлении источника,
испускающего монохроматическое излучение частотой
540 1012 Гц, энергетическая сила света которого в этом
направлении составляет 1/683 Вт/ср.
Моль – количество вещества системы, содержащей столько же
структурных элементов, сколько содержится атомов в углероде –
12 массой 0,012 кг.
45.
радиан (rad, рад) - единица плоского угла, равная внутреннемууглу между двумя радиусами окружности, длина дуги между
которыми равна радиусу;
стерадиан (sr, ср) - единица телесного угла. Стерадиан равен
телесному углу с вершиной в центре сферы, вырезающему на
поверхности этой сферы площадь, равную площади квадрата со
стороной, равной радиусу сферы.
R
R
46.
Для более детального изучения установленныхединиц измерений следует обратиться к
ГОСТ 8.417-2002 “Единицы величин”.
В нем, кроме единиц СИ, приведены:
1. Внесистемные единицы, допустимые к применению
наравне с единицами СИ.
(Например, единицы времени: минута, час, сутки, неделя).
2.Единицы относительных и логарифмических
величин.
(Например, процент, промилле).
3.Внесистемные единицы, временно допустимые к
применению.
(Например, в морской навигации единицы: длины –
морская миля (1852м), скорости – узел (0,514 м/с).
4. Правила образования наименований и обозначений
десятичных кратных и дольных единиц.
5. Правила написания обозначений единиц.
47.
Множ.Приставка СИ
Наименование
Русское
Межд.
10 15.
10 12.
10 9.
10 6.
10 3.
10 2.
10 1.
10 -1.
10 -2.
10 -3.
10 -6.
10 -9.
10 -12.
10 -15
пета
тера
гига
мега
кило
гекто
дека
деци
санти
милли
микро
нано
пико
фемто
peta
tera
giga
mega
kilo
hecto
deca
deci
centi
milli
micro
nano
pico
femto
Обозначение
Русское
Межд.
П
Т
Г
М
к
г
да
д
с
м
мк
н
п
ф
P
T
G
M
k
h
da
d
c
m
n
p
f
48.
Приставки используются, чтобы избежать большихили малых числовых значений, но следует обращать
внимание на то, что дольные и кратные единицы не
являются когерентными единицами СИ.
Чтобы использовать только когерентные единицы, в
процессе вычислений все величины необходимо
выражать в единицах СИ, а кратные и дольные
единицы рекомендуется подставлять только в
конечный результат.
Кратные и дольные единицы выбирают таким образом,
чтобы числовые значения величины находились в
диапазоне 0,1 – 1000.
49.
Приставки “гекто”, “деци”, “дека”, “санти” должныиспользоваться, когда применение других приставок
неудобно. Присоединение к наименованию единицы
двух и более приставок подряд не допускается.
Например, вместо наименования единицы
микро-микрофарад следует писать пикофарад.
В связи с тем, что наименование основной единицы –
килограмма – содержит приставку “кило”, для
образования кратных и дольных единиц массы
используется дольная единица грамм и приставки
необходимо присоединять к слову “грамм”, например
миллиграмм (мг) вместо микрокилограмм (мккг).
Дольную единицу массы – грамм – допускается
применять без присоединения приставки.
50.
Вопросы для самопроверки:1. Как взаимосвязаны метрология, стандартизация и
сертификация?
2. Что является качественной и количественной
характеристикой физической величины?
3. Как можно представить значение физической величины?
4. Какие величины называются физическими?
5. Если 5 человек заказали в кафе по 200 г томатного сока,
сколько они выпили вместе?
6. Если в Париже 68 0F, а в Москве 20 оС, то где теплее?
10 минут. Время пошло.
51.
52.
Система СГСОсновные
единицы:
сантиметр (длина)
грамм (масса)
секунда (время)
Система СИ
Основные
единицы:
метр (длина)
килограмм (масса)
секунда (время)
Система МКГСС
Основные
единицы:
метр (длина)
килограмм-сила
секунда (время)
Класс LMT
Класс LMT
Класс LFT
РАЗМЕРНОСТЬ ОПРЕДЕЛЯЕТСЯ КЛАССОМ СИСТЕМЫ ЕДИНИЦ.
Пример:
Сила в системе СИ определяется на основе уравнения
взаимосвязи
F = m a, размерность LMT-2
Сила в системе МКГСС относится к основным единицам и ее
размерность будет F
53.
МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦС
развитием
торговли
и
промышленности
различия
в единицах, применяемых для практических измерений, стали создавать
большие неудобства, что и привело к идее создания единой для всех
стран системы мер.
Система мер под девизом “На все времена, для всех народов”
была разработана в конце XVIII века во Франции
В разработке системы принимали участие французские ученые
Ж.-Л.Лагранж
(1736–1813)
Ш.-М.Талейран (1754–1838)
и др.
54.
Было решено за основу системы положить единицу длины – 1метр, равный одной десятимиллионной части четверти земного
меридиана, проходящего через Париж.
За единицу веса (в то время масса и вес считались одной и той
же величиной) был принят вес одного кубического дециметра
чистой воды при температуре ее наибольшей плотности (около
+4 оС).
Принятая французским парламентом система мер (получившая
название метрической), еще не была системой единиц в
современном понимании, так как перечень величин, охваченных
ею, был мал. Да и в самой Франции она была введена только в
1840 г.
К несомненным достоинствам системы следует отнести
десятичный принцип образования кратных и дольных единиц.
В основу создания метрической системы были положены
принципы, которые соблюдаются и в настоящее время
55.
“Надо обратиться к самой природе, почерпнувоснову системы мер в ее недрах, и суметь
найти в ней же способы поверки…”
Ван Свинден
Основные принципы
метрической системы
• неизменность единиц,
взятых из природы
• построение на десятичной
основе
• международный характер
• связь единиц длины, массы,
объема и площади
56.
20 мая 1875 г.Германия
Австро-Венгрия
подписание в Париже на
Бельгия
специально созванной
Аргентина
дипломатической конференции
Дания
Метрической конвенции –
США
первого межправительственного
Испания
Франция
соглашения в области
Италия
метрологии
Перу
Португалия
Россия
Швеция
Норвегия
Швейцария
Турция
Венесуэла
57.
“Под числом мы понимаем не столько множествоединиц, сколько отвлеченное отношение какойнибудь величины к величине такого же рода,
принятой за единицу”
И. Ньютон
“… Числа можно получать не только путем счета, но и путем
деления одного числа на другое, т.е. число можно получать
через отношение одного числа к другому. Точнее говоря, под
числом будем понимать отвлеченное отношение одной
величины к другой величине того же рода, принятой нами за
единицу. ”
Из трудов Насирэддина Туси
58.
“… наука начинается … с тех пор, какначинают измерять; точная наука
немыслима без меры”
“В природе мера и вес суть главные
орудия познания”
Точные измерения позволяют подтвердить или
опровергнуть наши представления о
веществах и явлениях.
В 1895 г. Рэлеем и Рамсеем при измерениях
плотности атмосферного воздуха как смеси
азота и кислорода был открыт аргон (1 %
содержания в атмосфере)
Открытие дейтерия было сделано на
основании измерений средней массы
естественного водорода.
























































 Физика
Физика