Энергетический спектр носителей заряда. Зонная структура энергетического спектра кристалла

1.

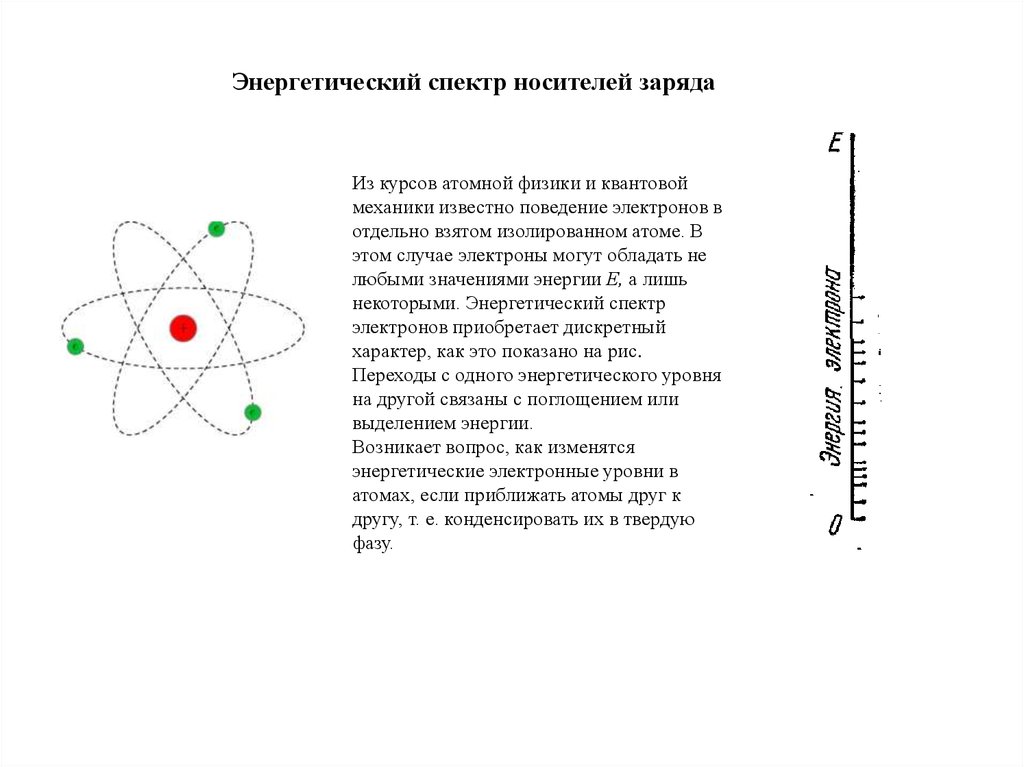
Энергетический спектр носителей заряда
Из курсов атомной физики и квантовой
механики известно поведение электронов в
отдельно взятом изолированном атоме. В
этом случае электроны могут обладать не
любыми значениями энергии Е, а лишь
некоторыми. Энергетический спектр
электронов приобретает дискретный
характер, как это показано на рис.
Переходы с одного энергетического уровня
на другой связаны с поглощением или
выделением энергии.
Возникает вопрос, как изменятся
энергетические электронные уровни в
атомах, если приближать атомы друг к
другу, т. е. конденсировать их в твердую
фазу.

2.

Первое следствие сближения атомов в кристалле
Упрощенная картина такого одномерного кристалла приведена на рис. .
Рассмотрим какие силы действуют в отдельном атоме, и какие — в кристалле. В
изолированном атоме существуют сила притяжения ядром атома всех своих электронов
и сила отталкивания между электронами. В кристалле из-за близкого расстояния
между атомами возникают новые силы. Это — силы взаимодействия между ядрами,
между электронами, принадлежащими разным атомам, и между всеми ядрами и всеми
электронами. Под влиянием этих дополнительных сил энергетические уровни
электронов в каждом из атомов кристалла каким-то образом должны измениться. Одни
уровни понизятся, другие повысятся на шкале энергий. В этом состоит первое
следствие сближения атомов.

3.

Обобществление электронов в кристалле
Второе следствие связано с тем, что электронные оболочки атомов, в особенности, внешние
могут не только соприкасаться друг с другом, но способны даже перекрыться. В результате
этого электрон с одного уровня в каком-либо из атомов может перейти на уровень в соседнем
атоме без затраты энергии и, таким образом, свободно перемещаться от одного атома к
другому. В связи с этим нельзя утверждать, что данный электрон принадлежит какому-нибудь
одному определенному атому, наоборот, электрон в такой ситуации принадлежит всем атомам
кристаллической решетки одновременно. Иными словами, происходит обобществление
электронов. Разумеется, что полное обобществление происходит лишь с теми электронами,
которые находятся на внешних электронных оболочках. Чем ближе электронная оболочка к
ядру, тем сильнее ядро удерживает электрон на этом уровне и препятствует перемещению
электронов от одного атома к другому.

4.

Зонная структура энергетического спектра кристалла
Совокупность обоих следствий сближения атомов
приводит к появлению на энергетической шкале вместо
отдельных уровней целых энергетических зон (рис. 1.1,
г), т. е. областей таких значений энергий, которыми
может обладать электрон, находясь в пределах твердого
тела. Ширина зоны должна зависеть от степени связи
электрона с ядром. Чем больше эта связь, тем меньше
расщепление уровня, т. е. тем уже зона. В
изолированном атоме имеются запрещенные значения
энергии, которыми не может обладать электрон.
Естественно ожидать, что нечто аналогичное будет и в
твердом теле. Между зонами (теперь уже не уровнями)
могут быть запрещенные зоны. Характерно, что если в
отдельном атоме расстояния между уровнями будут невелики, то в кристалле запрещенный участок может
исчезнуть за счет перекрытия образующихся
энергетических зон.
Таким образом, энергетический спектр электронов в
кристалле имеет зонную структуру.

5.

Количественное решение задачи о спектре электронов в
кристалле с помощью уравнения Шредингера.
Это одно из видов уравнения Шредингера
Это уравнение относиться к свободному движению частицы. Если же частица движется в
силовом поле, то связанные с ней волны описываются так называемой волновой функцией ψ.
После различных преобразований аналитическое выражение уравнения
Шредингера для кристалла имеет вид
После раскрытия неопределенности получим
Решение этого трансцендентного уравнения можно найти для любого φ графически. Для этого
обозначим левую часть в этом уравнении F (λа) и построим график этой функции в зависимости от λа.
Вид функции F (λа) показан на рис.

6.

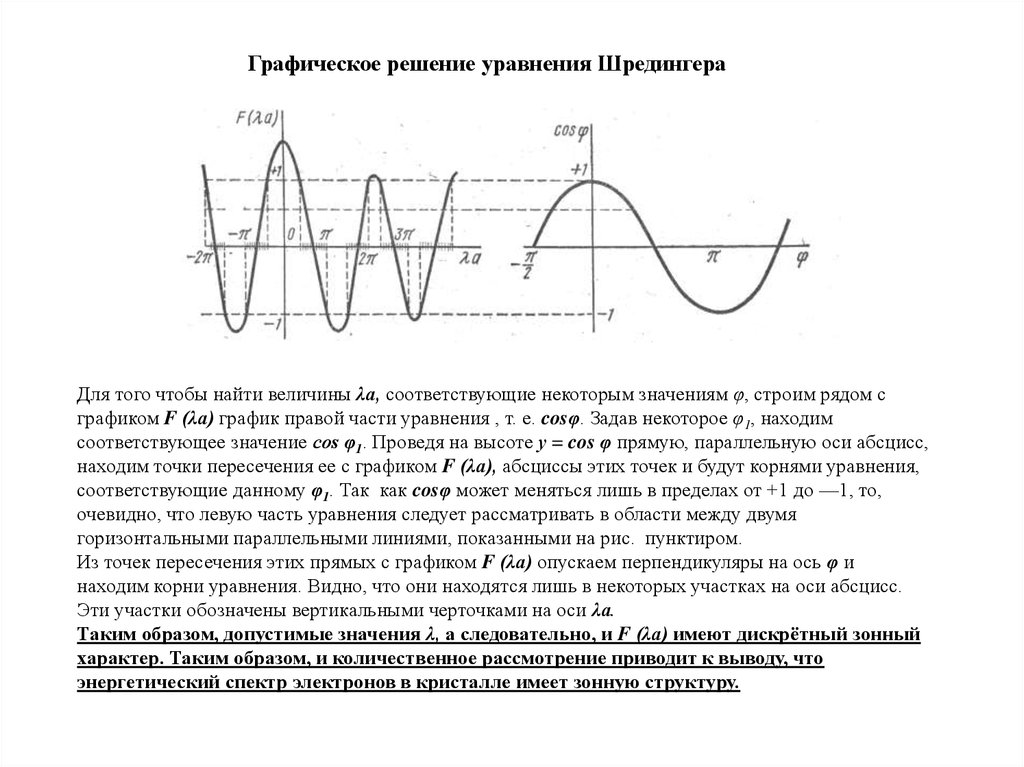
Графическое решение уравнения Шредингера
Для того чтобы найти величины λа, соответствующие некоторым значениям φ, строим рядом с
графиком F (λа) график правой части уравнения , т. е. cosφ. Задав некоторое φ1, находим
соответствующее значение cos φ1. Проведя на высоте у = cos φ прямую, параллельную оси абсцисс,
находим точки пересечения ее с графиком F (λа), абсциссы этих точек и будут корнями уравнения,
соответствующие данному φ1. Так как cosφ может меняться лишь в пределах от +1 до —1, то,
очевидно, что левую часть уравнения следует рассматривать в области между двумя
горизонтальными параллельными линиями, показанными на рис. пунктиром.
Из точек пересечения этих прямых с графиком F (λа) опускаем перпендикуляры на ось φ и
находим корни уравнения. Видно, что они находятся лишь в некоторых участках на оси абсцисс.
Эти участки обозначены вертикальными черточками на оси λа.
Таким образом, допустимые значения λ, а следовательно, и F (λа) имеют дискрётный зонный
характер. Таким образом, и количественное рассмотрение приводит к выводу, что
энергетический спектр электронов в кристалле имеет зонную структуру.

7.

Металлы и полупроводники
В изолированном атоме выше валентного уровня находятся уровни энергии, на которых хотя
электронов и нет, но они могут там находиться при возбуждении атомов. Для этого валентному
электрону необходимо преодолеть энергетический барьер, равный потенциалу возбуждения атома.
Точно так же и в кристалле выше валентной зоны имеется полностью свободная от
электронов зона, которую называют зоной проводимости. Заполнение зоны проводимости
может начаться только если электроны в валентной зоне получат
дополнительную
энергию,
достаточную для преодоления энергетического барьера, равного ширине запрещенной зоны, лежащей между валентной зоной и зоной проводимости.
Случай б. Валентная зона заполнена
полностью, но запрещенная зона между валентной
зоной и зоной проводимости отсутствует (рис. 1.2,
б). Такой кристалл будет хорошо проводить
электрический ток и его электропроводность не
будет зависеть (или почти не будет· зависеть) от
температуры. Таким образом, этот случай
соответствует металлическому кристаллу.
.
Случай в и г. Валентная зона заполнена полностью и не перекрыта с зоной проводимости
(рис. 1.2, в и 1.2, г). Это случаи, когда перемещение электронов под действием
электрического поля не может происходить до тех пор, пока каким-либо способом, например
нагревом, не будет переведена часть электронов из валентной зоны в зону проводимости. Т. е.
эти случаи описывают кристаллы, электропроводность которых должна повышаться с
увеличением температуры. Такие кристаллы называют полупроводниками

8.

В металлах возможны два случая:
зона проводимости заполнена частично. При температуре 1 К энергия теплового
движения kT 10 4 эВ значительно больше энергии между соседними уровнями зоны
( 10 22 эВ), электроны легко попадают в зону проводимости, металл хорошо
проводит ток; валентная и свободная зоны перекрыты.
В диэлектрикахвалентная и свободная зоны целиком заполнены и разделены
запрещенной зоной шириной в несколько эВ. При реальных температурах электроны
из валентной зоны не могут попасть в зону проводимости.
В полупроводниках ширина запрещенной зоны мала Е 1эВ, переброс электронов
становится возможным за счет теплового движения.

9.

Анализ степени заполнения зон позволяет в дальнейшем
исключить из рассмотрения все глубокие зоны, лежащие
ниже валентной, так как электроны в этих зонах не
участвуют в прохождении электрического тока через
кристалл. Таким образом, зонную структуру, которую
рассмотрим в дальнейшем, будем изображать так, как она
показана на рис.
Обычно принято для краткости изображать лишь потолок валентной зоны, обозначаемый Еυ
подразумевая, что сама валентная зона располагается ниже этого уровня. Точно так же принято
изображать дно зоны проводимости, т. е. ее нижний уровень, обозначаемый ес. Ширину
запрещенной зоны принято обозначать Eg.
Однако надо помнить, что в связи с статистическим
распределением электронов на уровнях, правильней будет
изображать зонную структуру, как показано на нижнем рис.
Вместо валентной зоны – потолок валентной зоны,
Вместо зоны проводимости- дно зоны проводимости

10.

Неприменимость ньютоновской механики для электронов доказывают обычно на основании
известного в квантовой механики принципа неопределенности, при котором неопределенность в
величине скорости электрона оказывается больше самой скорости, что, конечно, является
абсурдом. Таким образом, для электрона в кристалле понятие о мгновенной скорости теряет
смысл. Остается лишь понятие о средней скорости электрона.
Чему же равна средняя скорость электрона в кристалле? Ее можно определить как
групповую скорость волн, с помощью которых описывается электрон.
vГ 1 / dE / dk
dA vГ dtF
F
F dE
dt
dk
dk
dt
1 d 2E
a
F
dk 2
2
m 2
(d E dk 2 )
За время dt внешняя сила F совершает работу по
перемещению электрона.
Отсюда находим.
Дифференцируя vГ по времени получим ускорение электрона
в виде
Сравнивая это выражение с законом Ньютона для обычных
тел можно увидеть полное сходство, если трактовать как
аналог массы величину
Эту величину называют эффективной массой. Смысл введения эффективной массы заключается в
том, что с ее помощью учитывают совместное действие периодического потенциального поля и
внешней силы на электрон в кристалле. Посредством введения эффективной массы удалось сложные
законы движения электронов в кристалле свести к законам, которые по форме (только по форме!)
совпадают с хорошо известными законами классической механики. Следует понимать, что
эффективная масса ничего общего не имеет с обычной массой, т. е. она не является мерой инерции и
не связана с силами тяготения.

11.

Рассмотренная выше зонная структура явилась следствием существования
внутреннего периодического поля, которое до сих пор принималось идеально правильным.
Если будут иметь место какие-либо нарушения идеальности периодического поля, то они
повлекут за собой и нарушения идеальности зонной структуры.
Дефекты, способные при ненарушенных валентных связях в
кристалле отдавать электроны в зону проводимости, называют
донорами, а полупроводник, содержащий доноры, называют
полупроводником с электронной электропроводностью или
полупроводником п-типа.
Дефекты, способные воспринимать электроны из валентной
зоны, называют акцепторами, а полупроводники, содержащие
акцепторы, называют или полупроводниками с дырочной
электропроводностью или полупроводниками р-типа.
Уровни дефектов, на которых они расположены, не лежат ни в
зоне проводимости, ни в валентной зоне.
Они располагаются в запрещенной зоне полупроводника
Необходимо помнить, что доноры могут отдавать электроны не только в зону
проводимости, а любому из дефектов, имеющих акцепторную природу. Соответственно,
акцепторы, наряду с захватом электронов из валентной зоны могут в принципе
воспринимать электроны от любых доноров, имеющихся в кристалле.

12.

Элементы статистической физики
Носители заряда, как всякие частицы в условиях термодинамического
равновесия, должны подчиняться статистическим закономерностям. Их отличие,
например, от обычных газовых частиц заключается в том, что они подчиняются
квантовым; законам.
Они могут обладать не любыми значениями энергии, а дискретными. В
одном состоянии не может находиться более одного электрона. Эти отличия
приводят к особенностям статистических закономерностей, которым
подчиняются носители заряда. Для их понимания следует вспомнить основные
положения статистической физики.
Понятие о функции распределения.
В общем числе частиц имеются такие, координаты которых лежат в
интервалах:
x-x+Δx,
y-y+Δy,
z-z+Δz
а составляющие импульсов соответственно между значениями
px- px+Δpx,
py- py+Δpy,
pz- pz+Δpz,
Если количество таких частиц будет ΔN, то они составят долю, равную ΔN/N,
от всех частиц. Количество частиц будет возрастать (или убывать)
пропорционально изменению интервалов Δx, Δy, Δz, Δpx, Δpy, Δpz.

13.

Функция распределения
Коэффициент пропорциональности w в свою очередь может являться функцией
координат и импульсов, а кроме того, и времени:
ΔN =w(x,у, z, рх,ру, рг, t) Δx Δy Δz Δpx Δpy Δpz
Так как
ΔxΔyΔz =ΔV - элемент объема в пространстве координат,
ΔpxΔpyΔpz =Δω - элемент объема в пространстве импульсов, a
ΔV Δω = Δγ - элемент объема в фазовом пространстве, то
ΔN = w Δγ
Таким образом, w имеет простой физический смысл — она определяет число
электронов, содержащихся в данном фазовом промежутке, рассчитанное на единицу
объема фазового пространства.
Можно написать:
ΔN/N = Δγ w/N
где функция (распределения)
w/N=f
есть относительная концентрация частиц, содержащихся в данном фазовом
промежутке, рассчитанная на единицу фазового объема. Или, функция
f – это вероятность попадания частицы в данный фазовый промежуток,
рассчитанная на единицу фазового объема.

14.

Функция распределения Максвелла— Больцмана
В классической физике частицы предполагаются различимыми, причем в данном
энергетическом состоянии может находиться неограниченное число классических частиц. Примером
таких классических частиц является молекулярный газ. Эти частицы описываются хорошо известной
в классической физике функцией распределения Максвелла— Больцмана:
f М( E, T ) exp(
М
F
n
M E
kT
)
где μМ - представляет собой термодинамический параметр,
называемый химическим потенциалом. Химический потенциал
выражает изменение свободной энергии системы при изменении
числа частиц этой системы на единицу, при неизменных
температуре и объеме системы.
Как видно из рисунка, с уменьшением температуры число
частиц с малыми значениями энергии неограниченно возрастает.
При температуре абсолютного нуля все частицы займут самое
нижнее энергетическое состояние.
Графики функции распределения Максвелла-Больцмана (а) и распределение частиц по
энергиям (в) при трех различных значениях температуры.

15.

Функция распределения Бозе - Эйнштейна
В отличие от классических частиц элементарные частицы микромира: фотоны, фононы,
электроны, протоны, нейтроны и др. — являются неразличимыми частицами и, следовательно,
в общем случае не подчиняются статистике Максвелла—Больцмана. Распределение таких
частиц по энергиям зависит от того, подчиняются ли частицы принципу Паули. (Австрийский физик
Вольфганг Паули — один из нескольких европейских физиков-теоретиков, сформулировавших в конце 1920-х — начале 1930-х
годов основные принципы и постулаты квантовой механики. Принцип, носящий его имя, является одним из основополагающих в
этом разделе физической науки. Проще всего представить себе, в чем именно заключается принцип Паули, если сравнить электроны
с автомобилями на многоярусной крытой стоянке. В каждый бокс помещается только одна машина, а после того, как все боксы на
нижнем этаже стоянки заняты, автомобилям приходится в поисках свободного места заезжать на следующий этаж. Так же и
электроны в атомах — на каждой орбите вокруг ядра их помещается не больше, чем там имеется «парковочных мест», а после того,
как все места на орбите заняты, следующий электрон ищет себе место на более высокой орбите).
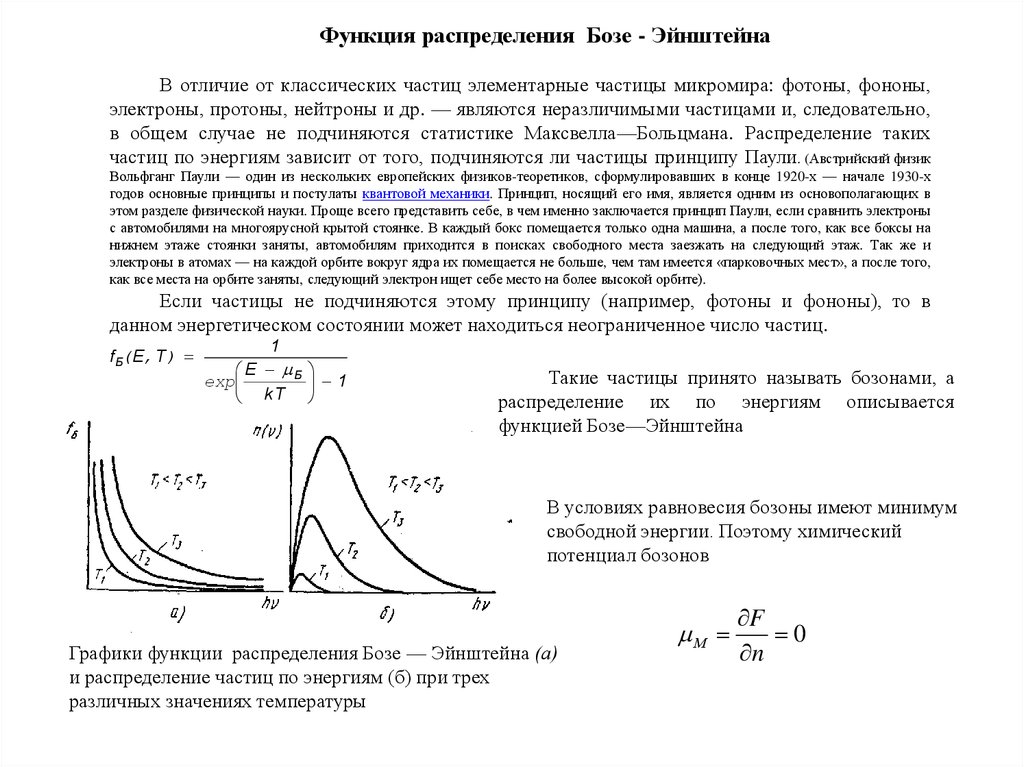
Если частицы не подчиняются этому принципу (например, фотоны и фононы), то в
данном энергетическом состоянии может находиться неограниченное число частиц.
f Б( E, T )
1
E Б
exp
1
kT
Такие частицы принято называть бозонами, а
распределение их по энергиям описывается
функцией Бозе—Эйнштейна
В условиях равновесия бозоны имеют минимум
свободной энергии. Поэтому химический
потенциал бозонов
Графики функции распределения Бозе — Эйнштейна (а)
и распределение частиц по энергиям (б) при трех
различных значениях температуры
М
F
0
n

16.

Функция распределения Ферми—Дирака
Если частицы подчиняются принципу Паули (например, электроны, нейтроны и др.),
то в каждом энергетическом состоянии одновременно не может быть более одной частицы.
В этих условиях функция распределения, выражающая среднее число частиц в данном
энергетическом состоянии, будет представлять собой вероятность заполнения данного
состояния. Расчетом наиболее вероятного распределения по энергетическим уровням
неразличимых частиц, подчиняющихся принципу Паули, получают формулу ·
fФ( E, T )
1
E Ф
exp
1
kT
получившую название функции распределения Ферми—Дирака.
Частицы,
описываемые
этой
функцией
распределения,
получили; название фермионов.
Как видно из формулы,. последним заполненным состоянием будет энергетический уровень,
высота которого, отсчитанная от дна зоны проводимости, равна химическому потенциалу ЕF = μФ.
Этот энергетический уровень ЕF получил название уровня Ферми. Все энергетические уровни,
лежащие выше уровня Ферми, свободны, а значение функции распределения для этих уровней равно
нулю (fФ(Е>EF) = 0). Описанное распределение электронов по энергиям при Т = 0°К показано на рис.,а
ступенчатой линией.

17.

На рис. для сравнения приведены различные кривые распределения частиц.
Видно, что значения функций распределения
при малых энергиях в случае статистики МаксвеллаБольцмана и Бозе-Эйнштейна значительно больше,
чем в случае статистики Ферми-Дирака. Следует,
однако, отметить, что при
E Ф
exp
1
kT
статистики Бозе-Эйнштейна и Ферми-Дирака переходят в статистику МаксвеллаБольцмана, которую можно рассматривать как предельный случай этих двух квантовых
статистик.
Исходя из выше изложенного видно что
-в оптоэлектронике (фотоны) необходимо использовать распределение БозеЭйнштейна,
-в микроэлектронике (электроны) распределение Ферми-Дирака.

18.

Равновесная концентрация носителей
В общем случае концентрация свободных носителей заряда в кристалле может быть вычислена
интегрированием произведения плотности квантовых состояний g(E) на функцию распределения fF(E)
по всем энергетическим уровням системы в соответствии с формулой.
n(E)dE=f(E,T)g(E)dE
Для
определения концентрации электронов в зоне проводимости интегрирование следует
производить от уровня дна зоны проводимости Ес до верхнего уровня Етак Поскольку функция
распределения быстро уменьшается с ростом энергии, то значение верхнего предела интегрирования
без заметной погрешности расчета может быть сколь угодно увеличено или взято равным
бесконечности. После интегрирования для электронов и дырок получим
E EF
n N c exp C
kT
E EV
p NV exp F
kT
где EF - энергия Ферми равная химическому потенциалу μ
NC –эффективная плотность состояний в зоне проводимости.
NV –эффективная плотность состояний в валентной зоне.
В собственном полупроводнике условие нейтральности определяется
равенством концентраций электронов и дырок p=n.
1
n p n i ( NC NV )
2
E EV
exp C
2
kT

19.

Легированный полупроводник.
Если в полупроводнике содержатся примеси или дефекты, образующие донорные или
акцепторные уровни в запрещенной зоне, то появляются дополнительные электронные
переходы, изменяющие концентрацию носителей заряда и положение уровня Ферми.
Концентрация электронов в зоне проводимости и дырок в валентной зоне в этом случае
описывается теми же выражениями, однако энергия уровня Ферми уже является функцией
концентрации примесей. Для доноров в электронном полупроводнике и для акцепторов в
дырочном получим
nn ( N D N C )
1
2
E ED
exp C
2
kT
1
E EV
pP ( N A N D ) 2 exp A
2
kT
Если в образце имеются оба сорта примесей — доноры и акцепторы, то тип проводимости
определяется по преобладающей примеси. Если, например, концентрация доноров ND больше
концентрации акцепторов NA, то при Т = 0 К все акцепторные уровни будут заполнены электронами,
перешедшими с доноров.
При повышении температуры все донорные уровни опустошатся и концентрация электронов
станет постоянной и равной разности числа доноров и акцепторов:
n = ND –NA
Аналогичные закономерности наблюдаются в дырочном полупроводнике, содержащем некоторое
количество доноров.
p = NA – ND
Обычно в полупроводнике всегда имеется большее или меньшее количество неосновной примеси,
т. е. доноров в дырочном полупроводнике и акцепторов в электронном полупроводнике. Отношение
числа неосновных центров к основным (ND/NA или NA/ND. соответственно) называют степенью
компенсации, а образцы, содержащие оба вида центров, — компенсированными.

20.

Неравновесные носители тока
Помимо теплового возбуждения, приводящего к возникновению равновесных носителей тока,
возможны и другие способы обогащения полупроводника электронами и дырками: генерация их
светом, потоком заряженных частиц, введение (инжекция) через контакт и т. д. Действие подобных
агентов приводит к появлению дополнительных, избыточных, против равновесной концентрации,
свободных носителей. В момент возникновения избыточные носители не будут находиться в тепловом
равновесии с решеткой. По этой причине их называют неравновесными носителями.
С течением времени, вследствие взаимодействия с решеткой энергия неравновесных носителей
непрерывно уменьшается и в конце концов выравнивается с энергией равновесных носителей. Расчет
показывает, что такое выравнивание происходит примерно за 10 -10с, что значительно меньше среднего
времени жизни носителей в полупроводнике.
Поэтому практически в течение всего времени своего существования избыточные носители
обладают такой же энергией и другими свойствами, что и равновесные носители
При неизменной интенсивности внешнего агента концентрация избыточных носителей растет вначале
быстро, а затем, вследствие непрерывно увеличивающейся скорости рекомбинации, рост замедляется и
в конце концов устанавливается стационарное состояние, при котором скорость генерации носителей
равна скорости их рекомбинации. Этому состоянию отвечает постоянная концентрация носителей в
полупроводнике, равная n для электронов и p для дырок. Концентрация избыточных носителей в этих
условиях равна:
Δп=п— п0 и Δp=p—p0
Если в полупроводнике нет объемного заряда то Δn =Δp Это условие называется условием
электронейтральности полупроводника.

21.

Уравнение непрерывности
Процесс образования избыточных носителей
называют процессом генерации электроннодырочных пар.
Обратный процесс сваливания электронов из
зоны проводимости в валентную зону называют
процессом рекомбинации носителей.
Пусть в полупроводнике р-типа в направлении оси x существует положительный градиент
концентрации электронов (неосновных носителей) dn/dx>0. Такой градиент может
быть создан, например, инжекцией электронов с одного конца полупроводника.
Предположим далее, что в том же направлении х действует электрическое поле
напряженности Ex.
Выделим в полупроводнике слой толщиной dх, расположенный перпендикулярно оси х, с
площадью поперечного сечения 1 см2 (рис. ). Объем этого слоя равен dх.
Обозначим концентрацию электронов в слое в момент времени t через п(х,t), а в момент t+dt
через п(х, t+dt). Тогда изменение числа электронов в слое за время dt будет равно:
[n(x,t+dt)-n(x,t)]dx =(∂n/∂t)dtdx.
Изменение числа электронов в слое вызывается протеканием в нем процессов генерации и
рекомбинации носителей, а также диффузией и дрейфом носителей, возникающим под
действием градиента концентрации и внешнего поля.

22.

Генерация носителей. За время dt в слое объемом dх ионизирующий фактор создает
gdxdt электронов, где g — скорость генерации электронов.
Рекомбинация электронов. Вследствие рекомбинации ежесекундно в единице объема
полупроводника уничтожается R = -(n-n0)/τn электронов. За время dt в объеме dх
убыль числа электронов составит: - [(n-n0)/ τn]dxdt.
Диффузия и дрейф носителей. Наличие градиента концентрации и внешнего поля Ex. в
направлении оси х приводит к тому, что поток электронов Jп(х), втекающий в слой dх, не
равен потоку Jп(х+dх), вытекающему из слоя. Изменение числа электронов в слое за
время dt, вызванное различием этих потоков, составит:
J n ( x) J n ( x dx) dt J n dxdt
x
Полное изменение числа электронов в слое за время dt (уравнение непрерывности для избыточных
электронов и дырок) будет равно:
J
n n0
n
n g
t
x
n
J p
p p0
p
g
t
x
p
При наличии в полупроводнике электрического поля Ex и градиента концентрации электронов ток
будет складываться из двух составляющих:
дрейфовой, обусловленной направленным движением электронов под действием внешнего поля и
диффузионой, вызванной диффузией электронов.

23.

Дрейфовый ток. Дрейфовое движение электронов и дырок совершается в структуре
полупроводника под действием электрического поля и является направленным.
Дрейфовый ток равен:
JЭ = nun Ex
где un — подвижность электронов; n — их концентрация.
Диффузионный ток. Ток, обусловленный диффузией электронов, пропорционален
градиенту их концентрации:
JD = Dп(∂п/∂х)
Коэффициент пропорциональности Dn называется коэффициентом диффузии.
Полный ток, обусловленный движением электронов, равен:
Jn = nun Ex + Dп(∂п/∂х)
Аналогичное выражение можно получить для тока, обусловленного движением дырок:
Jp = nup Ex + Dp(∂p/∂х)
Знак минус у диффузионной составляющей указывает на то, что диффузионный ток дырок
направлен противоположно градиенту их концентрации (в сторону уменьшения
концентрации дырок).
Связь между изменением концентрации носителей в элементарном объеме полупроводника
и током, проходящим через этот объем, устанавливается уравнением непрерывности
n n0
n
2n
n
Dn 2 x u n
g
t
x
n
x
p p0
p
2 p
p
Dp 2 xu p
g
t
x
n
x

24.

Электропроводность.
Под действием электрического поля свободные носители заряда в полупроводнике приобретают направленное движение,
называемое дрейфом. При этом движущиеся носители непрерывно сталкиваются с узлами кристаллической решетки,
примесями и другими всевозможными дефектами, т. е. испытывают рассеяние. Ускоренное движение под действием поля
возможно только в коротких интервалах между столкновениями, на длине свободного пробега. После каждого
столкновения электрон должен заново «набирать» скорость. В результате средняя дрейфовая скорость электронов и дырок
оказывается вполне определенной величиной, пропорциональной напряженности поля:
Коэффициент пропорциональности μ есть подвижность носителей.
Плотность дрейфового тока определяется законом Ома: где σ – удельная проводимость
С другой стороны плотность тока пропорциональна концентрации свободных
носителей и скорости дрейфа .
Дрейф электронов и дырок (как разноименных зарядов) под действием электрического поля происходит в
противоположных направлениях, поэтому суммарная плотность дрейфового тока в кристалле
I = e (nμn + p μp) Ex
Коэффициент пропорциональности между напряженностью поля Ex и плотностью тока I составляет удельную
проводимость
σ = e(nμn + pμp)
Собственная электропроводимость обусловлена генерацией электронно-дырочных пар, а примесная — ионизацией
атомов примеси.
1
E EV
n p ni ( N C NV ) 2 exp C
2kT
Измерив электропроводность σ как функцию температуры и изобразим результаты на графике в полулогарифмическом
масштабе:
Наклон прямой позволяет, таким образом, определить ширину запрещенной зоны ΔE:

25.

Расчет ширины запрещенной зоны полупроводника
по температурной зависимости сопротивления
Сопротивление полупроводника определяется формулой
И значит:
Полупроводниковое сопротивление
помещается в термостатируемую
камеру, температура в которой
измеряется термометром. Температура
камеры задается и поддерживается
током термостатирующей жидкости.
Сопротивление образца измеряется
мостовым методом с помощью прибора
"Мост универсальный Е7-4",при
помощи правой ручки “Отсчет”.
Экспериментальную зависимость сопротивления от
температуры удобно изображать графически в координатах l
nR и 1/Т. График представляет собой прямую линию, тангенс
угла наклона которой к оси 1/Т равен:

26.

Фотопроводимость. Появление в твердом теле избыточных носителей может вызывать свет,
падающий на полупроводник. Процесс внутреннего освобождения носителей под действием света
называется внутренним фотоэффектом. Повышение концентрации носителей заряда вследствие
генерации их светом вызывает повышение проводимости полупроводника. Эту дополнительную
проводимость называют фотопроводимостью в отличие от темновой проводимости, обусловленной
тепловым возбуждением носителей. Возбуждение дополнительных носителей может происходить с
примесных уровней и из валентной зоны.
В соответствии с этим различают примесную и собственную фотопроводимости
Обозначим через Ф интенсивность света, через α
коэффициент поглощения света и через β - квантовый
выход Тогда число избыточных носителей, ежесекундно
генерируемых в единице объема полупроводника, будет
равно: g = βαФ
Стационарная концентрация избыточных носителей будет
равна, очевидно, произведению скорости генерации на
время их жизни τ:
Δn0 = βαФτn Δp0 = βαФτp
стационарная фотопроводимость полупроводника будет
равна:
σФ = eβαФ(unτn + upτp)

27.

Определение ширины запрещенной зоны
по краю собственного поглощения
Все типы электронов определяют взаимодействия света с твердым телом, которые можно
классифицировать как взаимодействия с сохранением кванта энергии (пропускание, рассеяние и отражение
света твердым телом) и взаимодействия с превращением кванта энергии, в результате которых образуются
частицы, не имеющие электрического заряда (фотолюминесценция, превращение в теплоту, генерация
экситонов), или частицы с зарядом (внутренний и внешний фотоэффект, генерация пары электрон-дырка).
Во всех взаимодействиях с превращением кванта энергии имеет место поглощение света. Среди
механизмов поглощения света в твердом теле можно выделить собственное поглощение, обусловленное
переходами между энергетическими зонами твердого тела.
Собственное или фундаментальное поглощение света в
полупроводниках, обусловленное переходами электронов из
валентной зоны в зону проводимости в результате поглощения
ими фотонов, энергия которых превышает ширину запрещенной
зоны, является характеристическим для вещества, поскольку оно
определяется структурой зон. Спектр поглощения представляет
собой непрерывную кривую, более или менее круто спадающую в
области больших длин волн (рис.).

28.

Коэффициент поглощения света частоты ν при прямых межзонных переходах определяется вероятностью
такого перехода и числом состояний в валентной зоне и зоне проводимости, разделенных энергетическим
расстоянием hν. Очевидно, что при прямых переходах каждому состоянию в валентной зоне с данным
значением волнового вектора ki соответствует только одно состояние в зоне проводимости с тем же
значением ki , то есть при переходе энергия электрона в валентной зоне Ei и энергия электрона в зоне
проводимости Ej однозначно определяются энергией фотона hν. Вблизи k =0 зависимость E(k)
представляет собой параболу (рис.).
Если вероятность перехода не зависит от энергии (прямой переход), то
коэффициент поглощения света для прямых межзонных переходов равен
Таким образом, собственное межзонное поглощение будет иметь место,
если энергия фотона превышает ширину запрещенной зоны, то есть
собственное поглощение имеет сплошной спектр, длинноволновая
граница которого определяется условием
Схема стандартных, или параболических,
зон в полупроводниках. EC - EV = Eg
Для коэффициента поглощения света в случае запрещенного прямого межзонного перехода может быть
получено выражение (непрямые переходы):
Таким образом, длина волны λгр , соответствующая границе собственного поглощения, позволяет по
формуле определить ширину запрещенной энергетической зоны, а зависимость коэффициента поглощения
от частоты вблизи края собственного поглощения - тип оптического перехода:
для разрешенного (прямого) перехода α(ν) ~ ν 1/2 , для запрещенных (непрямые переходы)- α(ν) ~ ν 3/2

29.

Поглощение света слоем полупроводника конечной толщины.
При падении светового пучка интенсивностью I0 на поверхность слоя полупроводника толщиной d
часть его RI0 отражается на границе раздела воздух/полупроводник (R - френелевский коэффициент
отражения), а оставшаяся часть (1- R)I0 проходит внутрь полупроводника. По мере распространения внутри
слоя интенсивность света согласно закону Бугера-Ламберта экспоненциально уменьшается и после
частичного отражения света на второй границе раздела полупроводник/воздух из слоя выходит световой
поток с интенсивностью, определенной следующим образом (рис.):
где D = α d - оптическая плотность слоя толщиной d,
α – коэффициент поглощения полупроводника.
В случае, когда оптическая плотность образца D < 1, интенсивность
прошедшего через него светового потока будет являться суммой
интенсивностей всех составляющих его компонентов и пропускание
образца можно оценить как
Изменение интенсивности светового пучка
при его прохождении через слой
полупроводника
В случае, когда D > 1, справедливым становится выражение
Величина α у полупроводниковых материалов меняется в широких пределах: от 10-2 до 105 см-1.. С
допустимой погрешностью по измеренным значениям R, T и d можно определить коэффициент поглощения:

30.

Схема установки для определения спектра поглощения полупроводника
Излучение лампы накаливания (1) фокусируется линзой (2) на входную щель монохроматора УМ-2 (3). Изображение
сплошного спектра излучения лампы формируется в плоскости выходной щели монохроматора. Перемещая
диспергирующую призму прибора с помощью барабана длин волн (4), можно через выходную щель пропускать
свет различных диапазонов спектра излучения лампы (1). Этот квазимонохроматический поток падает на приемную
площадку фотодиода ФД-24 (5), кожух которого надевается непосредственно на корпус выходной щели УМ-2. Ток
фотодиода регистрируется с помощью чувствительного цифрового вольтметра GDM-8135 (6), работающего в режиме
гальванометра: он измеряет падение напряжения на входном сопротивлении вольтметра, обусловленное током
фотодиода. Перед входной щелью УМ-2 устанавливается исследуемый образец (7), заключенный между двумя
стеклянными пластинами, или стеклянные пластины без образца (8) (последние необходимы для учета
френелевского отражения от стеклянных пластин). Блок (9) служит для питания лампы накаливания (1).
Для построения градуировочного графика прибора УМ-2 вместо лампы накаливания устанавливается ртутная лампа
(типа ДРШ-250) (на рис. 7 не приведена).

31.

Определение ширины запрещенной зоны Eg и типа межзонного перехода.
1. Используя экспериментальные данные по пропусканию Т, рассчитать коэффициент поглощения
полупроводника для различных частот по формуле
Например: данные по исследуемому образцу: d = 20 мкм, R = 0,15.
Составить таблицу по нижеприведенной форме:
2. Построить графическую зависимость α2 = f (hν).
3. Выявить на графике участок спектра, где
экспериментальные точки удовлетворяют линейной
зависимости. Наличие такого участка показывает, что
межзонный оптический переход является прямым
разрешенным переходом.
4. Экстраполировать линейную зависимость до пересечения
ее с осью абсцисс.
Точка пересечения определяет ширину запрещенной зоны
Eg, выраженную в эВ.