Похожие презентации:
Расчет по деформациям железобетонных конструкций. (Тема 14)
1. Расчет по деформациям
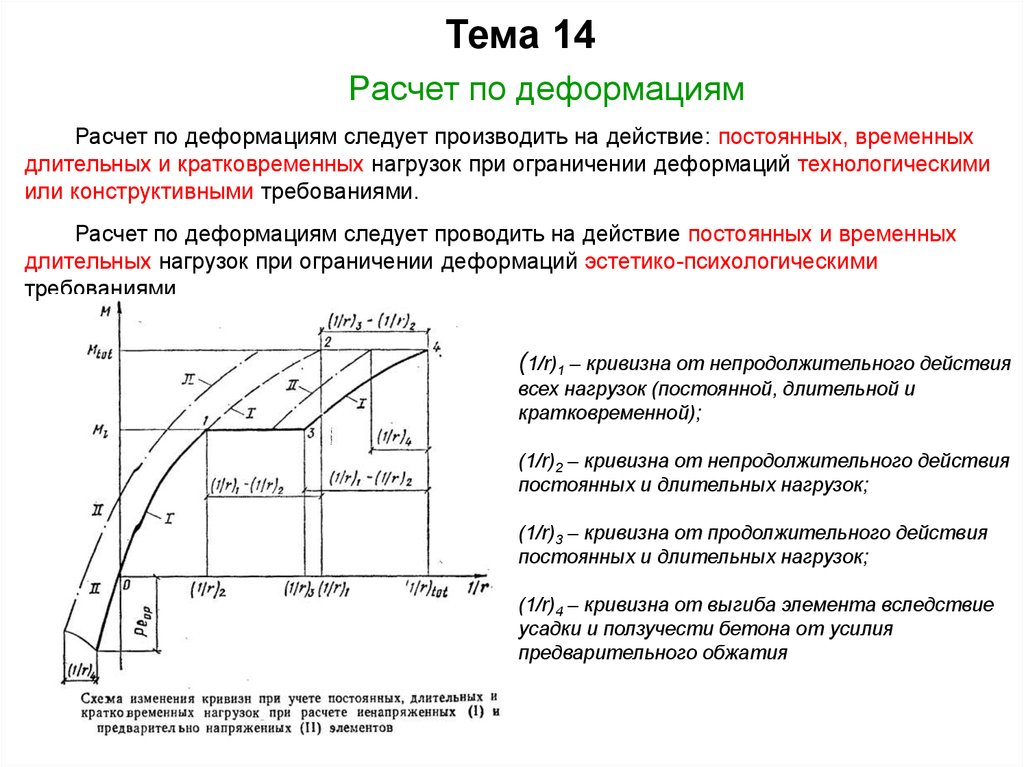
Тема 14Расчет по деформациям
Расчет по деформациям следует производить на действие: постоянных, временных
длительных и кратковременных нагрузок при ограничении деформаций технологическими
или конструктивными требованиями.
Расчет по деформациям следует проводить на действие постоянных и временных
длительных нагрузок при ограничении деформаций эстетико-психологическими
требованиями.
(1/r)1 – кривизна от непродолжительного действия
всех нагрузок (постоянной, длительной и
кратковременной);
(1/r)2 – кривизна от непродолжительного действия
постоянных и длительных нагрузок;
(1/r)3 – кривизна от продолжительного действия
постоянных и длительных нагрузок;
(1/r)4 – кривизна от выгиба элемента вследствие
усадки и ползучести бетона от усилия
предварительного обжатия
2.
Определение кривизны железобетонных элементов.Для элементов без предварительного напряжения полную кривизну
определяют по формуле:
- для участков без трещин в растянутой зоне
1 1 1
r r 1 r 2
где (1/r)1 и (1/r)2 – кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и
временных нагрузок
- для участков с трещинами
1 1 1 1
r r 1 r 2 r 3
где:
(1/r)1 – кривизна от непродолжительного действия всех нагрузок, на которые производят
расчет по деформациям;
(1/r)2 – кривизна от непродолжительного действия постоянных и длительных нагрузок;
(1/r)3 – кривизна от продолжительного действия постоянных и длительных нагрузок.
3.
Для предварительно напряженных элементов полную кривизну определяют поформуле:
для участков без трещин в растянутой зоне:
1 1 1 1
r r 1 r 2 r 3
где (1/r)1 и (1/r)2 – кривизны соответственно от непродолжительного действия
кратковременных нагрузок и от продолжительного действия постоянных и длительных
нагрузок нагрузок.
(1/r)3 – кривизна от непродолжительного действия усилия предварительного обжатия P
(т.е. при действии M = P eop).
для участков с трещинами
1 1 1 1
r r 1 r 2 r 3
где (1/r)1 – кривизна от непродолжительного действия всех нагрузок, на которые
производят расчет по деформациям;
(1/r)2 – кривизна от непродолжительного действия постоянных и длительных нагрузок;
(1/r)3 – кривизна от продолжительного действия постоянных и длительных нагрузок.
4.
На участках элемента без трещин кривизну определяют как для сплошного приведенногосечения в стадии I напряженно-деформированного состояния:
1 M
r Bпр
где Bпр – жесткость приведенного сечения (при продолжительном действии нагрузки с
учетом ползучести бетона).
Bпр E b1 I red
Ired – момент инерции приведенного поперечного сечения, включающего в себя площадь
поперечного сечения только сжатой зоны бетона и площади сечения сжатой и
растянутой арматуры, умноженные на коэффициент приведения арматуры к бетону
sl
Es
Eb,red
Eb1 – модуль деформации сжатого бетона
при непродолжительном действии нагрузки
Eb1 0.85 Eb
при продолжительном действии нагрузки
Eb
Eb1
1 b,cr
b,cr - коэффициент ползучести бетона
5.
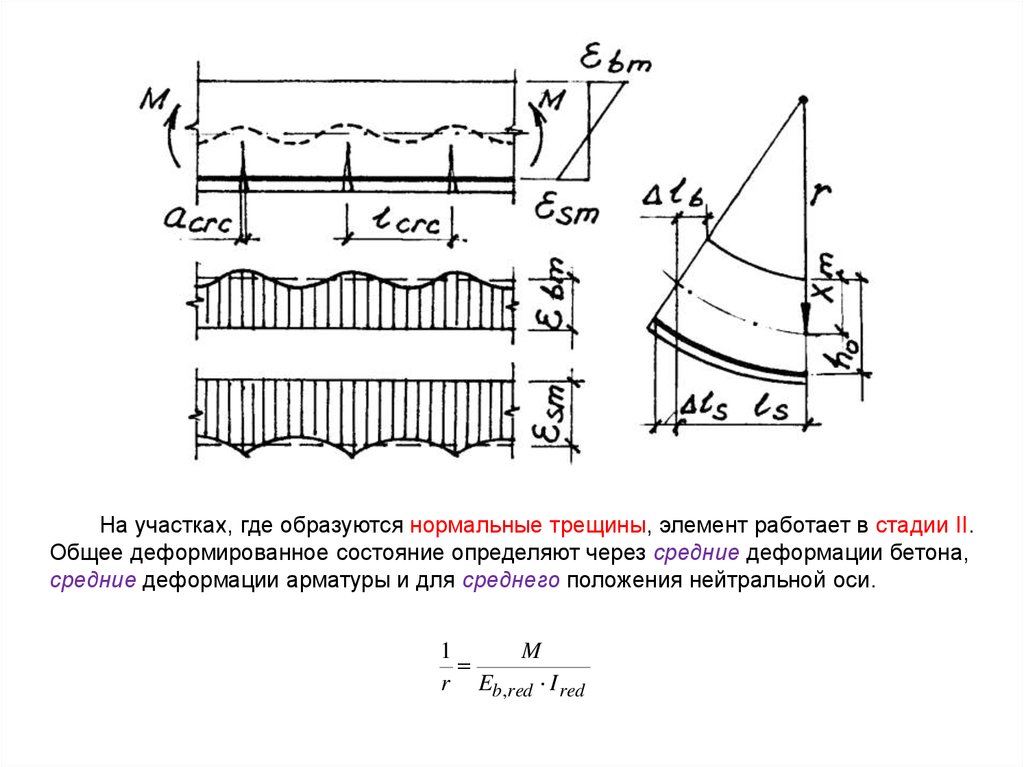
На участках, где образуются нормальные трещины, элемент работает в стадии II.Общее деформированное состояние определяют через средние деформации бетона,
средние деформации арматуры и для среднего положения нейтральной оси.
1
M
r Eb,red I red
6.
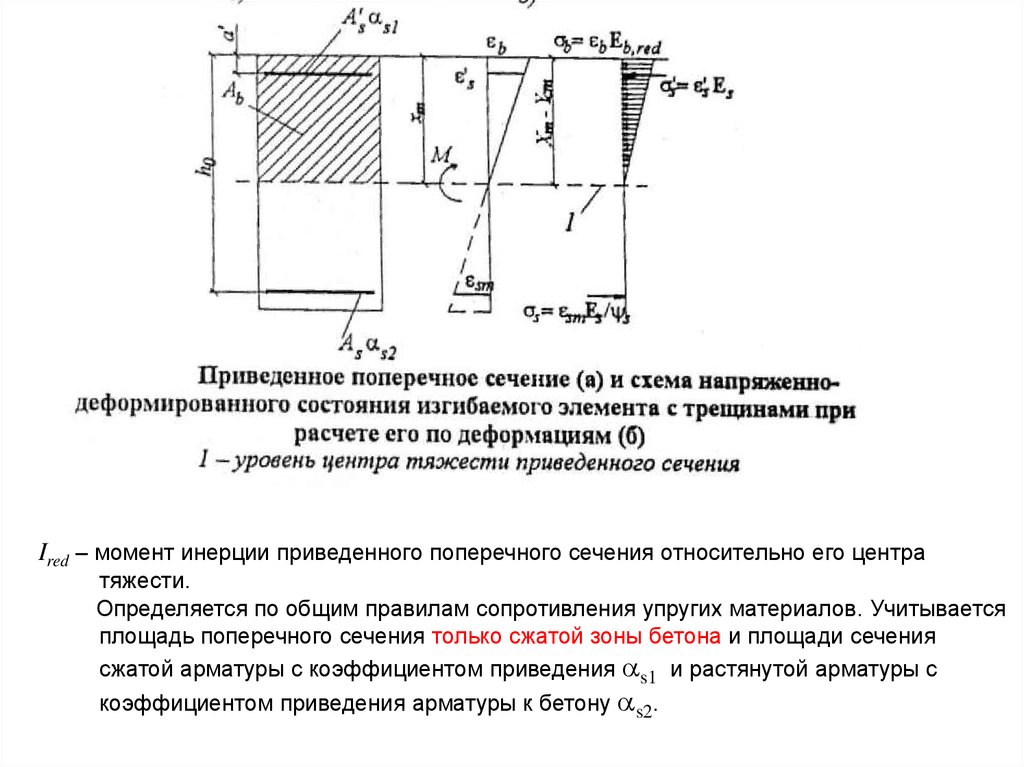
Ired – момент инерции приведенного поперечного сечения относительно его центратяжести.
Определяется по общим правилам сопротивления упругих материалов. Учитывается
площадь поперечного сечения только сжатой зоны бетона и площади сечения
сжатой арматуры с коэффициентом приведения s1 и растянутой арматуры c
коэффициентом приведения арматуры к бетону s2.
7.
I red I b I s s 2 I s s1Ib, Is, I's - моменты инерции площадей сечения соответственно сжатой зоны бетона,
растянутой и сжатой арматуры относительно центра тяжести приведенного без учета
бетона растянутой зоны поперечного сечения.
Высоту сжатой зоны бетона определяют из решения уравнения:
Sb s 2 S s s1 S ' s
где Sb, Ss и S’s – статические моменты соответственно сжатой зоны бетона, площадей
растянутой и сжатой арматуры относительно нейтральной оси.
Для прямоугольных тавровых и двутавровых сечений высоту сжатой зоны можно
определить по формуле:
h f
a
2
z
x h0 z 2 s s 2 s s1 f
h
2
h
0
0
где
z s s 2 s s1 f
s
As
;
b h0
A
s s ;
b h0
f
b f b h f
b h0
8.
Eb,red – приведенный модуль деформации сжатого бетона, принимаемый равным:E b,red
R b,ser
b1,red
Значения коэффициентов приведения для сжатой арматуры : s1
Для растянутой арматуры
s 2
Es
;
s E b,red
Es
;
E b,red
s – коэффициент, учитывающий неравномерное распределение относительных
деформаций растянутой арматуры между трещинами.
Можно определять эти коэффициенты приведения по упрощенным формулам:
s2
s1
s1
300
R b,ser
s1
;
s
- при непродолжительном действии нагрузки;
560 - при продолжительном действии нагрузки и нормальной влажности
R b,ser окружающего воздуха (w = 40…75%);
9.
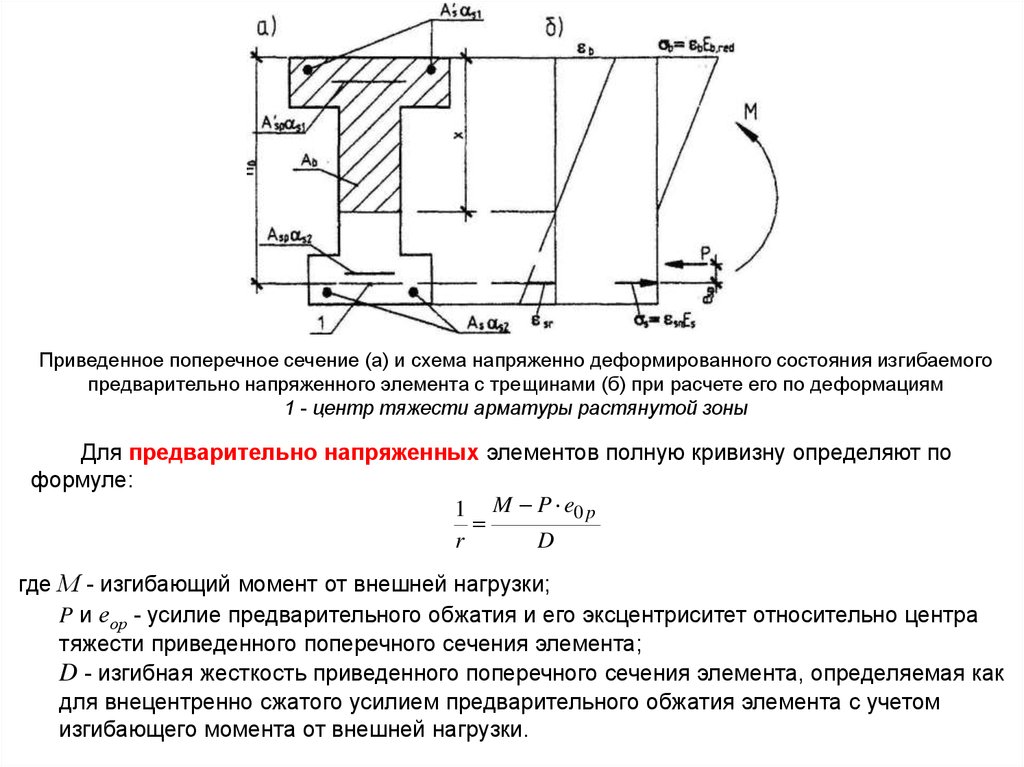
Приведенное поперечное сечение (а) и схема напряженно деформированного состояния изгибаемогопредварительно напряженного элемента с трещинами (б) при расчете его по деформациям
1 - центр тяжести арматуры растянутой зоны
Для предварительно напряженных элементов полную кривизну определяют по
формуле:
1 M P e0 p
r
D
где М - изгибающий момент от внешней нагрузки;
P и еор - усилие предварительного обжатия и его эксцентриситет относительно центра
тяжести приведенного поперечного сечения элемента;
D - изгибная жесткость приведенного поперечного сечения элемента, определяемая как
для внецентренно сжатого усилием предварительного обжатия элемента с учетом
изгибающего момента от внешней нагрузки.
10.
Для прямоугольных, тавровых и двутавровых элементов безпредварительного напряжения можно проводить расчет по упрощенной
формуле:
- определяется по табл. 4.5 Пособия к СП 63.13330.2012 в зависимости
от величин:
- определяется по табл. 4.6 Пособия к СП 63.13330.2012 в зависимости
от величин:
11.
Полная кривизна:1
P
r S red Eb,red
где Sred – статический момент приведенного поперечного сечения относительно нейтральной оси
Eb,red – приведенный модуль деформации сжатого бетона, который вычисляется как для
элементов без предварительного напряжения.
Высоту сжатой зоны x определяют из решения уравнения:
I red M
esp h0 x
S red
P
где Ired – момент инерции приведенного поперечного сечения относительно его
нейтральной оси,
esp – расстояние от точки приложения усилия обжатия P до центра тяжести растянутой
арматуры
12.
Для прямоугольных, тавровых и двутавровых элементов можно проводить расчетпо упрощенной формуле при:
h f 0.3 h
a s 0.2 h 0
и
1
M
r c b h03 Eb,red
Коэффициент с определяется в зависимости от f, s2, es/h
es
M
esp
P
As Asp
;
b h0
f
0.5
b f b h f Asp As s1
b h0
h f
h0
;








 Строительство
Строительство








