Предварительный эксперимент и методы его анализа

1. Раздел 2. ЭКСПЕРИМЕНТАЛЬНО-СТАТИСТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ

Раздел 2.
ЭКСПЕРИМЕНТАЛЬНОСТАТИСТИЧЕСКИЕ МЕТОДЫ
МОДЕЛИРОВАНИЯ
Тема 1.
Предварительный
эксперимент и методы его
анализа

2. 1.1. Экспериментирование как метод получения информации о системе

Информация - это некоторая
последовательность сведений, знаний,
которые актуализируемы (получаемы,
передаваемы, преобразуемы, сжимаемы
и/или регистрируемы) с помощью
некоторых знаков (символьного,
образного, жестового, звукового,
сенсомоторного типа)
2

3. 1.1. Экспериментирование как метод получения информации о системе

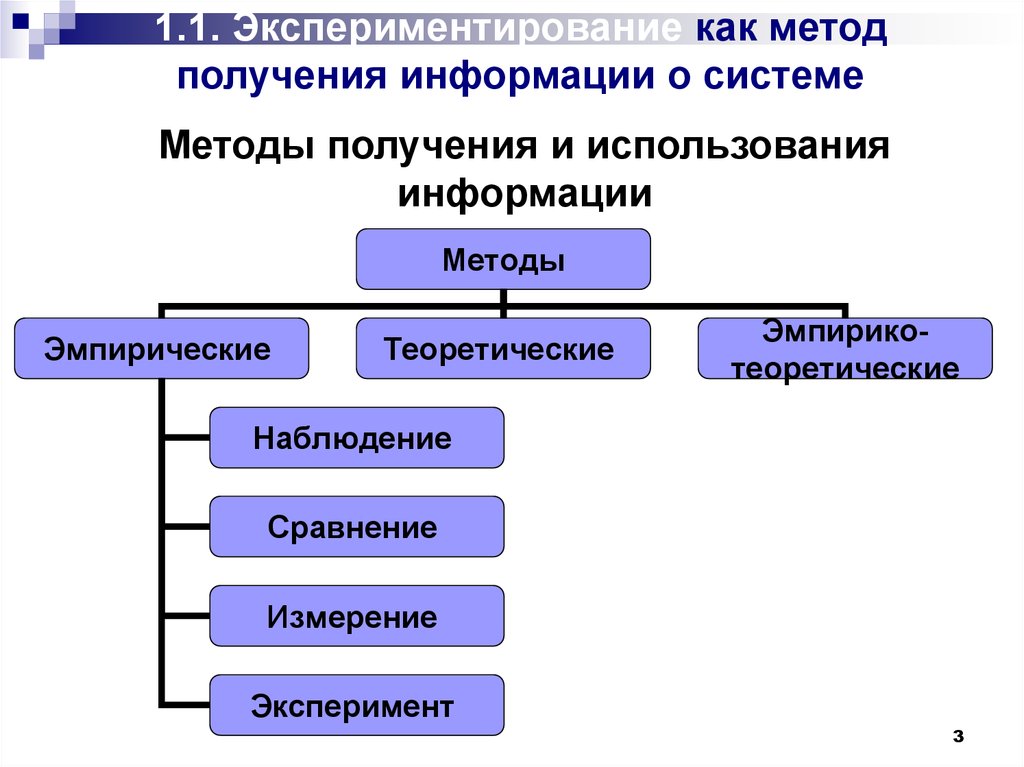
Методы получения и использования
информации
Методы
Эмпирические
Теоретические
Эмпирикотеоретические
Наблюдение
Сравнение
Измерение
Эксперимент
3

4. 1.1. Экспериментирование как метод получения информации о системе

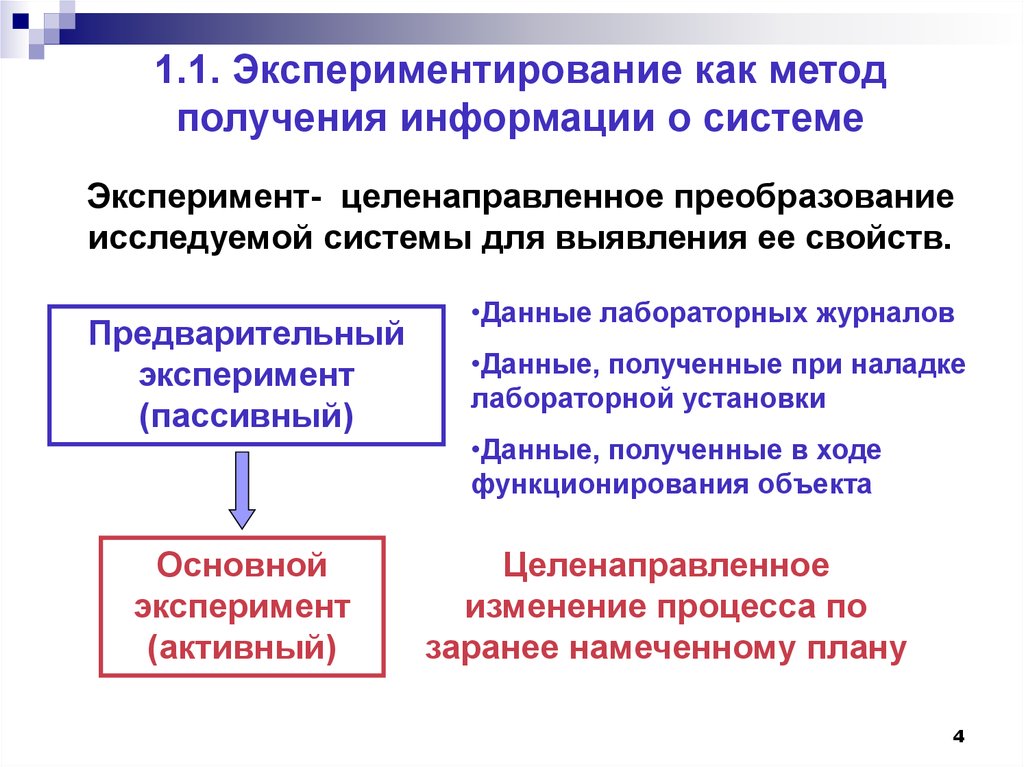
Эксперимент- целенаправленное преобразование
исследуемой системы для выявления ее свойств.
Предварительный
эксперимент
(пассивный)
Основной
эксперимент
(активный)
•Данные лабораторных журналов
•Данные, полученные при наладке
лабораторной установки
•Данные, полученные в ходе
функционирования объекта
Целенаправленное
изменение процесса по
заранее намеченному плану
4

5. 1.1. Экспериментирование как метод получения информации о системе

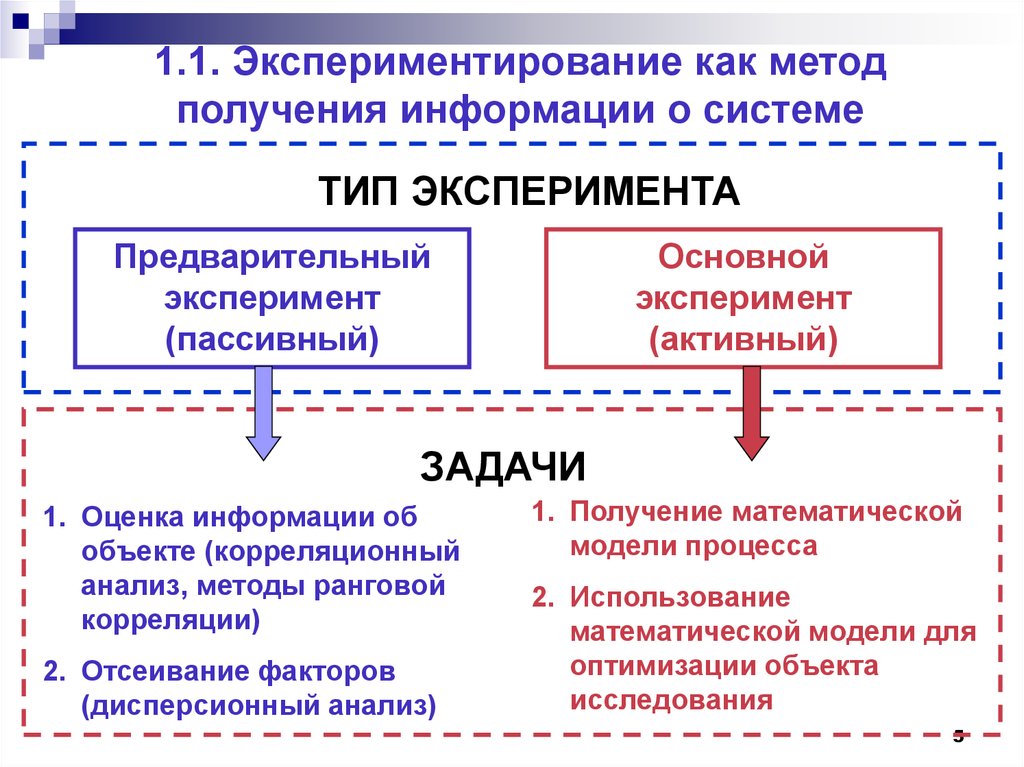
ТИП ЭКСПЕРИМЕНТА
Предварительный
эксперимент
(пассивный)
Основной
эксперимент
(активный)
ЗАДАЧИ
1. Оценка информации об
объекте (корреляционный
анализ, методы ранговой
корреляции)
2. Отсеивание факторов
(дисперсионный анализ)
1. Получение математической
модели процесса
2. Использование
математической модели для
оптимизации объекта
исследования
5

6. 1.2. Генеральная совокупность и случайная выборка

Выборка
(выборочная
совокупность)
-
часть
объектов из генеральной совокупности, отобранных
для изучения, с целью получения информации о
всей генеральной совокупности.
Генеральная
совокупность
-
все
допустимые
значения случайной величины
Выборка,
которая
генеральной
репрезентативной.
сохраняет
совокупности,
все
свойства
называется
6

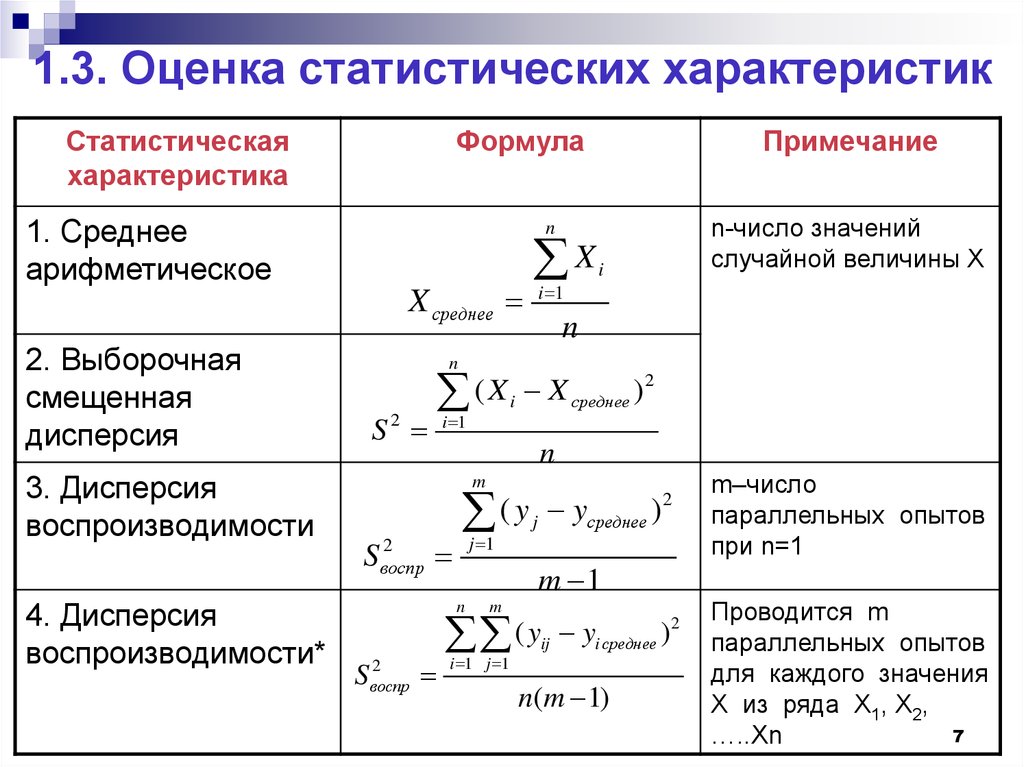
7. 1.3. Оценка статистических характеристик

Статистическая
характеристика
1. Среднее
арифметическое
2. Выборочная
смещенная
дисперсия
3. Дисперсия
воспроизводимости
4. Дисперсия
воспроизводимости*
Формула
Примечание
n-число значений
случайной величины Х
n
X среднее
X
i 1
i
n
n
S2
2
(
X
X
)
i среднее
i 1
n
m
2
Sвоспр
(y
j 1
m 1
n
2
Sвоспр
yсреднее )
j
2
m
( y
i 1 j 1
ij
yi среднее )
n(m 1)
2
m–число
параллельных опытов
при n=1
Проводится m
параллельных опытов
для каждого значения
Х из ряда Х1, Х2,
7
…..Хn

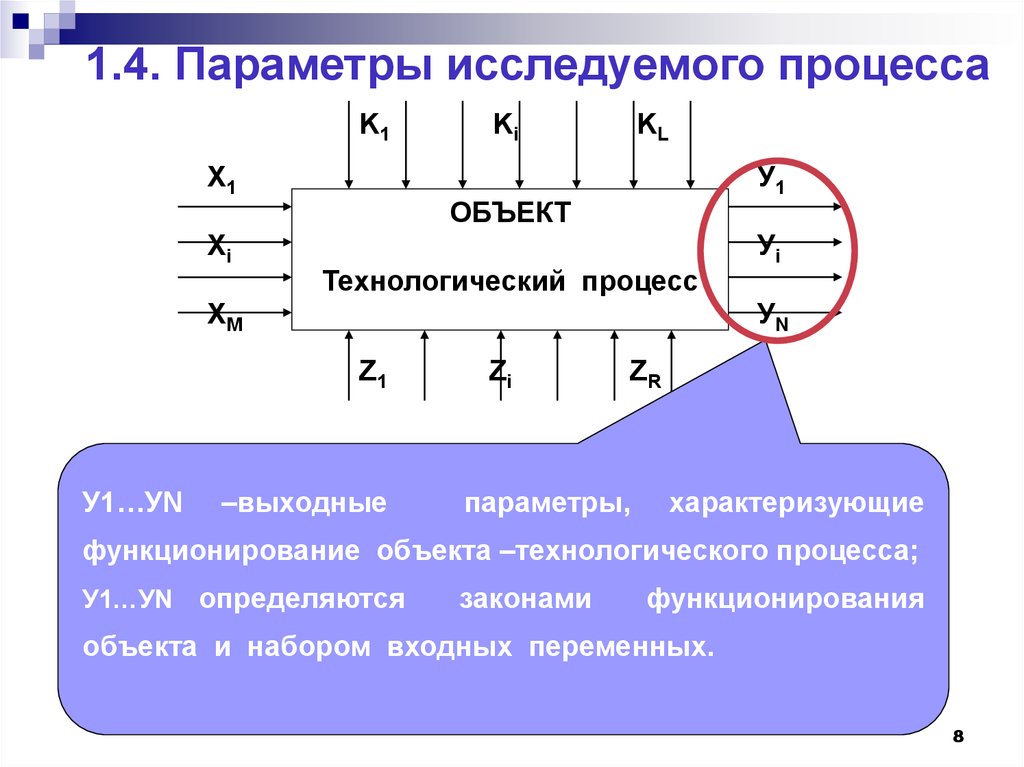
8. 1.4. Параметры исследуемого процесса

K1
Х1
Хi
Ki
KL
У1
ОБЪЕКТ
Технологический процесс
ХM
УN
Z1
У1…УN
Уi
–выходные
Zi
ZR
параметры,
характеризующие
функционирование объекта –технологического процесса;
У1…УN определяются
законами
функционирования
объекта и набором входных переменных.
8

9. 1.4. Параметры исследуемого процесса

Выходные
параметры
Технологические
Техникоэкономические
Степень
конверсии
мономера
Себестоимость
Выход полимера
Прибыль
на ед.продукции
ММР
9

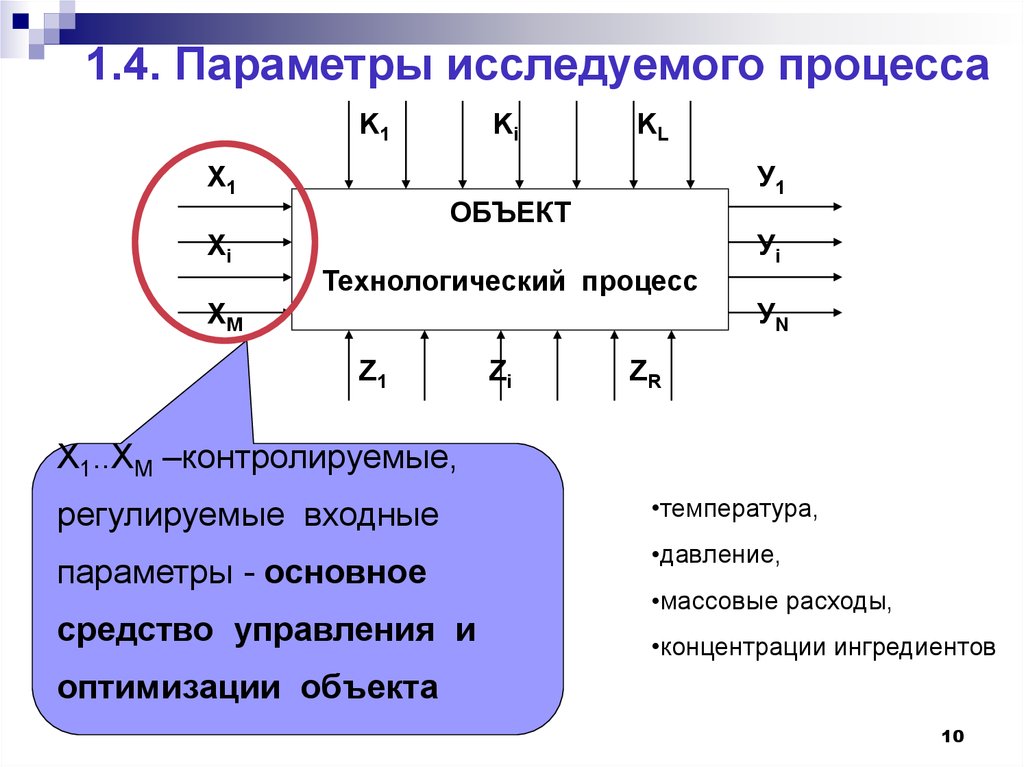
10. 1.4. Параметры исследуемого процесса

K1
Х1
Хi
Ki
KL
У1
ОБЪЕКТ
Технологический процесс
ХM
Уi
УN
Z1
Zi
ZR
Х1..ХМ –контролируемые,
регулируемые входные
•температура,
параметры - основное
•давление,
средство управления и
•массовые расходы,
•концентрации ингредиентов
оптимизации объекта
10

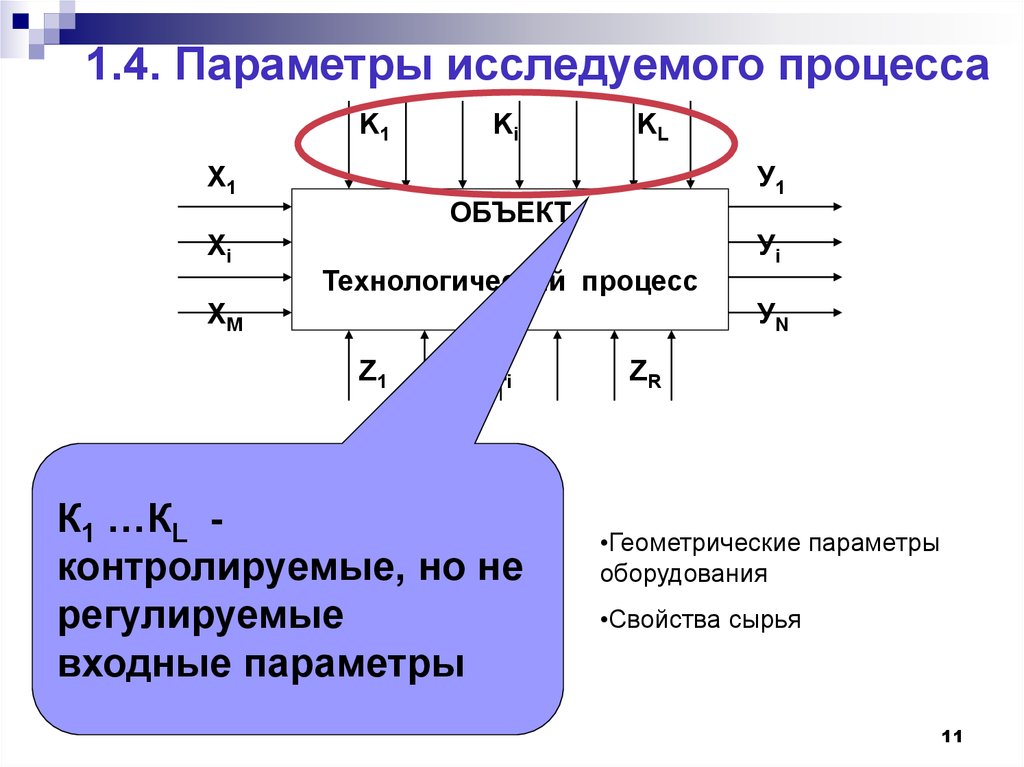
11. 1.4. Параметры исследуемого процесса

K1
Х1
Хi
Ki
KL
У1
ОБЪЕКТ
Технологический процесс
ХM
Уi
УN
Z1
Zi
К1 …КL контролируемые, но не
регулируемые
входные параметры
ZR
•Геометрические параметры
оборудования
•Свойства сырья
11

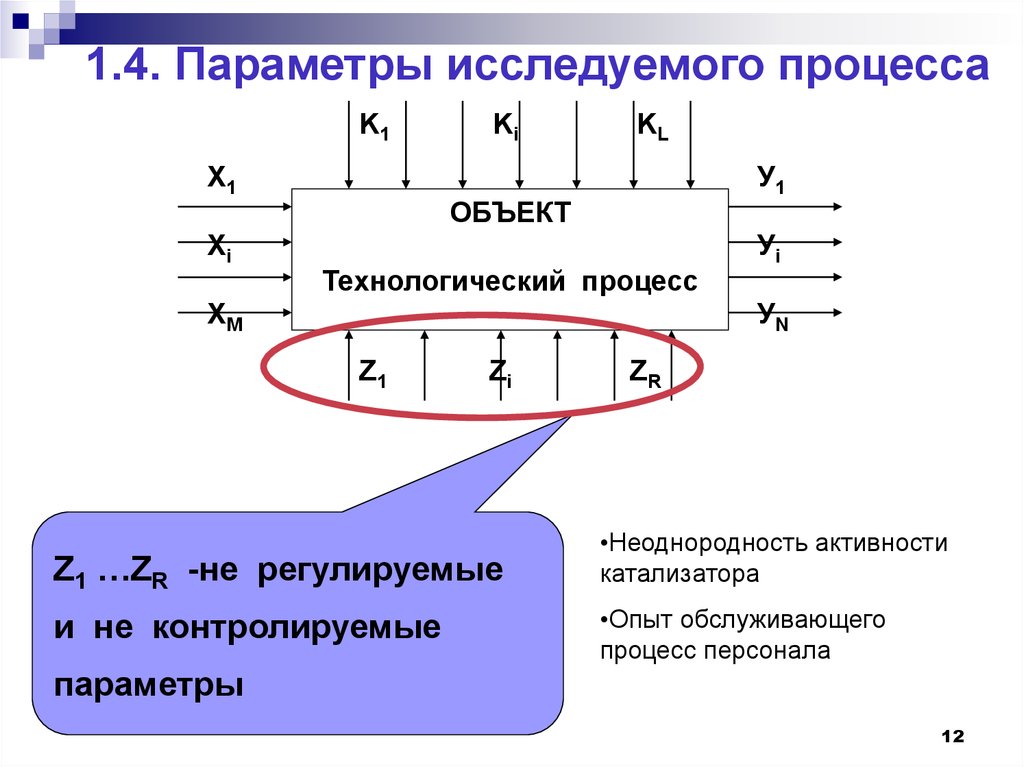
12. 1.4. Параметры исследуемого процесса

K1
Х1
Хi
Ki
KL
У1
ОБЪЕКТ
Технологический процесс
ХM
Уi
УN
Z1
Zi
Z1 …ZR -не регулируемые
и не контролируемые
ZR
•Неоднородность активности
катализатора
•Опыт обслуживающего
процесс персонала
параметры
12

13.

K1
Х1
Хi
Ki
KL
У1
ОБЪЕКТ
Технологический процесс
ХM
Уi
УN
Z1
Zi
ZR
Задача исследователя сводится к анализу связи У и
(Х,Z,К) или чаще всего У и (Х,К).
Основными результатами анализа являются:
Сформированные уравнения связи
(расчетные, проектные уравнения) У =f (Х,К);
Набор констант (параметров) уравнений связи;
Алгоритмы решения этих уравнений
13

14. 1.3. Этапы предварительного эксперимента и его анализа

Выбор переменных состояния (выходных параметров)
Выбор факторов (входных параметров)
Проведение эксперимента
Дисперсионный анализ
Корреляционный анализ
Регрессионный анализ
14

15. 1.3. Этапы предварительного эксперимента и его анализа

Этап 1. Выбор переменных состояния
(выходных параметров)
Требования к переменной состояния:
1. Должна иметь количественную характеристику
2. Должна однозначно измерять объект
исследования
3. Должна иметь область определения, заданную
технологическими или принципиальными
ограничениями
15

16. 1.3. Этапы предварительного эксперимента и его анализа

Этап 2. Выбор факторов
(входных параметров)
Требования к факторам:
1. Должны быть регулируемыми с помощью
определенного устройства, точность измерения
факторов которым должна быть известной и
достаточно высокой
16

17. 1.3. Этапы предварительного эксперимента и его анализа

Этап 4. Корреляционный анализ
—
метод
обработки
заключающийся
в
статистических
изучении
(корреляции)
между
сравниваются
коэффициенты
данных,
коэффициентов
переменными.
При
корреляции
этом
между
одной парой или множеством пар признаков, для
установления
между
ними
статистических
взаимосвязей
17

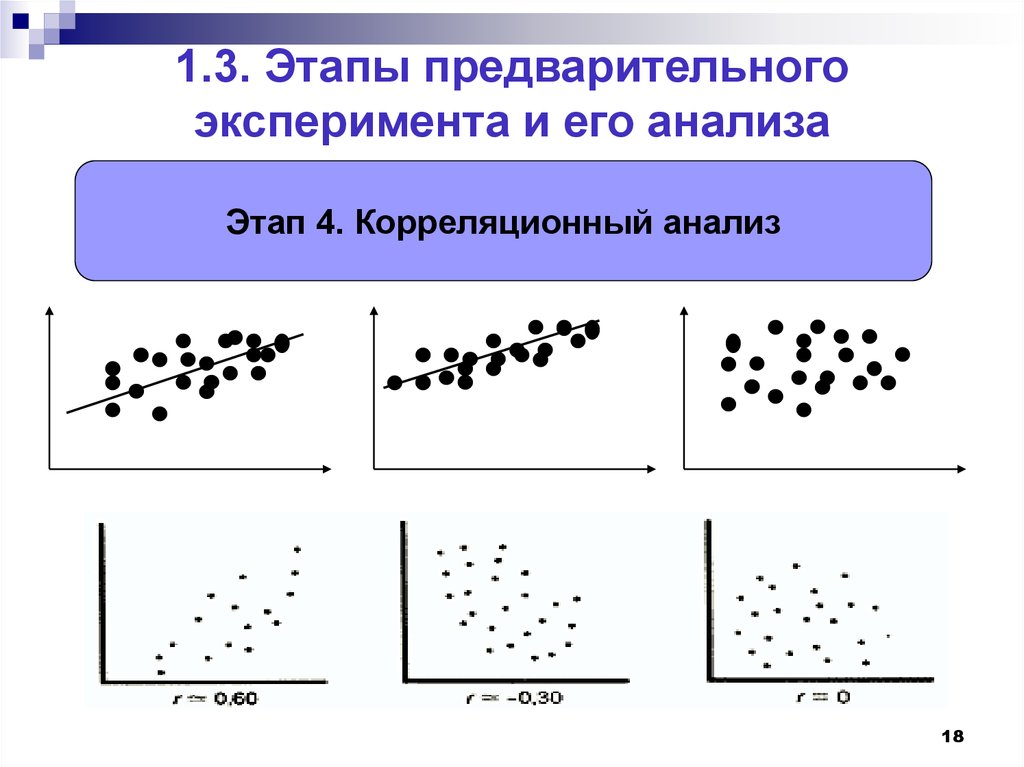
18. 1.3. Этапы предварительного эксперимента и его анализа

Этап 4. Корреляционный анализ
18

19. 1.3. Этапы предварительного эксперимента и его анализа

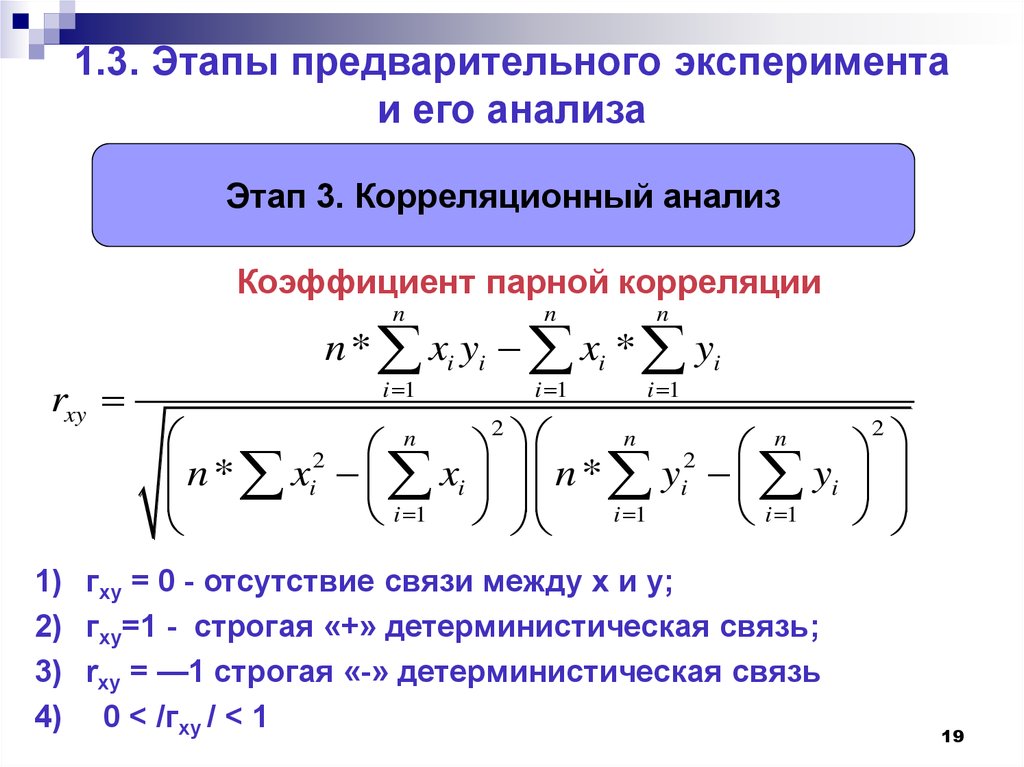
Этап 3. Корреляционный анализ
Коэффициент парной корреляции
rxy
n
n
n
i 1
i 1
i 1
n * xi yi xi * yi
2
2
n
n
n
2
2
n * xi xi n * yi yi
i
1
i
1
i
1
1) гху = 0 - отсутствие связи между х и y;
2) гxy=1 - строгая «+» детерминистическая связь;
3) rxy = —1 строгая «-» детерминистическая связь
4) 0 < /гxy / < 1
19

20. 1.3. Этапы предварительного эксперимента и его анализа

Этап 5. Регрессионный анализ
Уравнения для расчета
коэффициентов линейной
однофакторной регрессии
n
a1
Y a0 a1 X
n
x y
i 1
i
i 1
n
i
2
n xi yi
i 1
2
xi n xi
i 1
i 1
n
n
20

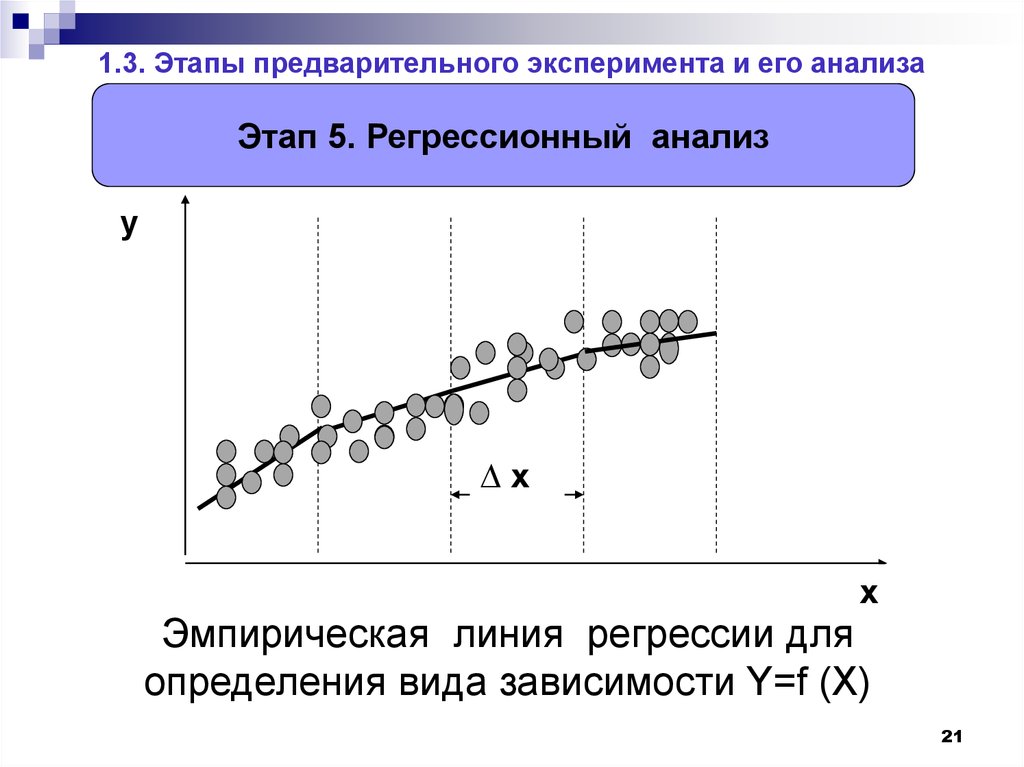
21. 1.3. Этапы предварительного эксперимента и его анализа

Этап 5. Регрессионный анализ
у
∆х
х
Эмпирическая линия регрессии для
определения вида зависимости Y=f (Х)
21

22.

Виды однофакторных регрессионных моделей
и расчет коэффициентов регрессии
22

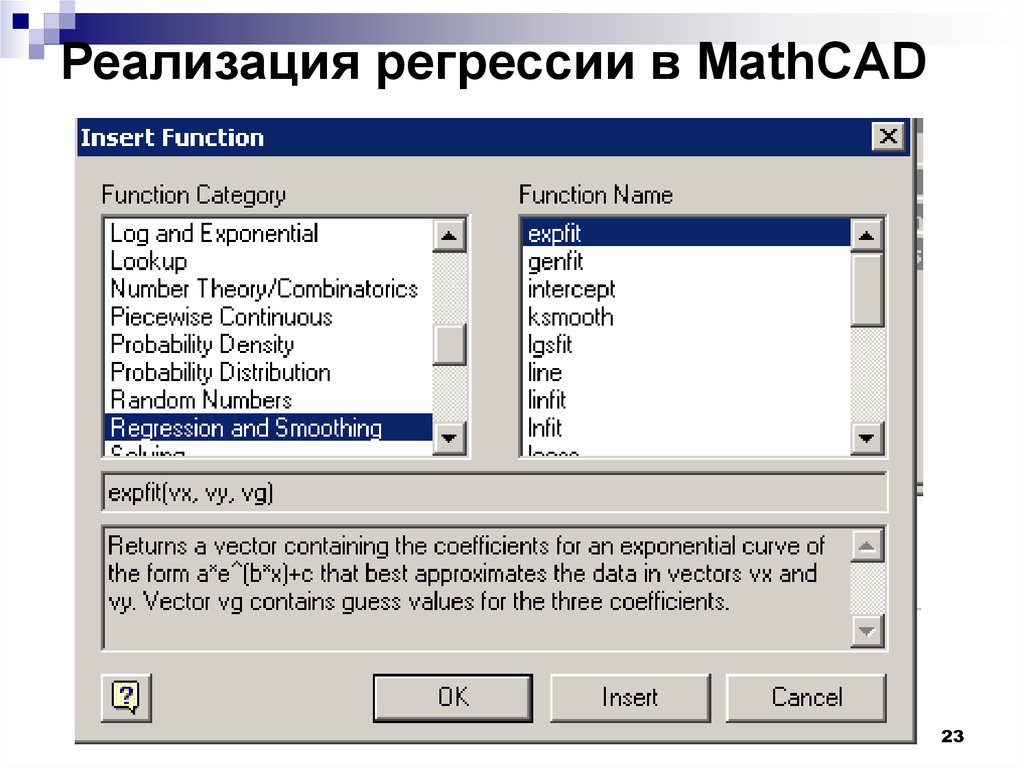
23. Реализация регрессии в MathCAD

23

24. Реализация однофакторной регрессии в Excel

Шаг 1 – Внесение экспериментальных
данных
24

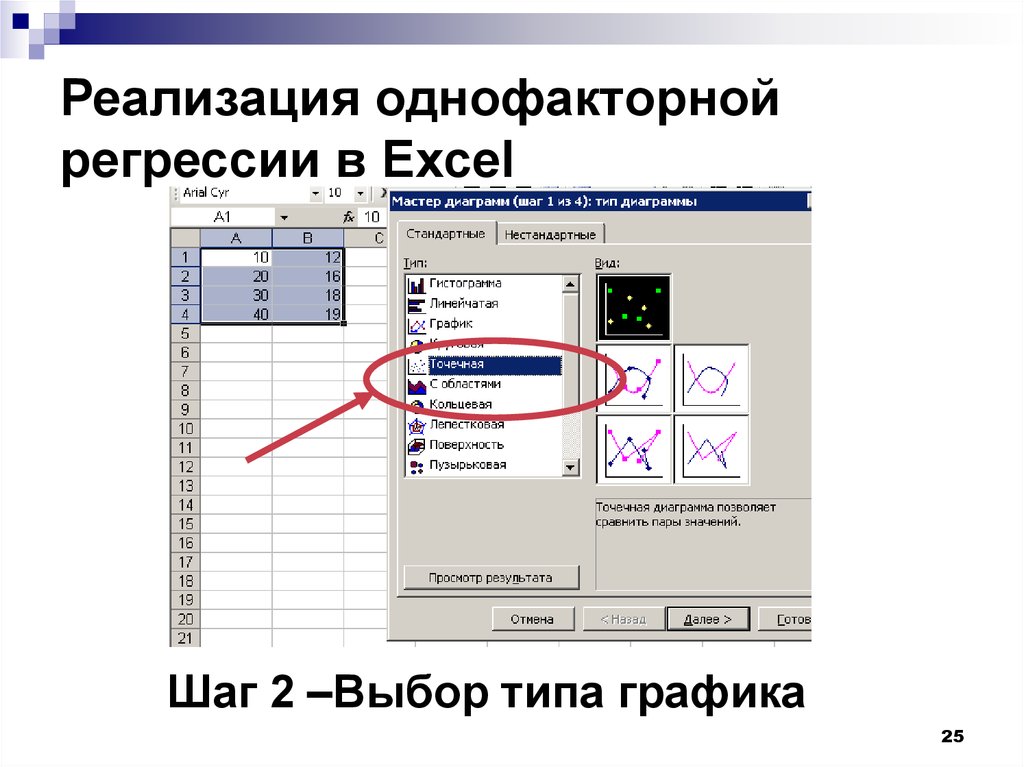
25. Реализация однофакторной регрессии в Excel

Шаг 2 –Выбор типа графика
25

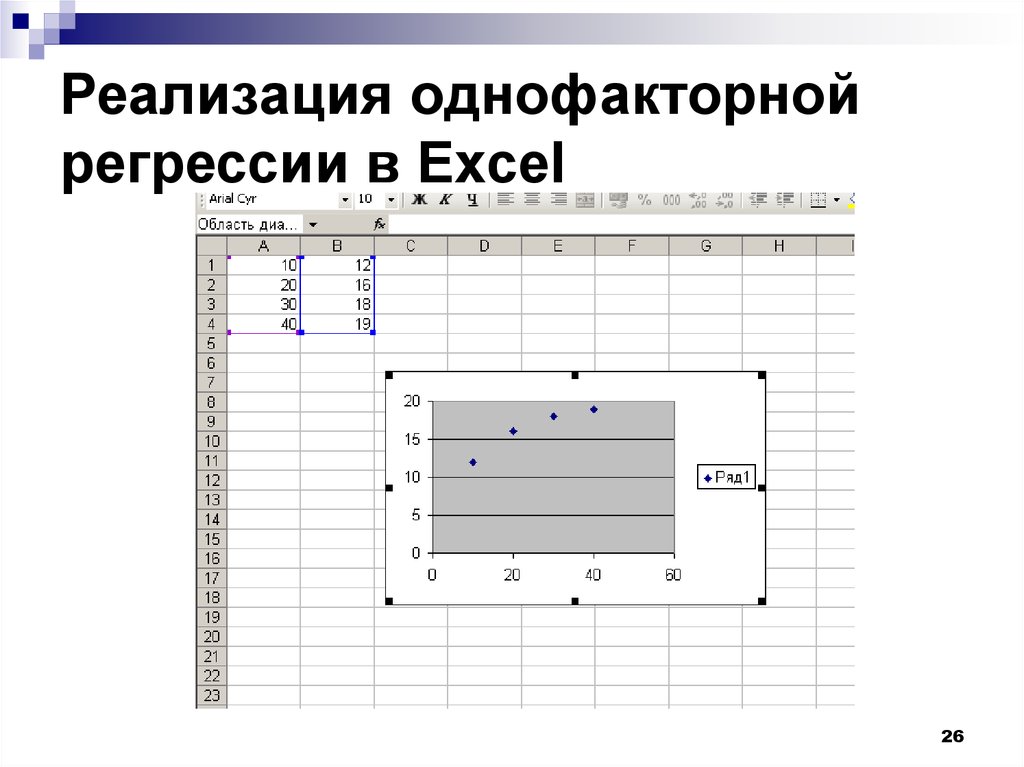
26. Реализация однофакторной регрессии в Excel

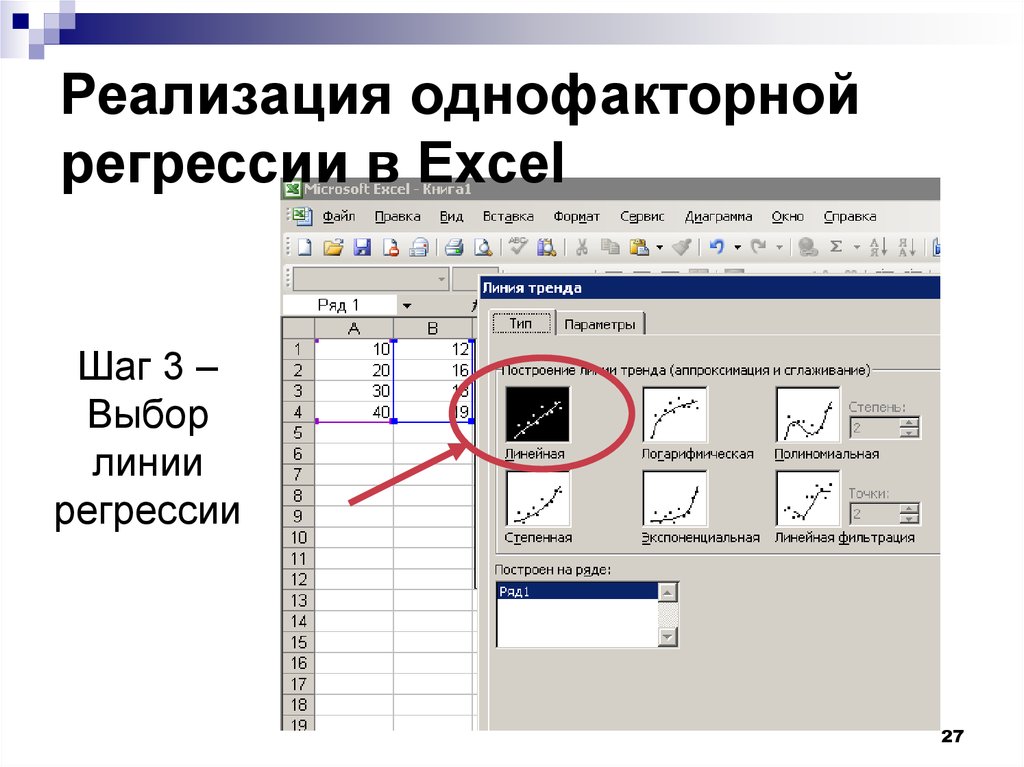
26

27. Реализация однофакторной регрессии в Excel

Шаг 3 –
Выбор
линии
регрессии
27

28. Реализация однофакторной регрессии в Excel

28

29. Реализация однофакторной регрессии в Excel

29