Аттестационная работа. Способы решения квадратных уравнений

1. Аттестационная работа

Слушателя курсов повышения квалификации по программе:
«Проектная и исследовательская деятельность как способ
формирования метапредметных результатов обучения в
условиях реализации ФГОС»
Сагитова Альмира Рашитовна
Фамилия, имя, отчество
МАОУ СОШ № 70 город Тюмень
Образовательное учреждение, район
На тему:
«Способы решения квадратных уравнений»
1

2.

Социологический опрос
Способы решения квадратного уравнения
Метод выделения квадрата двучлена
Метод разложения левой части уравнения на
множители способом группировки
Решение уравнения по формулам дискриминанта
и корней квадратного уравнения
Решение уравнения, используя теорему Виета.
Решение уравнения графическим способом.
Неверно решили уравнение
Количество учащихся
0
0%
2
2,5 %
53
67 %
4
0
20
5%
0%
25,5 %

3.

Актуальность проблемы
Теория уравнений занимает ведущее место в
алгебре и математике в целом. Сила теории уравнений
в том, что не только имеет теоретическое значение
для познания естественных законов, но и служит
практическим целям. Большинство жизненных задач
сводится к решению различных видов уравнений, и
чаще это уравнения квадратного вида.

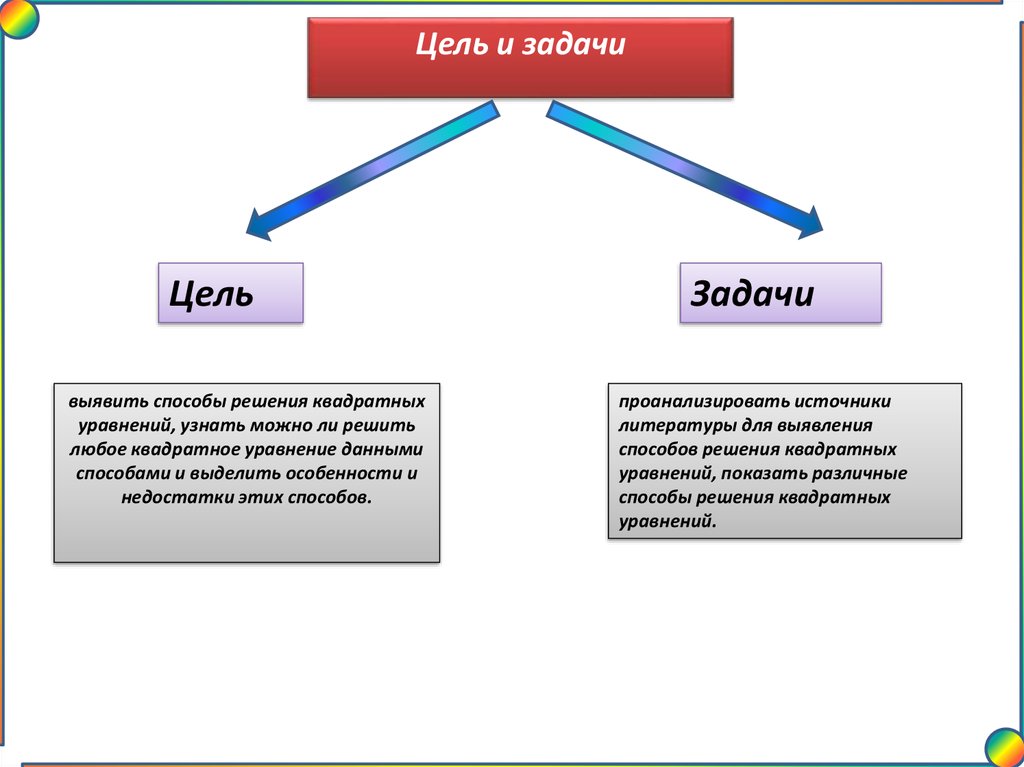
4.

Цель и задачи
Цель
выявить способы решения квадратных
уравнений, узнать можно ли решить
любое квадратное уравнение данными
способами и выделить особенности и
недостатки этих способов.
Задачи
проанализировать источники
литературы для выявления
способов решения квадратных
уравнений, показать различные
способы решения квадратных
уравнений.

5.

Объект исследования:
квадратные уравнения.
Предмет исследования:
способы решения
квадратных уравнений.

6.

Гипотеза:
существуют ли другие способы
решения квадратного уравнения и
имеют ли они право на жизнь?
Методы исследования:
анализ литературы, социологичес кий опрос, наблюдение, сравнение и
обобщение результатов.

7.

Этапы выполнения
исследовательской работы:
Сбор данных
Обработка данных
Анализ данных

8.

Сбор данных
История возникновения квадратных уравнений
Др.Индия 499 г.
Диофант
Др. Вавилон
Европа 13 – 17 в.

9.

Сбор данных
Способы решения квадратных уравнений
Разложение левой части на множители
Метод выделения полного квадрата
По формуле
С использованием теоремы Виета
(прямой и обратной)
Основные
Графический способ
По свойствам коэффициентов
Способом «переброски»
С помощью циркуля и линейки
С помощью номограммы
Геометрический способ
Дополнительные

10.

По свойствам коэффициентов
Свойства:

11.

Способом «переброски»
Умножив обе части уравнения на а, получим
Пусть
, откуда
Тогда получим уравнение с новой переменной
Его корни у1 и у2. Окончательно

12.

С помощью циркуля и линейки
Данный способ заключается в том, чтобы при
нахождении корней уравнения
отметить в системе координат точки
и А(0;1); провести окружность с центром в точке S и
радиусом SA. Абсциссы точек пересечения с осью
Ох есть корни исходного уравнения
Радиус окружности больше ординаты центра
, окружность пересекает ось
Ох в двух точках
, где
корни исходного уравнения.
Радиус окружности равен ординате центра
, окружность пересекает ось
Ох в одной точке
где
корень
исходного уравнения.
Радиус окружности меньше ординаты центра
, окружность не имеет общих
точек с осью Ох. В этом случае исходное уравнение
не имеет корней.

13.

С помощью номограммы
Это старый и незаслуженно забытый способ
решения квадратных уравнений. Номограмма взята из
«Четырѐхзначных математических таблиц»
В.М.Брадиса. При помощи этой номограммы
приближѐнно можно найти положительные корни
конкретного уравнения
Для этого надо на оси р взять точку M с координатой р, на
оси q – точку N с координатой q и провести прямую MN. Каждая
точка пересечения прямой MN с кривой Г даѐт положительный
корень уравнения.
Построенная прямая MN может пересекаться с кривой Г:
в двух точках (в этом случае оба корня данного уравнения
положительны);
в одной точке (в этом случае второй корень уравнения
отрицателен);
может касаться кривой (в этом случае у уравнения
кратный положительный корень);
может не иметь с кривой Г ни одной общей точки (в этом
случае либо оба корня уравнения отрицательны, либо у него
вообще нет действительных корней).

14.

Геометрический способ
Рассмотрим, как древние греки решали уравнение
Решение представлено на рисунке, где
или
Выражения
и 16 + 9
геометрически представляют собой один и
тот же квадрат со стороной 5. Поэтому

15.

Обработка данных
Разложение левой части
уравнения на множители
Метод выделения
полного квадрата
Ответ: -4,5; 1.

16.

Обработка данных
По формуле
С использованием
формул Виета
имеет два разных
по знаку корня
больший по модулю
корень отрицательный
Ответ: -4,5; 1.

17.

Обработка данных
Способом «переброски»
Перебросим коэффициент а = 2 к
свободному члену и получим
уравнение:
По свойству коэффициентов
Так как
то
из которого по формулам Виета
Корнями исходного уравнения будут
Ответ: -4,5; 1.

18.

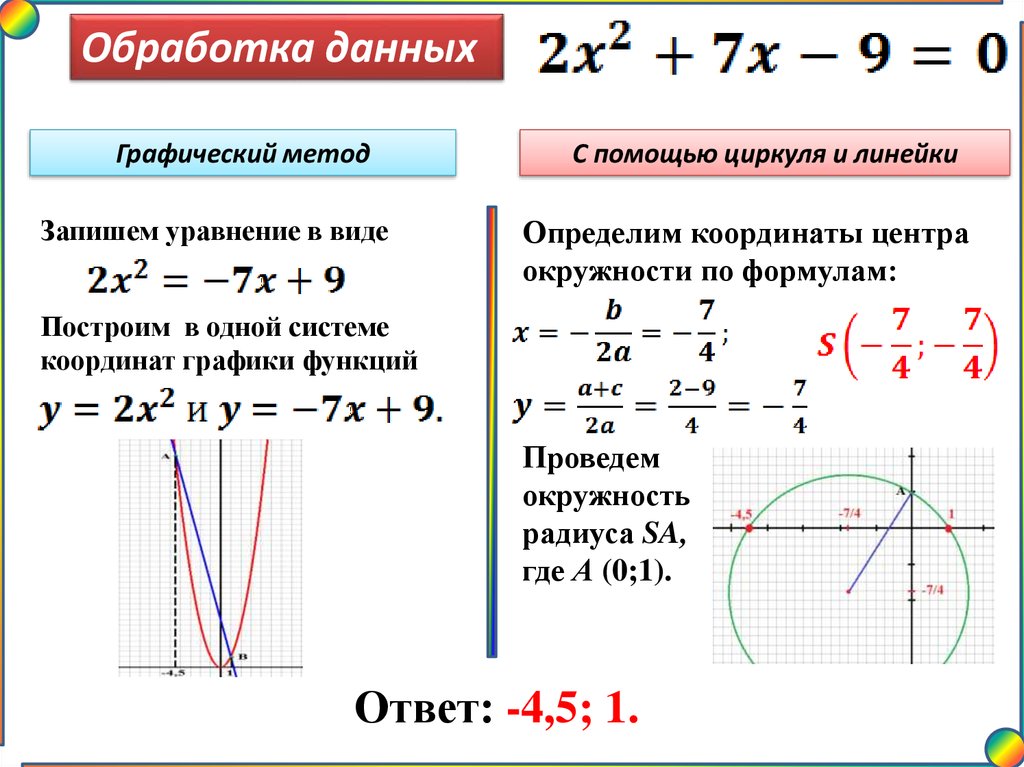
Обработка данных
Графический метод
Запишем уравнение в виде
С помощью циркуля и линейки
Определим координаты центра
окружности по формулам:
Построим в одной системе
координат графики функций
Проведем
окружность
радиуса SA,
где А (0;1).
Ответ: -4,5; 1.

19.

Обработка данных
С помощью номограммы
Представим уравнение в виде:
Номограмма дает
положительный
корень
Геометрический способ
Представим уравнение в виде:
Площадь полученного
квадрата:
Так как
отрицательный
корень
, то:
Таким образом, получили уравнение:
Ответ: -4,5; 1.

20.

Анализ данных
Данные способы решения заслуживают внимания, поскольку
они не все отражены в школьных учебниках математики.
Овладение данными способами поможет учащимся
экономить время и эффективно решать уравнения, так как
потребность в быстром решении обусловлена применением
тестовой системы вступительных экзаменов.
Одни квадратные уравнения можно решить разными способами, а
для других уравнений некоторые способы не применимы.
Основным в решении квадратных уравнений является правильно
выбрать рациональный способ решения и применить алгоритм
решения

21.

положительные стороны и недостатки
Название способа решения
квадратных уравнений
Разложение левой части
уравнения на множители
Положительные стороны
Недостатки
Дает возможность сразу увидеть корни
уравнения.
Метод выделения полного
квадрата
За минимальное количество действий можно
найти корни уравнений
По формуле
Можно применить ко всем квадратным
уравнениям.
Достаточно легкий способ, дает возможность
сразу увидеть корни уравнения.
Нужно правильно расчленить
слагаемые для
группировки.
Нужно правильно найти все
слагаемые для выделения
полного квадрата.
Нужно выучить формулы.
С использованием формул
Виета
Легко находятся только целые
корни.
Способом «переброски»
За минимальное количество действий можно Легко найти только целые корни.
найти корни уравнения, применяется
совместно со способом теоремы Виета.
По свойствам коэффициентов
Не требует особых усилий
Подходит только к некоторым
уравнениям
Графический способ
Наглядный способ
Могут быть не точности при
составлении графиков
С помощью циркуля и линейки
Наглядный способ
Могут быть не точности
С помощью номограммы
Наглядный способ, прост в применении.
Геометрический способ
Наглядный способ.
Не всегда под рукой имеется
номограмма.
Похож на способ выделения
полного квадрата

22.

Список использованной литературы
1. Плужников И.10 способов решения квадратных
уравнений//Математика в школе.-2004.-№41
2. Гусев В. А., Мордкович А. Г. Математика: Справочные
материалы: Книга для учащихся. – М.: Просвещение, 1988
3. Глейзер Г. И. История математики в школе. – М.:
просвещение, 1982
4. Брадис В. М. Четырехзначные математические таблицы
для средней школы. – м., просвещение, 1990
5. Дидактические материалы по алгебре.
6. http://revolution.allbeс.ru/
7. http://mat.1september.ru/2004/41/no42_01.htm