Похожие презентации:
Релятивистская механика материальной точки. Специальная, частная теория относительности. Постулаты Эйнштейна
1. Релятивистская механика материальной точки
Специальная (частная)теория относительности.
Постулаты Эйнштейна
2. Свет играет роль сигнала, который необходим для синхронизации часов, которые отсчитывают различные события.
• Классическая механика Ньютонаневерна при скоростях, стремящихся к
скорости света (v→c).
с = 3∙108 м/с (2,998∙108 м/с).
3.
Для описания движения тел соскоростями близкими к скорости света,
Эйнштейн создал релятивистскую
механику, которая учитывает
требования специальной теории
относительности.
Специальная теория относительности
(СТО) создана в 1905 г. Эйнштейном,
как физическая теория пространства и
времени для случая пренебрежимо
слабых гравитационных полей.
4. Основу теории образуют 2 постулата Эйнштейна:
1. Принцип относительности Эйнштейна;2. Принцип постоянства скорости света.
• Принцип относительности
Эйнштейна является
распространением механического
принципа относительности (принципа
относительности Галилея) на все без
исключения физические объекты.
5. Классический принцип относительности
Справедлив для классической механики,т.е. при v << c.
Формулировка классического принципа
относительности: законы динамики
одинаковы во всех инерциальных
системах отсчёта.
6. Преобразования координат Галилея
r r0 r .(1)Две системы отсчёта:
К – инерциальная система
отсчёта, неподвижная
(лабораторная система
отсчёта).
К' – система движется
равномерно и прямолинейно
относительно К со скоростью
v0 = const.
r радиус вектор материальной точки в системе К.
r радиус вектор материальной точки в системе К'.
r0 радиус вектор начала координат системы К' в системе К.
7.
В начальный момент времени (t = 0) началакоординат систем К и К' совпадают.
В дальнейшем система К' начинает двигаться
относительно К в направлении, совпадающем
с вектором r0 со скоростью v0.
r0 v0t.(2)
r v0t r .(3)
Уравнение (3) запишем в проекциях на оси
координат: x v t x ,
0x
y v0 y t y ,
z v0 z t z .
8. В частном случае, когда К' движется с v0 вдоль положительного направления оси х системы К:
x v0 x t x ,y y ,
(5)
– преобразования
z z ,
Галилея.
t t .
В классической механике считается, что ход времени
не зависит от относительного движения систем отсчёта
следовательно,
t t .
9. Теорема сложения скоростей
Продифференцируем уравнение (3) по времени:dr d v0 t r dr
v0
, (6) dt dt .
теорема
сложения
dt dt
dt
v v0 v .(7) скоростей Галилея.
v – скорость движения тела относительно К (абсолютная),
v' – скорость движения тела относительно К'
(относительная),
v0 – скорость движения системы К' относительно К
(переносная).
10.
Еслиv const, v0 const v v0 v const
F 0,
т.е. если в системе К на материальную
точку силы не действуют, то и в системе
К' на материальную точку силы не
действуют.
Если система отсчета движется с
постоянной скоростью относительно
инерциальной системы отсчёта, то она
также является инерциальной.
11. Классический принцип относительности
Продифференцируем уравнение (7) по времени:dv dv0 dv
.(8) a a , (9)
dt dt
dt
0
v0 const
dv
dt
m const ma ma .
12.
Ускорение движения материальной точкиявляется инвариантным (не меняется)
относительно инерциальной системы отсчёта.
Следовательно, второй закон Ньютона
(основное уравнение динамики) не меняет
своего вида при переходе от одной
инерциальной системы отсчета к другой.
Физический смысл: находясь в инерциальной
системе отсчёта никакими механическими
опытами нельзя обнаружить, движется
система или нет.
13.
Через 6 месяцев Земля вточке 3, путь, который
должен пройти свет
L L D
L L D
D
t t
c c c
c
можно определить с.
Рёмер получил значение
с = 214300 км/с.
14. Скорость света – инвариант относительно инерциальных систем отсчёта
• Фундаментальный интерес представляетвопрос о величине скорости света.
Впервые доказать конечность скорости
распространения света удалось Рёмеру в
1676 г. Он обнаружил, что затмение Ио –
крупнейшего спутника Юпитера совершается
не совсем регулярно со временем
(нарушается периодичность затмения).
При наблюдении затмения через 6 месяцев
Земля находится в диаметрально
расположенной точке своей орбиты вокруг
Солнца, и свет должен пройти до Земли уже
другой путь.
15.
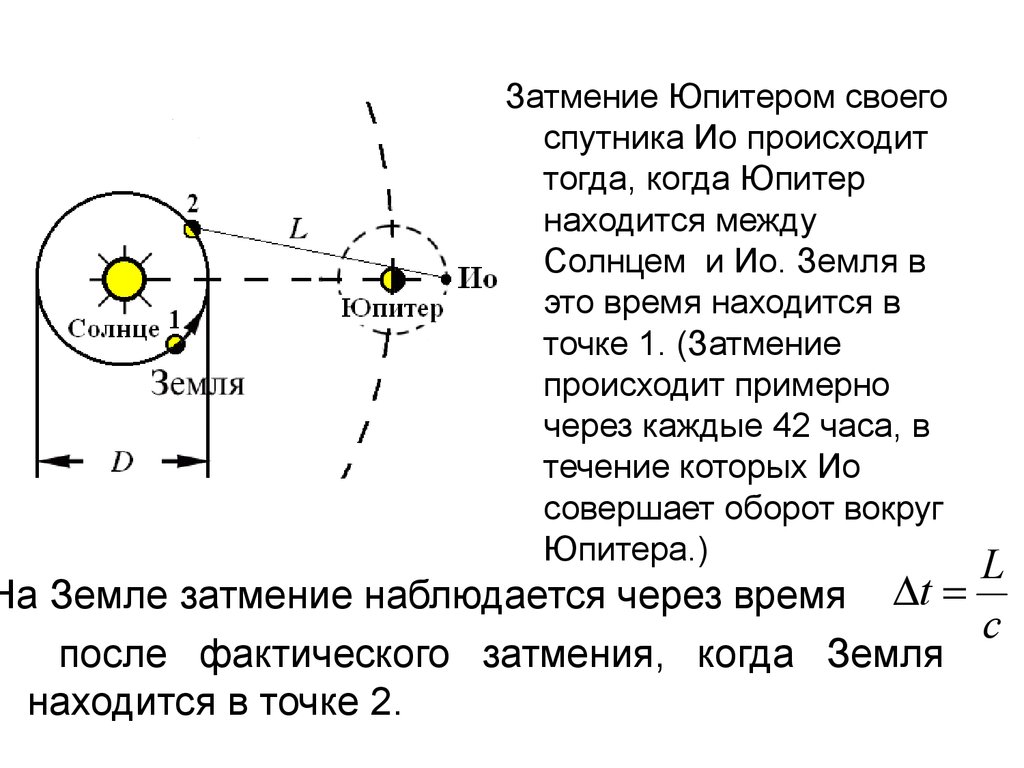
Затмение Юпитером своегоспутника Ио происходит
тогда, когда Юпитер
находится между
Солнцем и Ио. Земля в
это время находится в
точке 1. (Затмение
происходит примерно
через каждые 42 часа, в
течение которых Ио
совершает оборот вокруг
Юпитера.)
L
t
c
На Земле затмение наблюдается через время
после фактического затмения, когда Земля
находится в точке 2.
16. Пусть в системе К есть источник света, в К' – приёмник света.
Применяя преобразованияГалилея скорость света
относительно К':
c c v c ,
что не подтверждается
экспериментальными
результатами. c = const.
17.
Этот факт является одним из постулатов,лежащих в основе СТО.
Эйнштейн объяснил этот результат
свойствами пространства и времени:
с точки зрения движущегося наблюдателя
(система К') пространство
«сокращается» в направлении
v
1
движения в
раз, а интервал
c
времени dt по измерениям того же
v
1
наблюдателя уменьшается в
раз
c
2
2
dx dx
c const.
dt dt
18. ● Опыт Майкельсона –Морли (Майкельсон в 1881 г., Морли -1887 г.)
До опубликования в 1905 г. Эйнштейном теорииотносительности считалось, что световые
волны распространяются в особой среде –
эфире, подобно тому, как звук
распространяется в воздухе. Только по
отношению к покоящемуся эфиру скорость
света равна с. Для наблюдателя,
движущегося со скоростью v относительно
эфира,
c c v .
19. Опыт Майкельсона –Морли
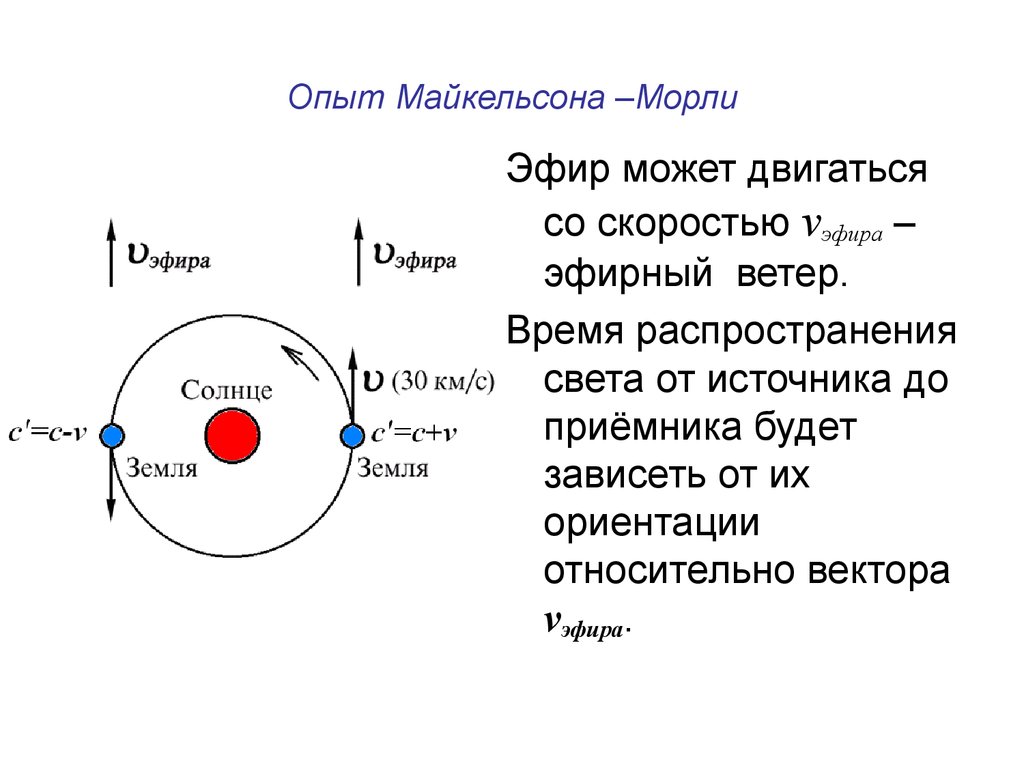
Эфир может двигатьсясо скоростью vэфира –
эфирный ветер.
Время распространения
света от источника до
приёмника будет
зависеть от их
ориентации
относительно вектора
vэфира.
20. Опыт Майкельсона –Морли
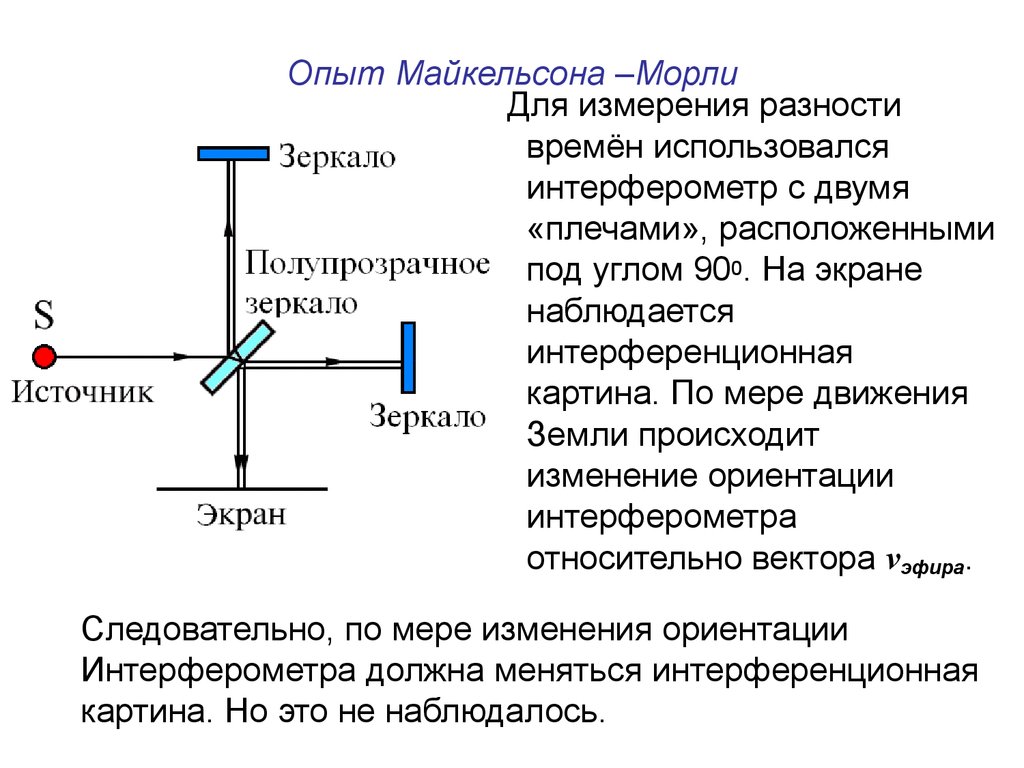
Для измерения разностивремён использовался
интерферометр с двумя
«плечами», расположенными
под углом 900. На экране
наблюдается
интерференционная
картина. По мере движения
Земли происходит
изменение ориентации
интерферометра
относительно вектора vэфира.
Следовательно, по мере изменения ориентации
Интерферометра должна меняться интерференционная
картина. Но это не наблюдалось.
21. Опыт Майкельсона –Морли
Следовательно, свет от источника винтерферометре всегда
распространяется со скоростью с
относительно источника света.
Вывод: скорость света с не зависит от
движения источника или наблюдателя.
22. ● Опыт Саде:
показано, что скорость рентгеновскихлучей, испускаемых источником,
который движется с v ~ 0,5c, остаётся
постоянной независимо от скорости
движения источника с точностью ±10 %.
23. ● Опыт Бертоцци:
нельзя ускорить частицу (электрон) доv > c.
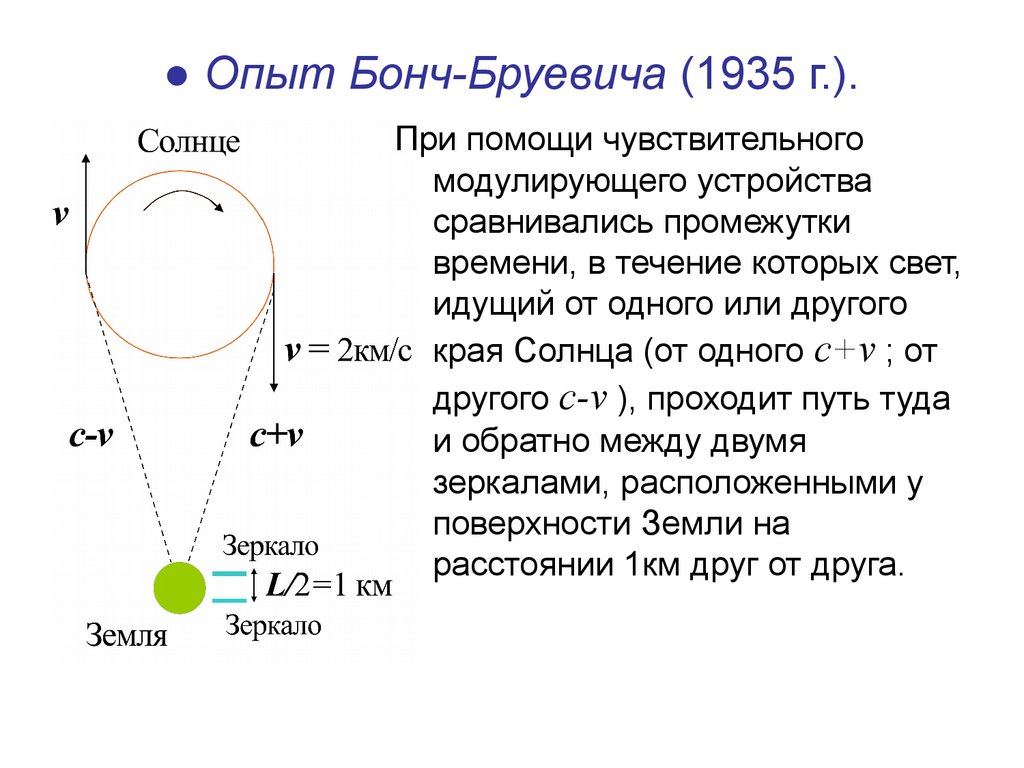
24. ● Опыт Бонч-Бруевича (1935 г.).
При помощи чувствительногомодулирующего устройства
сравнивались промежутки
времени, в течение которых свет,
идущий от одного или другого
края Солнца (от одного c+v ; от
другого c-v ), проходит путь туда
и обратно между двумя
зеркалами, расположенными у
поверхности Земли на
расстоянии 1км друг от друга.
25. Опыт Бонч-Бруевича
LL
t
0.
c v c v
∆t оказалось меньше погрешности
измерений.
c+v = c-v , следовательно, скорость света
с не зависит от скорости источника и
c=const.
26. Из опытов следует:
1. с инвариантна для всех инерциальныхСО.
2. с – максимальная возможная скорость
передачи сигнала, движения частицы,
полей взаимодействия.
• Эти выводы не согласуются с
представлениями об абсолютном
пространстве, абсолютном времени и
бесконечной скорости передачи
взаимодействия, на которых основана
механика Ньютона.
27.
Требовалось пересмотретьфундаментальные представления о
пространстве, времени, скорости
передачи взаимодействий для случая
движения с v ≈ c. Эта новая теория
должна была переходить в механику
Ньютона при v << c. Эйнштейн заложил
основы специальной теории
относительности (СТО).
28. Постулаты Эйнштейна
В основе СТО лежат постулаты Эйнштейна.I. Принцип относительности.
Не только механические, но и
электромагнитные, оптические и другие
явления в инерциальных системах
отсчета (ИСО) протекают одинаково.
ИСО равноправны, и нет таких опытов, с
помощью которых их можно различить.
29. Принцип относительности
распространяется на все явления. Всезаконы природы инвариантны по
отношению к переходу от одной ИСО к
другой. Если явления наблюдаются из
разных ИСО, то они могут отличаться
только из-за различных начальных
условий. Поэтому в законы природы
начальные условия не входят.
30. Постулаты Эйнштейна
II. Принцип постоянства (инвариантности)скорости света в вакууме.
Скорость света в вакууме не зависит от
скорости движения источника и приёмника,
т.е. является инвариантом относительно ИСО
8 м
~
~
с с 2,997928 0,000004 10 .
с
Постоянство скорости света –
фундаментальное свойство природы,
констатируемое как опытный факт.
31. II постулат Эйнштейна, как следствие I постулата
Объектом СТО является скорость передачиинформации от одной точки в другую, т.е.
скорость явлений, связанных причинноследственной связью.
Под скоростью передачи информации
понимают скорость передачи взаимодействия
(сигнала).
Сигнал – физическая порция энергии,
переносимая каким-либо материальным
объектом из одной точки в другую.
32. II постулат Эйнштейна, как следствие I постулата
Скорость света в вакууме c = const имаксимальная скорость передачи
информации, сигнала.
Если с – максимальная возможная
скорость передачи сигнала, то она
должна быть одинаковой во всех ИСО.
Если бы она была разной, то тогда
существовал бы способ различения
ИСО.
33. Преобразования Лоренца
Классические преобразования Галилеянесовместимы с постулатами
Эйнштейна.
Постулатам Эйнштейна удовлетворяют
преобразования Лоренца,
предложенные им в 1904 г., как
преобразования, относительно которых
инвариантны уравнения Максвелла.
34. Преобразования Лоренца
y'y
K
0'
0
z
K'
z'
v= co nst
x
Рассмотрим 2 ИСО: К и К'.
К' движется относительно К
с v = const – равномерно и
прямолинейно.
x ' В начальный момент
времени О и О' совпадают.
Пусть следим за точкой x' = 0' (начало отсчёта К' )
x vt.
из системы К
Если следим за точкой x = 0 из системы К'
x vt .
35. Преобразования Лоренца
Преобразования координат и времени всистемах К и К' должны быть такими, что если
x обращается в ноль, то x' тоже обращается в
ноль.
В соответствии с принципом относительности
все ИСО равноправны, пространственновременная связь (связь пространства и t)
должны во всех ИСО иметь одинаковый вид.
Этому требованию отвечают только линейные
x A x vt , (1)
преобразования:
x A x vt .(2)
36. Преобразования Лоренца
Если предположить, что в этих системахраспространяется световой сигнал, то в
соответствии со II постулатом скорость света
в вакууме – инвариант (постоянна).
x ct ; x ct .(3)
С учётом уравнений (1), (2), перепишем (3):
ct A ct vt At c v ;
ct A ct vt At c v .
(4)
37. Преобразования Лоренца
Перемножим уравнения системы (4):2
c
c tt A tt c v .(5) A 2
2
c v
2
2
A
2
2
1
2
v
1 2
c
1
, (7)
1
.(6)
2
v
1 2
c
т.к. оси направлены в
2
одну сторону, то
остается +А:
v
1
A
, (8) A
.(9)
2
2
c
v
1
1 2
c
38. Преобразования Лоренца
Уравнение (9) подставляем в (1), (2):x
x vt
1
2
, (10) x
x vt
1
2
.(10а)
В начальный момент времени: системы К
и К' совпадают, движение происходит
вдоль оси х: y y , z z .
39. Преобразования Лоренца
Найдём преобразование для времени.Из уравнения (10а) следует:
x 1 x vt подставляем(10)
2
x vt
v
t
2
1
v
t x 2
2
x 1 x vt
c
t
v
t
.
2
2
1
1
40. Преобразования Лоренца
Аналогично:v
t x 2
c
t
.
2
1
41. Преобразования Лоренца
Прямые преобразованияК→К' :
x
x vt
1
2
,
Обратные преобразования
К'→ К:
x
x vt
,
y y ,
z z,
1
y y ,
z z ,
v
t x 2
c .
t
2
1
v
t x 2
c
t
.
2
1
2
42. Классические преобразования Галилея:
x x vt ,y y ,
x x vt ,
y y,
z z,
z z ,
t t .
t t.
2
v
2
1,
При v << c:
преобразования
c
Лоренца переходят
в преобразования Галилея.
43. Следствия из преобразований Лоренца
1. Относительность одновременности.Пусть в системе К в точках с координатами x1 и x2
в моменты времени t1 и t2 происходят 2
события.
В системе К' им соответствуют координаты x'1 и
x'2, время t'1 и t'2.
44. Относительность одновременности
• Если x1 = x2, т.е. события происходят в однойточке и являются одновременными t1 = t2. Из
преобразований Лоренца следует:
x'1 = x'2, t'1 = t'2, т.е. эти события в системе
К' происходят в одной точке и являются
одновременными. Следовательно, эти
события для любых ИСО являются
одновременными и пространственно
t
совпадающими.
x vt
v
x 2
c
t
.
x
,
2
2
1
1
45. Относительность одновременности
• Если в системе К события: x1 ≠ x2 –пространственно разобщены,
но t1 = t2 – одновременны.
В системе К':
x1
x1 vt
1 2
vx1
t 2
c
t1
1 2
,
x 2
x2 vt
1 2
vx2
t 2
c ,
t 2
1 2
т.е. x'1 ≠ x'2, t'1 ≠ t'2, события остаются
пространственно разобщенными и
оказываются неодновременными.
,
46. Относительность одновременности
События одновременные в однойсистеме отсчёта не одновременны в
другой СО.
vx2
vx1
t 2 t 2
v x1 x2
c
c
t 2 t1
0
.
2
2
2
1
c 1
Знак определяется знаком выражения
v x1 x2 .
47. 2. Длина отрезка (стержня) в различных системах отсчёта Длина отрезка – разность координат его начала и конца, измеренных одновременно в вы
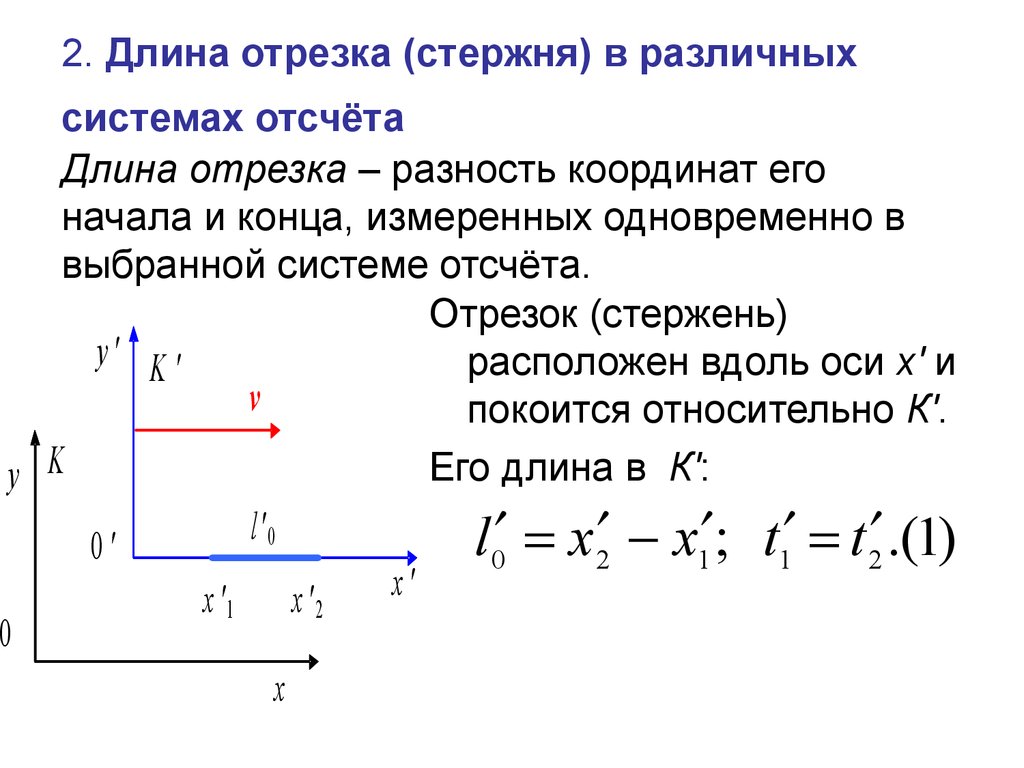
2. Длина отрезка (стержня) в различныхсистемах отсчёта
Длина отрезка – разность координат его
начала и конца, измеренных одновременно в
выбранной системе отсчёта.
Отрезок (стержень)
y' K '
расположен вдоль оси x' и
v
покоится относительно К'.
Его длина в К':
y K
l'
0
l0 x 2 x1 ; t1 t 2 .(1)
0'
x'
x '1 x '2
0
x
48. 2. Длина отрезка (стержня) в различных системах отсчёта
y' K 'v
y K
2. Длина отрезка (стержня) в
различных системах отсчёта
l' 0
0'
0
x '1
К' движется относительно К со скоростью v.
Длина отрезка в К:
l0
x2 vt 2
1 2
x1 vt1
1 2
x2 vt 2 x1 vt1
1 2
x '2
x'
x
; (2)
при t1 t 2
l
2
l.
l0
,
(
3
)
l
l
1
,
(
4
)
l
0
0
2
1
Длина стержня l'0 в системе, относительно которой
он покоится, больше длины стержня l в системе,
относительно которой он движется.
49.
y' K 'Стержень покоится в системе
К, К' движется относительно
К со скоростью v.
v
y K
0'
0
x'
l0
x1
x2
x
K : l0 x2 x1 ; t1 t2 .
x 2 vt2 x1 vt1
l0
2
1
l
(при t1 t2 )
.
2
1
K : l l0 1 l0 l .
2
Длина стержня l0 в системе, относительно которой
он покоится, больше длины стержня l' в системе,
относительно которой он движется.
50. 2. Длина отрезка (стержня) в различных системах отсчёта.
Линейные размеры тела, движущегосяотносительно ИСО, уменьшаются в
2
1 раз.
направлении движения в
Длина отрезка, измеренная в системе отсчёта,
в которой он покоится, называется его
собственной длиной. Собственная длина
всегда имеет наибольшее значение.
Длина отрезка зависит от выбора системы
отсчёта, т.е. относительная.
В классической механике:
v
v c 1 l l0 ; l l0 .
c
51. 3. Интервал времени в разных системах отсчёта
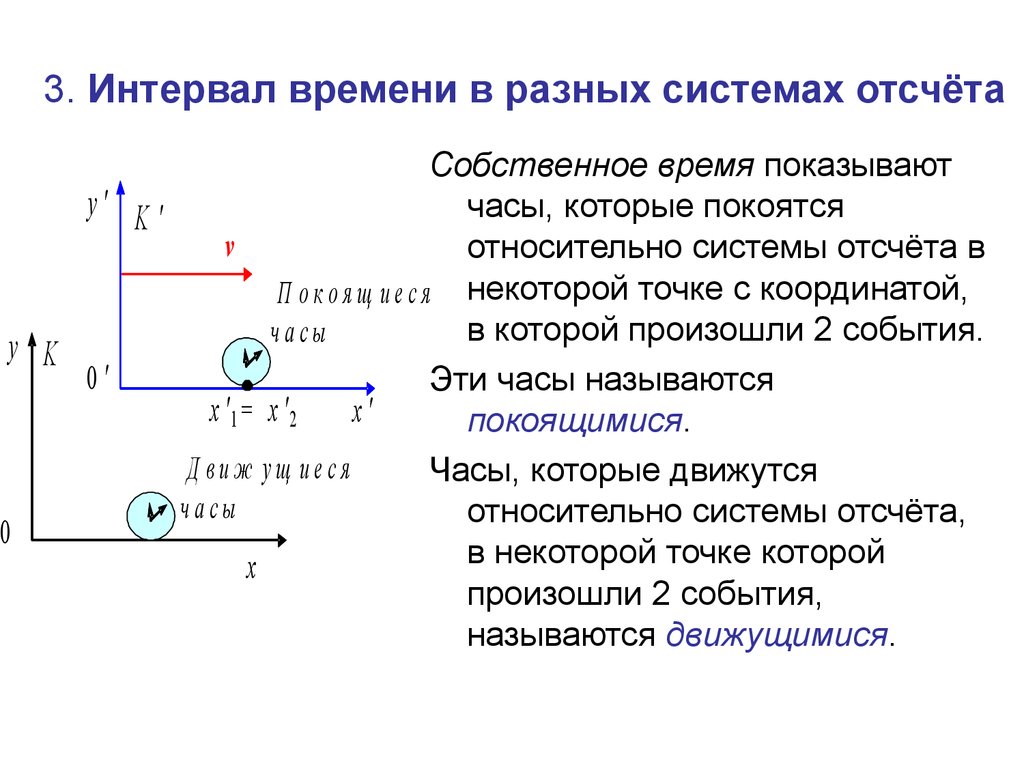
Собственное время показываютy' K '
часы, которые покоятся
v
относительно системы отсчёта в
П о к о я щ и е с я некоторой точке с координатой,
в которой произошли 2 события.
часы
y K
0'
Эти часы называются
x '1 = x '2
x'
покоящимися.
Д виж ущ иеся
Часы, которые движутся
часы
относительно системы отсчёта,
0
в некоторой точке которой
x
произошли 2 события,
называются движущимися.
52. Интервал времени в разных системах отсчёта
K : x1 x 2 ; 0 t 2 t1 (1) время между 2-мяy' K '
y K
событиями, которые
показывают покоящиеся часы.
v
П о коящ иеся
часы
0'
x '1 = x '2
x'
vx 2
vx1
t 2 2 t1 2
0
c
c
K : t 2 t1
.(
2
)
2
2
1
1
0
Д виж ущ иеся
часы
x
1 0 .(3) 0 .
2
Движущиеся часы показывают большее время.
53. Интервал времени в разных системах отсчёта
y' K 'y K
0
Часы покоятся в системе
v
К.
Д виж ущ иеся
2 события происходят в К
часы
в некоторой точке с
координатой x1 =x2.
x'
0'
П окоящ иеся
часы
x 1= x 2
x
K : 1 0 .(4)
0 .
движ .ч .
2
покоящ .ч .
Собственное время всегда имеет
наименьшее значение
54. Интервал времени в разных системах отсчёта
Интервал времени между событиямизависит от выбора системы отсчёта, т.е.
время относительно.
В классической механике:
v
v c 1 0 ; 0 .
c
55. Опыт с мюонами
Эти частицы рождаются на расстоянии 30 км отповерхности Земли и обнаруживаются вблизи
поверхности Земли, т.е. проходят путь S = 30 км.
Их собственное время жизни τ'0 = 2·10-6 с.
Если принять, что мюоны движутся со скоростью
света, то
8
6
S c связанной
2 Землёй,
10 600 м 30км.
В системе отсчёта,
0 3 10 с
существуют движущиеся часы. Поэтому время
жизни мюона с точки зрения земного
наблюдателя
0
;
S
S
.
0
2
1
56. «Парадокс близнецов (часов)»
Пусть осуществляется космический полёт соскоростью близкой к с, β = 0,99999.
Если покоящиеся часы связаны с космическим
кораблём, удаляющемся с v =βc, то для
наблюдателя, связанного с Землёй, ход часов
в космическом аппарате замедляется в
1 раз.
1
2
224, если 0 10 лет, то 2240 лет.
0
57. «Парадокс близнецов (часов)»
Но принцип относительности временисправедлив только для ИСО.
СО, связанные с близнецами, не эквивалентны.
Земная СО – ИСО, корабельная СО – НСО.
Следовательно, принцип относительности к
ним не применим.
58. Релятивистский закон сложения скоростей
В механике Ньютона теорема сложенияскоростей
Галилея:
K : u v u .
Т.к. движение происходит
вдоль оси х :
u x v u x ,
u y u y ,
u z u z .
59. Релятивистский закон сложения скоростей
В релятивистской механике.Проекции скорости материальной точки на
координатные оси в системе К:
dx
dy
dz
u x ; u y ; u z .(1)
dt
dt
dt
Проекции скорости материальной точки на
координатные оси в системе К':
dx
dy
dz
u x
; u y
; u z
.(2)
dt
dt
dt
60. Релятивистский закон сложения скоростей
Согласно преобразованиям Лоренца:x
x vt
1
2
,
y y ,
z z ,
v
t x 2
c .
t
2
1
dx dx vdt 1
u x
dt dt vdx 1 2
2
c
dx
v
ux v
dt
.(3)
dx
uxv
v
1 2
c
1 dt
2
c
2
61.
xx vt
1
2
,
y y,
z z ,
v
t x 2
c .
t
1 2
dy dy 1
u y
vdx
dt
dt 2
c
2
uy 1
.( 4)
uxv
1 2
c
2
uz 1
dz dz 1
u z
.(5)
vdx
uxv
dt
dt 2
1 2
c
c
2
2
u u x u y u z .
2
2
2
62. Релятивистский закон сложения скоростей
Если материальная точка движется в системе Квдоль оси х со скоростью с:
c v
u x c,
u x
c,
cv
1 2
c
т.е. скорость в системе К' равна с.
Следовательно, объект, распространяющийся
со скоростью с, будет иметь эту же скорость
относительно других систем независимо от
того, сколь быстро они движутся (согласие с II
постулатом Эйнштейна).
63. Релятивистский закон сложения скоростей
Систему отсчёта связывают сматериальным объектом, у которого
v < c.
С фотоном систему отсчёта связывать
нельзя, т.к. его v = c.
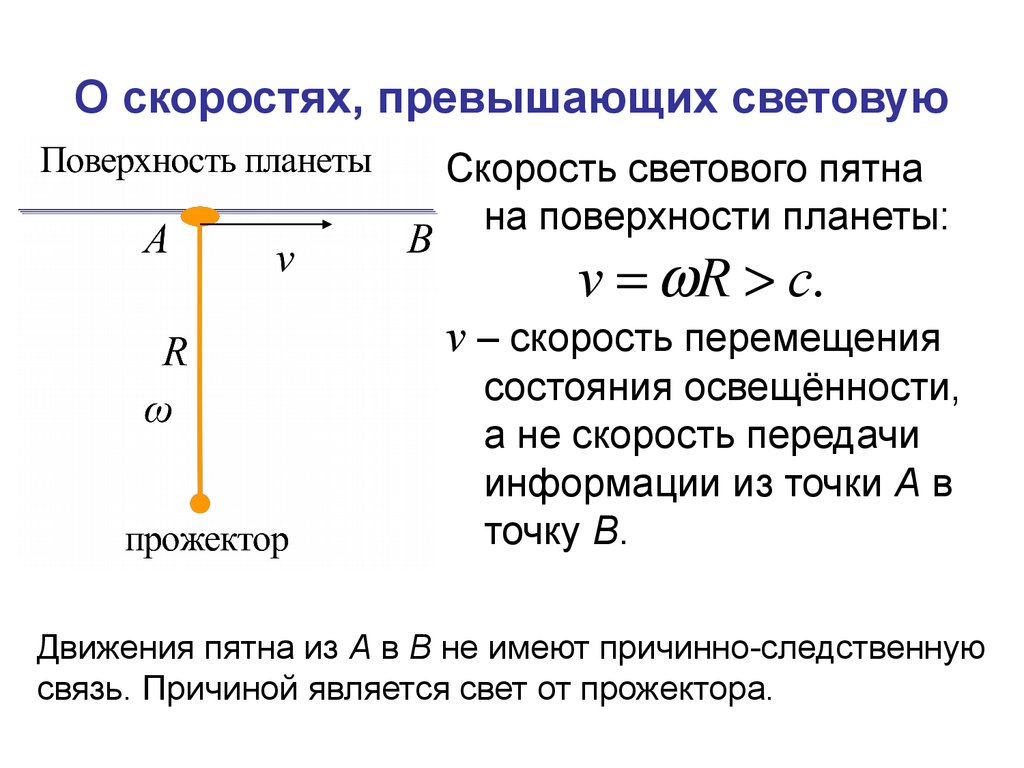
64. О скоростях, превышающих световую
Скорость светового пятнана поверхности планеты:
v R c.
v – скорость перемещения
состояния освещённости,
а не скорость передачи
информации из точки А в
точку В.
Движения пятна из А в В не имеют причинно-следственную
связь. Причиной является свет от прожектора.
65. Релятивистская динамика (3 закона Ньютона)
1. Постулат существованияинерциальных систем отсчёта.
Остаётся без изменения.
66. Релятивистская динамика (3 закона Ньютона)
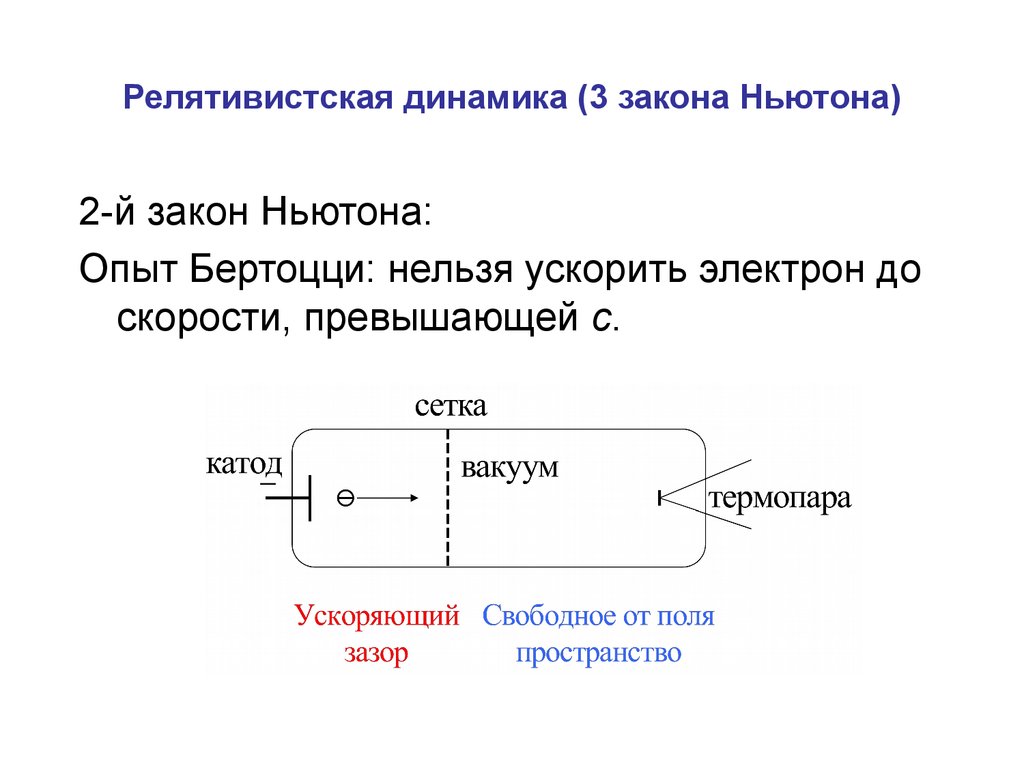
2-й закон Ньютона:Опыт Бертоцци: нельзя ускорить электрон до
скорости, превышающей с.
67. Релятивистская динамика
Термопара – для определения кинетическойэнергии, переходящей в тепло при ударе по
ней электронов.
2
2
p
mv
2
2
Ек
v Ек
2m
2
m
v Ек
2
линейная зависимость.
Свободное от поля пространство – для
измерения времени и скорости пролёта
электрона.
68. Релятивистская динамика
pТ еория
v2
(к л а с с и ч е с к а я 2 2
v Ек
м еханика)
m
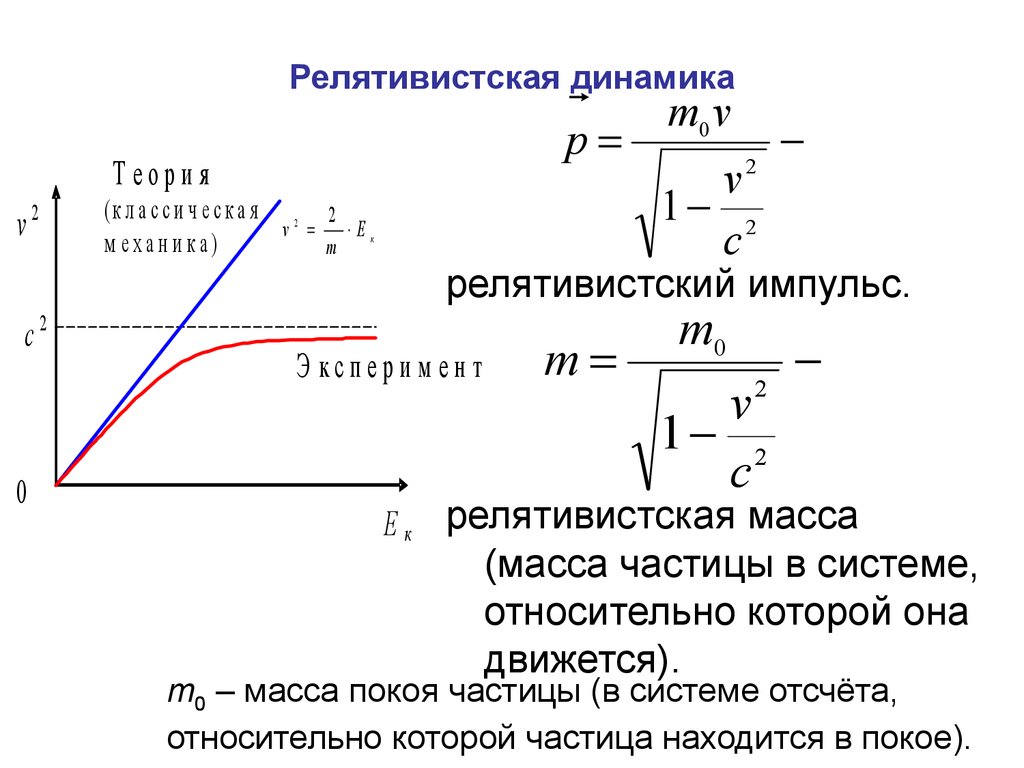
m0 v
2
v
1 2
c
релятивистский импульс.
c2
0
Э ксперим ент
m
m0
2
v
1 2
c
Е к релятивистская масса
(масса частицы в системе,
относительно которой она
движется).
m0 – масса покоя частицы (в системе отсчёта,
относительно которой частица находится в покое).
69.
Инертная масса не зависит от направлениядействия силы.
В релятивистской механике масса m(v)
утрачивает смысл коэффициента
пропорциональности между векторами а и F:
dp d m0 v
F
;
p
f
v
,
v
.
2
dt dt
v
1 2
c
70.
2F v v const.
m0
dv
a , F
a
2
dt
v
1 2
c
F || v
m0
F
a
2 3
v
1 2
c
m
m
m0
2
v
1 2
c
m0
v
1 2
c
2
.
.
3
71. Релятивистская динамика
В отличие от Ньютоновской механики векторсилы F в релятивистской механике не
является инвариантом (в различных СО F
имеет различные модули и направления).
В релятивистской механике понятие инертной
массы теряет смысл, и поэтому 2 закон
Ньютона записывается в виде:
d m0 v
F
.
2
dt
v
1 2
c
72. Релятивистская динамика
3-й закон Ньютона.В релятивистской механике работает
концепция близкодействия, в
соответствии с которой взаимодействие
передаётся от точки к точке с конечной
v = c. Время передачи взаимодействия
S
t .
v
73. Релятивистская динамика. 3-й закон Ньютона.
В точке 2 рождается заряженная частица q2. Вмомент её рождения на q2 действует сила со
стороны q1, а на q1 со стороны q2 силы не
действуют, т.к. для передачи взаимодействия
требуется время t.
Следовательно, 3-й закон Ньютона
нарушается.
74. Взаимодействие массы и энергии (формула Эйнштейна)
полнаяE
mc энергия
(1) тела или системы тел, из каких
2
бы видов энергии она не состояла бы. Е
связана с массой m тела соотношением (1).
релятивистская масса,
мера
m0
энергосодержания,
зависит от v тела.
m
v2
1 2
c
энергия покоя,
Ек – кинетическая энергия.
E E 0 E к , E 0 m0 c
2
75. Связь полной энергии и импульса
m0 cE
2
mc
2
2
v
1 2
c
2
v
2 4
2 4
2 4
2 2 2
2 4
m c 1 2 m0 c , m
c m
v c m0 c
c
E
p
2
2
E p c m c inv.
2
2
2
2
0
4
E m c p c E m c p c .
2
2
0
4
2
2
2
0
4
2
2
76. Связь кинетической энергии и импульса
E p c m c E2
2
2
2
0
4
2
0
(1) энергия покоя.
E E0 Eк E E 2 E0 Eк Е .(2)
2
2
0
2
к
(1) E
p c E 2 E0 E к Е p c Е
2
2
2
2
0
2
к
( 2)
1
p
Е к 2 Е0 Е к .
с
2
2
2
0
77. Частица с нулевой массой покоя
Законы Ньютоновской механики недопускают существование частицы с
нулевой массой, т.к. для них даже при
малых F ускорение а → ∞.
Существование частиц с m0 = 0 не
противоречит законам релятивистской
механики.
78. Частица с нулевой массой покоя
В соответствии с уравнениямиp
m0 v
2
v
1 2
c
,
E
m0 c
2
v2
1 2
c
частица с m0 = 0 обладает р ≠ 0 и Е ≠ 0, т.к. если
её v = c, то соотношение 0/0
представляет собой неопределённость, которая
может равняться конечному числу.
79. Частица с нулевой массой покоя
Пример: фотон m0 = 0, Е0 = 0,E pc; E h mc
2
h
p
; p mc
c
h
m 2 .
c






















































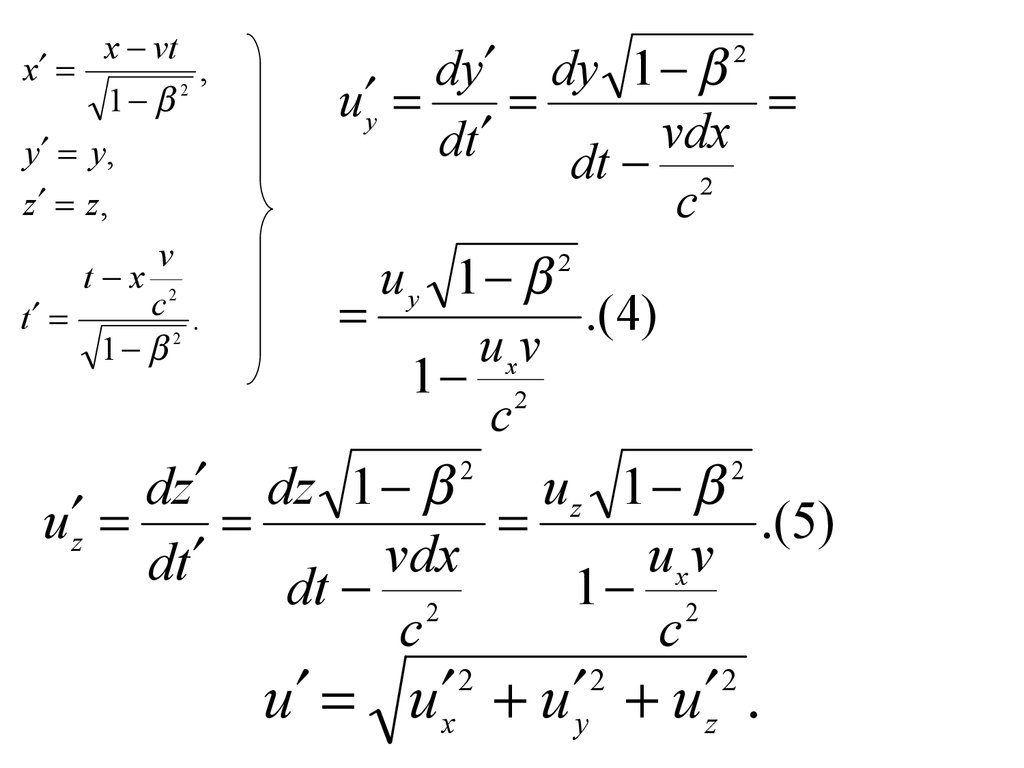





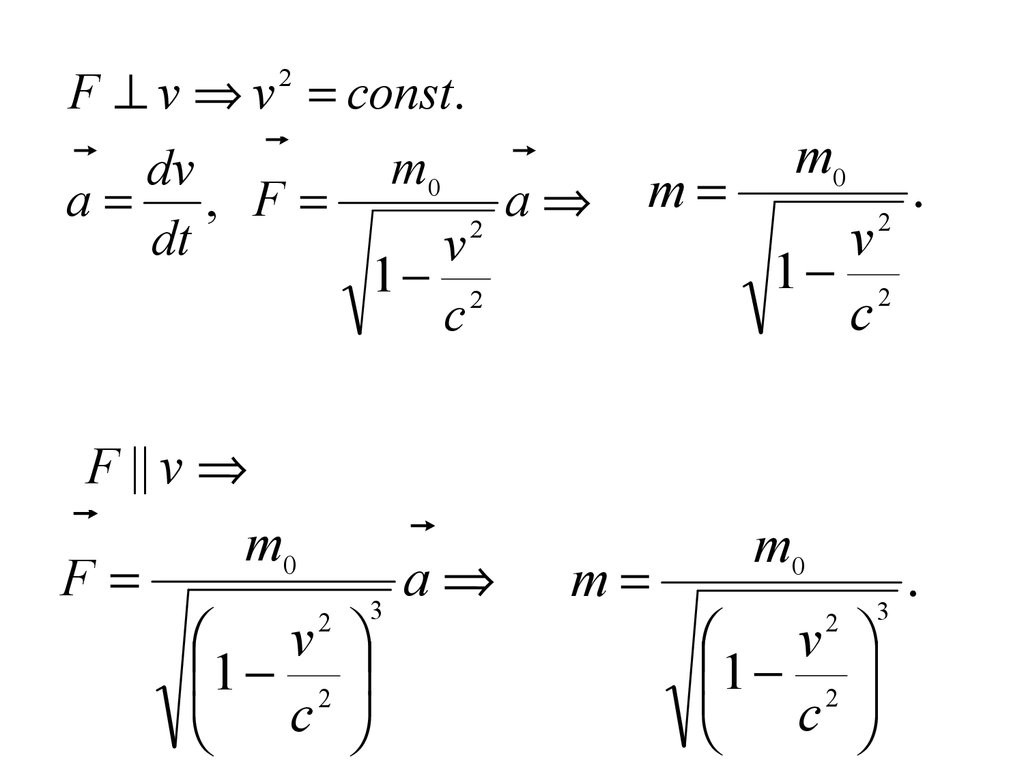









 Физика
Физика








