Семантика императивного языка While2

1. Семантика императивного языка While

1

2. Абстрактный синтаксис языка While

Синтаксические категории
p
B
D
C
е
bе
Program
Block
Decl
Cmd
Exp
BExp
I
x
bx
op
bop
n
Id
Var
BVar
Op
BOp
Num
2

3. Абстрактный синтаксис языка While

Определения
p
B
D
C
::= B
::= D ; C
::= var x | bvar bx | procedure I:C | D’; D”
::= skip | x := e | C’ ; C” | I
| if be then C’ else C”
| while be do C’ | begin B end
e ::= x | n | e’ op e” | if be then e’ else e”
be::= bx | T | F | Not be’| Equal (e,e’)
| be’ bop be”
op
::= + | - | * | div
bop ::= and | or
3

4. Естественная семантика языка While

• Отношение «вычисляет» определяется
утверждениями вида:
<С,s> s’,
где С – команда,
s - состояние переменных.
Правила.
[ass] <x:=e,s> s[x/A[e]s],
где A[e]s обозначает s├e Av
[skip] < skip,s> s.
4

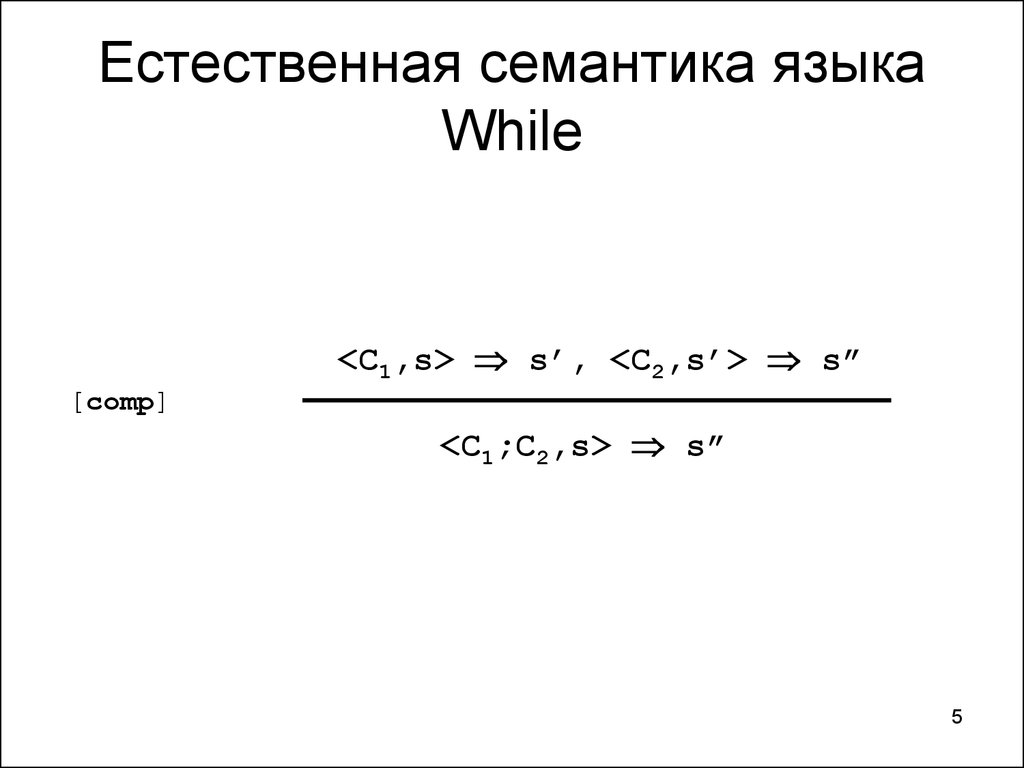
5. Естественная семантика языка While

<С1,s> s’, <С2,s’> s”
[comp]
<С1;С2,s> s”
5

6. Естественная семантика языка While

<С1,s> s’
[ift]
<if be then С1 else С2,s> s’
<С2,s> s’
[iff]
[B[be]s=T]
[B[be]s=F]
<if be then С1 else С2,s> s’
где B[be]s=bv обозначает s├be Bbv
6

7. Естественная семантика языка While

<С,s> s’ <while be do С,s’> s”
[whilet]
[B[be]s=T]
<while be do С,s> s”
[whilef]
[B[be]s=F]
<while be do С,s> s
7

8. Реализация на Прологе 1

:-op(880,xfx,:=).
:-op(890,xfx,[then,else,do]).
:-op(900,fy,[if,while]).
:-op(910,xfy,>>).
test (y:=1 >> while x>0 do
(y:= y*x >> x:=x-1)).
8

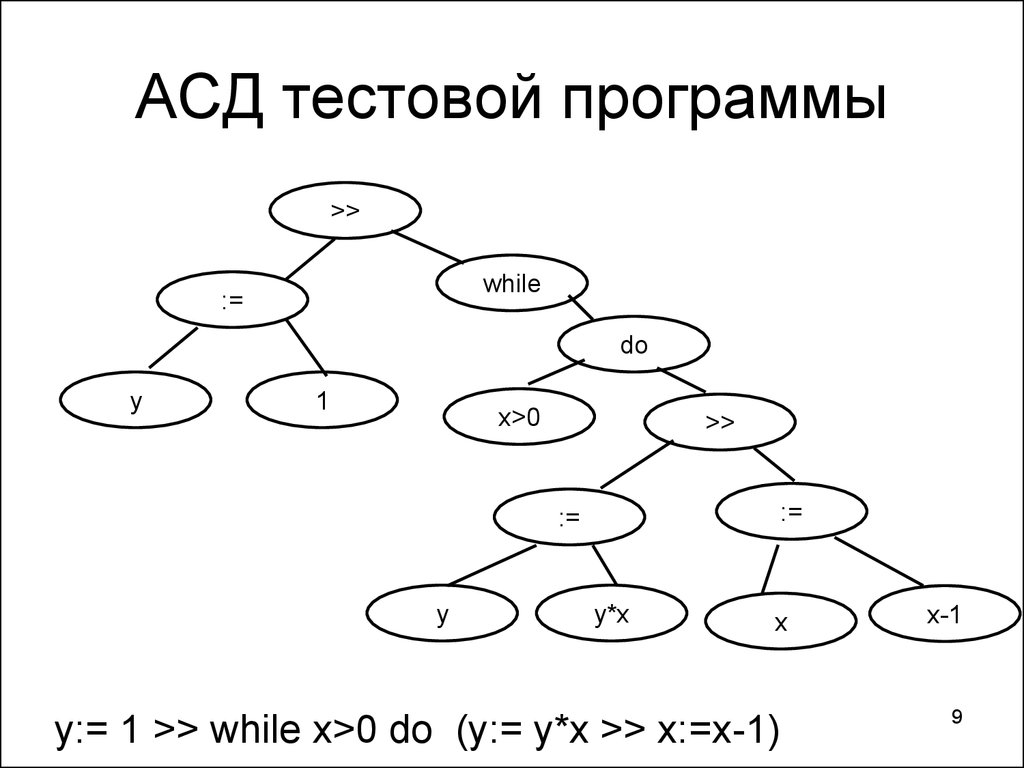
9. АСД тестовой программы

>>
while
:=
do
y
1
x>0
>>
:=
:=
y
y*x
x
y:= 1 >> while x>0 do (y:= y*x >> x:=x-1)
x-1
9

10. Реализация на Прологе 2

store(X,V,[],[X/V]) :- !.
store(X,V,[X/_|T],[X/V|T]) :- !.
store(X,V,[X1/V1|T],[X1/V1|Tn]) :store(X,V,T,Tn).
10

11. Реализация на Прологе 3

eval(X:=E,S,Sn) :arith(S,E,V),
store(X,V,S,Sn).
eval(skip,S,S).
eval(C1 >> C2,St0,St2) :eval(C1,St0,St1),
eval(C2,St1,St2).
11

12. Реализация на Прологе 4

eval(if B then C1 else _,St0,St1) :beval(St0,B,tt),!,
eval(C1,St0,St1).
eval(if _ then _ else C2,St0,St1) :eval(C2,St0,St1).
eval(while B do C, St0, St1) :beval(St0,B,tt),!,
eval(C >> (while B do C),St0,St1).
eval(while _ do _, St, St).
12

13. Семантическая эквивалентность команд

• Команды C1 и C2 семантически эквивалентны,
если для любых двух состояний s и s’
справедливо:
<C1,s> s’ <C2,s> s’
• Докажем, что команды
while be do C
и
if be then (C; while be do C)
else skip
семантически эквивалентны.
13

14. Доказательство

• Часть 1
Докажем, что если
<while be do C, s> s”
(1)
то и
< if be then (C; while be do C)
else skip, s> s”
(2)
• из истинности посылки (1) следует, что для неё
существует дерево вывода T. Корень этого
дерева может иметь одну из двух форм, в
зависимости от того, использовалось ли правило
[whilet] или [whilef] .
14

15. Доказательство (продолжение)

• В первом случае дерево T , будет иметь форму:
T1
T2
<while be do C, s> s”
где
T1
T2
-
дерево вывода с корнем <C,s> s’,
а
имеет корень <while be do C, s’> s” .
Более того B[b]s=T
.
15

16. Доказательство (продолжение)

• Использовав T1 и T2 как посылки правила [comp] получим
дерево:
T1
T2
<C; while be do C, s> s”
Учитывая, что B[be]s=T можно применив правило [ift]
получим дерево:
T1
T2
<C; while be do C, s> s”
<if be then (C; while be do C) else skip, s> s”
В нём получился вывод заключения (2)
16

17. Доказательство (продолжение)

• Во втором случае, когда использовалось правило [whilef]
и выполнялось условие B[b]s=F, тогда s = s” . Дерево
T будет иметь форму:
<while be do C, s> s
Используя аксиому [skip] получим
<skip,s> s,
а применив правило [iff] получим дерево вывода для (2):
<skip, s> s
<if be then (C; while be do C) else skip, s> s
В нём получился вывод заключения (2), если учесть, что
s = s” .
• Это завершает доказательство первой части.
17

18. Доказательство (продолжение)

• Часть 2
Докажем импликацию в обратном порядке: если
< if be then (C; while be do C)
else skip, s> s”
(2)
то и
<while be do C, s> s”
(1)
Для этого, имея дерево вывода T для (2), нужно
построить дерево вывода для (1) . Для (2) дерево
вывода могло быть построено только правилами
[ift] или [iff].
18

19. Доказательство (продолжение)

В первом случае, когда B[be]s=T, вершина (2) получена
из вершины
T1 = < C; while be do C, s> s”,
которая , в свою очередь как композиция операторов могла
быть получена только по правилу [comp] . Значит к T1 ведут
две ветви:
T2 = < C, s> s’,
T3 = < while be do C, s’> s”.
Теперь, если T2 и T3 в качестве посылок для правила
[whilet] получим дерево вывода для (1).
• Во втором случае, когда выполнялось условие B[b]s=F,
дерево T будет строиться по правилу [iff] и, тогда
получим ветвь для <skip, s> s”. На основании
аксиомы [skip] получим, что s = s” . Теперь, применив
аксиому [whilef] получим дерево вывода для (1).
19