Похожие презентации:
Теоретический материал по геометрии за курс 7-9 классов
1. Теоретический материал по геометрии за курс 7-9 классов
2. Углы
3.
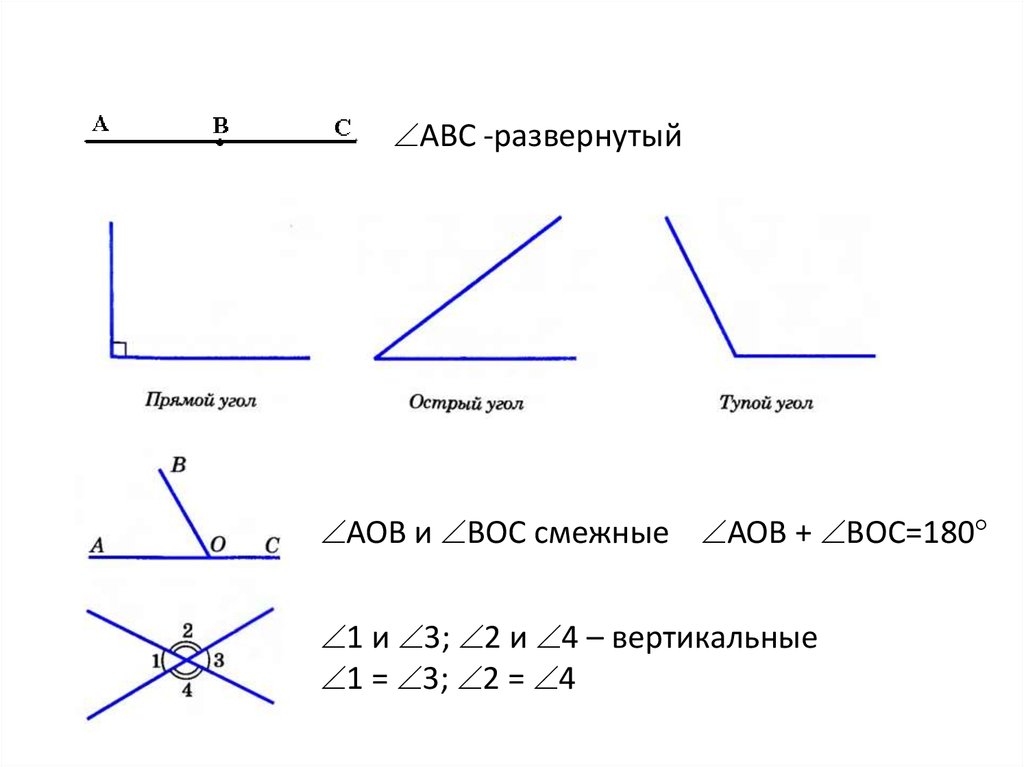
АВС -развернутыйАОВ и ВОС смежные АОВ + ВОС=180
1 и 3; 2 и 4 – вертикальные
1 = 3; 2 = 4
4.
5.
6.
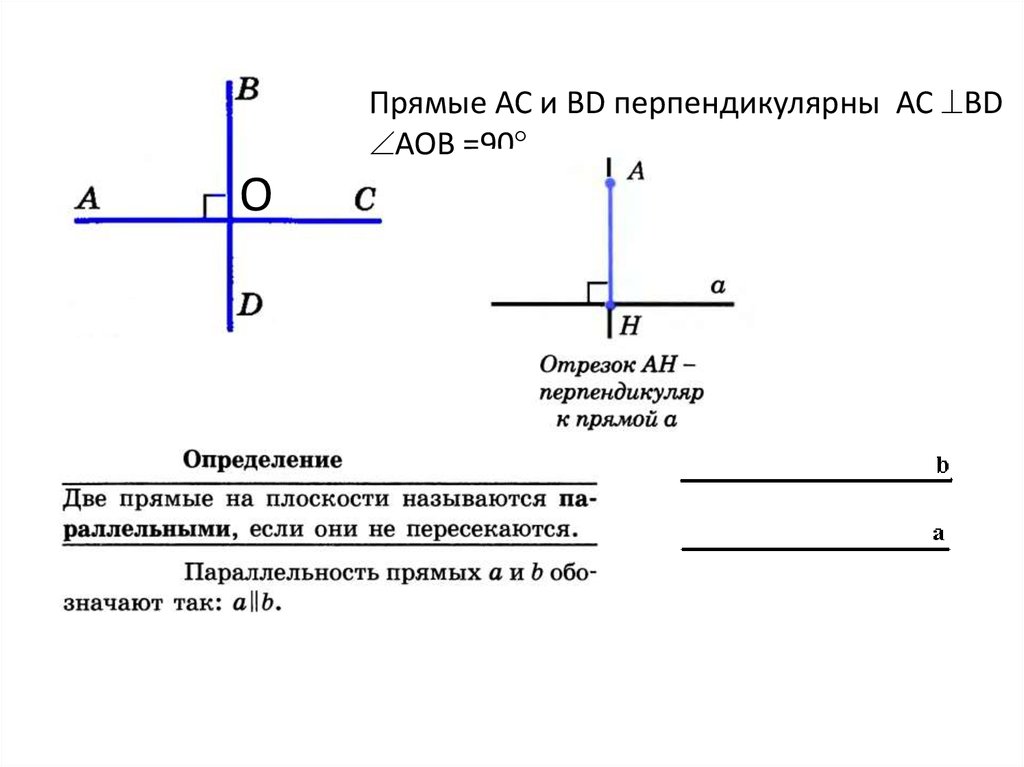
Прямые АС и BD перпендикулярны АС BDАОВ =90
О
7.
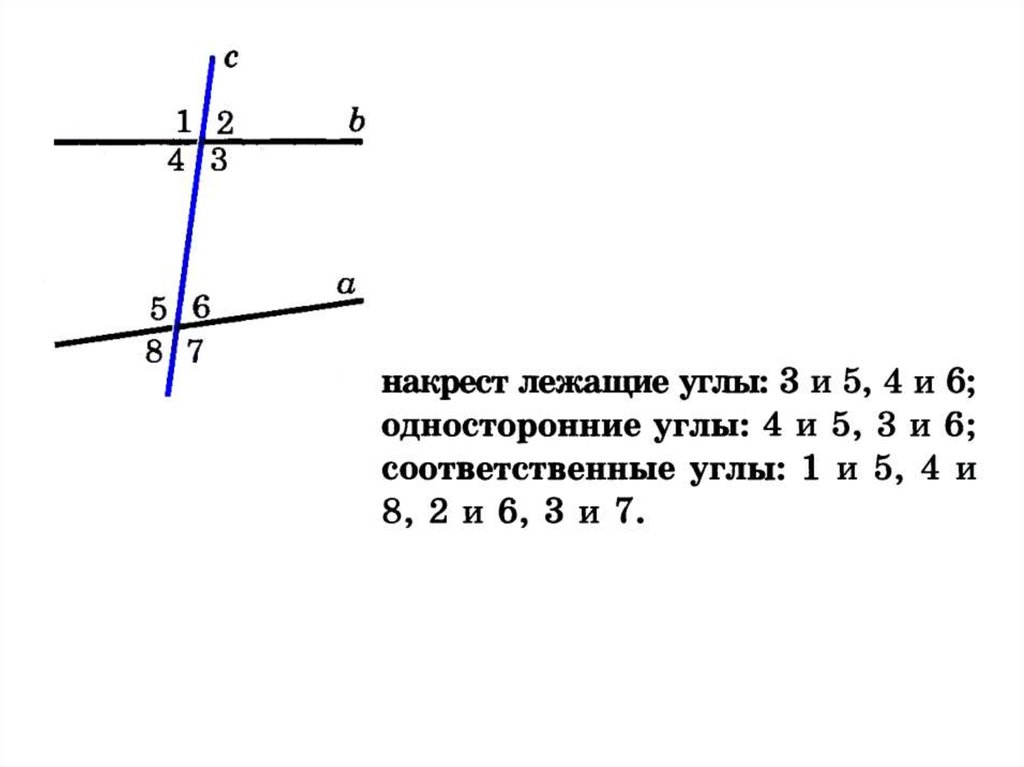
Признаки параллельности прямых8.
Аксиома параллельных прямыхСледствия из аксиомы параллельных прямых
Если a b, с
пересекает а, то с
пересекает b.
Если a с, b с, то
a b.
9.
Свойства параллельных прямых10.
11.
12.
13.
14.
15.
DE ABAB
DE
2
16.
Признаки равенства треугольников(I признак)
(II признак)
(III признак)
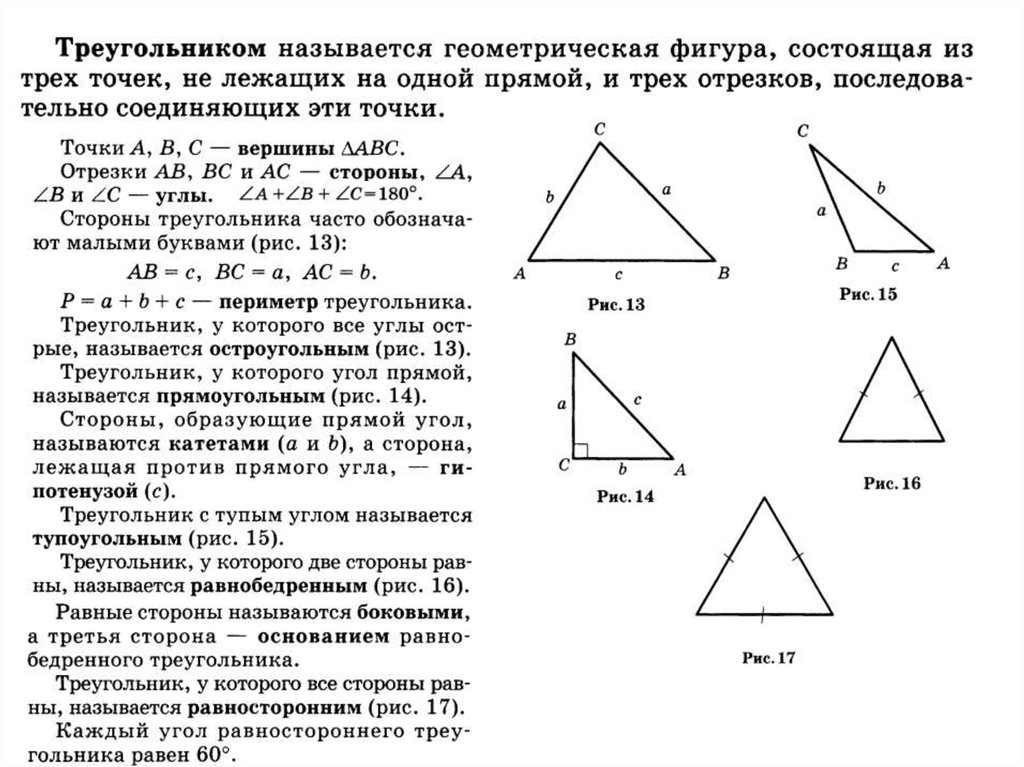
17.
Неравенство треугольника18.
Прямоугольный треугольник19.
4) В прямоугольномтреугольнике медиана,
проведенная к гипотенузе,
равна половине гипотенузы.
(Теорема Пифагора)
(Теорема обратная теореме Пифагора)
20.
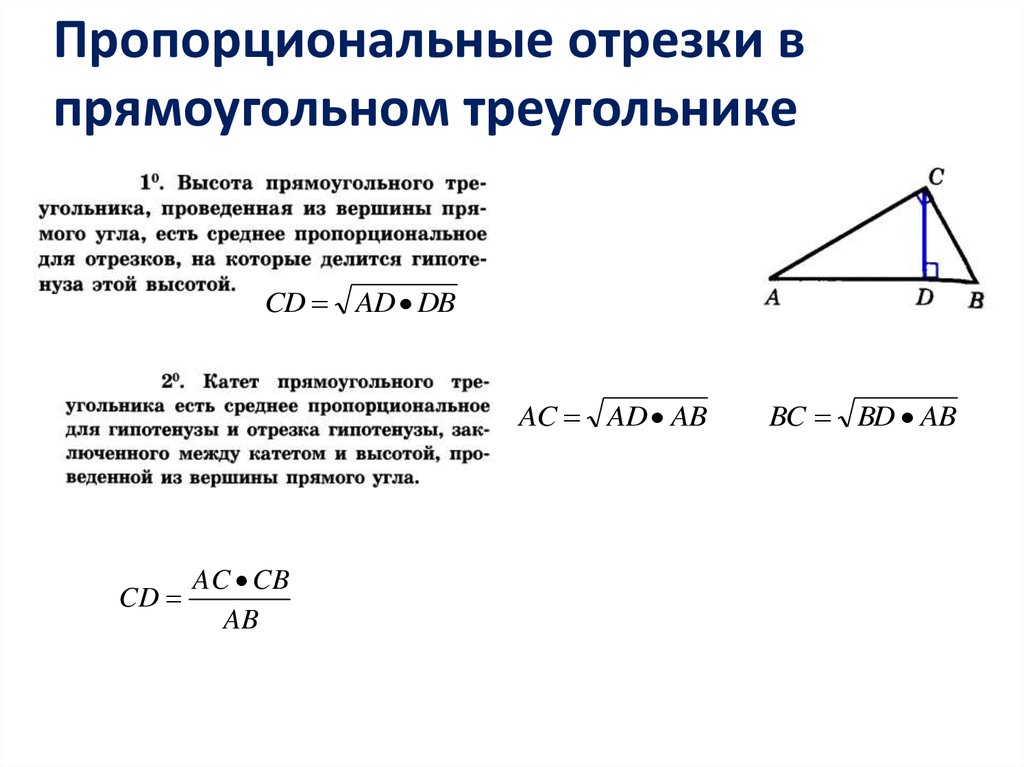
Пропорциональные отрезки впрямоугольном треугольнике
CD AD DB
AC AD AB
CD
AC CB
AB
BC BD AB
21.
Основное тригонометрическоетождество
22.
4 замечательные точки треугольника23.
24.
25.
26.
Свойство биссектрисы треугольникаCK KD
AC AB
27.
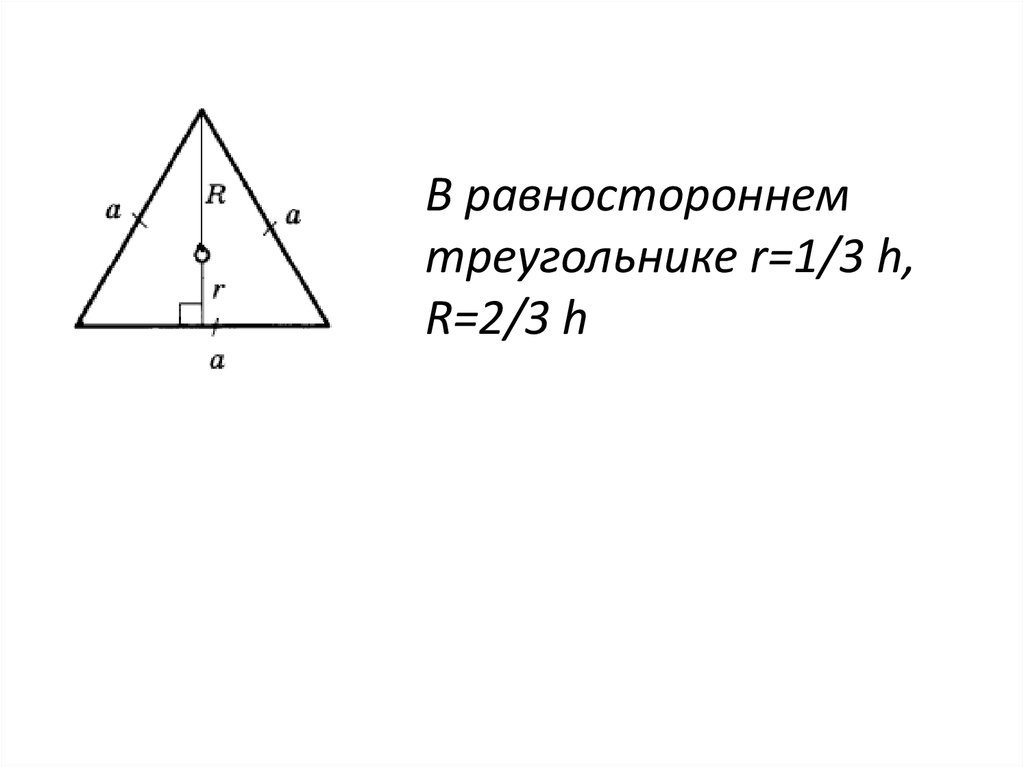
В равностороннемтреугольнике r=1/3 h,
R=2/3 h
28.
29.
Подобные треугольники30.
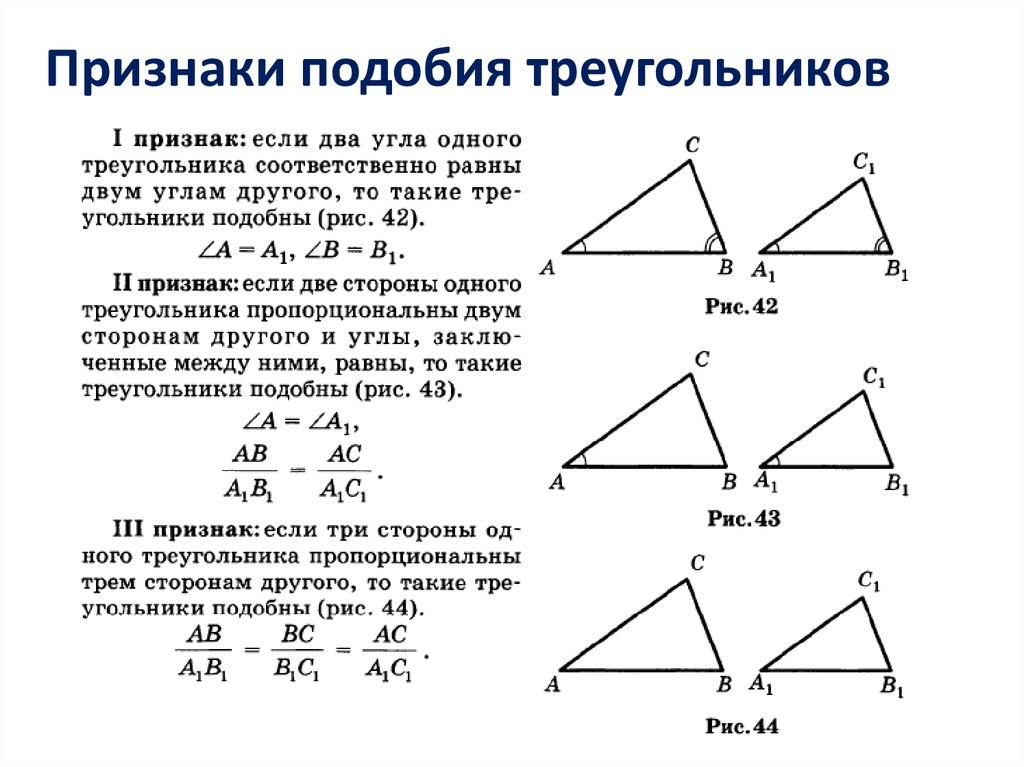
Признаки подобия треугольников31.
32.
Формулы площадей треугольников33.
34.
35.
ПараллелограммСвойства параллелограмма:
1. В параллелограмме противоположные стороны равны.
2. В параллелограмме противоположные углы равны.
3. В параллелограмме диагонали точкой пересечения делятся пополам.
4. Сумма двух углов, прилежащих к одной стороне, равна 180 .
5. Биссектриса угла параллелограмма отсекает равнобедренный
треугольник.
6. Биссектрисы двух углов параллелограмма, прилежащих к одной стороне,
взаимно перпендикулярны.
7. Биссектрисы противоположных углов параллелограмма параллельны
или совпадают.
8. В параллелограмме сумма квадратов диагоналей равна сумме квадратов
всех его сторон.
36.
37.
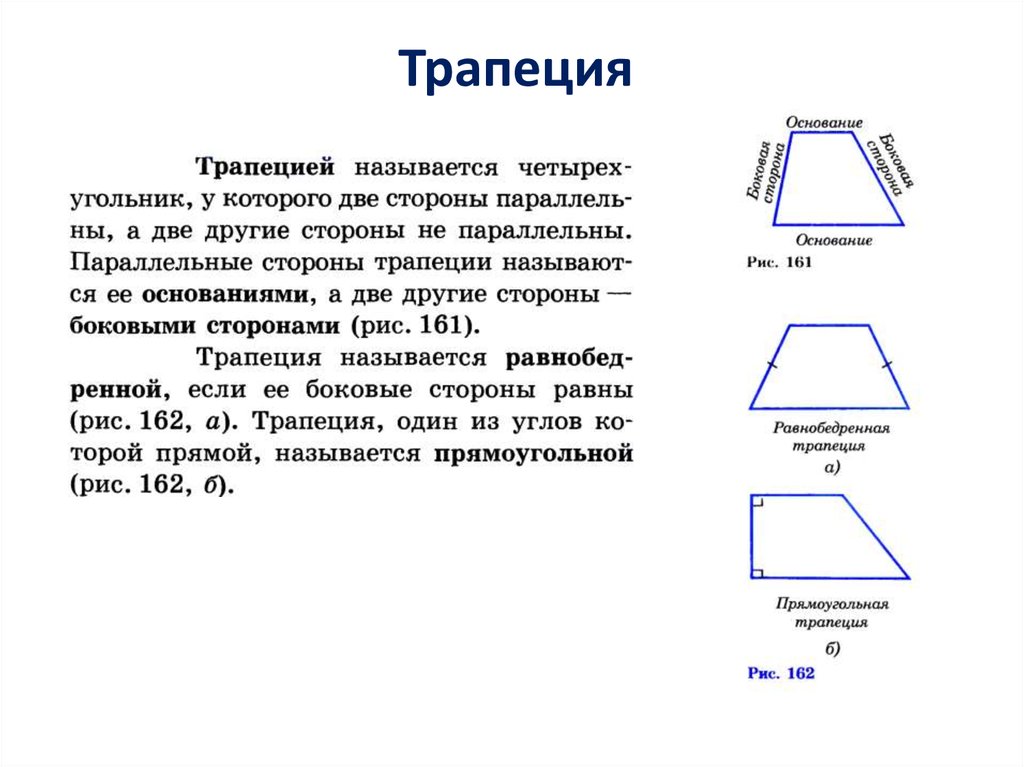
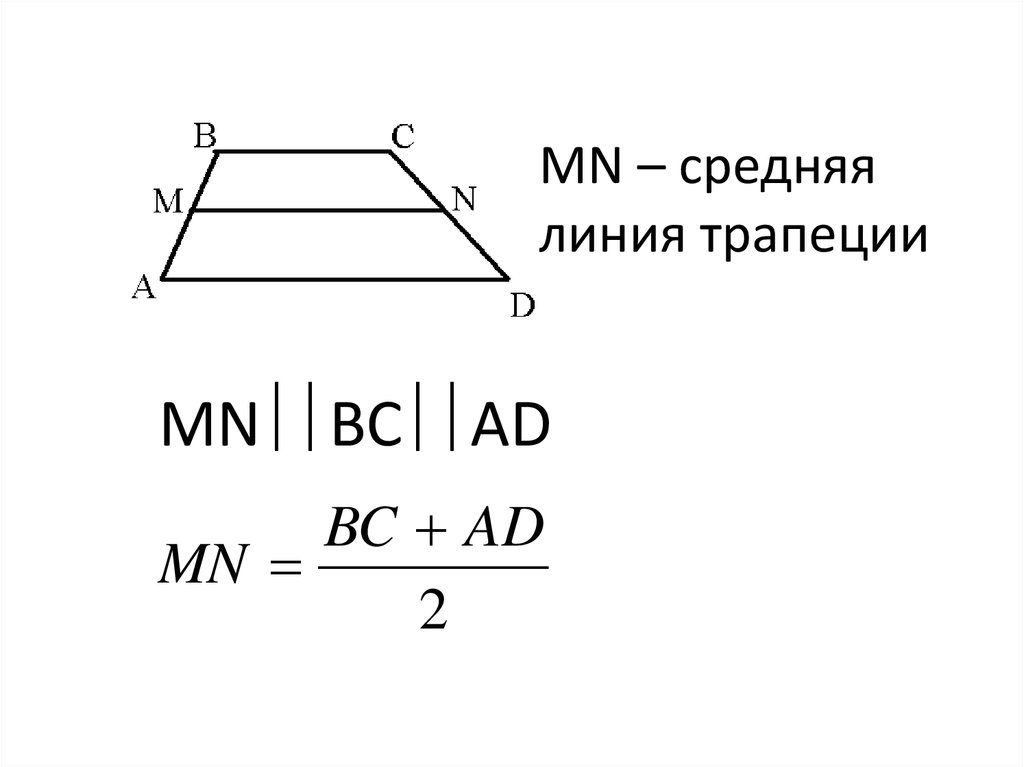
Трапеция38.
MN – средняялиния трапеции
MN BC AD
BC AD
MN
2
39.
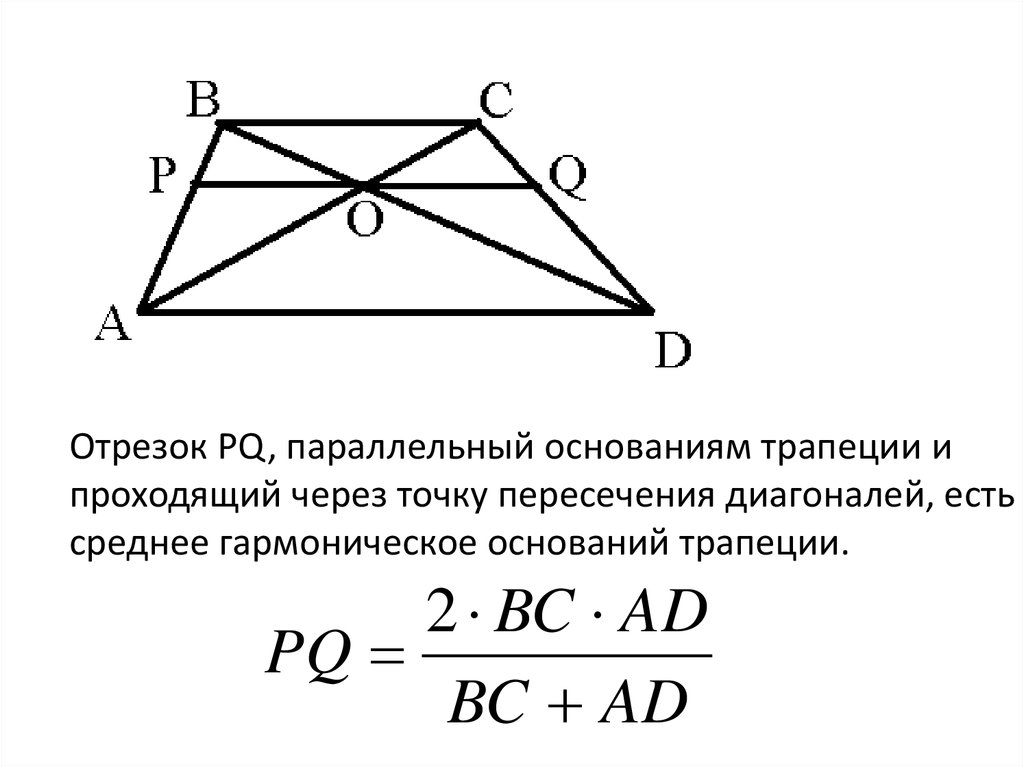
Отрезок PQ, параллельный основаниям трапеции ипроходящий через точку пересечения диагоналей, есть
среднее гармоническое оснований трапеции.
2 BC AD
PQ
BC AD
40.
В трапеции точка пересечения продолжений боковыхсторон, точка пересечения диагоналей и середины
оснований лежат на одной прямой.
41.
Прямоугольник42.
Ромб43.
Квадрат44.
45.
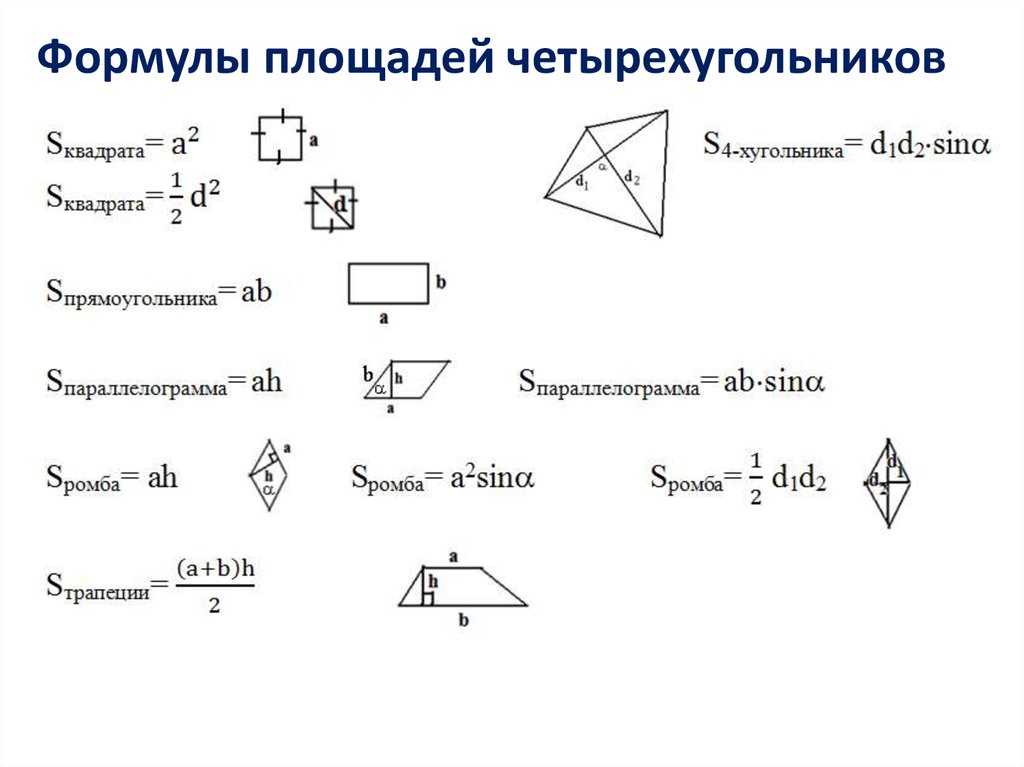
Формулы площадей четырехугольников46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
Формула для вычисления угла правильного nугольника57.
Правильный шестиугольник1. Диагонали правильного
шестиугольника делят его на 6
равных равносторонних
треугольника.
2. Сторона правильного
шестиугольника равна радиусу
описанной окружности.
3. Углы правильного шестиугольника
равны 120 .
4. Формула площади правильного
шестиугольника получается из
формулы площади правильного
треугольника:
2
6 a 3
S6
4
58.
59.
60.
61.
62.
Длина векторавычисляется по формуле

































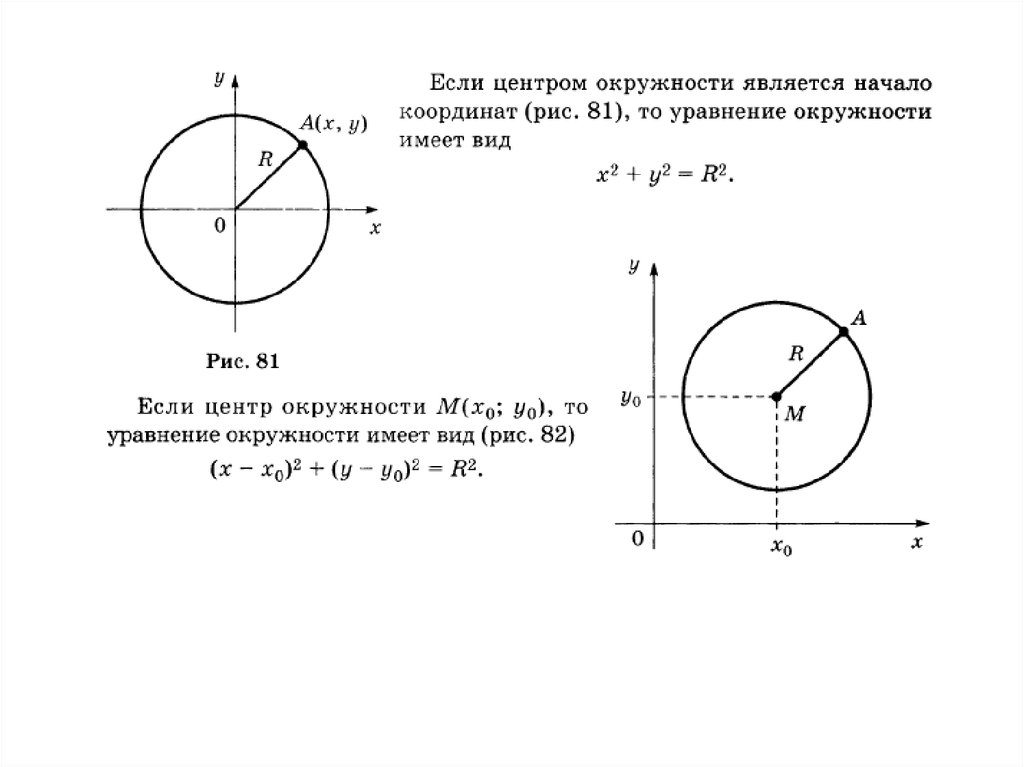








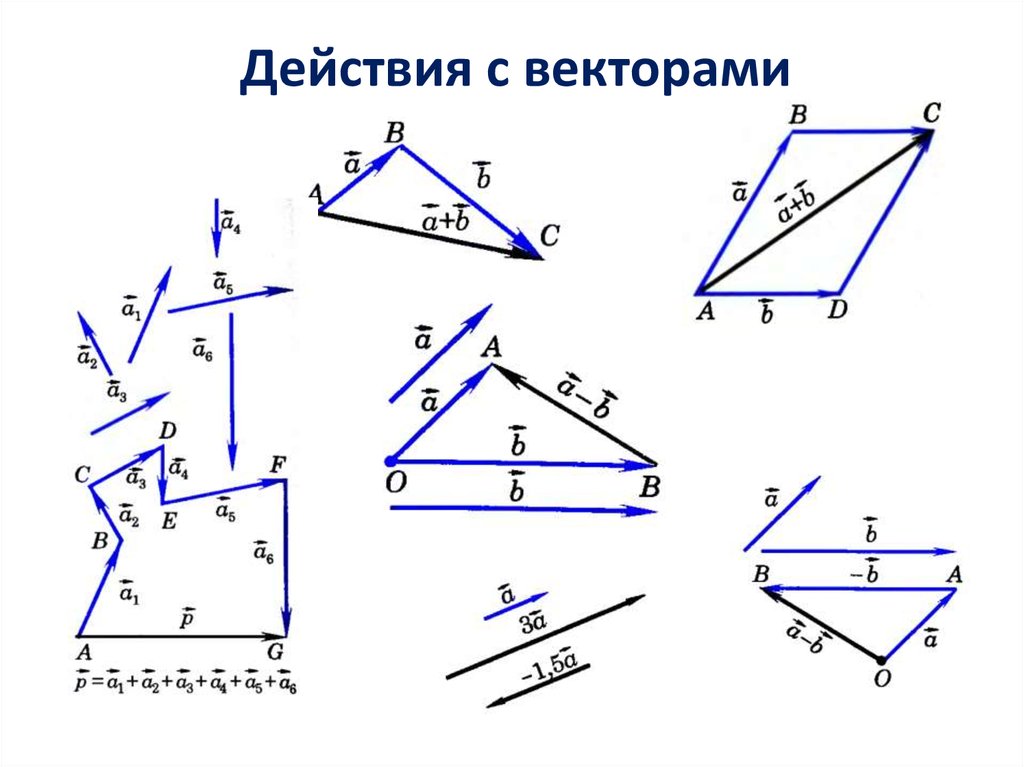



 Математика
Математика








