Похожие презентации:
Два подхода к измерению информации. (8 класс)
1.
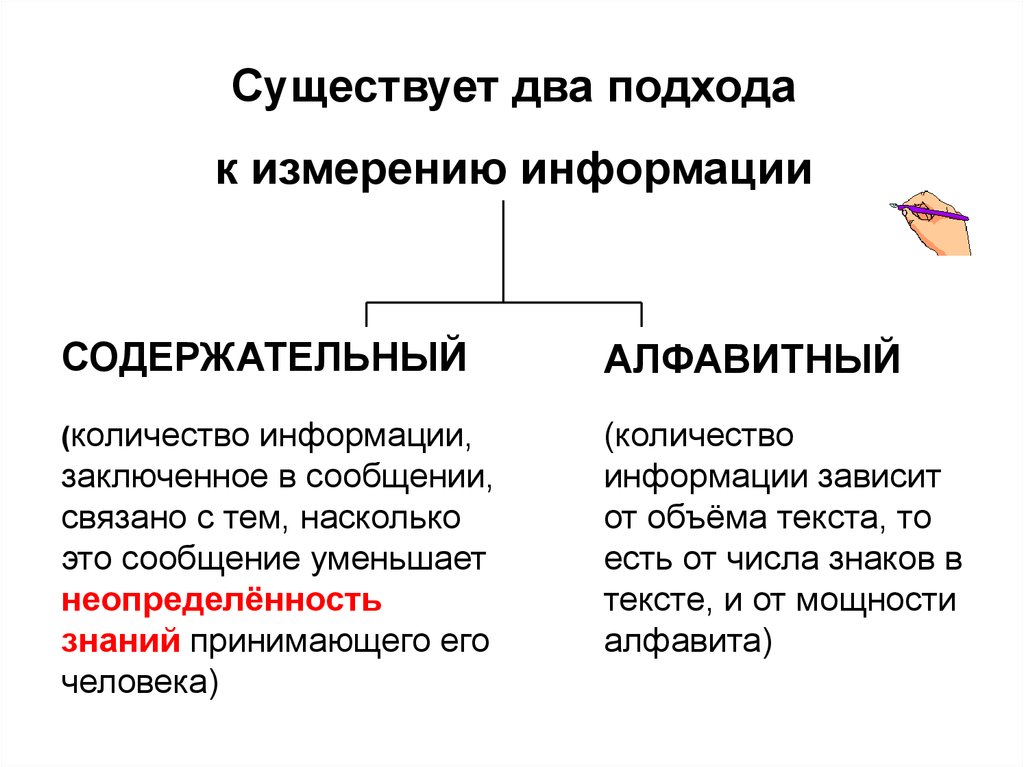
Существует два подходак измерению информации
СОДЕРЖАТЕЛЬНЫЙ
АЛФАВИТНЫЙ
(количество информации,
(количество
информации зависит
от объёма текста, то
есть от числа знаков в
тексте, и от мощности
алфавита)
заключенное в сообщении,
связано с тем, насколько
это сообщение уменьшает
неопределённость
знаний принимающего его
человека)
2. Алфавитный подход
3. Алфавитный подход
Алфавит – набор знаков, используемых при кодированииинформации с помощью некоторого языка.
Примеры:
АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
ABCDEFGHIJKLMNOPQRSTUVWXYZ
ХO
0123456789
32
26
2
10
С помощью языка двоичных чисел можно закодировать
символы любого алфавита, а значит, и любую
информацию, записанную на любом языке.
К. Поляков, 2006-2011
http://kpolyakov.narod.ru
4.
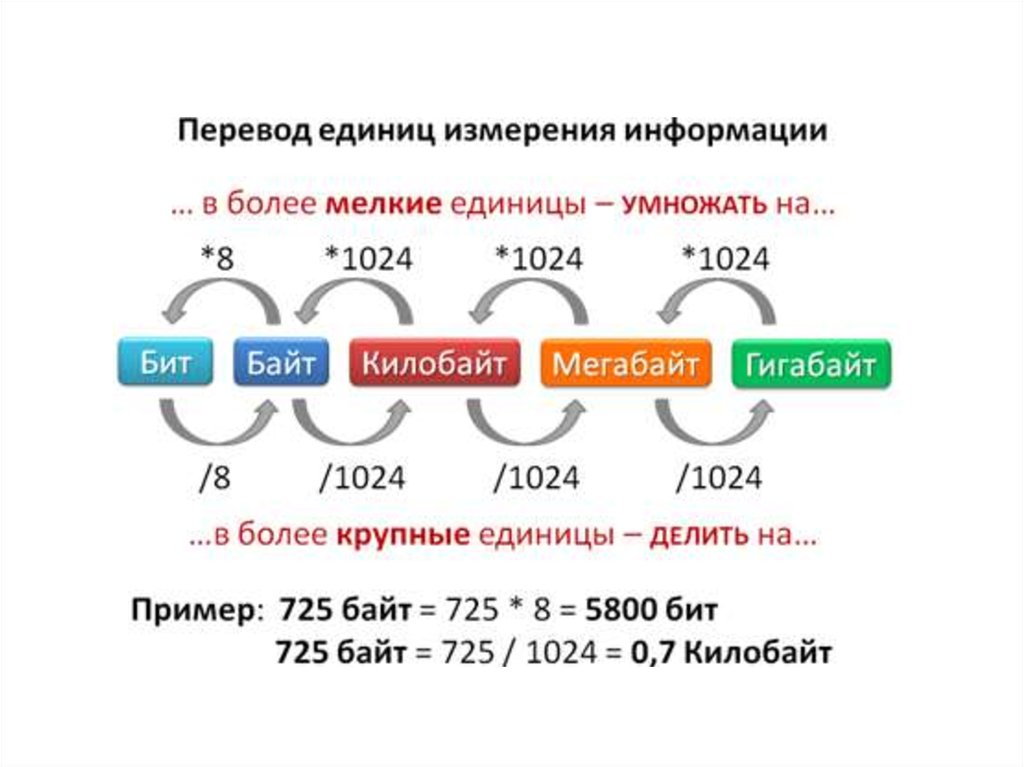
!1 байт – это 8 бит
1 символ=1 байт
(Буква, цифра, знак)
5. Запомни!
1 Кбайт=210= 1024 байт1 Мбайт=220=1024 Кбайт≈ 1.000.000 байт
1 Гбайт=230=1024Мбайт≈1.000.000.000байт
1 Тбайт= 240=1024 Гбайт
6.
7. Ответь на вопрос
Сколько МБ информации содержитсообщение объемом в 8192 КБ?
1) 1024;
2) 8388608;
3) 8;
4) 1;
Решение: 8192 КБ: 1024=8 МБ
информации, ответ 3)
8.
!Формула Хартли
N 2
I
Американский инженер Ральф Винтон Лайон Хартли сделал вклад в теорию
информации, введя в 1928 меру информации, которая называется хартлиевским
количеством информации.
Процесс получения информации рассматривается как выбор одного сообщения из
конечного наперёд заданного множества
N равновероятных сообщений, а
количество информации I, содержащееся в выбранном сообщении, определяет как
двоичный логарифм N.
9.
Для кодирования N символов произвольногоалфавита требуется
i - разрядный двоичный код
получили формулу 2i=N, в которой
N - мощность алфавита (количество вариантов или
символов алфавита)
i - информационный вес символа (количество
информации в битах)
10. Например:
ЗадачаАлфавит племени Пульти содержит 8 символов. Каков
информационный вес символа этого алфавита?
Решение:
N=8
N = 2i
i–?
Ответ: 3 бита.
8 = 2i.
i = 3.
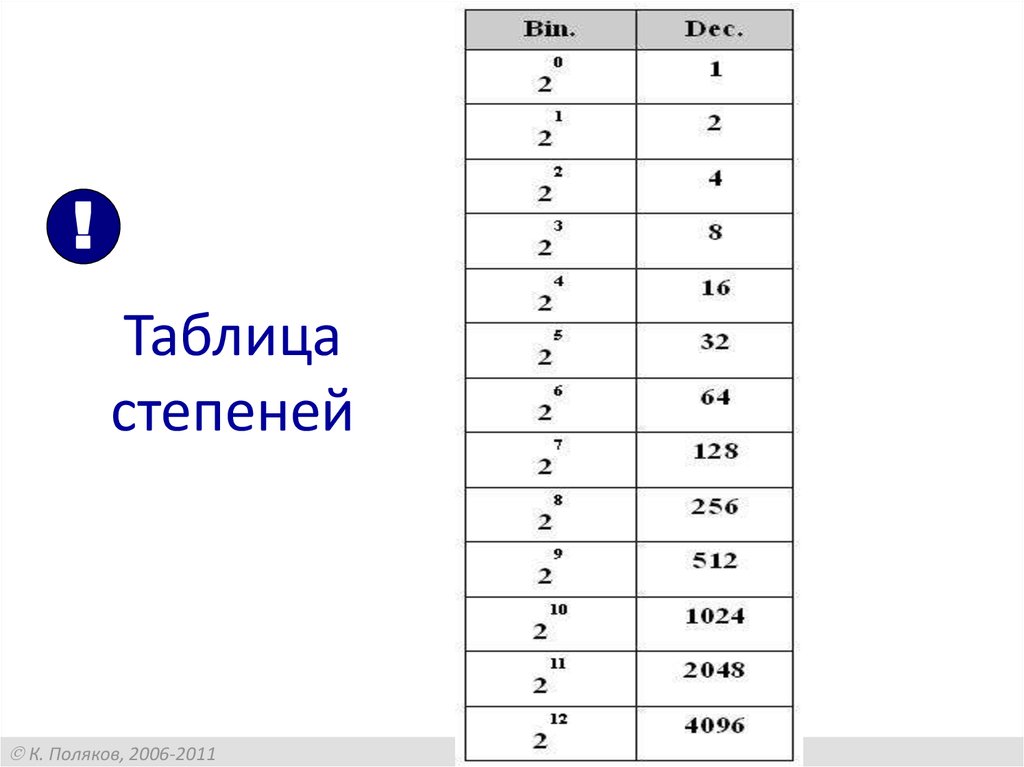
11. Таблица степеней
!Таблица
степеней
К. Поляков, 2006-2011
http://kpolyakov.narod.ru
12.
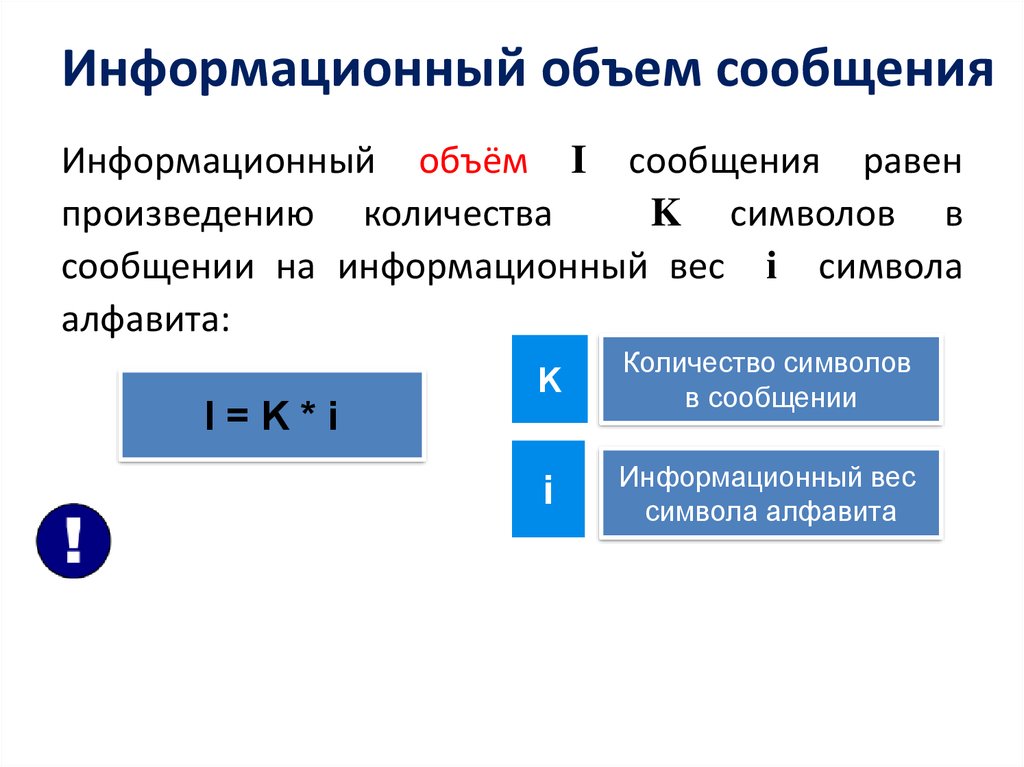
Информационный объем сообщенияИнформационный объём I сообщения равен
произведению количества
K символов в
сообщении на информационный вес i символа
алфавита:
K
Количество символов
в сообщении
i
Информационный вес
символа алфавита
I=K*i
13. Задача:
Задача. Определить объем информации в сообщенииПРИВЕТВАСЯ
для кодирования которого используется русский алфавит
(только заглавные буквы).
Решение:
считаем все символы (здесь К=10 символов)
мощность алфавита (N=32=25) – 32 символа
1 символ несет 5 бит информации- i
Тогда, I = K*i= 10·5 бит = 50 бит
К. Поляков, 2006-2011
http://kpolyakov.narod.ru
14.
ЗадачаСообщение, записанное буквами из 256символьного алфавита, содержит 50 символов.
Какой объем информации оно несет?
Дано: N=256 K= 50
I-?
Решение:
i
i
1) N= 2 256= 2
i = 8 бит
2) I = 8 бит * 50= 400 бит
3) I = 400 бит : 8= 50 байт.
Ответ: сообщение весит 50 байт.
15. Содержательный подход
16.
Неопределённость знания о результатенекоторого события – это число возможных
вариантов результата.
Например: подбрасывание монеты.
Неопределённость знания равно 2, т.к. у
монеты две стороны.
События (орел или решка), которые могут
произойти равновероятны (ни одно из событий
не имеет преимуществ перед другим).
17.
Пусть в некотором сообщении содержатсясведения о том, что произошло одно из N
равновероятных событий. Тогда количество
информации (заключенное в этом сообщении) i бит и число N связаны формулой:
18. Например:
В барабане для розыгрыша лотереи находится 32шара. Сколько информации содержит сообщение
о первом выпавшем номере.
Решение:
Количество возможных вариантов – 32
19.
ЗадачаСообщение о том, что Петя живет во втором
подъезде, несет 3 бита информации.
Сколько подъездов в доме?
Решение:
Дано: i=3
Найти: N - ?
2i = N
23 = 8
Ответ: 8 подъездов
20. Задача
В корзине лежат 8 мячей разного цвета (белый, красный,синий, желтый, зеленый, оранжевый, фиолетовый,
коричневый). Какое количество информации несет в себе
сообщение о том, что из корзины будет вынут мяч
красного цвета?
Решение:
Так как возможности вынуть мяч каждого из возможных
цветов равновероятны, то для определения количества
информации, содержащегося в сообщении о выпадении
мяча красного цвета, воспользуемся формулой N = 2i
Имеем 8=23 ;
Ответ: 3 бита
21. Задача
Проводятся две лотереи «4 из 32» и «5 из 64».Сообщение о результатах, какой из лотерей
несет больше информации?
Вытаскивание любого номера из
лотерейного барабана – события
равновероятные.
Поэтому в первой лотерее количество
информации в сообщении об одном
номере равно 5 бит (25 = 32), а во втором –
6 бит (26 = 64).
22.
Сообщение о 4-х номерах в первойлотерее несет 5 * 4 = 20 бит.
Сообщение о 5-ти номерах второй
лотереи несет 6 * 5 = 30 бит.
Следовательно, сообщение о результатах второй
лотереи несет больше информации, чем первой.
23. Задача
Врач-стоматолог принимает пациентов с 8 утра до 2 дня.На каждого пациента отводится по 30 минут. Какое
количество информации содержит сообщение о том, что
Петя записался на приём в 11:30?
Решение:
1. Нужно посчитать число вариантов, т.е. максимальное число
человек, которое может принять врач.
2. Он может принимать в:
8:00, 8:30, 9:00, 9:30, 10:00, 10:30, 11:00, 11:30, 12:00, 12:30,
13:00, 13:30. Т.е. (14-8)*2 = 12 пациентов.
3. Петя записался на прием в 11:30 - это один(!) из возможных
равновероятных вариантов, а значит несет информации: 12=2i
12=2i < 16=2i ; тогда
i= 4бита



















 Информатика
Информатика








